Uploaded byNicolas Bettenburg
Approximation Algorithms
The document discusses approximation algorithms for NP-complete problems. It introduces the idea of finding near-optimal solutions in polynomial time for problems where optimal solutions cannot be found efficiently. It provides examples of the vertex cover problem and set cover problem, describing greedy approximation algorithms that provide performance guarantees for finding near-optimal solutions for these problems. The document also discusses some open questions around whether these approximation ratios can be improved.
In this document
Powered by AI
Overview of NP-complete problems and the need for approximation algorithms that provide near-optimal solutions efficiently.Definition of approximation ratio and its significance in evaluating the quality of approximation algorithms.
Introduction to various NP-complete problems as identified by Richard Karp in 1972, including examples like CLIQUE and KNAPSACK.
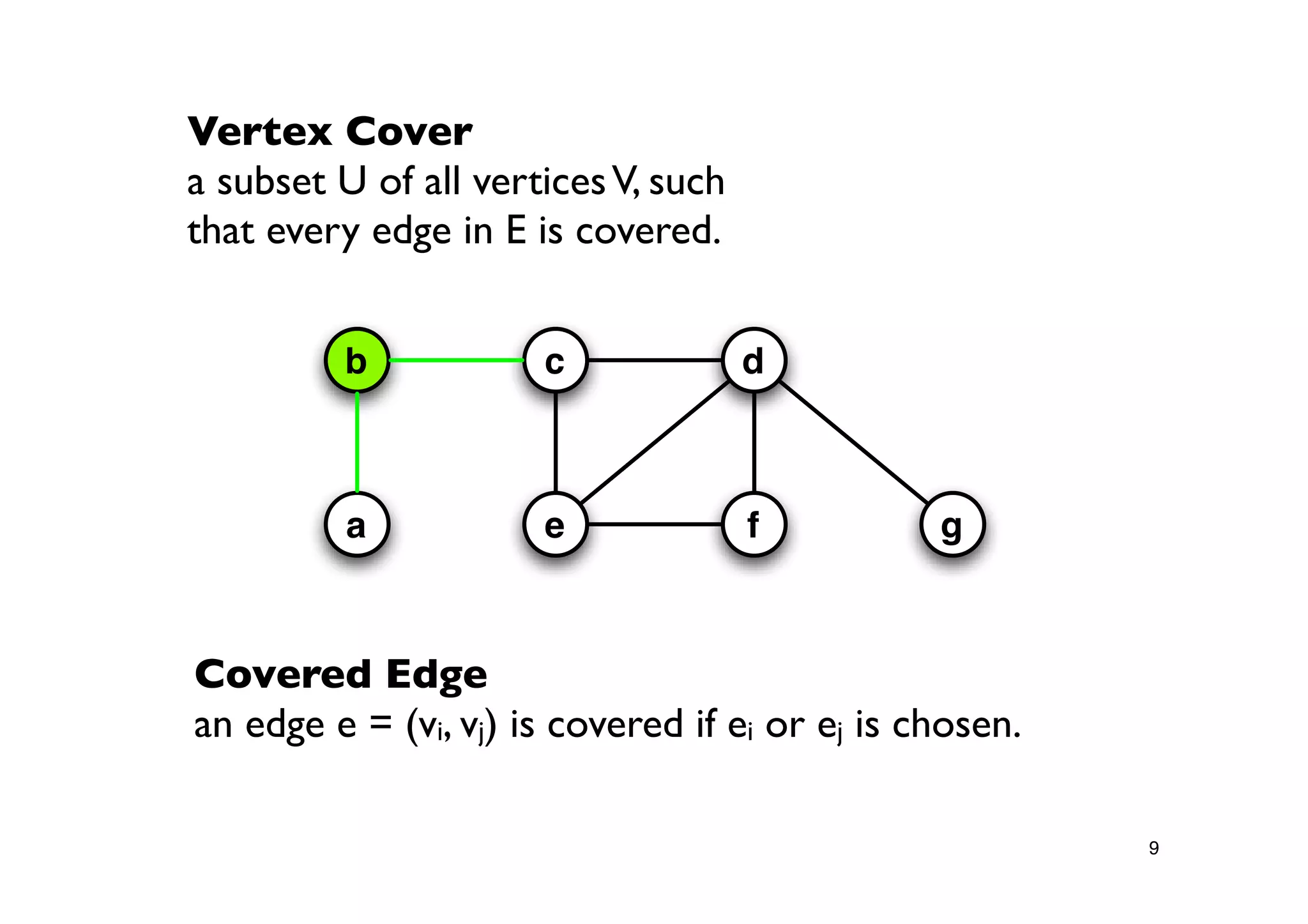
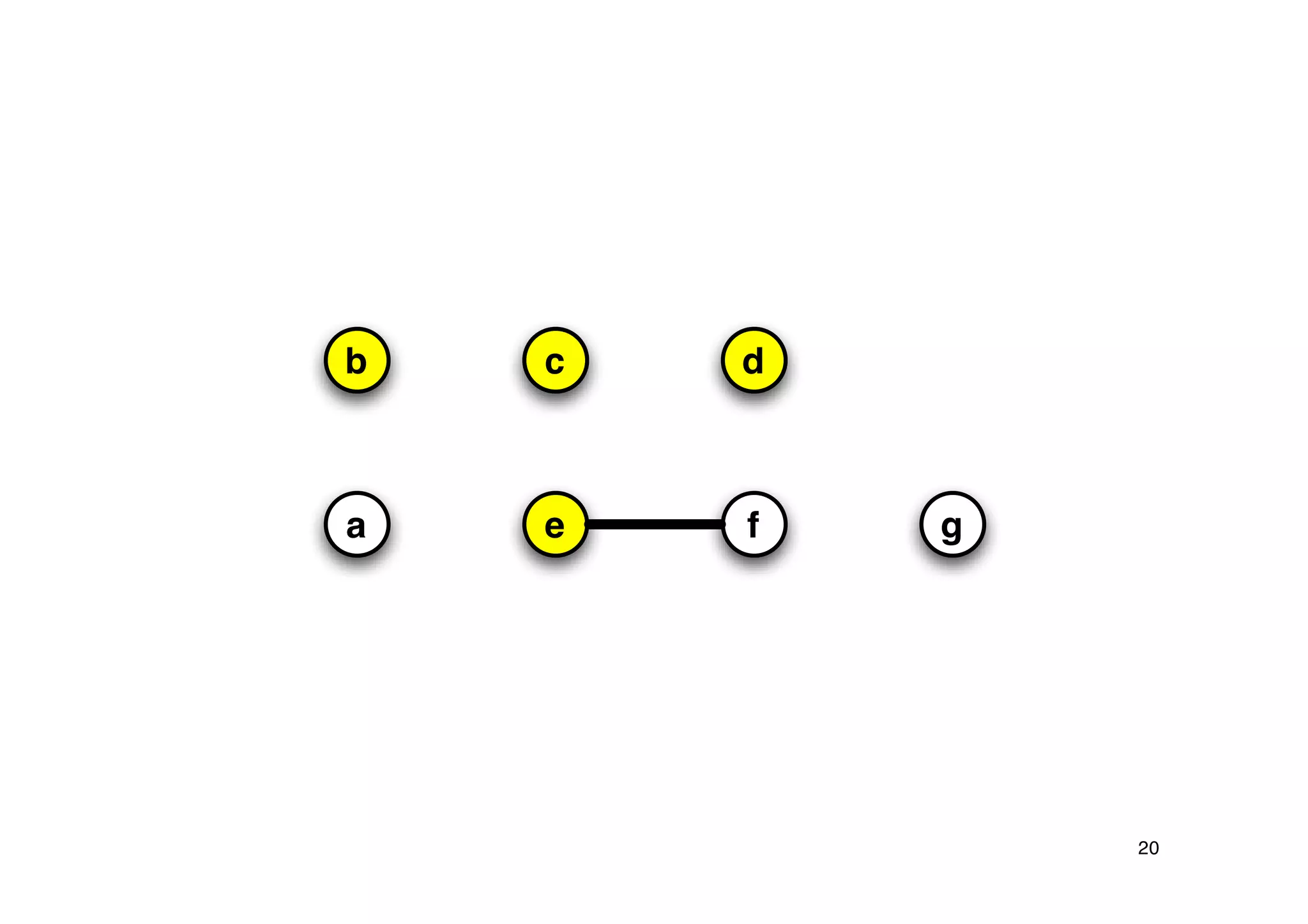
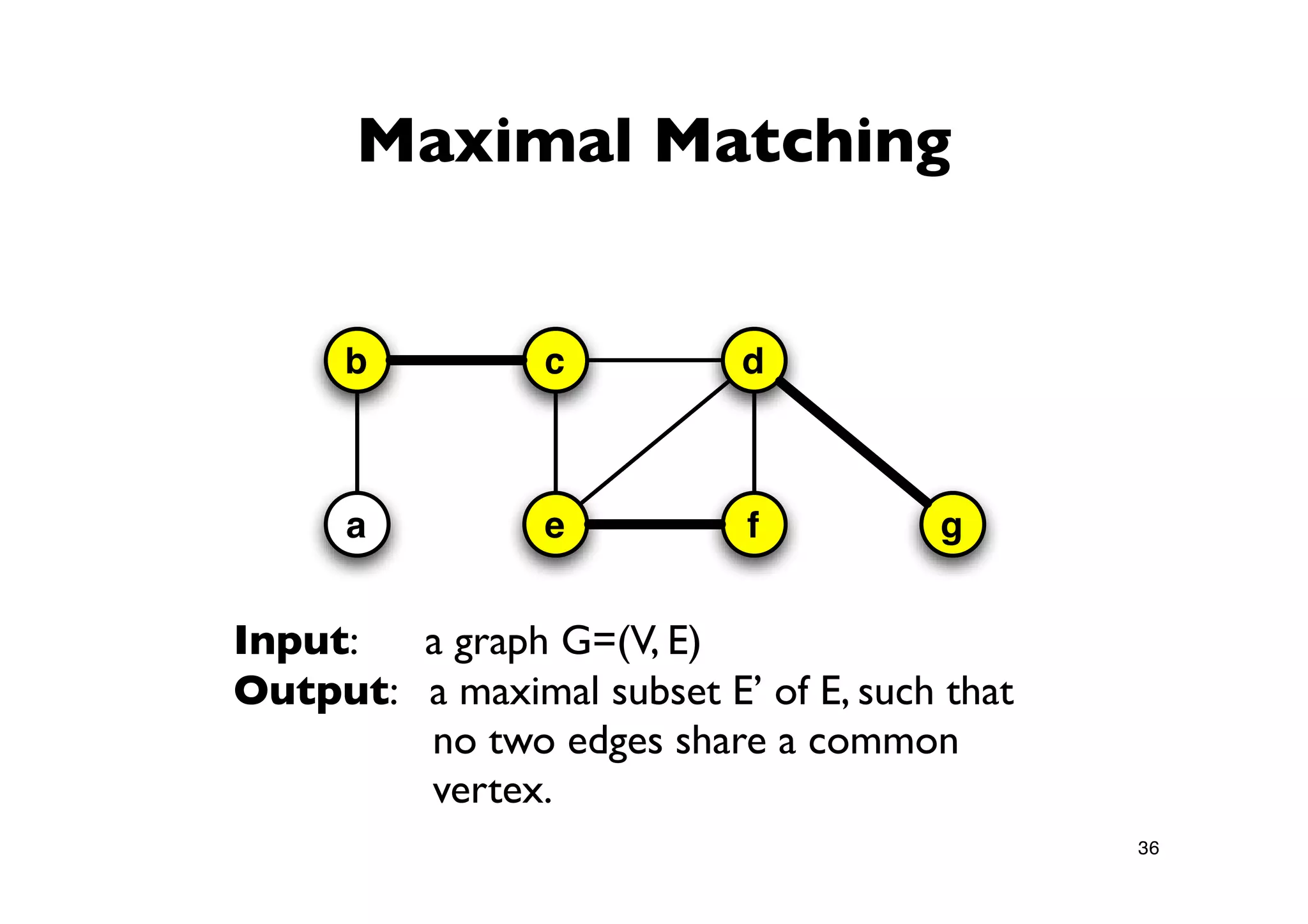
Explanation of the Vertex Cover problem, defining it as a selection of vertices that cover all edges in a graph.
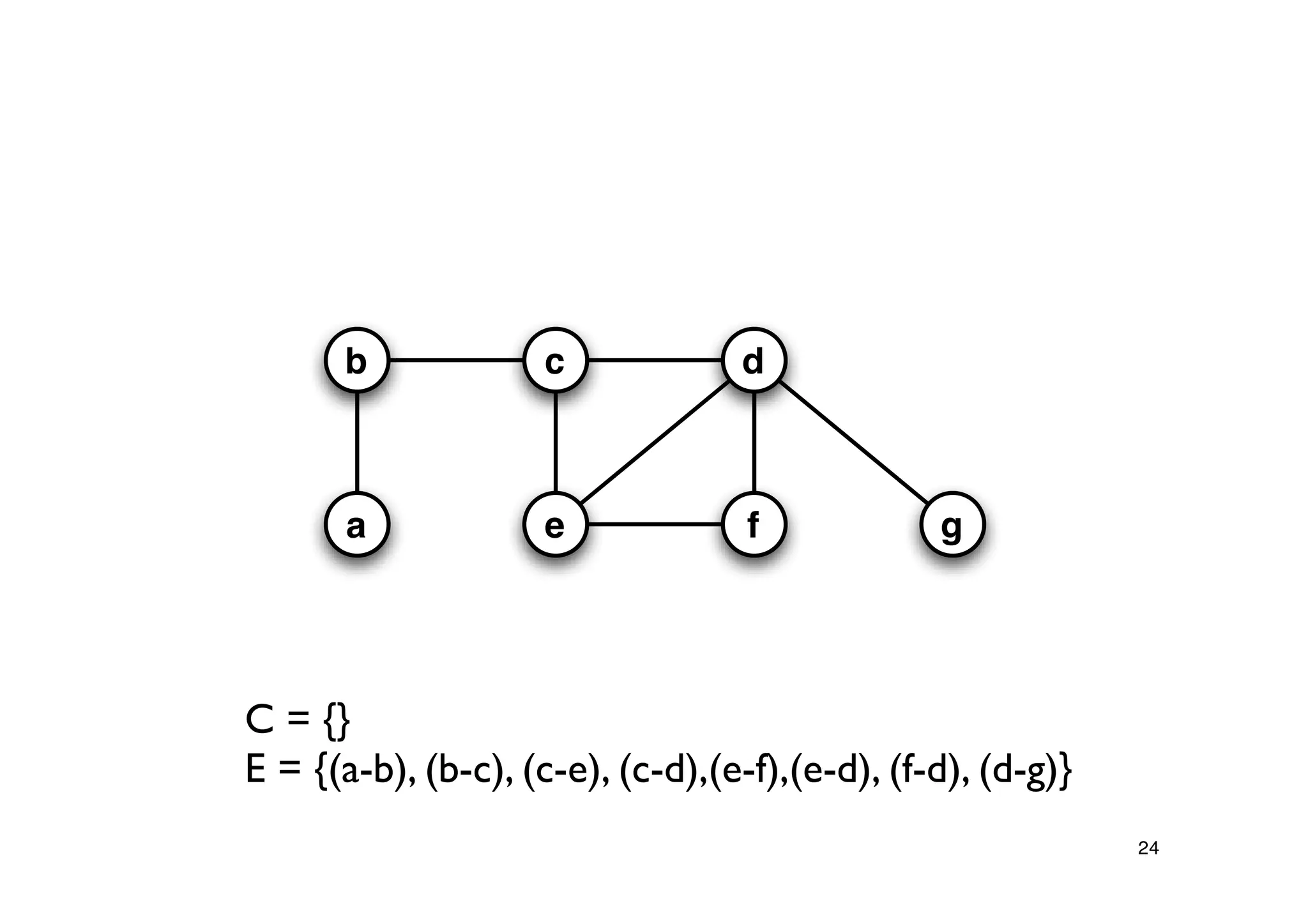
Detailing the Greedy-Vertex-Cover algorithm, highlighting the process of selecting vertices based on their degree.
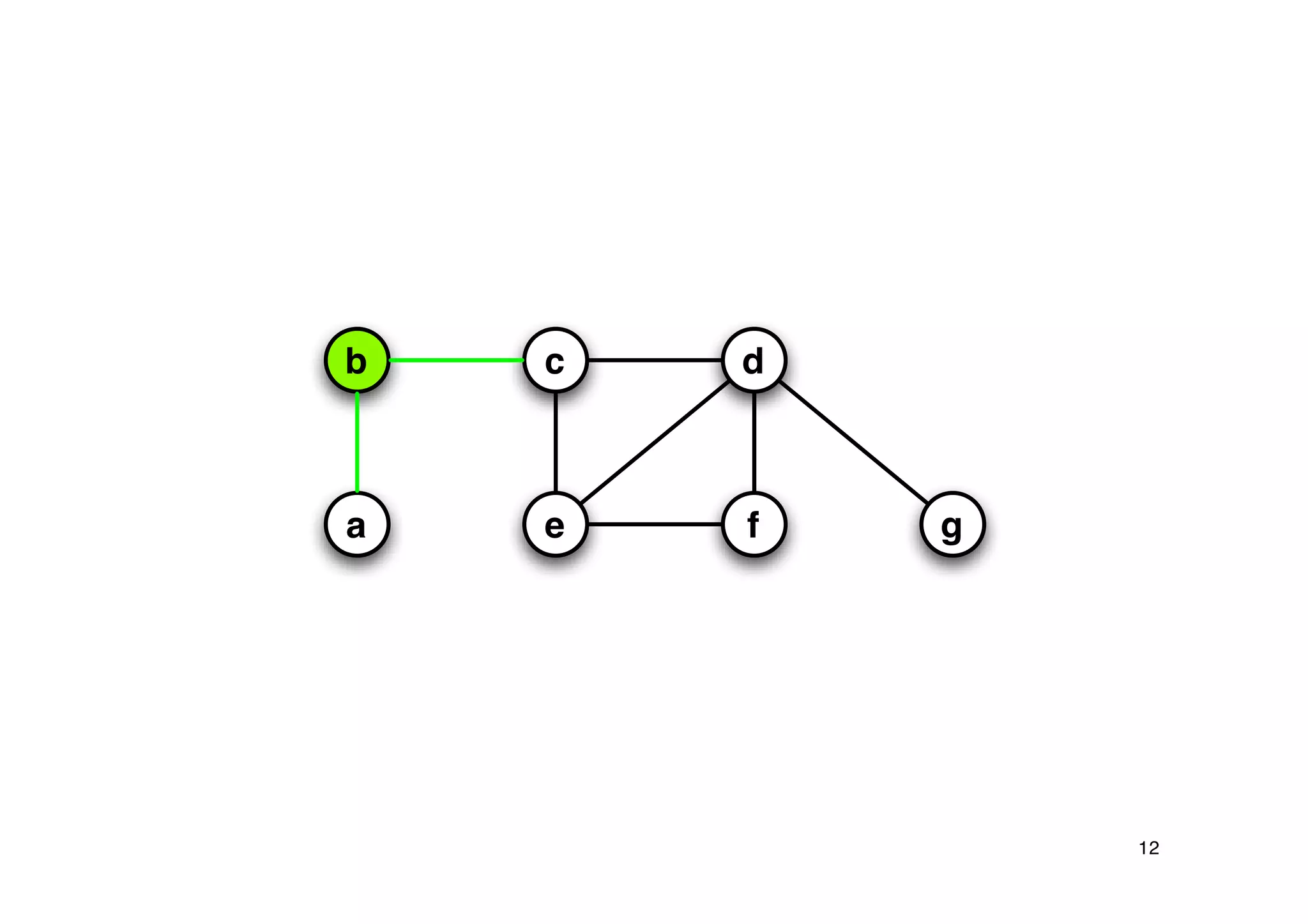
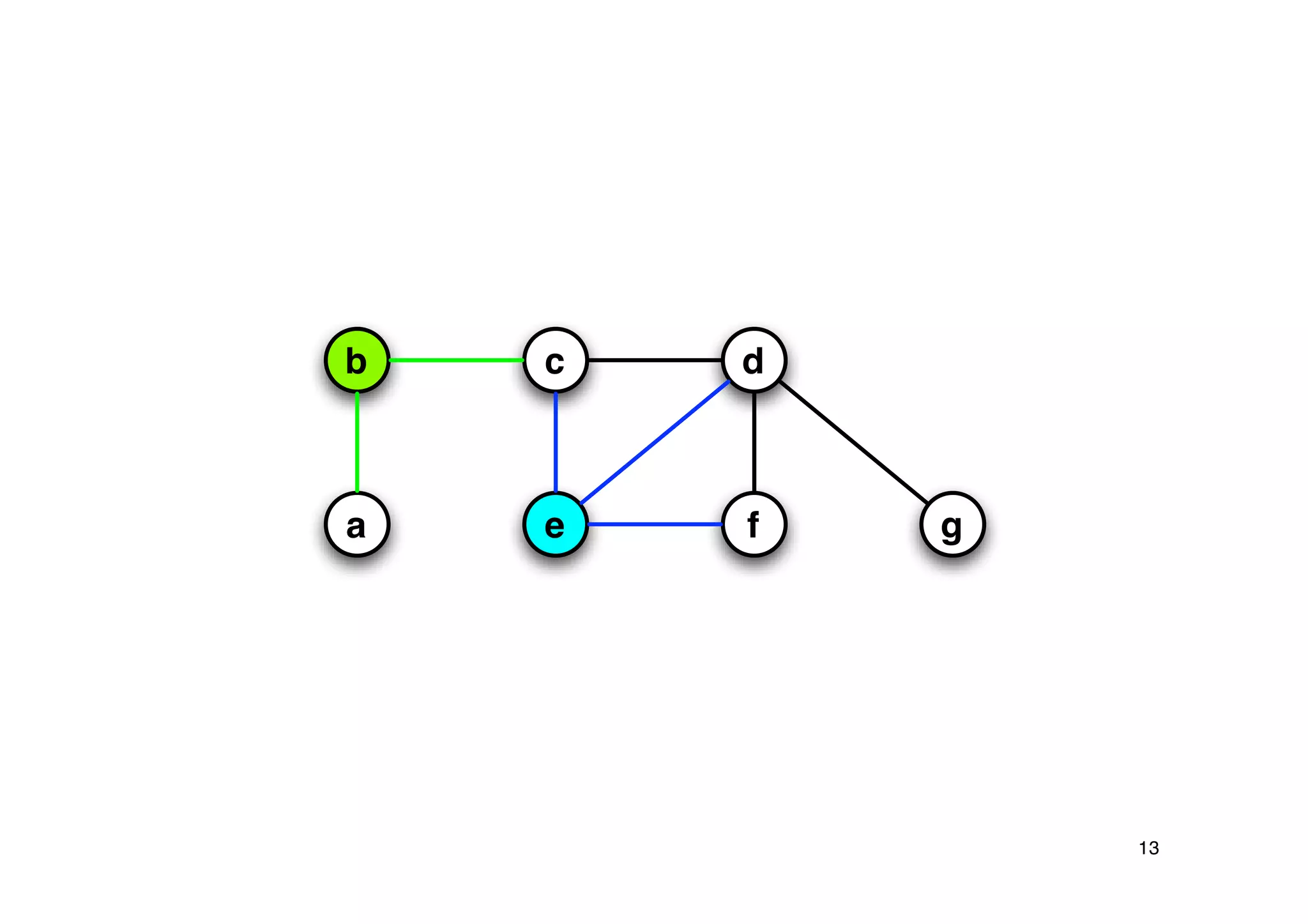
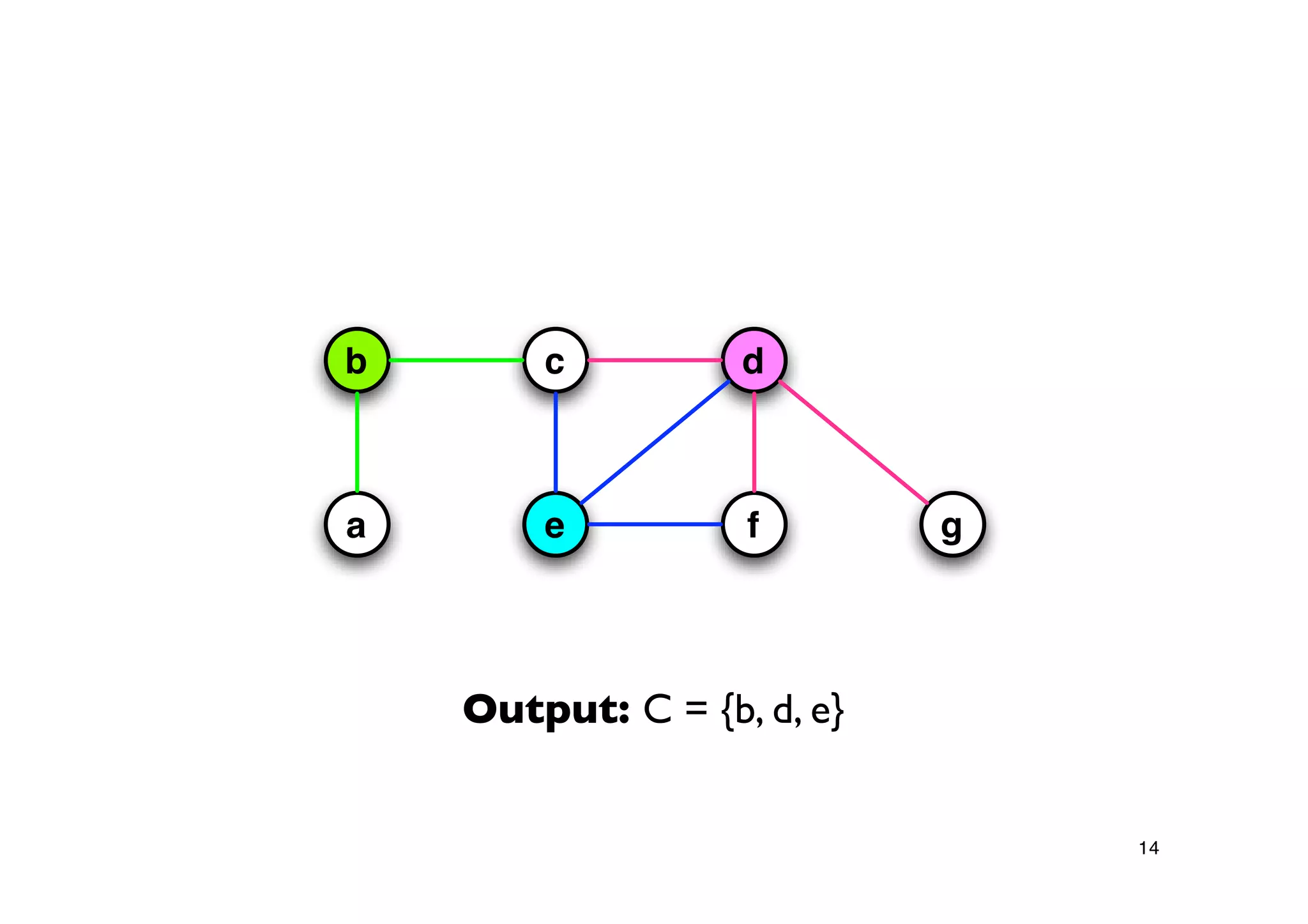
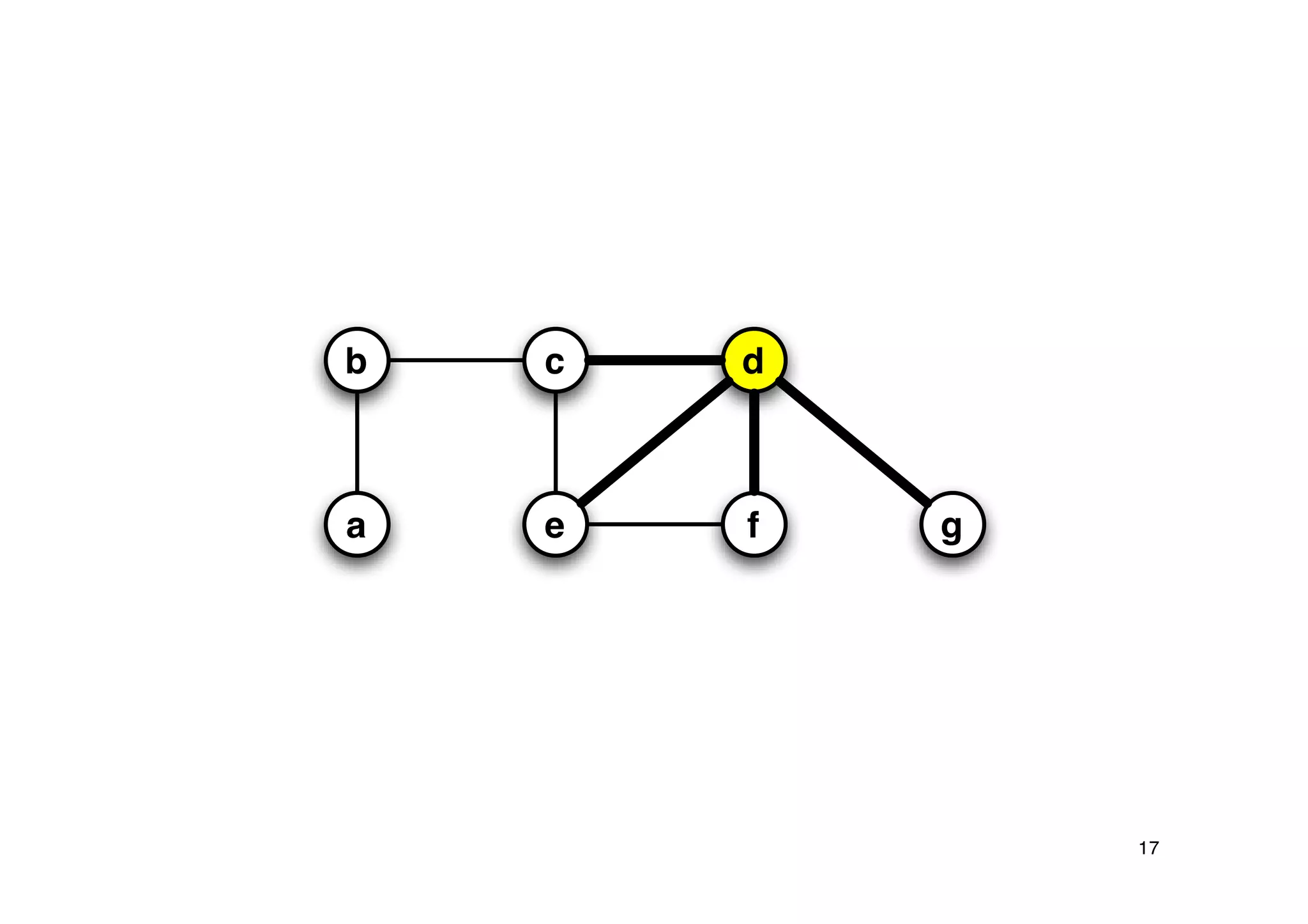
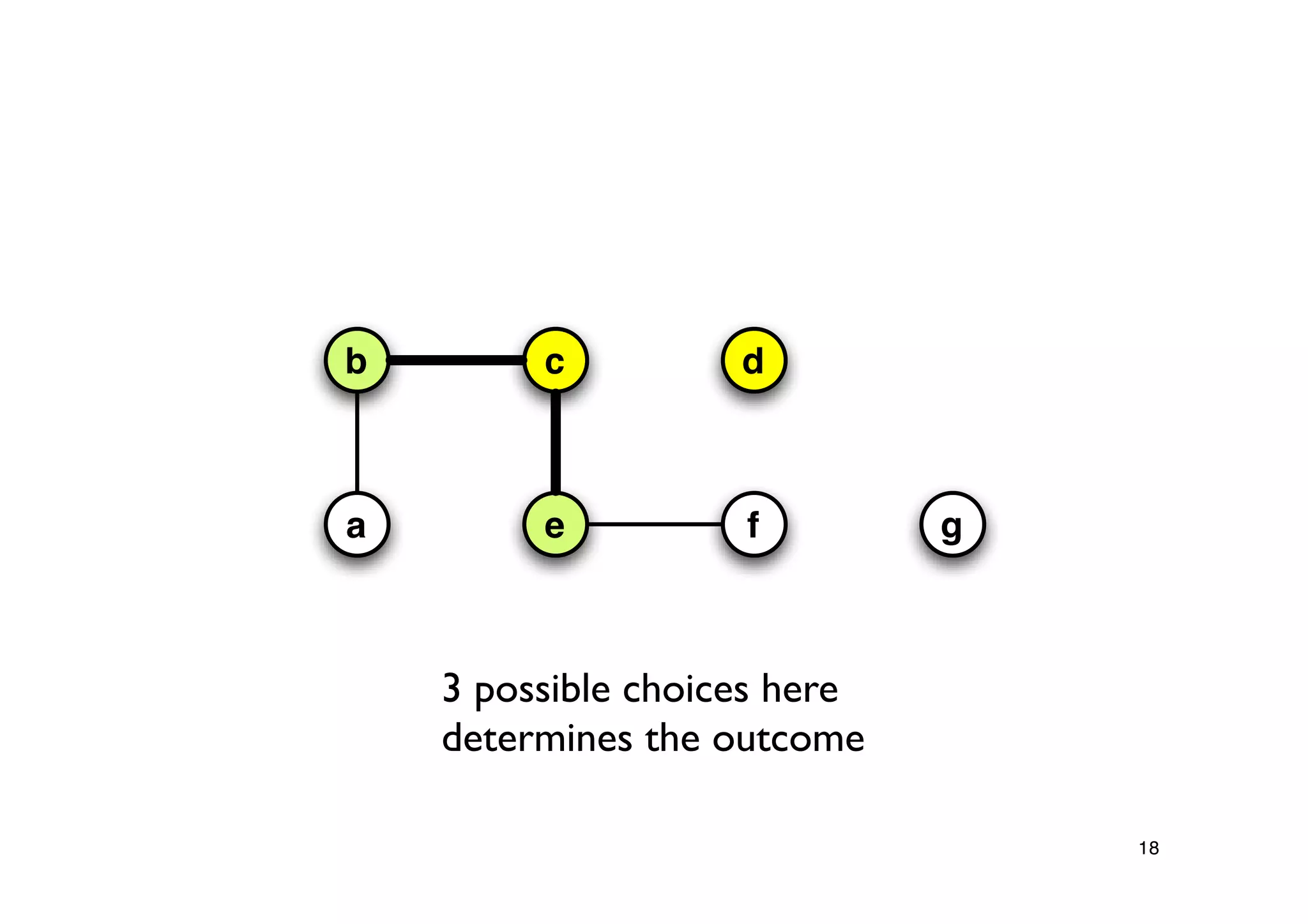
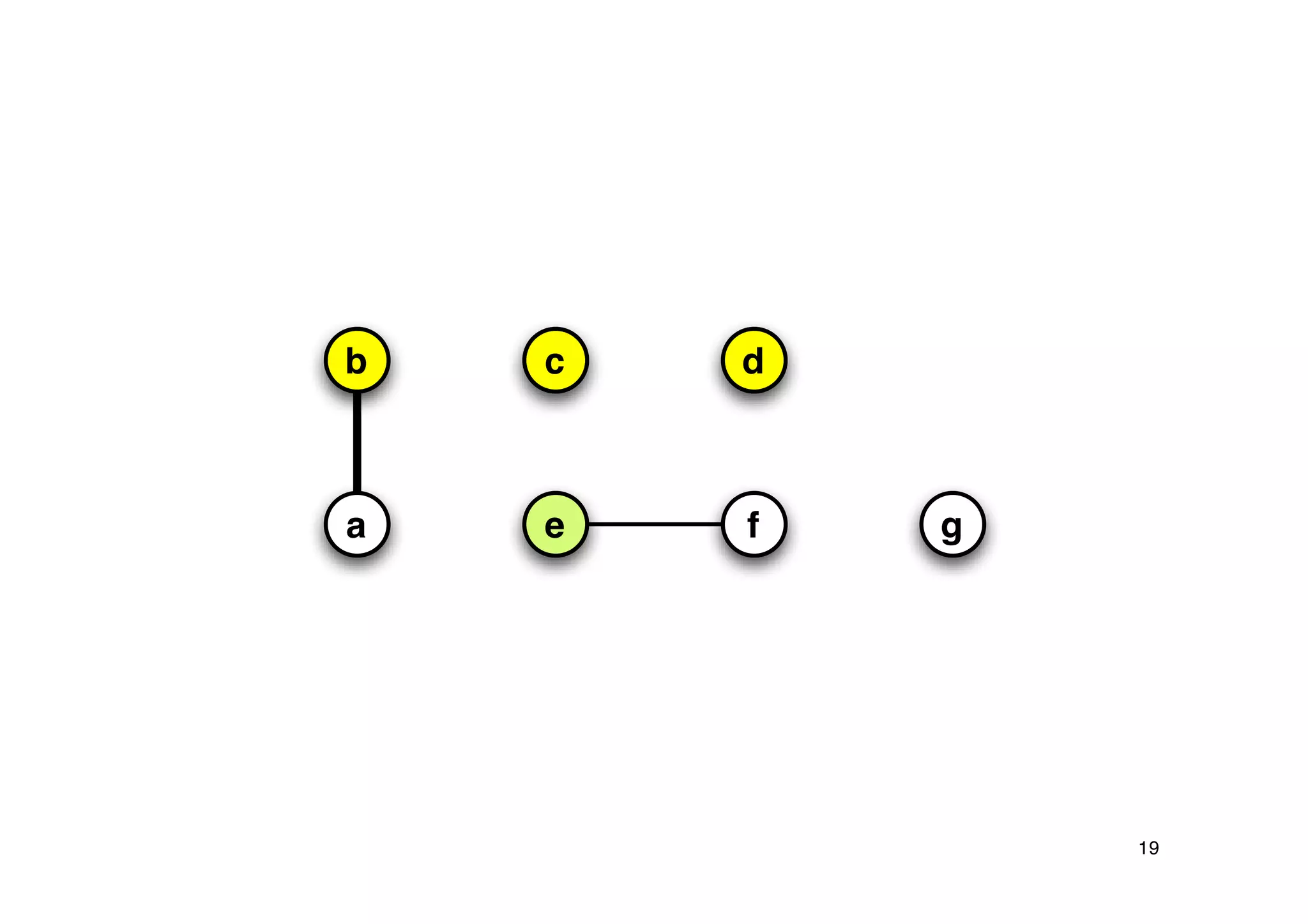
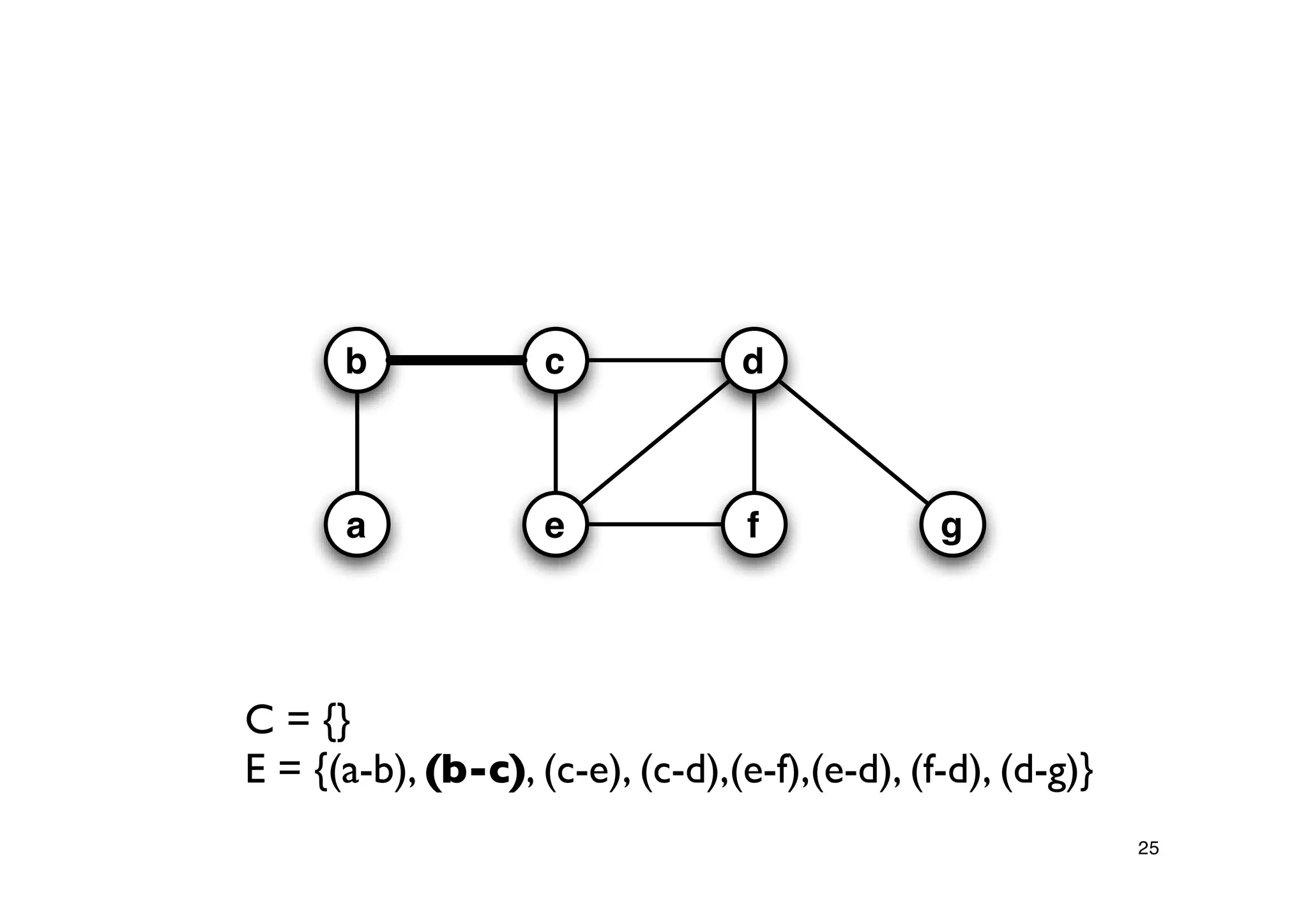
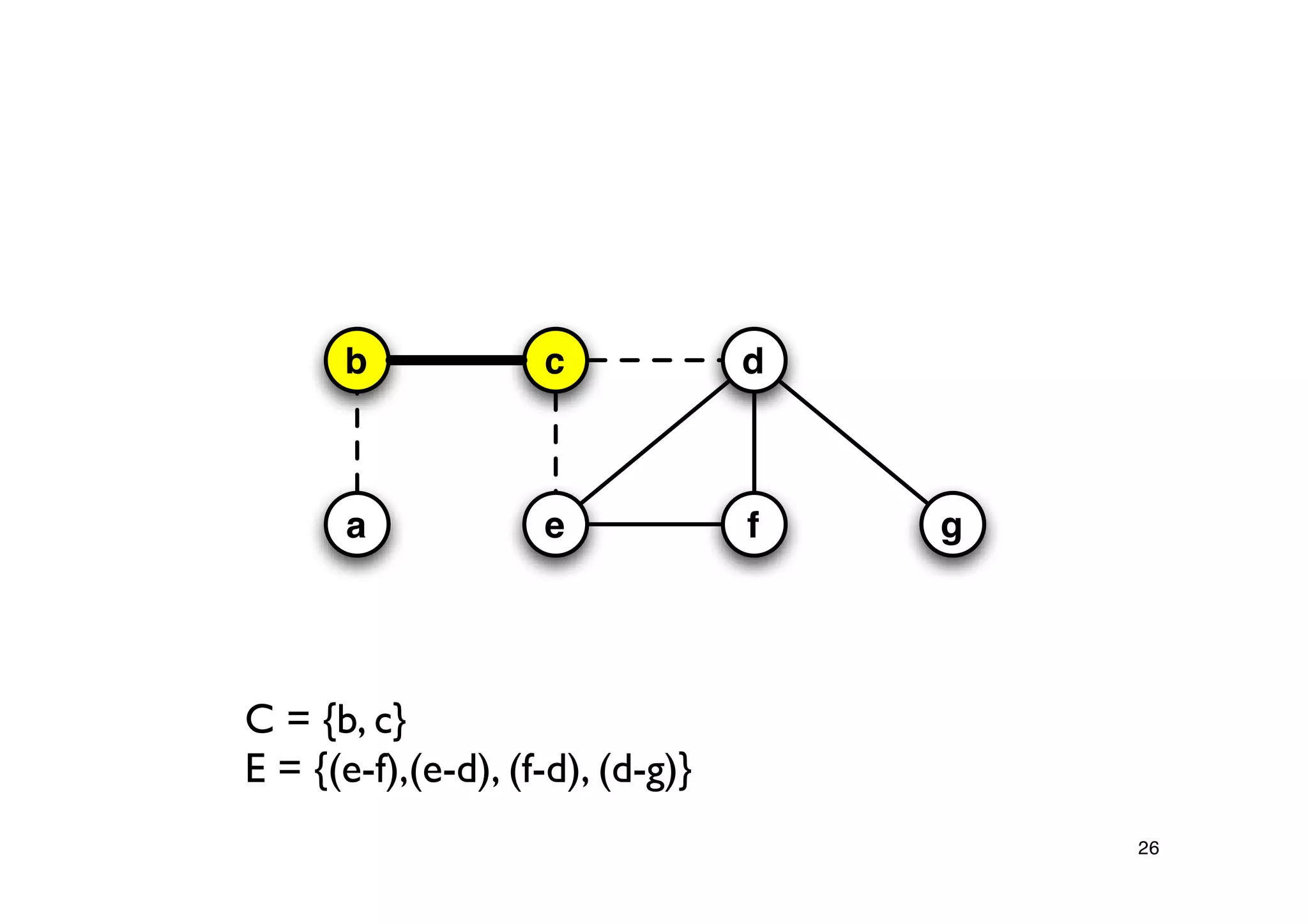
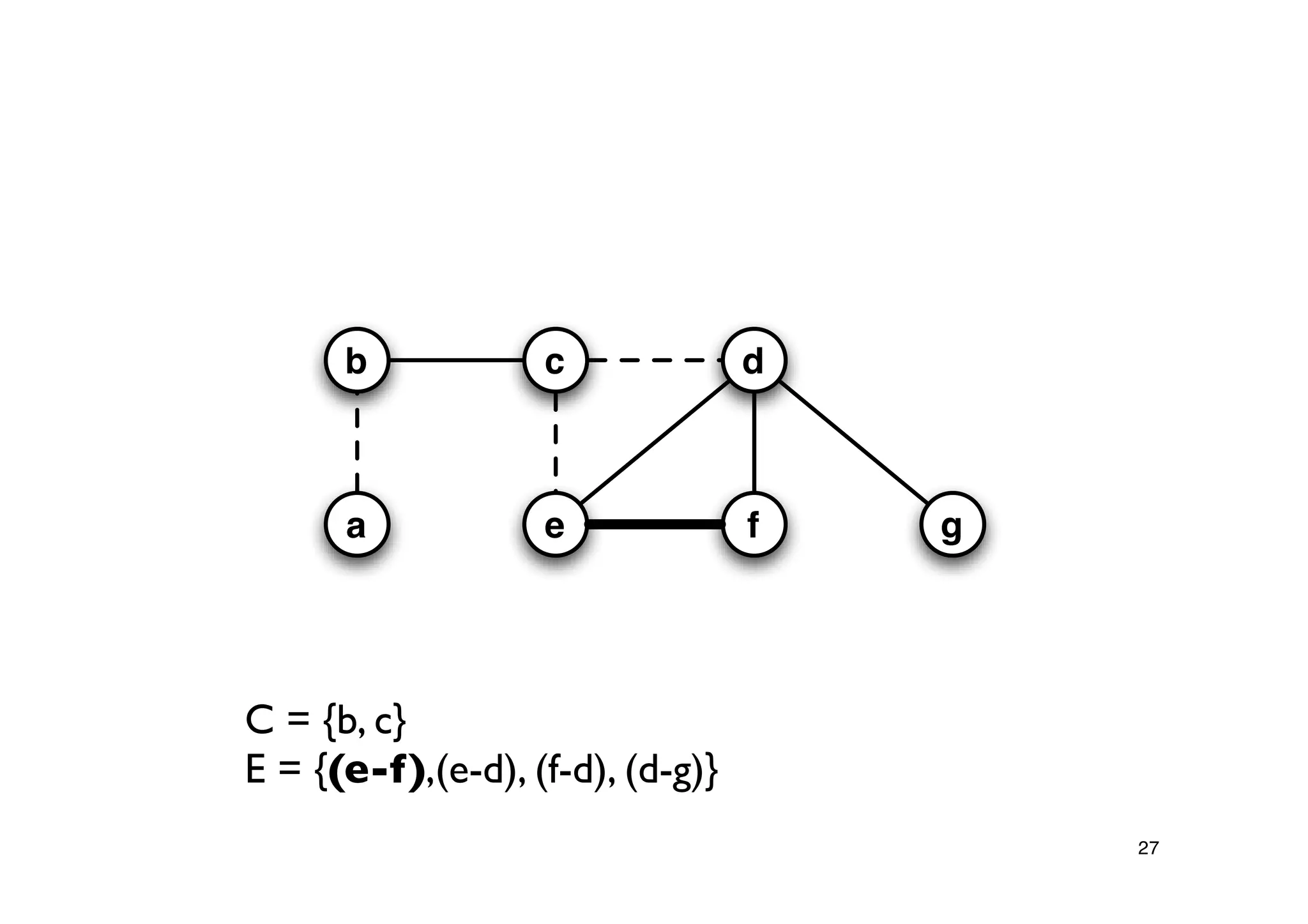
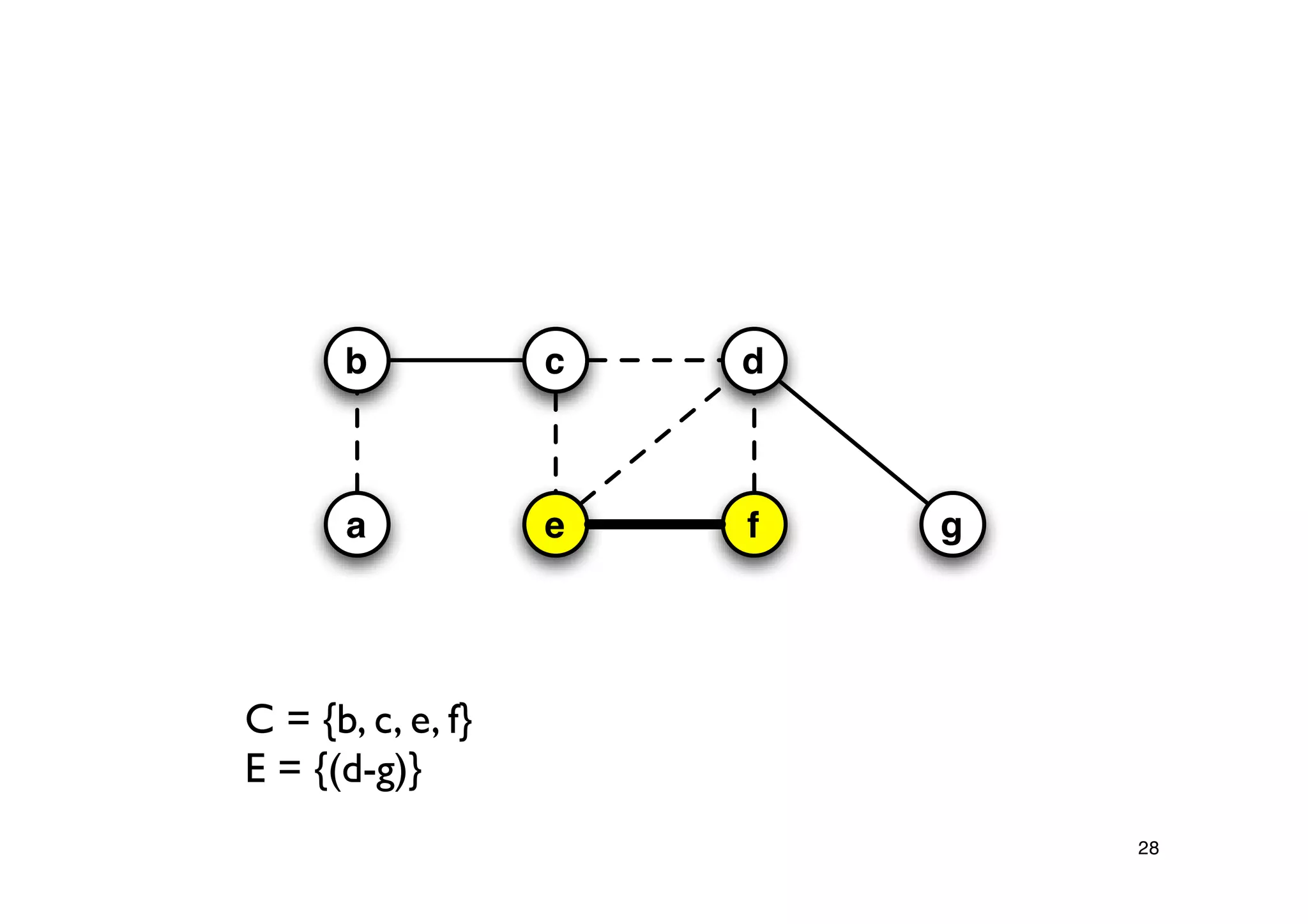
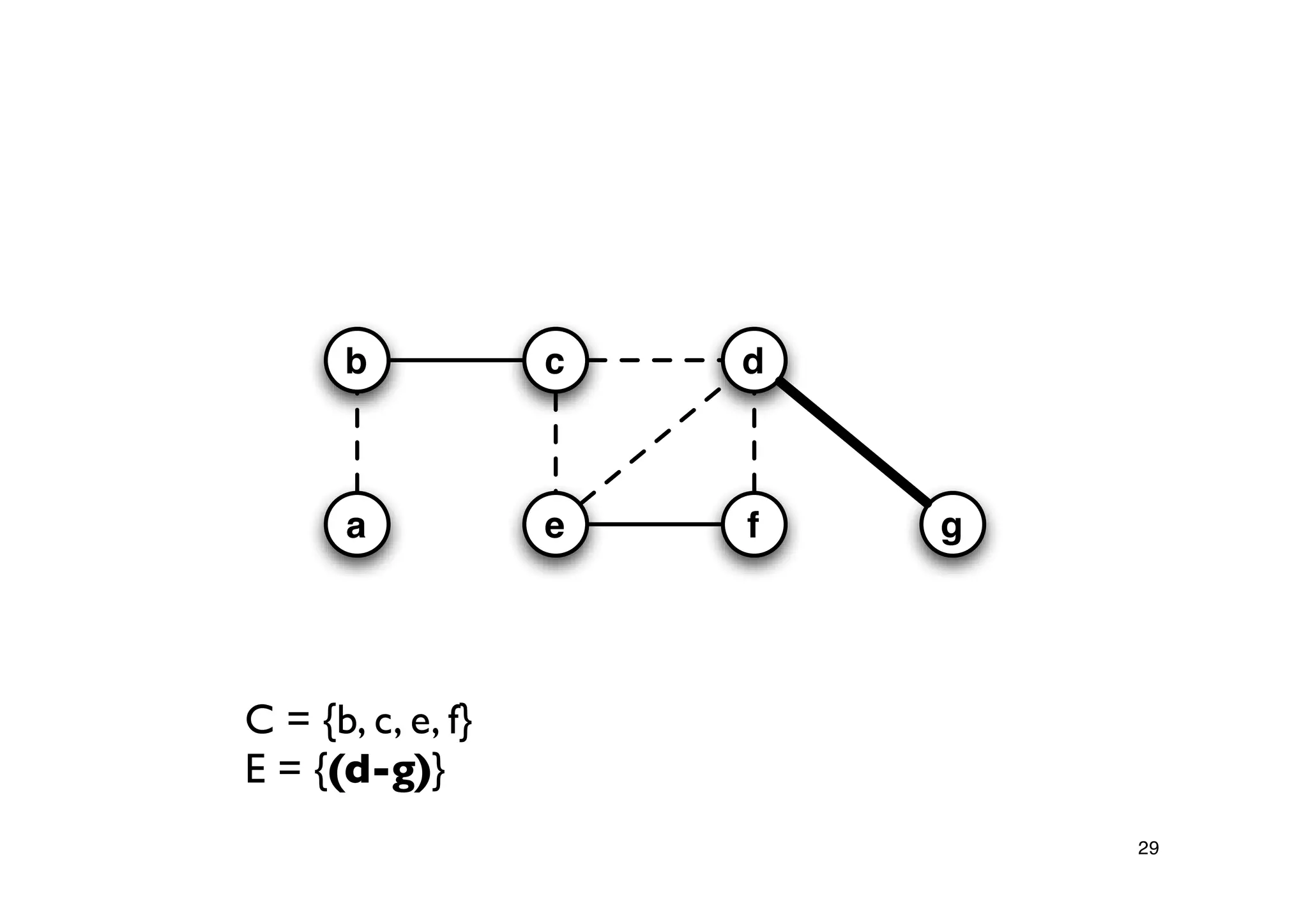
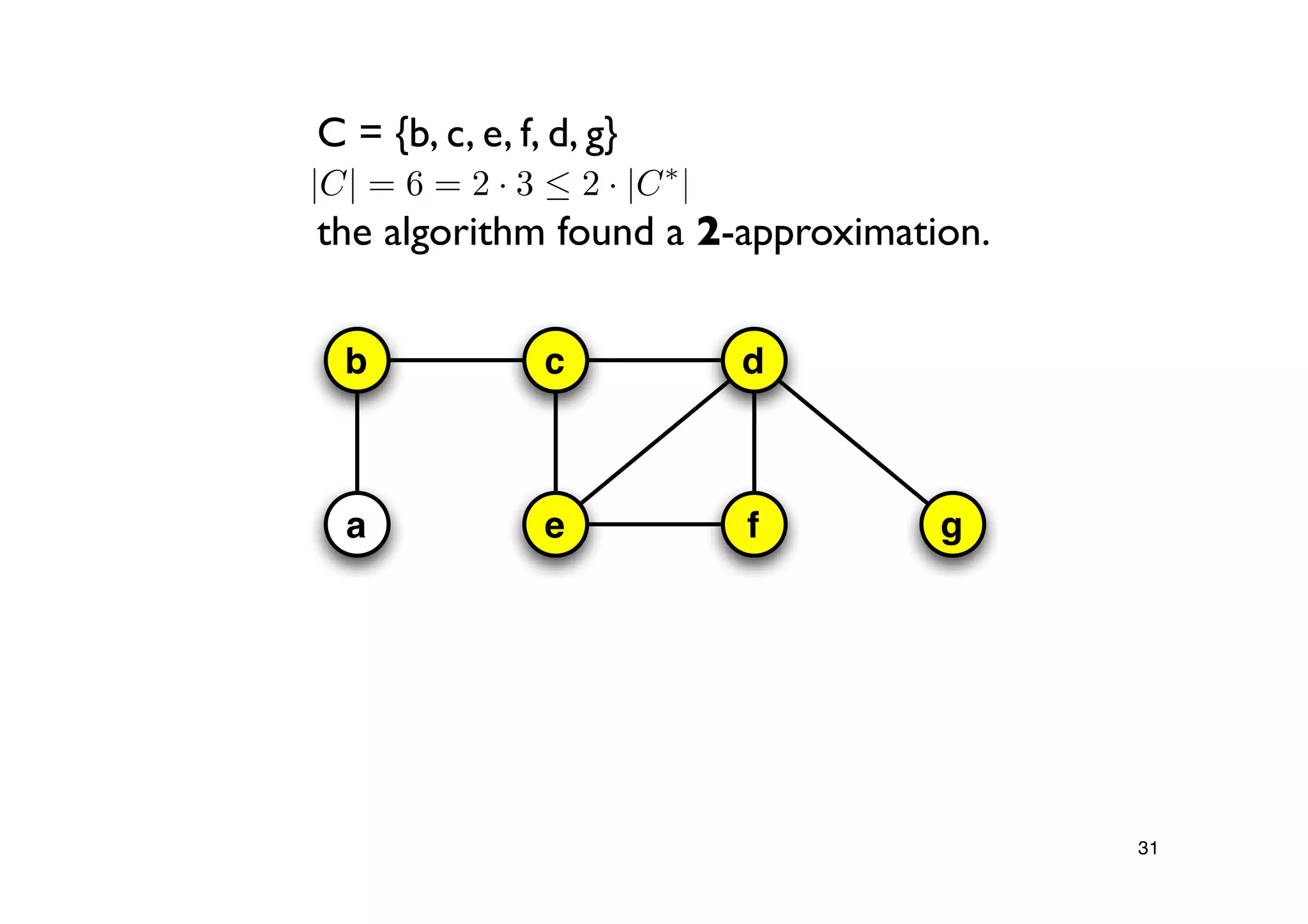
Explanation of the Approx-Vertex-Cover algorithm with its mechanism for producing a solution and its computational efficiency.
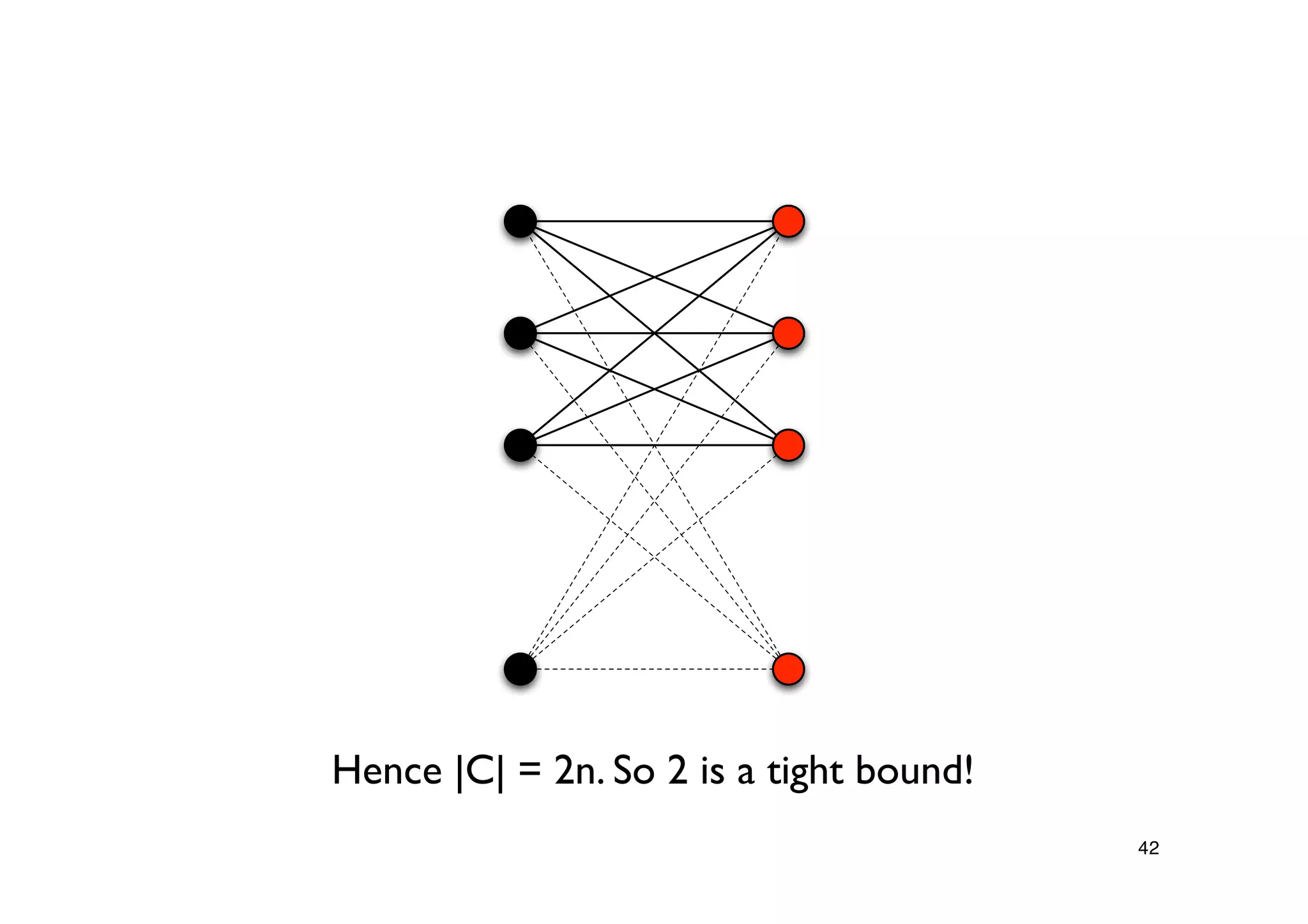
Steps proving the solution's correctness and its approximation factor compared to the optimal solution.
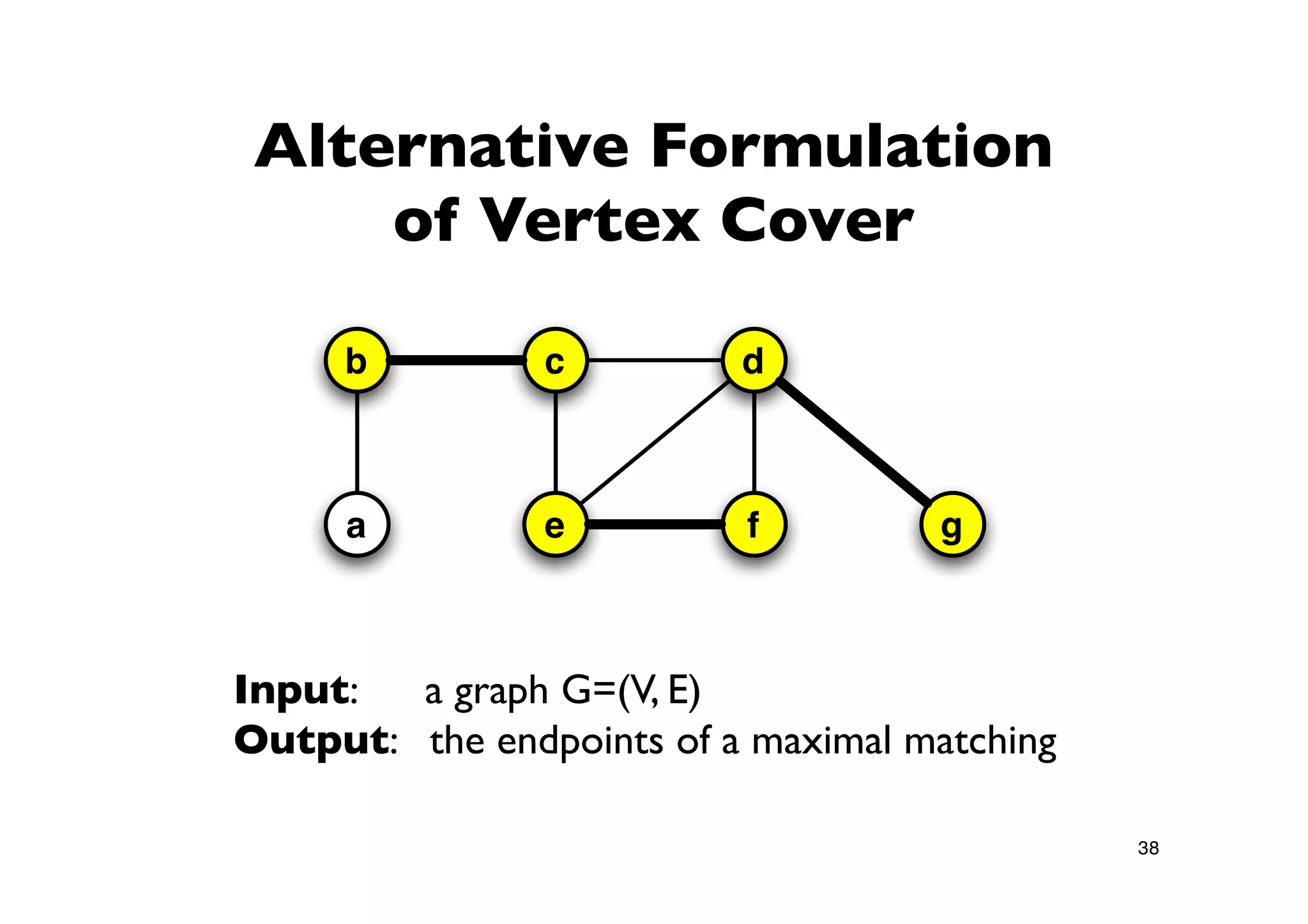
Discussion on the relationship between Maximal Matching and Minimal Vertex Cover in bipartite graphs, including König's Theorem.
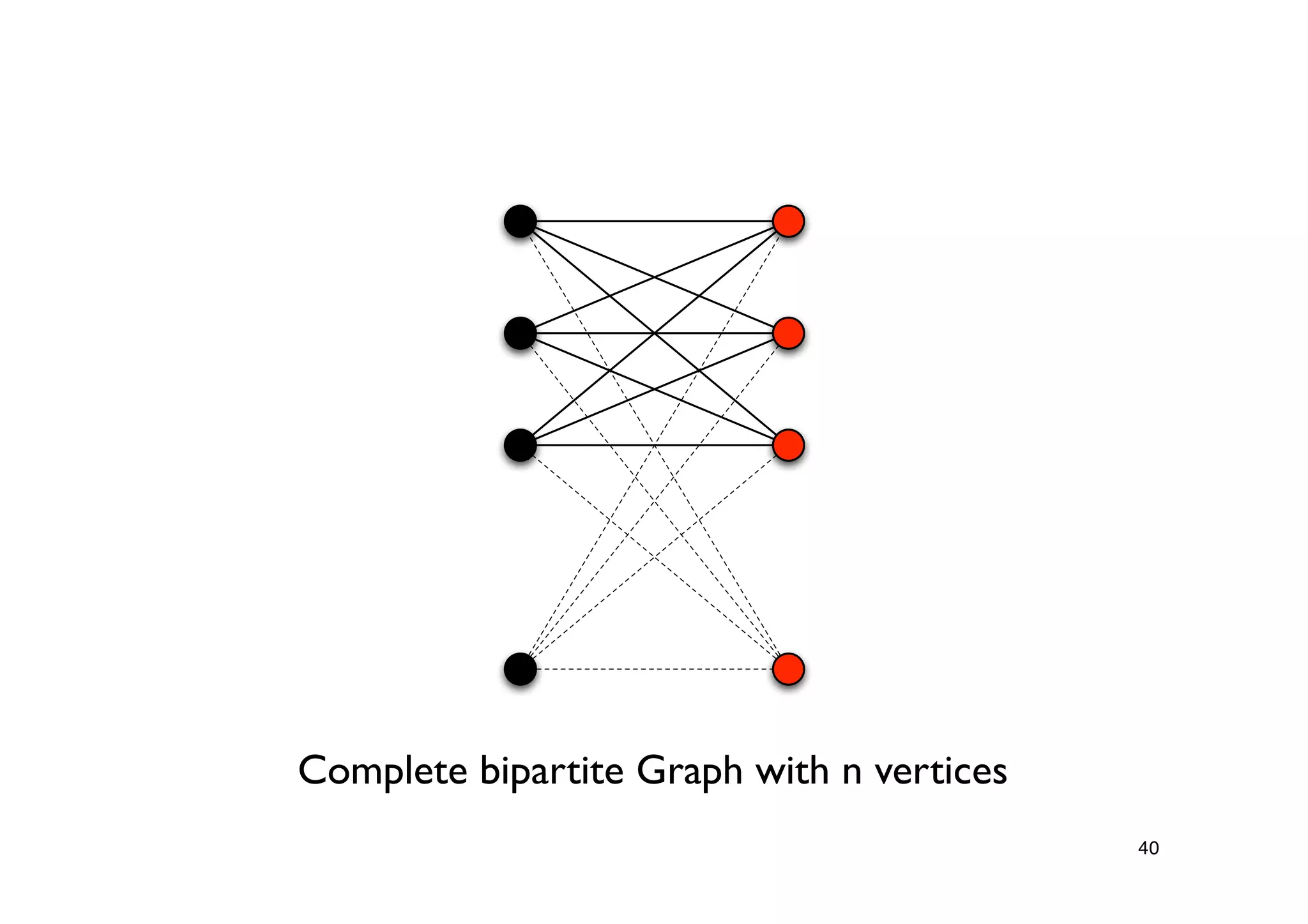
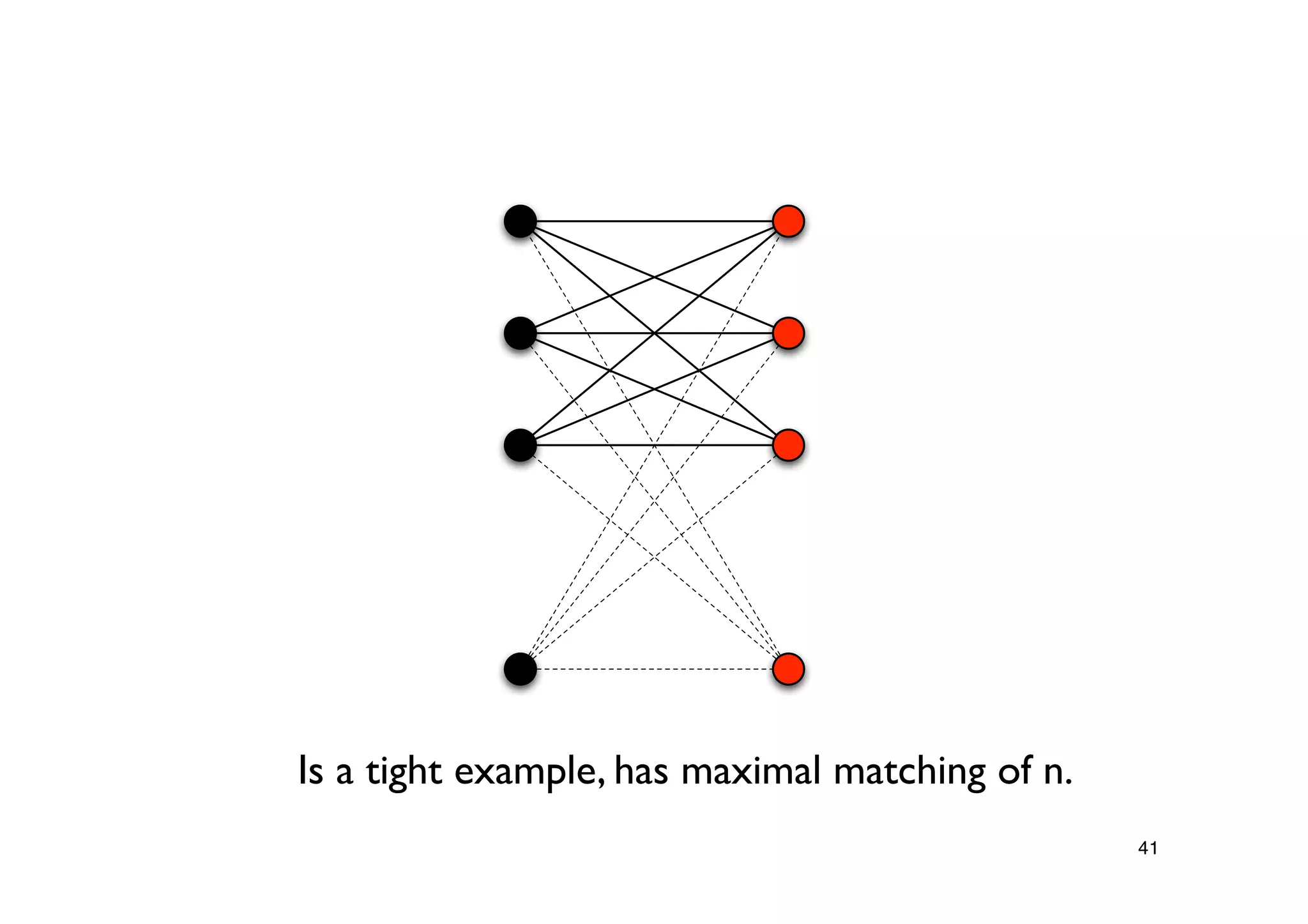
Exploration of known approximation bounds for Vertex Cover and advancements, including a parallel algorithm for efficient computation.
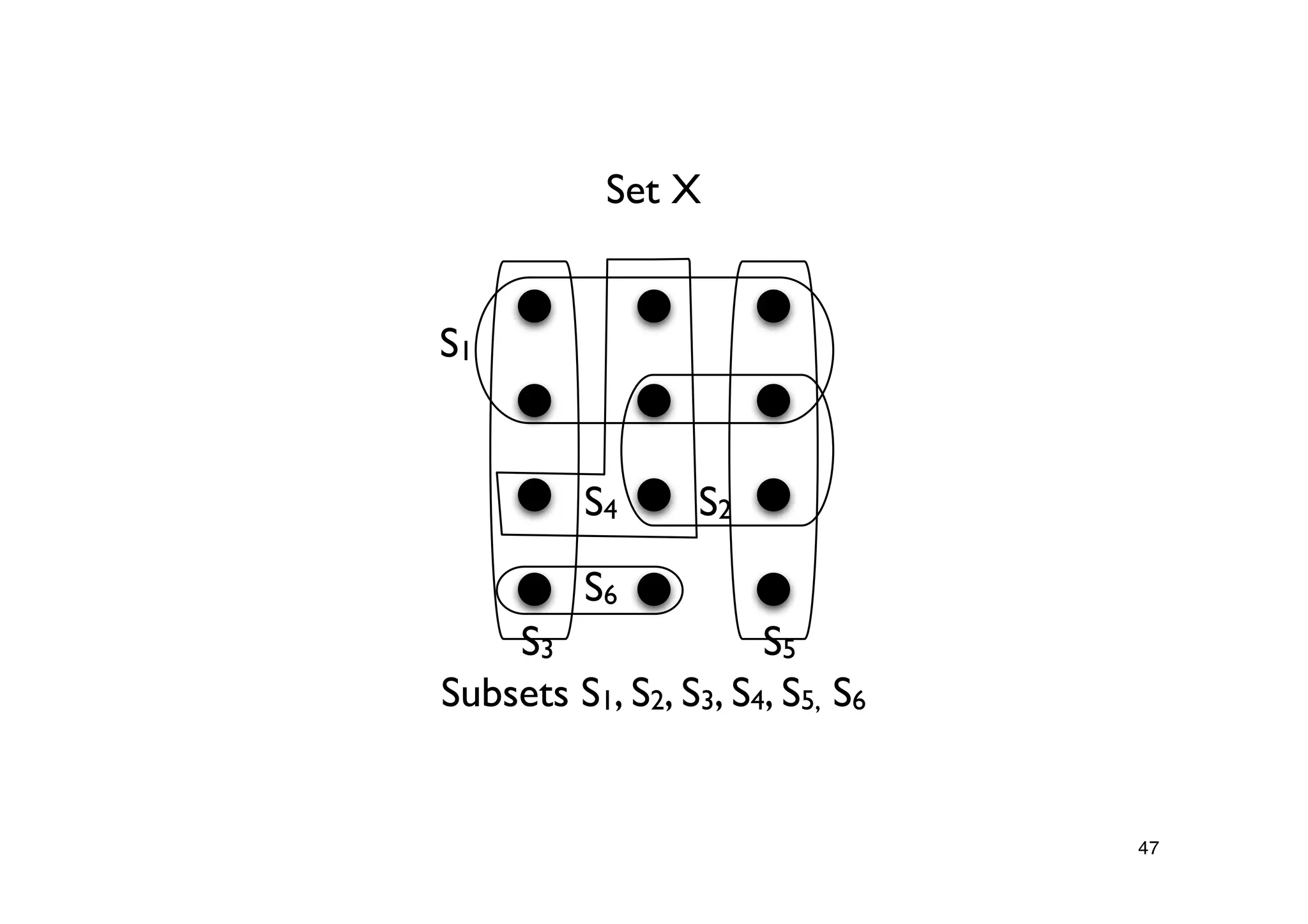
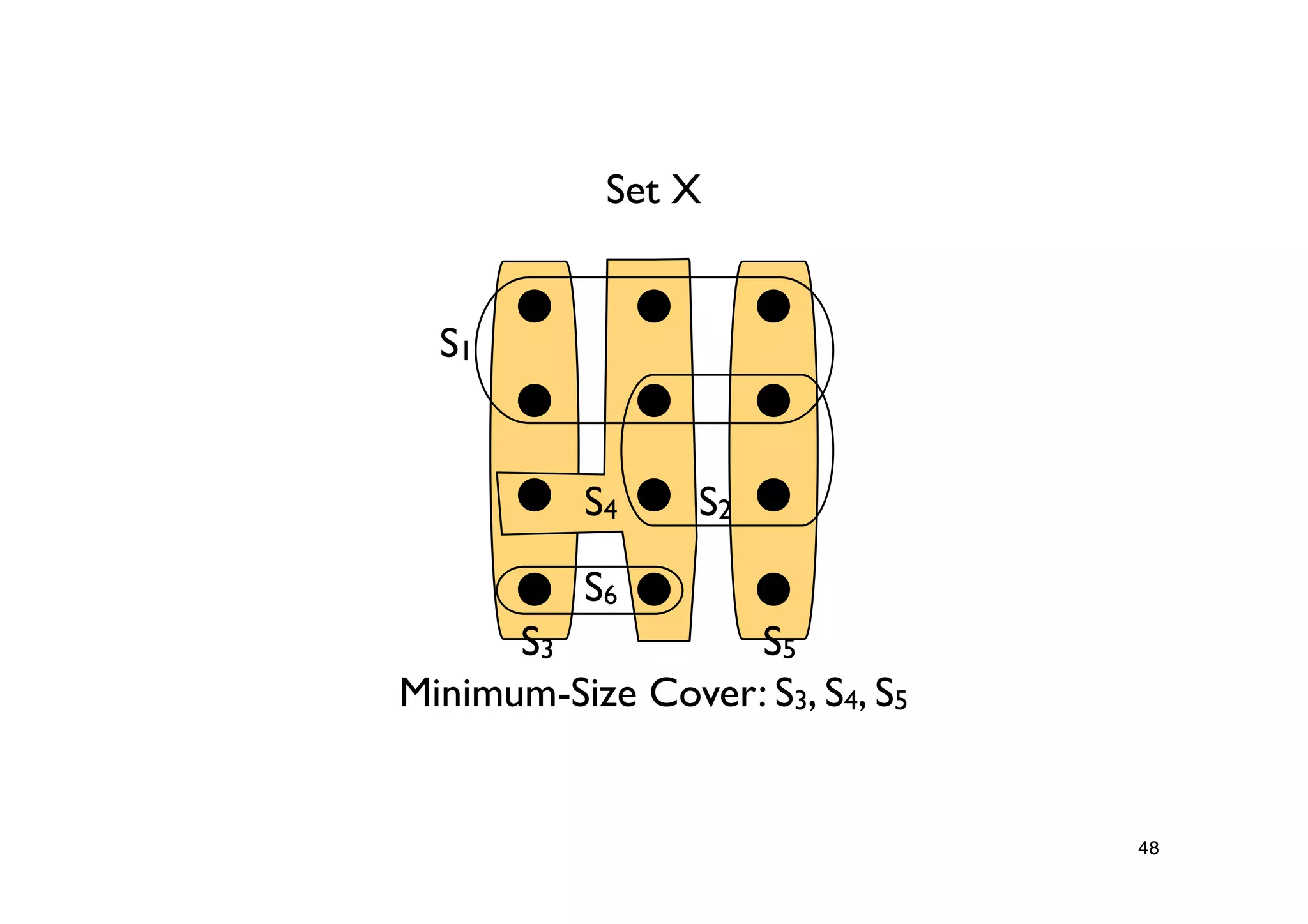
Introduction of the Set Cover problem, defining the task of covering set elements with minimum size subsets.Description of the Greedy-Set-Cover algorithm as an approximation algorithm and its performance analysis.
Open questions in research regarding approximation algorithms and a general discussion on the topic.