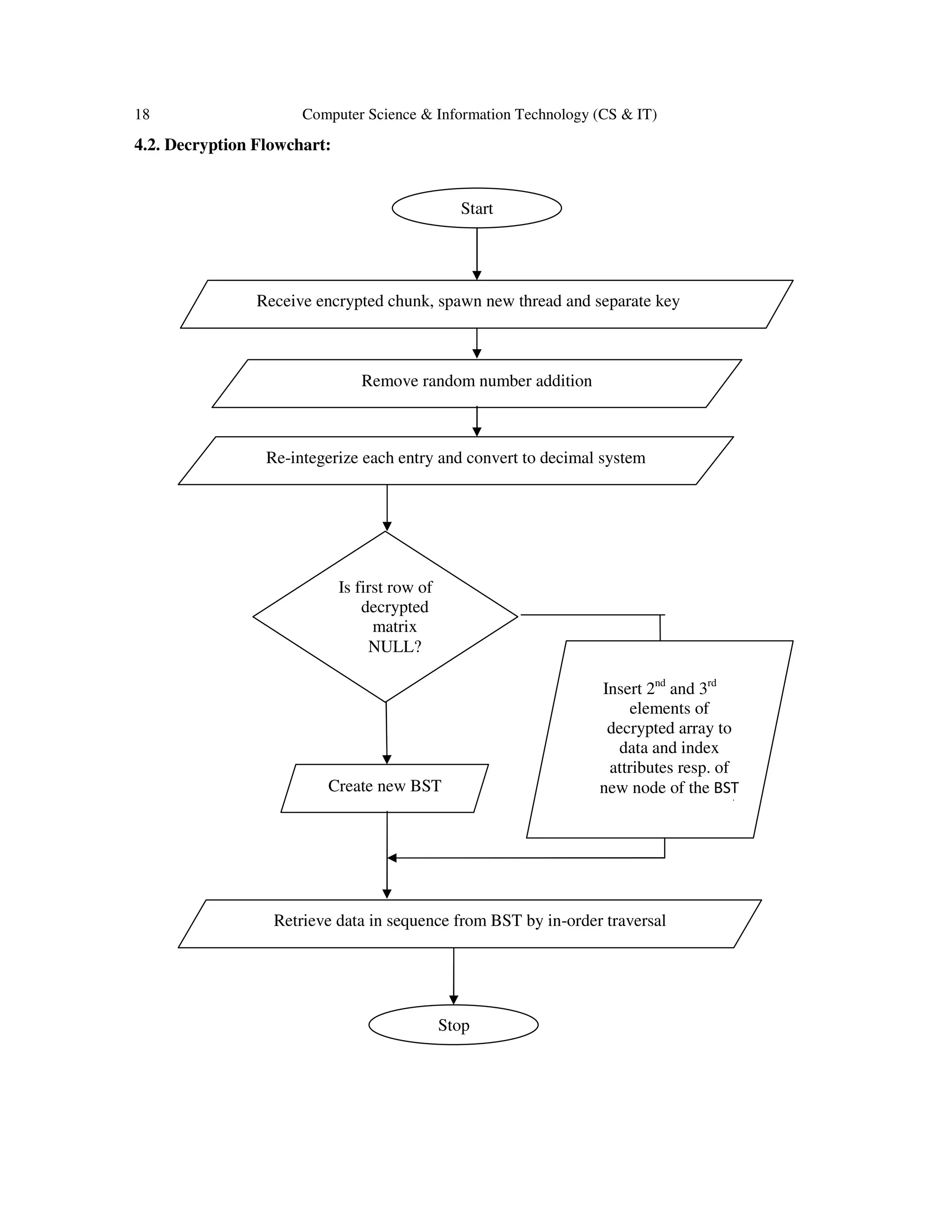
This document proposes a new cryptosystem with four levels of encryption and discusses how parallel programming can improve efficiency. The four encryption levels are: 1) matrix transformation, 2) fractionification, 3) random number addition, and 4) change of radix. Data is first fragmented and each chunk encrypted separately with a unique key. Parallel processing allows each chunk's encryption and decryption to occur simultaneously. The decryption operations reverse the encryption steps to recover the original data.







![Computer Science & Information Technology (CS & IT) 19 5. CONCLUSIONS The cryptosystem proposed in the paper works on four different layers of the encryption. All the layers cover the possible attacks on its inner layer making the encryption extremely complex to crack. The security factors of the system protect it against the cracking attacks. The polynomials and random number generators are left to the implementation for making the system flexible. This incurs the variation of complexity of encryption depending on the implementation. The parallel approach of programming adds to the efficiency of application significantly, as discussed in the section II. REFERENCES [1] Yi-Shiung Yeh, Tzong –Chen Wu, Chin Chen Chang and Wei Chizh Yang “A New Cryptosystem using Matrix Transformation”, Proceedings. 25th Annual IEEE International Carnahan Conference on Security Technology 1991 (Cat. No.91CH3031-2) [2] D. C. Lay “Linear Algebra” ISBN: 9781405846219, Chapters 1, 2 and 3 AUTHORS Parag A. Guruji Earned Bachelor of Technology degree in Computer Science and Engineering from Walchand College of Engineering, Sangli, India in May 2014. Working at ZLemma Analytics in Data Science team since June 2014](https://image.slidesharecdn.com/anewcryptosystemwithfourlevelsofencryptionandparallelprogramming-150826103115-lva1-app6892/75/A-new-cryptosystem-with-four-levels-of-encryption-and-parallel-programming-9-2048.jpg)