2DArrays_Matrix data structure and algorithm

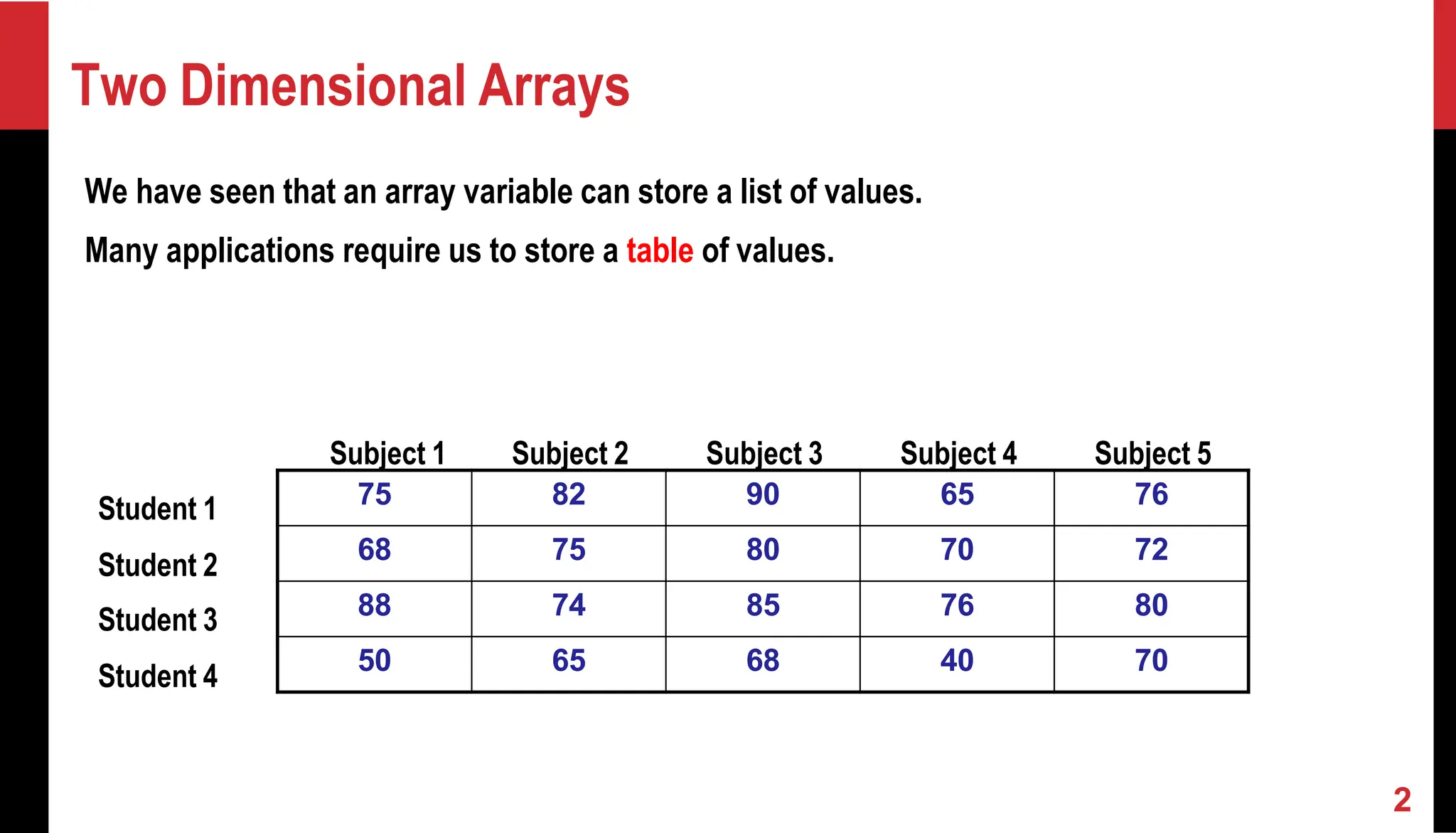
Two Dimensional Arrays We have seen that an array variable can store a list of values. Many applications require us to store a table of values. 75 82 90 65 76 68 75 80 70 72 88 74 85 76 80 50 65 68 40 70 Student 1 Student 2 Student 3 Student 4 Subject 1 Subject 2 Subject 3 Subject 4 Subject 5 2

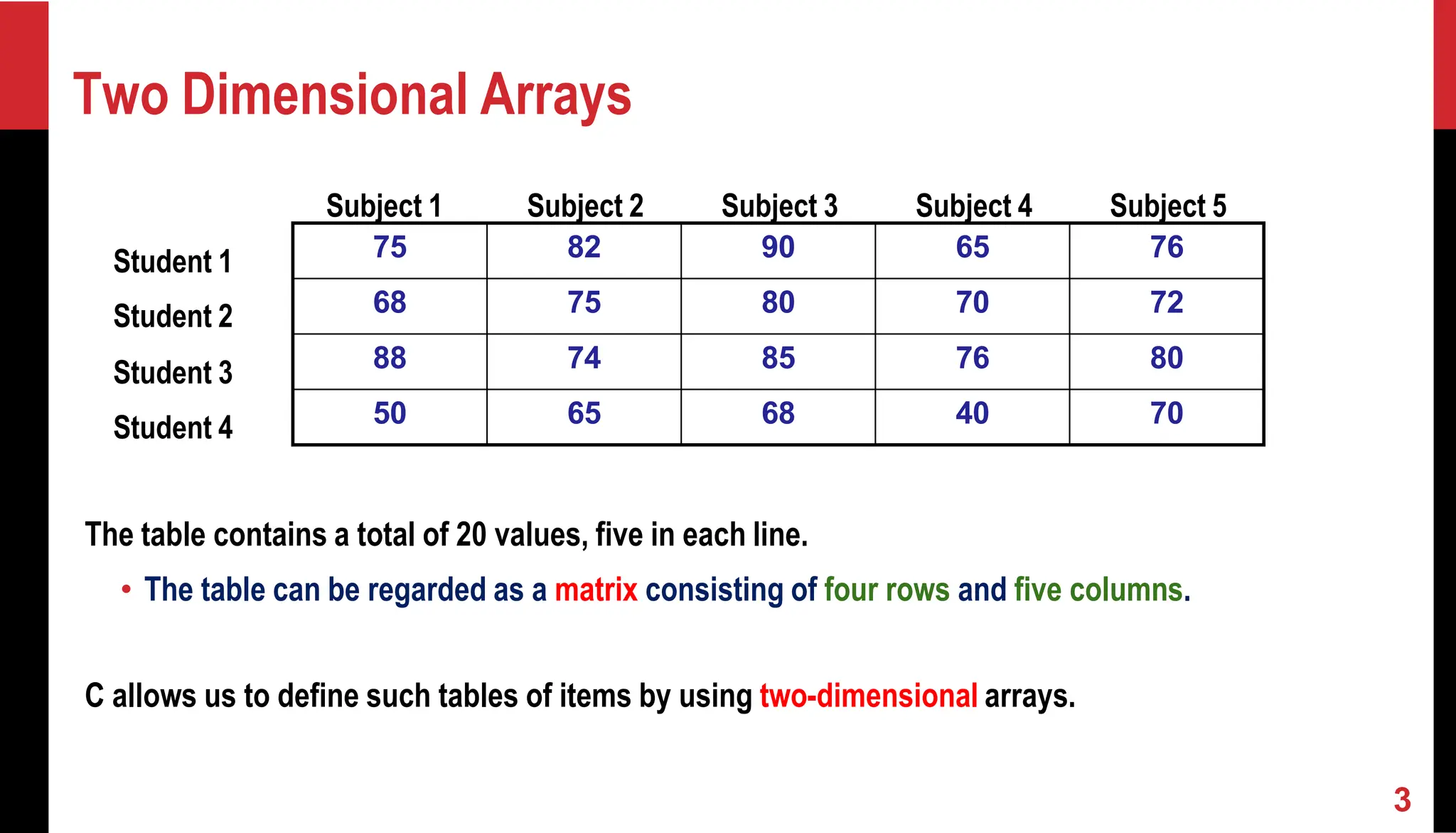
Two Dimensional Arrays 75 82 90 65 76 68 75 80 70 72 88 74 85 76 80 50 65 68 40 70 Student 1 Student 2 Student 3 Student 4 The table contains a total of 20 values, five in each line. • The table can be regarded as a matrix consisting of four rows and five columns. C allows us to define such tables of items by using two-dimensional arrays. Subject 1 Subject 2 Subject 3 Subject 4 Subject 5 3

Declaring 2-D Arrays General form: type array_name[row_size][column_size]; Examples: int marks[4][5]; float sales[12][25]; double matrix[100][100]; First index indicates row, second index indicates column. Both row index and column index start from 0 (similar to what we had for 1-d arrays) 4

Declaring 2-D Arrays int m[4][5]; m[0][0] m[0][1] m[0][2] m[0][3] m[0][4] m[1][0] m[1][1] m[1][2] m[1][3] m[1][4] m[2][0] m[2][1] m[2][2] m[2][3] m[2][4] m[3][0] m[3][1] m[3][2] m[3][3] m[3][4] Row 0 Row 1 Row 2 Row 3 Column0 Column1 Column2 Column3 Column4 5

Accessing Elements of a 2-D Array Similar to that for 1-D array, but use two indices. • First index indicates row, second index indicates column. • Both the indices should be expressions which evaluate to integer values. Examples: x[m][n] = 0; c[i][k] += a[i][j] * b[j][k]; val = sqrt( arr[j*3][k+1] ); 6

How is a 2-D array stored in memory? Starting from a given memory location (starting address of the array), the elements are stored row-wise in consecutive memory locations. • x: starting address of the array in memory • c: number of columns • k: number of bytes allocated per array element, e.g., sizeof(int) • a[i][j] is allocated memory location at address x + (i * c + j) * k a[0][0] a[0][1] a[0][2] a[0][3] a[1][0] a[1][1] a[1][2] a[1][3] a[2][0] a[2][1] a[2][2] a[2][3] Row 0 Row 1 Row 2 7

Array Addresses int main() { int a[3][5]; int i, j; for (i=0; i<3;i++) { for (j=0; j<5; j++) printf ("%un", &a[i][j]); printf ("n"); } return 0; } 3221224480 3221224484 3221224488 3221224492 3221224496 3221224500 3221224504 3221224508 3221224512 3221224516 3221224520 3221224524 3221224528 3221224532 3221224536 Output 8

How to read the elements of a 2-D array? By reading them one element at a time for (i=0; i<nrow; i++) for (j=0; j<ncol; j++) scanf (“%f”, &a[i][j]); • The ampersand (&) is necessary. • The elements can be entered all in one line or in different lines. We can also initialize a 2-D array at the time of declaration: int a[MAX_ROWS][MAX_COLS] = { {1,2,3}, {4,5,6}, {7,8,9} }; 9

How to print the elements of a 2-D array? By printing them one element at a time. for (i=0; i<nrow; i++) for (j=0; j<ncol; j++) printf (“%f ”, a[i][j]); for (i=0; i<nrow; i++) { for (j=0; j<ncol; j++) printf (“%f ”, a[i][j]); printf(“n”); } This will print all elements in one line. This will print the elements with one row in each line (matrix form). 10

Example: Matrix addition int main() { int a[100][100], b[100][100], c[100][100], p, q, m, n; printf (“Enter dimensions: ”); scanf (“%d %d”, &m, &n); for (p=0; p<m; p++) for (q=0; q<n; q++) scanf (“%d”, &a[p][q]); for (p=0; p<m; p++) for (q=0; q<n; q++) scanf (“%d”, &b[p][q]); for (p=0; p<m; p++) for (q=0; q<n; q++) c[p][q] = a[p][q] + b[p][q]; for (p=0; p<m; p++) { for (q=0; q<n; q++) printf (“%d ”, c[p][q]); printf (“n”); } return 0; }

A 2-D array is an array or 1-D arrays, and so a row pointer 12 #include <stdio.h> int main () { int i, j, A[4][5] = { { 7, 14, 3, 16, 6}, {11, 5, 9, 13, 18}, { 2, 15, 20, 1, 19}, {10, 4, 12, 17, 8} }; for (i=0; i<4; ++i) { for (j=0; j<5; ++j) printf("%p ", &A[i][j]); printf("n"); } printf("sizeof(A) = %3lu, A = %p, A + 1 = %pn", sizeof(A), A, A + 1); printf("sizeof(*A) = %3lu, *A = %p, *A + 1 = %pn", sizeof(*A), *A, *A + 1); printf("sizeof(&A) = %3lu, &A = %p, &A + 1 = %pn", sizeof(&A), &A, &A + 1); return 0; } Output 0x7ffc314fe100 0x7ffc314fe114 0x7ffc314fe128 0x7ffc314fe13c 0x7ffc314fe104 0x7ffc314fe118 0x7ffc314fe12c 0x7ffc314fe140 0x7ffc314fe108 0x7ffc314fe11c 0x7ffc314fe130 0x7ffc314fe144 0x7ffc314fe10c 0x7ffc314fe120 0x7ffc314fe134 0x7ffc314fe148 0x7ffc314fe110 0x7ffc314fe124 0x7ffc314fe138 0x7ffc314fe14c sizeof(A) = 80, A = 0x7ffc314fe100, A + 1 = 0x7ffc314fe114 sizeof(*A) = 20, *A = 0x7ffc314fe100, *A + 1 = 0x7ffc314fe104 sizeof(&A) = 8, &A = 0x7ffc314fe100, &A + 1 = 0x7ffc314fe150

Passing 2-d arrays to functions 13

Passing 2-D arrays to functions Similar to that for 1-D arrays. • The array contents are not copied into the function. • Rather, the address of the first element is passed. For calculating the address of an element in a 2-D array, the function needs: • The starting address of the array in memory (say, x) • Number of bytes per element (say, k) • Number of columns in the array, i.e., the size of each row (say, c) The above three pieces of information must be known to the function. a[i][j] is located at memory address x + (i * c + j) * k 14

Example int main() { b[15]25]; int a[15][25], … … add (a, b, 15, 25); … … } void add (int x[][25], int y[][25], int rows, int cols) { } We can also write int x[15][25], y[15][25]; The first dimension is ignored. But the second dimension must be given. 15

Example: Matrix addition with functions void AddMatrix( int A[][100], int B[][100], int C[][100], int x, int y) { int i, j; for (i=0; i<x; i++) for (j=0; j<y; j++) C[i][j] = A[i][j] + B[i][j]; } void ReadMatrix (int A[][100], int x, int y) { int i, j; for (i=0; i<x; i++) for (j=0; j<y; j++) scanf (“%d”, &A[i][j]); } 16

Example: Matrix addition int main() { int a[100][100], b[100][100], c[100][100], p, q, m, n; scanf (“%d%d”, &m, &n); ReadMatrix(a, m, n); ReadMatrix(b, m, n); AddMatrix(a, b, c, m, n); PrintMatrix(c, m, n); return 0; } void PrintMatrix (int A[][100], int x, int y) { int i, j; printf (“n”); for (i=0; i<x; i++) { for (j=0; j<y; j++) printf (“ %5d”, A[i][j]); printf(“n”); } }

Example: #include <stdio.h> int main() { int a[15][25], b[15][25], c[15][25]; int m, n; scanf (“%d %d”, &m, &n); for (p=0; p<m; p++) for (q=0; q<n; q++) scanf (“%d”, &a[p][q]); for (p=0; p<m; p++) for (q=0; q<n; q++) scanf (“%d”, &b[p][q]); add (a, b, m, n, c); for (p=0; p<m; p++) { for (q=0; q<n; q++) printf(“%f ”, c[p][q]); printf(“n”); } } void add (int x[][25], int y[][25], int m, int n, int z[][25]) { int p, q; for (p=0; p<m; p++) for (q=0; q<n; q++) z[p]q] = x[p][q] + y[p][q]; } Note that the number of columns has to be fixed in the function definition. • There is no difference between void add( int x[ ][25], … ) and void add( int x[15][25], … ) • Specifying the first dimension is not necessary, but not a mistake. 18

Example: Transpose of a matrix #include <stdio.h> void transpose (int x[][3], int n) { int p, q, t; for (p=0; p<n; p++) for (q=0; q<n; q++) { t = x[p][q]; x[p][q] = x[q][p]; x[q][p] = t; } } main() { int a[3][3], p, q; for (p=0; p<3; p++) for (q=0; q<3; q++) scanf (”%d”, &a[p][q]); transpose (a, 3); for (p=0; p<3; p++) { for (q=0; q<3; q++) printf (”%d ”, a[p][q]); printf (“n”); } } 19

Example: Transpose of a matrix #include <stdio.h> void transpose (int x[][3], int n) { int p, q, t; for (p=0; p<n; p++) for (q=0; q<n; q++) { t = x[p][q]; x[p][q] = x[q][p]; x[q][p] = t; } } main() { int a[3][3], p, q; for (p=0; p<3; p++) for (q=0; q<3; q++) scanf (”%d”, &a[p][q]); transpose (a, 3); for (p=0; p<3; p++) { for (q=0; q<3; q++) printf (”%d ”, a[p][q]); printf (“n”); } } This function is wrong. Why? 20

The Correct Version void transpose (int x[][3], int n) { int p, q, t; for (p = 0; p < n; p++) for (q = p; q < n; q++) { t = x[p][q]; x[p][q] = x[q][p]; x[q][p] = t; } } 10 20 30 40 50 60 70 80 90 10 40 70 20 50 80 30 60 90 21

Dynamically allocating 2-d arrays A brief discussion

You may recall … We have discussed the issue of dynamically allocating space for 1-D arrays • Using malloc()libraryfunction. int *ptr; ptr = (int*) malloc( 100 * sizeof(int) ); 23

How to dynamically allocate a 2-d array? Many variations possible: 1. Fixed number of rows, but variable number of columns 2. Variable number of rows, but fixed number of columns 3. Both number of rows and columns variable We will discuss only the first variation: Fixed number of rows, but variable number of columns 24

Fixed number of rows, but variable number of columns Let us assume the number of rows is fixed to 3. We can use an array of pointers of size 3, where the ith element of this array (a pointer) will point to the ith row of the 2-d array. int *r[3], i, c; printf (”Enter nos. of columns of the 2-d array:”); scanf(”%d”, &c); // each row will have c elements for (i=0;i<3;i++) r[i] = (int *) malloc(c*sizeof(int)); // allocate i-th row 25

Possible to have rows with different number of elements Dynamically allocated memory r[0] r[1] r[2] Statically allocated pointer array

#include <stdio.h> #include <stdlib.h> int main() { int *r[3], i, j, col; for (i=0; i<3; ++i) { col = 2 * (i+1); r[i] = (int *) malloc (col*sizeof(int)); for (j=0; j<col; ++j) r[i][j] = i + j; } for (i=0; i<3; ++i) { col = 2 * (i+1); for (j=0; j<col; ++j) printf("%d ", r[i][j]); printf("n"); } return 0; } 0 1 1 2 3 4 2 3 4 5 6 7 Output 27

We have studied only 2-d arrays. C allows arrays of higher dimensions as well. 28

Practice problems 1. Write a function that takes an n x n square matrix A as parameter (n < 100) and returns 1 if A is an upper- triangular matrix, 0 otherwise. 2. Repeat 1 to check for lower-triangular matrix, diagonal matrix, identity matrix. 3. Consider a n x n matrix containing only 0 or 1. Write a function that takes such a matrix and returns 1 if the number of 1’s in each row are the same and the number of 1’s in each column are the same; it returns 0 otherwise. 4. Write a function that reads in an m x n matrix A and an n x p matrix B, and returns the product of A and B in another matrix C. Pass appropriate parameters. 5. Write a function to find the transpose of a non-square matrix A in a matrix B. 6. Repeat the last exercise when the transpose of A is computed in A itself. Use no additional 2-d arrays. For each of the above, also write a main function that reads the matrices, calls the function, and prints the results (a message, the result matrix etc.)

2DArrays_Matrix data structure and algorithm

More Related Content

Similar to 2DArrays_Matrix data structure and algorithm

More from Sumni Uchiha

Recently uploaded

2DArrays_Matrix data structure and algorithm