DEV Community

Cover image for #010 DS&A - Time and Space Analysis
Omar
Omar

Posted on

#010 DS&A - Time and Space Analysis

#algorithms #computerscience #datastructres

Introduction

Nothing to say more than hello 👋,
In Case your wondering who is this man in the banner it's the Khwarizmi the inventor of algorithms concept.
Make sure to follow because I will start more advanced series in future.

Algorithms

Time and Space Analysis

Introduction to asymptotic

In order to solve any problem in computer science we usually write a program , before writing program it's better to write it in formal description which is called Algorithm .

let's say we have a problem P we need to write a program , let's say we write it in c , to write program we need first to write an Algorithm , let's say P have many solutions s1,s2,s3,s4.... the thing that will differ solution from another is time and memory , the science of it is called Design and analysis of algorithm.

some of the notations used in Algorithms are these:

Asymptotic notation

Big(oh) represented by O

image-20200914233224043

if time Increasing as input increasing so the the worst case or upper bound is C*g(n) and satisfy those conditions

f(n) <= C*g(n) ; n >= n0 ; c>0 , n0 >= 1 f(n) = O(g(n))
Enter fullscreen mode Exit fullscreen mode

let's take this example

f(n) = 3n+2 and g(n) = n f(n) = O(g(n)) f(n) <= C * g(n) , c > 0 , n0 >= 1 3n+2 <= c*n take c = 4 3n+2 <= 4n => n >= 2
Enter fullscreen mode Exit fullscreen mode

we can pick g(n) = n^2 or n^3 ... n^nbecause f(n) can be written with respect to g(n) but it is preferred to take the smallest one which is n

Big omega represented by Ω

image-20200915171717083

f(n) >= C*g(n) ; n >= n0 ; c>0 , n0 >= 1 f(n) = O(g(n))
Enter fullscreen mode Exit fullscreen mode

example

f(n) = 3n+2 and g(n) = n f(n) = O(g(n)) f(n) >= C * g(n) 3n+2 >= c*n take c = 1 and n0 >= 1 3n+2 = Ω(n)
Enter fullscreen mode Exit fullscreen mode

example 2

g(n) = 3n+2 g(n)=n^2 3n+2 ?= Ω(n^2) 3n+2 >= c*n^2 , n0
Enter fullscreen mode Exit fullscreen mode

We can not find a C that satisfy this solution , so we need to pick things lower than n like log(n) or log(log(n))

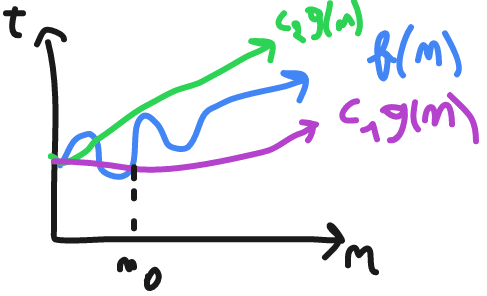
Big theta represented by Θ

image-20200915172753442

f(n) = Θ(g(n)) c1*g(n) <= f(n) <= c2*gn(n) ; c1,c2 > 0 , n >= n0
Enter fullscreen mode Exit fullscreen mode

example

f(n) = 3n+2 , g(n) = n f(n) <= C2*g(n) take c2 = 4 3n+2 <= 4n f(n) >= c1*g(n) take c1 = 1 3n+2 >= n , n0 >= 1
Enter fullscreen mode Exit fullscreen mode

O this mean their is no bigger time than this , and it's called worst case.

Ω this mean their is no better time than this , and it's called best case.

Θ this mean it's the average case , and it's called the average case.

we usually don't care about best case , we care about worst case. If the worst and best cases are the same we generally go for average case.

example: take this array with n elements

0 1 2 3 4 5 6 7
5 7 1 2 4 10 20 11

let's say we need to find element x , best case is Ω(1) , worst case is O(n), average case is Θ(n/2)= Θ(n)

Time Complexity Analysis

the f(n) is not the real time is just approximation time that program take to finish.

there is 2 types of Algorithms :

iterative: A() { for i=1 to n max(a,b) } recursive: A(n) { if() A(n/2) }
Enter fullscreen mode Exit fullscreen mode

any iterative can be written as recursive and vise versa.

If the Algorithm doesn't have loops or recursion time complexity is constant O(1) , if the time complexity is O(n^2+n) we take the biggest degree so we take it O(n^2)

examples

A() { int i; for(i = 1 to n) pf("text"); } time complexity : O(n)
Enter fullscreen mode Exit fullscreen mode 
A() { int i; for(i = 1 to n) for(j = 1 to n) pf("omar"); } time complexity : O(n^2)
Enter fullscreen mode Exit fullscreen mode 
A() { int i; while (s <= n) { i++; s = s+i; pf("omar"); } } time complexity : O(sqrt(n)) /* Analysing : s : 1 3 6 10 15 21 ... i : 1 2 3 4 5 6 ... s will stop on n let's say k is the final i and s is nothing but new i + all old i (6 = 3+2+1) so it will stop when it reach k(k+1)/2 > n (k^2+k)/2 > n k = O(sqrt(n)) */
Enter fullscreen mode Exit fullscreen mode 
A() { int i; for(i=1;i^2<=n;i++) pf("omar"); } time complexity : O(sqrt(n)) // Here all the cases are the same
Enter fullscreen mode Exit fullscreen mode 
A() { int i,j,k,n; for(i=1 ; i<n ; i++) { for(j=1;j<=i;j++) { for(k=1 ; k <= 100 ; k++) { pf("omar"); } } } } time complexity : O(n^2) /* Analysing : i = 1 , j = 1 time , k = 100 times i = 2 , j = 2 times , k = 200 times i = 3 , j = 3 times , k = 300 times ... i = n , j = n times , k = j*100 times 1*100+2*100+3*100+...+n*100 = 100 (1+2+3+...+n) = 100 (n(n+1)/2) = O(n^2) */
Enter fullscreen mode Exit fullscreen mode 
int i,j,k,n; for(i = 1 ; i <= n ;i++) { for(j=1 ; j <= i^2 ; j++) { for(k=1 ; k <= n/2 ; k++) { pf("omar"); } } } time complexity : O(n^4) /* Analysing : i = 1 , j = 1 time , k = n/2 * 1 i = 2 , j = 4 times , k = n/2 * 4 i = 3 , j = 9 times , k = n/2 * 9 ... i = n , j = n^2 times , k = n/2 * n^2 times n/2 * 1 + n/2 *4 + n/2 * 9 + ... + n/2 * n^2 = n/2 * (n(n+1)(2n+1))/6 = O(n^4) */
Enter fullscreen mode Exit fullscreen mode 
A() { for(i = 1 ; i < n ; i = i*2) pf("omar"); } time complexity : O(log(n)) /* Analysing : i : 1 , 2 , 4 ... n 2^0 , 2^1 , 2^2 ... 2^k 2^k = n => k = log(n) = O(log(n)) since i is multiplied by 2 every step so log here is base 2 if i is multiplied by k we say log of base k */
Enter fullscreen mode Exit fullscreen mode 
A() { int i,j,k; for(i=n/2 ; i <= n ; i++) for(j=1 ; j <= n2 ; j++) for(k=1 ; k <= n ; k=k*2) pf("omar"); } time complexity : O(n^2 * log(n)) /* Analysing : n/2 * n/2 * log(n) = O(n^2 * log(n)) */
Enter fullscreen mode Exit fullscreen mode 
A() { int i,j,k; for(i=n/2 ; i <= n ; i++) // n/2 for(j=1 ; j <= n ; i = 2*k) // log n for(k=1 ; k <= n ; k = k*2) // log n pf("omar"); } time complexity : O(n*(log(n))^2)
Enter fullscreen mode Exit fullscreen mode 
A() { // assume n >= 2 while(n>1) { n = n/2; } } time complexity : O(log(n))
Enter fullscreen mode Exit fullscreen mode 
A() { for(i = 1 ; i <= n ; i++) // n for(j = 1 ; j <= n ; i = j+i) // pf("omar") } time complexity : O(n*log(n)) /* Analysing : i = 1 , j = 1 to n ; n times i = 2 , j = 1 to n ; n/2 times i = 3 , j = 1 to n ; n/3 times ... i = n , j = 1 to n ; n/n times n(1+ 1/2 + 1/3 + ... + 1/n ) = n (log n) = O(n * log(n)) */
Enter fullscreen mode Exit fullscreen mode 
A() { int n = (2^2)^k; for(i=1;i<=n;i++) // n { j = 2 while(j <= n) { j = j^2; pf("omar"); } } } time complexity : O(log(log(n))) /* Analysing : k = 1 ; n = 4 ; j = 2,4 ; n * 2 times k = 2 ; n = 16 ; j = 2,4,16 ; n * 3 times k = 3 ; n = (2^2)^3 ; j = 2^1,2^2,2^4,2^8 ; n * 4 times n = (2^2)^k => log n = 2^k => log(log(n))=k n*(k+1) = n(log(log(n)) + 1) = O(log(log(n))) */
Enter fullscreen mode Exit fullscreen mode

Time analysis of recursive 

A(n) { if(...) return A(n/2)+A(n/2); } T(n) = c+2*T(n/2)
Enter fullscreen mode Exit fullscreen mode 
A(n) { if(n>1) return A(n-1); } T(n) = 1 + T(n-1) = 1 + 1 + T(n-2) = 2+1+T(n-3) = k+T(n-k) // k = n-1 = (n-1)+T(1) = n-1+1 = n
Enter fullscreen mode Exit fullscreen mode

back substitution

T(n-1) = 1+T(n-2) -> 2 T(n-2) = 1+T(n-3) -> 3
Enter fullscreen mode Exit fullscreen mode 
T(n) = n + T(n) T(n-1) = (n-1)+T(n-2) T(n-2) = (n-2)+T(n-3) ----------------------- T(n) = n + T(n-1) = n + (n-1) + T(n-2) = n + (n-1) + (n-2) + T(n-3) = n + (n-1) + (n-2)+...+(n-k)+T(n-(k+1)) with n-(k+1)=1 => n-k-1=1 => k=n-2 = n+(n-1)+(n-2)+...+(n-(n-2))+T(n-(n-2+1)) = n+(n-1)+(n-2)+...+1 = n(n-1)/2 = O(n^2)
Enter fullscreen mode Exit fullscreen mode

recursive tree method

T(n) = 2*T(n/2) + C ; n>1 = C ; n = 1
Enter fullscreen mode Exit fullscreen mode

image-20200917021118588

T(1) = T(n/n) c+2c+4c+...+nc c(1+2+4+...+n) c(1+2+4+...+2^k) c(1 (2^(k+1) - 1) / (2-1) ) c(2^k+1 - 1) c(2n-1) O(n)
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2*T(n/2)+n ; n > 1 = 1 ; n = 1
Enter fullscreen mode Exit fullscreen mode

image-20200917025850624

comparing various functions

let's say we have two functions n^2 and n^3 they have n^2 as common so I rewrite it as 1 and n .

If f(n) is given and g(n) is given we take biggest degree and compare them. If they are constants like 2 and 4 we consider them the same.

examples

2^n n^2 n log(2) 2 log(n) n 2*log(n) consider n = 2^100 2^100 2*log(2^100) 2^100 200 2^100 >>>>>>>>>>>>>>>>>>> 200 so 2^n growing very large
Enter fullscreen mode Exit fullscreen mode 
3^n 2^n n*log(3) n*log(2) cancel n and compare it log(3) log(2)
Enter fullscreen mode Exit fullscreen mode 
n^2 n*log(n) concel common terms n*n n*log(n) n > log(n)
Enter fullscreen mode Exit fullscreen mode 
n log(n)^100 log(n) 100*log(log(n)) take n = 2^128 128 100*log(128) 128 700 let's take n = 1024 1024 100*log(1024) 1024 1000 so n growing larger
Enter fullscreen mode Exit fullscreen mode 
n^log(n) n*log(n) log(n)*log(n) log(n)+log(log(n)) for n = 10^1024 1024*1024 1034 for n = (2^2)^20 2^20*2^20 2^20+20 so n^log(n) is larger
Enter fullscreen mode Exit fullscreen mode 
sqrt(log(n)) log(log(n)) 1/2 * log(log(n)) log(log(log(n))) take n = (2^2)^10 5 3.5
Enter fullscreen mode Exit fullscreen mode 
n^(sqrt(n)) n^log(n) sqrt(n)*log(n) log(n)*log(n) sqrt(n) log(n) 1/2 * log(n) log(log(n)) n = 2^128 64 7
Enter fullscreen mode Exit fullscreen mode 
f(n) = { n^3 0<n<10000 n^2 n>=10000 } g(n) = { n 0 < n < 100 n^3 n > 100 }
Enter fullscreen mode Exit fullscreen mode
0-99 100-9999 10,000 ....
f(n) n^3 n^3 n^2
g(n) n n^3 n^3

we take care about the function in infinity so g(n) is bigger in infinity

Masters theorem

first there is a different between log^2(n) and (log(n))^2 , because (log(n))^2 = log(n) * log(n) and log^2(n) = log(log(n))

masters theorem used to solve reclusive problems

Lightbox

examples

T(n) = 3T(n/2) + n^2 a = 3 , b = 2 , k = 2 p=0 a < b^k 3 < 4 so it's the case 3)a so T(n) = O(n^2 * log^0(n))
Enter fullscreen mode Exit fullscreen mode 
T(n) = 4*T(n/2) + n^2 a=4 , b=2 , k=2 , p=0 4=2^2 so it's case 2)a T(n) = O(n^log(4) * log(n)) = O(n^2*log(n))
Enter fullscreen mode Exit fullscreen mode 
T(n) = T(n/2)+n^2 a=1 , b=2 , k=2 , p=0 1 < 2^2 it's case 3)a T(n) = O(n^2 * log^0(n)) = O(n^2)
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2^n*T(n/2)+n^n master theoreme is not applied
Enter fullscreen mode Exit fullscreen mode 
T(n) = 16*T(n/4)+n a = 16 b=4 k=1 p=0 16>4 so it's 1)
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2*T(n/2)+n*log(n) a=2 b=2 k=1 p=1 2=2 , p>-1 so it's 2)a
Enter fullscreen mode Exit fullscreen mode

if it doesn't directly look like theorem we need to refactoring it

T(n) = 2*T(n/2)+n/log(n) = 2T(n/2)+n*log^-1(n) a=2 , b =2 , k=1 p=-1 s = 2^1 so it's case 2)b
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2*T(n/4)+n^0.51 a=2 b=4 k=051 p=0 2 < 4^0.51 case 3)a
Enter fullscreen mode Exit fullscreen mode 
T(n) = 05*T(n/2)+1/n a=0.5 not valid
Enter fullscreen mode Exit fullscreen mode 
T(n) = 6*T(n/3)+n^2*log(n) a=6 b=3 k=2 p=1 6 < 3^2 so it's 3)a
Enter fullscreen mode Exit fullscreen mode 
T(n) = 64 T(n/8) - n^2 * log(n) can not apply master theorem
Enter fullscreen mode Exit fullscreen mode 
T(n) = 7*T(n/3)+n^2 a=7 b=3 k=2 p=0 7 < 3^2 case 3)a
Enter fullscreen mode Exit fullscreen mode 
T(n) = 4*T(n/2)+log(n) a=4 b=2 k=0 p=1 4 > 2^0 case 1
Enter fullscreen mode Exit fullscreen mode 
T(n) = sqrt(2)*T(n/2)+log(n) a=sqrt(2) b=2 k=0 p=1 sqrt(2) > 2^0 case 1
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2*T(n/2)+sqrt(n) a=2 b=2 k=1/2 p=0 2>2^1/2 case 1
Enter fullscreen mode Exit fullscreen mode 
T(n) = 3*T(n/2)+n a=3 b=2 k=1 p=0 3 > 2^1 case 1
Enter fullscreen mode Exit fullscreen mode 
T(n) = 3*T(n/3)+sqrt(n) a=3 b=3 k=1/2 p=0 3>3^1/2 case 1
Enter fullscreen mode Exit fullscreen mode 
T(n) = 4*T(n/2)+C*n a=4 b=2 k=1 p=0 4 > 2^1 case 3)b
Enter fullscreen mode Exit fullscreen mode 
T(n)=3*T(n/4)+(n*log(n)) a=3 b=4 k=1 p=1 3 < 4 case 3)a
Enter fullscreen mode Exit fullscreen mode

Analysis Space Complexity

same as time complexity we have space complexity for Iterative programs and recursive programs. Some times we sacrifice time for space.

Algo(A,1,n) { int i; for(i=1 to n) A[i] = 0; }
Enter fullscreen mode Exit fullscreen mode

this space complexity is constant O(1) because we don't take the initial input into count. So we calculate extra spaces such as i

Algo(A,1,n) { int i; create B[n]; for(i=1 to n) B[i] = A[i]; }
Enter fullscreen mode Exit fullscreen mode

the amount of space required is O(n) because we declare B[n] that contain n element. Same as Time complexity we didn't take in count the constants in other word we take higher degree.

Algo(A,1,n) { create B[n,n]; int i,j; for(i=1 to n) for(j=1 to n) B[i,j]=A[i] }
Enter fullscreen mode Exit fullscreen mode

space complexity is O(n^2)

A(n) { if(n>=1) { A(n-1); pf(n); } }
Enter fullscreen mode Exit fullscreen mode

because the program is small we are going to use the tree method , take n=3

image-20200919192742044

image-20200919192808057

the output is 1 2 3 because every time I end call I print it

the space complexity is the number of stacks which is O(kn) where k is constant so we write it as O(n)

time complexity is T(n) = T(n-1)+1 it's not form where we can apply master theorem so we gonna use back substitution

T(n) =T(n-1)+1 T(n-1)=T(n-2)+1 T(n-2)=T(n-3)+1 T(n) = T(T(n-2)+1)+1 = T(n-2) +2 = (T(n-3)+1) +2 = T(n-3)+3 = T(n-k)+k = T(n-n)+n = T(0)+n = 1+n = O(n)
Enter fullscreen mode Exit fullscreen mode

so time and space complexity is O(n)

A(n) { if(n>=1) { A(n-1); pf(n); A(n-1); } }
Enter fullscreen mode Exit fullscreen mode

number of recursive calls are

A(3) = 15 = 2^(3+1) - 1 A(2) = 7 = 2^(2+1) - 1 A(1) = 3 = 2^(1+1) - 1 A(n) = (2^n) - 1
Enter fullscreen mode Exit fullscreen mode

this is not the space complexity because the stack will only need 4 cells A(0),A(1),A(2),A(3) in the stack in order to compute it where the stack will start to empty it self every time it reach A(0) , so it's (n+1)*k where k is the size occupied by one cell in stack so space complexity is nothing more than O(nk) = O(n).

To optimize it We can use Dynamic programming which is to store the already computed values for not compute them again.

A(n) -> T(n) { if(n>=1) { A(n-1); -> T(n-1) pf(n); -> 1 A(n-1); -> T(n-1) } }
Enter fullscreen mode Exit fullscreen mode 
T(n) = 2*T(n-1)+1 ; n > 0 T(n-1) = 2*T(n-2)+1 T(n-2) = 2*T(n-3)+1 T(n) = 2(2T(n-2)+1) = 4T(n-2)+2+1 = 4(2T(n-3)+1)+2+1 = 8T(n-3)+7 = 2^k * T(n-k) + 2^(k-1)+...+2^2+2+1 = 2^n * T(0)+2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1 = 2^n + 2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1 = O(2^n+1) = O(2^n)
Enter fullscreen mode Exit fullscreen mode

the time complexity is very big O(2^n) we can lower it with Dynamic Programming as we said.

Top comments (0)