Program to find out the critical and pseudo-critical edges in a graph in Python

Suppose, we are given a graph that contains n vertices numbered 0 to n -1. The graph is undirected and each edge has a weight. So given the graph, we have to find out the critical and the pseudo-critical edges in the graphs MST. An edge is called a critical edge if deletion of that edge causes the MST weight to increase. A pseudo-critical edge is an edge that can appear in all the graphs MSTs, but not all. We find out the index of the edges given the graph as input.

So, if the input is like

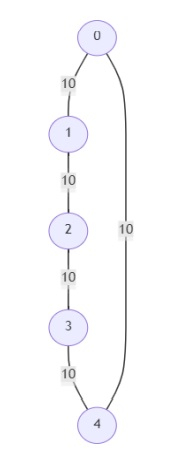
and number of vertices is 5, then the output will be [[], [0, 1, 2, 3, 4]] There are no critical edges in the given graph and all the edges are pseudo-critical. As all the edges have the same weight, any 3 edges from the graph will make an MST.

To solve this, we will follow these steps −

• Define a function find_mst() . This will take num_vertices, graph, init := null, exl := null

• Define one helper function visit() . This will take u

• k[u] := True

• for each v, w in of graph[u, an empty list], do

  • if exl and u is in exl and v is in exl, then

    • go for next iteration

  • if not k[v] is True, then

    • push triplet (w,u,v) into heap tmp

• res := 0

• k := a new list of size num_arrays containing value False

• tmp := a new heap

• if init is non-null, then

  • u := init

  • v := init

  • w := init

  • res := res + w

  • k[u] := True

  • k[v] := True

  • visit(u) or visit(v)

• otherwise,

  • visit(0)

• while tmp is not empty, do

  • w := pop smallest item from heap tmp

  • u := pop smallest item from heap tmp

  • v := pop smallest item from heap tmp

  • if k[u] and k[v] is non-zero, then

    • go for next iteration

  • res := res + w

  • if not k[u] is True, then

    • visit(u)

  • if not k[v] is True, then

    • visit(v)

• return res if all of k are True, otherwise return infinity

• From the main method, do the following:

• graph := given graph

• temp := find_mst(num_vertices, graph)

• c_edge := a new list

• p_edge := a new list

• for i in range 0 to size of edges, do

  • if find_mst(num_vertices, graph, exl = edges[i, index 2 to end]) > temp, then

    • insert i at the end of c_edge

  • otherwise, if find_mst(num_vertices, graph, init = edges[i]) is same as temp, then

    • insert i at the end of p_edge

• return [c_edge, p_edge]

Example

Let us see the following implementation to get better understanding

from heapq import heappop, heappush def solve(num_vertices, edges):    graph = dict()    for u, v, w in edges:       graph.setdefault(u, []).append((v, w))       graph.setdefault(v, []).append((u, w))    temp = find_mst(num_vertices, graph)    c_edge, p_edge = [], []    for i in range(len(edges)):       if find_mst(num_vertices, graph, exl = edges[i][:2]) > temp:          c_edge.append(i)       elif find_mst(num_vertices, graph, init = edges[i]) == temp:          p_edge.append(i)    return [c_edge, p_edge] def find_mst(num_vertices, graph, init = None, exl = None):    def visit(u):       k[u] = True       for v, w in graph.get(u, []):          if exl and u in exl and v in exl:             continue          if not k[v]:             heappush(tmp, (w, u, v))    res = 0    k = [False] * num_vertices    tmp = []    if init:     u, v, w = init res += w k[u] = k[v] = True visit(u) or visit(v) else: visit(0) while tmp: w, u, v = heappop(tmp) if k[u] and k[v]: continue res += w if not k[u]: visit(u) if not k[v]: visit(v) return res if all(k) else inf print(solve(5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]))

Input

5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]] 

Output

[[], [0, 1, 2, 3, 4]]