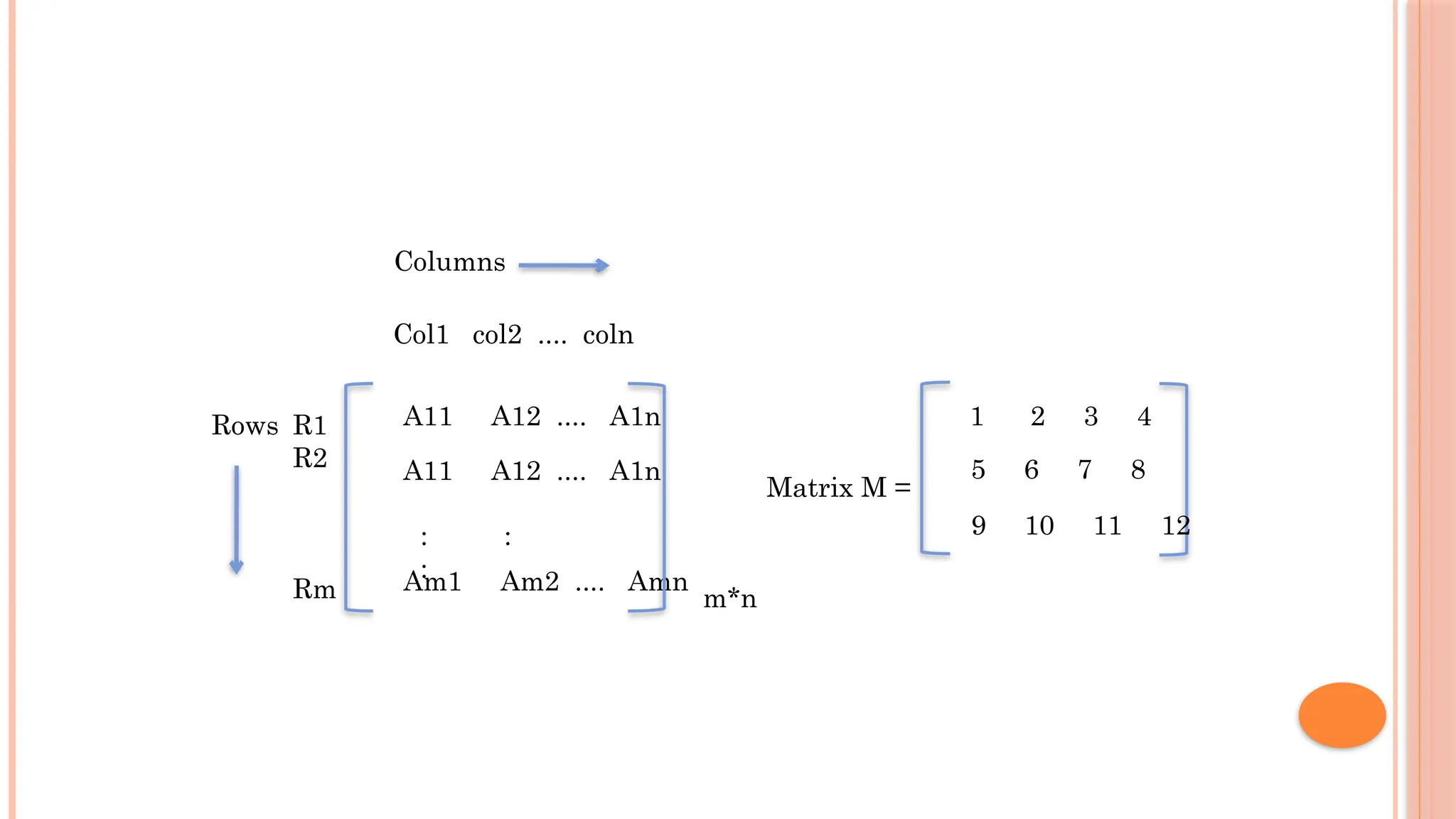
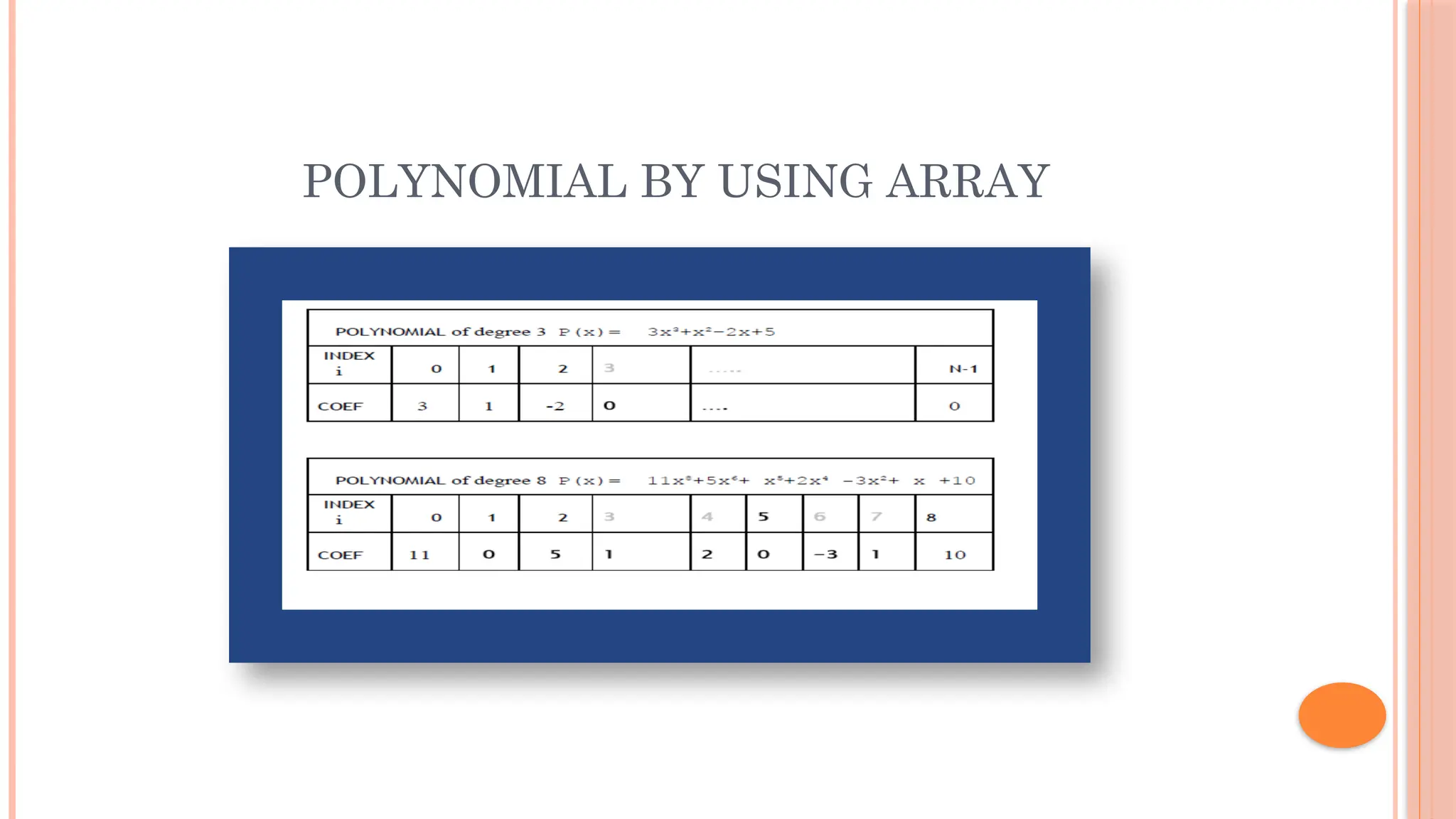
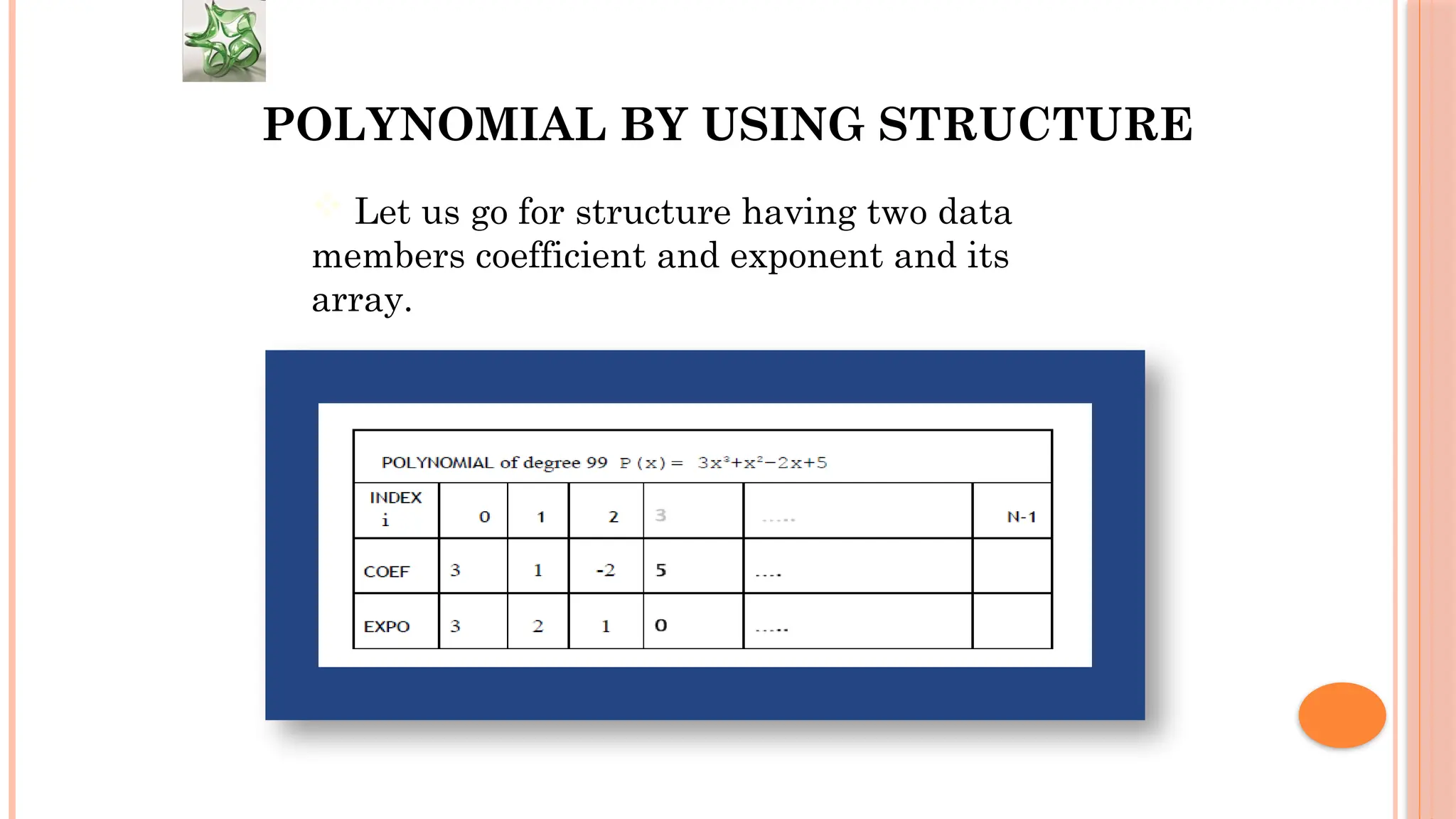
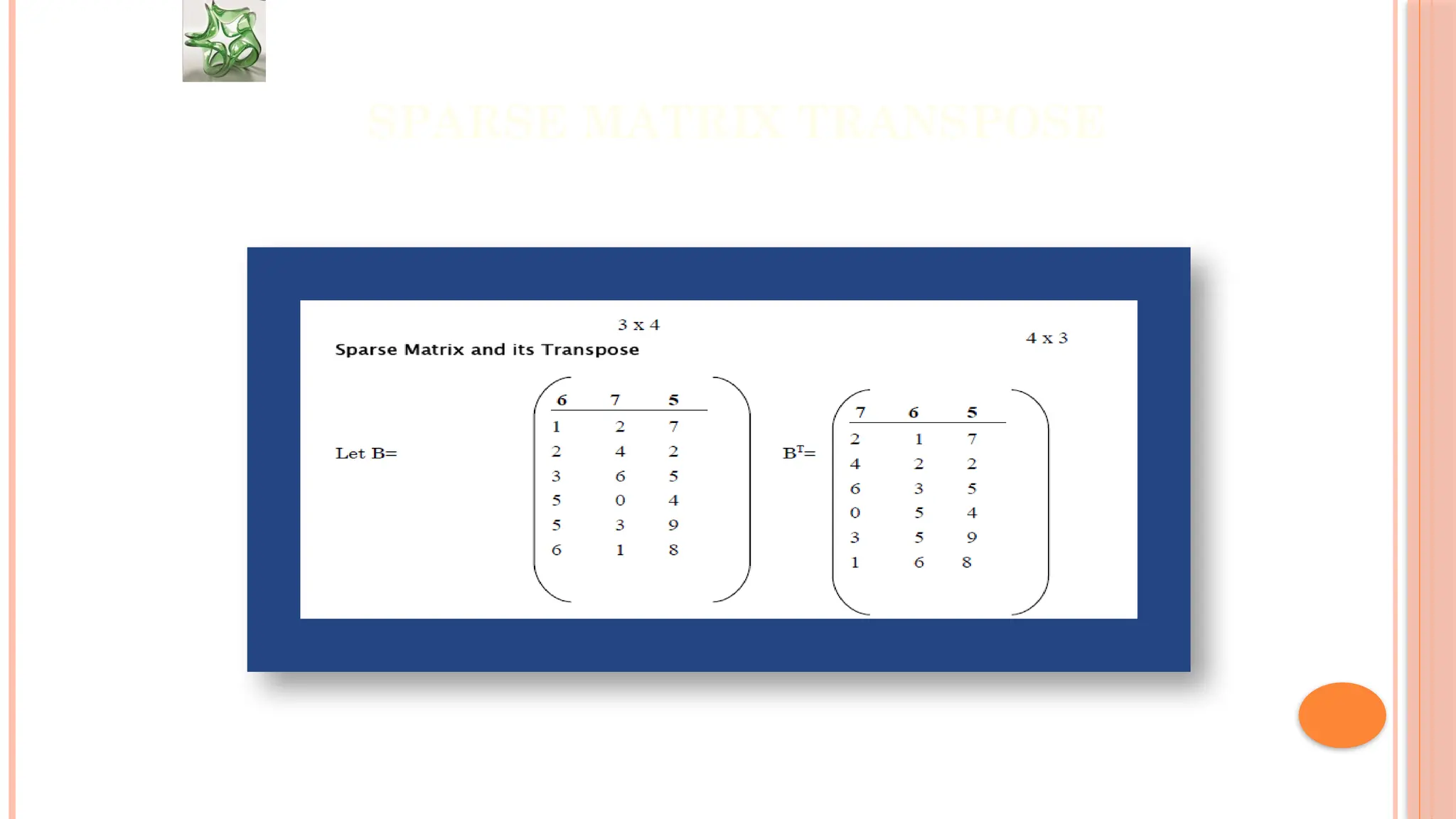
The document discusses linear data structures, particularly arrays, emphasizing their sequential organization and operations such as creation, storage, and access. It covers memory representation, including row-major and column-major formats for multi-dimensional arrays, and the concept of ordered lists and polynomial representations. Additionally, it outlines the advantages and disadvantages of arrays as a fundamental data structure in computer science.


![ARRAYS If we intend to store a group of data together in a sequential manner in computer’s memory, then arrays can be one of the possible data structures. An array is a finite ordered collection of homogeneous data elements which provides direct access (or random access) to any of its elements. An array as a data structure is defined as a set of pairs (index, value) such that with each index a value is associated. • index — indicates the location of an element in an array. • value - indicates the actual value of that data element. • Declaration of an array in ‘C++’: int A[20];](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-3-2048.jpg)





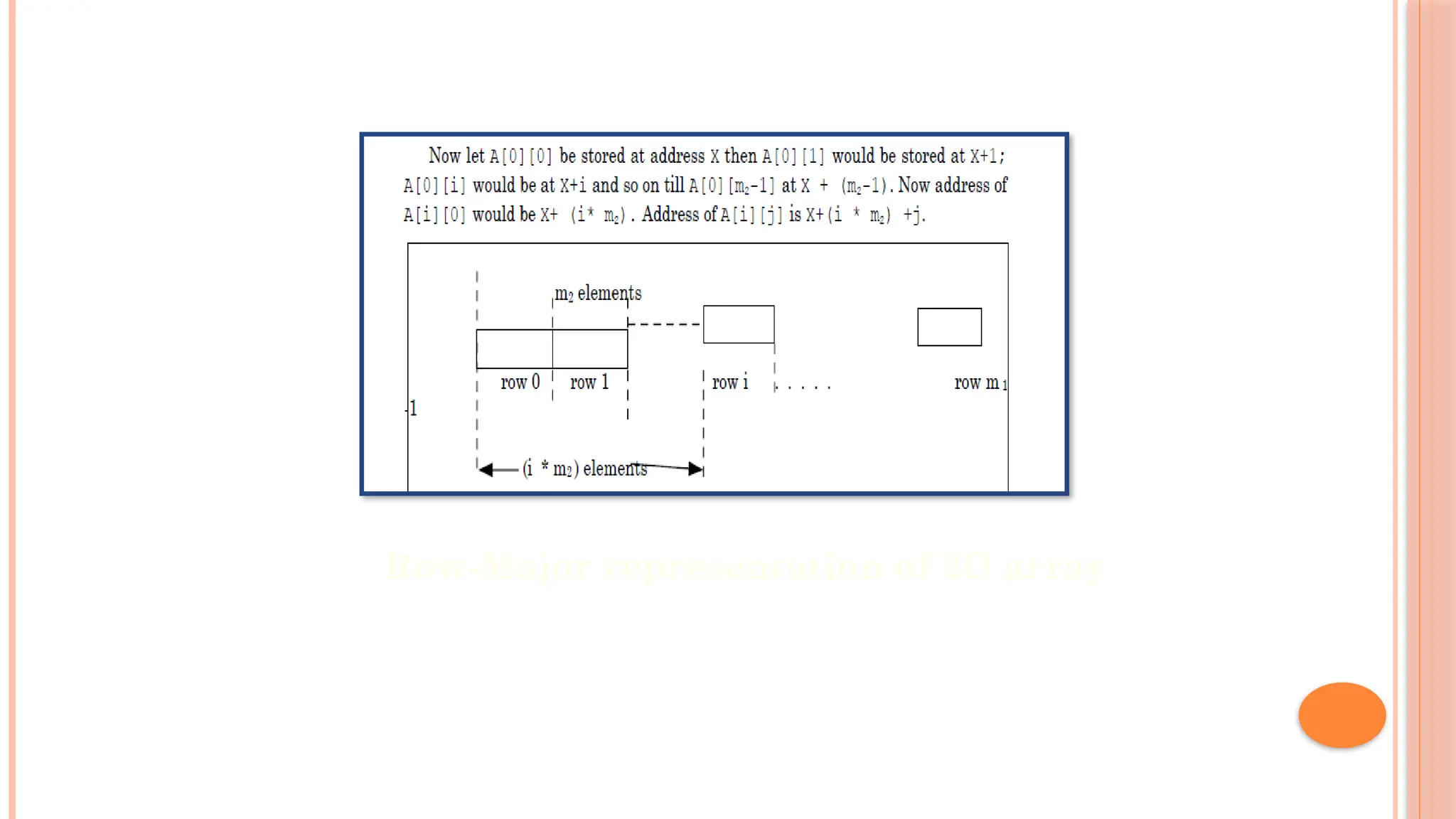
![ROW MAJOR ARRANGEMENT Address of A[i][j] = base addr + (col_index * total no. of rows + row_index) element size Row 0 Row 1 Row m-1 Row 0 Row 1 Row m-1 Memory Location Row-major arrangement in memory , in row major representation](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-10-2048.jpg)
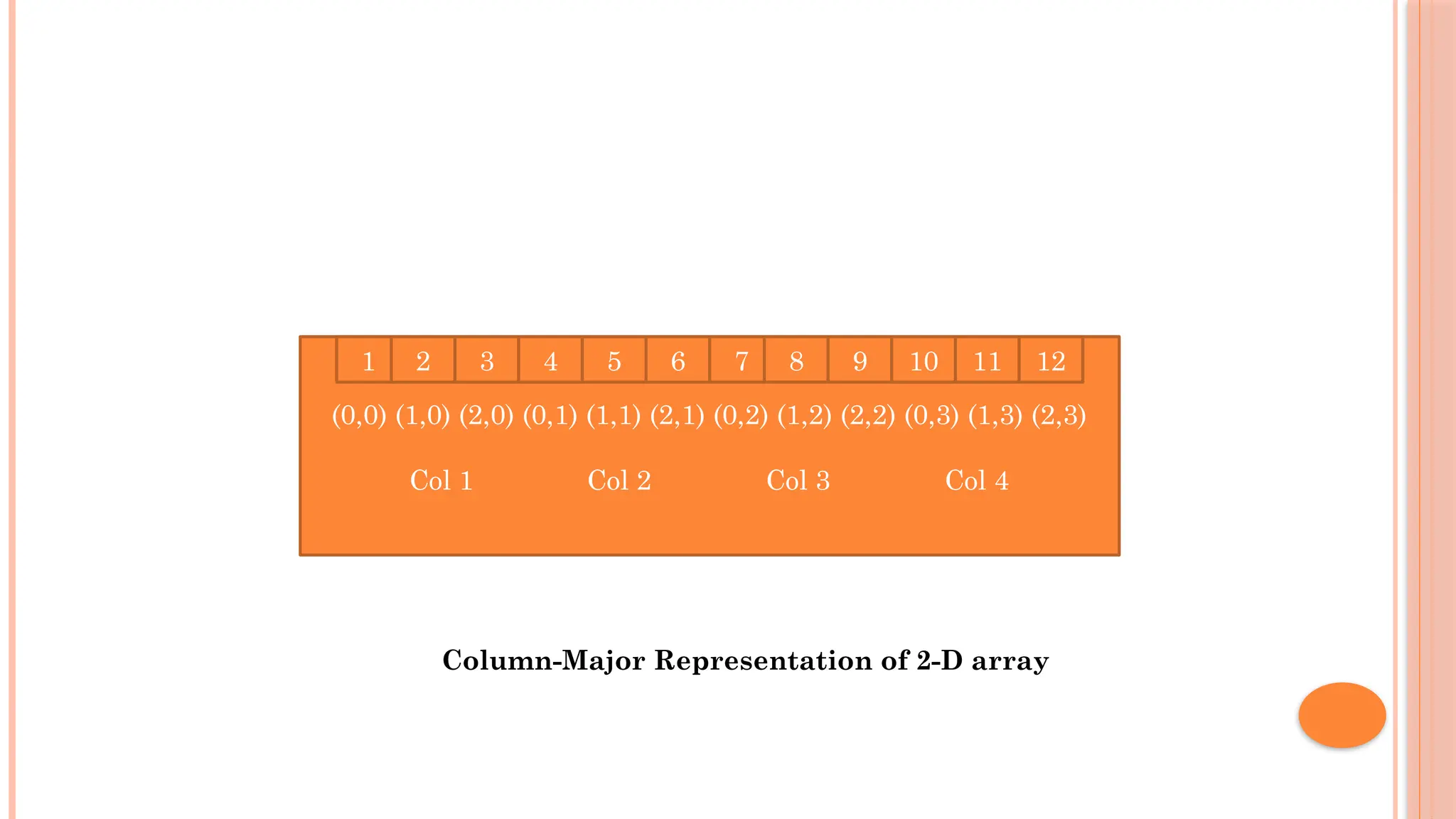
![COLUMN-MAJOR ARRANGEMENT Address of A[i][j] = base addr + (row_index * total no. of columns + col_index) *element size col1 col2 Col n-1 Col 0 Col 1 Col 2 Memory Location … Column-major arrangement in memory , in column major representation](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-11-2048.jpg)


![Three dimensions row-major arrangement (i*m2*m3) elements A[0][m2][m3] A[1][m2][m3] A[i][m2][m3] A[m1-1][m2]](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-16-2048.jpg)








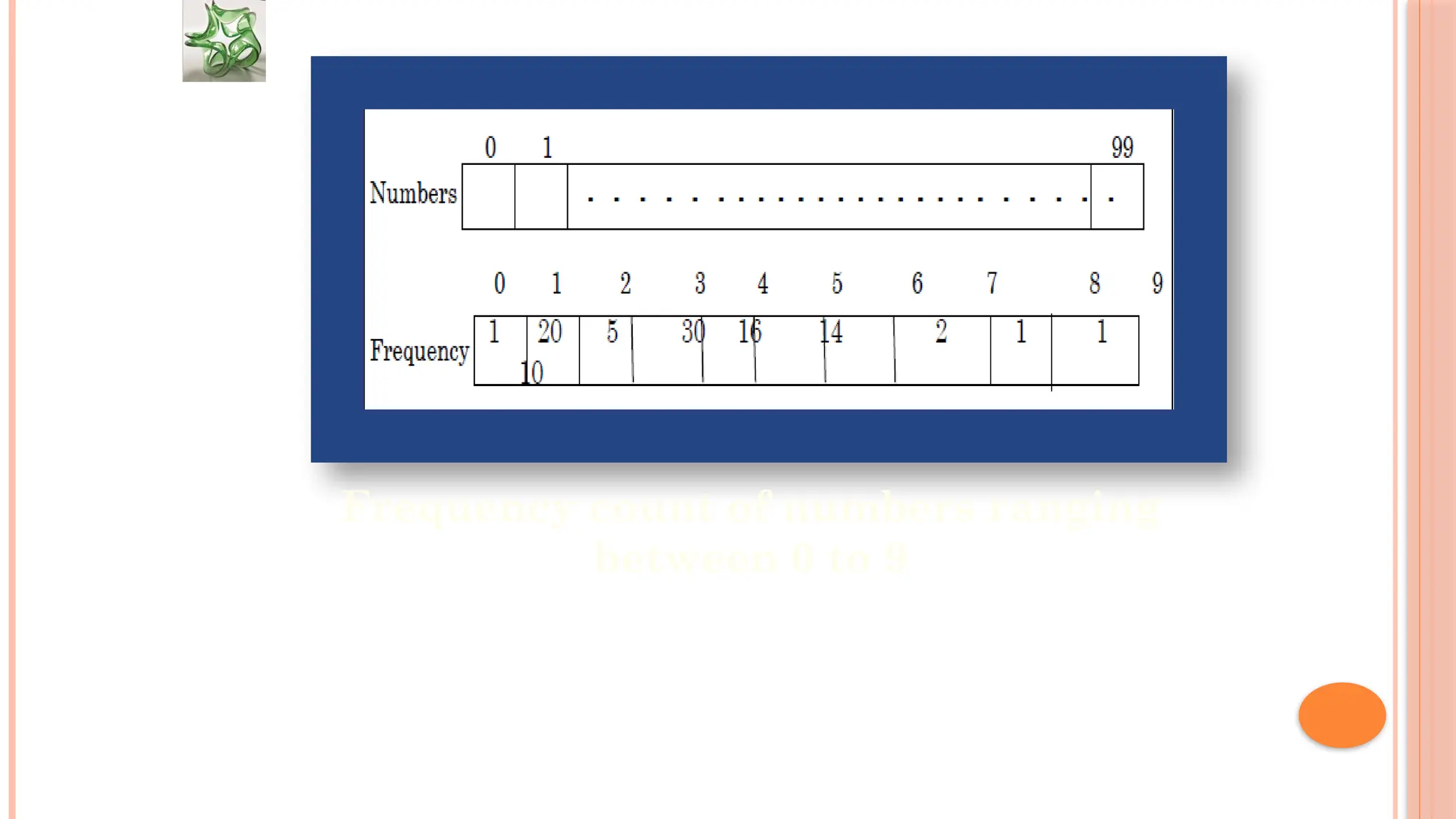
![AN ARRAY FOR FREQUENCY COUNT We can use array to store the number of times a particular element occurs in any sequence. Such occurrence of particular element is known as frequency count. void Frequency_Count ( int Freq[10 ], int A [ 100]) { int i; for ( i=0;i<10;i++) Freq[i]=0; for ( i=0;i<100;i++) Freq[A[i] ++; }](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-27-2048.jpg)








![BASICALLY A STRING IS STORED AS A SEQUENCE OF CHARACTERS IN ONE-DIMENSIONAL CHARACTER ARRAY SAY A. CHAR A[10] ="STRING" ; EACH STRING IS TERMINATED BY A SPECIAL CHARACTER THAT IS NULL CHARACTER ‘0’. THIS NULL CHARACTER INDICATES THE END OR TERMINATION OF EACH STRING.](https://image.slidesharecdn.com/u2-250119152234-c721e773/75/U2-pptx-Advanced-Data-Structures-and-Algorithms-38-2048.jpg)



