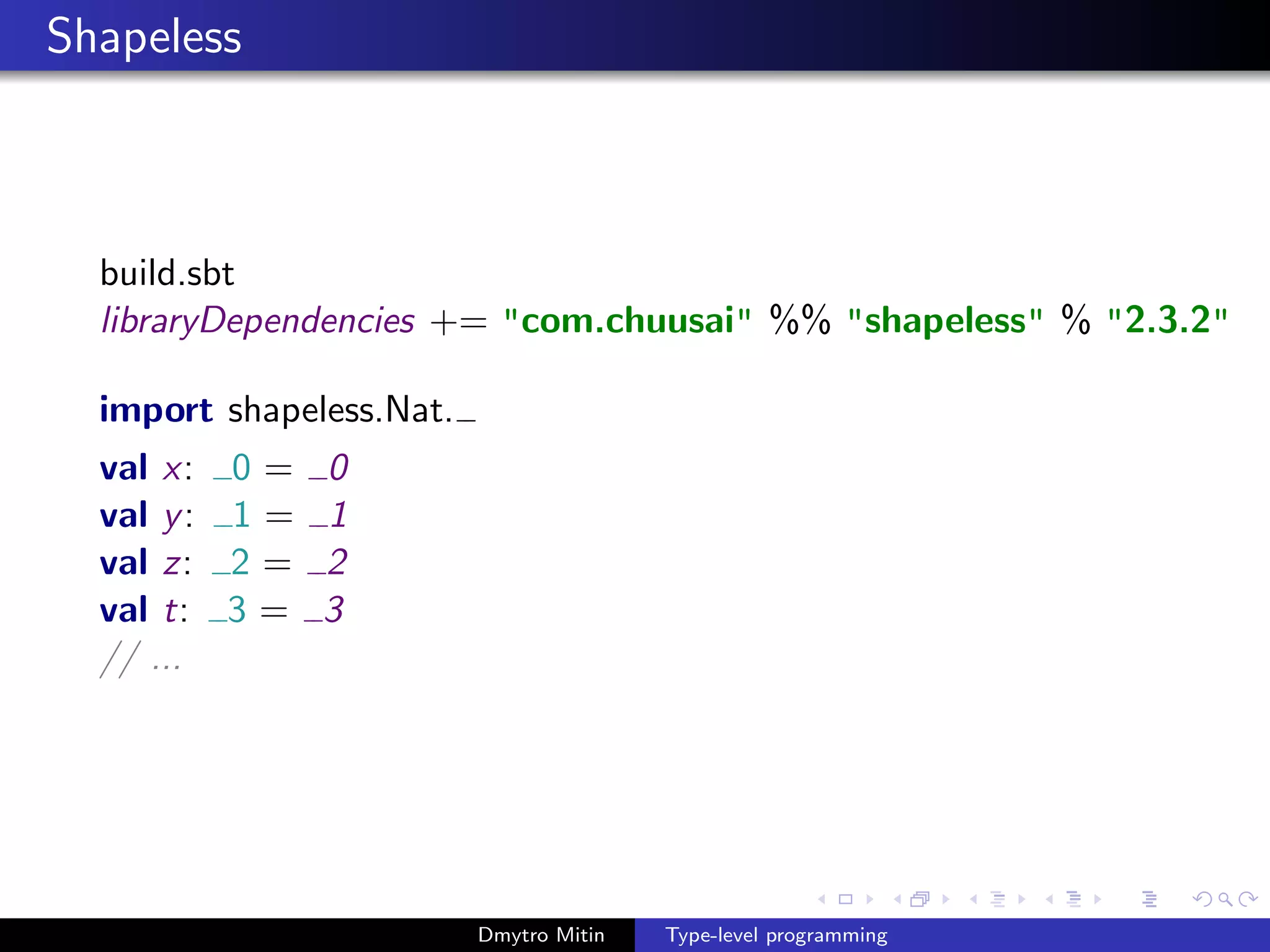
This document discusses type-level programming in Scala, including defining type-level versions of booleans, natural numbers, and functions like factorials and Fibonacci numbers. It shows how to represent true and false as types True and False with type-level operations like not, &&, and ||. It also defines a type-level representation of natural numbers using sealed traits like Nat and Succ, and shows how to define type-level factorials and Fibonacci functions recursively over these number types. Finally, it mentions using the Shapeless library to work with type-level numbers.
![Type-level programming Value level Type level ADT values: val x object X Members: def x, val x type X def f(x) type F[X] a.b A#B x : T X <: T new A(b) A[B] Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-2-2048.jpg)
: C } case object True extends Bool { def not: Bool = False def &&(b: Bool): Bool = b def ||(b: Bool): Bool = True def ifElse[C](t: => C, f: => C): C = t } case object False extends Bool { def not: Bool = True def &&(b: Bool): Bool = False def ||(b: Bool): Bool = b def ifElse[C](t: => C, f: => C): C = f } Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-3-2048.jpg)
![Type-level booleans sealed trait Bool { type Not <: Bool type && [B <: Bool] <: Bool type || [B <: Bool] <: Bool type IfElse[C, T <: C, F <: C] <: C } type True = True.type type False = False.type case object True extends Bool { type Not = False type && [B <: Bool] = B type || [B <: Bool] = True type IfElse[C, T <: C, F <: C] = T } Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-4-2048.jpg)
![Type-level booleans case object False extends Bool { type Not = True type && [B <: Bool] = False type || [B <: Bool] = B type IfElse[C, T <: C, F <: C] = F } implicitly[False# Not =:= True] implicitly[(True# && [False]) =:= False] implicitly[(True# || [False]) =:= True] implicitly[False# IfElse[Any, Int, String] =:= String] // compile time! Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-5-2048.jpg)

![Type-level natural numbers sealed trait Nat { type This >: this.type <: Nat type ++ = Succ[This] type + [ <: Nat] <: Nat type * [ <: Nat] <: Nat } final object Zero extends Nat { type This = Zero type + [X <: Nat] = X type * [ <: Nat] = Zero } type Zero = Zero.type final class Succ[N <: Nat] extends Nat { type This = Succ[N] type + [X <: Nat] = Succ[N# + [X]] type * [X <: Nat] = (N# * [X])# + [X] } Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-7-2048.jpg)
![Type-level natural numbers type 0 = Zero type 1 = 0 # ++ type 2 = 1 # ++ type 3 = 2 # ++ type 4 = 3 # ++ type 5 = 4 # ++ type 6 = 5 # ++ type 7 = 6 # ++ type 8 = 7 # ++ implicitly[False# IfElse[Nat, 2, 4] =:= 4] implicitly[ 2# + [ 3] =:= 5] implicitly[ 2# * [ 3] =:= 6] Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-8-2048.jpg)

![Type-level factorial sealed trait Factorial[N <: Nat] { type Res <: Nat } implicit object factorial0 extends Factorial[ 0] { type Res = 1 } implicit def factorial[N <: Nat, X <: Nat](implicit fact: Factorial[N] { type Res = X } ) = new Factorial[Succ[N]] { type Res = X# * [Succ[N]] } implicitly[Factorial[ 0] { type Res = 1 }] implicitly[Factorial[ 1] { type Res = 1 }] implicitly[Factorial[ 2] { type Res = 2 }] implicitly[Factorial[ 3] { type Res = 6 }] Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-10-2048.jpg)
![Type-level Fibonacci numbers sealed trait Fibonacci[N <: Nat] { type Res <: Nat } implicit object fibonacci0 extends Fibonacci[ 0] { type Res = 0 } implicit object fibonacci1 extends Fibonacci[ 1] { type Res = 1 } implicit def fibonacci[N <: Nat, X <: Nat, Y <: Nat](implicit fib1: Fibonacci[N] { type Res = X }, fib2: Fibonacci[Succ[N]] { type Res = Y } ) = new Fibonacci[Succ[Succ[N]]] { type Res = X# + [Y] } implicitly[Fibonacci[ 0] { type Res = 0 }] implicitly[Fibonacci[ 1] { type Res = 1 }] implicitly[Fibonacci[ 2] { type Res = 1 }] implicitly[Fibonacci[ 3] { type Res = 2 }] implicitly[Fibonacci[ 4] { type Res = 3 }] implicitly[Fibonacci[ 5] { type Res = 5 }] implicitly[Fibonacci[ 6] { type Res = 8 }] Dmytro Mitin Type-level programming](https://image.slidesharecdn.com/typelevel-170323115739/75/Type-level-programming-11-2048.jpg)