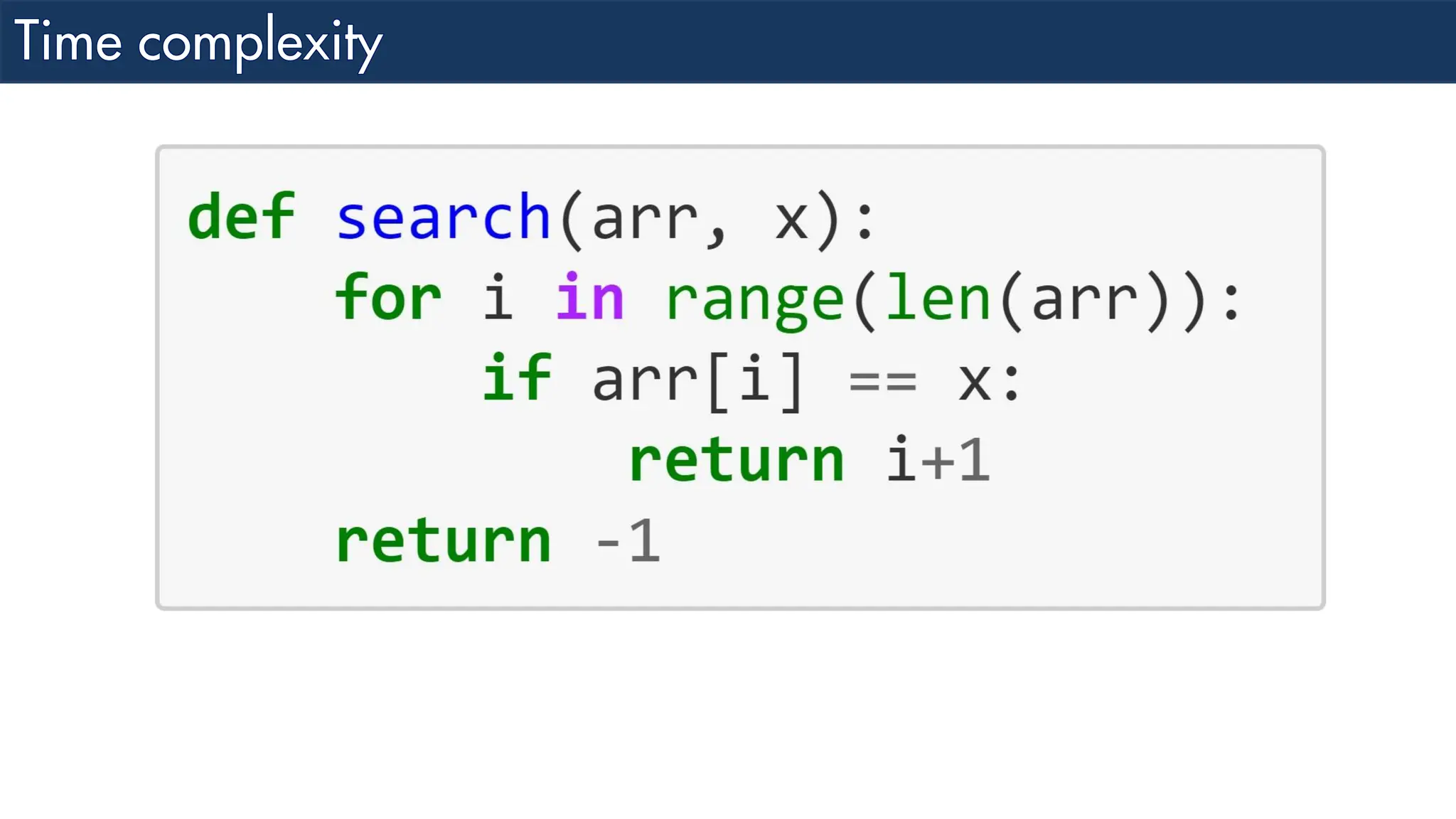
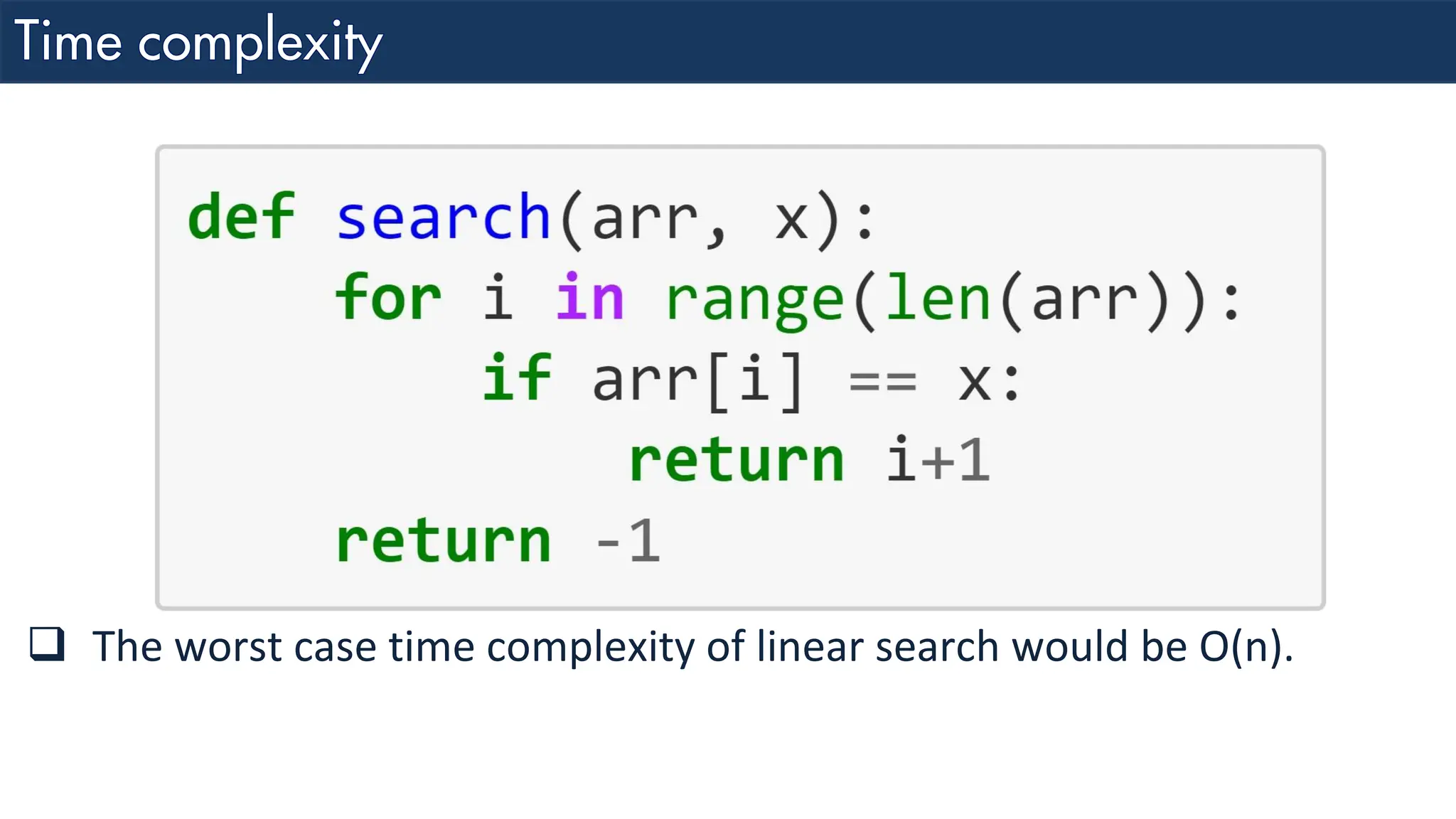
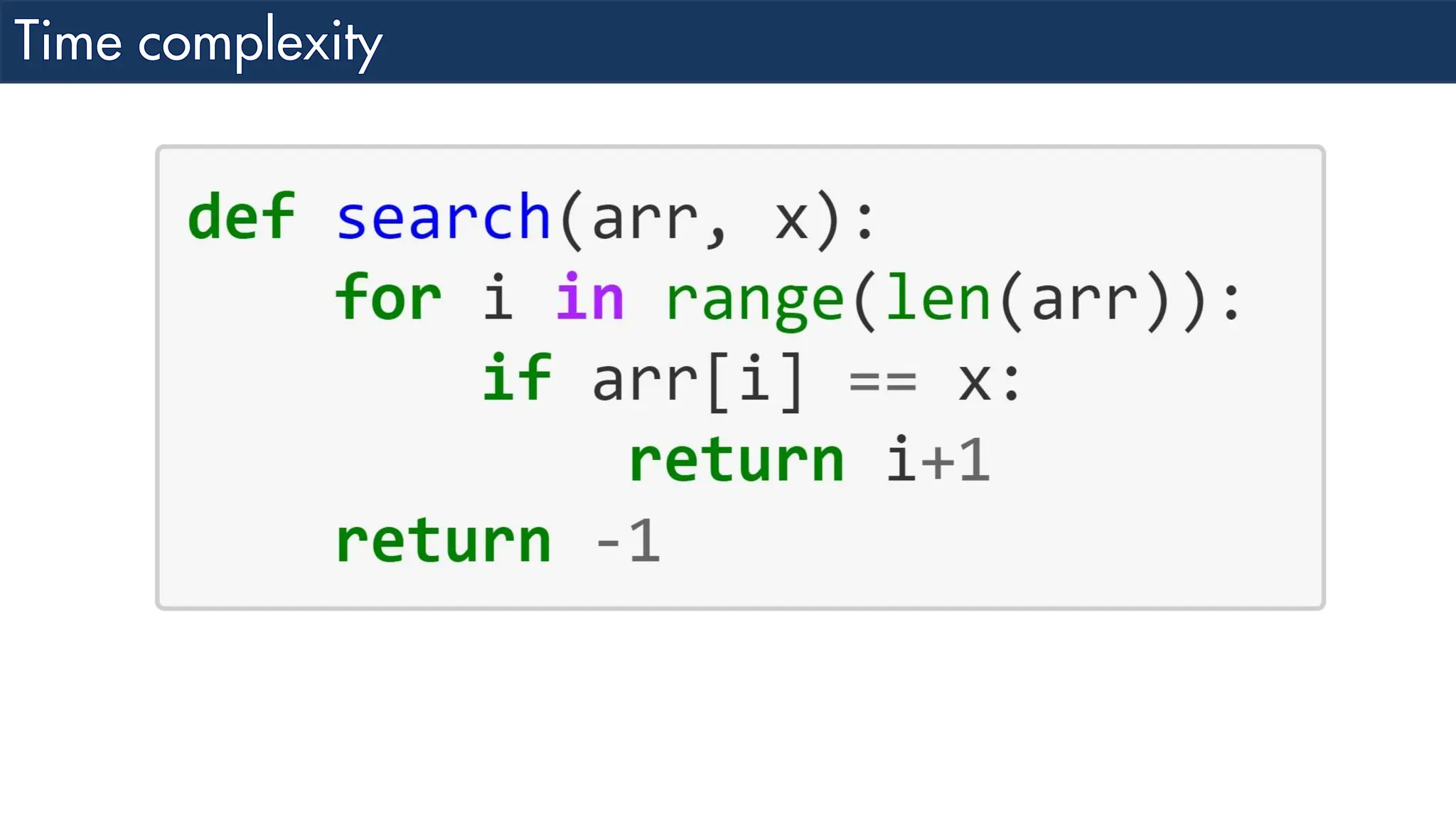
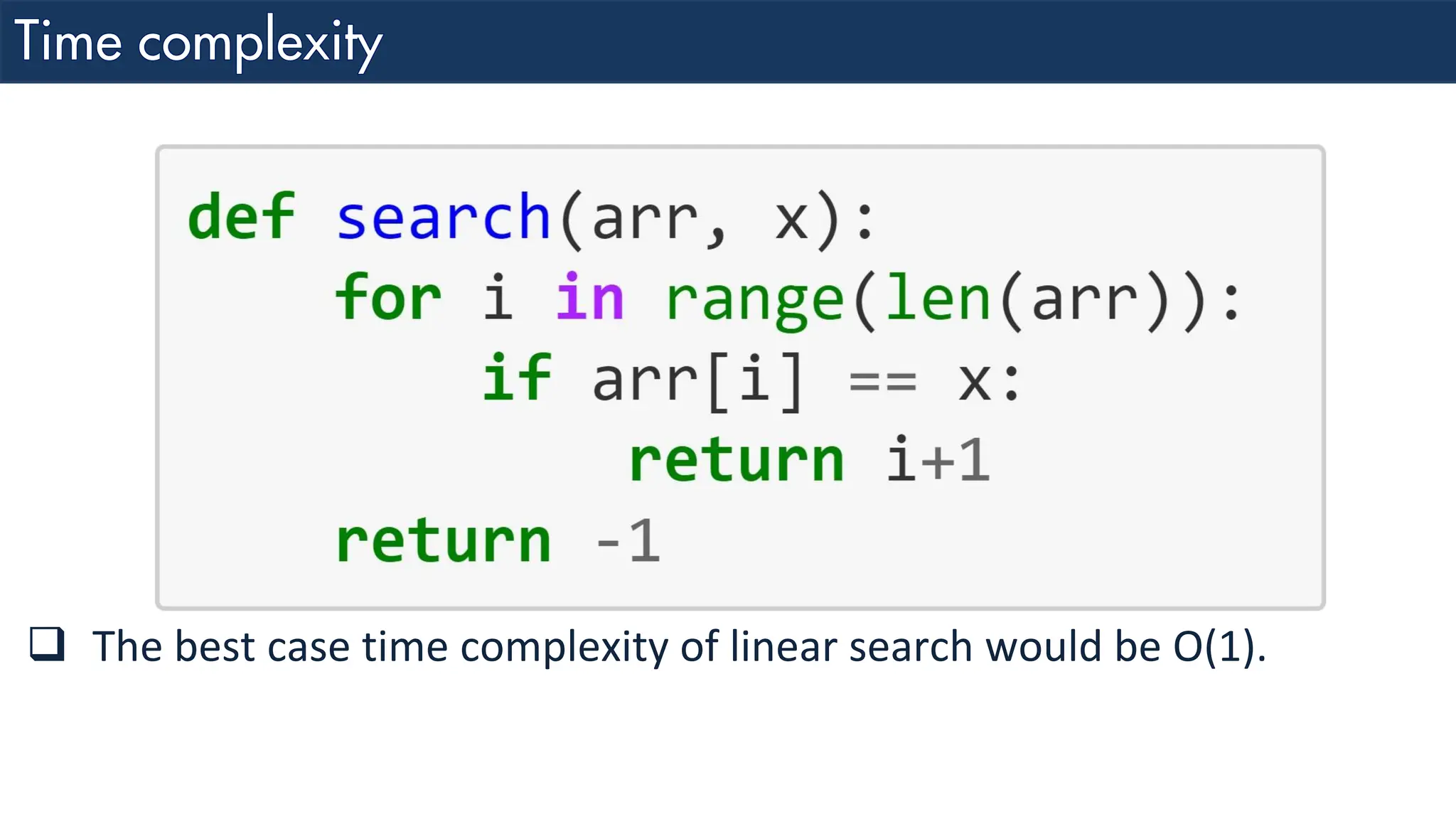
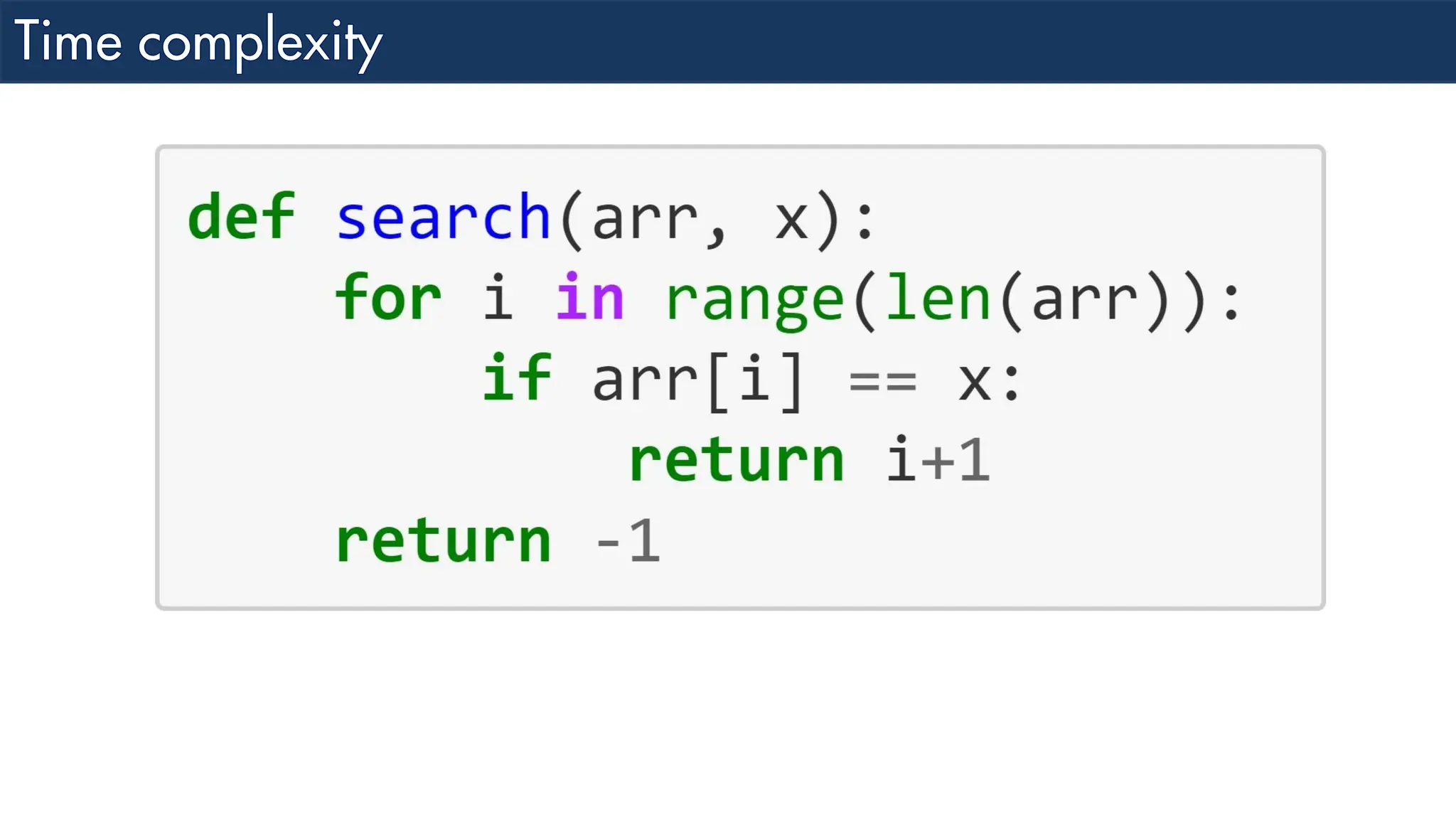
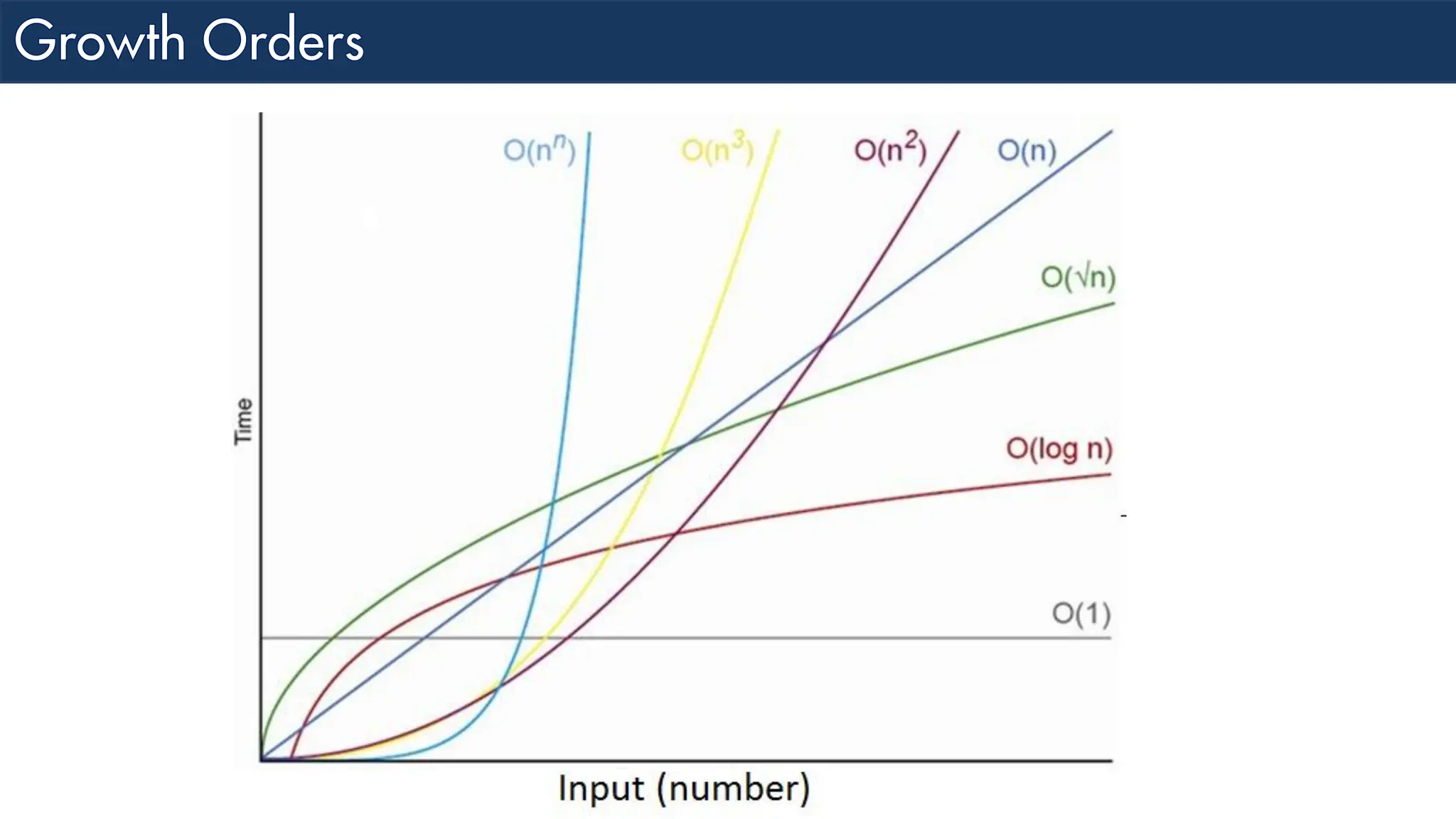
The document discusses the analysis and design of algorithms, focusing on time complexity through worst, average, and best case scenarios. It explains different notations such as Big O, Omega, and Theta for expressing time complexities, as well as examples of linear search in different cases. Additionally, it covers how to combine time complexities of loops and provides insight into specific time complexity calculations.