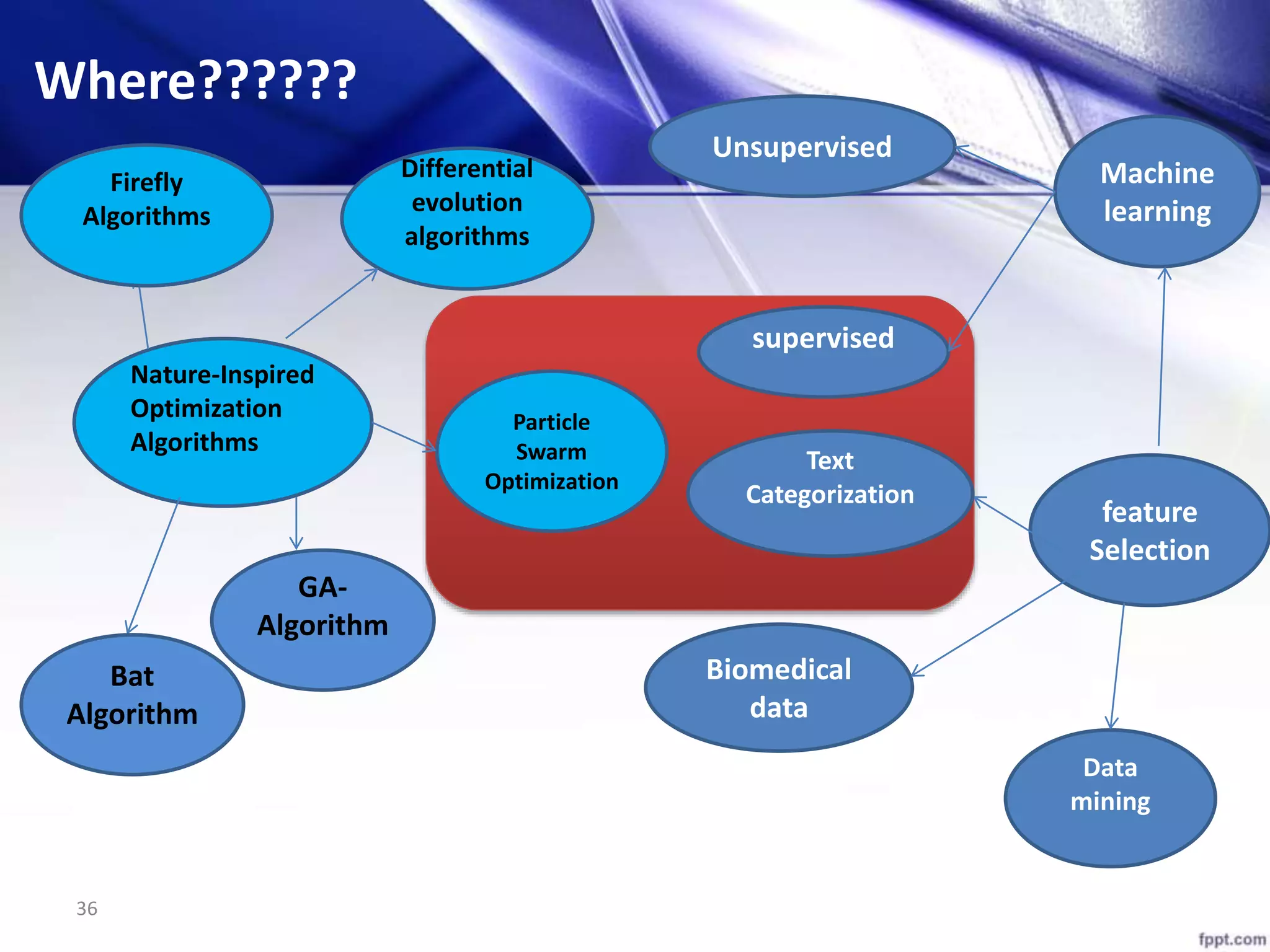
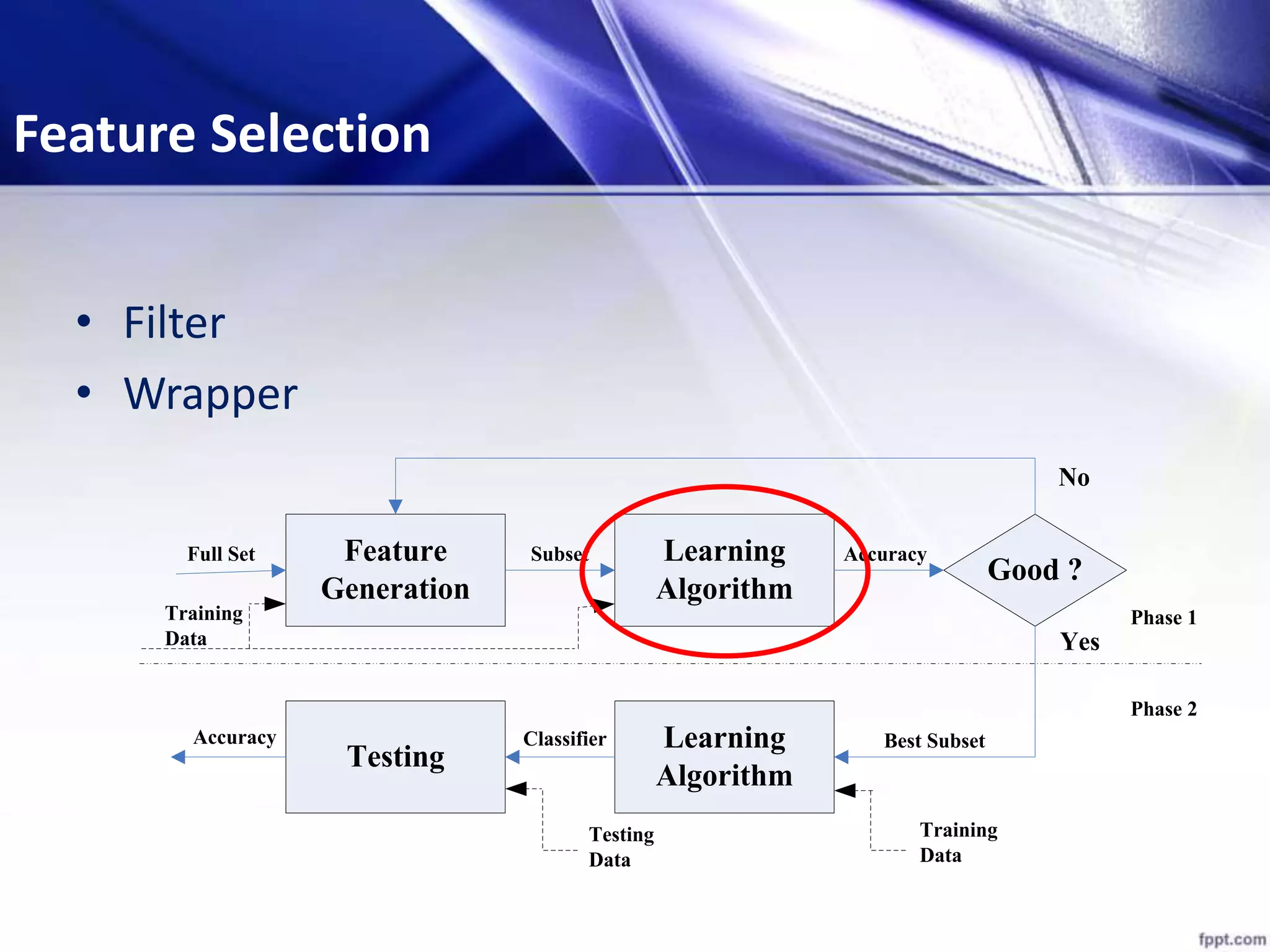
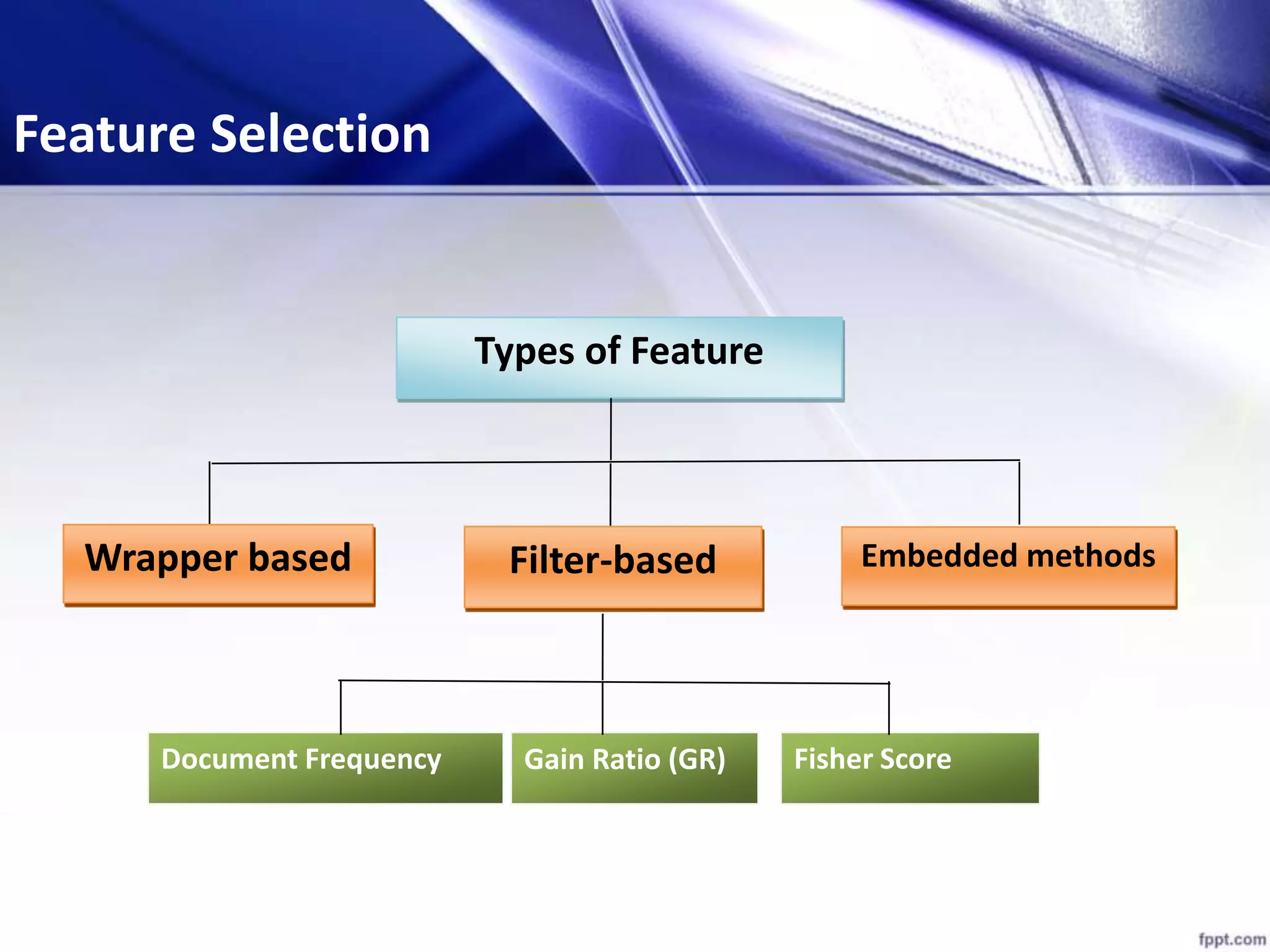
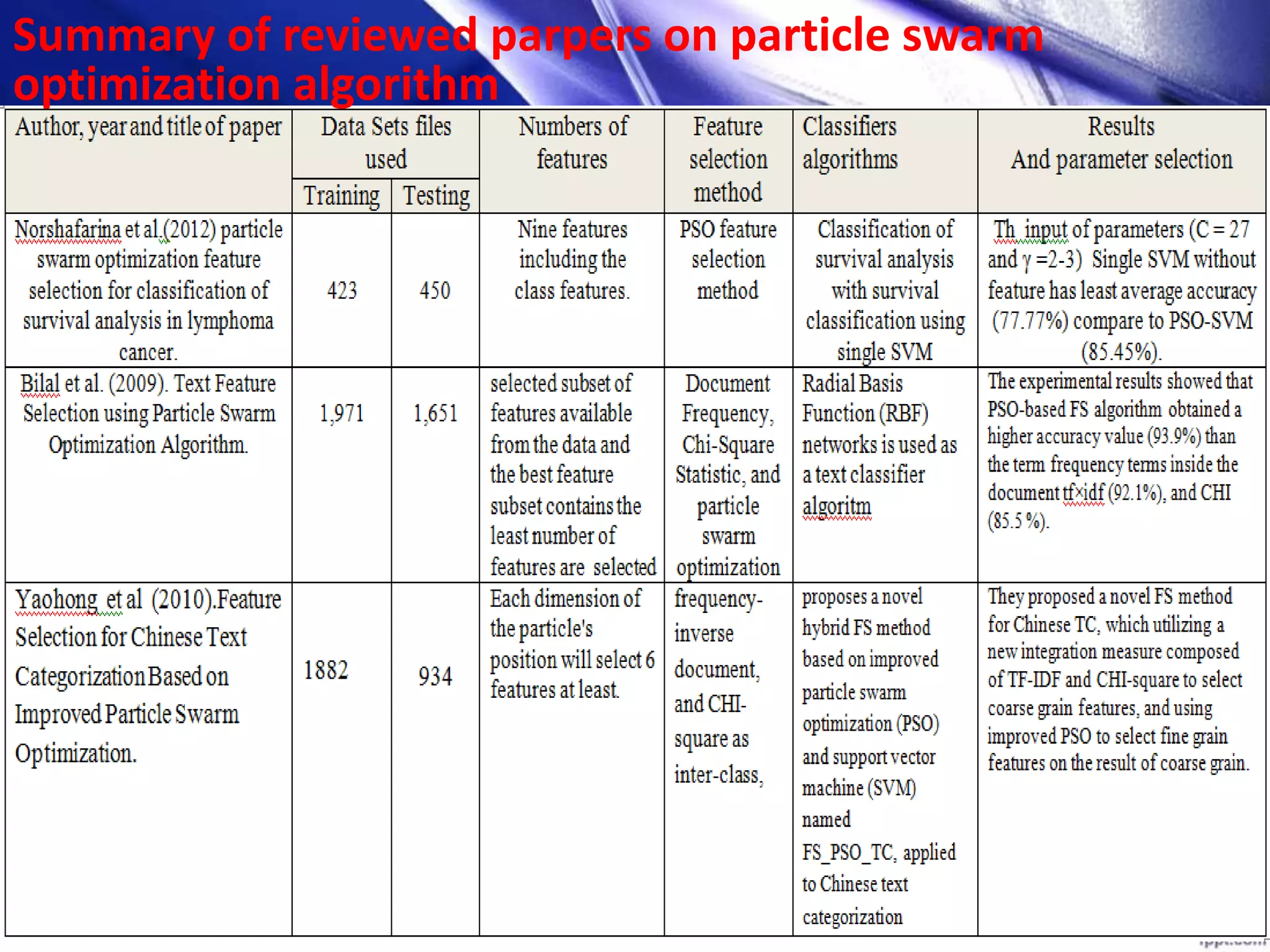
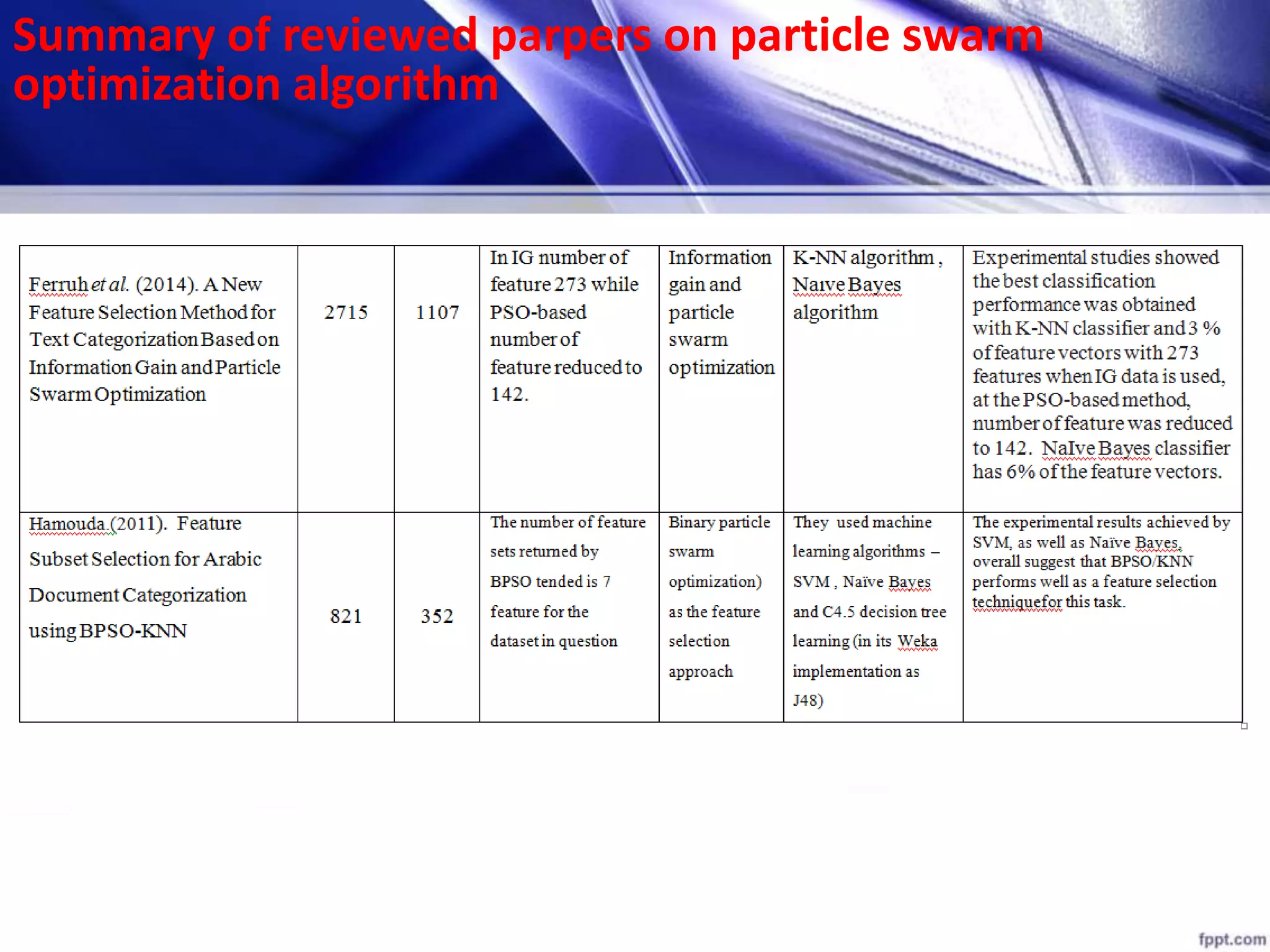
This document discusses using particle swarm optimization (PSO) for feature selection in text categorization. It provides an introduction to PSO, explaining how it was inspired by bird flocking behavior. The document outlines the PSO algorithm, parameters, and concepts like particle velocity and position updating. It also discusses feature selection techniques like filter and wrapper methods and compares different feature utility measures that can be used.











![The following weighting function is usually utilized in (1) w = wMax-[(wMax-wMin) x iter]/maxIter (2) where wMax= initial weight, wMin = final weight, maxIter = maximum iteration number, iter = current iteration number. si k+1 = si k + Vi k+1 (3) CONCEPT OF PSO](https://image.slidesharecdn.com/psofeatureselection-151224171905/75/TEXT-FEUTURE-SELECTION-USING-PARTICLE-SWARM-OPTIMIZATION-PSO-12-2048.jpg)



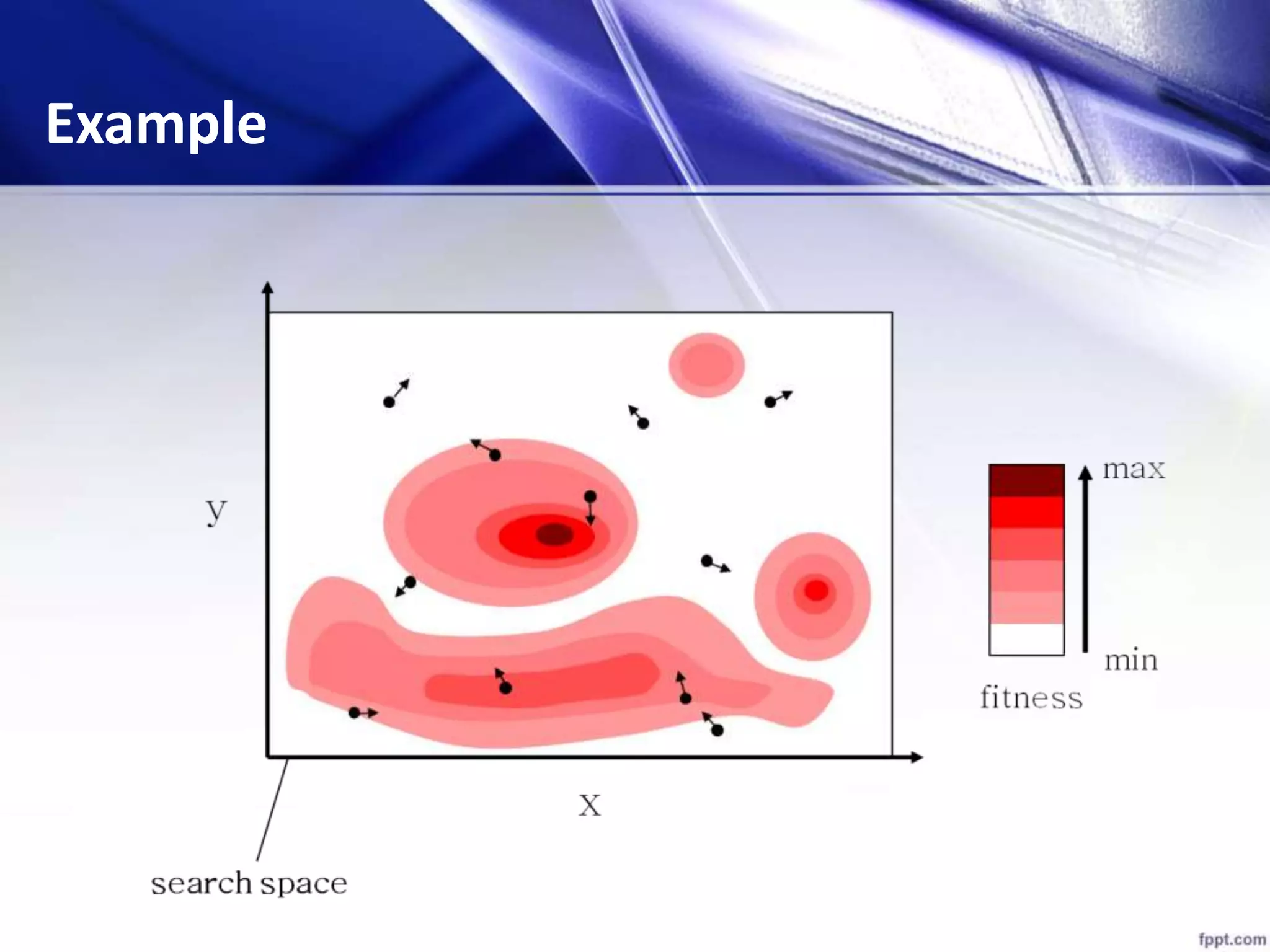
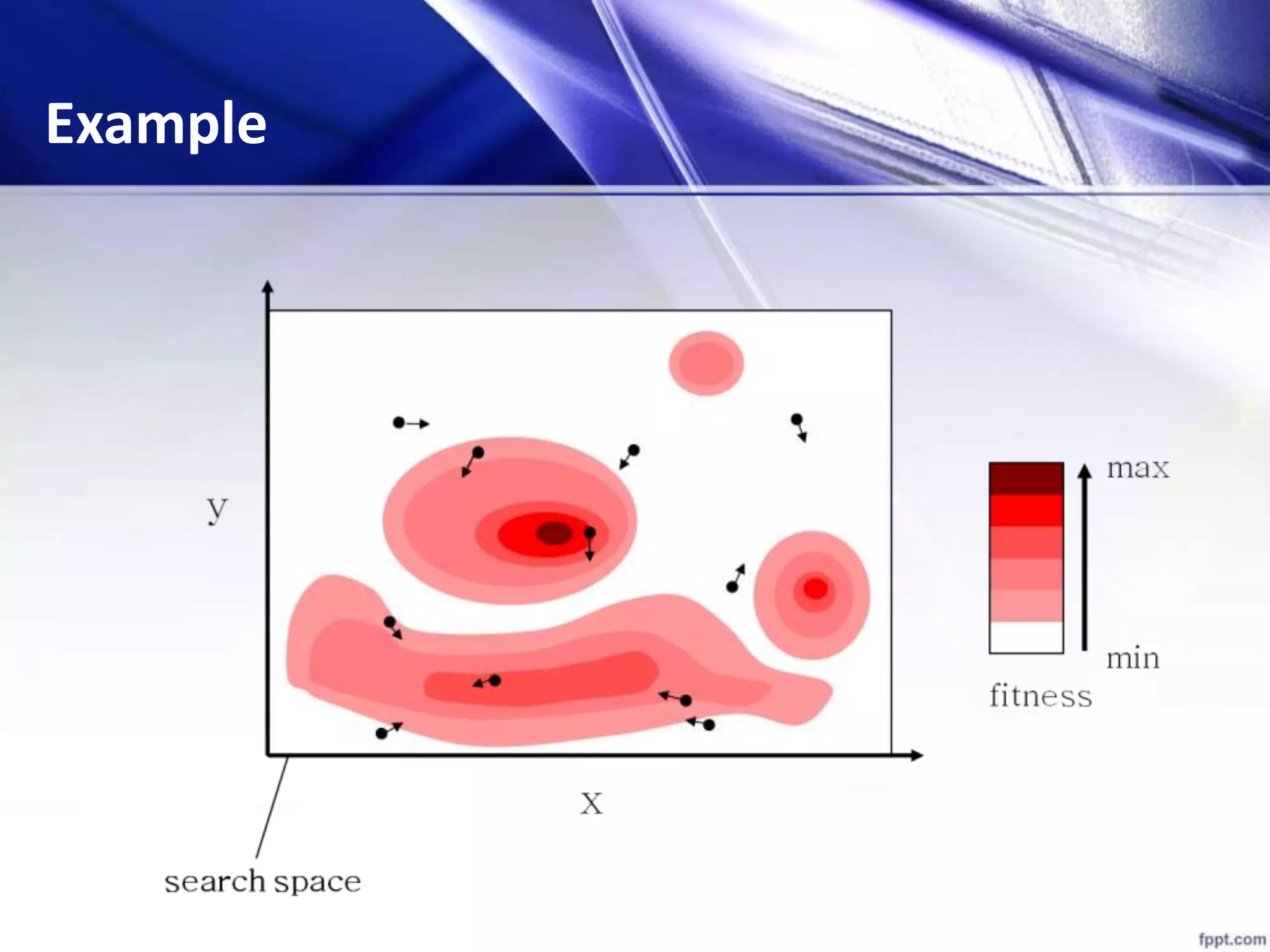

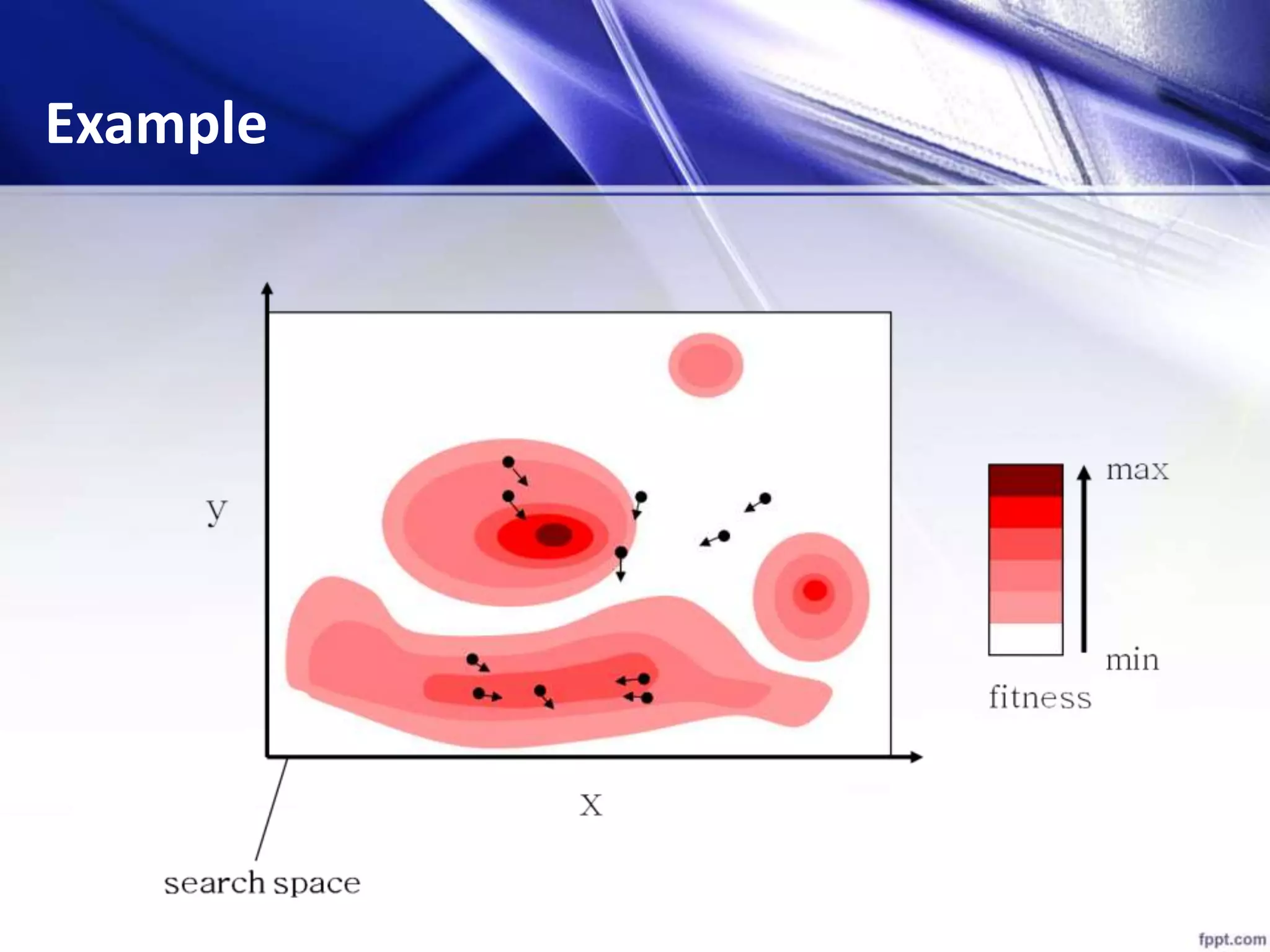
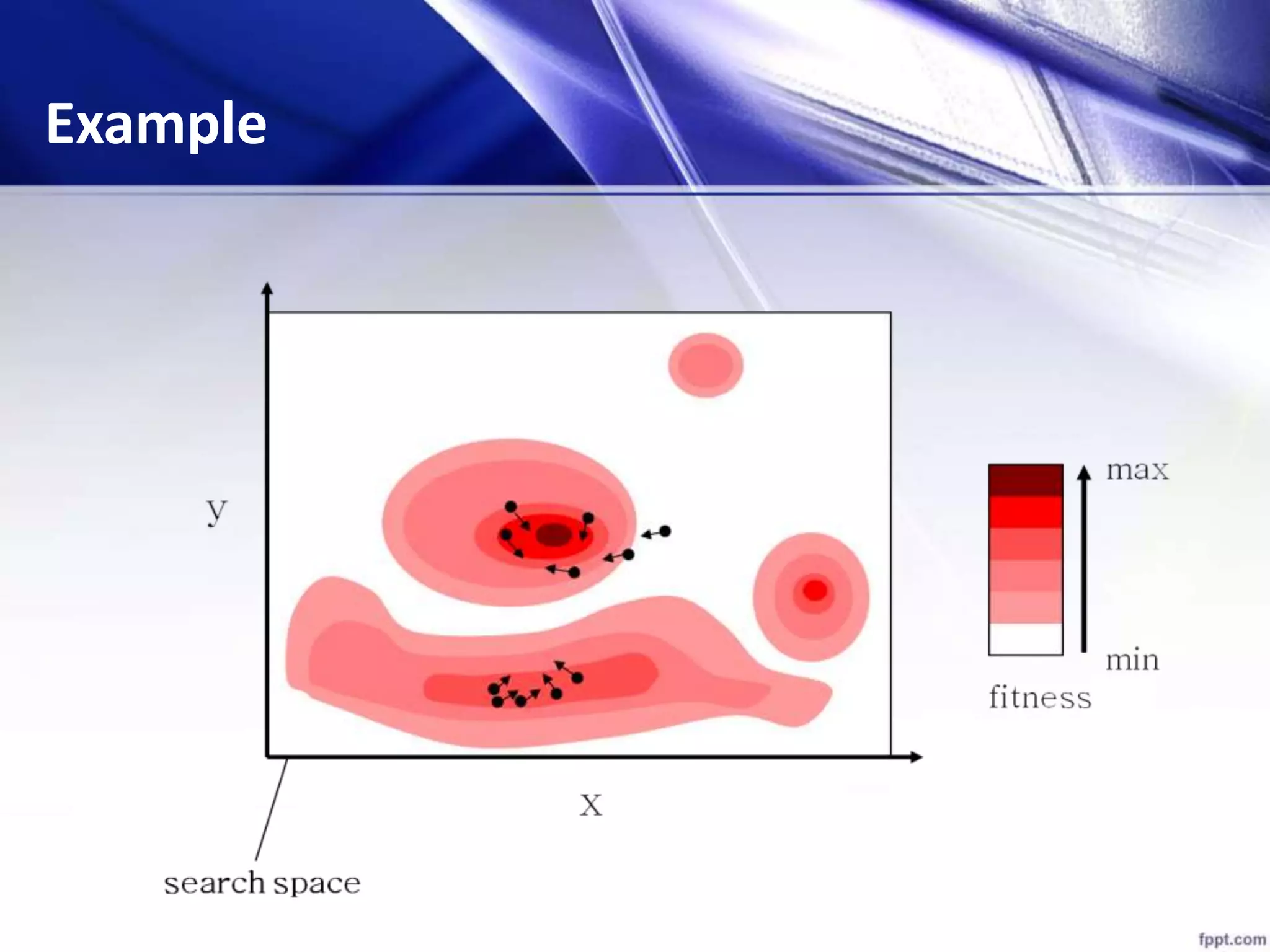


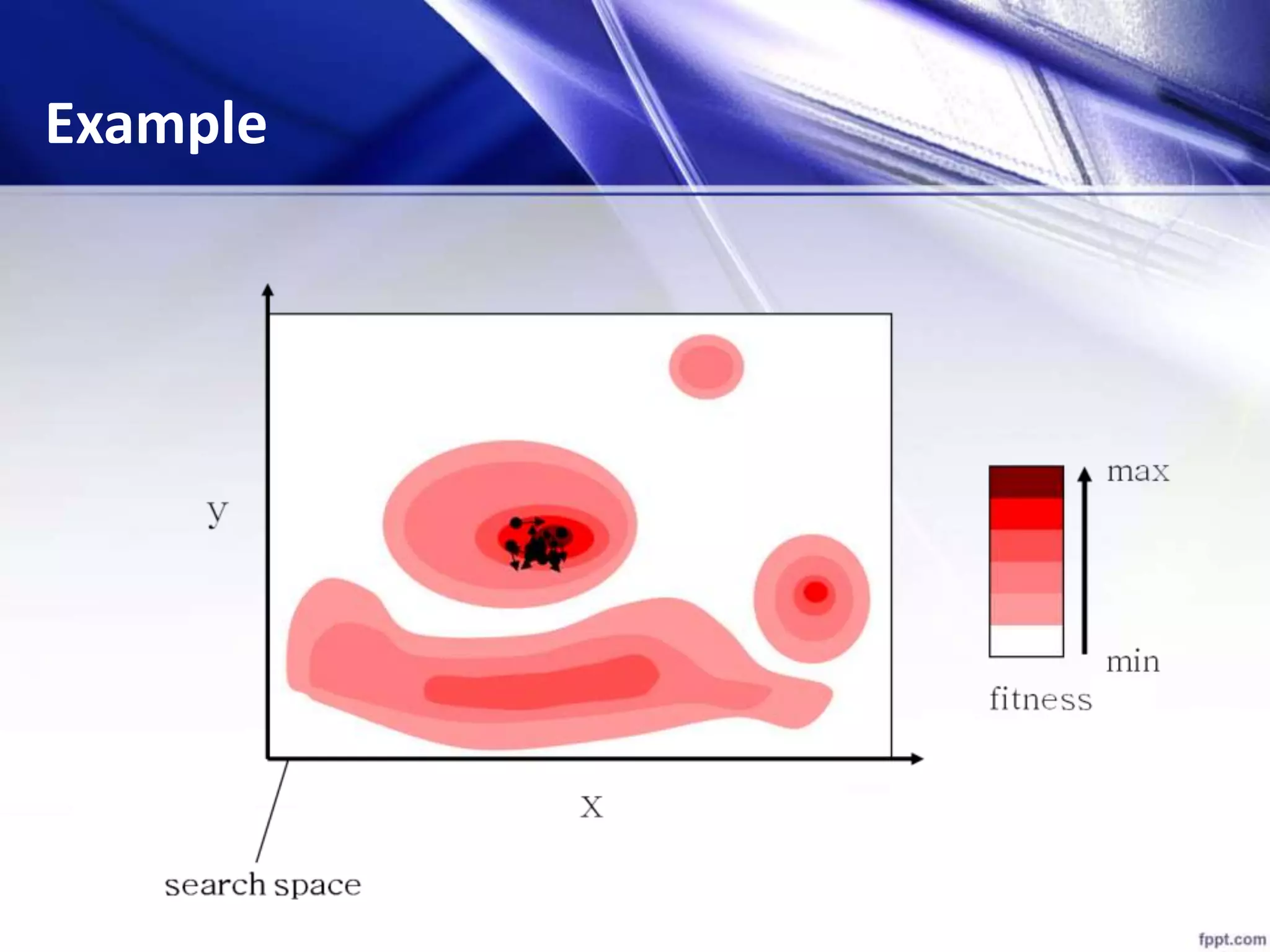

![[x*] = PSO() P = Particle_Initialization(); For i=1 to it_max For each particle p in P do fp = f(p); If fp is better than f(pBest) pBest = p; end end gBest = best p in P; For each particle p in P do v = v + c1*rand*(pBest – p) + c2*rand*(gBest – p); p = p + v; end end Algorithm - Parameters](https://image.slidesharecdn.com/psofeatureselection-151224171905/75/TEXT-FEUTURE-SELECTION-USING-PARTICLE-SWARM-OPTIMIZATION-PSO-25-2048.jpg)