This presentation provides a clear and concise overview of popular string matching algorithms used in computer science, especially in areas like text search, bioinformatics, and compiler design. 🔍 Topics Covered: What is String Matching? Naive Algorithm (Brute Force) Knuth-Morris-Pratt (KMP) Algorithm Rabin-Karp Algorithm


![String Matching •We formalize the string-matching problem as follows. We assume that the text is an array T[1.. n] of length n and that the pattern is an array P[ 1..m] of length m≤ n. •We further assume that the elements of P and T are characters drawn from a finite alphabet . For example, we may have = {0,1} or = ,a, b, …, z-. The character arrays P and T are often called strings of characters.](https://image.slidesharecdn.com/unit5-250505065536-4351080a/75/String-Matching-Algorithms-Naive-KMP-Rabin-Karp-3-2048.jpg)
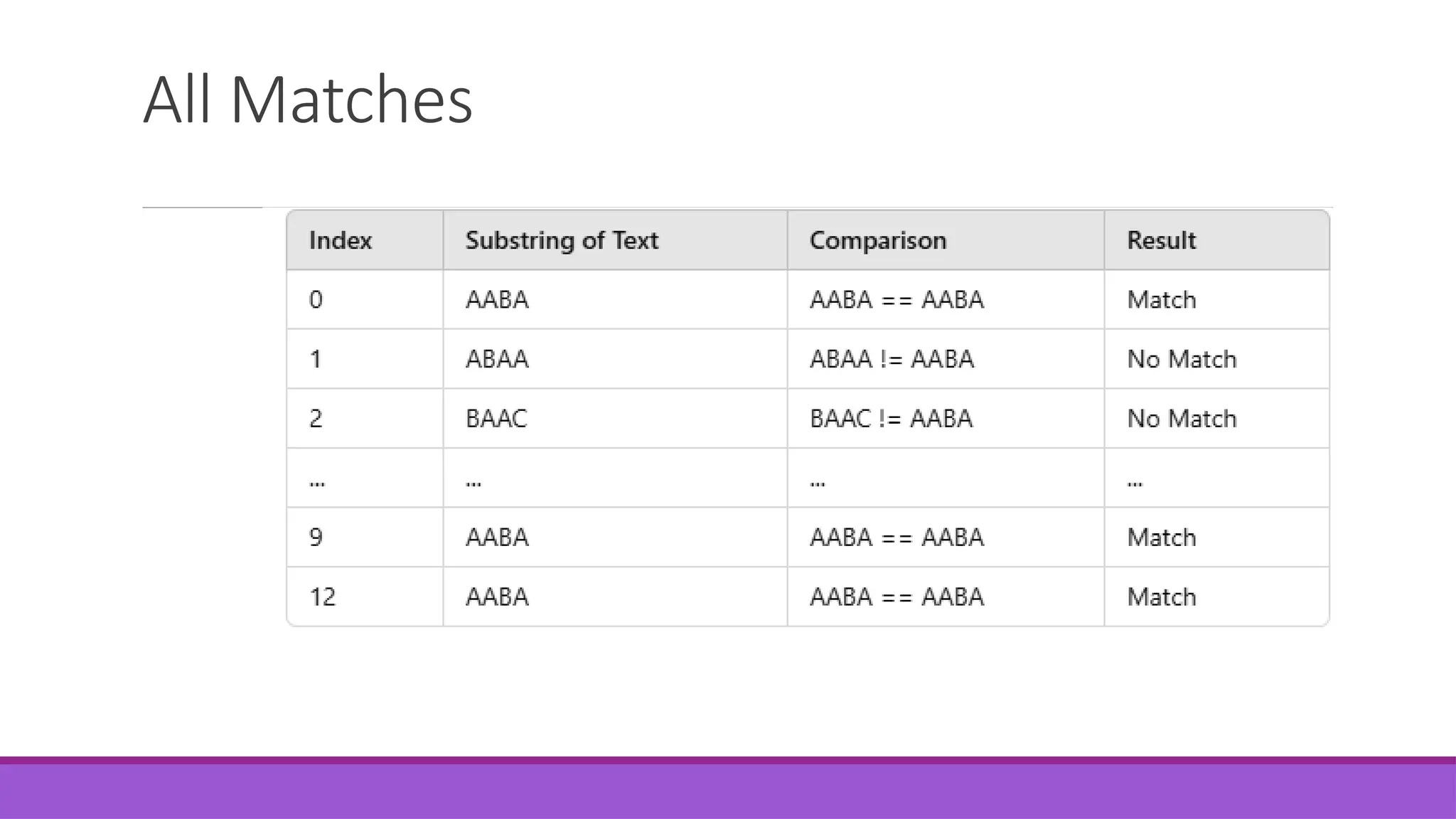
![String Matching we say that pattern P occurs with shift s in text T (or, equivalently, that pattern P occurs beginning at position s + 1 in text T ) if 0 ≤ s ≤ n-m and T*s+1… s +m+ = P*1…m+ (that is, if T[s+j] = P[j], for 1 ≤ j ≤ m). If P occurs with shift s in T , then we call s a valid shift; otherwise, we call s an invalid shift. The string matching problem is the problem of finding all valid shifts with which a given pattern P occurs in a given text T](https://image.slidesharecdn.com/unit5-250505065536-4351080a/75/String-Matching-Algorithms-Naive-KMP-Rabin-Karp-4-2048.jpg)