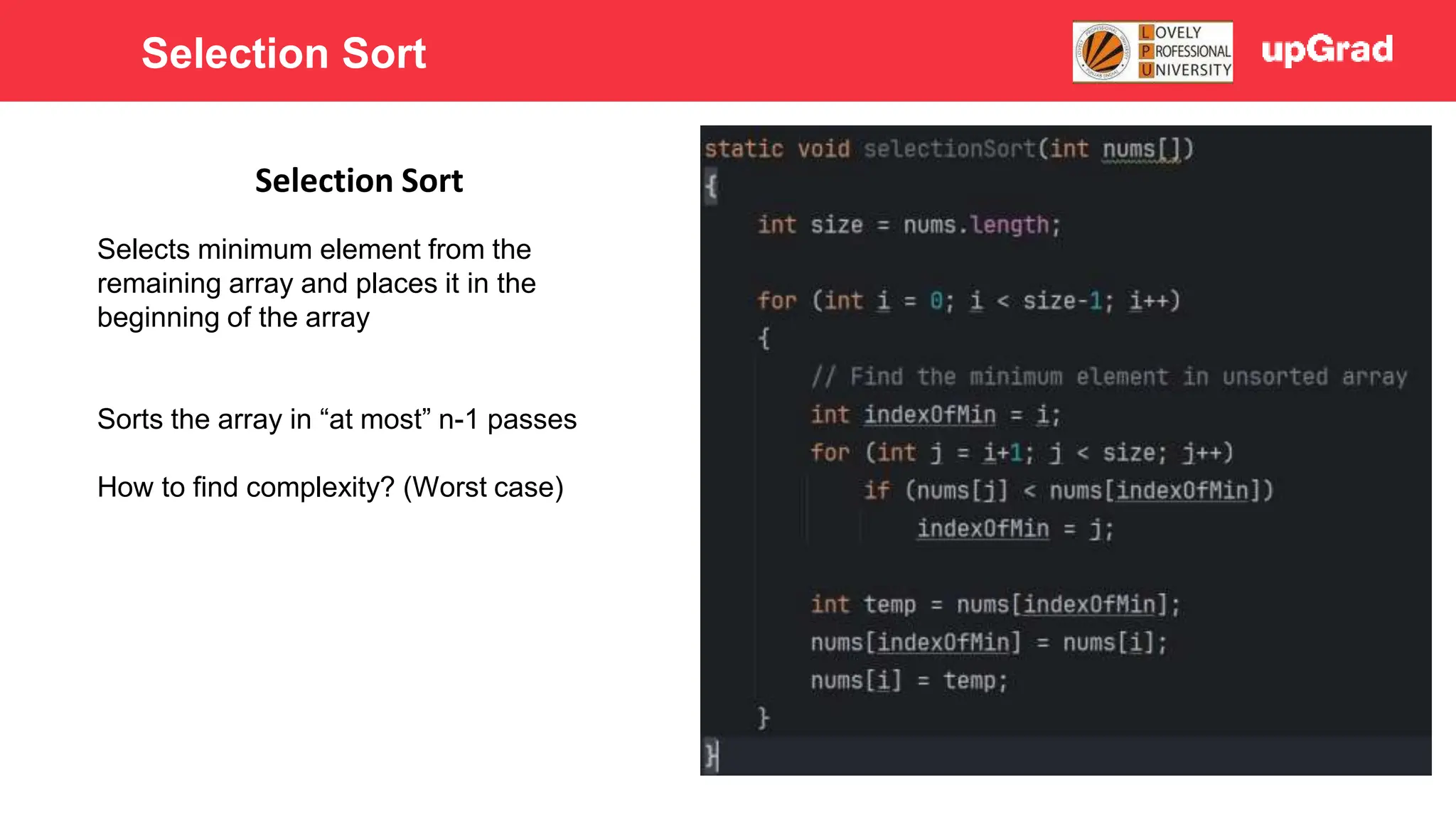
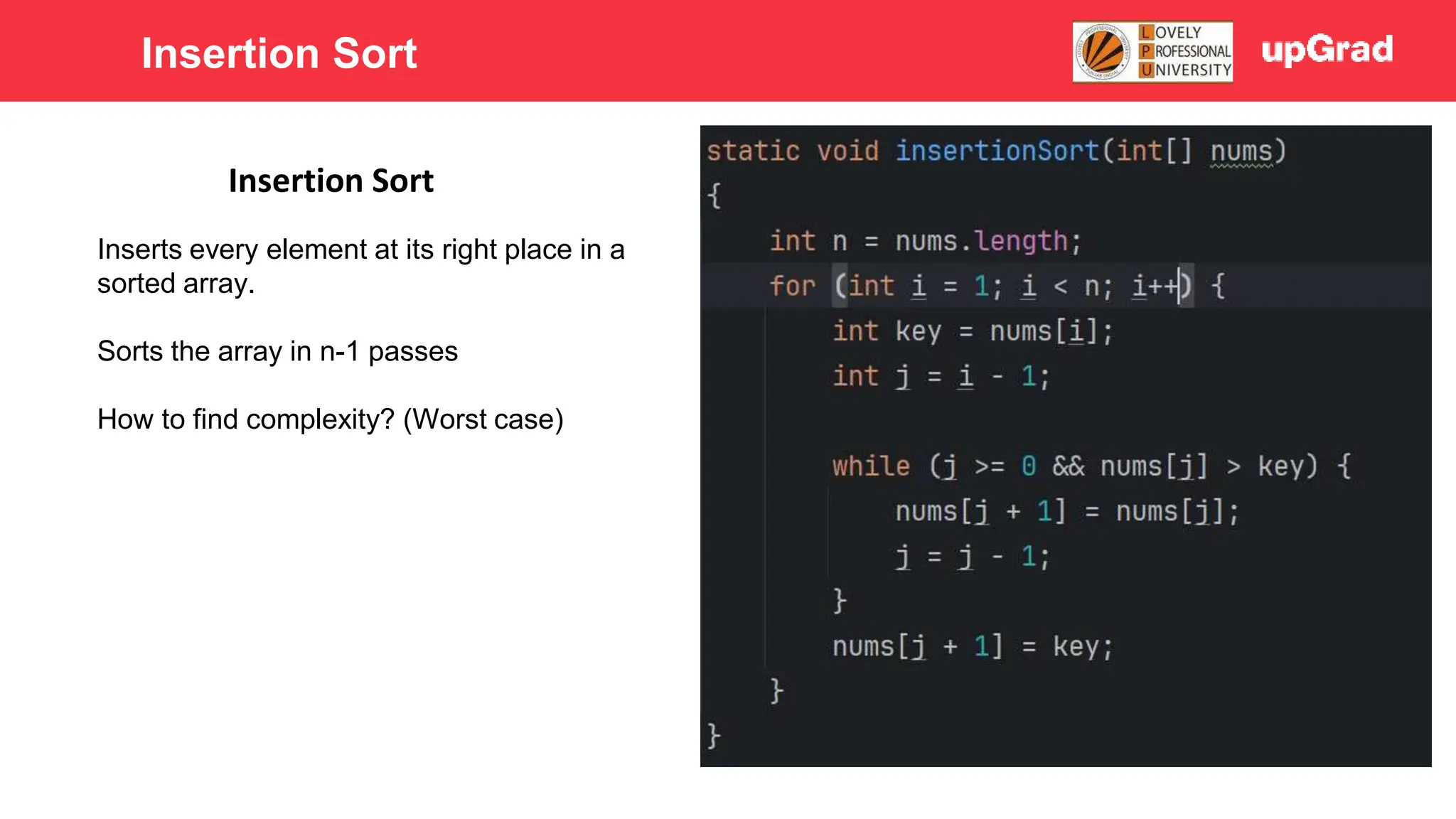
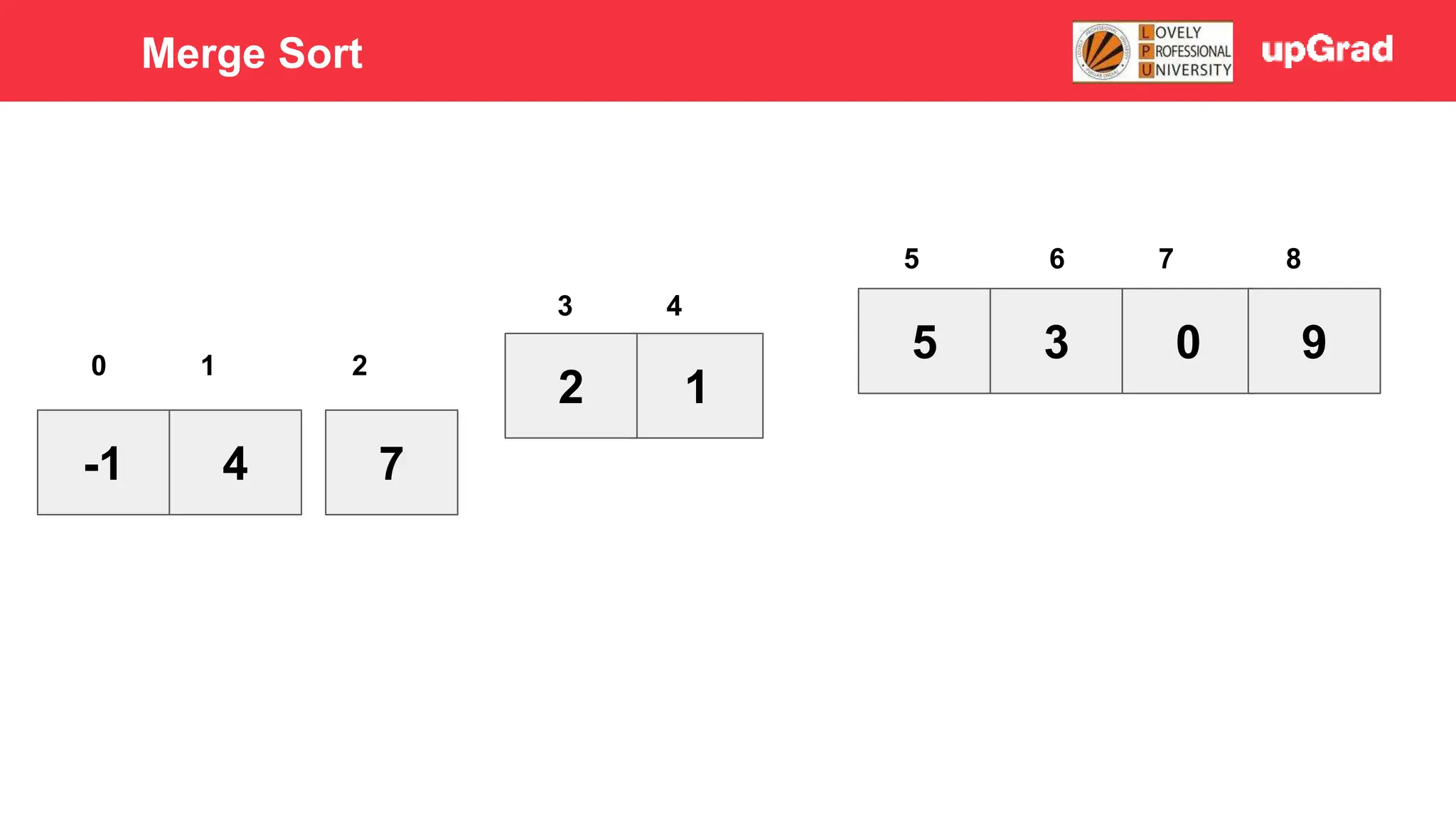
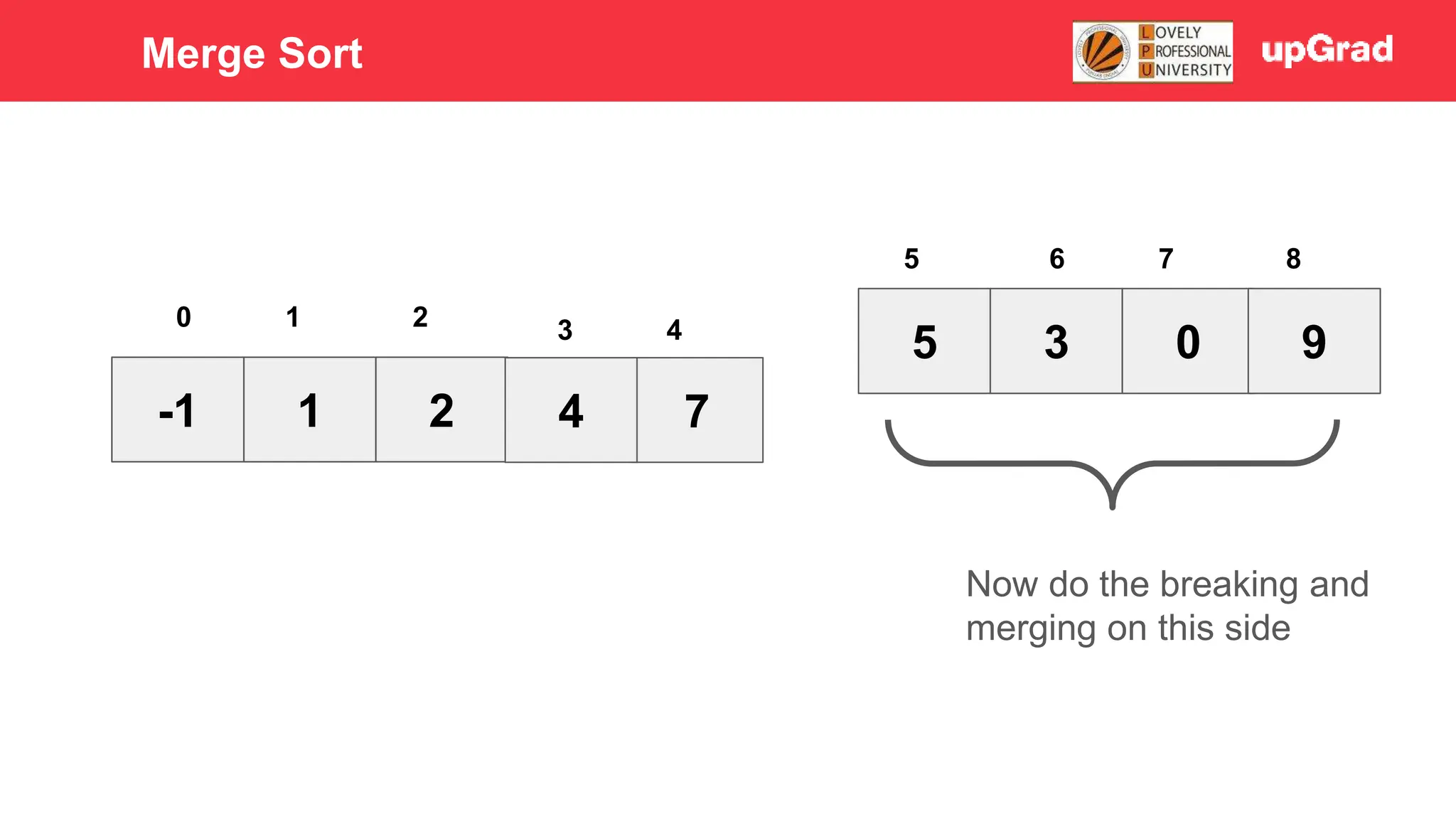
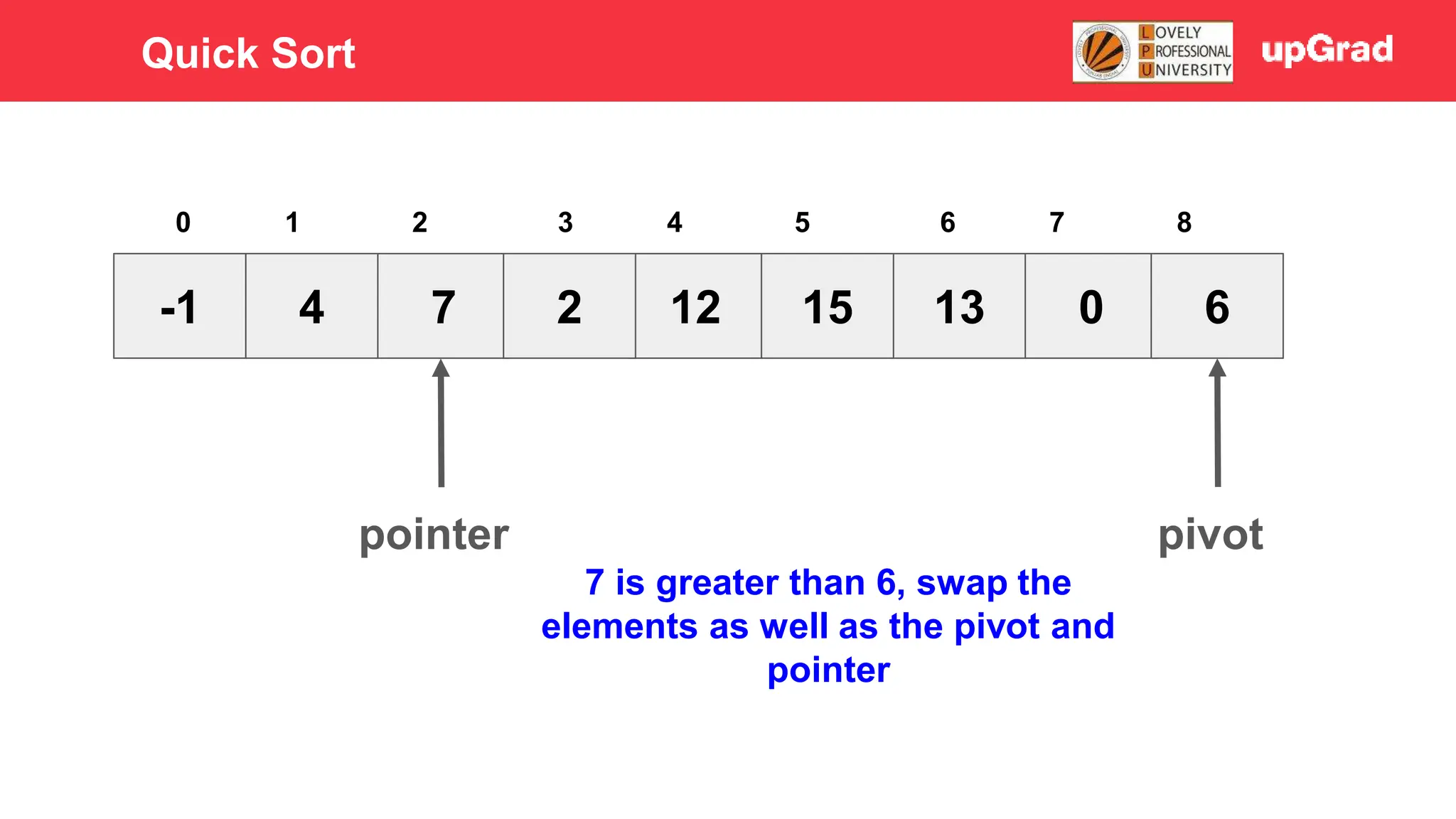
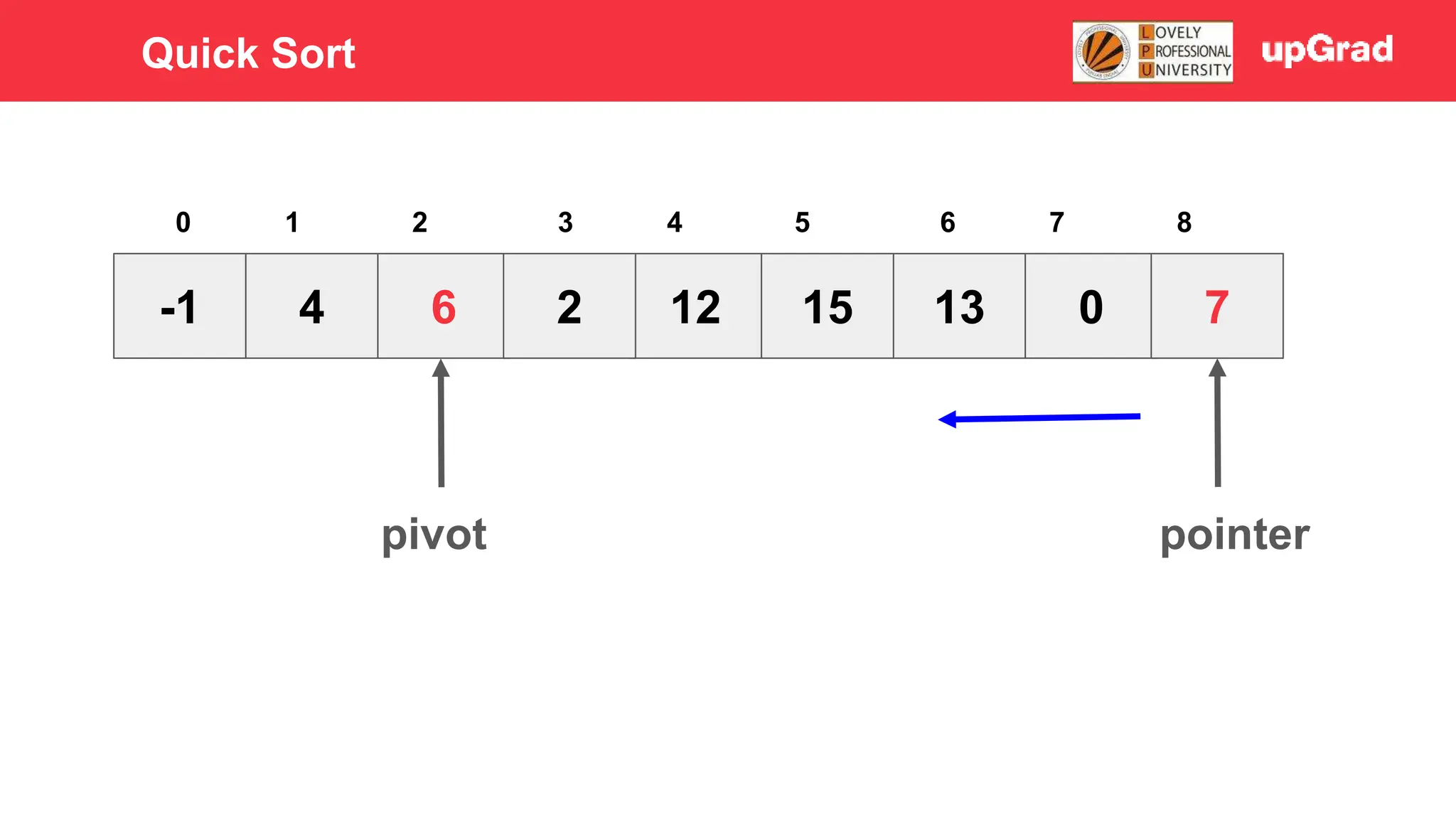
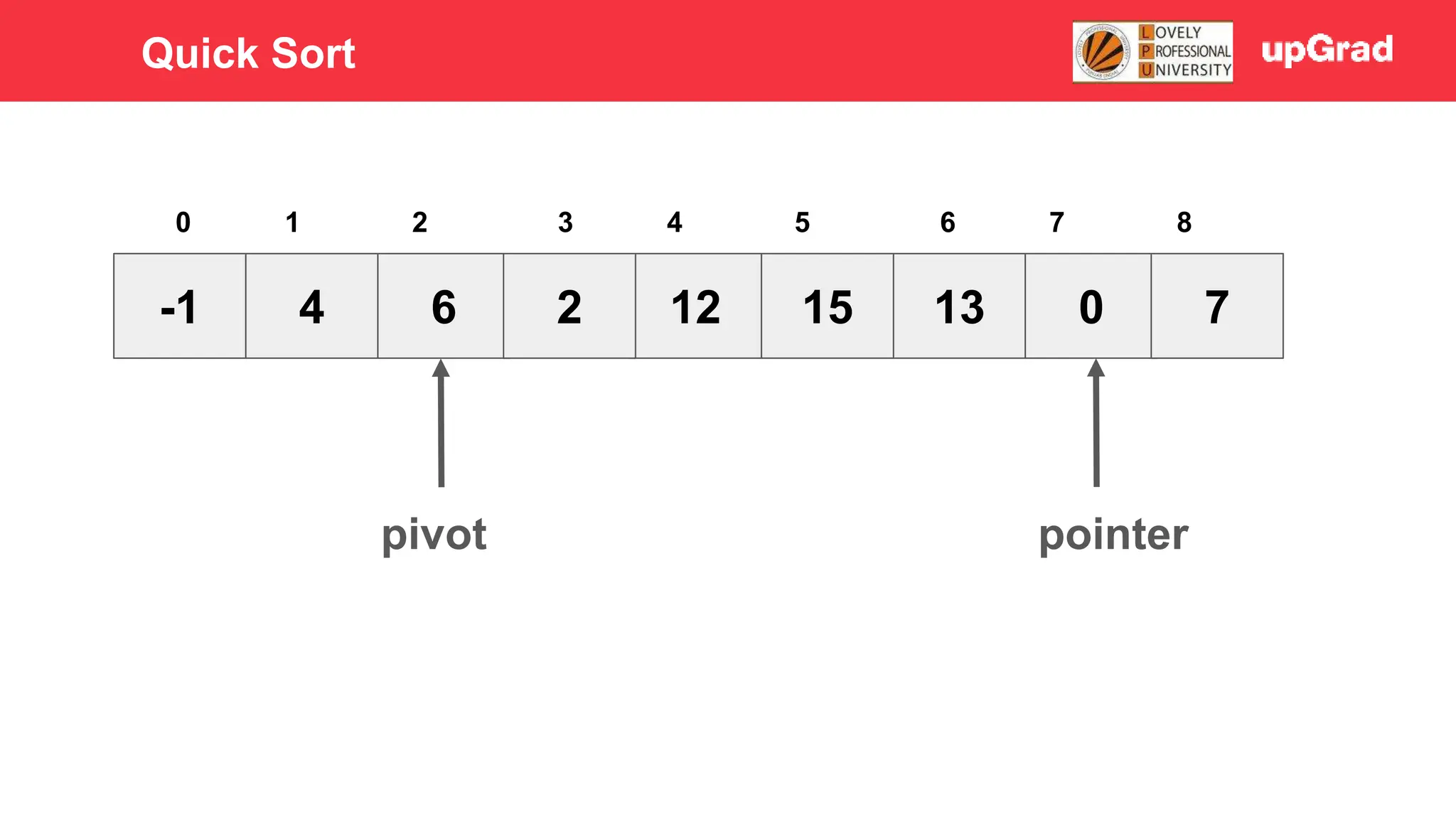
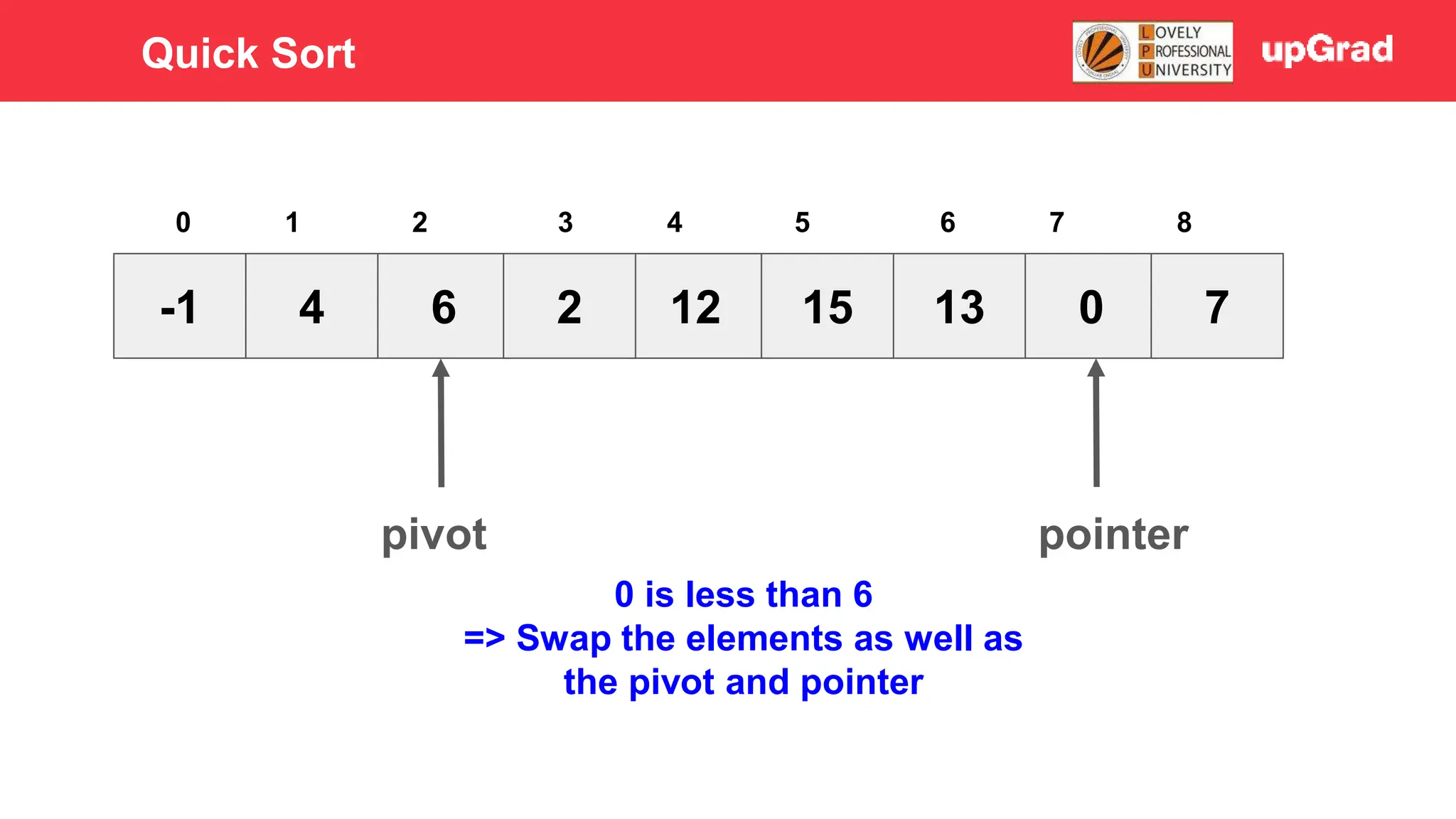
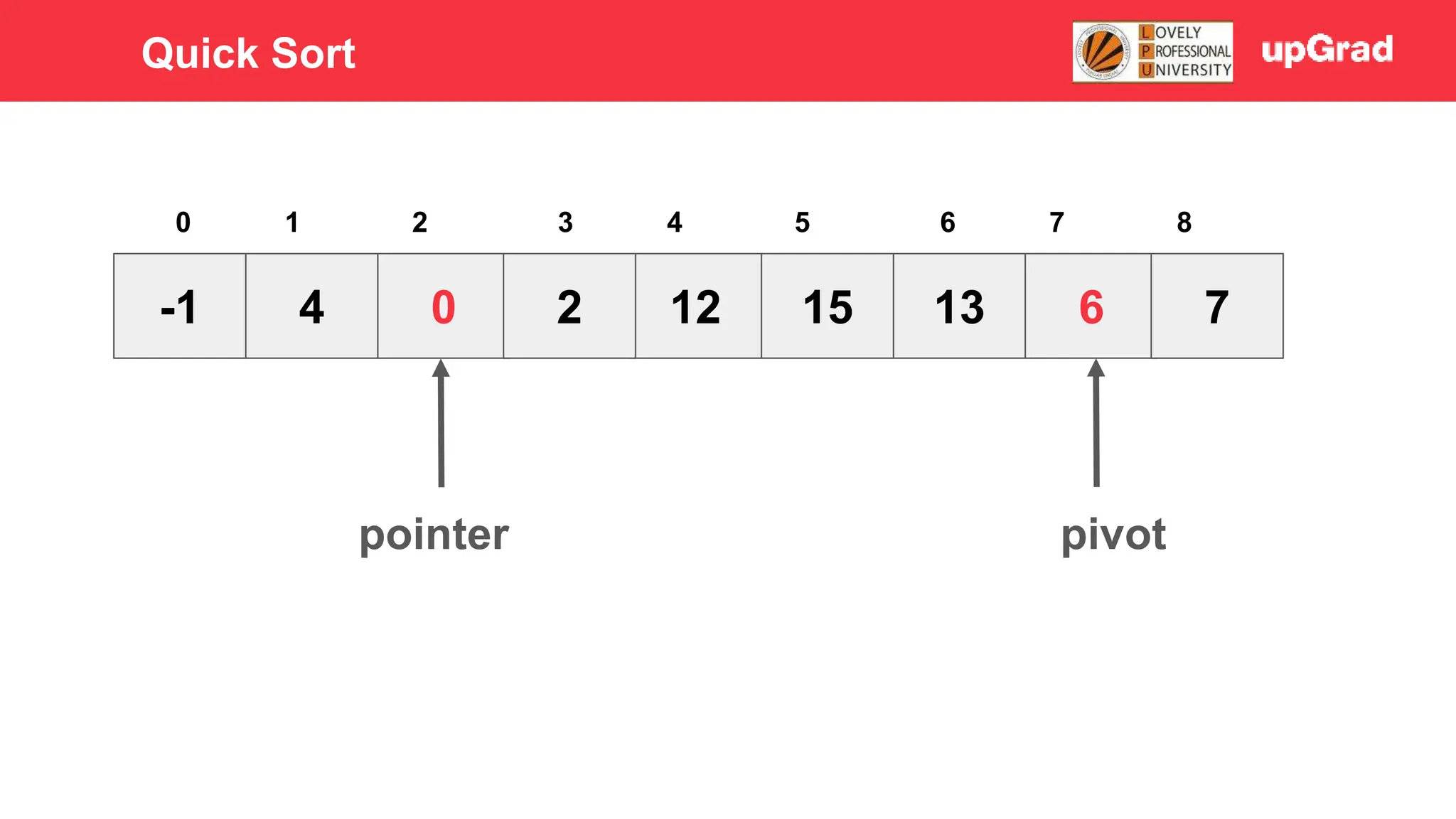
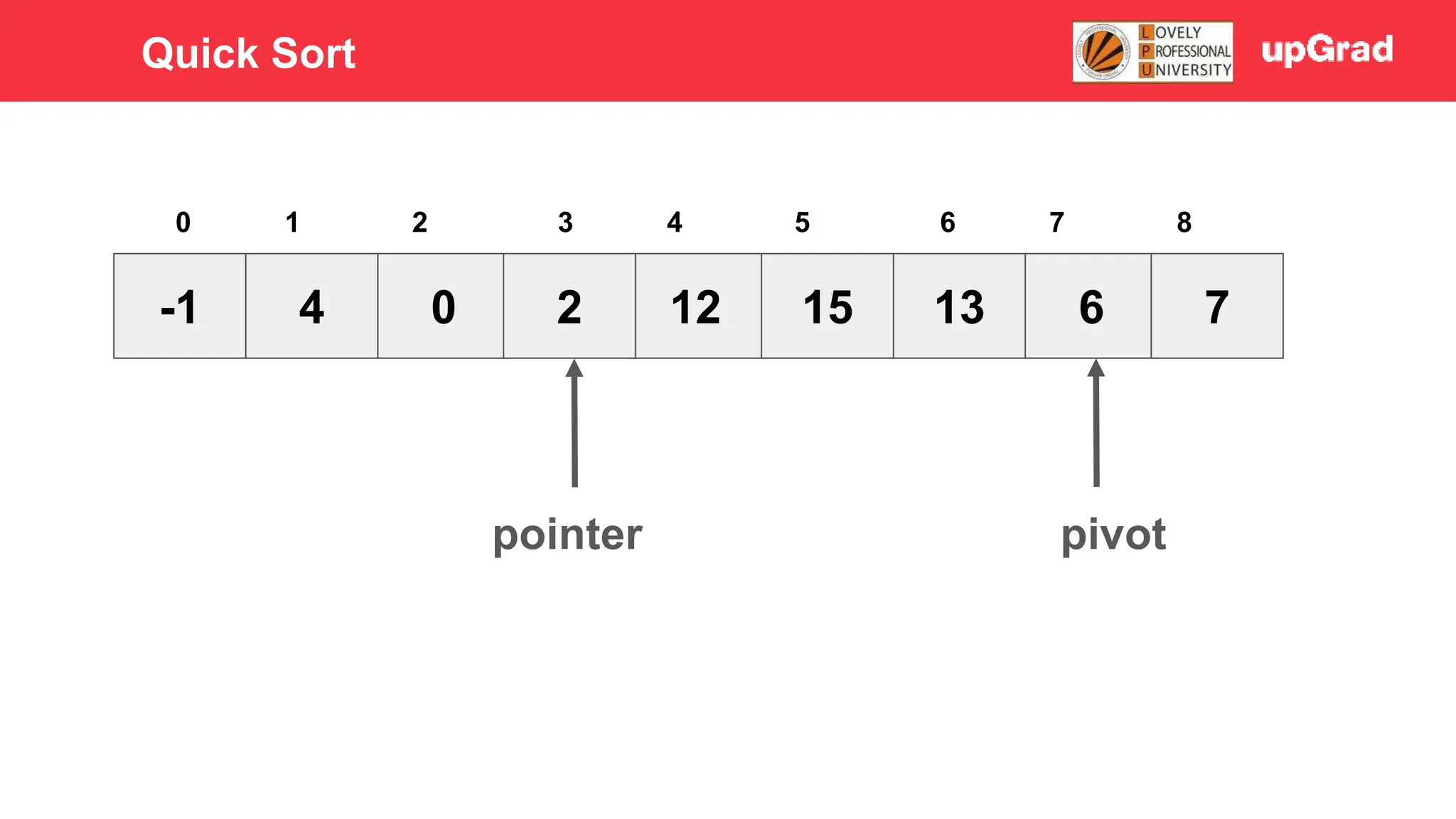
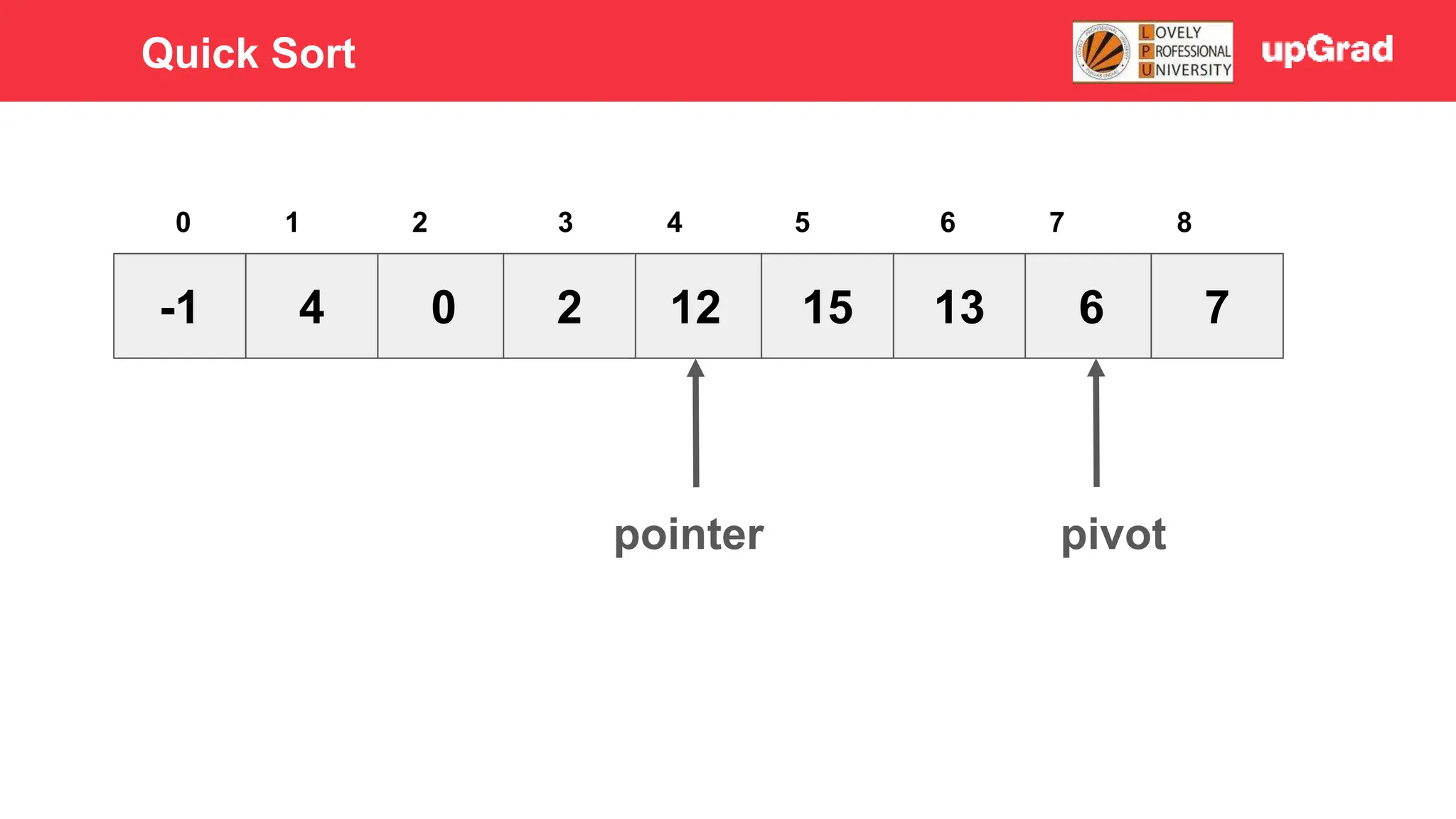
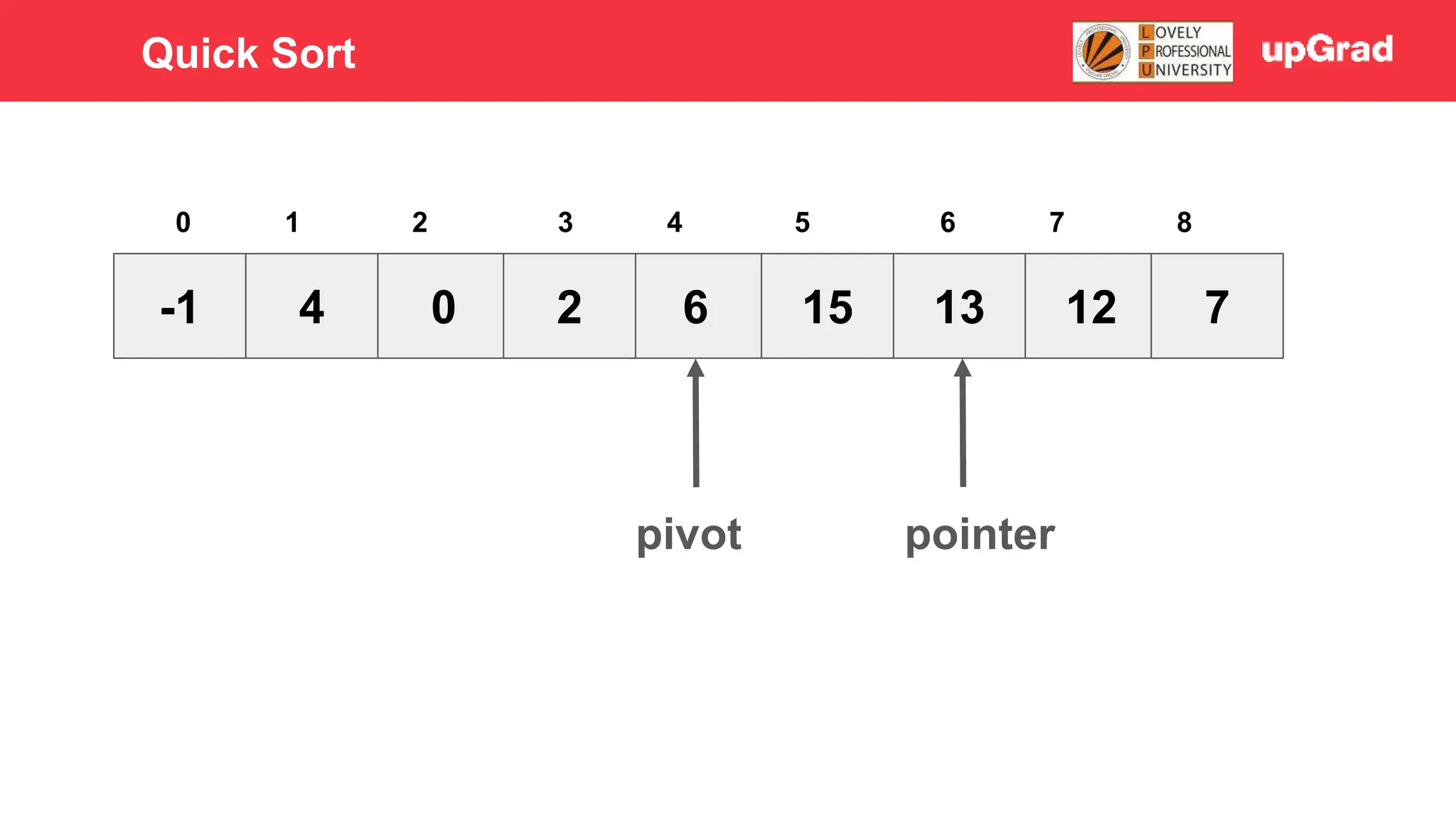
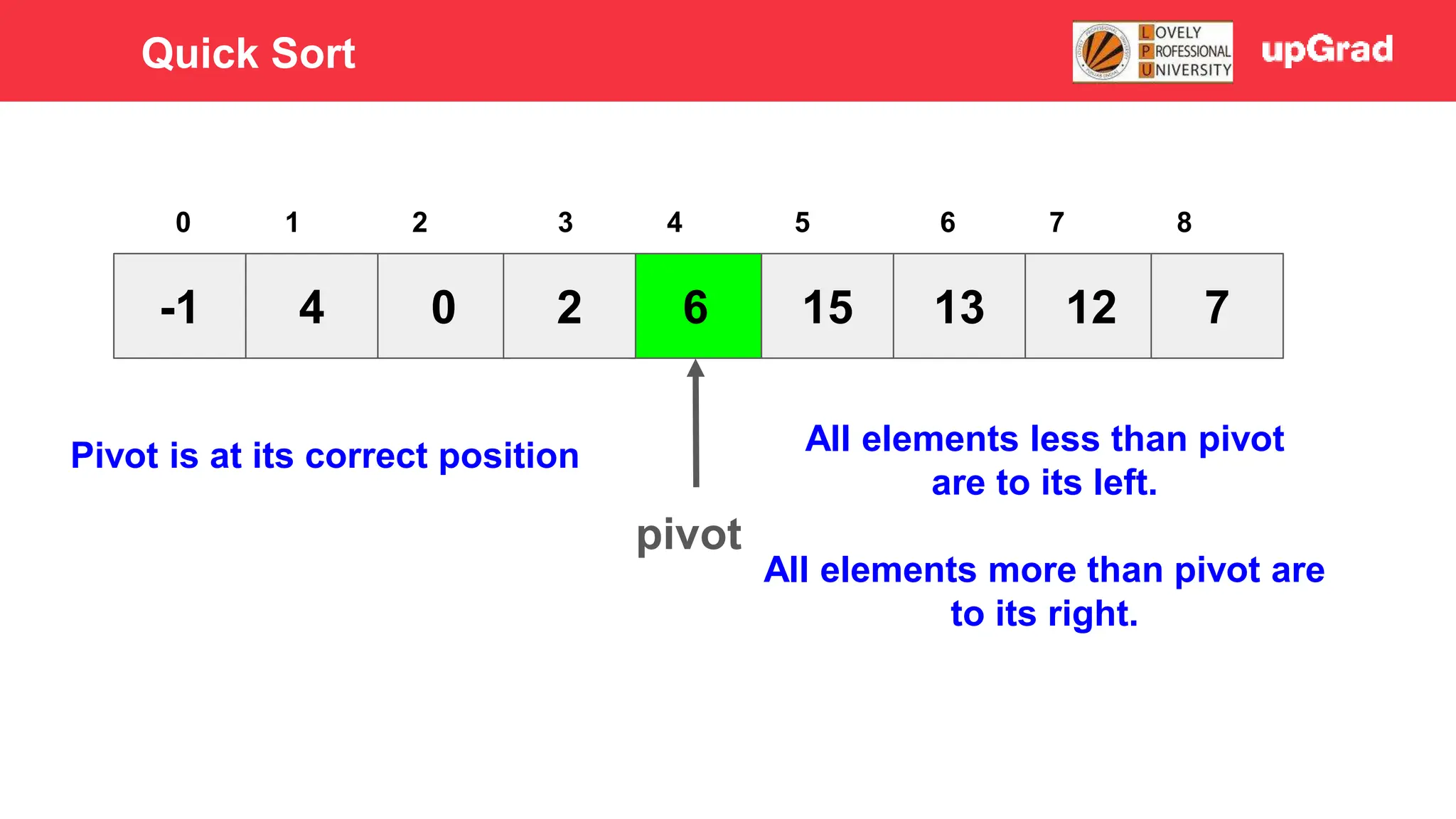
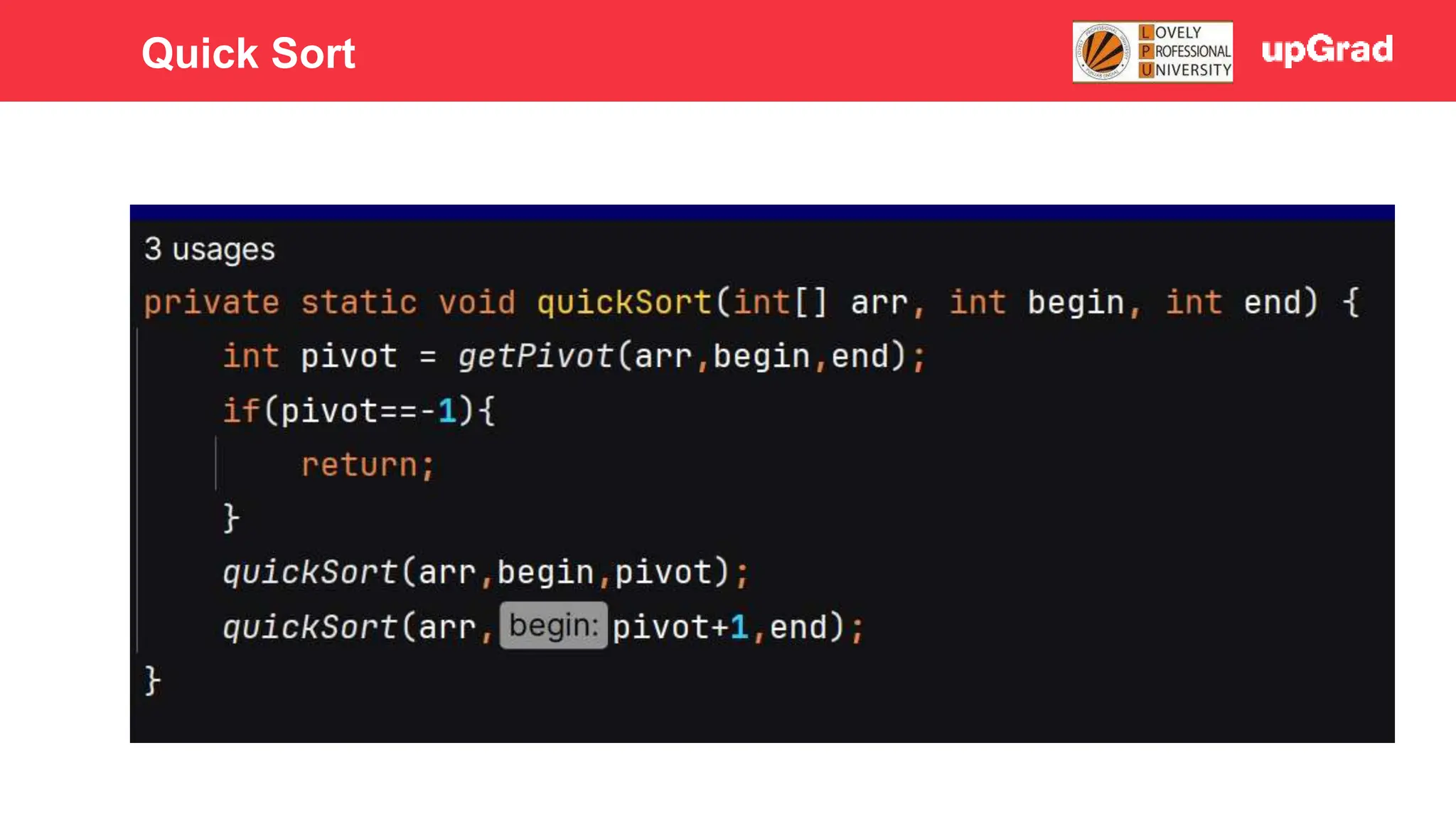
1) The document discusses various sorting algorithms like bubble sort, selection sort, insertion sort, merge sort, quick sort and heap sort. 2) It provides detailed explanations of how merge sort and quick sort algorithms work, including examples with diagrams showing the sorting process step-by-step. 3) Merge sort has a time complexity of O(n log n) as it recursively divides the array into halves and then merges the sorted halves, while quick sort selects a pivot element and partitions the array into elements less than and greater than the pivot in O(n) time on average.




![Merge Sort T(N) = 2.T(N/2) + cN T(N) = 2.[2T(N/4)+cN/2] + cN = 4.T(N/4) + 2.cN/2 + cN = 4.T(N/4) + 2.cN = 22.T(N/22) + 2.cN Now, 4.T(N/4) + 2.cN can be further solved to obtain = 8.T(N/8) + 3.cN = 23.T(N/23) + 3.cN Say T(N) = 2k.T(N/2k) + k.cN (if mergeSort goes for k recursions)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-7-2048.jpg)













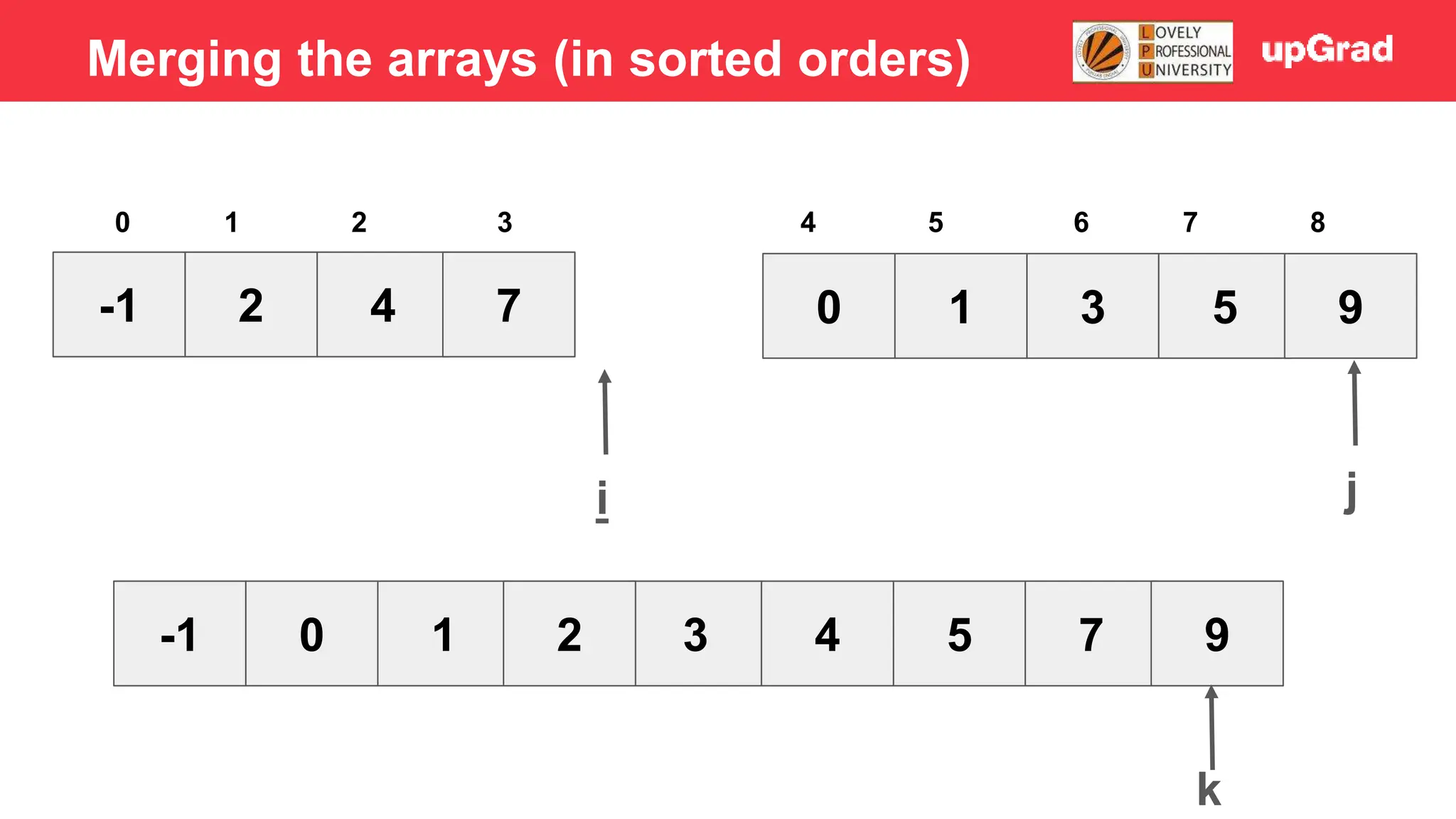
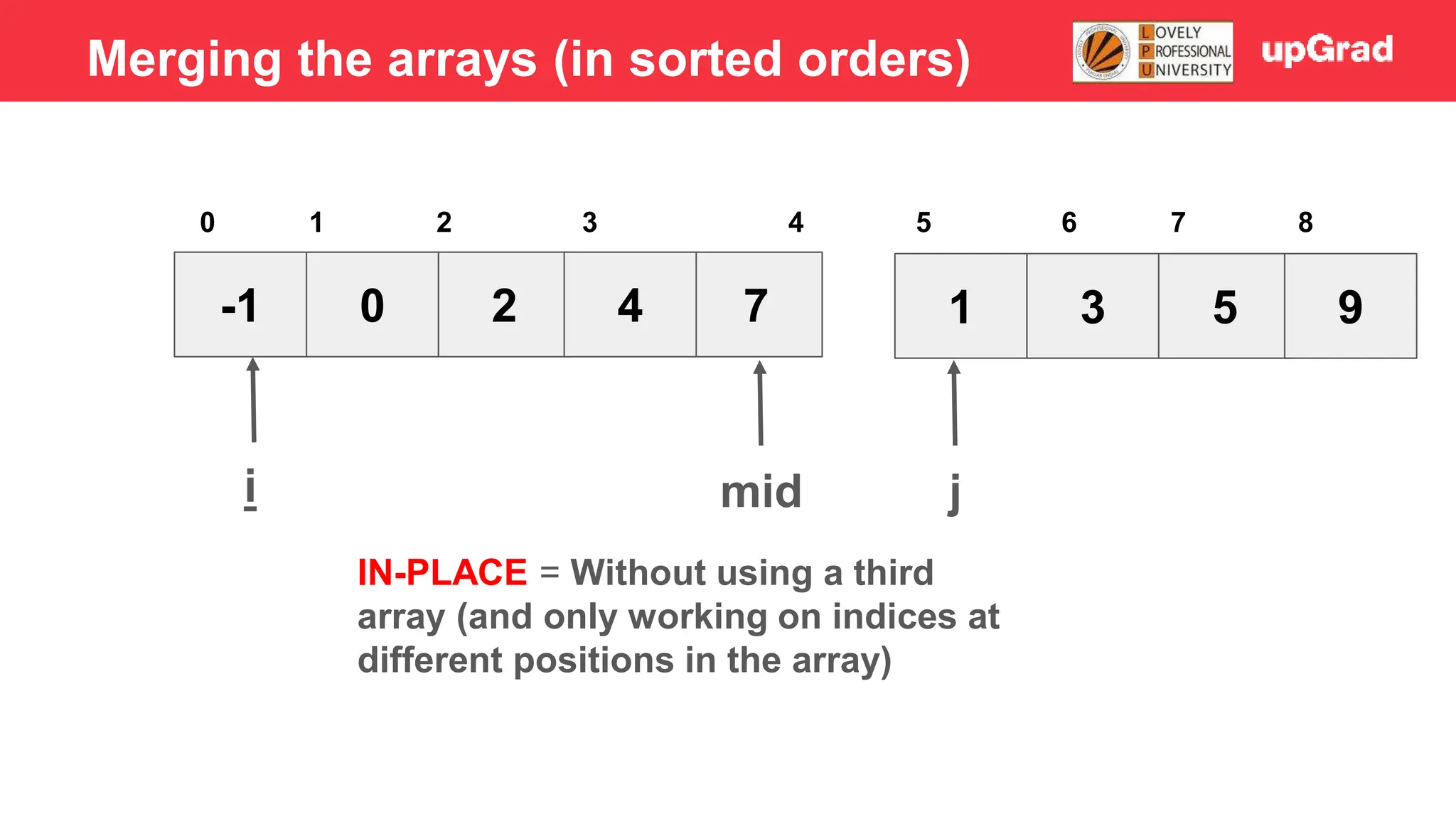
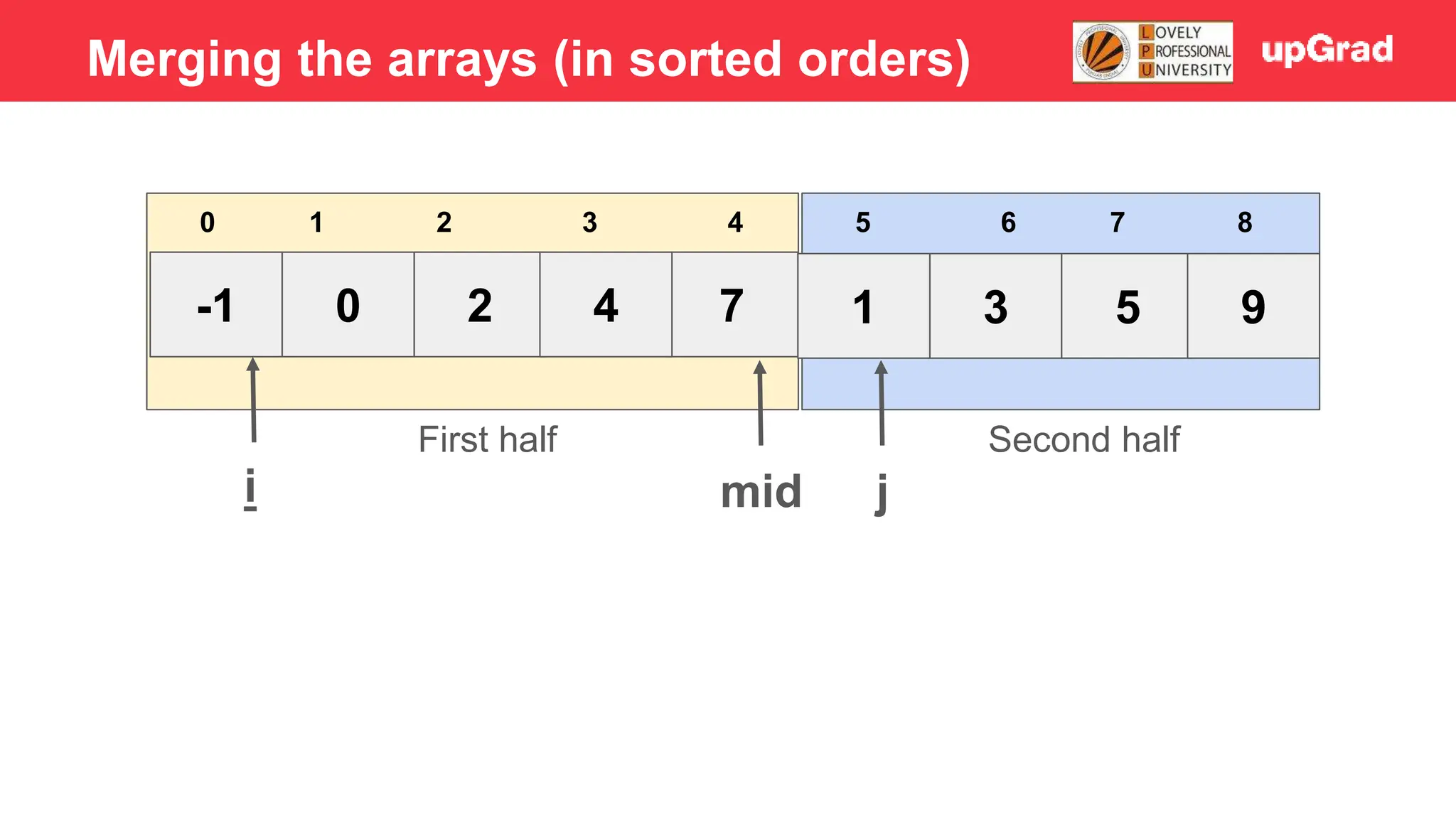
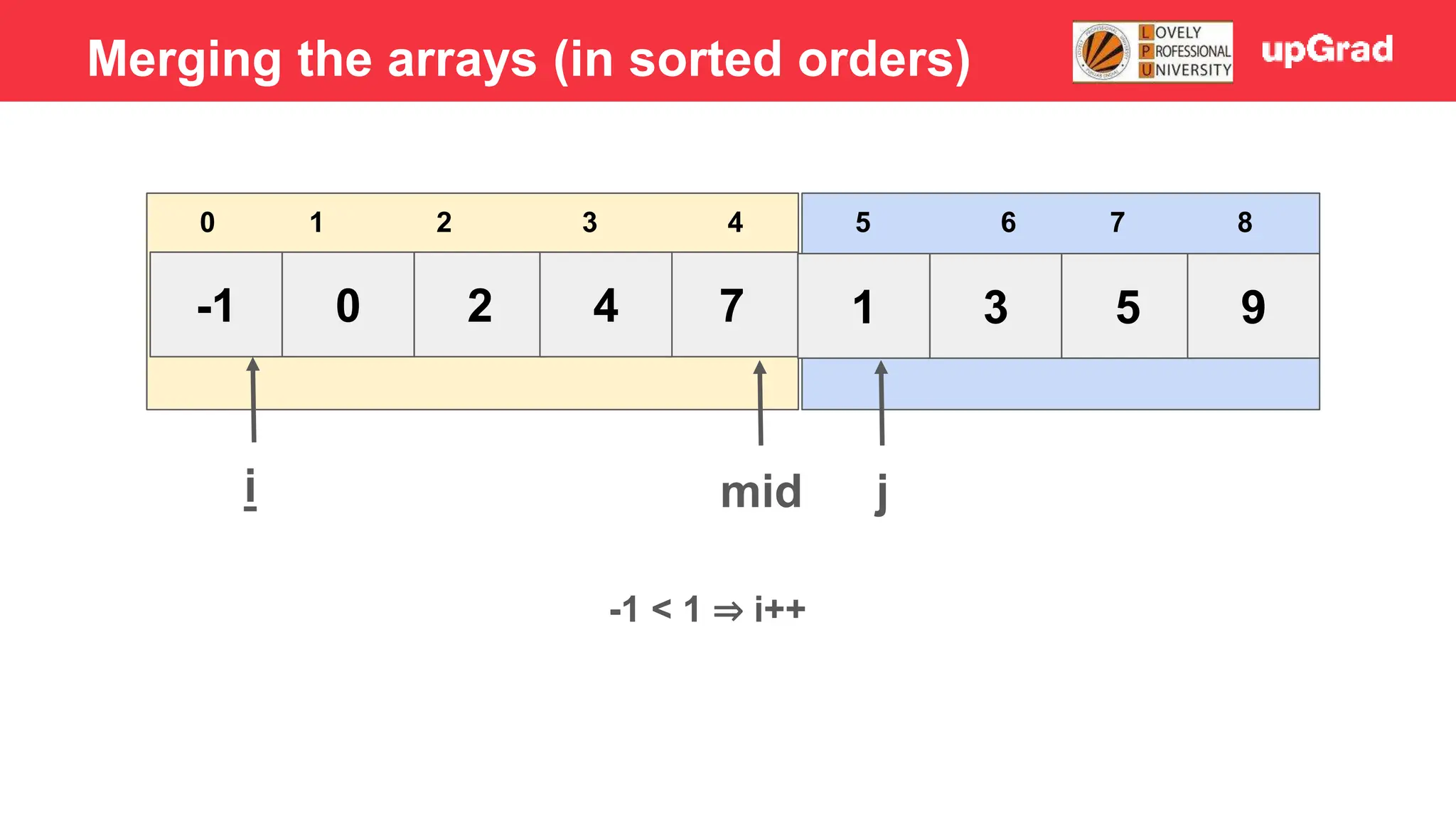
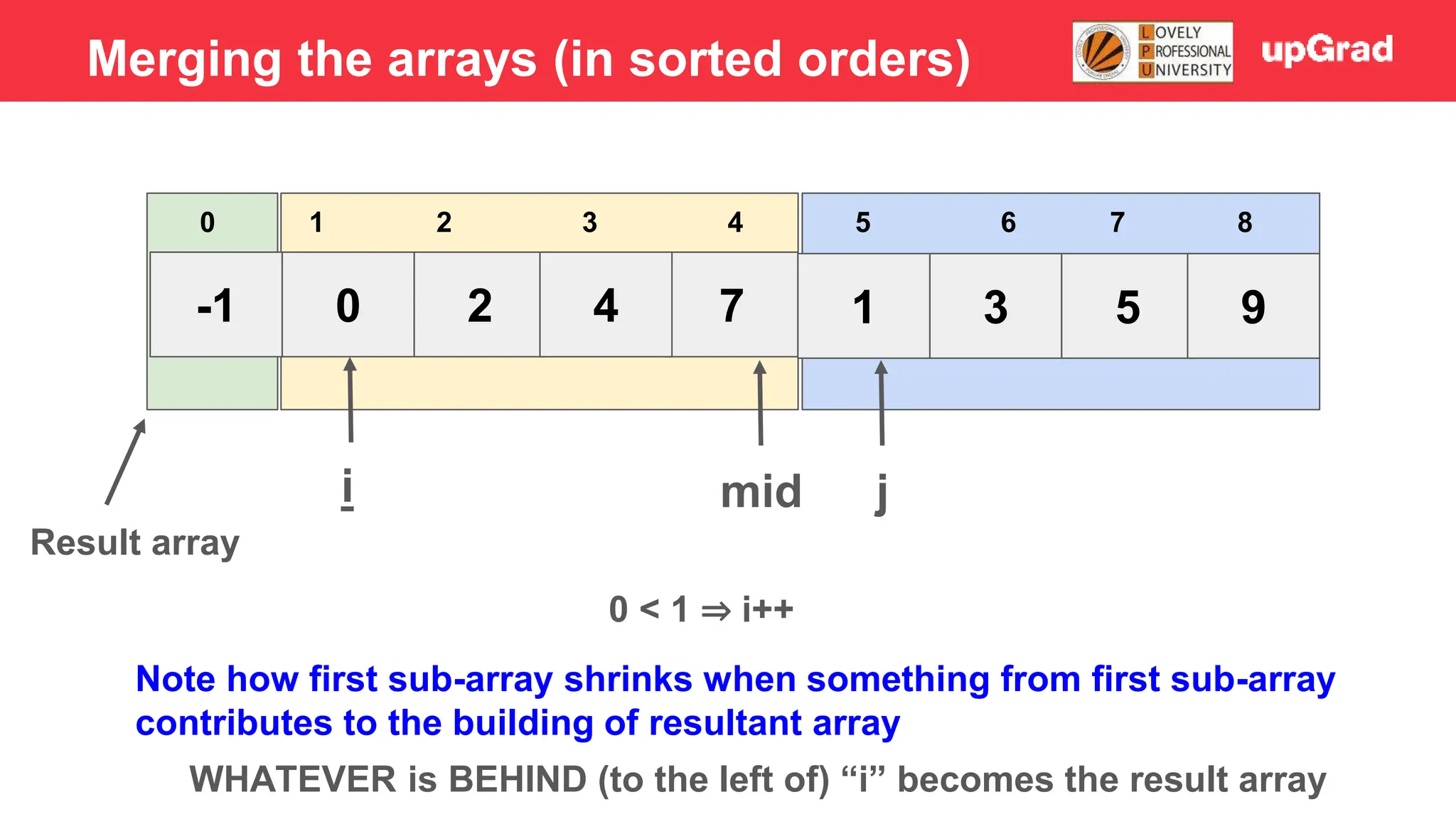

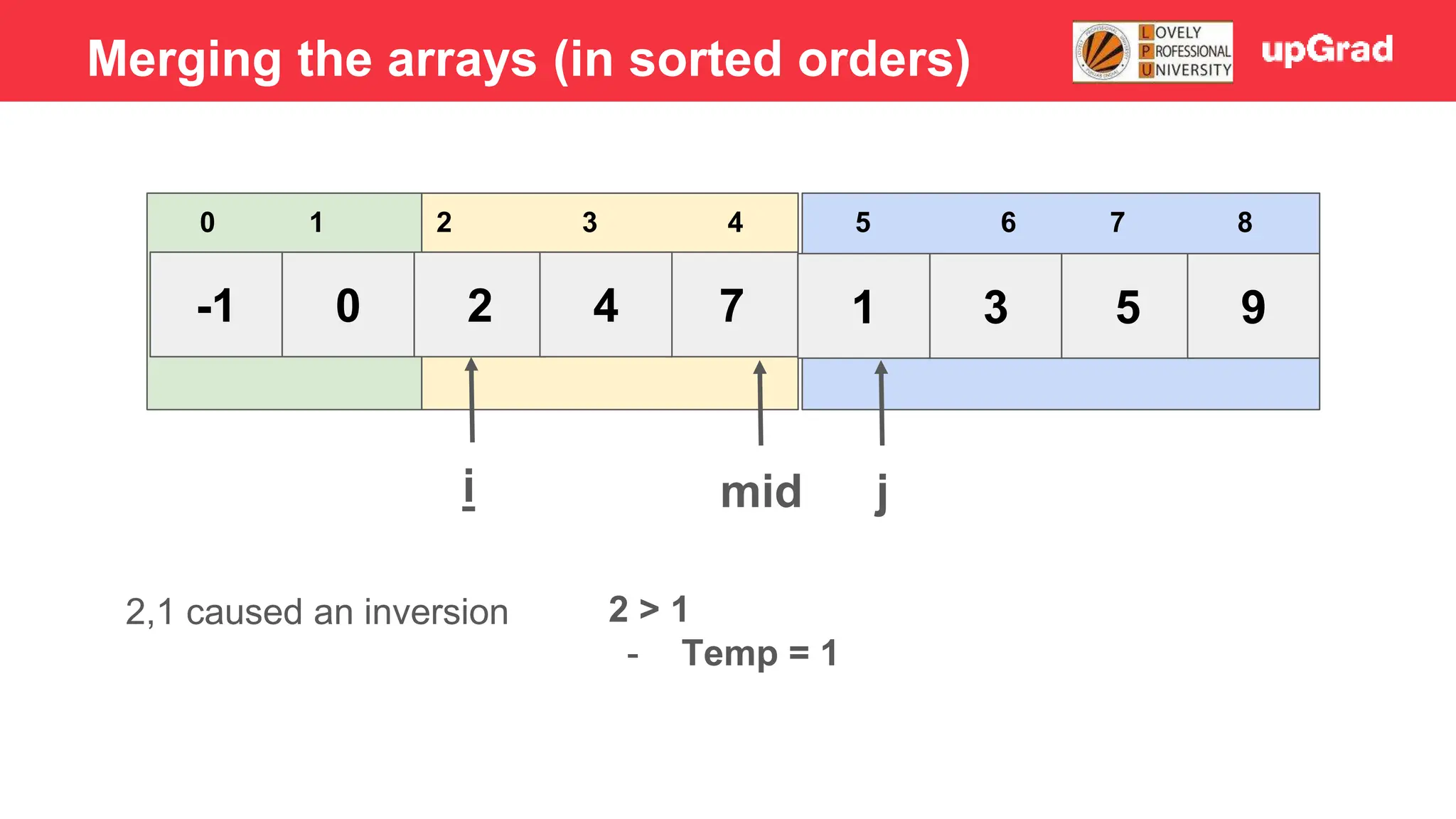
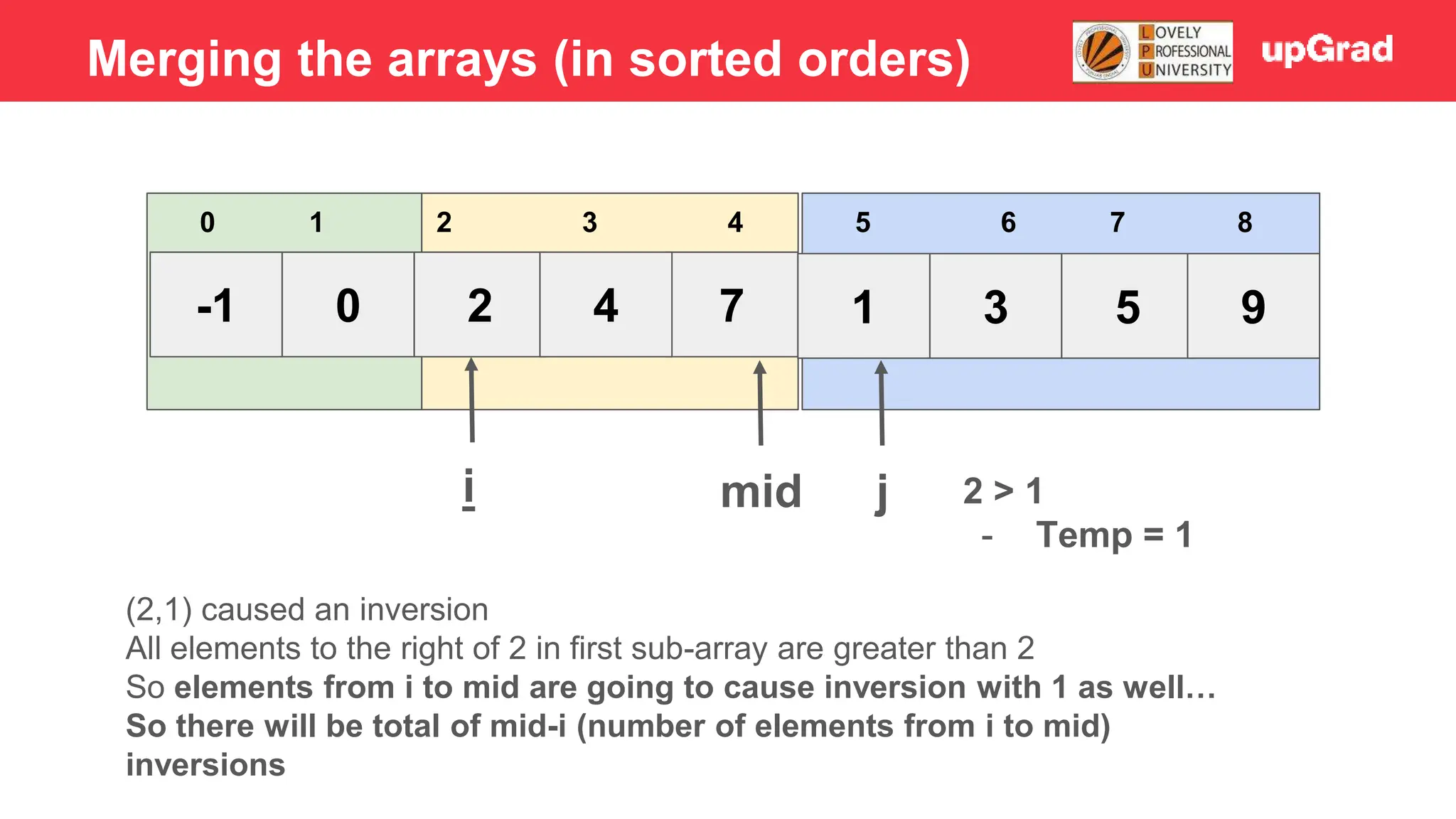
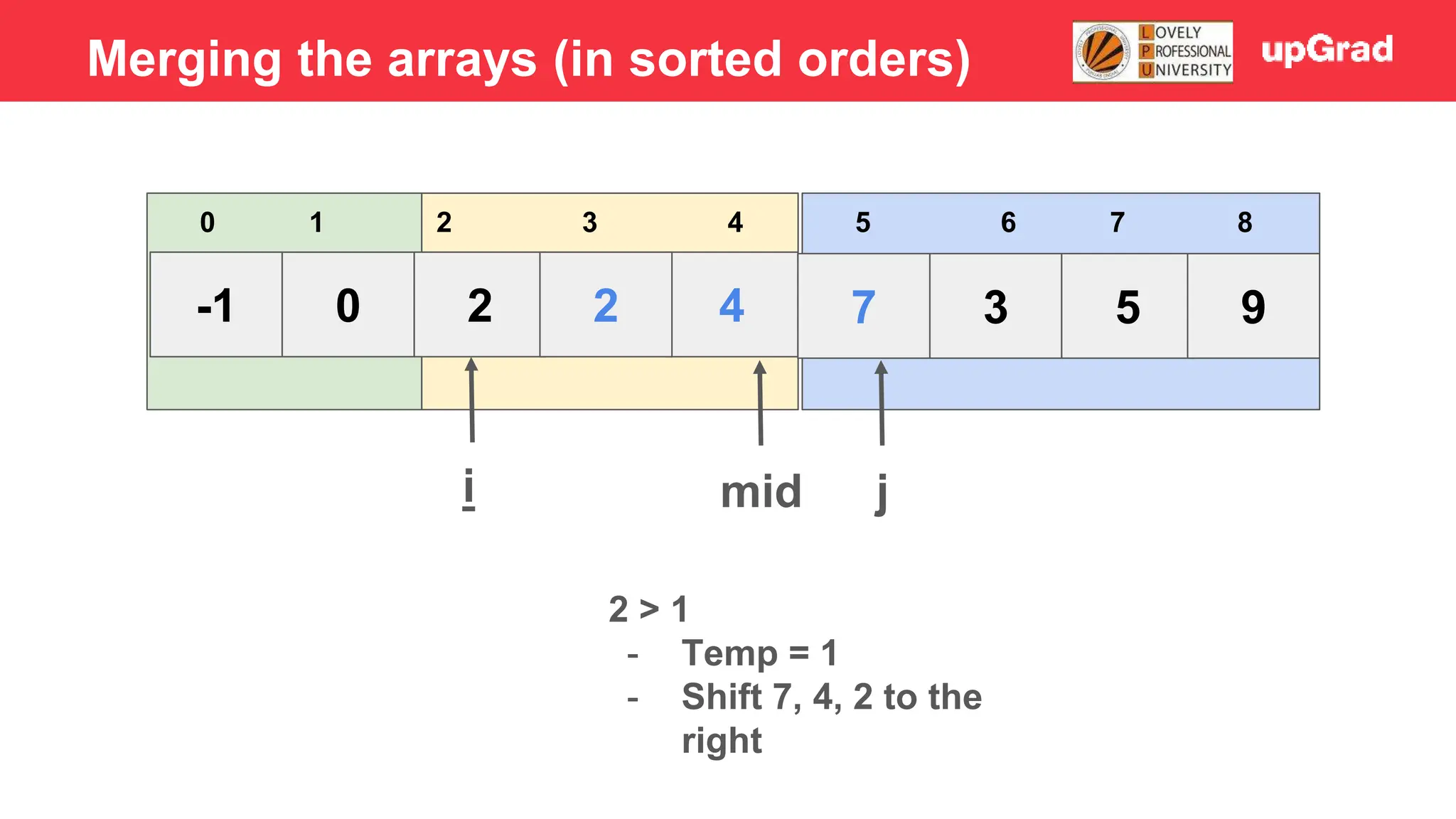
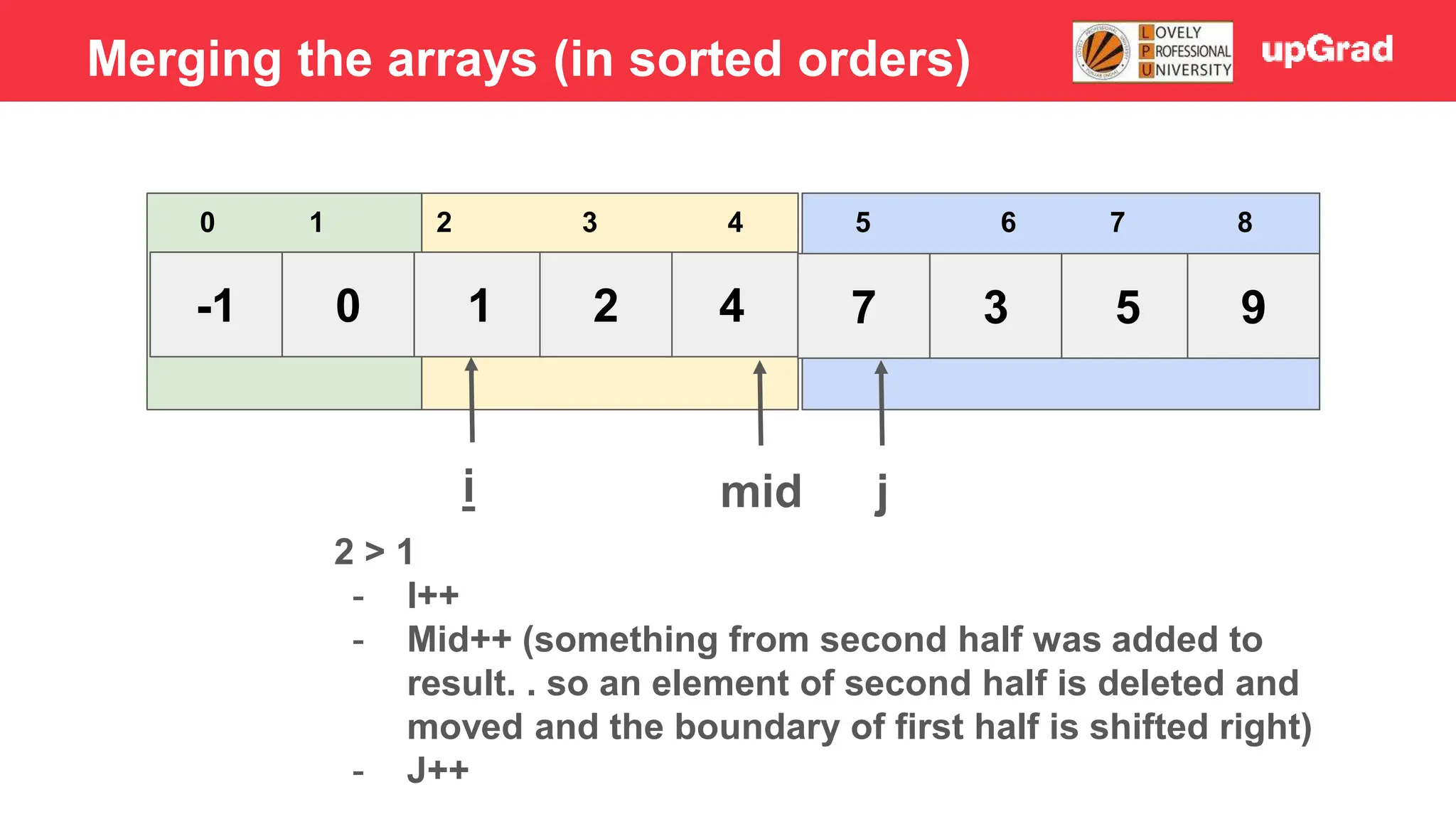
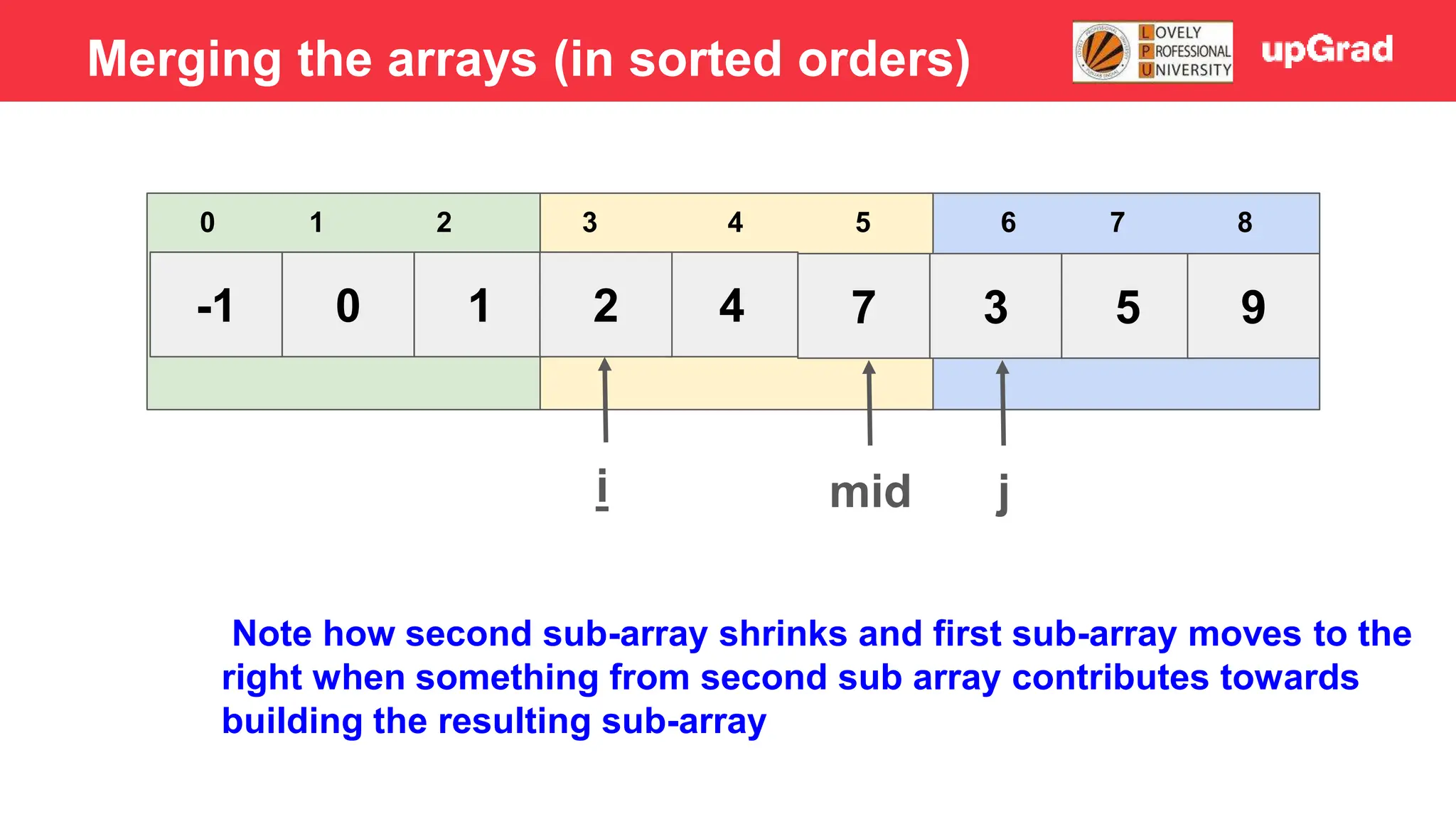
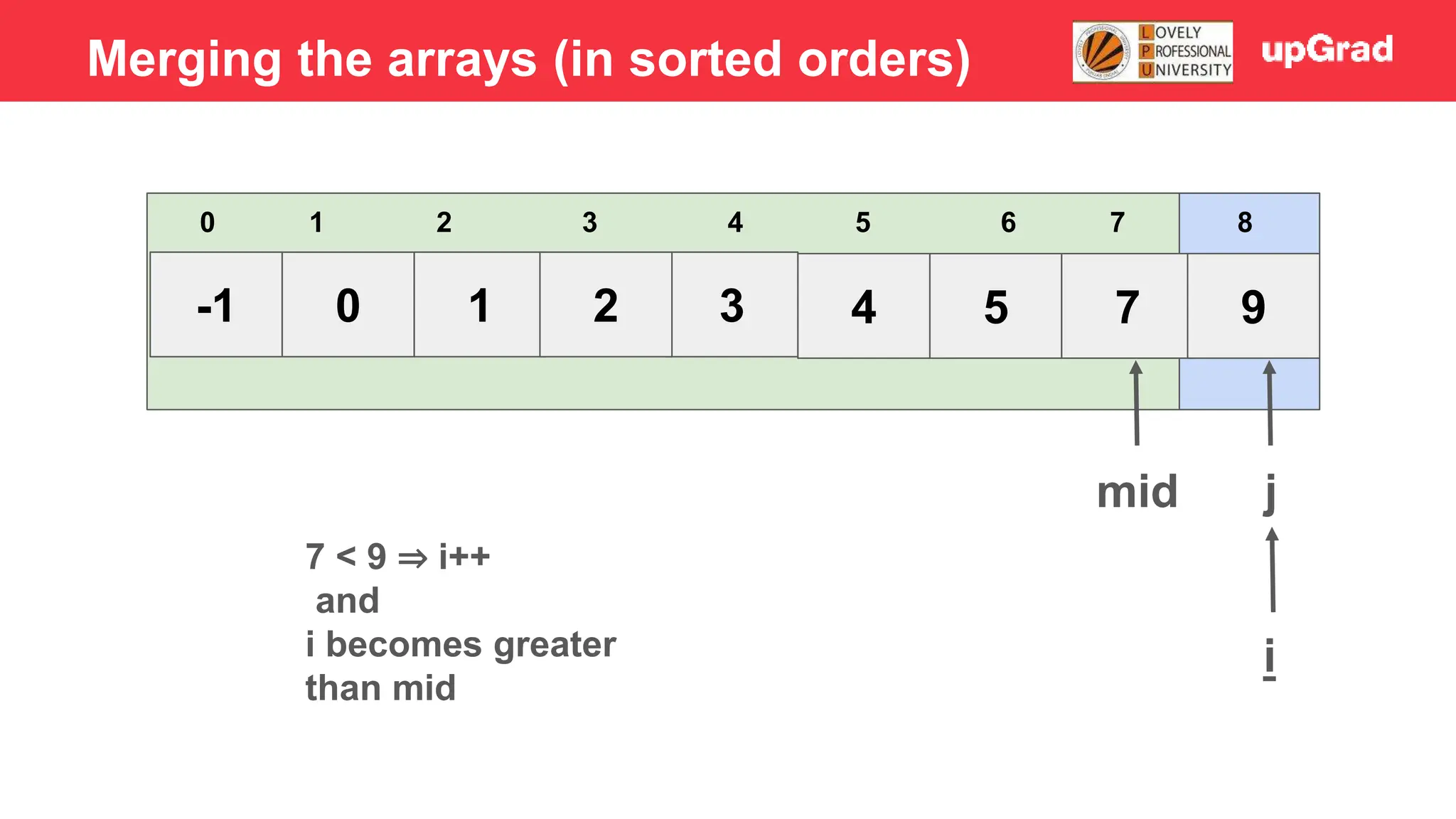
![-1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - Temp = 1 - Shift 7, 4, 2 to the right - Arr[i] = temp Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-32-2048.jpg)
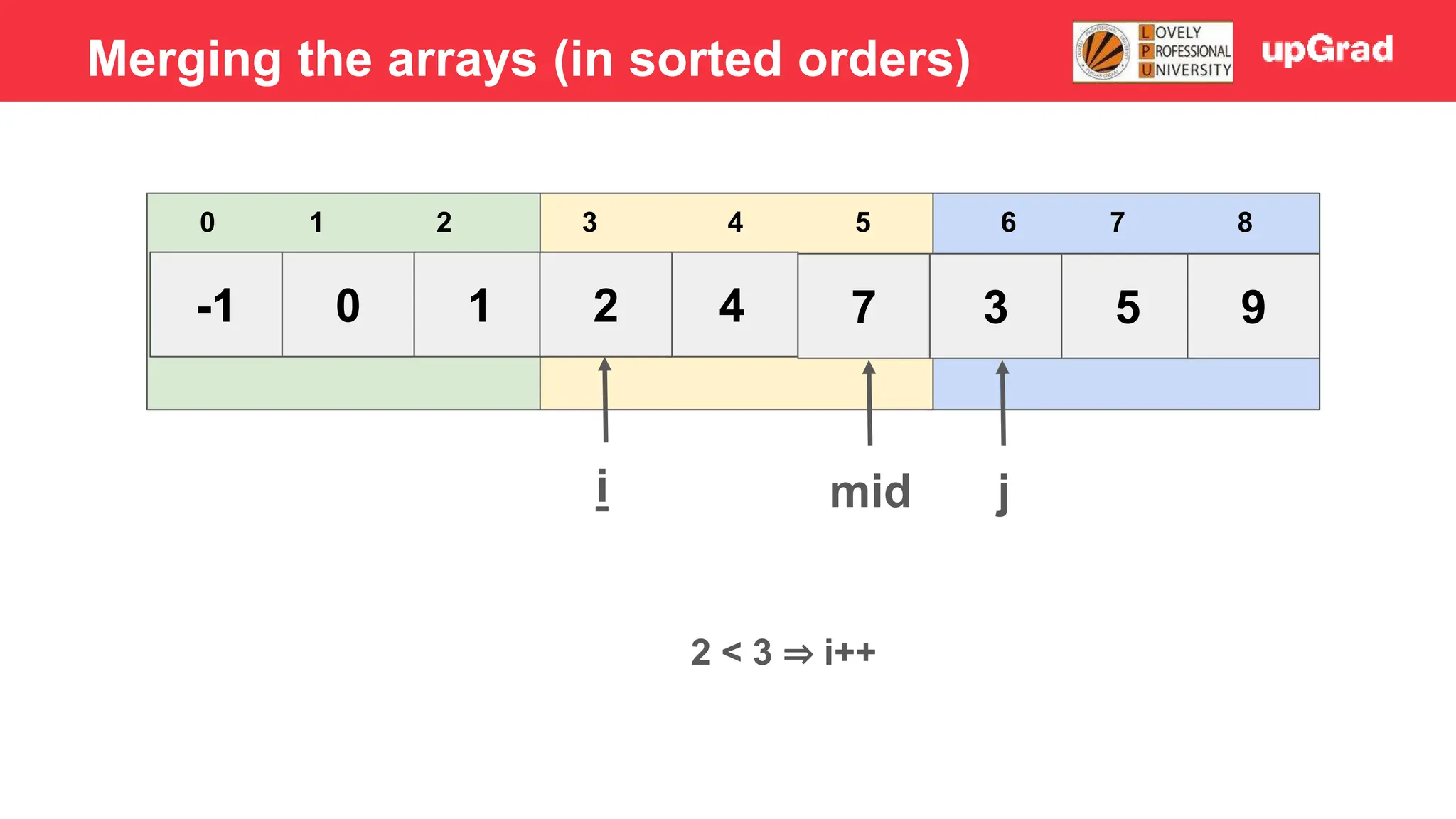
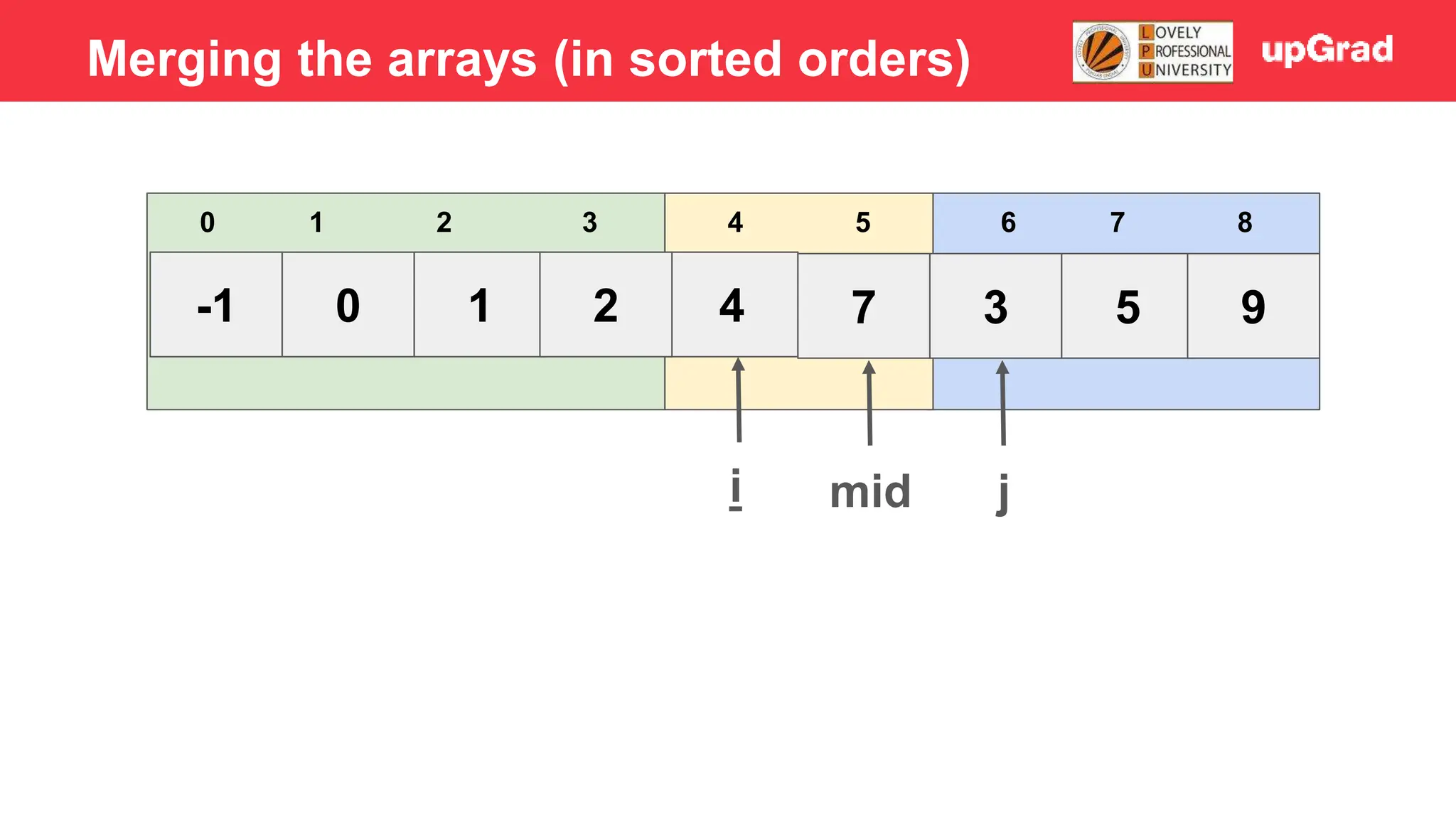

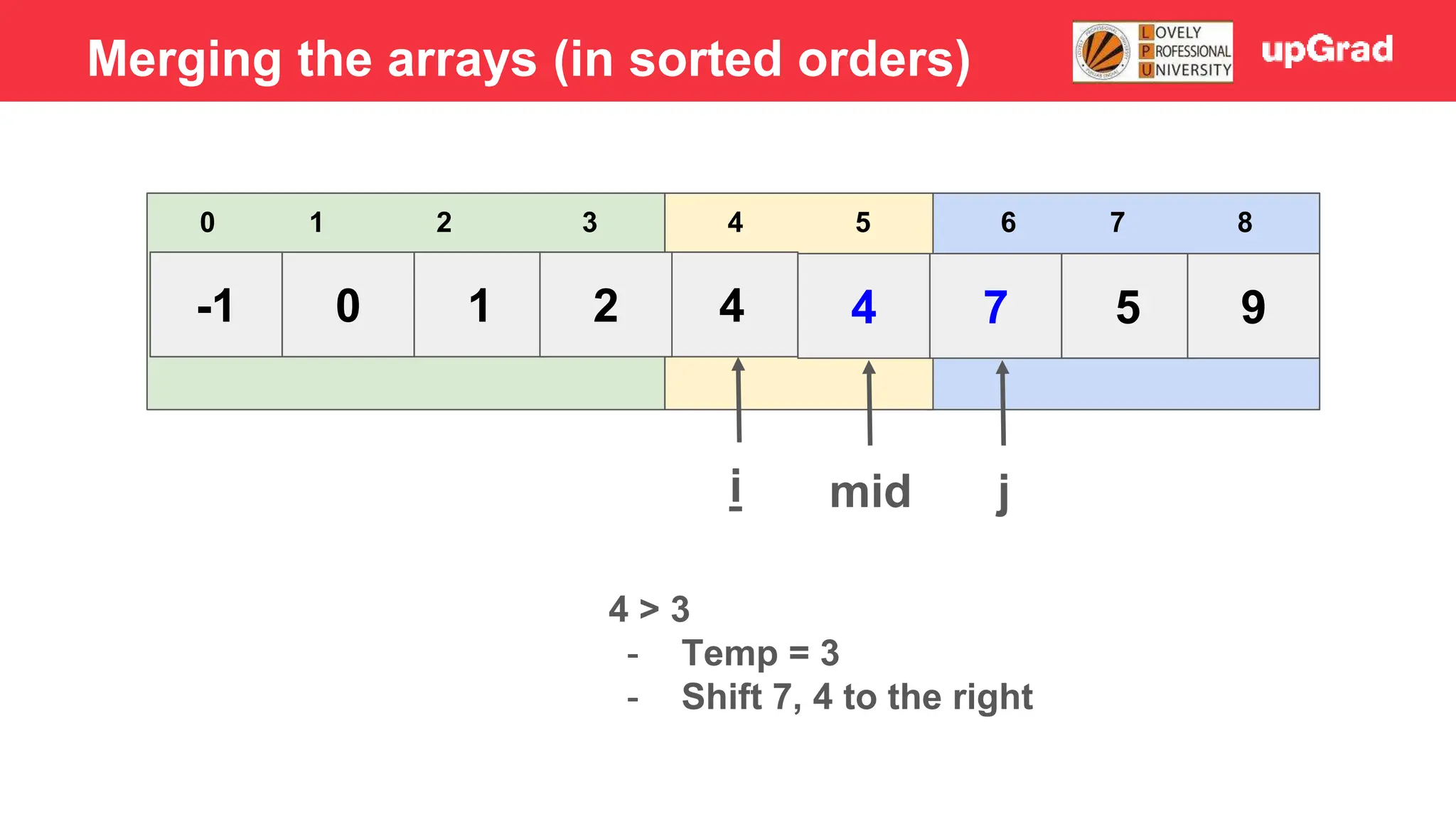
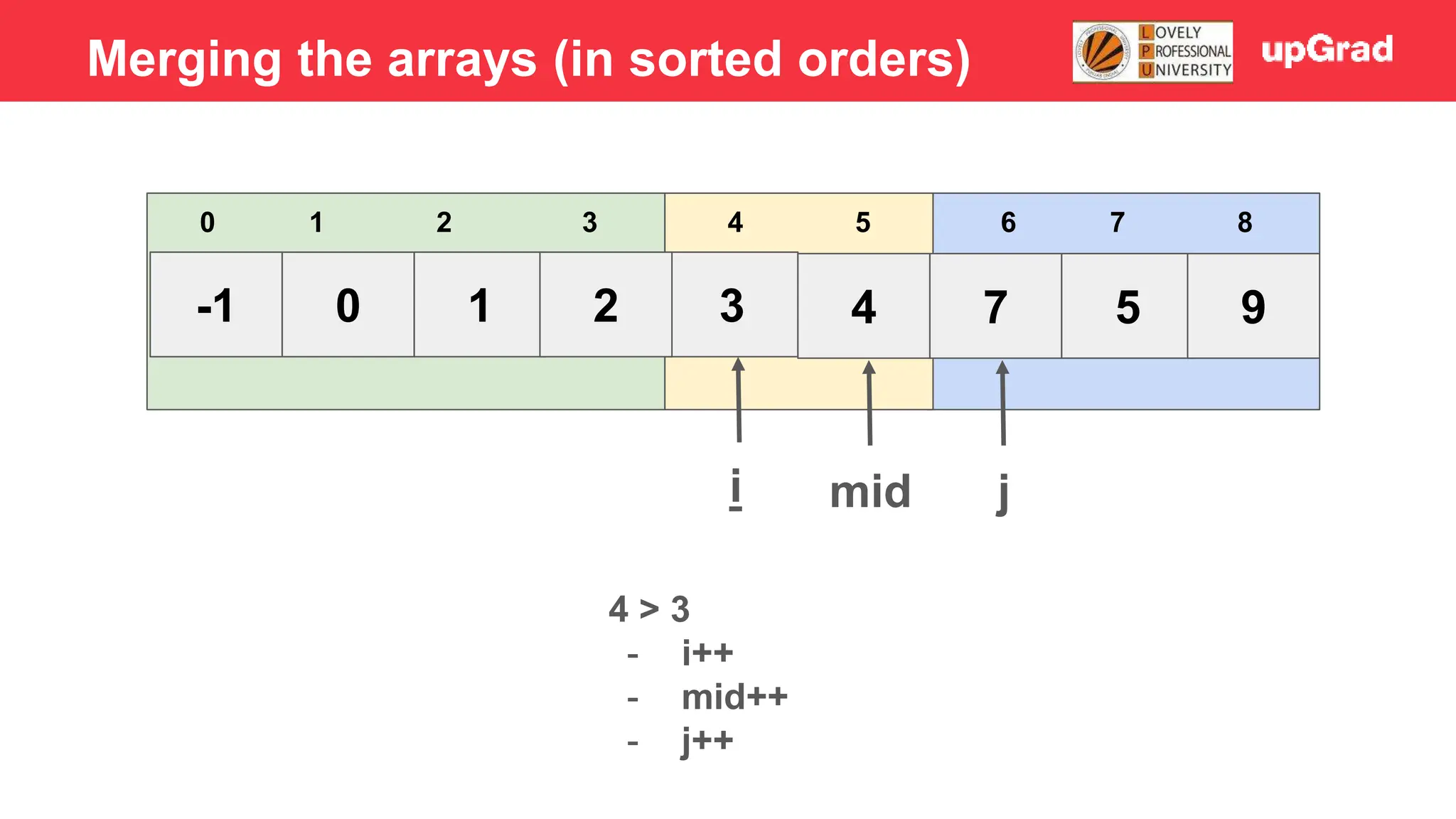
![-1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - Temp = 3 - Shift 7, 4 to the right - Arr[i] = temp Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-39-2048.jpg)
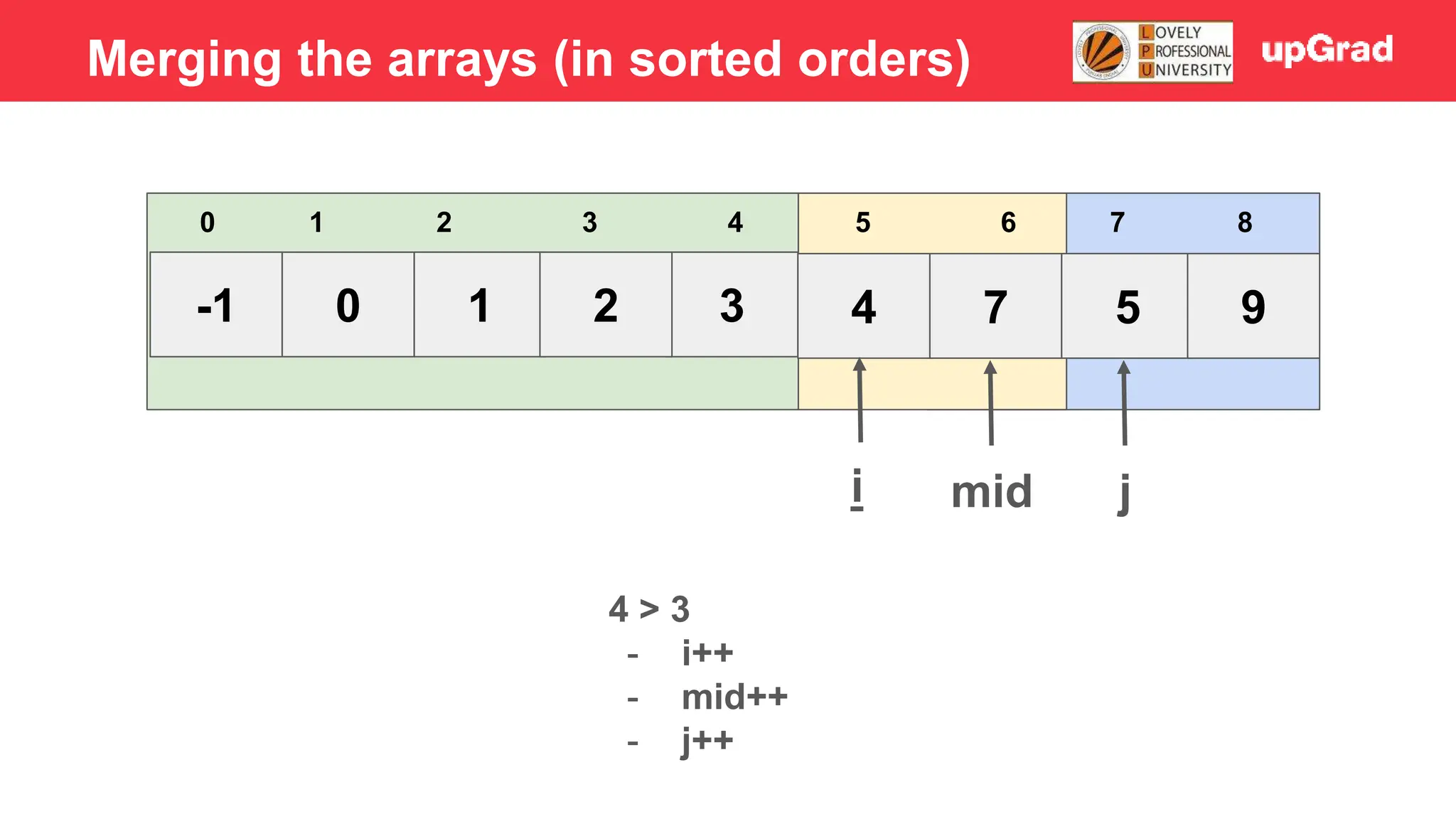
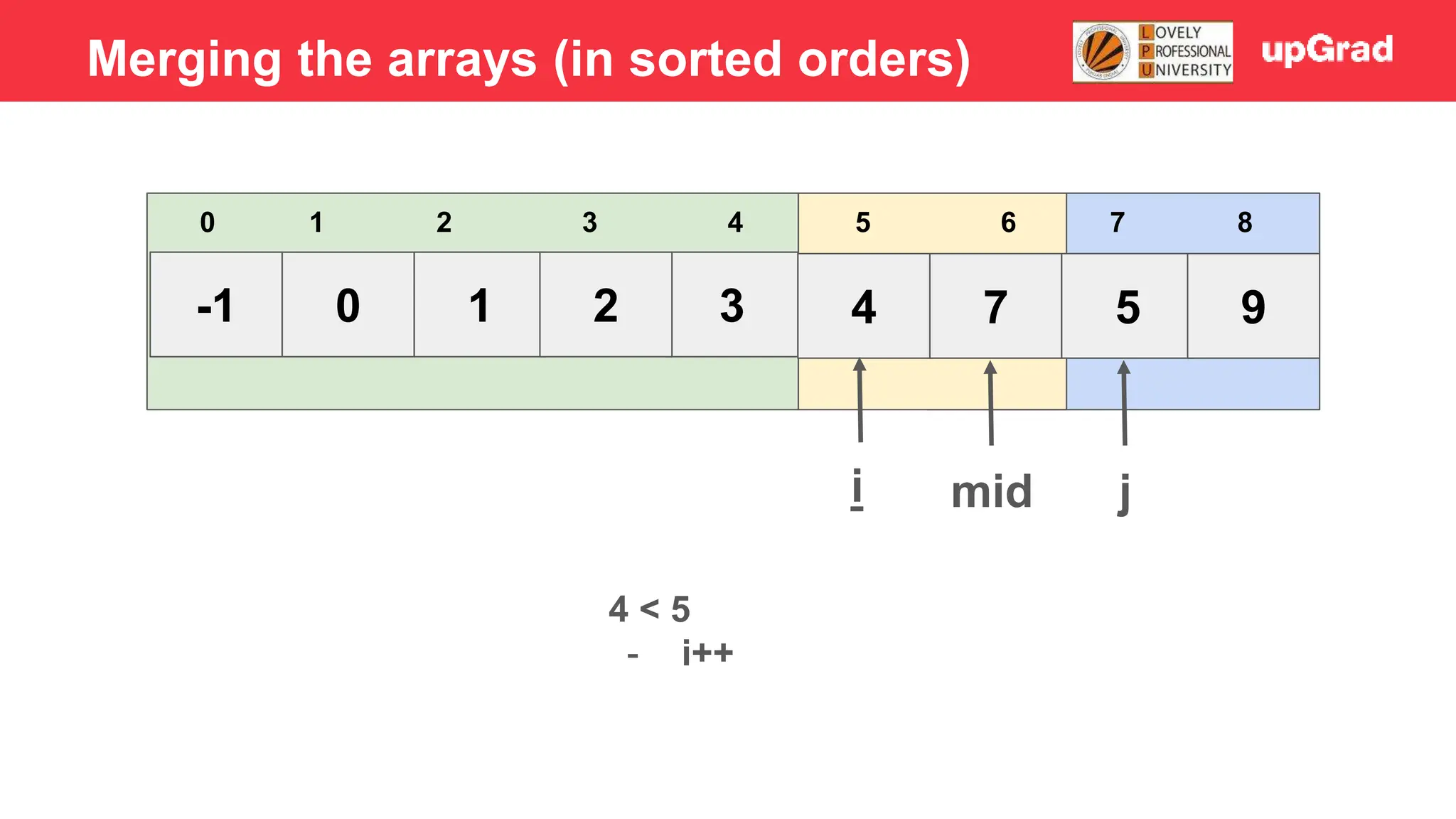
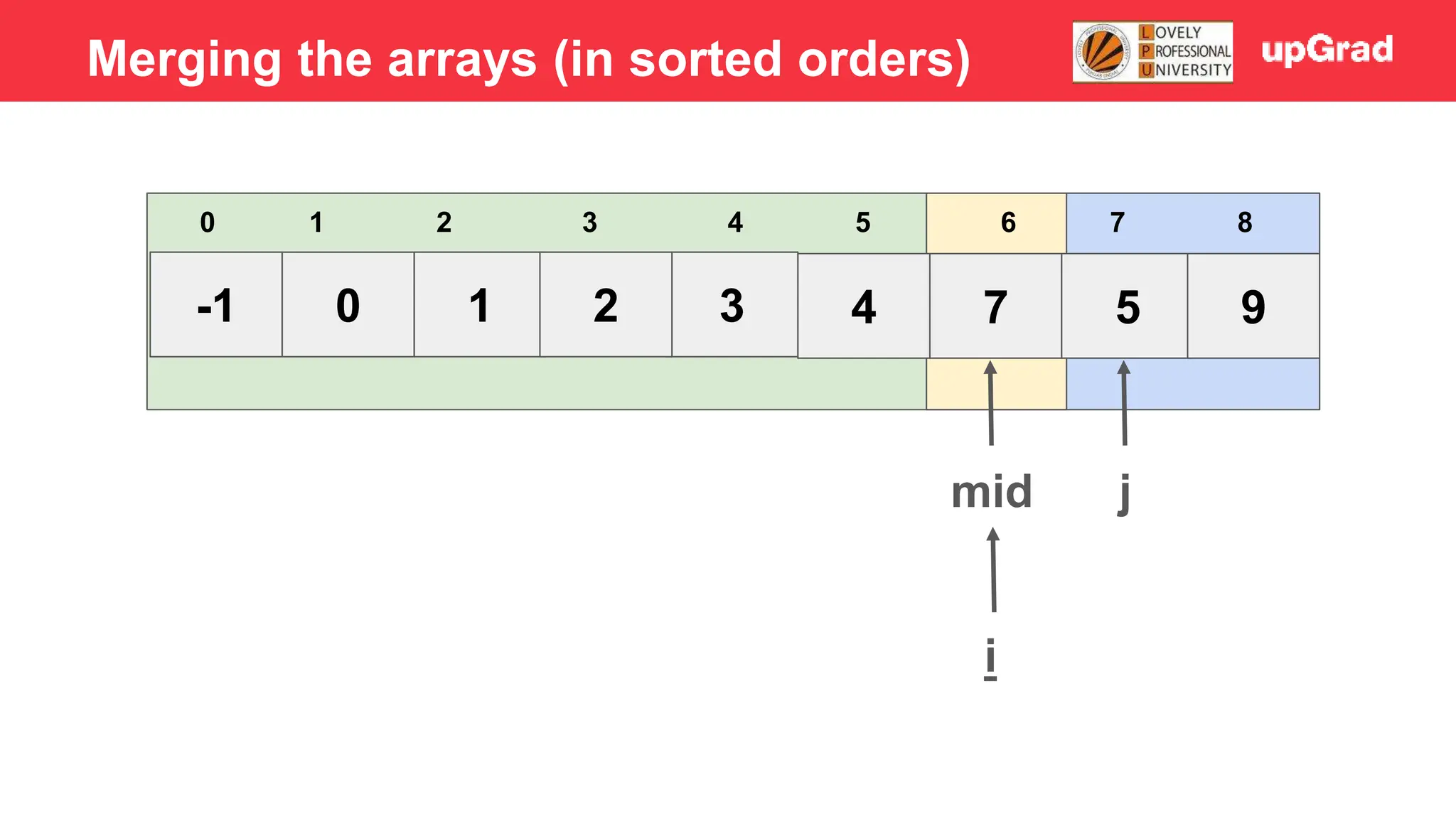
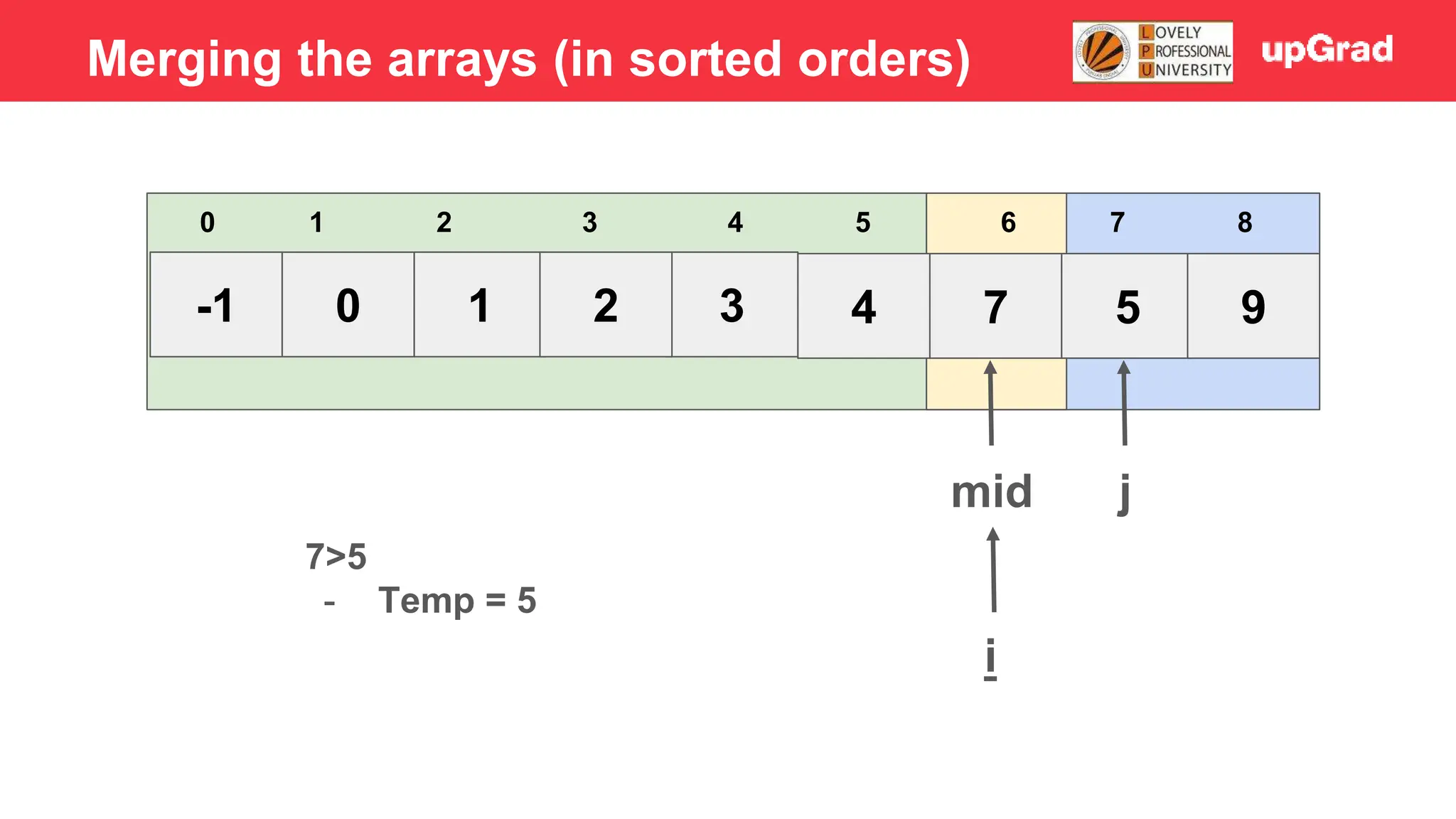

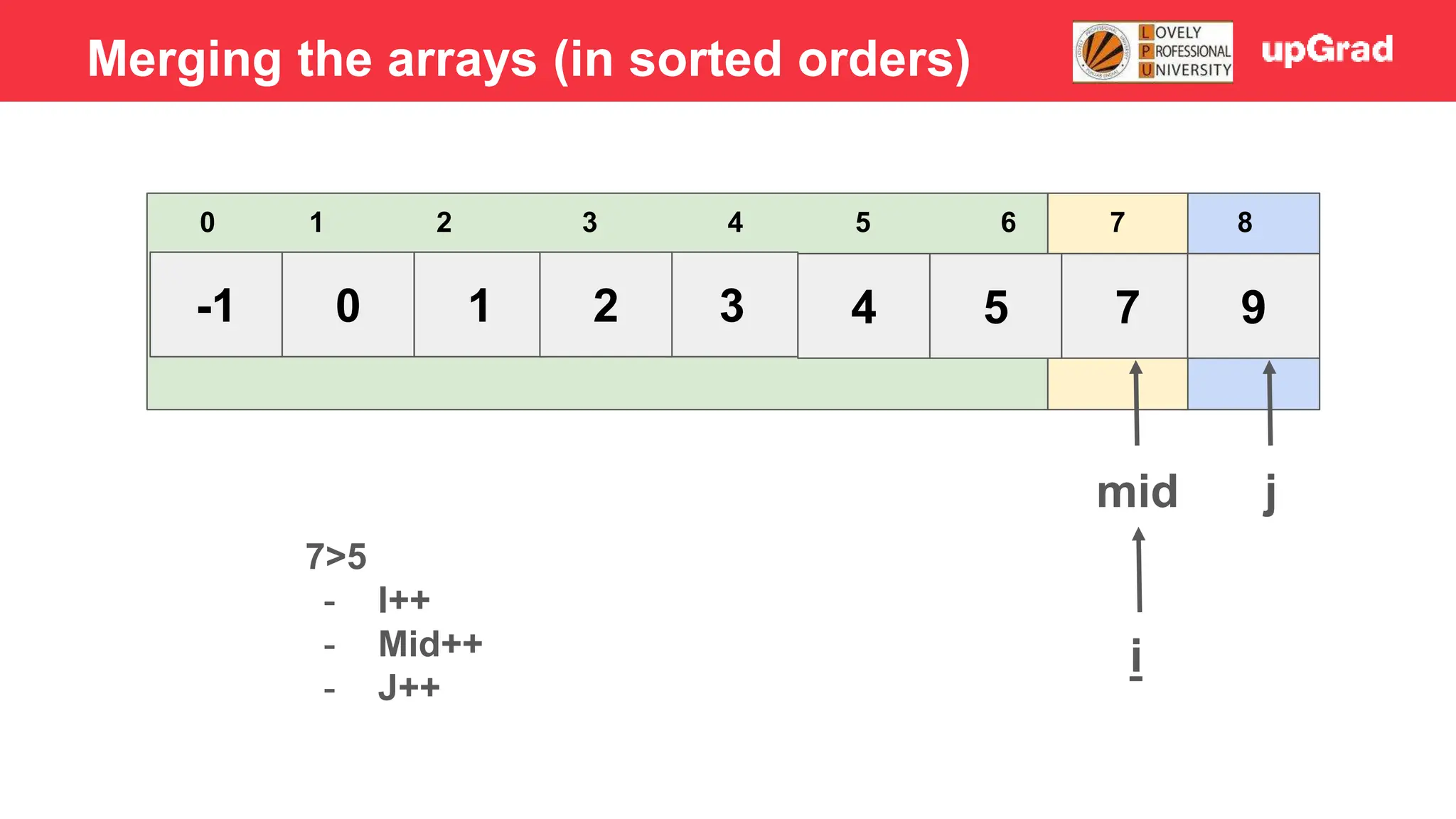
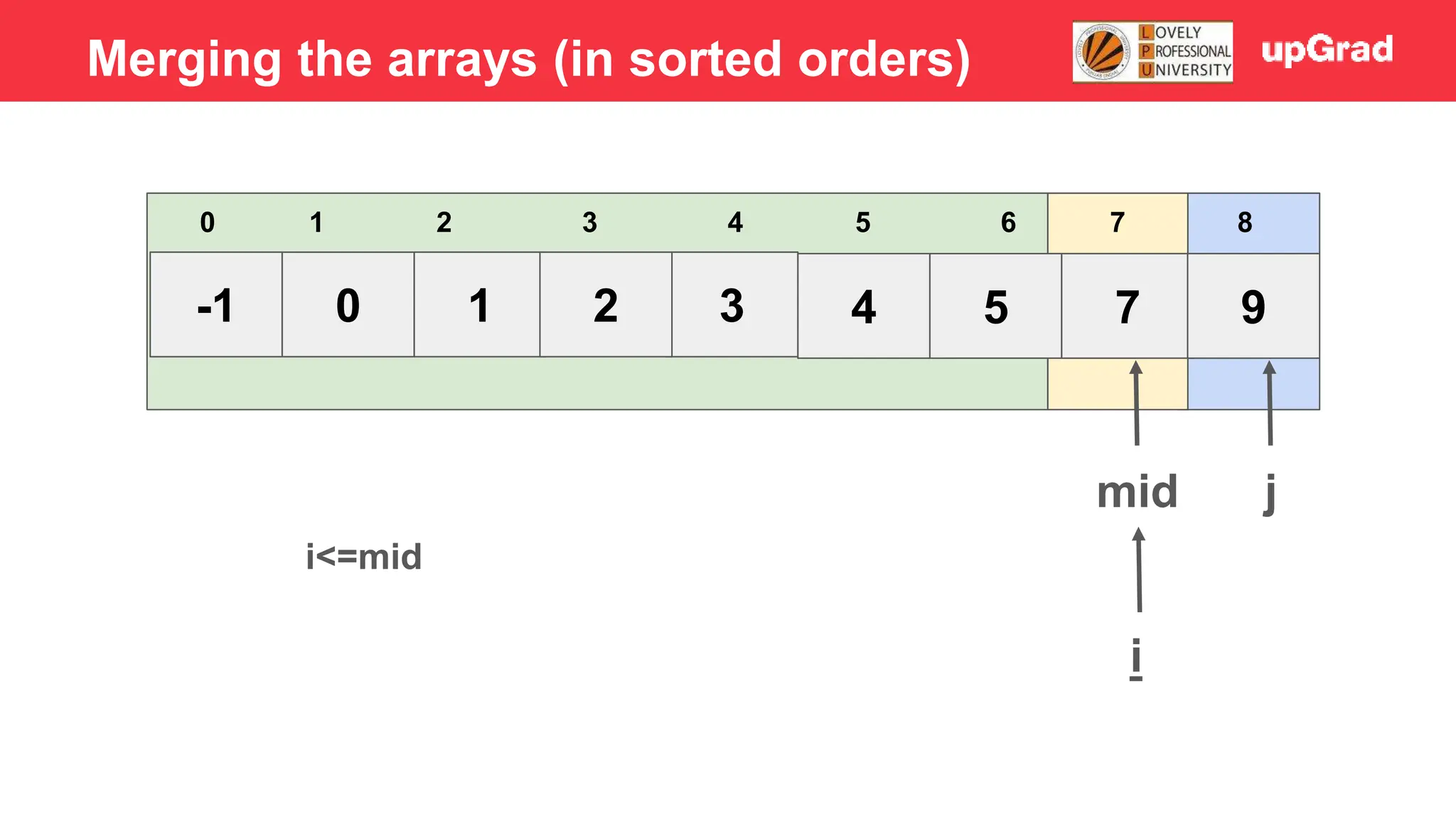
![-1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 i j mid 7>5 - Temp = 5 - Shift 7 to right - Arr[i] = temp Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-46-2048.jpg)












![1 9 7 4 0 5 3 2 -1 maxHeapify Method: maxHeapify(arr, N, currentIndex) Arr = the array containing elements [Root is at 0] N = the length of current heap currentIndex = where maxHeapification starts Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-72-2048.jpg)








![1 9 7 4 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 We have sent zero down the heap. . which may violate heap property with its own children. . [Note: IndexOfLargest will be at a position from where the largest element was picked for swapping,i.e, Left child or right child. If the swapping happened at all] Therefore, call maxHeapify(arr, N=9, currentIndex = indexOfLargest) currentIndex leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-81-2048.jpg)









![7 4 -1 1 5 -1 3 0 9 3 4 5 0 1 2 6 7 8 Now do the mixheapify on index 5 Left child index of index 5 is 11 [outside the range of current heap] Right child is also outside the range of current Heap (that is 8) Therefore no more swapping is involved maxHeapify(arr, N=8, currentIndex = 0) Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/75/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-91-2048.jpg)




