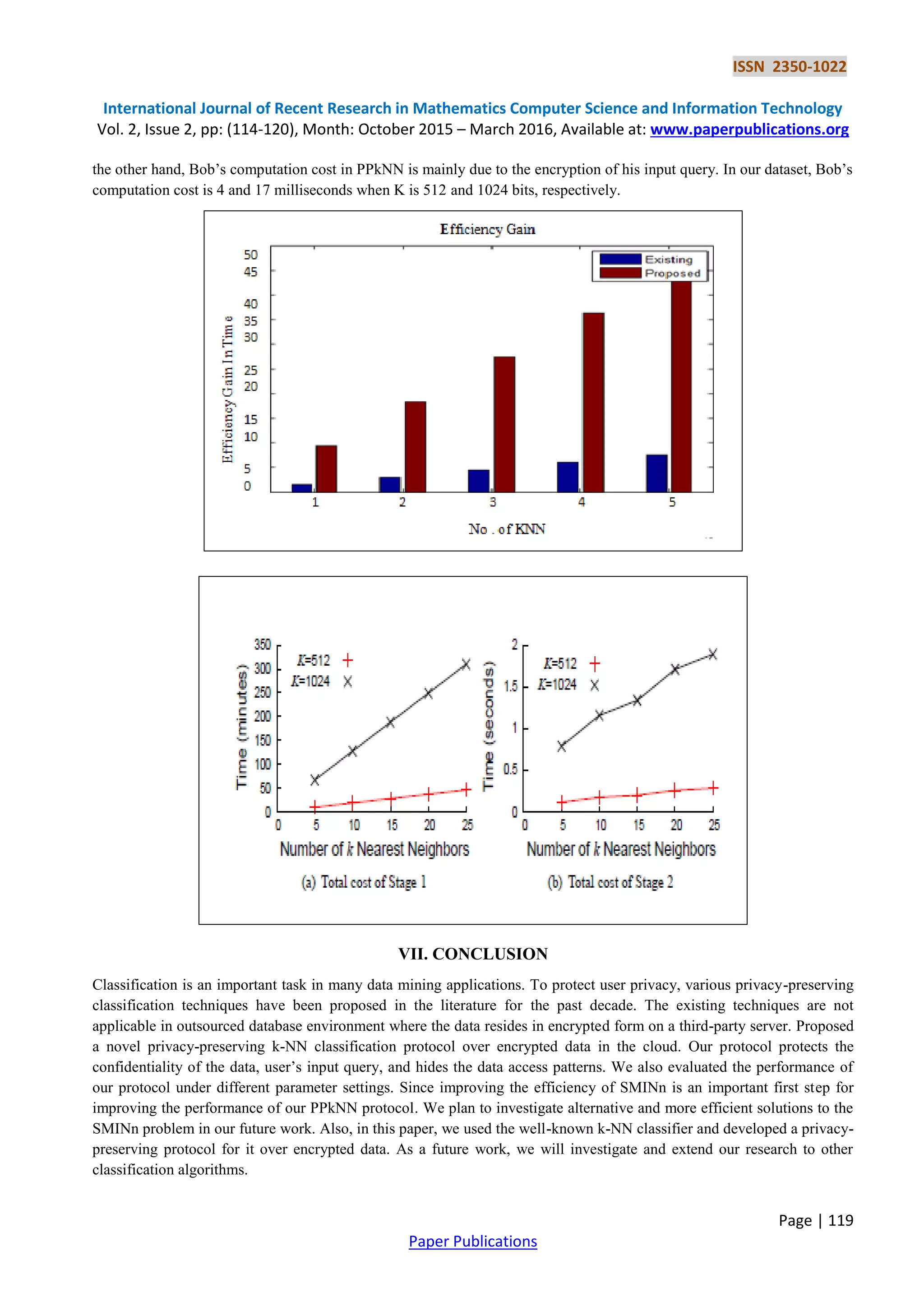
This document presents a novel privacy-preserving k-nearest neighbor (ppknn) classification protocol designed for securely classifying data outsourced to the cloud. The protocol addresses key privacy issues such as confidentiality of encrypted data, user query privacy, and protection of data access patterns, utilizing the Paillier cryptosystem for encryption. Experimental analysis demonstrates the protocol's efficiency and security under a semi-honest model, highlighting its advancements over existing methods in handling sensitive data.


![ISSN 2350-1022 International Journal of Recent Research in Mathematics Computer Science and Information Technology Vol. 2, Issue 2, pp: (114-120), Month: October 2015 – March 2016, Available at: www.paperpublications.org Page | 116 Paper Publications • Stage 2 - Secure Computation of Majority Class (SCMCk): Following from Stage 1, C1 and C2 jointly compute the class label with a majority voting among the k-nearest neighbors of q. At the end of this step, only Bob knows the class label corresponding to his input query record q. The main steps involved in the proposed PPkNN protocol are as shown in Algorithm. We now explain each of the two stages in PPkNN in detail. The Paillier cryptosystem is an additive homomorphic and probabilistic asymmetric encryption scheme. The encryption scheme is semantically secure. We simply use the well-known Paillier scheme in our implementations. However, to be more specific, in this paper we use the original Paillier cryptosystem. Key generation : Randomly generate the prime numbers p and q. Calculate : n = p*q and phi= (p-1)*(q-1) Find : g=n+1 and λ=lcm (p-1,q-1) μ=(L(gλ modn2 ))-1 mod n Where, L (u) = u-1/n u = gλ modn2 Encryption : C=gm .rn modn2 Where, C=cipher text m=message Decryption : D=Lt*μ mod n Where, t=c λ mod n2 Lt= (t-1)/n 3.1. Stage 2: Secure Computation of Majority Class (SCMCk): Without loss of generality, suppose Alice’s dataset D consists of w unique class labels denoted by c = (c1, . .cw). We assume that Alice outsources her list of encrypted classes to C1. That is, Alice outsources (Epk (c1), . ,Epk (cw)) to C1 along with her encrypted database D′ during the data outsourcing step. Note that, for security reasons, Alice may add dummy categories into the list to protect the number of class labels, i.e., w from C1 and C2. However, for simplicity, we assume that Alice does not add any dummy categories to c. During Stage 2, C1 with private inputs Ʌ=(Epk(c1), . . . ,Epk(cw)) and Ʌ′ = (Epk(c1’), . . . ,Epk(ck’)), and C2 with sk securely compute Epk(cq). Here cq denotes the majority class label among c1’, . . . , ck’. At the end of stage 2, only Bob knows the class label cq. The overall steps involved in Stage 2 are shown in Algorithm. To start with, C1 and C2 jointly compute the encrypted frequencies of each class label using the k-nearest set as input. That is, they compute Epk(f (ci)) using(Ʌ,Ʌ′) as C1’s input to the secure frequency (SF) protocol, for 1 ≤ i ≤ w. The output (Epk (f(c1)), . . . ,Epk(f(cw))) is known only to C1. Then, C1 with Epk(f (ci)) andC2 with sk involve in the secure bit decomposition (SBD) protocol to compute [f (ci)], that is, vector of encryptions of the individual bits of f (ci), for 1 ≤ I ≤ w. After this, C1 and C2 jointly involve in the SMAXw protocol. Briefly, SMAXw utilizes the sub-routine SMAX to eventually compute ([fmax], Epk (cq)) in an iterative fashion. Here [fmax] =[max(f(c1), . . . , f(cw))] and cq denotes the majority class out of Ʌ′. At the end, the output ([fmax], Epk (cq)) is known only to C1. After this,C1 computes q = Epk(cq + rq),where rq is a random number in ZN known only to C1. Then, C1 sends q to C2 and rq to Bob. Upon receiving q, C2 decrypts it to get the randomized majority class label ′q = Dsk(q) and sends it to Bob. Finally, upon receiving rq from C1 and ′q from C2, Bob computes the output class label corresponding to q as cq = q − rq mod N. 3.2. Security Analysis of PPkNN under the Semi-honest Model: Here we provide a formal security proof for the proposed PPkNN protocol under the semi-honest model. Due to the encryption of q and by semantic security of the Paillier cryptosystem, Bob’s input query q is protected from Alice, C1 and C2 in our PPkNN protocol.](https://image.slidesharecdn.com/secureencrypteddata-604-170106063828/75/Secure-Encrypted-Data-in-Cloud-Based-Environment-3-2048.jpg)
![ISSN 2350-1022 International Journal of Recent Research in Mathematics Computer Science and Information Technology Vol. 2, Issue 2, pp: (114-120), Month: October 2015 – March 2016, Available at: www.paperpublications.org Page | 117 Paper Publications Algorithm: SCMCk (Epk (c1’), . . . ,Epk (ck’)) → cq Require: (Epk (c1), . . . , Eok (cw)), (Epk (c1′), . . . ,Epk(ck′))are known only to C1; sk is known only to C2 1: C1 and C2: (a). (Epk(f(c1)), . . . ,E(f(cw))) ← SF(Ʌ,Ʌ’), where Ʌ =(Epk(c1), . . . ,Epk(cw)), Ʌ ′ = (Epk(c1′), . . . ,Epk(ck′)) (b). for i = 1 to w do: • [f (ci)] ← SBD(Epk(f (ci))) (c). ([fmax],Epk(cq)) ← SMAXw(Ψ1, . . . , Ψw), where Ψi = ([f (ci)],Epk (ci)), for 1 ≤ i ≤ w 2: C1: (a). γq ← Epk(cq) * Epk(rq), where rq ∈R ZN (b). Send γq to C2 and rq to Bob 3: C2: (a). Receive γq from C1 (b). γ′q ← Dsk(γq); send γ′q to Bob 4: Bob: (a). Receive rq from C1 and γ′q from C2 (b). cq ← γ′q − rq mod N The goal of PPkNN is to protect data confidentiality and hide data access patterns. In this paper, to prove a protocol’s security under the semi-honest model, we adopted the well-known security definitions from the literature of secure multiparty computation (SMC). IV. SYSTEM OVERVIEW Read the car evaluation dataset from KDD. It consists of 1,728 records and six attributes. There is a separate class attribute and the dataset is categorized into four different classes. Encrypt the dataset attribute-wise, using the Bitwise XOR operation. The Bitwise XOR operation split the string data by removing comas. Strings are converted into binary format using ASCII keyword. Convert the binary values into encrypted format by using Paillier cryptosystem. The Paillier cryptosystem is a public-key encryption scheme. It consists of 3 schemes: Key generation Encryption Decryption The encrypted data send to cloud. Then the cloud will search the similar data. That data’s are grouped together, and then collect the features of neighboring data by using SRKNN. From that data, find the majority class by means of SCMC and produce the classify data. Then analyze the efficiency of our solution through various experiments. Fig: Architecture Design](https://image.slidesharecdn.com/secureencrypteddata-604-170106063828/75/Secure-Encrypted-Data-in-Cloud-Based-Environment-4-2048.jpg)

![ISSN 2350-1022 International Journal of Recent Research in Mathematics Computer Science and Information Technology Vol. 2, Issue 2, pp: (114-120), Month: October 2015 – March 2016, Available at: www.paperpublications.org Page | 120 Paper Publications REFERENCES [1] C. C. Agrawal and P. S. Yu. A general survey of privacy-preserving data mining models and algorithms. Privacy- preserving data mining, pages 11–52, 2008. [2] R. Agrawal, J. Kiernan, R. Srikant, and Y. Xu. Order preserving encryption for numeric data. In ACM SIGMOD, pages 563–574, 2004. [3] R. Agrawal and R. Srikant. Privacy-preserving data mining. In ACM Sigmod Record, volume 29, pages 439– 450.ACM, 2000. [4] H. Hu, J. Xu, C. Ren, and B. Choi. Processing private queries over untrusted data cloud through privacy homomorphism. In IEEE ICDE, pages 601–612, 2011. [5] R. J. Bayardo and R. Agrawal. Data privacy through optimal k-anonymization. In IEE ICDE, pages 217–228, 2005. [6] X. Xiao, F. Li, and B. Yao, “Secure nearest neighbor revisited,” in Proc. IEEE Int. Conf. Data Eng., 2013, pp. 733– 744. [7] Y. Elmehdwi, B. K. Samanthula, and W. Jiang, “Secure k-nearest neighbor query over encrypted data in outsourced environments,” in Proc. IEEE 30th Int. Conf. Data Eng., 2014, pp. 664–675. [8] Y. Qi and M. J. Atallah, “Efficient privacy-preserving k-nearest neighbor search,” in Proc. IEEE 28th Int. Conf. Distrib. Comput.Syst. 2008, pp. 311–319. [9] M. Bohanec and B. Zupan. The UCI KDD Archive. University of California, Department of Information and Computer Science, Irvine, CA, 1997. [10] Y. Huang, D. Evans, J. Katz, and L. Malka, “Faster secure two-party computation using garbled circuits,” in Proc. 20th USENIX Conf. Security, 2011, pp. 35–35.](https://image.slidesharecdn.com/secureencrypteddata-604-170106063828/75/Secure-Encrypted-Data-in-Cloud-Based-Environment-7-2048.jpg)