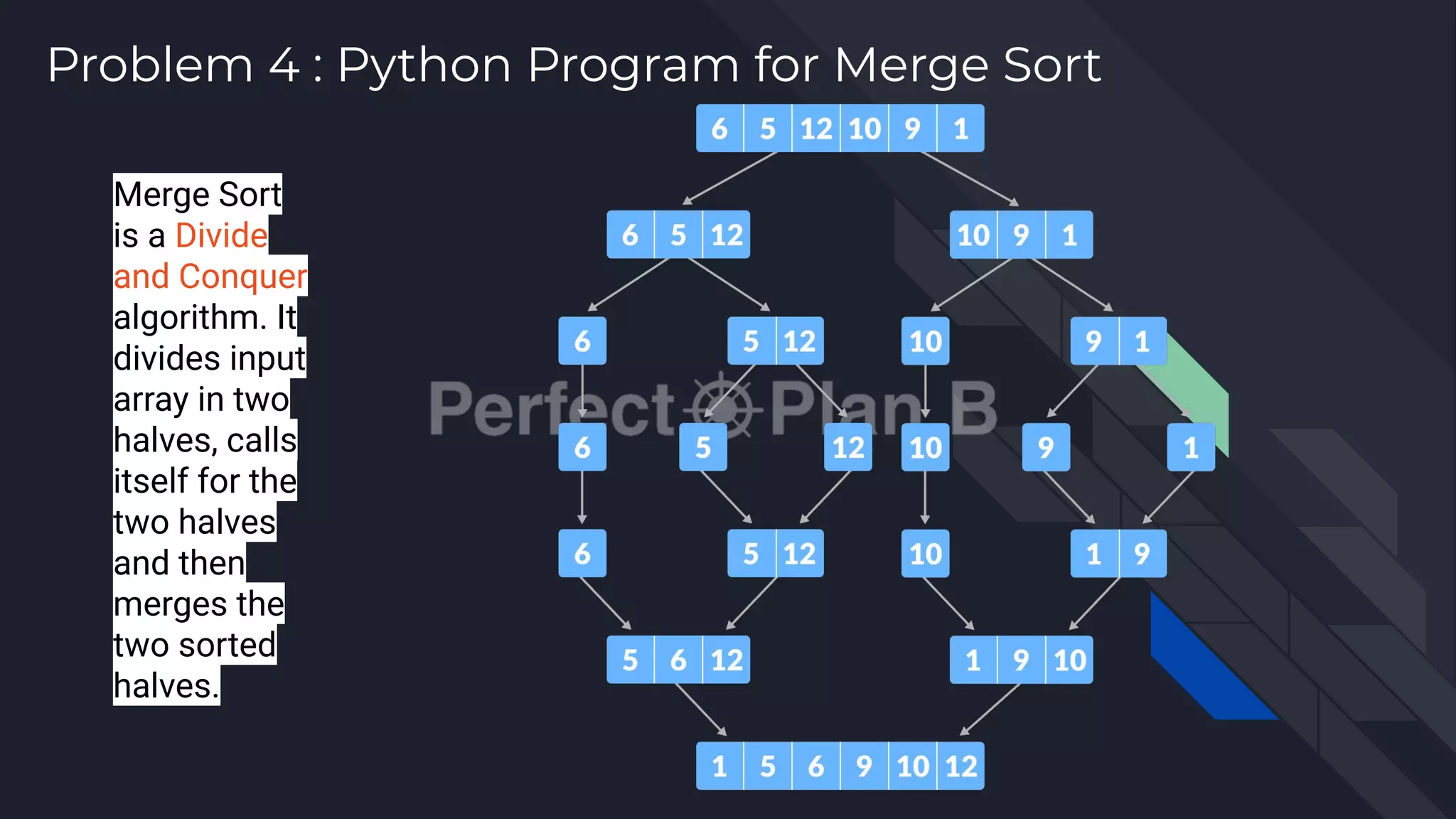
The document provides Python code solutions for common sorting and searching algorithms, including linear search, binary search, quicksort, and merge sort. It includes examples and explanations of how each algorithm works. Problems 1 and 2 cover linear and binary search algorithms to find a target value in a list. Problems 3 and 4 provide recursive and iterative implementations of quicksort and merge sort algorithms to fully sort a list from lowest to highest values.

![Problem 1 : Python Program for Linear Search Problem: Given an array arr[] of n elements, write a function to search a given element x in arr[]. Examples : Input : arr[] = {10, 20, 80, 30, 60, 50, 110, 100, 130, 170} x = 110; Output : 6 Element x is present at index 6 Input : arr[] = {10, 20, 80, 30, 60, 50, 110, 100, 130, 170} x = 175; Output : -1 Element x is not present in arr[].](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-2-2048.jpg)
![Solution: Python Program for Linear Search # Searching an element in a list/array in python # can be simply done using 'in' operator # Example: # if x in arr: # print arr.index(x) # If you want to implement Linear Search in python # Linearly search x in arr[] # If x is present then return its location # else return -1 def search(arr, x): for i in range(len(arr)): if arr[i] == x: return i return -1](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-3-2048.jpg)
![Problem 2 : Python Program for Binary Search (Recursive and Iterative) Examples: Input : [2, 3, 4, 10, 40] X = 10 Output : Element is present at index 3](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-4-2048.jpg)
![Solution : Python Program for Binary Search (Recursive and Iterative) # Python 3 program for recursive binary search. # Returns index of x in arr if present, else -1 def binary_search(arr, low, high, x): # Check base case if high >= low: mid = (high + low) // 2 # If element is present at the middle itself if arr[mid] == x: return mid # If element is smaller than mid, then it can only # be present in left subarray elif arr[mid] > x: return binary_search(arr, low, mid - 1, x) # Else the element can only be present in right subarray else: return binary_search(arr, mid + 1, high, x) else: # Element is not present in the array return -1 # Test array arr = [ 2, 3, 4, 10, 40 ] x = 10 # Function call result = binary_search(arr, 0, len(arr)-1, x) if result != -1: # In Python 2: print "Element present at index %d" % result print("Element is present at index", str(result)) else: # In Python 2: print "Element not present in array" print("Element is not present in array")](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-5-2048.jpg)
![Solution : Python Program for Binary Search (Iterative) # Iterative Binary Search Function # It returns index of x in given array arr if present, # else returns -1 def binary_search(arr, x): low = 0 high = len(arr) - 1 # optimization: pooled variable mid = 0 while low <= high: mid = (high + low) // 2 # Check if x is present at mid if arr[mid] < x: low = mid + 1 # If x is greater, ignore left half elif arr[mid] > x: high = mid - 1 # If x is smaller, ignore right half else: return mid # If we reach here, then the element was not present return -1 # Test array arr = [ 2, 3, 4, 10, 40 ] x = 10 # Function call result = binary_search(arr, 0, len(arr)-1, x) if result != -1: # In Python 2: print "Element present at index %d" % result print("Element is present at index", str(result)) else: # In Python 2: print "Element not present in array" print("Element is not present in array")](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-6-2048.jpg)

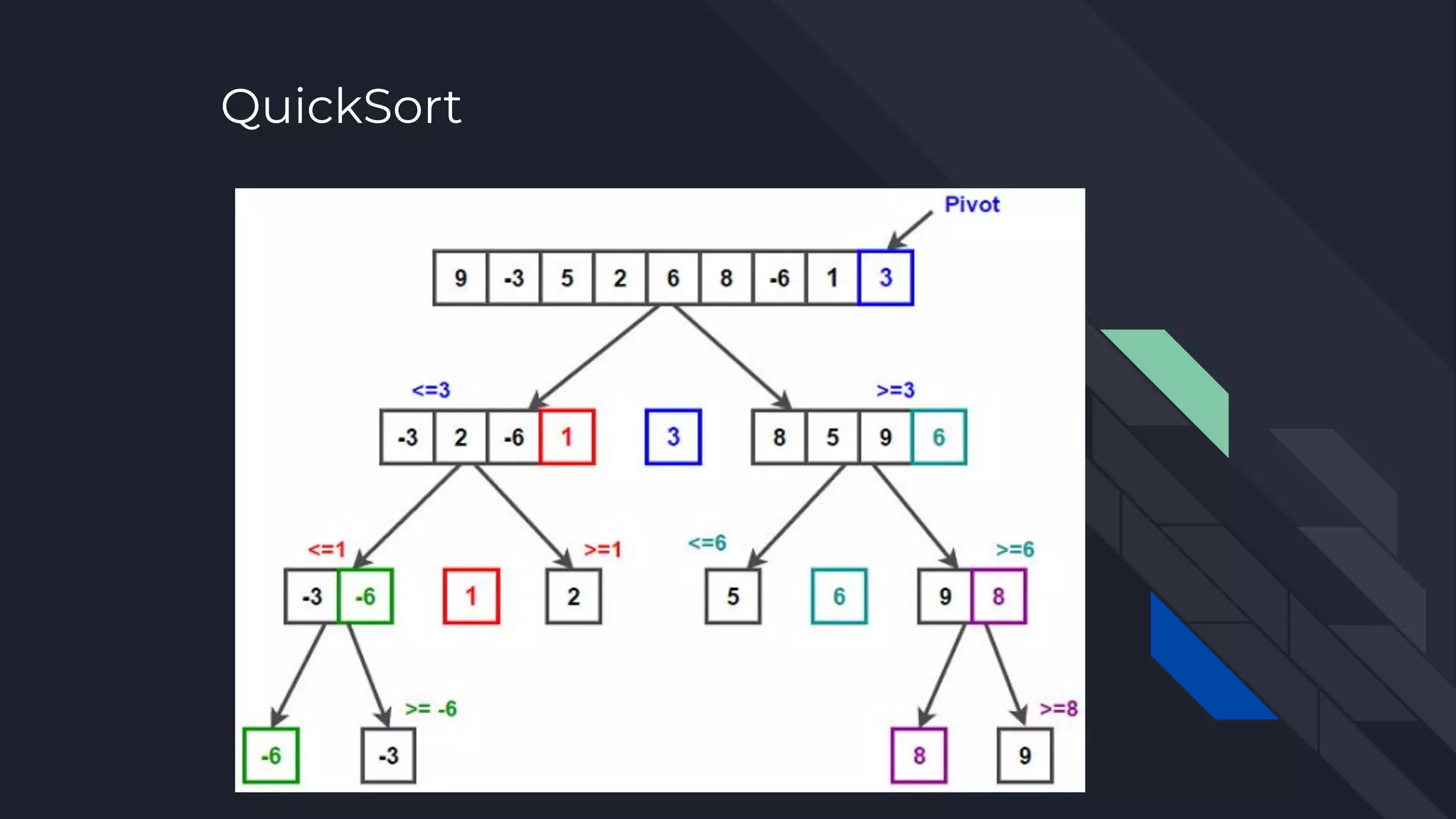
![Solution : Python Program for QuickSort (PseudoCode) /* low --> Starting index, high --> Ending index */ quickSort(arr[], low, high) { if (low < high) { /* pi is partitioning index, arr[p] is now at right place */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Before pi quickSort(arr, pi + 1, high); // After pi } }](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-9-2048.jpg)
![Solution : Python Program for QuickSort # Python program for implementation of Quicksort Sort # This function takes last element as pivot, places # the pivot element at its correct position in sorted # array, and places all smaller (smaller than pivot) # to left of pivot and all greater elements to right # of pivot def partition(arr,low,high): i = ( low-1 ) # index of smaller element pivot = arr[high] # pivot for j in range(low , high): # If current element is smaller than or # equal to pivot if arr[j] <= pivot: # increment index of smaller element i = i+1 arr[i],arr[j] = arr[j],arr[i] arr[i+1],arr[high] = arr[high],arr[i+1] return ( i+1 ) # The main function that implements QuickSort # arr[] --> Array to be sorted, # low --> Starting index, # high --> Ending index # Function to do Quick sort def quickSort(arr,low,high): if low < high: # pi is partitioning index, arr[p] is now # at right place pi = partition(arr,low,high) # Separately sort elements before # partition and after partition quickSort(arr, low, pi-1) quickSort(arr, pi+1, high) # Driver code to test above arr = [10, 7, 8, 9, 1, 5] n = len(arr) quickSort(arr,0,n-1) print ("Sorted array is:") for i in range(n): print ("%d" %arr[i]),](https://image.slidesharecdn.com/searchingsortingandcomplexityanalysisinds-221106170522-6c00dbd4/75/Searching-Sorting-and-Complexity-analysis-in-DS-pdf-10-2048.jpg)