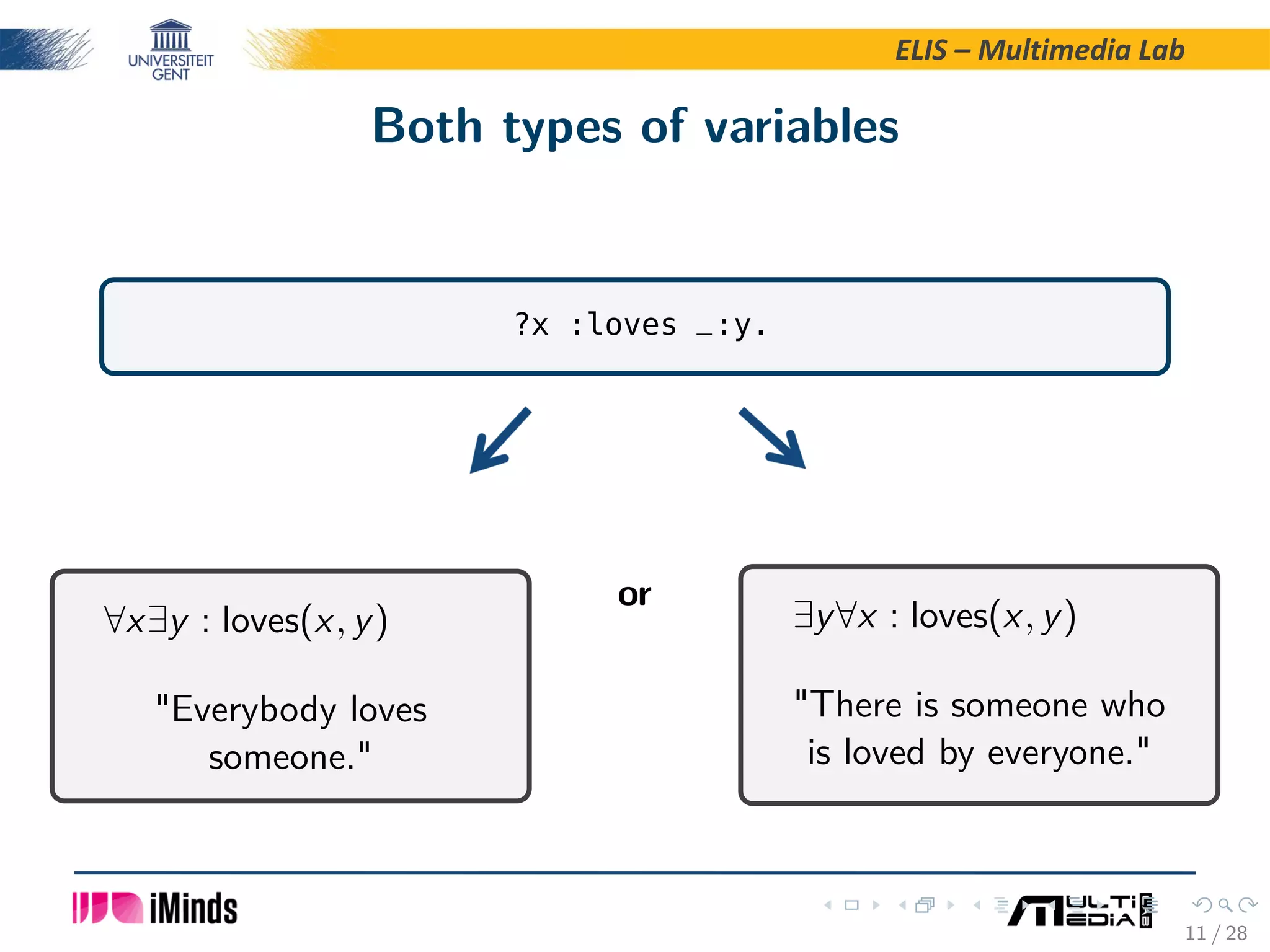
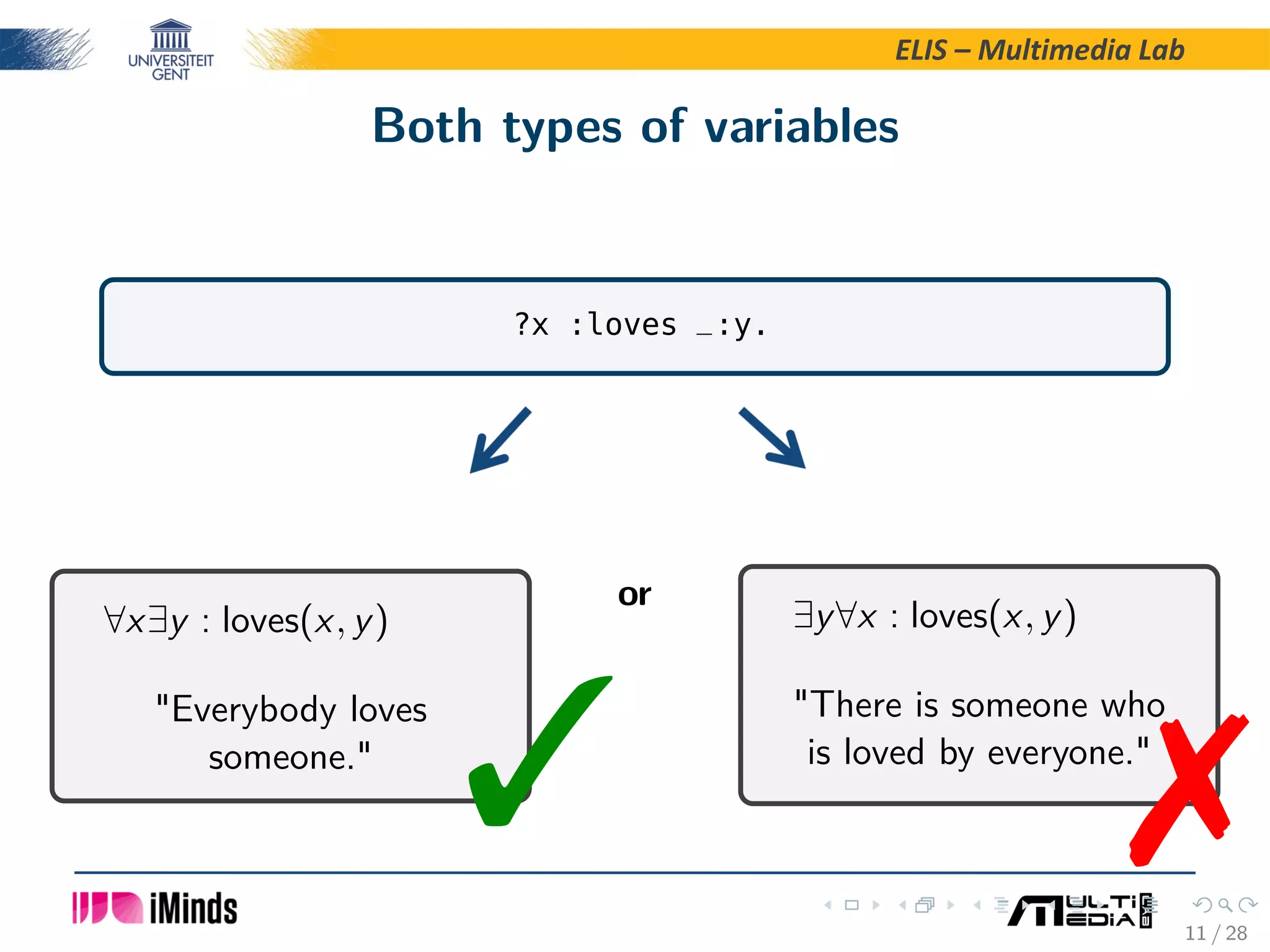
The document discusses the semantics of Notation3 logic, which is a rule logic for the Semantic Web invented by Tim Berners-Lee and Dan Connolly. Notation3 logic allows for implicit quantification using blank nodes and variables starting with question marks. The semantics of Notation3 logic is not fully defined, though implementations provide some guidance. The paper proposes handling implicit quantification by defining the scope of existential variables as the formula they occur in, while universal variables have scope that includes descendant formulas. A formal semantics is introduced using substitutions and their component-wise and total applications to formulas.







































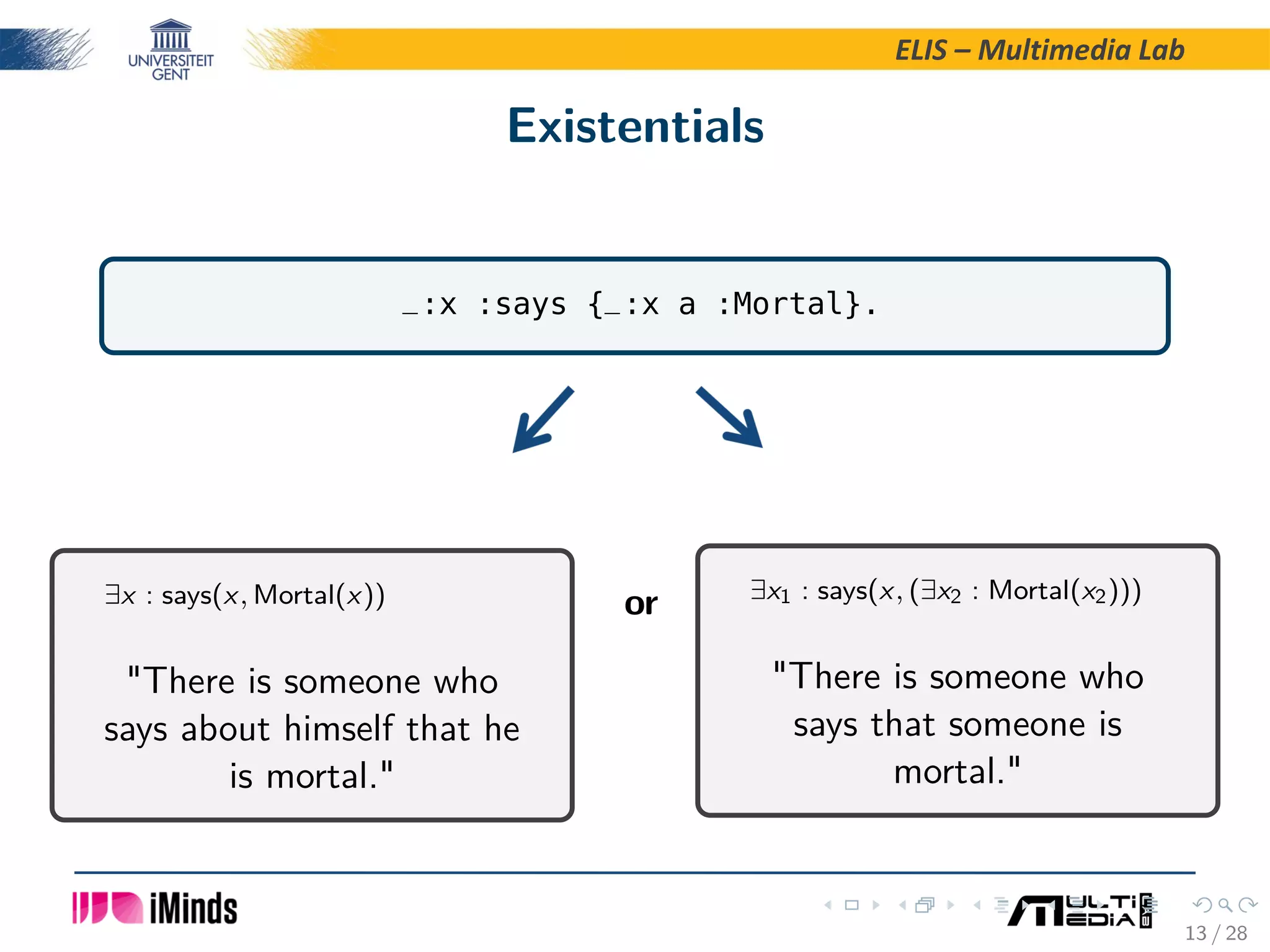

![ELIS – Multimedia Lab Existentials “When formulae are nested, _: blank nodes syntax [is] used to only identify blank node in the formula it occurs directly in. It is an arbitrary temporary name for a symbol which is existentially quantified within the current formula (not the whole file). They can only be used within a single formula, and not within nested formulae.” Source: W3C Team submission; cwm and EYE give the same result. 14 / 28](https://image.slidesharecdn.com/doerthearndtsemanticsofn3-151008084420-lva1-app6891/75/RuleML-2015-Semantics-of-Notation3-Logic-A-Solution-for-Implicit-Quantification-44-2048.jpg)






















































