Python crash course libraries numpy-1, panda.ppt

Python Crash Course Python Crash Course Numpy Numpy

Scientific Python? Scientific Python? • Extra features required: – fast, multidimensional arrays – libraries of reliable, tested scientiﬁc functions – plotting tools • NumPy is at the core of nearly every scientific Python application or module since it provides a fast N-d array datatype that can be manipulated in a vectorized form. 2

What is NumPy? What is NumPy? • NumPy is the fundamental package needed for scientific computing with Python. It contains: – a powerful N-dimensional array object – basic linear algebra functions – basic Fourier transforms – sophisticated random number capabilities – tools for integrating Fortran code – tools for integrating C/C++ code

NumPy documentation NumPy documentation • Official documentation – http://docs.scipy.org/doc/ • The NumPy book – http://web.mit.edu/dvp/Public/numpybook.pdf • Example list – https://docs.scipy.org/doc/numpy/reference/routines.html

Arrays – Numerical Python (Numpy) Arrays – Numerical Python (Numpy) • Lists ok for storing small amounts of one-dimensional data • But, can’t use directly with arithmetical operators (+, -, *, /, …) • Need efﬁcient arrays with arithmetic and better multidimensional tools • Numpy • Similar to lists, but much more capable, except ﬁxed size >>> a = [1,3,5,7,9] >>> print(a[2:4]) [5, 7] >>> b = [[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]] >>> print(b[0]) [1, 3, 5, 7, 9] >>> print(b[1][2:4]) [6, 8] >>> import numpy >>> a = [1,3,5,7,9] >>> b = [3,5,6,7,9] >>> c = a + b >>> print c [1, 3, 5, 7, 9, 3, 5, 6, 7, 9]

Numpy – N-dimensional Array manpulations Numpy – N-dimensional Array manpulations The fundamental library needed for scientific computing with Python is called NumPy. This Open Source library contains: • a powerful N-dimensional array object • advanced array slicing methods (to select array elements) • convenient array reshaping methods and it even contains 3 libraries with numerical routines: • basic linear algebra functions • basic Fourier transforms • sophisticated random number capabilities NumPy can be extended with C-code for functions where performance is highly time critical. In addition, tools are provided for integrating existing Fortran code. NumPy is a hybrid of the older NumArray and Numeric packages, and is meant to replace them both.

Numpy – Creating arrays Numpy – Creating arrays • There are a number of ways to initialize new numpy arrays, for example from – a Python list or tuples – using functions that are dedicated to generating numpy arrays, such as arange, linspace, etc. – reading data from files

The ndarray data structure The ndarray data structure • NumPy adds a new data structure to Python – the ndarray – An N-dimensional array is a homogeneous collection of “items” indexed using N integers – Defined by: 1. the shape of the array, and 2. the kind of item the array is composed of 8

Array shape Array shape • ndarrays are rectangular • The shape of the array is a tuple of N integers (one for each dimension) 9

Array item types Array item types • Every ndarray is a homogeneous collection of exactly the same data-type – every item takes up the same size block of memory – each block of memory in the array is interpreted in exactly the same way 10

Some ndarray methods Some ndarray methods • ndarray. tolist () – The contents of self as a nested list • ndarray. copy () – Return a copy of the array • ndarray. fill (scalar) – Fill an array with the scalar value 11

Some NumPy functions Some NumPy functions abs() add() binomial() cumprod() cumsum() floor() histogram() min() max() multipy() polyfit() randint() shuffle() transpose() 12

Numpy – Creating vectors Numpy – Creating vectors • From lists – numpy.array # as vectors from lists >>> a = numpy.array([1,3,5,7,9]) >>> b = numpy.array([3,5,6,7,9]) >>> c = a + b >>> print(c) [4, 8, 11, 14, 18] >>> type(c) (<type 'numpy.ndarray'>) >>> c.shape (5,)

Numpy – Creating matrices Numpy – Creating matrices >>> l = [[1, 2, 3], [3, 6, 9], [2, 4, 6]] # create a list >>> a = numpy.array(l) # convert a list to an array >>>print(a) [[1 2 3] [3 6 9] [2 4 6]] >>> a.shape (3, 3) >>> print(a.dtype) # get type of an array int64 # or directly as matrix >>> M = array([[1, 2], [3, 4]]) >>> M.shape (2,2) >>> M.dtype dtype('int64') #only one type >>> M[0,0] = "hello" Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: invalid literal for long() with base 10: 'hello‘ >>> M = numpy.array([[1, 2], [3, 4]], dtype=complex) >>> M array([[ 1.+0.j, 2.+0.j], [ 3.+0.j, 4.+0.j]])

Numpy – Matrices use Numpy – Matrices use >>> print(a) [[1 2 3] [3 6 9] [2 4 6]] >>> print(a[0]) # this is just like a list of lists [1 2 3] >>> print(a[1, 2]) # arrays can be given comma separated indices 9 >>> print(a[1, 1:3]) # and slices [6 9] >>> print(a[:,1]) [2 6 4] >>> a[1, 2] = 7 >>> print(a) [[1 2 3] [3 6 7] [2 4 6]] >>> a[:, 0] = [0, 9, 8] >>> print(a) [[0 2 3] [9 6 7] [8 4 6]]

Numpy – Creating arrays Numpy – Creating arrays • Generation functions >>> x = arange(0, 10, 1) # arguments: start, stop, step >>> x array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) >>> numpy.linspace(0, 10, 25) array([ 0. , 0.41666667, 0.83333333, 1.25 , 1.66666667, 2.08333333, 2.5 , 2.91666667, 3.33333333, 3.75 , 4.16666667, 4.58333333, 5. , 5.41666667, 5.83333333, 6.25 , 6.66666667, 7.08333333, 7.5 , 7.91666667, 8.33333333, 8.75 , 9.16666667, 9.58333333, 10. ]) >>> numpy.logspace(0, 10, 10, base=numpy.e) array([ 1.00000000e+00, 3.03773178e+00, 9.22781435e+00, 2.80316249e+01, 8.51525577e+01, 2.58670631e+02, 7.85771994e+02, 2.38696456e+03, 7.25095809e+03, 2.20264658e+04])

Numpy – Creating arrays Numpy – Creating arrays # a diagonal matrix >>> numpy.diag([1,2,3]) array([[1, 0, 0], [0, 2, 0], [0, 0, 3]]) >>> b = numpy.zeros(5) >>> print(b) [ 0. 0. 0. 0. 0.] >>> b.dtype dtype(‘float64’) >>> n = 1000 >>> my_int_array = numpy.zeros(n, dtype=numpy.int) >>> my_int_array.dtype dtype(‘int32’) >>> c = numpy.ones((3,3)) >>> c array([[ 1., 1., 1.], [ 1., 1., 1.], [ 1., 1., 1.]])

Numpy – array creation and use Numpy – array creation and use >>> d = numpy.arange(5) # just like range() >>> print(d) [0 1 2 3 4] >>> d[1] = 9.7 >>> print(d) # arrays keep their type even if elements changed [0 9 2 3 4] >>> print(d*0.4) # operations create a new array, with new type [ 0. 3.6 0.8 1.2 1.6] >>> d = numpy.arange(5, dtype=numpy.float) >>> print(d) [ 0. 1. 2. 3. 4.] >>> numpy.arange(3, 7, 0.5) # arbitrary start, stop and step array([ 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])

Numpy – array creation and use Numpy – array creation and use >>> x, y = numpy.mgrid[0:5, 0:5] # similar to meshgrid in MATLAB >>> x array([[0, 0, 0, 0, 0], [1, 1, 1, 1, 1], [2, 2, 2, 2, 2], [3, 3, 3, 3, 3], [4, 4, 4, 4, 4]]) # random data >>> numpy.random.rand(5,5) array([[ 0.51531133, 0.74085206, 0.99570623, 0.97064334, 0.5819413 ], [ 0.2105685 , 0.86289893, 0.13404438, 0.77967281, 0.78480563], [ 0.62687607, 0.51112285, 0.18374991, 0.2582663 , 0.58475672], [ 0.72768256, 0.08885194, 0.69519174, 0.16049876, 0.34557215], [ 0.93724333, 0.17407127, 0.1237831 , 0.96840203, 0.52790012]])

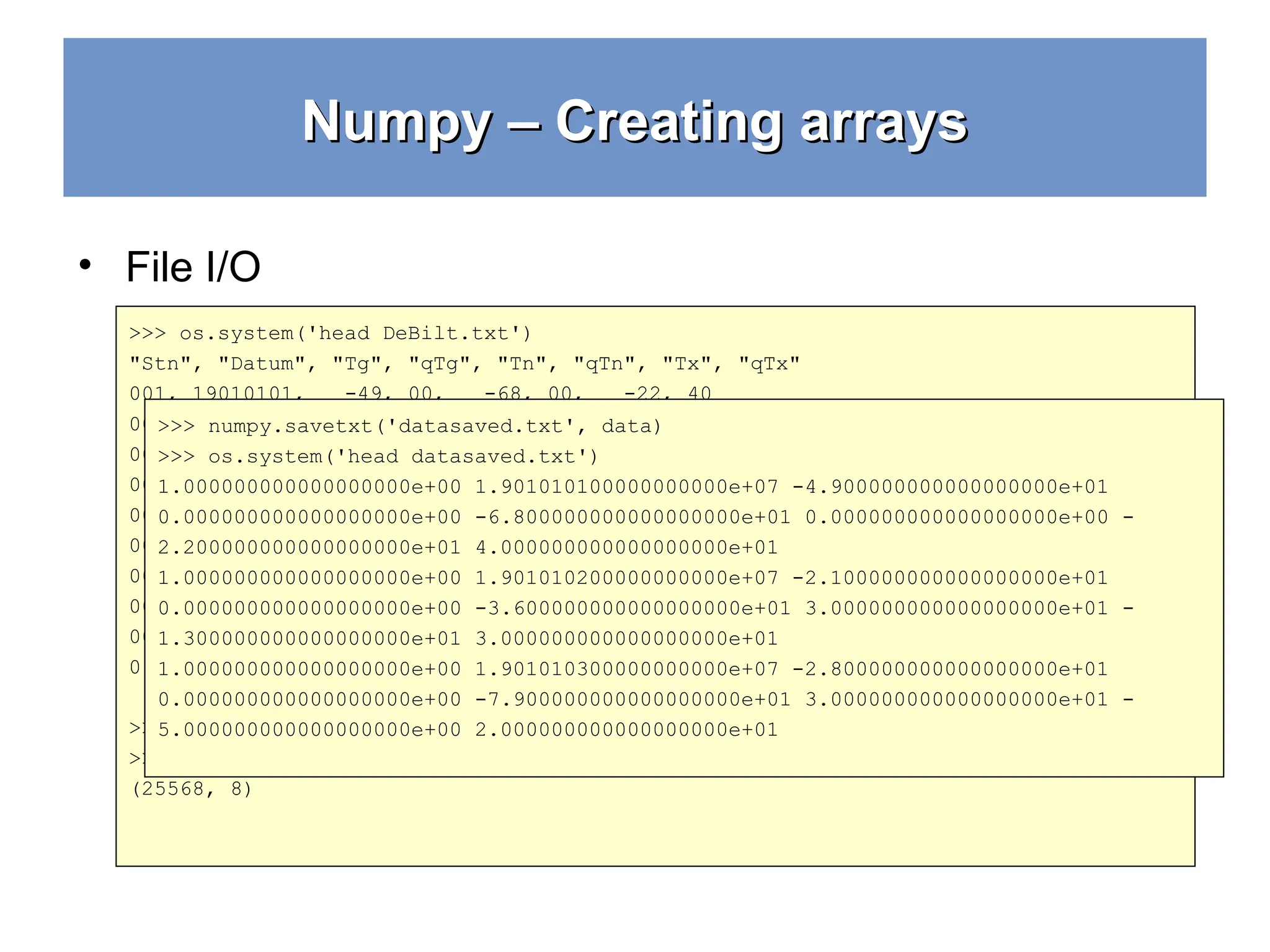
Numpy – Creating arrays Numpy – Creating arrays • File I/O >>> os.system('head DeBilt.txt') "Stn", "Datum", "Tg", "qTg", "Tn", "qTn", "Tx", "qTx" 001, 19010101, -49, 00, -68, 00, -22, 40 001, 19010102, -21, 00, -36, 30, -13, 30 001, 19010103, -28, 00, -79, 30, -5, 20 001, 19010104, -64, 00, -91, 20, -10, 00 001, 19010105, -59, 00, -84, 30, -18, 00 001, 19010106, -99, 00, -115, 30, -78, 30 001, 19010107, -91, 00, -122, 00, -66, 00 001, 19010108, -49, 00, -94, 00, -6, 00 001, 19010109, 11, 00, -27, 40, 42, 00 0 >>> data = numpy.genfromtxt('DeBilt.txt‘, delimiter=',‘, skip_header=1) >>> data.shape (25568, 8) >>> numpy.savetxt('datasaved.txt', data) >>> os.system('head datasaved.txt') 1.000000000000000000e+00 1.901010100000000000e+07 -4.900000000000000000e+01 0.000000000000000000e+00 -6.800000000000000000e+01 0.000000000000000000e+00 - 2.200000000000000000e+01 4.000000000000000000e+01 1.000000000000000000e+00 1.901010200000000000e+07 -2.100000000000000000e+01 0.000000000000000000e+00 -3.600000000000000000e+01 3.000000000000000000e+01 - 1.300000000000000000e+01 3.000000000000000000e+01 1.000000000000000000e+00 1.901010300000000000e+07 -2.800000000000000000e+01 0.000000000000000000e+00 -7.900000000000000000e+01 3.000000000000000000e+01 - 5.000000000000000000e+00 2.000000000000000000e+01

Numpy – Creating arrays Numpy – Creating arrays >>> M = numpy.random.rand(3,3) >>> M array([[ 0.84188778, 0.70928643, 0.87321035], [ 0.81885553, 0.92208501, 0.873464 ], [ 0.27111984, 0.82213106, 0.55987325]]) >>> >>> numpy.save('saved-matrix.npy', M) >>> numpy.load('saved-matrix.npy') array([[ 0.84188778, 0.70928643, 0.87321035], [ 0.81885553, 0.92208501, 0.873464 ], [ 0.27111984, 0.82213106, 0.55987325]]) >>> >>> os.system('head saved-matrix.npy') NUMPYF{'descr': '<f8', 'fortran_order': False, 'shape': (3, 3), } Ï< £¾ðê? sy²æ?$÷ÒVñë?Ù4ê?%dn¸í?Ã[Äjóë?Ä,ZÑ?Ç ÎåNê?ó7L{êá?0 >>>

Numpy - ndarray Numpy - ndarray • NumPy's main object is the homogeneous multidimensional array called ndarray. – This is a table of elements (usually numbers), all of the same type, indexed by a tuple of positive integers. Typical examples of multidimensional arrays include vectors, matrices, images and spreadsheets. – Dimensions usually called axes, number of axes is the rank [7, 5, -1] An array of rank 1 i.e. It has 1 axis of length 3 [ [ 1.5, 0.2, -3.7] , An array of rank 2 i.e. It has 2 axes, the first [ 0.1, 1.7, 2.9] ] length 3, the second of length 3 (a matrix with 2 rows and 3 columns

Numpy – ndarray attributes Numpy – ndarray attributes • ndarray.ndim – the number of axes (dimensions) of the array i.e. the rank. • ndarray.shape – the dimensions of the array. This is a tuple of integers indicating the size of the array in each dimension. For a matrix with n rows and m columns, shape will be (n,m). The length of the shape tuple is therefore the rank, or number of dimensions, ndim. • ndarray.size – the total number of elements of the array, equal to the product of the elements of shape. • ndarray.dtype – an object describing the type of the elements in the array. One can create or specify dtype's using standard Python types. NumPy provides many, for example bool_, character, int_, int8, int16, int32, int64, float_, float8, float16, float32, float64, complex_, complex64, object_. • ndarray.itemsize – the size in bytes of each element of the array. E.g. for elements of type float64, itemsize is 8 (=64/8), while complex32 has itemsize 4 (=32/8) (equivalent to ndarray.dtype.itemsize). • ndarray.data – the buffer containing the actual elements of the array. Normally, we won't need to use this attribute because we will access the elements in an array using indexing facilities.

Numpy – array creation and use Numpy – array creation and use >>> x = np.array([1,2,3,4]) >>> y = x >>> x is y True >>> id(x), id(y) (139814289111920, 139814289111920) >>> x[0] = 9 >>> y array([9, 2, 3, 4]) >>> x[0] = 1 >>> z = x[:] >>> x is z False >>> id(x), id(z) (139814289111920, 139814289112080) >>> x[0] = 8 >>> z array([8, 2, 3, 4]) Two ndarrays are mutable and may be views to the same memory: >>> x = np.array([1,2,3,4]) >>> y = x.copy() >>> x is y False >>> id(x), id(y) (139814289111920, 139814289111840) >>> x[0] = 9 >>> x array([9, 2, 3, 4]) >>> y array([1, 2, 3, 4])

Numpy – array creation and use Numpy – array creation and use >>> a = numpy.arange(4.0) >>> b = a * 23.4 >>> c = b/(a+1) >>> c += 10 >>> print c [ 10. 21.7 25.6 27.55] >>> arr = numpy.arange(100, 200) >>> select = [5, 25, 50, 75, -5] >>> print(arr[select]) # can use integer lists as indices [105, 125, 150, 175, 195] >>> arr = numpy.arange(10, 20 ) >>> div_by_3 = arr%3 == 0 # comparison produces boolean array >>> print(div_by_3) [ False False True False False True False False True False] >>> print(arr[div_by_3]) # can use boolean lists as indices [12 15 18] >>> arr = numpy.arange(10, 20) . reshape((2,5)) [[10 11 12 13 14] [15 16 17 18 19]]

Numpy – array methods Numpy – array methods >>> arr.sum() 145 >>> arr.mean() 14.5 >>> arr.std() 2.8722813232690143 >>> arr.max() 19 >>> arr.min() 10 >>> div_by_3.all() False >>> div_by_3.any() True >>> div_by_3.sum() 3 >>> div_by_3.nonzero() (array([2, 5, 8]),)

Numpy – array methods - sorting Numpy – array methods - sorting >>> arr = numpy.array([4.5, 2.3, 6.7, 1.2, 1.8, 5.5]) >>> arr.sort() # acts on array itself >>> print(arr) [ 1.2 1.8 2.3 4.5 5.5 6.7] >>> x = numpy.array([4.5, 2.3, 6.7, 1.2, 1.8, 5.5]) >>> numpy.sort(x) array([ 1.2, 1.8, 2.3, 4.5, 5.5, 6.7]) >>> print(x) [ 4.5 2.3 6.7 1.2 1.8 5.5] >>> s = x.argsort() >>> s array([3, 4, 1, 0, 5, 2]) >>> x[s] array([ 1.2, 1.8, 2.3, 4.5, 5.5, 6.7]) >>> y[s] array([ 6.2, 7.8, 2.3, 1.5, 8.5, 4.7])

Numpy – array functions Numpy – array functions • Most array methods have equivalent functions • Ufuncs provide many element-by-element math, trig., etc. operations – e.g., add(x1, x2), absolute(x), log10(x), sin(x), logical_and(x1, x2) • See http://numpy.scipy.org >>> arr.sum() 45 >>> numpy.sum(arr) 45

Numpy – array operations Numpy – array operations >>> a = array([[1.0, 2.0], [4.0, 3.0]]) >>> print a [[ 1. 2.] [ 3. 4.]] >>> a.transpose() array([[ 1., 3.], [ 2., 4.]]) >>> inv(a) array([[-2. , 1. ], [ 1.5, -0.5]]) >>> u = eye(2) # unit 2x2 matrix; "eye" represents "I" >>> u array([[ 1., 0.], [ 0., 1.]]) >>> j = array([[0.0, -1.0], [1.0, 0.0]]) >>> dot (j, j) # matrix product array([[-1., 0.], [ 0., -1.]])

Numpy – statistics Numpy – statistics >>> a = np.array([1, 4, 3, 8, 9, 2, 3], float) >>> np.median(a) 3.0 >>> a = np.array([[1, 2, 1, 3], [5, 3, 1, 8]], float) >>> c = np.corrcoef(a) >>> c array([[ 1. , 0.72870505], [ 0.72870505, 1. ]]) >>> np.cov(a) array([[ 0.91666667, 2.08333333], [ 2.08333333, 8.91666667]]) In addition to the mean, var, and std functions, NumPy supplies several other methods for returning statistical features of arrays. The median can be found: The correlation coefficient for multiple variables observed at multiple instances can be found for arrays of the form [[x1, x2, …], [y1, y2, …], [z1, z2, …], …] where x, y, z are different observables and the numbers indicate the observation times: Here the return array c[i,j] gives the correlation coefficient for the ith and jth observables. Similarly, the covariance for data can be found::

Using arrays wisely Using arrays wisely • Array operations are implemented in C or Fortran • Optimised algorithms - i.e. fast! • Python loops (i.e. for i in a:…) are much slower • Prefer array operations over loops, especially when speed important • Also produces shorter code, often more readable

Numpy – arrays, matrices Numpy – arrays, matrices >>> import numpy >>> m = numpy.mat([[1,2],[3,4]]) or >>> a = numpy.array([[1,2],[3,4]]) >>> m = numpy.mat(a) or >>> a = numpy.array([[1,2],[3,4]]) >>> m = numpy.asmatrix(a) For two dimensional arrays NumPy defined a special matrix class in module matrix. Objects are created either with matrix() or mat() or converted from an array with method asmatrix(). Note that the statement m = mat(a) creates a copy of array 'a'. Changing values in 'a' will not affect 'm'. On the other hand, method m = asmatrix(a) returns a new reference to the same data. Changing values in 'a' will affect matrix 'm'.

Numpy – matrices Numpy – matrices >>> a = array([[1,2],[3,4]]) >>> m = mat(a) # convert 2-d array to matrix >>> m = matrix([[1, 2], [3, 4]]) >>> a[0] # result is 1-dimensional array([1, 2]) >>> m[0] # result is 2-dimensional matrix([[1, 2]]) >>> a*a # element-by-element multiplication array([[ 1, 4], [ 9, 16]]) >>> m*m # (algebraic) matrix multiplication matrix([[ 7, 10], [15, 22]]) >>> a**3 # element-wise power array([[ 1, 8], [27, 64]]) >>> m**3 # matrix multiplication m*m*m matrix([[ 37, 54], [ 81, 118]]) >>> m.T # transpose of the matrix matrix([[1, 3], [2, 4]]) >>> m.H # conjugate transpose (differs from .T for complex matrices) matrix([[1, 3], [2, 4]]) >>> m.I # inverse matrix matrix([[-2. , 1. ], [ 1.5, -0.5]]) Array and matrix operations may be quite different!

Numpy – matrices Numpy – matrices • Operator *, dot(), and multiply(): • For array, '*' means element-wise multiplication, and the dot() function is used for matrix multiplication. • For matrix, '*'means matrix multiplication, and the multiply() function is used for element-wise multiplication. • Handling of vectors (rank-1 arrays) • For array, the vector shapes 1xN, Nx1, and N are all different things. Operations like A[:,1] return a rank-1 array of shape N, not a rank-2 of shape Nx1. Transpose on a rank-1 array does nothing. • For matrix, rank-1 arrays are always upgraded to 1xN or Nx1 matrices (row or column vectors). A[:,1] returns a rank-2 matrix of shape Nx1. • Handling of higher-rank arrays (rank > 2) • array objects can have rank > 2. • matrix objects always have exactly rank 2. • Convenience attributes • array has a .T attribute, which returns the transpose of the data. • matrix also has .H, .I, and .A attributes, which return the conjugate transpose, inverse, and asarray() of the matrix, respectively. • Convenience constructor • The array constructor takes (nested) Python sequences as initializers. As in array([[1,2,3],[4,5,6]]). • The matrix constructor additionally takes a convenient string initializer. As in matrix("[1 2 3; 4 5 6]")

Numpy – array mathematics Numpy – array mathematics >>> a = np.array([1,2,3], float) >>> b = np.array([5,2,6], float) >>> a + b array([6., 4., 9.]) >>> a – b array([-4., 0., -3.]) >>> a * b array([5., 4., 18.]) >>> b / a array([5., 1., 2.]) >>> a % b array([1., 0., 3.]) >>> b**a array([5., 4., 216.]) >>> a = np.array([[1, 2], [3, 4], [5, 6]], float) >>> b = np.array([-1, 3], float) >>> a array([[ 1., 2.], [ 3., 4.], [ 5., 6.]]) >>> b array([-1., 3.]) >>> a + b array([[ 0., 5.], [ 2., 7.], [ 4., 9.]]) >>> a = np.array([[1, 2], [3, 4], [5, 6]], float) >>> b = np.array([-1, 3], float) >>> a * a array([[ 1., 4.], [ 9., 16.], [ 25., 36.]]) >>> b * b array([ 1., 9.]) >>> a * b array([[ -1., 6.], [ -3., 12.], [ -5., 18.]]) >>>

Numpy – array mathematics Numpy – array mathematics >>> A = np.array([[n+m*10 for n in range(5)] for m in range(5)]) >>> v1 = arange(0, 5) >>> A array([[ 0, 1, 2, 3, 4], [10, 11, 12, 13, 14], [20, 21, 22, 23, 24], [30, 31, 32, 33, 34], [40, 41, 42, 43, 44]]) >>> v1 array([0, 1, 2, 3, 4]) >>> np.dot(A,A) array([[ 300, 310, 320, 330, 340], [1300, 1360, 1420, 1480, 1540], [2300, 2410, 2520, 2630, 2740], [3300, 3460, 3620, 3780, 3940], [4300, 4510, 4720, 4930, 5140]]) >>> >>> np.dot(A,v1) array([ 30, 130, 230, 330, 430]) >>> np.dot(v1,v1) 30 >>> Alternatively, we can cast the array objects to the type matrix. This changes the behavior of the standard arithmetic operators +, -, * to use matrix algebra. >>> M = np.matrix(A) >>> v = np.matrix(v1).T >>> v matrix([[0], [1], [2], [3], [4]]) >>> M*v matrix([[ 30], [130], [230], [330], [430]]) >>> v.T * v # inner product matrix([[30]]) # standard matrix algebra applies >>> v + M*v matrix([[ 30], [131], [232], [333], [434]])

Introduction to language Introduction to language End

Python crash course libraries numpy-1, panda.ppt

More Related Content

Similar to Python crash course libraries numpy-1, panda.ppt

More from janaki raman

Recently uploaded

Python crash course libraries numpy-1, panda.ppt