BS
Uploaded byBenjamin Sach
PDF, PPTX1,159 views

Pattern Matching Part Two: Suffix Arrays

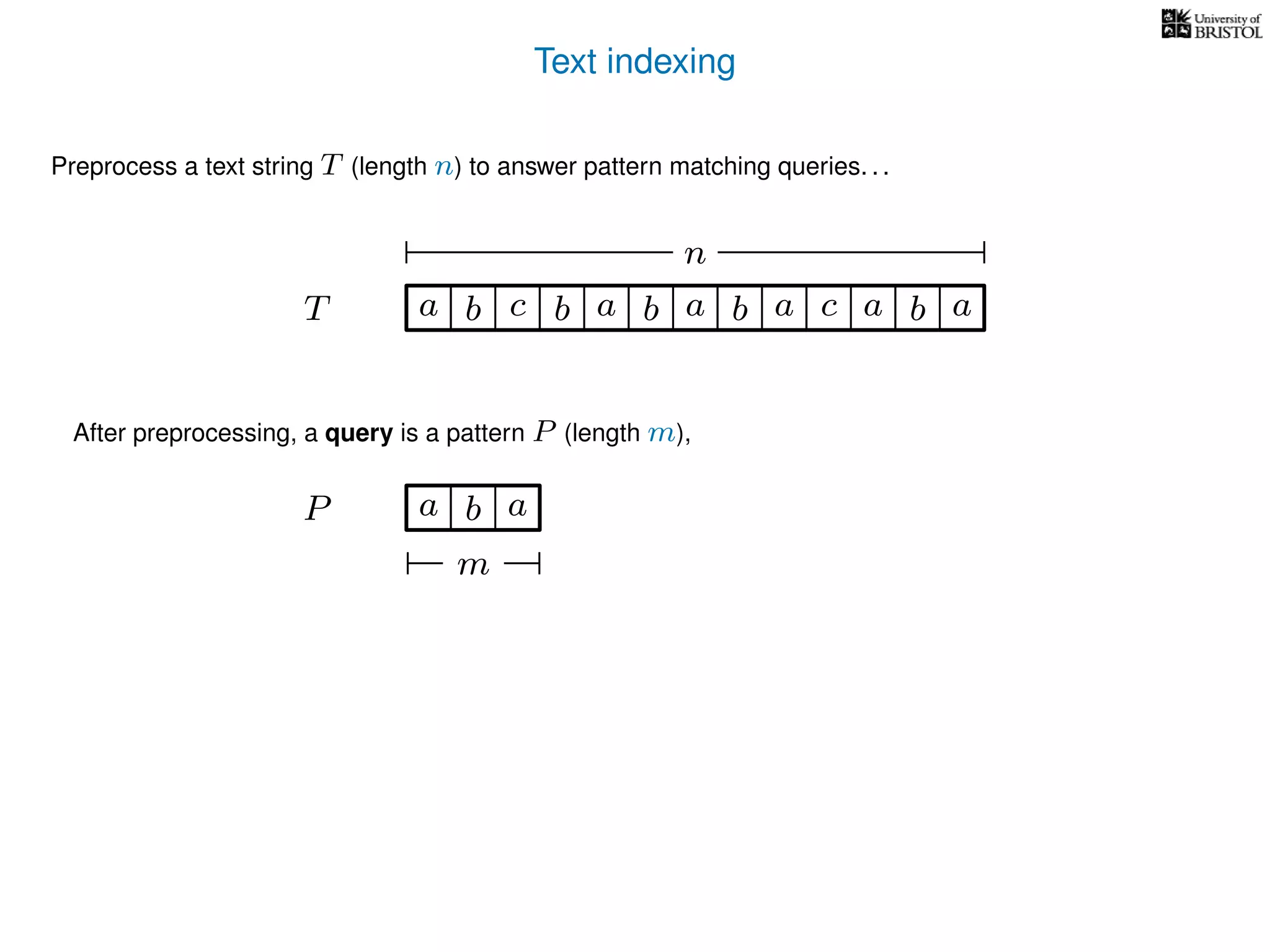
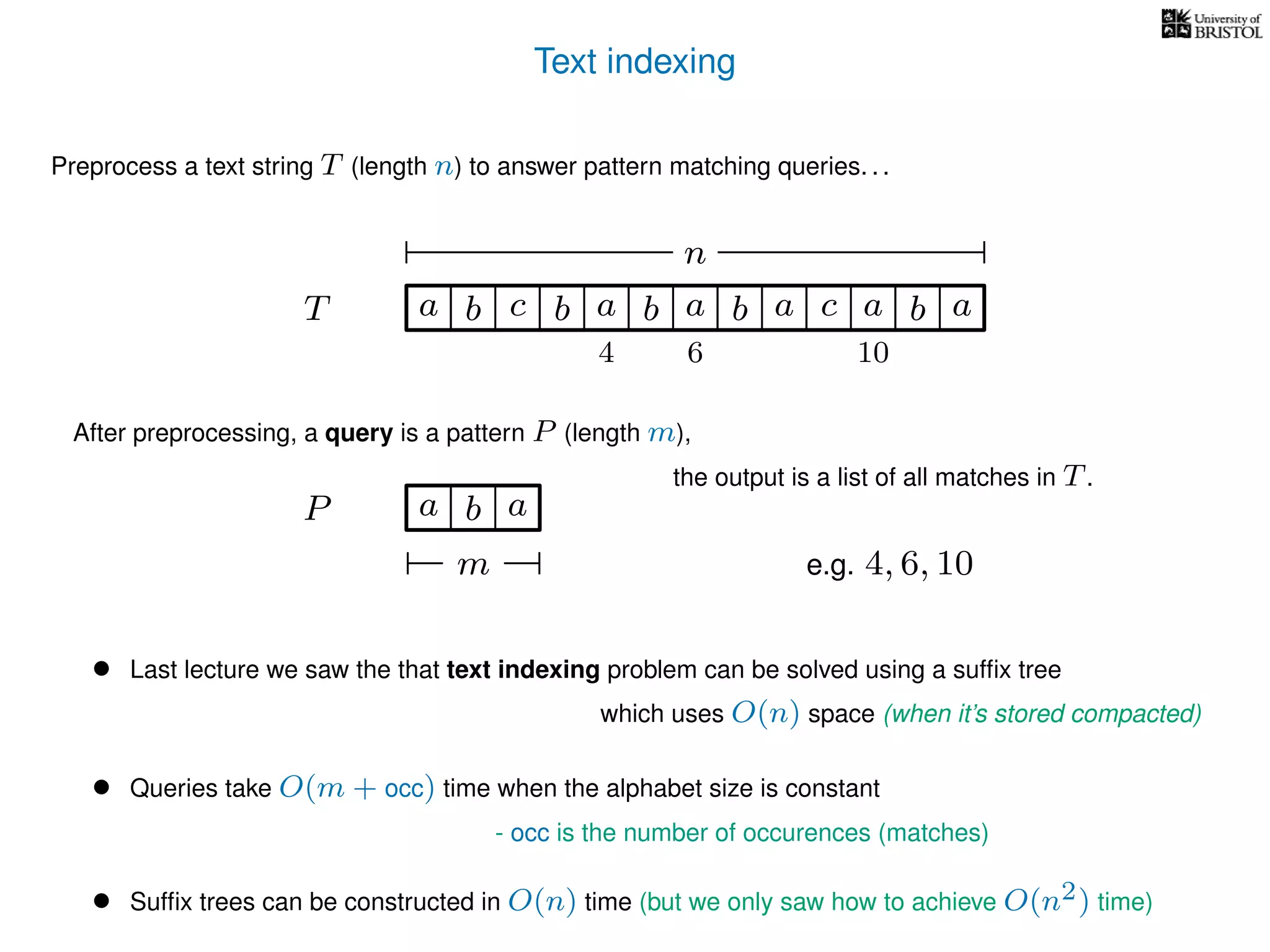
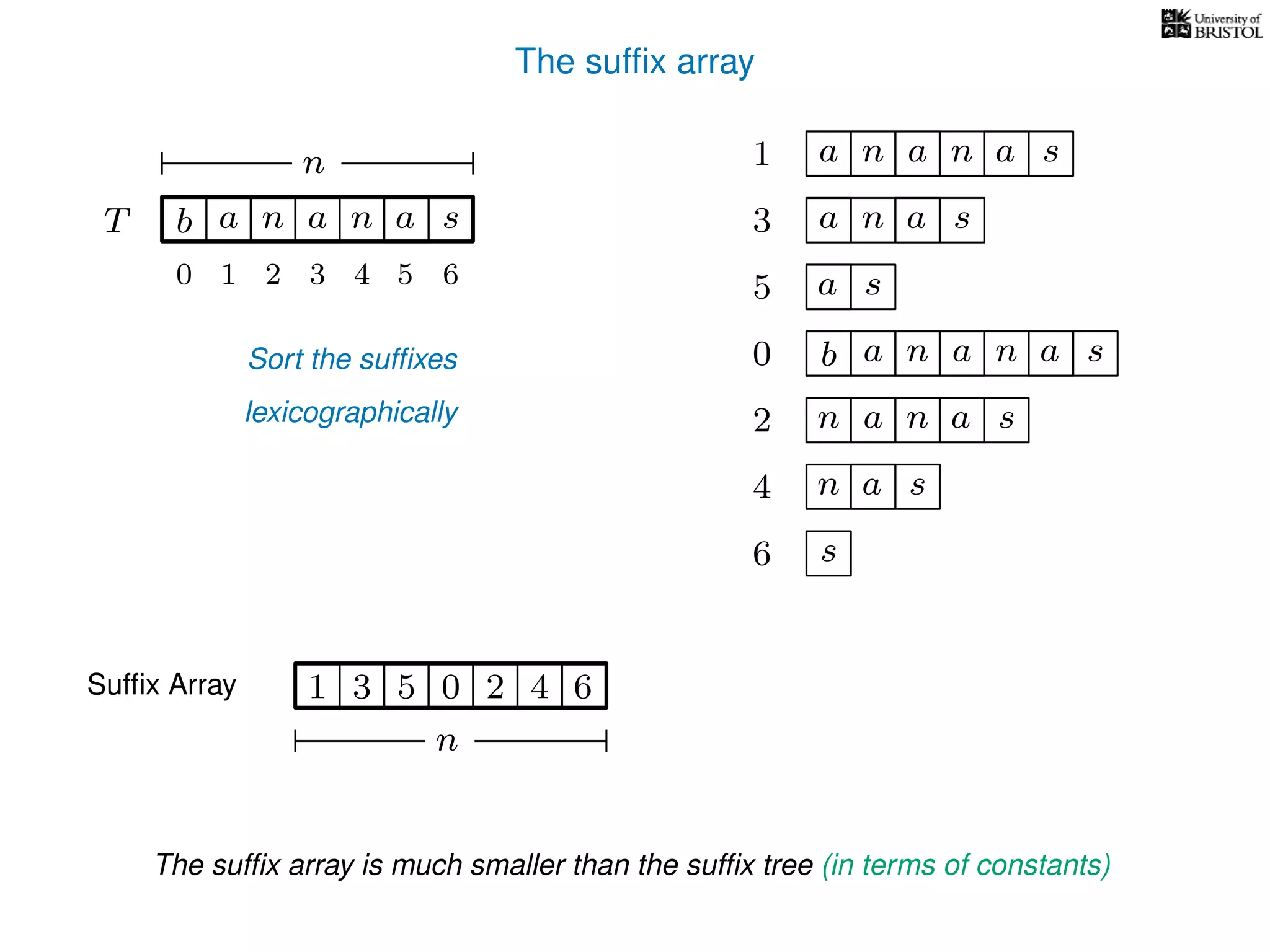
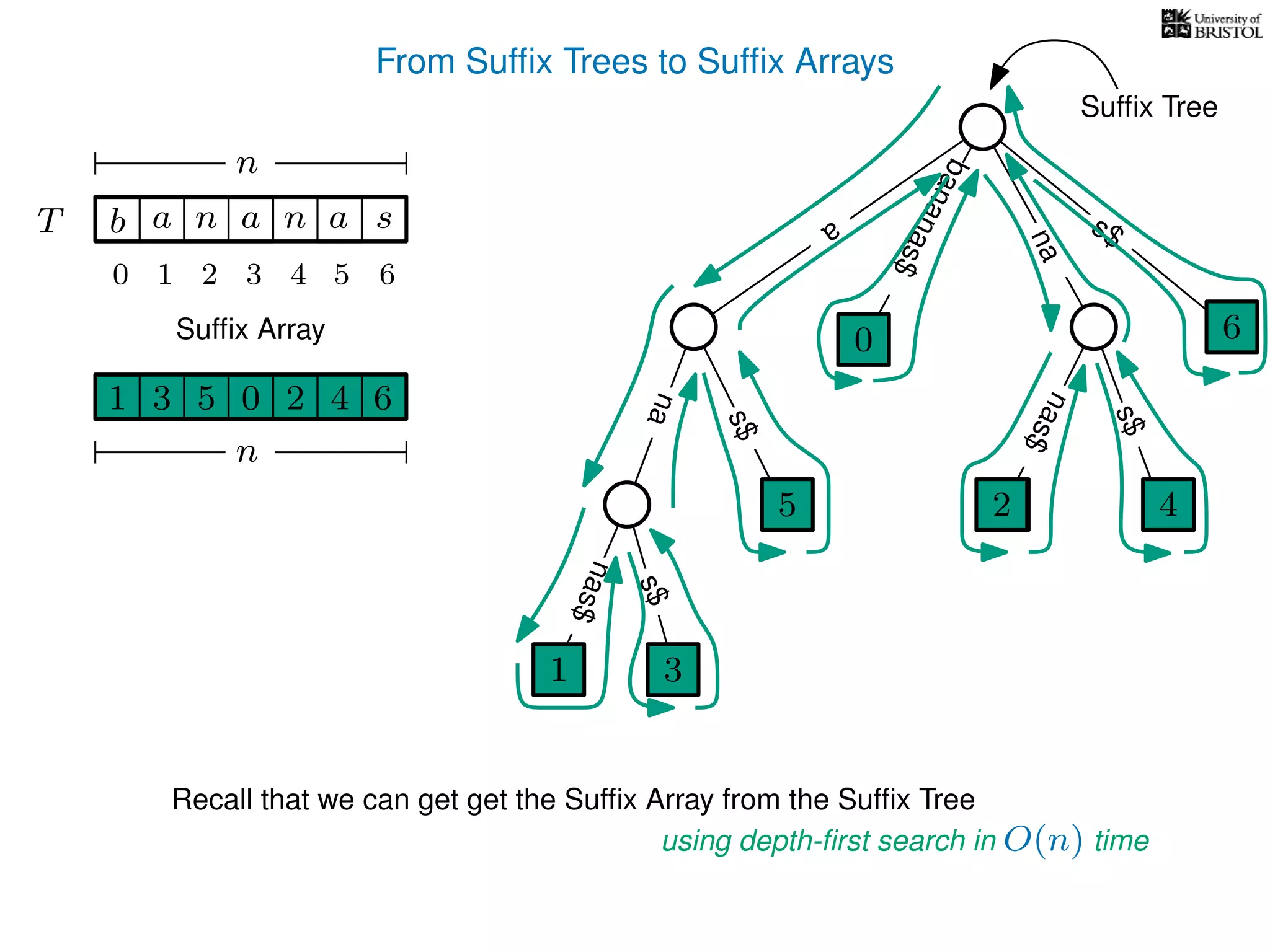
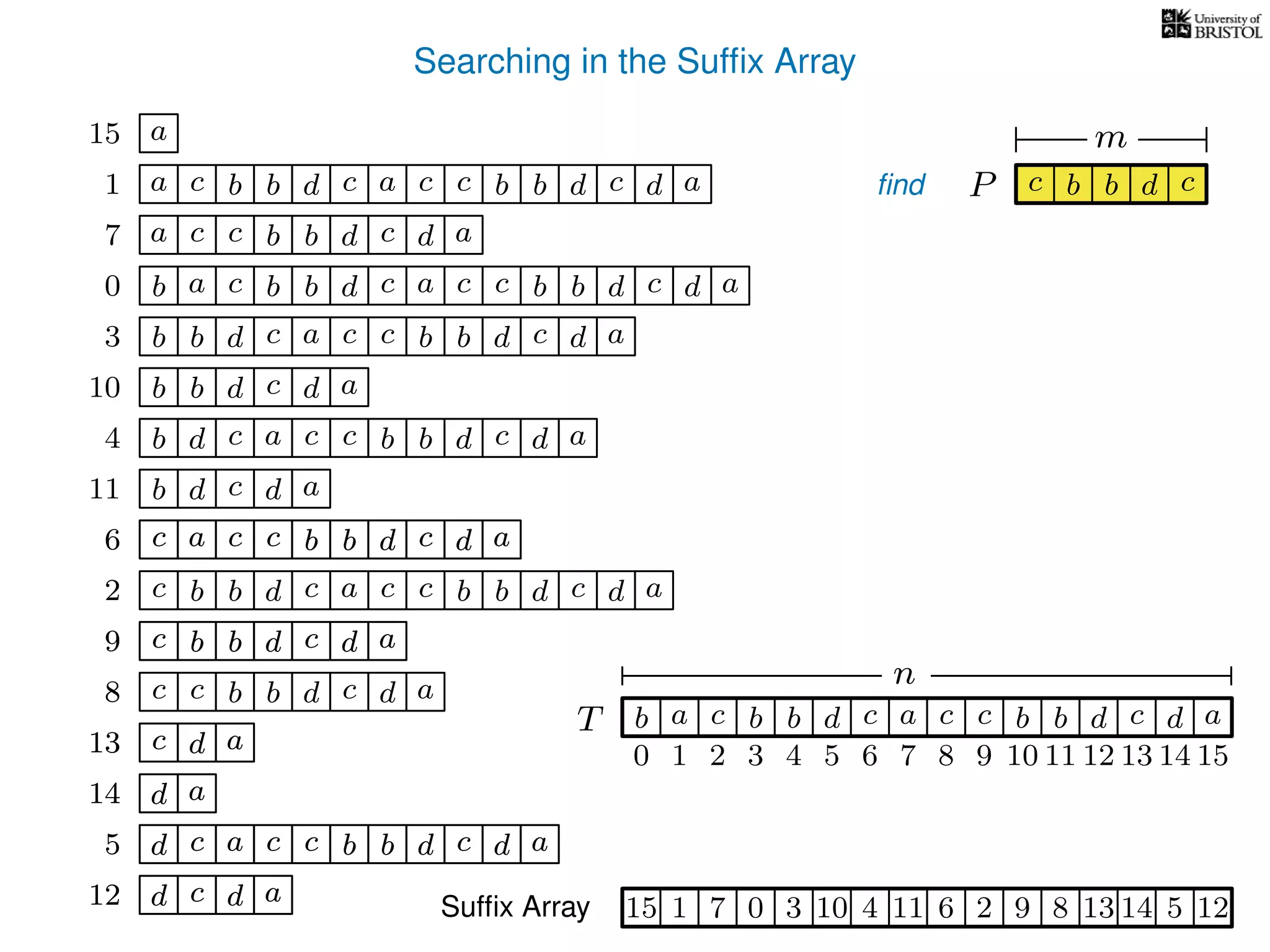
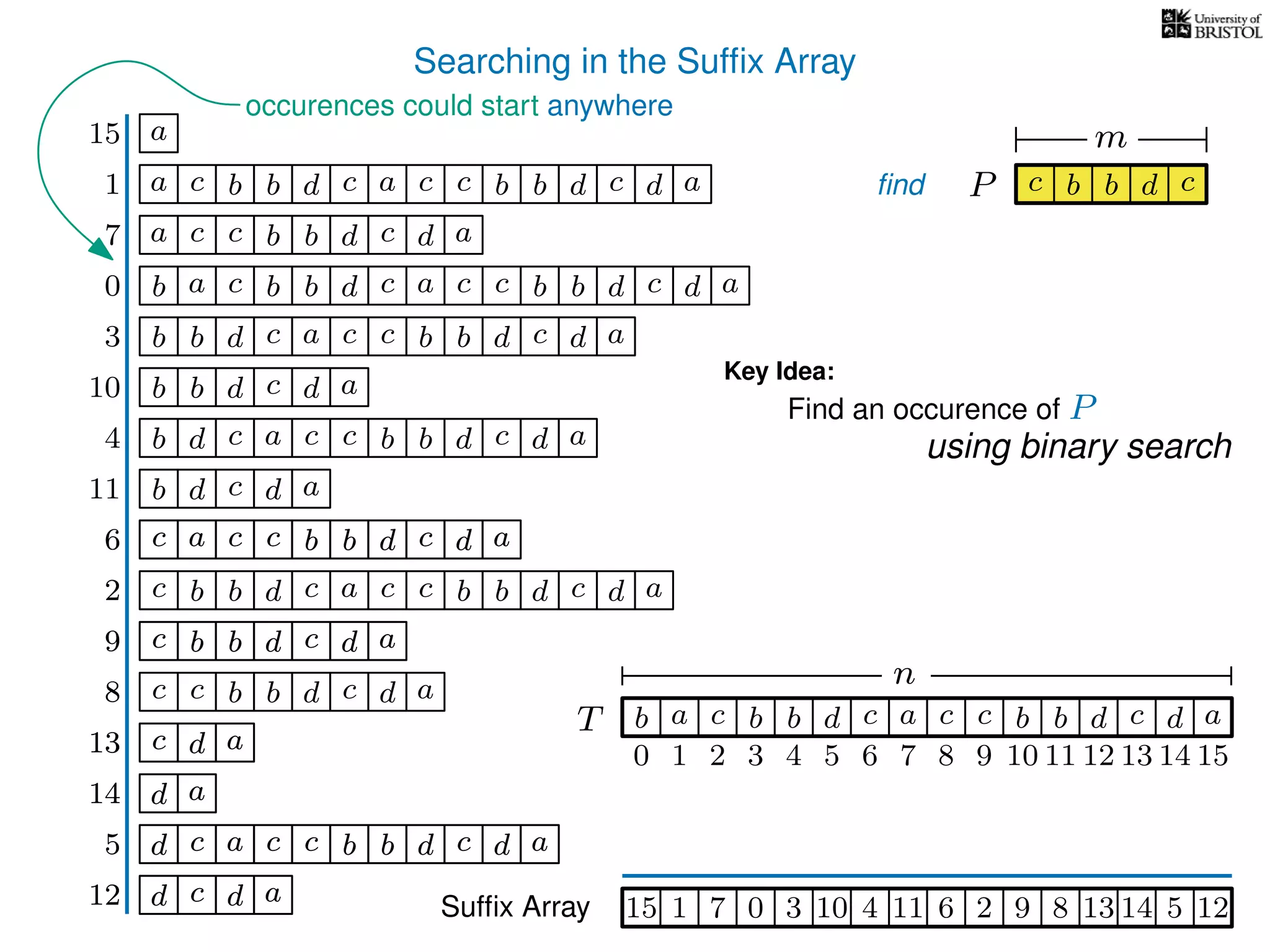
The document discusses advanced algorithms for text indexing and pattern matching using suffix arrays and trees. It explains the processes of preprocessing a text string to answer pattern matching queries, the efficiency of suffix trees in terms of space and query time, and how to construct suffix arrays. It also highlights the lexicographical sorting of suffixes and the transition from suffix trees to suffix arrays for more compact representation.

Download as PDF, PPTX
1 / 171
2 / 171
3 / 171
4 / 171
5 / 171
6 / 171
7 / 171
8 / 171
9 / 171
10 / 171
11 / 171
12 / 171
13 / 171
14 / 171
15 / 171
16 / 171
17 / 171
18 / 171
19 / 171
20 / 171
21 / 171
22 / 171
23 / 171
24 / 171
25 / 171
26 / 171
27 / 171
28 / 171
29 / 171
30 / 171
31 / 171
32 / 171
33 / 171
34 / 171
35 / 171
36 / 171
37 / 171
38 / 171
39 / 171
40 / 171
41 / 171
42 / 171
43 / 171
44 / 171
45 / 171
46 / 171
47 / 171
48 / 171
49 / 171
50 / 171
51 / 171
52 / 171
53 / 171
54 / 171
55 / 171
56 / 171
57 / 171
58 / 171
59 / 171
60 / 171
61 / 171
62 / 171
63 / 171
64 / 171
65 / 171
66 / 171
67 / 171
68 / 171
69 / 171
70 / 171
71 / 171
72 / 171
73 / 171
74 / 171
75 / 171
76 / 171
77 / 171
78 / 171
79 / 171
80 / 171
81 / 171
82 / 171
83 / 171
84 / 171
85 / 171
86 / 171
87 / 171
88 / 171
89 / 171
90 / 171
91 / 171
92 / 171
93 / 171
94 / 171
95 / 171
96 / 171
97 / 171
98 / 171
99 / 171
100 / 171
101 / 171
102 / 171
103 / 171
104 / 171
105 / 171
106 / 171
107 / 171
108 / 171
109 / 171
110 / 171
111 / 171
112 / 171
113 / 171
114 / 171
115 / 171
116 / 171
117 / 171
118 / 171
119 / 171
120 / 171
121 / 171
122 / 171
123 / 171
124 / 171
125 / 171
126 / 171
127 / 171
128 / 171
129 / 171
130 / 171
131 / 171
132 / 171
133 / 171
134 / 171
135 / 171
136 / 171
137 / 171
138 / 171
139 / 171
140 / 171
141 / 171
142 / 171
143 / 171
144 / 171
145 / 171
146 / 171
147 / 171
148 / 171
149 / 171
150 / 171
151 / 171
152 / 171
153 / 171
154 / 171
155 / 171
156 / 171
157 / 171
158 / 171
159 / 171
160 / 171
161 / 171
162 / 171
163 / 171
164 / 171
165 / 171
166 / 171
167 / 171
168 / 171
169 / 171
170 / 171
171 / 171
Advanced Algorithms – COMS31900 Pattern Matching part two Suffix Arrays Benjamin Sach
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T.
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. e.g. 4, 6, 10 4 6 10
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree • Queries take O(m + occ) time when the alphabet size is constant - occ is the number of occurences (matches) e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
Text indexing T Preprocess a text string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree • Queries take O(m + occ) time when the alphabet size is constant - occ is the number of occurences (matches) • Suffix trees can be constructed in O(n) time (but we only saw how to achieve O(n2) time) e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
The suffix array T b n aaT a sn n
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa snsuffix 1
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs:
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller) just a fancy name for the order the strings would appear in the dictionary In lexicographical ordering we sort strings based on the first symbol that differs:
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order If the symbols don’t have a natural order, we use their binary representation in memory b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller) just a fancy name for the order the strings would appear in the dictionary In lexicographical ordering we sort strings based on the first symbol that differs:
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
The suffix array T b n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 10 2 3 4 5 6
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n The suffix array is much smaller than the suffix tree (in terms of constants) 10 2 3 4 5 6
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n The suffix array is much smaller than the suffix tree (in terms of constants) 10 2 3 4 5 6
From Suffix Trees to Suffix Arrays a s$ nas$ nas$ nas$ s$ na s$ bananas$ 1 3 5 0 2 4 6 T b n aaT a sn n Suffix Array Suffix Tree 1 0 625 43 n Recall that we can get get the Suffix Array from the Suffix Tree 1 3 5 0 2 4 6 10 2 3 4 5 6 using depth-first search in O(n) time
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 157 100 1 43 112 1396 1485 12 c db cb a c bc c d adb
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find c db cb a c bc c d adb m
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: = c db cb a c bc c d adb c db cb m c db cb occurences must start in here Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: = c db cb a c bc c d adb c db cb m c db cb occurences must start in here we found a match! Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? m Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings m Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings so O(m log n) time in total m Find an occurence of P using binary search
Searching in the Suffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings so O(m log n) time in total This method generalises to O(m log n + occ) time m to find all occ occurences. Find an occurence of P using binary search by continuing the binary search (we will skip the details)
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences Do we really need to build the suffix tree to construct the suffix array? This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T =
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 R1 is split into blocks of length 3
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 R2 is also split into blocks of length 3
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 3
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 we assume that the bit representation of each symbol uses O(log n) bits. (which is a common and realistic assumption) This can be done by sorting the blocks in O(n) time using radix sort
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 How do we compute the suffix array for R ? Recursion! (Notice that R has length 2n/3)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : what use1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : what use1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 a b d ob a a b b a d d oa b b a d is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5 Suffix is smaller than suffix 1 55
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 ob b a d $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $ Suffix is smaller than suffix 7 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $ Suffix is smaller than suffix 2 5
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling,
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y suffix 0 is a y 1 24 111058 7 followed by suffix 1
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 1 24 111058 7
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank:
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank:
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Suffix array for just B0 6 09 3
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Suffix array for just B0 6 09 3 How do we merge these?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . .
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ?1 6
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3)
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3) It takes O(1) time to decide that 1 is smaller
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3) It takes O(1) time to decide that 1 is smaller 1
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 (a, 4) (a, 5) ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 (a, 4) (a, 5) Again, it takes O(1) time to decide that is smaller6 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 which is smaller, suffix or4 9 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 )4(which is smaller, suffix or4 9 ? is smaller
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 )4(which is smaller, suffix or4 9 ? is smaller
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8which is smaller, suffix or 9 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 +a= +b= 9 10 8 9 which is smaller, suffix or 9 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 +a= +b= 9 10 8 9 Uh oh! how do we compare 9 10to ? which is smaller, suffix or 9 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 Uh oh! how do we compare 9 10to ? +a= +b= 9 8 d a + + 11 10 It still takes O(1) time to decide that is smaller9 which is smaller, suffix or 9 ?
The DC3 method y a b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 Overall this merging phase takes O(n) time (because processing each suffix takes O(1) time)
The DC3 method Theorem The DC3 algorithm constructs a suffix array in O(n) time.
The DC3 method Theorem The DC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n)
The DC3 method Theorem The DC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n) radix sorting and merging recursion to construct a suffix array of size 2n/3
The DC3 method Theorem The DC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n) Solving this recurrence gives T(n) ∈ O(n). radix sorting and merging recursion to construct a suffix array of size 2n/3
The suffix array T b n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences We can construct the suffix array in O(n) time This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)

More Related Content

PDF
Pattern Matching Part One: Suffix Trees
byBenjamin Sach
 
PPT
Pattern matching
byshravs_188
 
PDF
Trie Data Structure
byHitesh Mohapatra
 
PPT
String kmp
bythinkphp
 
PPTX
Tries data structures
byJothi Ramasamy
 
PPT
String searching
bythinkphp
 
PDF
String matching, naive,
byAmit Kumar Rathi
 
PPTX
String matching algorithms-pattern matching.
bySwapan Shakhari
 
Pattern Matching Part One: Suffix Trees
byBenjamin Sach
 
Pattern matching
byshravs_188
 
Trie Data Structure
byHitesh Mohapatra
 
String kmp
bythinkphp
 
Tries data structures
byJothi Ramasamy
 
String searching
bythinkphp
 
String matching, naive,
byAmit Kumar Rathi
 
String matching algorithms-pattern matching.
bySwapan Shakhari
 

What's hot

PDF
International Journal of Engineering and Science Invention (IJESI)
byinventionjournals
 
PPT
POST’s CORRESPONDENCE PROBLEM
byRajendran
 
PDF
Application of fourier series to differential equations
byTarun Gehlot
 
PDF
Lex analysis
bySuhit Kulkarni
 
PPTX
Boyer more algorithm
byKritika Purohit
 
PPTX
String matching algorithms
byDepartment of Computer Science, University of Peshawar
 
PDF
Parseval's Theorem
byCOMSATS Abbottabad
 
PPTX
the fourier series
bysafi al amu
 
PPTX
Theory of computation / Post’s Correspondence Problems (PCP)
byTechnical Advisor at Iraqi Government
 
PDF
Fuzzy α^m-Separation Axioms
bypaperpublications3
 
PPT
String matching algorithms
byDr Shashikant Athawale
 
PPTX
Application of tries
byTech_MX
 
PDF
Object-Oriented Programming 5
byWarawut
 
PDF
Cut and Count
byASPAK2014
 
PPTX
Basics of Mathematical Cryptography
byNeha Gupta
 
PDF
25 String Matching
byAndres Mendez-Vazquez
 
DOCX
15 practical grep command examples in linux
byTeja Bheemanapally
 
PDF
Fourier Series of Music by Robert Fustero
byRobertFustero
 
PPTX
String matching Algorithm by Foysal
byFoysal Mahmud
 
PPT
Seq db searching
byEr Puspendra Tripathi
 
International Journal of Engineering and Science Invention (IJESI)
byinventionjournals
 
POST’s CORRESPONDENCE PROBLEM
byRajendran
 
Application of fourier series to differential equations
byTarun Gehlot
 
Lex analysis
bySuhit Kulkarni
 
Boyer more algorithm
byKritika Purohit
 
String matching algorithms
byDepartment of Computer Science, University of Peshawar
 
Parseval's Theorem
byCOMSATS Abbottabad
 
the fourier series
bysafi al amu
 
Theory of computation / Post’s Correspondence Problems (PCP)
byTechnical Advisor at Iraqi Government
 
Fuzzy α^m-Separation Axioms
bypaperpublications3
 
String matching algorithms
byDr Shashikant Athawale
 
Application of tries
byTech_MX
 
Object-Oriented Programming 5
byWarawut
 
Cut and Count
byASPAK2014
 
Basics of Mathematical Cryptography
byNeha Gupta
 
25 String Matching
byAndres Mendez-Vazquez
 
15 practical grep command examples in linux
byTeja Bheemanapally
 
Fourier Series of Music by Robert Fustero
byRobertFustero
 
String matching Algorithm by Foysal
byFoysal Mahmud
 
Seq db searching
byEr Puspendra Tripathi
 

Similar to Pattern Matching Part Two: Suffix Arrays

PDF
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
PDF
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
PDF
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
PPTX
Suffix Tree and Suffix Array
byHarshit Agarwal
 
PDF
A taxonomy of suffix array construction algorithms
byunyil96
 
PPT
Lec18
byNikhil Chilwant
 
PPTX
Suffix arrays
byStrand Life Sciences Pvt Ltd
 
DOC
Compiler Design QA
byDr. C.V. Suresh Babu
 
PDF
Approximate Indexing: Gapped Suffix Array
byKH Park (박경훈)
 
PPT
Overview_of_a_computational_model_-_Languages_1.ppt
bySanthoshS508159
 
PDF
C++ CoreHard Autumn 2018. Text Formatting For a Future Range-Based Standard L...
bycorehard_by
 
PPT
4888009.pptnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
byRAtna29
 
PDF
Mod1.pdf
bySanthoshS508159
 
PPT
13 Strings and text processing
bymaznabili
 
PDF
32 -longest-common-prefix
bySanjeev Gupta
 
PPT
Lec-02 Languages for finite automata FA
byNidaAslam30
 
PPT
Lecture 1,2
byshah zeb
 
PPTX
Automata definitions
bySajid Marwat
 
PPTX
Boyer-Moore-algorithm-Vladimir.pptx
byssuserf56658
 
PDF
The Next Best String
byKevlin Henney
 
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
Space Efficient Suffix Array Construction using Induced Sorting LMS Substrings
byijistjournal
 
Suffix Tree and Suffix Array
byHarshit Agarwal
 
A taxonomy of suffix array construction algorithms
byunyil96
 
Lec18
byNikhil Chilwant
 
Suffix arrays
byStrand Life Sciences Pvt Ltd
 
Compiler Design QA
byDr. C.V. Suresh Babu
 
Approximate Indexing: Gapped Suffix Array
byKH Park (박경훈)
 
Overview_of_a_computational_model_-_Languages_1.ppt
bySanthoshS508159
 
C++ CoreHard Autumn 2018. Text Formatting For a Future Range-Based Standard L...
bycorehard_by
 
4888009.pptnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
byRAtna29
 
Mod1.pdf
bySanthoshS508159
 
13 Strings and text processing
bymaznabili
 
32 -longest-common-prefix
bySanjeev Gupta
 
Lec-02 Languages for finite automata FA
byNidaAslam30
 
Lecture 1,2
byshah zeb
 
Automata definitions
bySajid Marwat
 
Boyer-Moore-algorithm-Vladimir.pptx
byssuserf56658
 
The Next Best String
byKevlin Henney
 

More from Benjamin Sach

PDF
Approximation Algorithms Part Four: APTAS
byBenjamin Sach
 
PDF
Approximation Algorithms Part Three: (F)PTAS
byBenjamin Sach
 
PDF
Approximation Algorithms Part Two: More Constant factor approximations
byBenjamin Sach
 
PDF
Approximation Algorithms Part One: Constant factor approximations
byBenjamin Sach
 
PDF
van Emde Boas trees
byBenjamin Sach
 
PDF
Orthogonal Range Searching
byBenjamin Sach
 
PDF
Pattern Matching Part Two: k-mismatches
byBenjamin Sach
 
PDF
Pattern Matching Part Three: Hamming Distance
byBenjamin Sach
 
PDF
Lowest Common Ancestor
byBenjamin Sach
 
PDF
Range Minimum Queries
byBenjamin Sach
 
PDF
Hashing Part Two: Cuckoo Hashing
byBenjamin Sach
 
PDF
Hashing Part Two: Static Perfect Hashing
byBenjamin Sach
 
PDF
Hashing Part One
byBenjamin Sach
 
PDF
Probability Recap
byBenjamin Sach
 
PDF
Bloom Filters
byBenjamin Sach
 
PDF
Dynamic Programming
byBenjamin Sach
 
PDF
Minimum Spanning Trees (via Disjoint Sets)
byBenjamin Sach
 
PDF
Shortest Paths Part 1: Priority Queues and Dijkstra's Algorithm
byBenjamin Sach
 
PDF
Depth First Search and Breadth First Search
byBenjamin Sach
 
PDF
Shortest Paths Part 2: Negative Weights and All-pairs
byBenjamin Sach
 
Approximation Algorithms Part Four: APTAS
byBenjamin Sach
 
Approximation Algorithms Part Three: (F)PTAS
byBenjamin Sach
 
Approximation Algorithms Part Two: More Constant factor approximations
byBenjamin Sach
 
Approximation Algorithms Part One: Constant factor approximations
byBenjamin Sach
 
van Emde Boas trees
byBenjamin Sach
 
Orthogonal Range Searching
byBenjamin Sach
 
Pattern Matching Part Two: k-mismatches
byBenjamin Sach
 
Pattern Matching Part Three: Hamming Distance
byBenjamin Sach
 
Lowest Common Ancestor
byBenjamin Sach
 
Range Minimum Queries
byBenjamin Sach
 
Hashing Part Two: Cuckoo Hashing
byBenjamin Sach
 
Hashing Part Two: Static Perfect Hashing
byBenjamin Sach
 
Hashing Part One
byBenjamin Sach
 
Probability Recap
byBenjamin Sach
 
Bloom Filters
byBenjamin Sach
 
Dynamic Programming
byBenjamin Sach
 
Minimum Spanning Trees (via Disjoint Sets)
byBenjamin Sach
 
Shortest Paths Part 1: Priority Queues and Dijkstra's Algorithm
byBenjamin Sach
 
Depth First Search and Breadth First Search
byBenjamin Sach
 
Shortest Paths Part 2: Negative Weights and All-pairs
byBenjamin Sach
 

Recently uploaded

PPTX
Historical Development and Evolution of Indian Knowledge system
byBanaras Hindu University
 
PPTX
Session 6 - Behavioral Events Interview.pptx
byUmanganElementarySch
 
PDF
Writing Against Empire, An Interview.pdf
byyalehistoricalreview
 
PPTX
PULSE.pptx. UNDERSTANDING PULSE,PHYSIOLOGY,CHARACTERSTICS, FACTORS AFFECTING,...
byPompi Begum
 
PDF
World Sight day 2025/Love your eyes/.pdf
byanmols3059
 
PPTX
Common problems or challenges faced by Indian adolescents
byDr. Harpal Kaur
 
PPTX
Nature, definition and Scope of Indian Knowledge system
byBanaras Hindu University
 
DOCX
Mid-Year-Review-Form school year 2025-2026
byCATHERINENIEVES3
 
PPTX
The law of Triads pptx(Science 8 week 5)
byAnnabelAlarcon
 
PPTX
UNIT -1 INTRODUCTION OF PSYCHOLOGY IN GNM.pptx
byPoojaSen20
 
PDF
2025 Bonner Congress Strategy Session– Student Leadership Bonner and Beyond.pdf
byBonner Foundation
 
PDF
'25 BC Powering Pathways– Career Connections and National Bonner Alumni Advis...
byBonner Foundation
 
PPTX
How to Manage Vehicle Model in Odoo 18 Fleet
byCeline George
 
PDF
'25 BC An Hour with Bonner Alumni–Meet, Mingle, Move.pdf
byBonner Foundation
 
PDF
Slit lamp parts 2/ppt/notes/download.pdf
byanmols3059
 
PDF
Retinal anatomy and physiology/ppt/ .pdf
byanmols3059
 
PDF
BIOCHEMISTRY INTRODUCTION - UNIT 1 FOR BSC NURSING.pdf
byPriyanshu Anand
 
PPTX
How to Create Automatic Transfers in Odoo Accounting
byCeline George
 
PDF
2025 Bonner Congress Opening Engage Now.pdf
byBonner Foundation
 
PDF
Function of Words in Context_V-N-ADJ-ADV.pdf
byNetziValdelomar1
 
Historical Development and Evolution of Indian Knowledge system
byBanaras Hindu University
 
Session 6 - Behavioral Events Interview.pptx
byUmanganElementarySch
 
Writing Against Empire, An Interview.pdf
byyalehistoricalreview
 
PULSE.pptx. UNDERSTANDING PULSE,PHYSIOLOGY,CHARACTERSTICS, FACTORS AFFECTING,...
byPompi Begum
 
World Sight day 2025/Love your eyes/.pdf
byanmols3059
 
Common problems or challenges faced by Indian adolescents
byDr. Harpal Kaur
 
Nature, definition and Scope of Indian Knowledge system
byBanaras Hindu University
 
Mid-Year-Review-Form school year 2025-2026
byCATHERINENIEVES3
 
The law of Triads pptx(Science 8 week 5)
byAnnabelAlarcon
 
UNIT -1 INTRODUCTION OF PSYCHOLOGY IN GNM.pptx
byPoojaSen20
 
2025 Bonner Congress Strategy Session– Student Leadership Bonner and Beyond.pdf
byBonner Foundation
 
'25 BC Powering Pathways– Career Connections and National Bonner Alumni Advis...
byBonner Foundation
 
How to Manage Vehicle Model in Odoo 18 Fleet
byCeline George
 
'25 BC An Hour with Bonner Alumni–Meet, Mingle, Move.pdf
byBonner Foundation
 
Slit lamp parts 2/ppt/notes/download.pdf
byanmols3059
 
Retinal anatomy and physiology/ppt/ .pdf
byanmols3059
 
BIOCHEMISTRY INTRODUCTION - UNIT 1 FOR BSC NURSING.pdf
byPriyanshu Anand
 
How to Create Automatic Transfers in Odoo Accounting
byCeline George
 
2025 Bonner Congress Opening Engage Now.pdf
byBonner Foundation
 
Function of Words in Context_V-N-ADJ-ADV.pdf
byNetziValdelomar1
 

Pattern Matching Part Two: Suffix Arrays

  • 1.
    Advanced Algorithms –COMS31900 Pattern Matching part two Suffix Arrays Benjamin Sach
  • 2.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n
  • 3.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m
  • 4.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T.
  • 5.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. e.g. 4, 6, 10 4 6 10
  • 6.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
  • 7.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree • Queries take O(m + occ) time when the alphabet size is constant - occ is the number of occurences (matches) e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
  • 8.
    Text indexing T Preprocess atext string T (length n) to answer pattern matching queries. . . ba b c a b a cb a a b a n After preprocessing, a query is a pattern P (length m), P a b a m the output is a list of all matches in T. • Last lecture we saw the that text indexing problem can be solved using a suffix tree • Queries take O(m + occ) time when the alphabet size is constant - occ is the number of occurences (matches) • Suffix trees can be constructed in O(n) time (but we only saw how to achieve O(n2) time) e.g. 4, 6, 10 4 6 10 which uses O(n) space (when it’s stored compacted)
  • 9.
    The suffix array Tb n aaT a sn n
  • 10.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
  • 11.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa snsuffix 1
  • 12.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
  • 13.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn
  • 14.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order
  • 15.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs:
  • 16.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
  • 17.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
  • 18.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a
  • 19.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
  • 20.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
  • 21.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c<
  • 22.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a
  • 23.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a
  • 24.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 25.
    The suffix array Tb n aaT a sn n 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s Sort the suffixes lexicographically 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 26.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 27.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 28.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 29.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order In lexicographical ordering we sort strings based on the first symbol that differs: b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller)
  • 30.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller) just a fancy name for the order the strings would appear in the dictionary In lexicographical ordering we sort strings based on the first symbol that differs:
  • 31.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn • The symbols themselves must have an order throughout we will use alphabetical order If the symbols don’t have a natural order, we use their binary representation in memory b a<a a b c< b c< a (in a ‘tie’, the shorter string is smaller) just a fancy name for the order the strings would appear in the dictionary In lexicographical ordering we sort strings based on the first symbol that differs:
  • 32.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn
  • 33.
    The suffix array Tb n aaT a sn n Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 10 2 3 4 5 6
  • 34.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
  • 35.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
  • 36.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n 10 2 3 4 5 6
  • 37.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n The suffix array is much smaller than the suffix tree (in terms of constants) 10 2 3 4 5 6
  • 38.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n The suffix array is much smaller than the suffix tree (in terms of constants) 10 2 3 4 5 6
  • 39.
    From Suffix Treesto Suffix Arrays a s$ nas$ nas$ nas$ s$ na s$ bananas$ 1 3 5 0 2 4 6 T b n aaT a sn n Suffix Array Suffix Tree 1 0 625 43 n Recall that we can get get the Suffix Array from the Suffix Tree 1 3 5 0 2 4 6 10 2 3 4 5 6 using depth-first search in O(n) time
  • 40.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 157 100 1 43 112 1396 1485 12 c db cb a c bc c d adb
  • 41.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find c db cb a c bc c d adb m
  • 42.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m Find an occurence of P using binary search
  • 43.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
  • 44.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
  • 45.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences could start anywhere Find an occurence of P using binary search
  • 46.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
  • 47.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
  • 48.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences could start anywhere Find an occurence of P using binary search
  • 49.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c d adb> c db cb a c bc c d adb m c db cb occurences must start in here Find an occurence of P using binary search
  • 50.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 51.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 52.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 53.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 54.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 55.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb < c bc db c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 56.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 57.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m occurences must start in here Find an occurence of P using binary search
  • 58.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: = c db cb a c bc c d adb c db cb m c db cb occurences must start in here Find an occurence of P using binary search
  • 59.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: = c db cb a c bc c d adb c db cb m c db cb occurences must start in here we found a match! Find an occurence of P using binary search
  • 60.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb m Find an occurence of P using binary search
  • 61.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? m Find an occurence of P using binary search
  • 62.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings m Find an occurence of P using binary search
  • 63.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings so O(m log n) time in total m Find an occurence of P using binary search
  • 64.
    Searching in theSuffix Array 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 4 b c dba cb a c dbc cb d a c dba cb a c bc c d adb db cb a c bc c d adb d cb a c bc c d adb d c a c bc c d adb c a c bc c d adb a c bc c d adb c bc c d adb c b c d adb c d a d a a c d ad c d adb b c d adb 2 5 6 8 9 12 13 14 d c a c bc c d adb c a c bc c d adb c b c d adb c d a d a c d ad b c dbT a cb a c dbc cb d a n 15 7 100Suffix Array 1 43 11 2 1396 148 5 12 c db cbP 157 100 1 43 112 1396 1485 12 find Key Idea: c db cb a c bc c d adb How long does this take? O(m) time to compare two strings so O(m log n) time in total This method generalises to O(m log n + occ) time m to find all occ occurences. Find an occurence of P using binary search by continuing the binary search (we will skip the details)
  • 65.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences
  • 66.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)
  • 67.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences Do we really need to build the suffix tree to construct the suffix array? This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)
  • 68.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T =
  • 69.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1
  • 70.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1
  • 71.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2
  • 72.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2
  • 73.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
  • 74.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 R1 is split into blocks of length 3
  • 75.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
  • 76.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
  • 77.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 R2 is also split into blocks of length 3
  • 78.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
  • 79.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2
  • 80.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol)
  • 81.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1
  • 82.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2
  • 83.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 3
  • 84.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34
  • 85.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 5
  • 86.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56
  • 87.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7
  • 88.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 we assume that the bit representation of each symbol uses O(log n) bits. (which is a common and realistic assumption) This can be done by sorting the blocks in O(n) time using radix sort
  • 89.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7
  • 90.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
  • 91.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
  • 92.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7
  • 93.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70
  • 94.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7
  • 95.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 How do we compute the suffix array for R ? Recursion! (Notice that R has length 2n/3)
  • 96.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : 1 2 3 4 5 6 70 0 1 6 4 2 5 3 7
  • 97.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : what use1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 is this?!
  • 98.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $R1 = b d ob a a b b a d $R2 = $ a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: Introduce a new “filler symbol” $. B2 contains indices with i mod 3 = 2 Number the blocks in lexicographical order ($ is the smallest symbol) 1 2 4 34 56 7 let R = 1 2 4 34 56 7 compute the suffix array of R : what use1 2 3 4 5 6 70 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
  • 99.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
  • 100.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 is this?!
  • 101.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 a b d ob a a b b a d d oa b b a d is this?! 1 5
  • 102.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d is this?! 1 5
  • 103.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d is this?! 1 5
  • 104.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ is this?! 1 5
  • 105.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ is this?! 1 5
  • 106.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ is this?! 1 5
  • 107.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5
  • 108.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5
  • 109.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R a b d ob a a b b a d d oa b b a d a b d ob a a b b a d $ b d ob a a b b a d $ $ d oa b b a d $ $ their order is given by the suffix array of R : is this?! 1 5 Suffix is smaller than suffix 1 55
  • 110.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?!
  • 111.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7
  • 112.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 ob b a d $ b d ob a a b b a d $ $
  • 113.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
  • 114.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
  • 115.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $
  • 116.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 ob b a d7 d oa b b a d $ $ ob b a d $ b d ob a a b b a d $ $ Suffix is smaller than suffix 7 5
  • 117.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?!
  • 118.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2
  • 119.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
  • 120.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
  • 121.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $
  • 122.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 Take any two suffixes in B1 ∪ B2 and find them in R their order is given by the suffix array of R : is this?! d oa b b a d5 b d ob a a b b a d2 d oa b b a d $ $ b d ob a a b b a d $ $ Suffix is smaller than suffix 2 5
  • 123.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 compute the suffix array of R : what use 0 1 6 4 2 5 3 7 0 1 2 3 4 5 6 7 is this?!
  • 124.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7
  • 125.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7
  • 126.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling,
  • 127.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, 1 24 111058 7
  • 128.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7
  • 129.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7
  • 130.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 a b d ob a a b b a d $ b d ob a a b b a d $ $ Concatenate R1 and R2 to obtain R: B2 contains indices with i mod 3 = 2 0 1 2 3 4 5 6 7 The suffix array of R : 0 1 6 4 2 5 3 7 after relabelling, we have the suffix array of just the suffixes from B1 ∪ B2 1 24 111058 7 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0)
  • 131.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0)
  • 132.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 24 111058 7
  • 133.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7
  • 134.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 1 24 111058 7
  • 135.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y 1 24 111058 7
  • 136.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y suffix 0 is a y 1 24 111058 7 followed by suffix 1
  • 137.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y 1 24 111058 7
  • 138.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 1 24 111058 7
  • 139.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank:
  • 140.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank:
  • 141.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort
  • 142.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
  • 143.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 How do we find the ordering of the suffixes from B0? (where i mod 3 = 0) Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
  • 144.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6)
  • 145.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Suffix array for just B0 6 09 3
  • 146.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 Each suffix i ∈ B0 is represented by (T[i], r) where r is the rank of suffix (i + 1) 1 24 111058 7 (the ranks are given by the array below) rank: We then sort in O(n) time using radix sort y a b d ob a a b b a d d ob a a b b a d oa b b a d oa d 0 3 6 9 = + 1y = + 4b = + 7a = +a 10 (y, 0) (b, 1) (a, 4) (a, 6) Suffix array for just B0 6 09 3 How do we merge these?
  • 147.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these?
  • 148.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . .
  • 149.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ?1 6
  • 150.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2
  • 151.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3)
  • 152.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3) It takes O(1) time to decide that 1 is smaller
  • 153.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . which is smaller, suffix or ? + 7a= 1 6 6 1 +a= 2 (a, 4) (a, 3) It takes O(1) time to decide that 1 is smaller 1
  • 154.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 ?
  • 155.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 ?
  • 156.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 (a, 4) (a, 5) ?
  • 157.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 which is smaller, suffix or4 6 + 7a=6 4 +a= 5 (a, 4) (a, 5) Again, it takes O(1) time to decide that is smaller6 ?
  • 158.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6
  • 159.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 which is smaller, suffix or4 9 ?
  • 160.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 )4(which is smaller, suffix or4 9 ? is smaller
  • 161.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 )4(which is smaller, suffix or4 9 ? is smaller
  • 162.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8which is smaller, suffix or 9 ?
  • 163.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 +a= +b= 9 10 8 9 which is smaller, suffix or 9 ?
  • 164.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 +a= +b= 9 10 8 9 Uh oh! how do we compare 9 10to ? which is smaller, suffix or 9 ?
  • 165.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 8 Uh oh! how do we compare 9 10to ? +a= +b= 9 8 d a + + 11 10 It still takes O(1) time to decide that is smaller9 which is smaller, suffix or 9 ?
  • 166.
    The DC3 method ya b d ob a a b b a d 1 2 3 4 5 6 7 8 9 10 110 T = B1 contains indices with i mod 3 = 1 B2 contains indices with i mod 3 = 2 Suffix array for just B1 ∪ B2 1 2 3 4 5 6 70 1 24 111058 7 Suffix array for just B0 6 09 3 How do we merge these? Merge them like in mergesort. . . 1 6 4 Overall this merging phase takes O(n) time (because processing each suffix takes O(1) time)
  • 167.
    The DC3 method Theorem TheDC3 algorithm constructs a suffix array in O(n) time.
  • 168.
    The DC3 method Theorem TheDC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n)
  • 169.
    The DC3 method Theorem TheDC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n) radix sorting and merging recursion to construct a suffix array of size 2n/3
  • 170.
    The DC3 method Theorem TheDC3 algorithm constructs a suffix array in O(n) time. Proof Suppose T(n) is the running time. We have T(n) = T(2n/3) + O(n) Solving this recurrence gives T(n) ∈ O(n). radix sorting and merging recursion to construct a suffix array of size 2n/3
  • 171.
    The suffix array Tb n aaT a sn n Suffix Array 1 0 625 4 Sort the suffixes lexicographically 0 b n aaa sn n aa1 a sn 2 n aa sn 4 a sn 5 a s 6 s 3 aa sn 3 n P aa n m an Finding an occurrence of a pattern (length m) takes O(m log n) time Finding all occurrences takes O(m log n + occ) time where occ is the number of occurences We can construct the suffix array in O(n) time This can be further improved to O(m + log n + occ) time (using LCP queries which we will see in a future lecture)