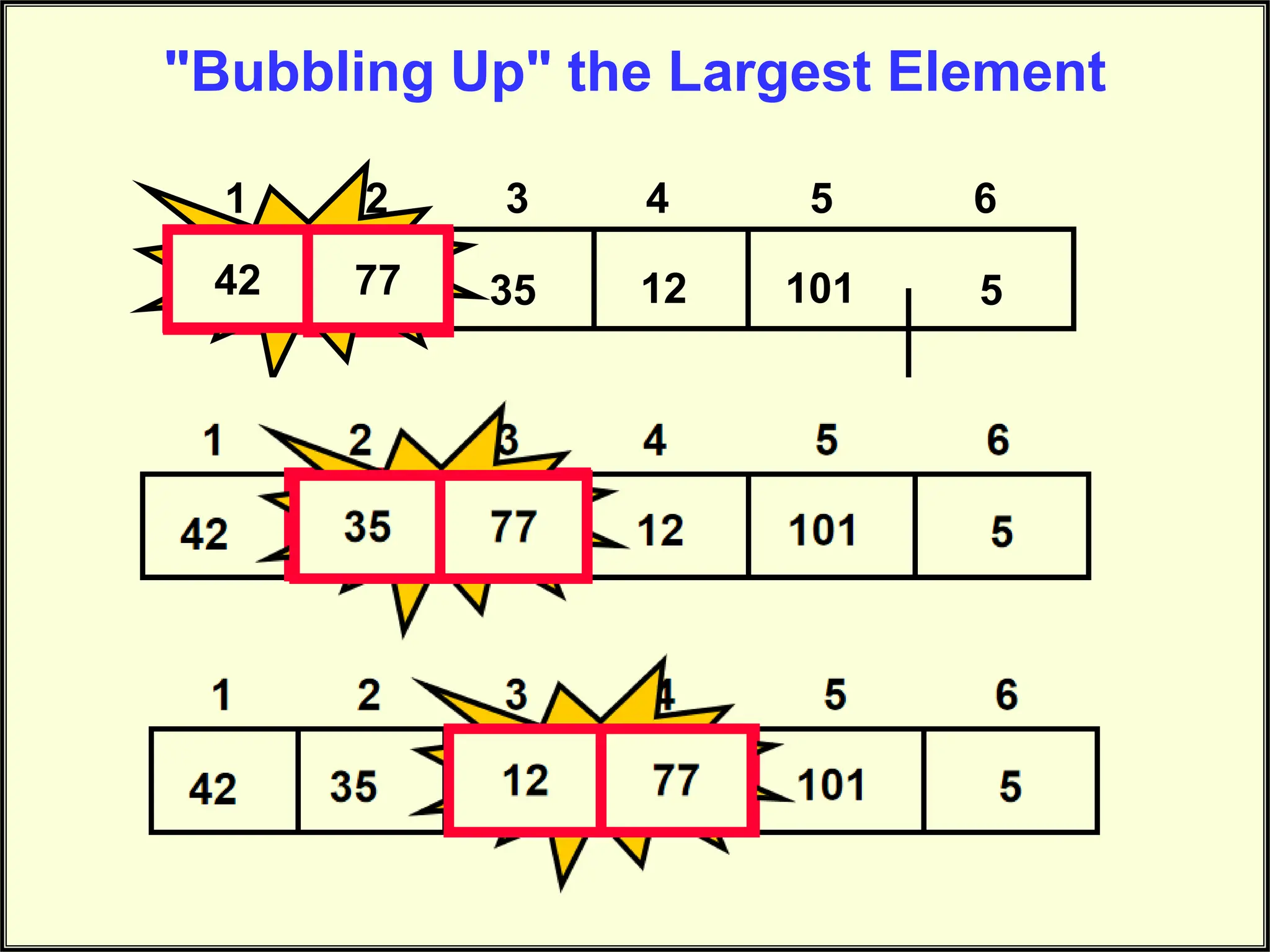
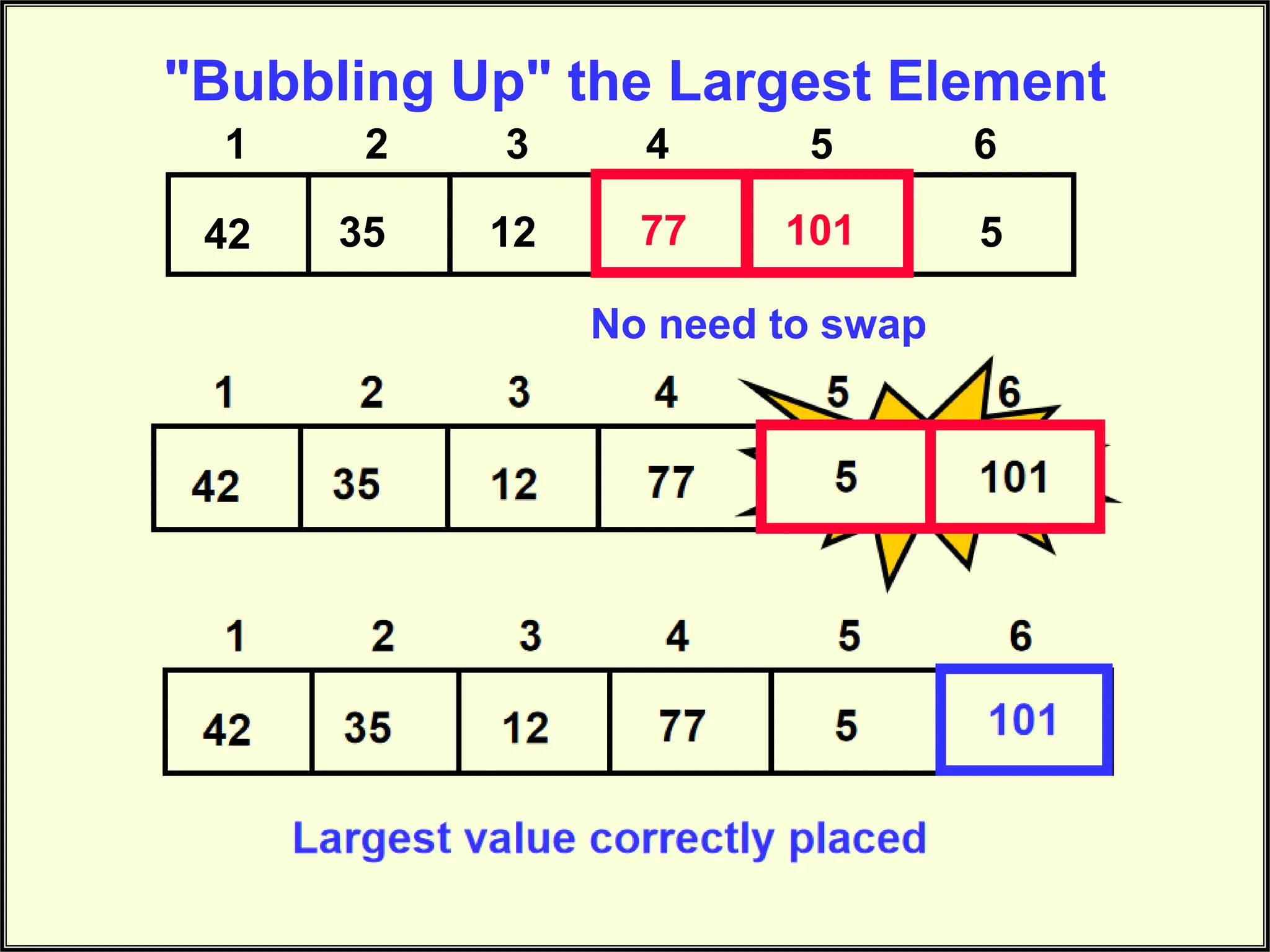
The document describes the bubble sort algorithm. Bubble sort works by repeatedly comparing adjacent elements and swapping them if they are in the wrong order, causing the largest elements to "bubble" to the top of the list. This process is repeated, each time allowing the next largest element to bubble to the top, until the entire list is sorted after N-1 passes through the list. The algorithm is simple but inefficient for large lists, as it compares and swaps elements multiple times.






![// Optimized java implementation of Bubble sort import java.io.*; class GFG { // An optimized version of Bubble Sort static void bubbleSort(int arr[], int n) { int i, j, temp; boolean swapped; for (i = 0; i < n - 1; i++) { swapped = false; for (j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // Swap arr[j] and arr[j+1] temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; swapped = true; } } // If no two elements were // swapped by inner loop, then break if (swapped == false) break; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) System.out.print(arr[i] + " "); System.out.println(); } // Driver program public static void main(String args[]) { int arr[] = { 64, 34, 25, 12, 22, 11, 90 }; int n = arr.length; bubbleSort(arr, n); System.out.println("Sorted array: "); printArray(arr, n); } }](https://image.slidesharecdn.com/bublesort-240304101419-10873307/75/MYSQL-DATABASE-MYSQL-DATABASE-MYSQL-DATABASE-BUBLESORT-pptx-9-2048.jpg)

