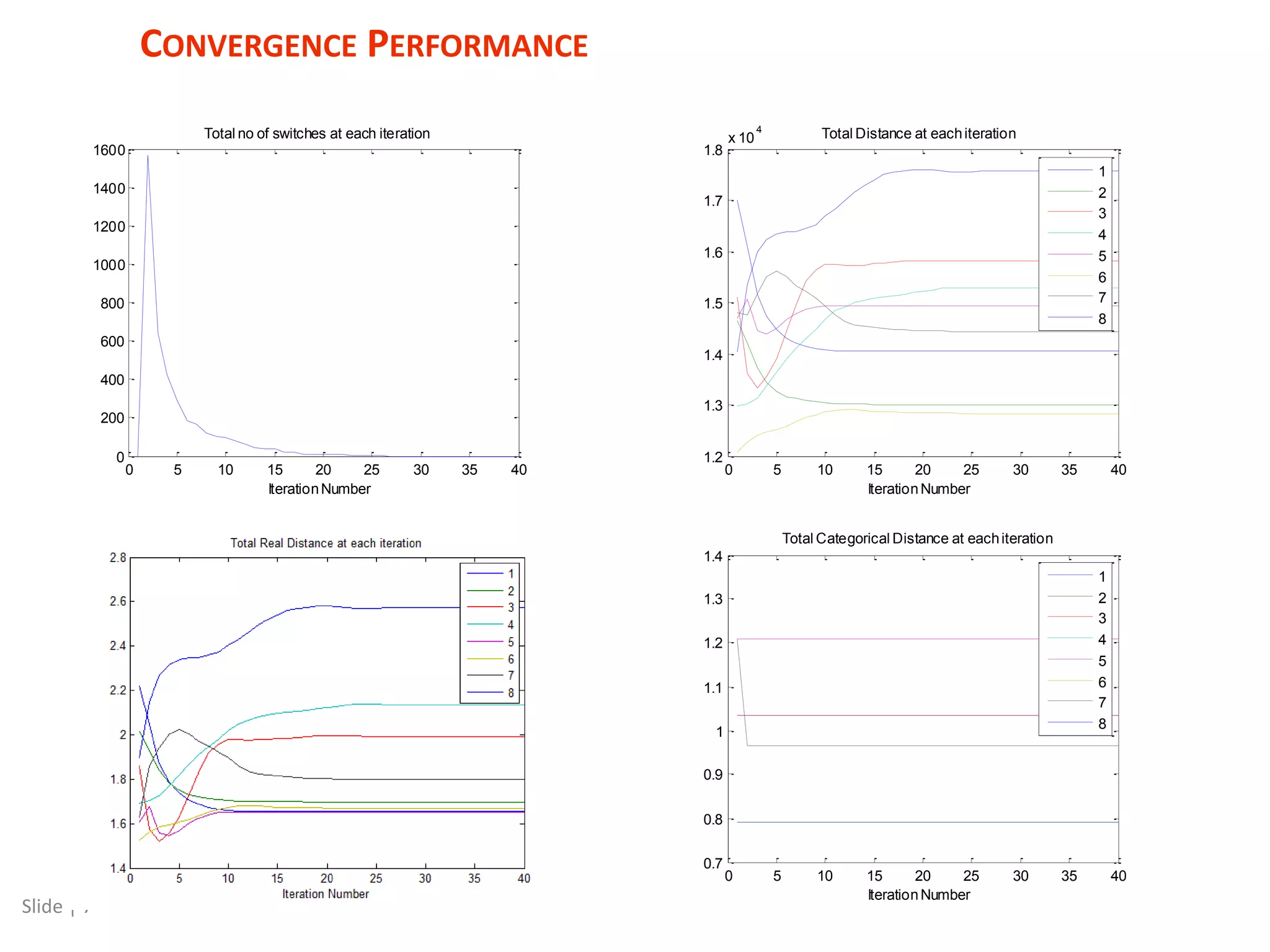
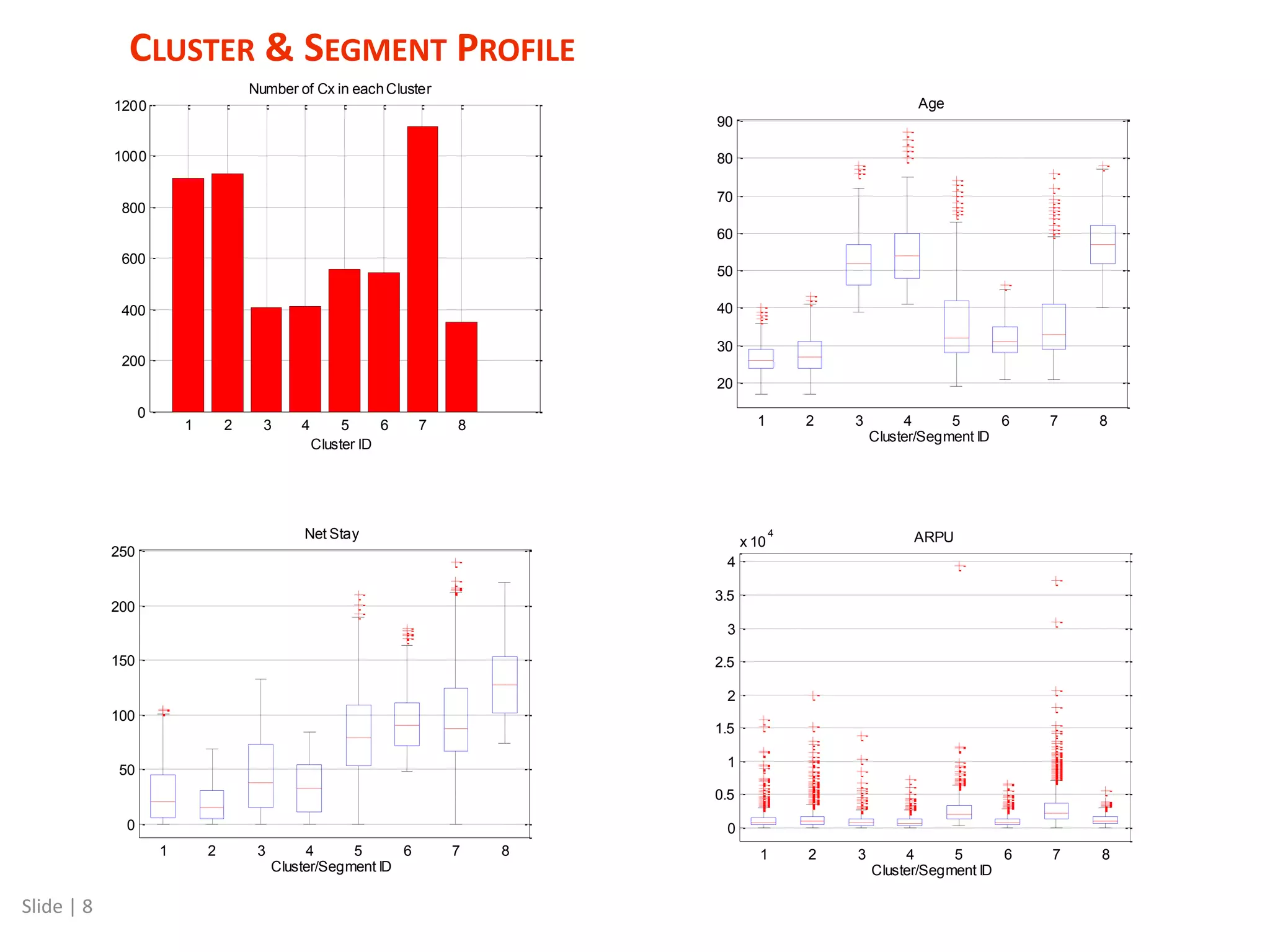
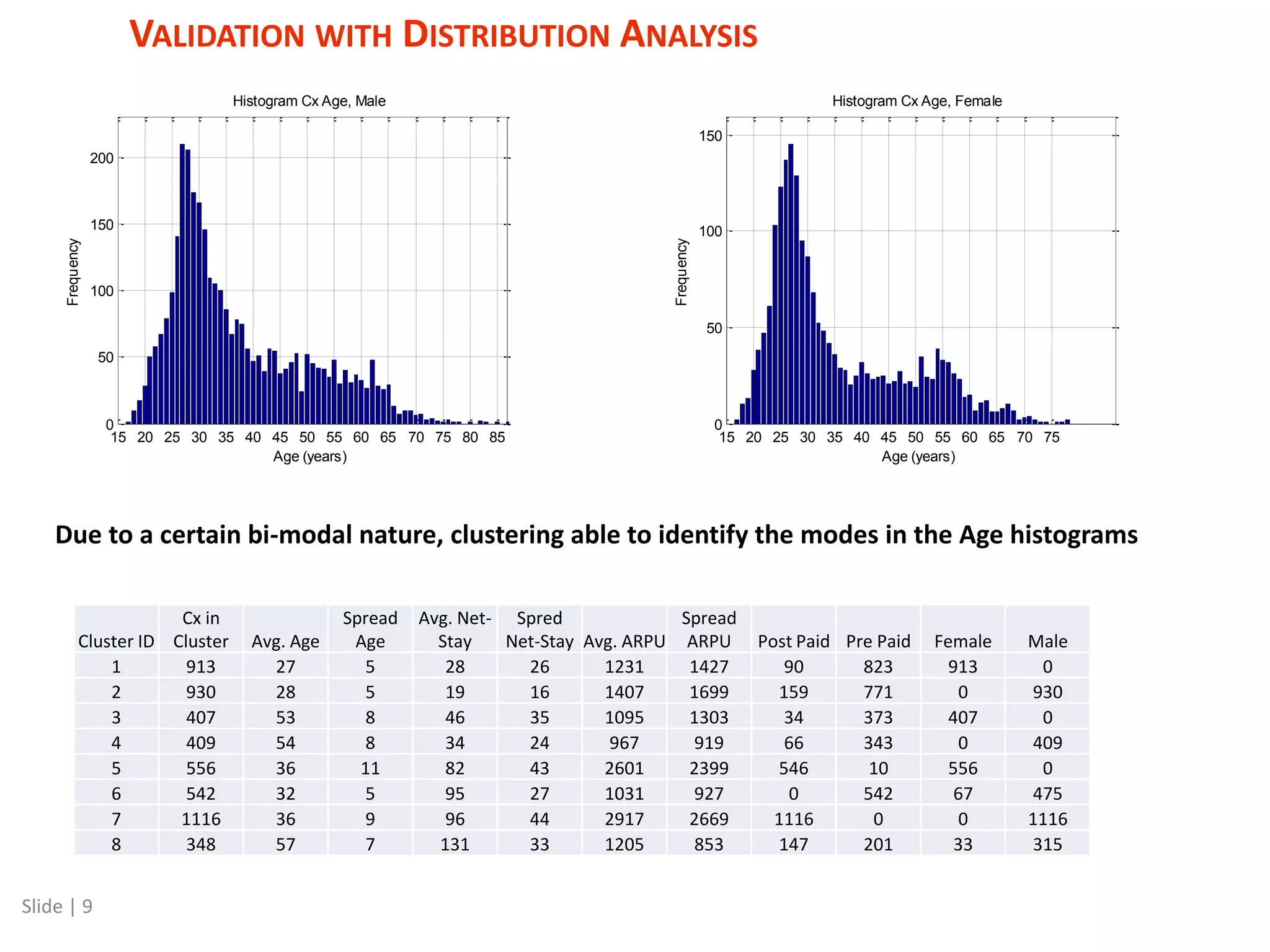
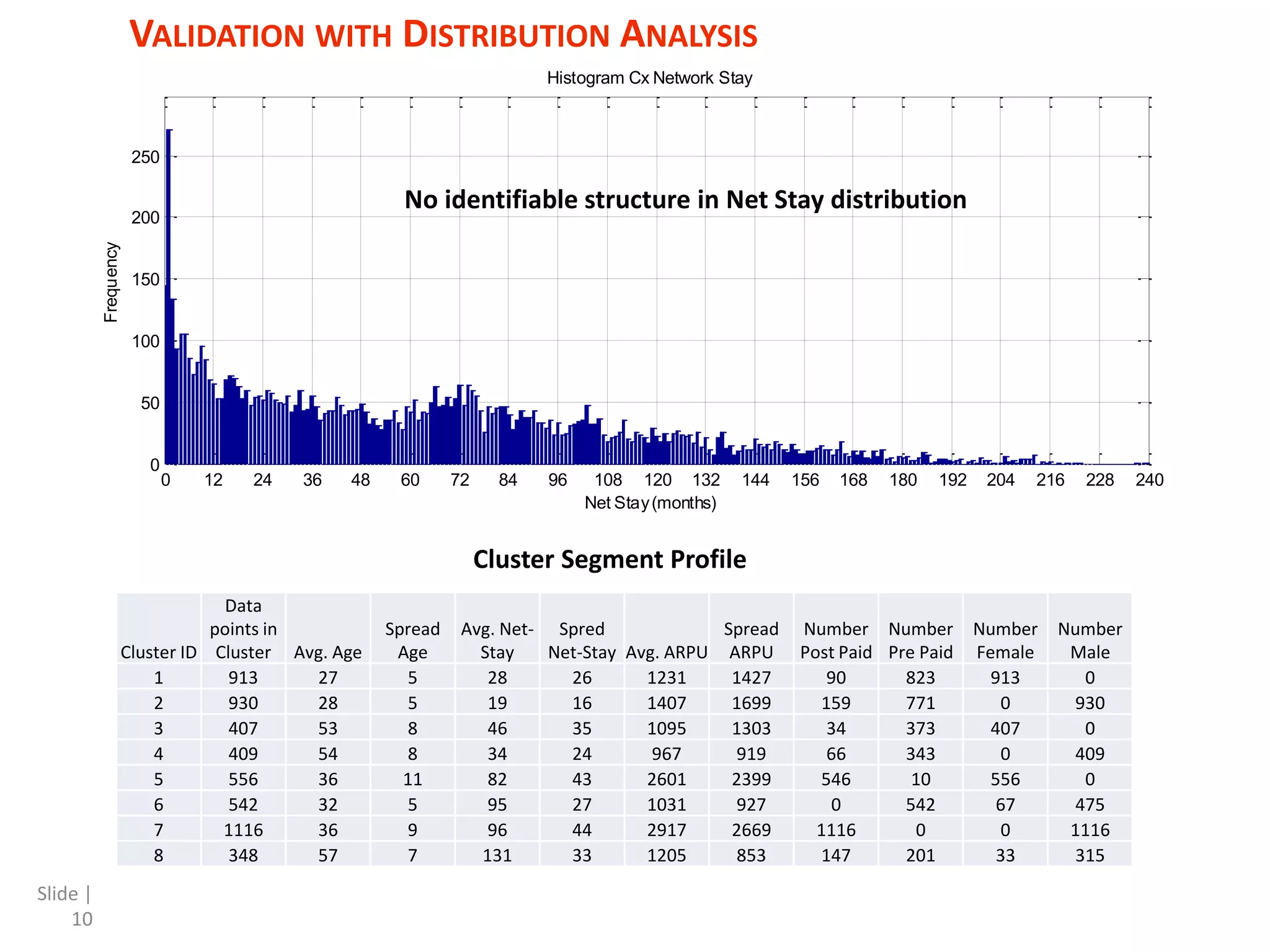
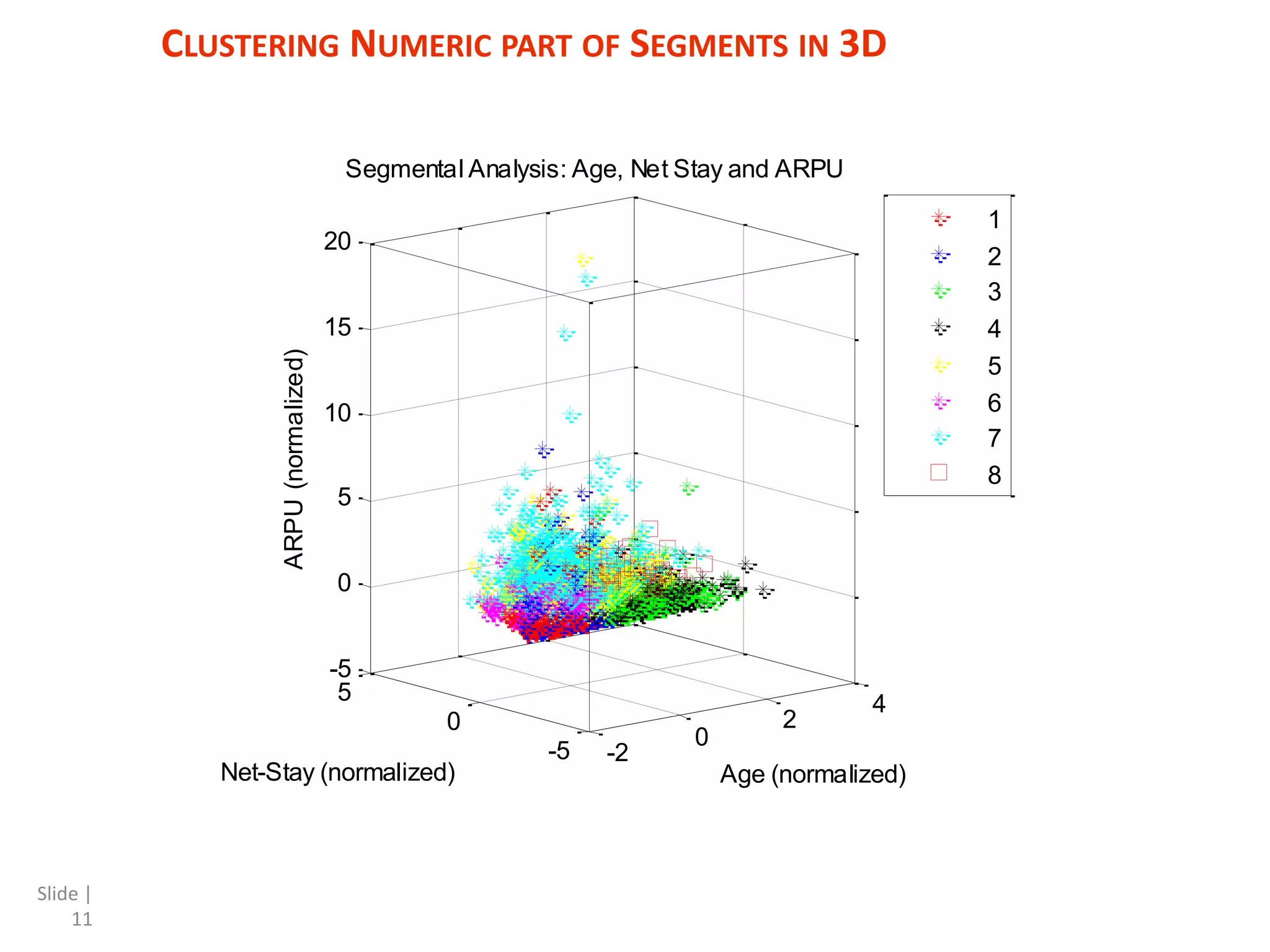
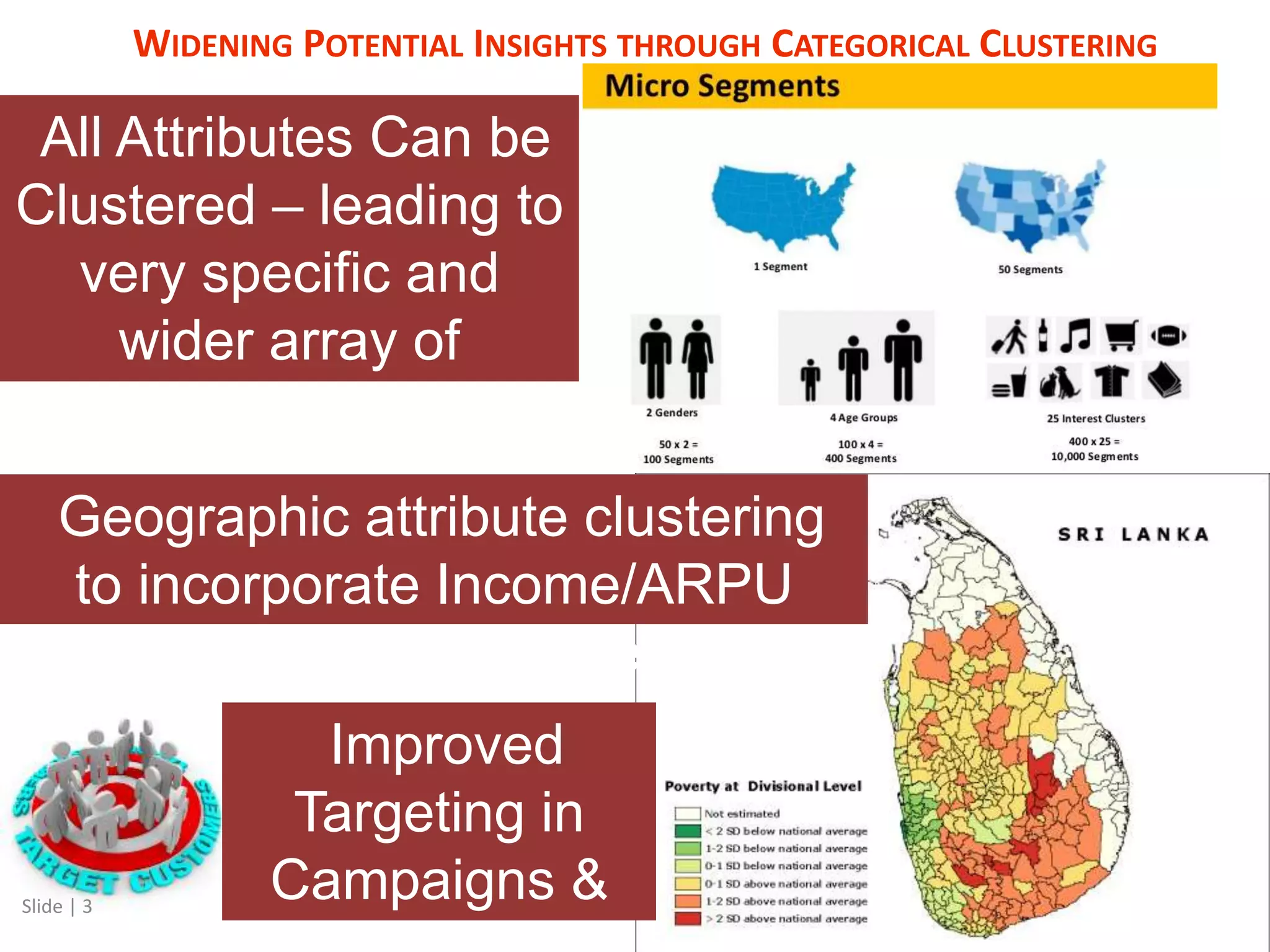
The document discusses a mixed numeric and categorical attribute clustering algorithm, detailing its advantages for improved campaign targeting and insights into micro-segments. It introduces the mixed k-prototypes algorithm, which combines numeric and categorical attributes to create specific segments while discussing convergence performance and validation through distribution analysis. The algorithm's sensitivity to initial conditions and flexibility in clustering various attributes are noted, alongside considerations for potential local minima in optimization.


![CONCEPT UNDERLYING THE MIXED K PROTOTYPES ALGORITHM [1] Slide | 4 point “d” and point “c” may switch sides depending on how similar the numeric part and categorical part of the point is similar to the numeric and categorical part of the centroid (prototype) Influence or contribution of Numeric and Categorical Attributes of a data point can be controlled via a parameter “gamma” Point “a” may switch if the categorical part is closer to the categorical centroid (prototype) more than its numeric part is close to the numeric part of the centroid. Numeric and Categorical Attributes parts of a data point can be considered separately and two sets of centroids act as attractors for each Attribute type in each cluster Numeric Attribute1 Shapes represent two values of a single categorical variable Numeric Attribute2 [1]. Huang, CSIRO, Australia](https://image.slidesharecdn.com/mixednumericandcategoricalattributeclusteringalgorithm-170211052656/75/Mixed-Numeric-and-Categorical-Attribute-Clustering-Algorithm-4-2048.jpg)
![MIXED K PROTOTYPES ALGORITHM [1] Slide | 5 Distance measure to a prototype (center) of two parts – numeric and categorical Numeric Attributes - Euclidian Distance Categorical Attributes – Dissimilarity Measure Centroid of Numeric Attributes – a simple average of the points in that cluster Includes “Yij” a fuzzy membership function if we wish to go in that direction](https://image.slidesharecdn.com/mixednumericandcategoricalattributeclusteringalgorithm-170211052656/75/Mixed-Numeric-and-Categorical-Attribute-Clustering-Algorithm-5-2048.jpg)
![MIXED K PROTOTYPES ALGORITHM [1] Slide | 6 Minimize the total cost “E” which is the sum of the distances to the numeric and categorical parts of the centroid (prototype) Centroid of Categorical attributes determined on highest frequency of attribute value in each cluster](https://image.slidesharecdn.com/mixednumericandcategoricalattributeclusteringalgorithm-170211052656/75/Mixed-Numeric-and-Categorical-Attribute-Clustering-Algorithm-6-2048.jpg)