Minimization of Localization Error using Connectivity based Geometrical Method in Wireless Sensor Networks

Minimization of Localization Error using Connectivity based Geometrical Method in Wireless Sensor Networks

• 1.
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 131 Copyright © 2018. IJEMR. All Rights Reserved. Volume-8, Issue-5, October 2018 International Journal of Engineering and Management Research Page Number: 131-136 DOI: doi.org/10.31033/ijemr.8.5.14 Minimization of Localization Error using Connectivity based Geometrical Method in Wireless Sensor Networks Sita Kumari. CH1 and Dr. S.P. Setty2 1 Assistant Professor, Department of Information Technology, Gayatri Vidya Parishad College of Engineering(A), INDIA 2 Professor, Department of Computer Science and Systems Engineering, Andhrauniversity College of Engineering, INDIA 1 Corresponding Author: sitha_kumari@gvpce.ac.in ABSTRACT Many localization schemes are designed for finding the geographical coordinates of the unlocalized node in the network. Still, it is a difficult problem to find accurate and efficient localization schemes in the Wireless Sensor Networks (WSNs). We proposed a new method, connectivity based WSN node localization using one of the geometrical method namely centroid of a triangle. By developing the centroid of a triangle from the WSN network model in terms of localization requirements. The simulation outcomes have shown that the modified centroid (centroid_T) performs marginally better than the existing centroid method with a marginally increase in the computation process. We also observe the variation of localization error with various anchor nodes, radio range, and network size. Keywords— Centroid of a Triangle, Localization, WSN I. INTRODUCTION Wireless Sensor Network (WSN) is a wireless intelligent network. It has ten to thousand sensor nodes. These nodes are communicating through radio waves and infrared medium. Each sensor node integration of a sensing device, a processing circuit, a communication unit, a power source, and required software[1][2]. The sensing device is the combination of sensors and ADC. The sensors are gathering the raw information externally and fed to the ADC. The ADC provides the corresponding information and interacts with the processing unit. The processing circuit performing computations according to the requirements given by software instructions. The results are stored into memory or transferred to another sensor node through the communication unit. The communication unit is the combination of transmitter and receiver, it transmitting and receiving the data among the sensor nodes. Finally, power source generates the power for processing and transmission of data to among the nodes. In WSNs, many of the applications such as target detection [3][4], forest fire detection, monitoring of the environment[5], traffic monitoring[5], hospital management[6], and industrial applications[5] require the position of the data that is localization, because the data received from any sensor nodes remain meaningless until it correlated with information about the position. Localization is the process of finding the physical coordinates of the sensor nodes with the help of known reference nodes or Global Positioning System (GPS). Basically, sensor nodes have limited computational power, radio communication range, and battery lifetime, there is a need for efficient and reliable localization methods. Localization is an interesting and important research area, many authors are proposed many localization algorithms, still, it requires accurate and minimum power with low-cost localization methods. When the developer design localization methods, they should consider following properties [7]. i. The developer must consider minimum power and cost of hardware because basically, WSN nodes are low power, low communication coverage area. ii. The localization is suitable in three dimensional(3D) node deployment models. iii. The Global Positioning System(GPS) is not suitable for in all environments because signal problems and it needs more hardware. If ever sensor node has GPS it requires more hardware, then cost and power consumption increase. iv. Node density is also an important factor when localization methods are implemented because more reference nodes (Anchor nodes)
• 2.
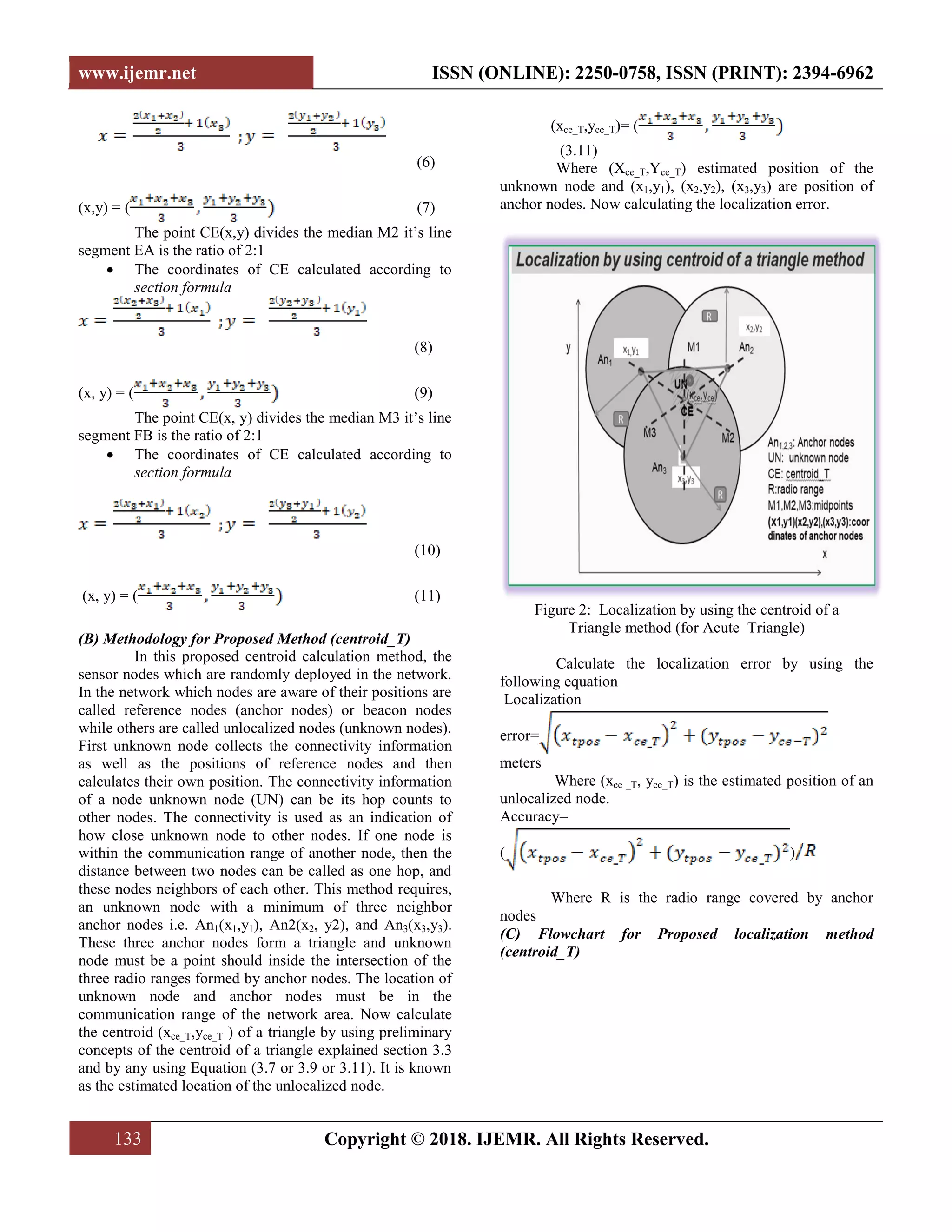
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 132 Copyright © 2018. IJEMR. All Rights Reserved. provide better accuracy but energy consumption is also increasing, So optimum number of anchors are required. v. The designed localization algorithms should be universal, not for particular applications it should applicable indoor as well as outdoor localization applications Localization methods have classified according to different criteria such as mode of operations, measurement and calculations, importance of accuracy, hardware complexity, network architecture, and node deployment models. According to measurement and classifications, the localization methods have divided into range-based and range-free methods. In the range-based localization method, the position of unlocalized nodes can be estimated with the help of distance or time difference or angle or signal strenth between the unknown node and reference nodes. Examples of range based methods[8] are TDOA, TOA, AOA, RSSI. In range-free methods the position is calculated, connectivity between reference nodes in terms of hop count only no need of distance between reference nodes. The well-known methods for range-free localization[9] are Centroid, Weighted centroid, DV-hop, Improved DV-hop, APIT, Bounding box, Amorphous, II. RELATED WORK The centroid is a simple range-free localization scheme introduced by Bulusu et al., [10]. Centroid uses a regular mesh topology of nodes which are known their positions and serve as reference points or anchors. These anchors send their location information as an announcement called beacons in periodically. The beacon consists of a reference location and connectivity metric based on received packets are used to rate the connectivity between an unknown node and its available reference locations. In equation 1 NoBrecv and NoBsend denote the number of beacons received from and sent by the ith anchor node in a time period t. If the receiving node receives the beacons grater than the threshold value in period t, then the nodes are considered with in a radio range. (1) Where CM is connectivity metric NoBrecv(i,t) is Number of Beacons received i th anchor in time period ‘t’ NoBsend(i,t) is Number of Beacons send i th anchor in time period ‘t’ Those anchors connectivity count CMi > CMthresh are considered for localization. The authors propose to set CMthresh = 90, i.e., only anchors with high delivery ratios are assumed to be connected to the unknown node. The set of ‘m’ anchors chosen reference points are used to estimate the location of the unlocalized node by using given Equation (2) (xest,yest)=( (2) Where (Xest, Yest) estimation position of the unlocalised node, (x1,y1), (x2,y2), ….( xm, ym) locations of ‘m’anchors. III. METHODOLOGY (A) Localization by using the centroid of a triangle (centroid_T) Preliminary concepts for proposed method Where the three medians intersect in a triangle is called centroid[11]. Let ABC be a triangle and their coordinates are A(x1,y1), B(x2,y2), and C(x3,y3). D, E, and F are the mid points and M1, M2, and M3 are the medians of a triangle. Figure 1: Calculation of centroid of a Triangle The centroid CE(x, y) derived as follows D is the mid-point of line segment AB of a triangle and the coordinates of D can be determined using mid-point formula ( (3) E is the mid-point of line segment BC of a triangle and the coordinates of E can be determined using mid-point formula • ( (4) F is the mid-point of line segment CA of a triangle and the coordinates of F can be determined using mid-point formula • ( (5) The point CE (x,y) divides the median M1 it’s line segment DC is the ratio of 2:1 • The coordinates of CE calculated according to section formula (x,y)
• 3.
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 133 Copyright © 2018. IJEMR. All Rights Reserved. (6) (x,y) = ( (7) The point CE(x,y) divides the median M2 it’s line segment EA is the ratio of 2:1  The coordinates of CE calculated according to section formula (8) (x, y) = ( (9) The point CE(x, y) divides the median M3 it’s line segment FB is the ratio of 2:1  The coordinates of CE calculated according to section formula (10) (x, y) = ( (11) (B) Methodology for Proposed Method (centroid_T) In this proposed centroid calculation method, the sensor nodes which are randomly deployed in the network. In the network which nodes are aware of their positions are called reference nodes (anchor nodes) or beacon nodes while others are called unlocalized nodes (unknown nodes). First unknown node collects the connectivity information as well as the positions of reference nodes and then calculates their own position. The connectivity information of a node unknown node (UN) can be its hop counts to other nodes. The connectivity is used as an indication of how close unknown node to other nodes. If one node is within the communication range of another node, then the distance between two nodes can be called as one hop, and these nodes neighbors of each other. This method requires, an unknown node with a minimum of three neighbor anchor nodes i.e. An1(x1,y1), An2(x2, y2), and An3(x3,y3). These three anchor nodes form a triangle and unknown node must be a point should inside the intersection of the three radio ranges formed by anchor nodes. The location of unknown node and anchor nodes must be in the communication range of the network area. Now calculate the centroid (xce_T,yce_T ) of a triangle by using preliminary concepts of the centroid of a triangle explained section 3.3 and by any using Equation (3.7 or 3.9 or 3.11). It is known as the estimated location of the unlocalized node. (xce_T,yce_T)= ( (3.11) Where (Xce_T,Yce_T) estimated position of the unknown node and (x1,y1), (x2,y2), (x3,y3) are position of anchor nodes. Now calculating the localization error. Figure 2: Localization by using the centroid of a Triangle method (for Acute Triangle) Calculate the localization error by using the following equation Localization error= meters Where (xce _T, yce_T) is the estimated position of an unlocalized node. Accuracy= ( ) Where R is the radio range covered by anchor nodes (C) Flowchart for Proposed localization method (centroid_T)
• 4.
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 134 Copyright © 2018. IJEMR. All Rights Reserved. Figure 3: Flow chart for the proposed method IV. EXPERIMENTAL SETUP AND RESULTS ANALYSIS (A) Simulation environment For verifying the performance of the proposed method, a number of simulations have been conducting by using MATLAB R2015a. In this experiment, initial network size is 40m X 40m square area and numbers of sensor nodes are randomly deployed and a radio range of each node is 20meters, which is used to communicate the nodes wirelessly and hop distance between anchor nodes is 10meters it indicates anchor nodes are connected in a single hop. With the help of these simulation parameters to calculate estimate position and localization error by varying anchor density, radio range, and network sizes. Figure 4 shows the simulation environment for localization by using centroid of the triangle (centroid_T). Figure 4: simulation environment for centroid of a Triangle (centroid_T) (B) Experimental Results and Analysis Figure 5: Variation of relative localization error with Radio ranges of centroid and centroid_T Figure 5 shows the Relative Localization error (RLE) with various radio ranges. In both methods the RLE is decreasing by increasing the radio range because communication range increasing more number of reference
• 5.
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 135 Copyright © 2018. IJEMR. All Rights Reserved. nodes are available for an unknown node, then the distance between anchor nodes are decreasing. If the distance is decreasing, the error is also decreasing. When the communication range is 20meters, the RLE has decreased by 7.88 % in the centroid_T method as compared to the existing centroid method. Figure 6: Variation of Relative Localization Error with anchor nodes of centroid and centroid_T Figure 6 shows, when the anchor node amount is minimum, the RLE has decreased by 4.99% in the centroid_T method as compared to the existing centroid method. Figure 7: Variation of Relative Localization Error with anchor nodes of centroid and centroid_T The figure 7 shows, when the network size is 40sq.m, the RLE has decreased by 8.66% in the centroid_T method as compared to the existing centroid method. In both the methods the localization error is increasing when increasing the network size. Figure 8: Variation of Relative Localization Error with Simulation rounds of centroid and centroid_T The RLE of both methods is maintained study state error when increasing the number of simulation rounds. V. CONCLUSION Location of data is very important in certain applications of WSNs, So localization plays a major role in the WSNs. When comparing with range-based localization methods, the rage free localization methods have less cost and less complexity. Simulation results demonstrate under the various parameters which are effective to the localization error like anchor amount, radio range and network size. The accuracy of the calculated position is directly related to the anchor nodes in the sensor field and radio-range. We can archive high accuracy with more number of anchor nodes, but at the same time, energy consumption and cost is increased. The existing centroid localization method and modified centroid localization method comparatively observed, it found that the localization error is minimized when increasing the radio range, anchor nodes, and error is increasing when the network size is increasing. The simulation outcomes have shown that the modified centroid (centroid_T) performs marginally better than the existing centroid method.
• 6.
  www.ijemr.net ISSN (ONLINE):2250-0758, ISSN (PRINT): 2394-6962 136 Copyright © 2018. IJEMR. All Rights Reserved. REFERENCES [1] Hu. F, Cao. X. (2010). Wireless sensor networks: Principles and practice. (1st ed.). CRC Press: Taylor & Francis Group. [2] Waltenegus Da, & Christian. P. (2010). Fundamentals of wireless sensor networks: Theory and practice. Wiley Publications. Available at: https://pdfs.semanticscholar.org/e87f/5253451603be6ef1b5 d56700ed8048a33d61.pdf. [3] F. Akyildiz, Su. W, Y., & Cayirci. E. (2002). Wireless sensor networks: A survey. Computer Networks, 38(4), 393-422. [4] M.Haenggi. (2005). Opportunities and challenges in wireless sensor networks in handbook of sensor networks. Compact Wireless and Wired Sensing Systems, New York, USA: CRC Press. pp.1-11. [5] M.A Perillo & Heinzelman, W.B. (2004). Wireless sensor network protocols. Available at: https://pdfs.semanticscholar.org/6aee/ed25f71a283ccf5320 4fac00358d3b90d5da.pdf. [6] Yick Jennifer, Mukherjee Biswanath, & Ghosal Dipak. (2008). Wireless sensor network survey. Computer Networks, 52(12), 2292-2330. [7] Ali Alrajeh Nabil, Maryam Bashir, & Shams Bilal. (2013). Localization Techniques in Wireless Sensor Networks. International Journal of Distributed Sensor Network, 1-9. doi.org/10.1155/2013/304628. [8] Wang, Jing, Gosh, R.K., Das, & K Sajal. (2010). A survey on sensor localization. Journal of Control Theory and Applications, 8(1), 2-11. [9] Nicolescu, D., Nath, B. (2003). DV based positioning in ad hoc networks. Telecommunication Systems, 22(1), 267- 280. [10] Bulusu. N, Heidemann. J, & Estrin. D. (2000). GPS- less low-cost outdoor localization for very small devices. IEEE Personal Communications Magazine, 7(5), 28-32. [11] https://www.mathopenref.com