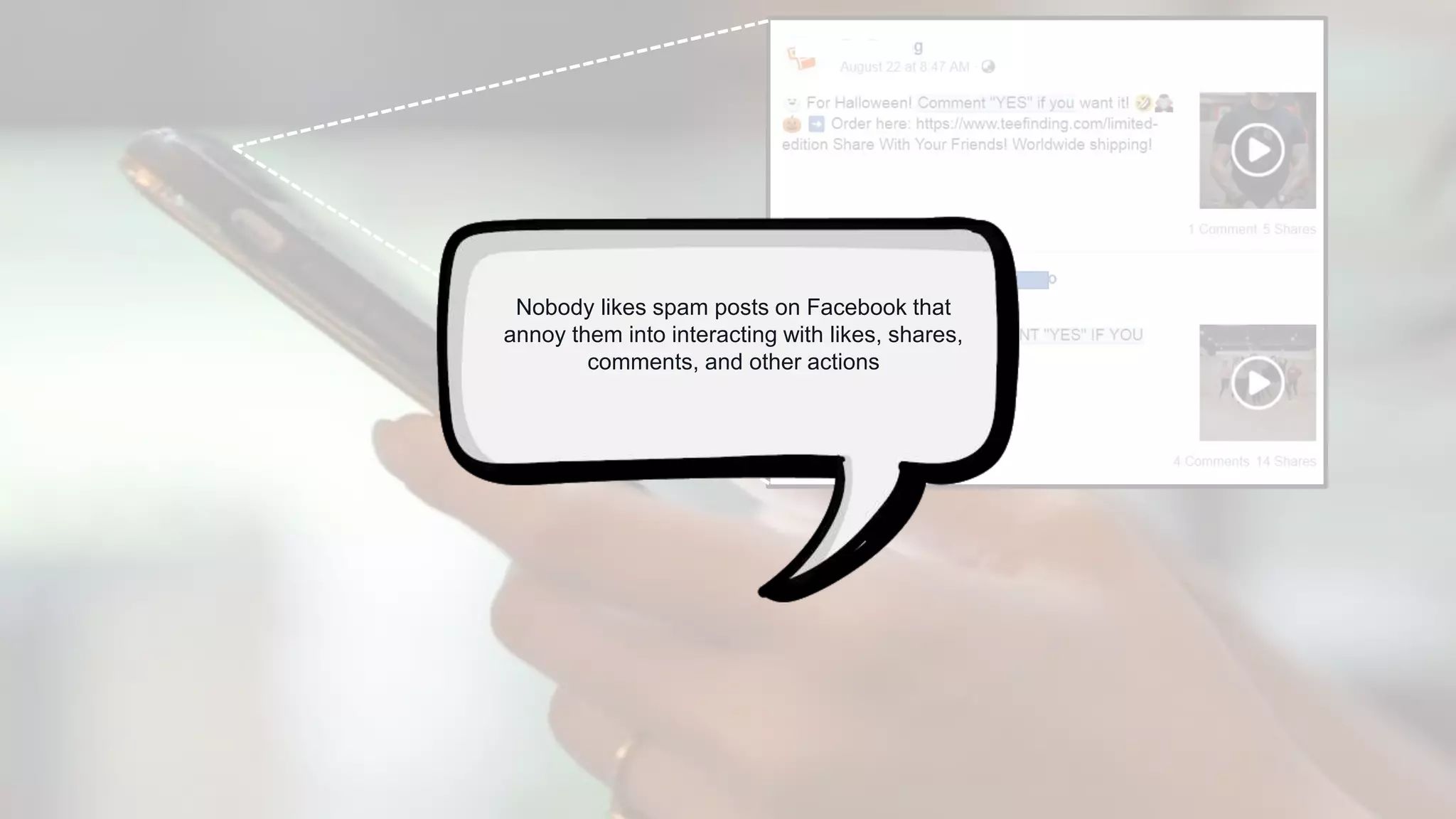
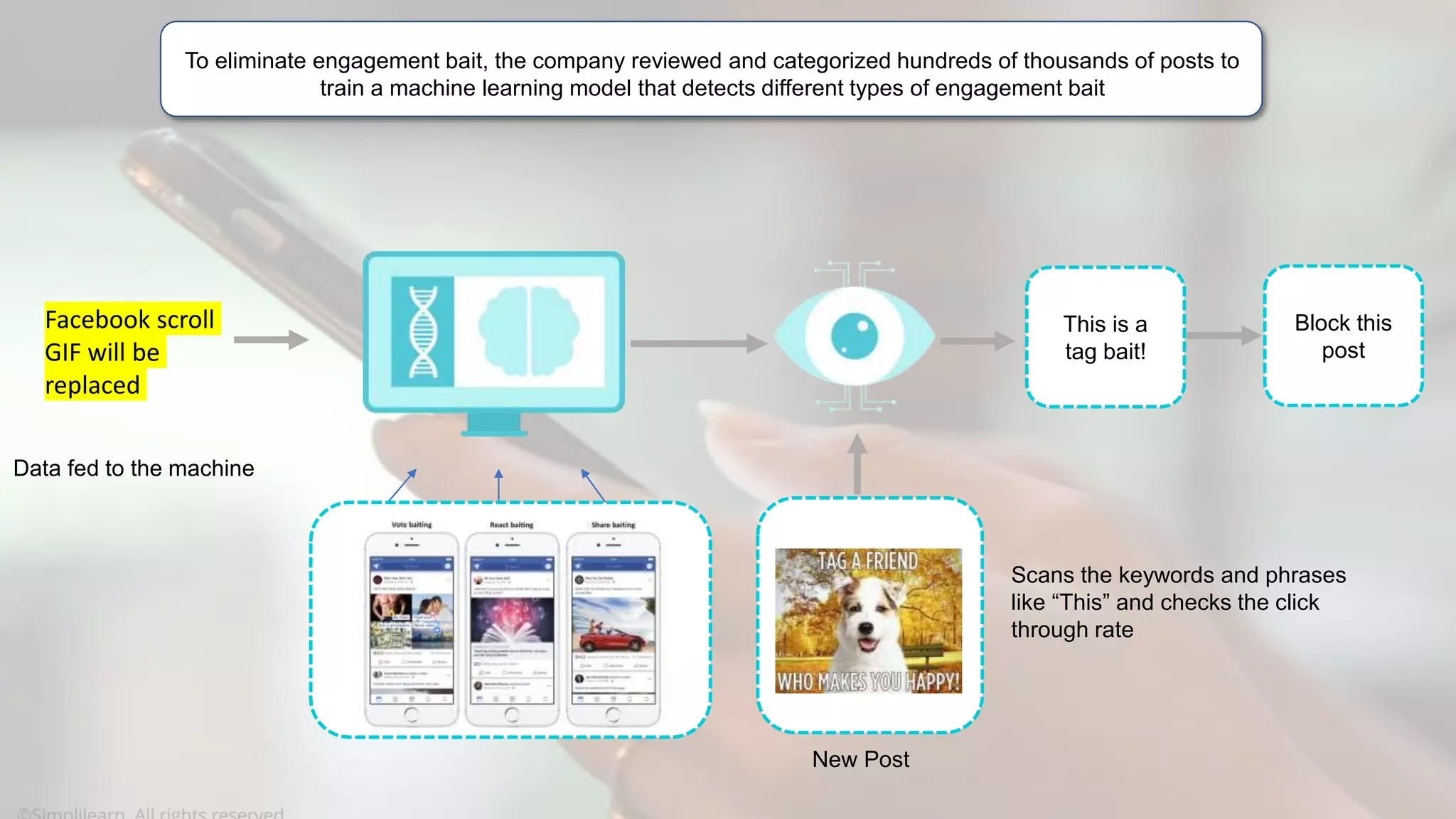
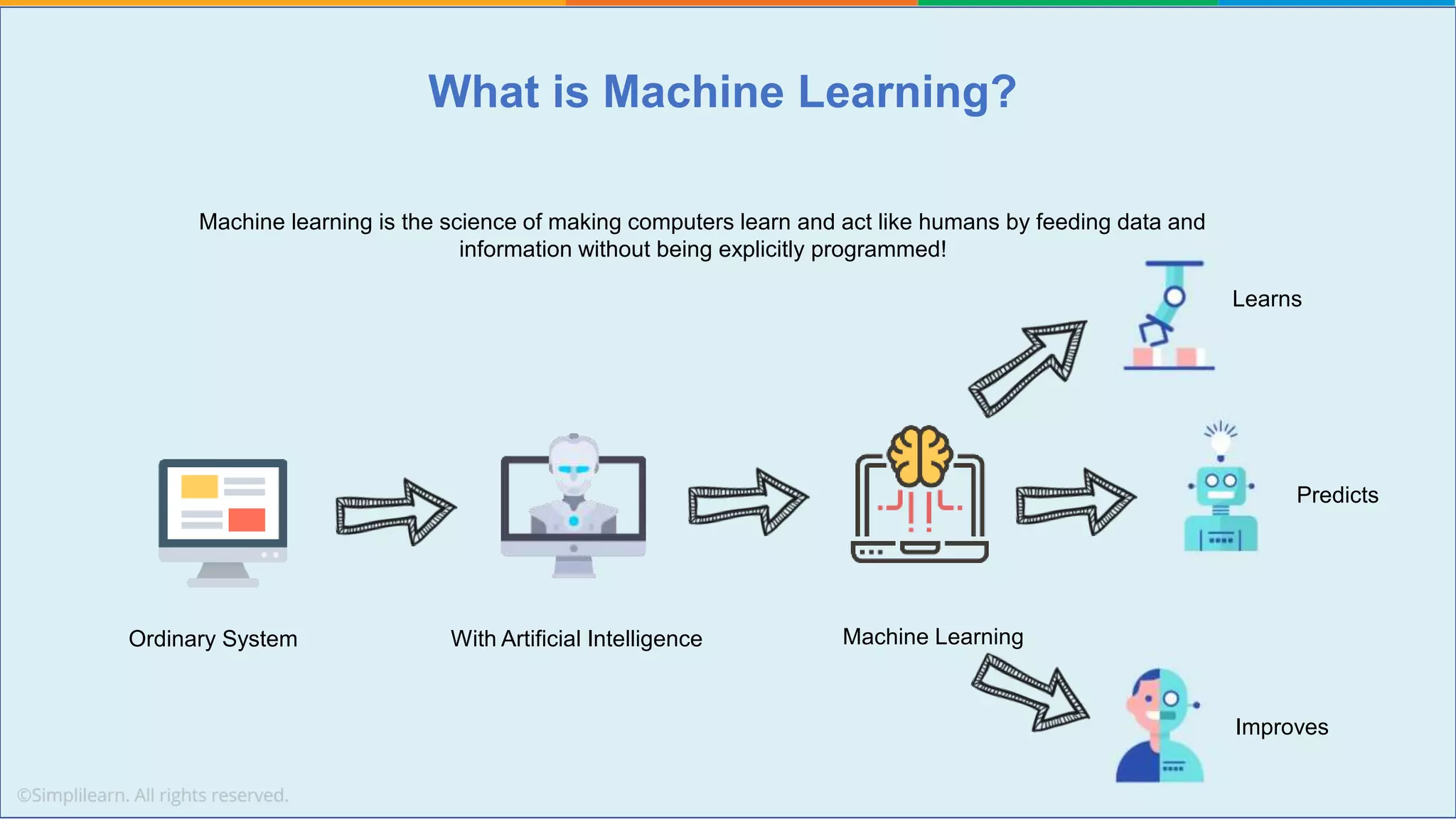
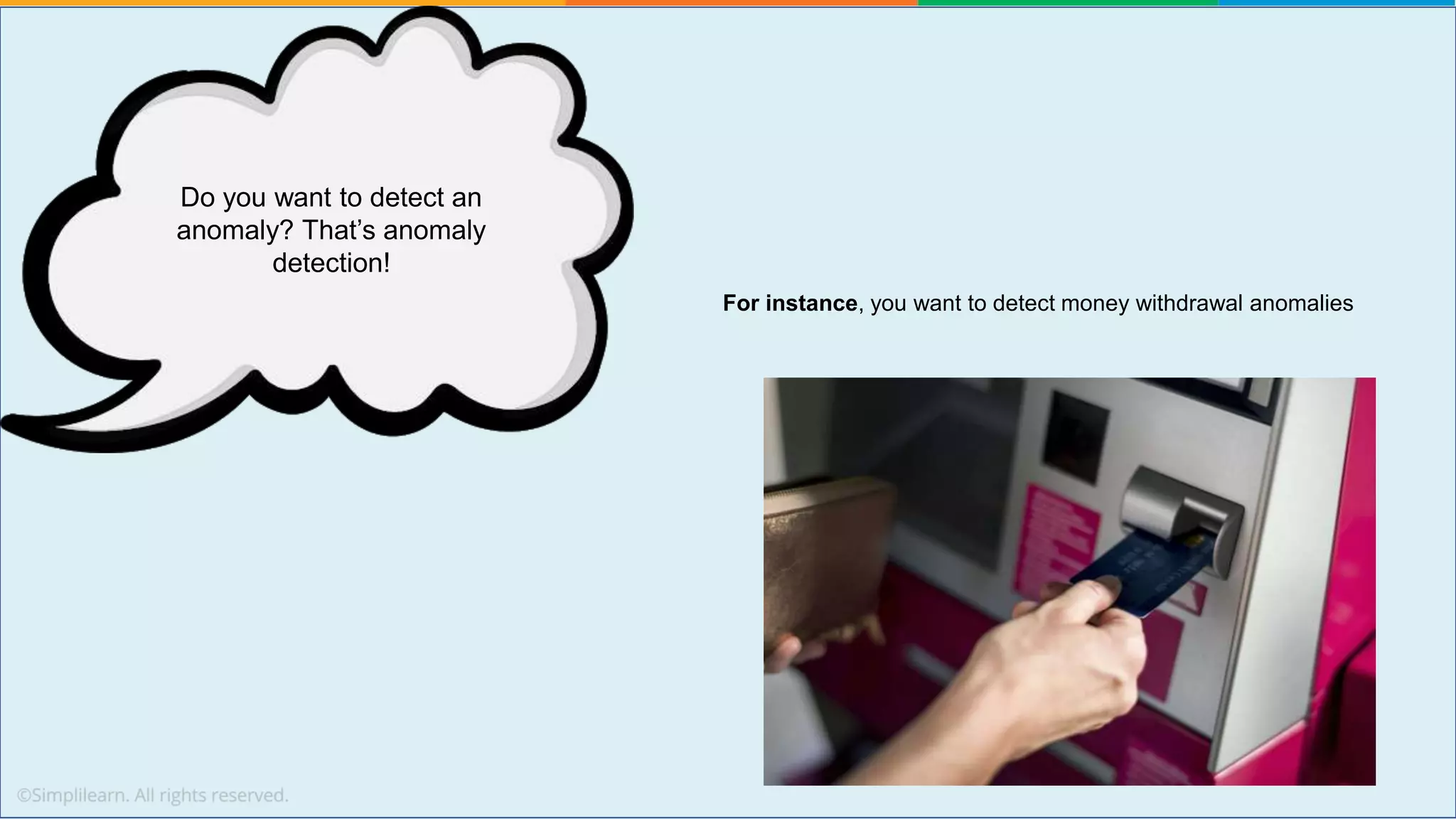
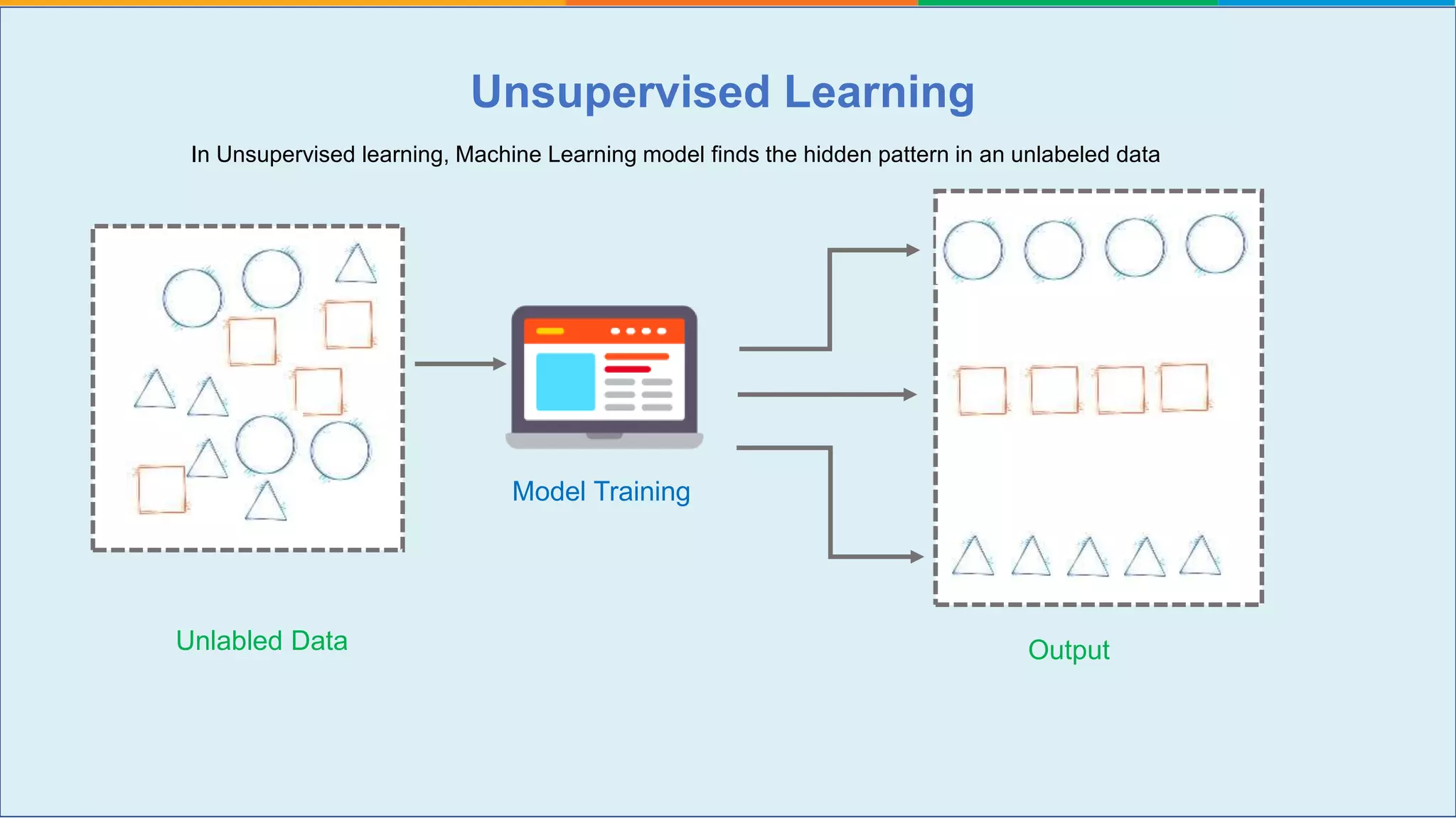
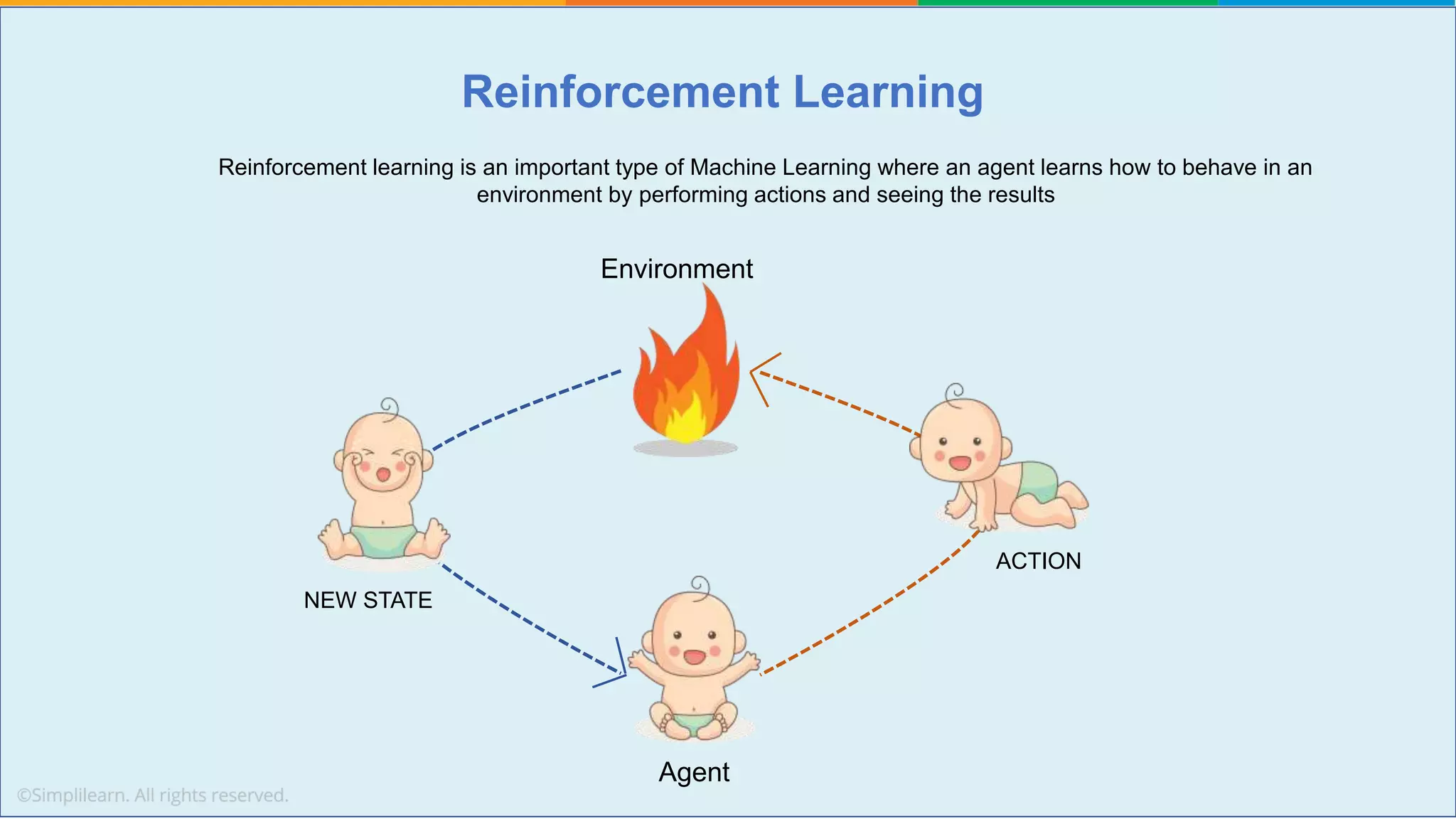
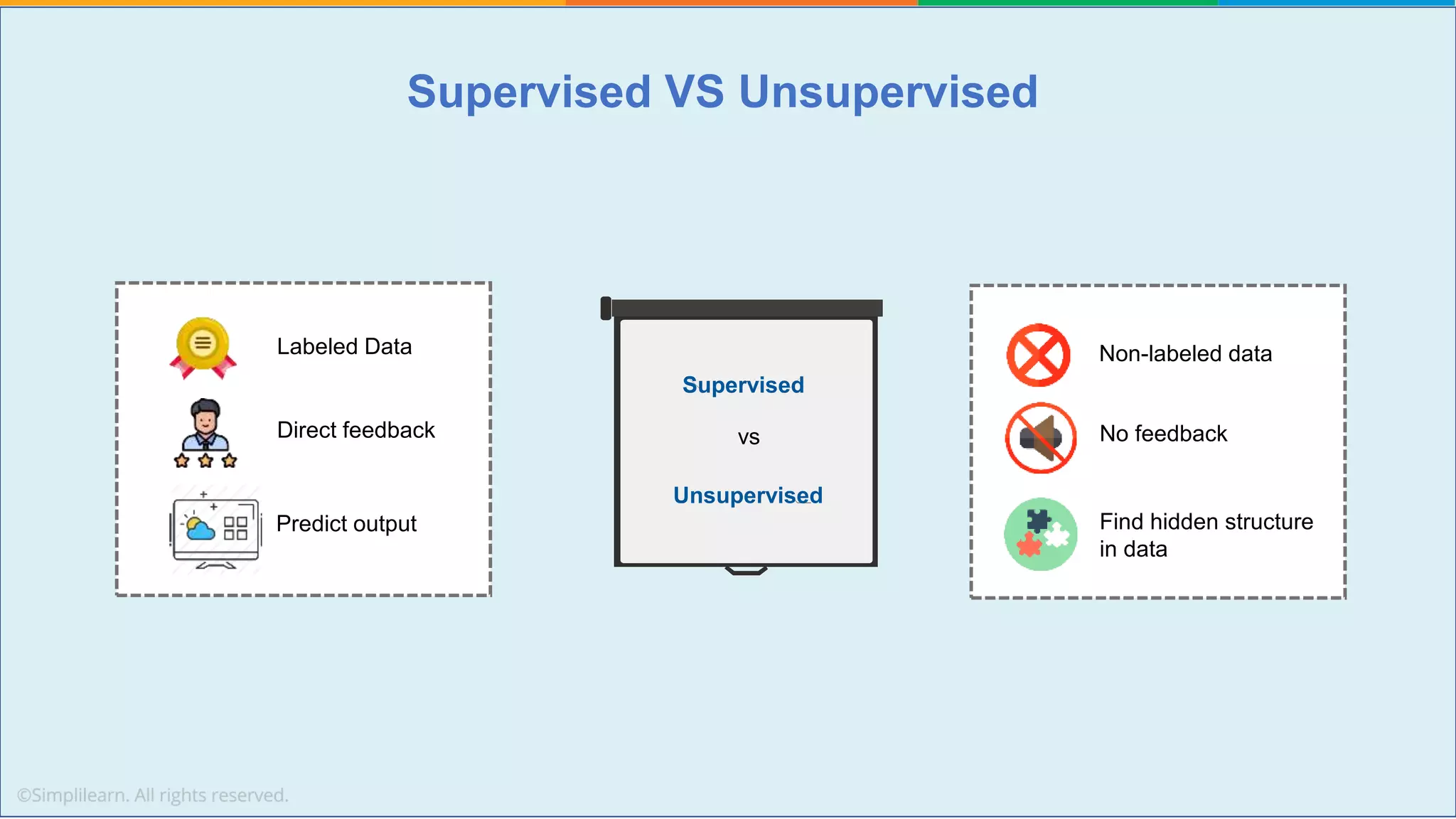
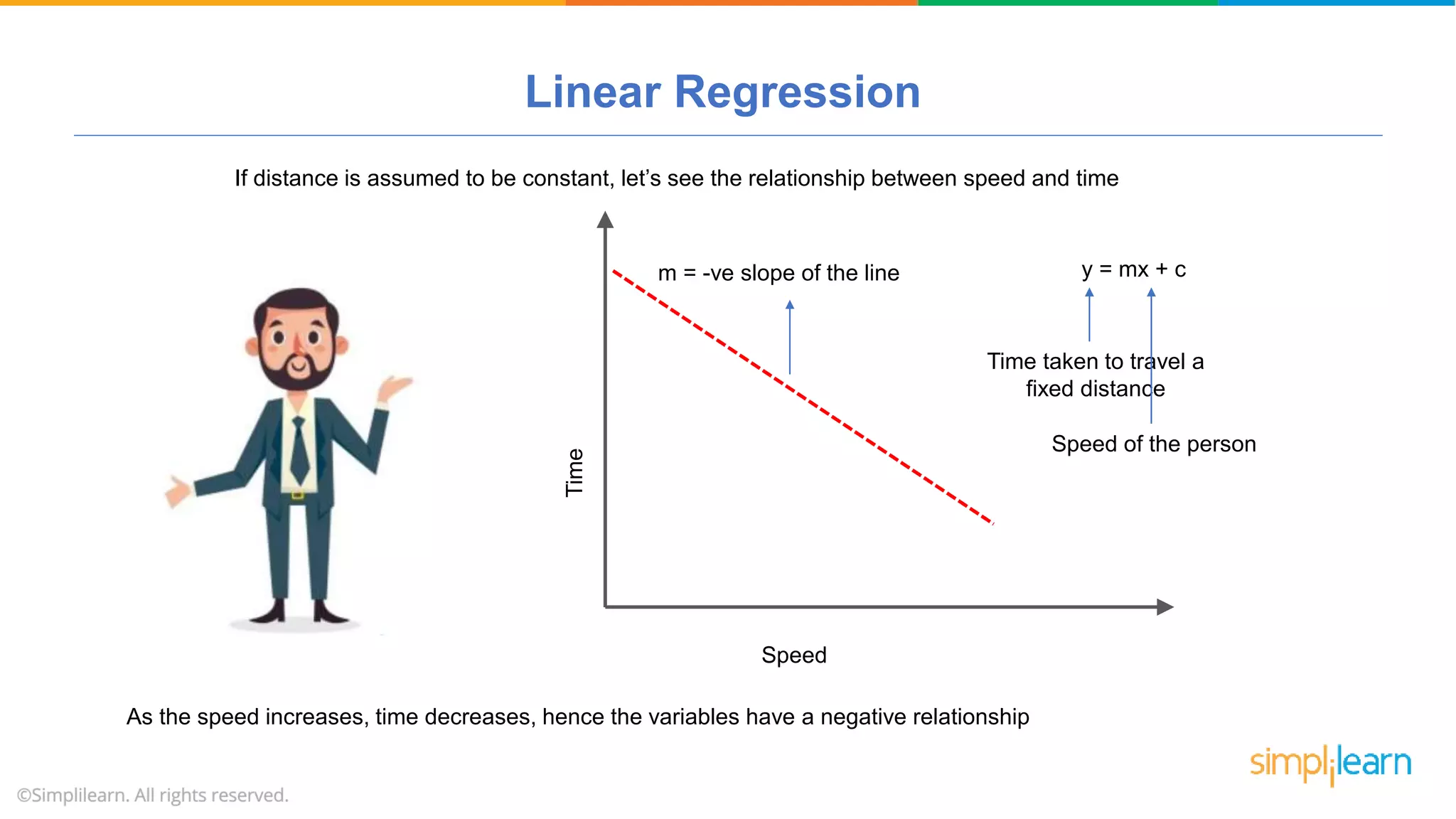
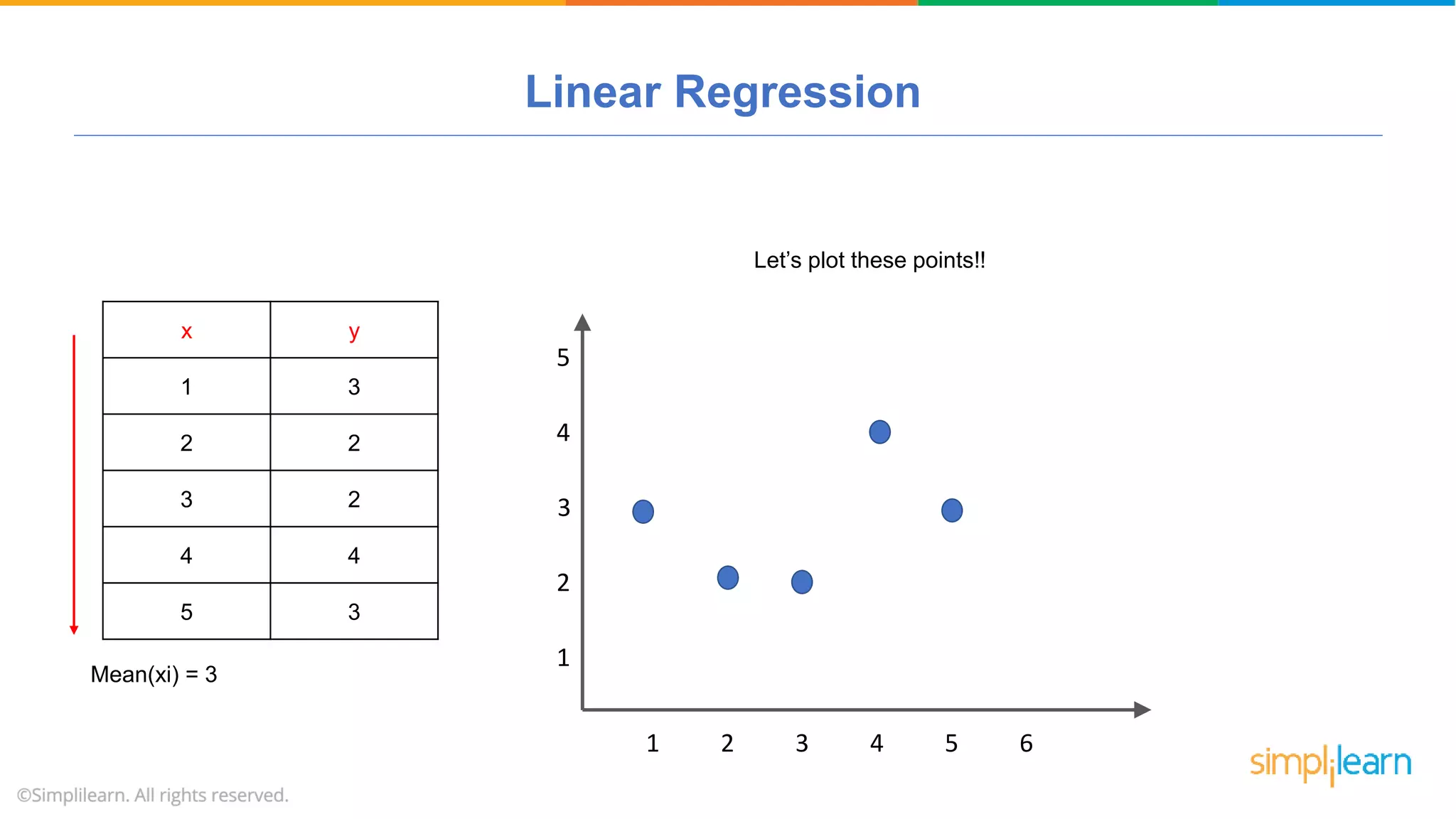
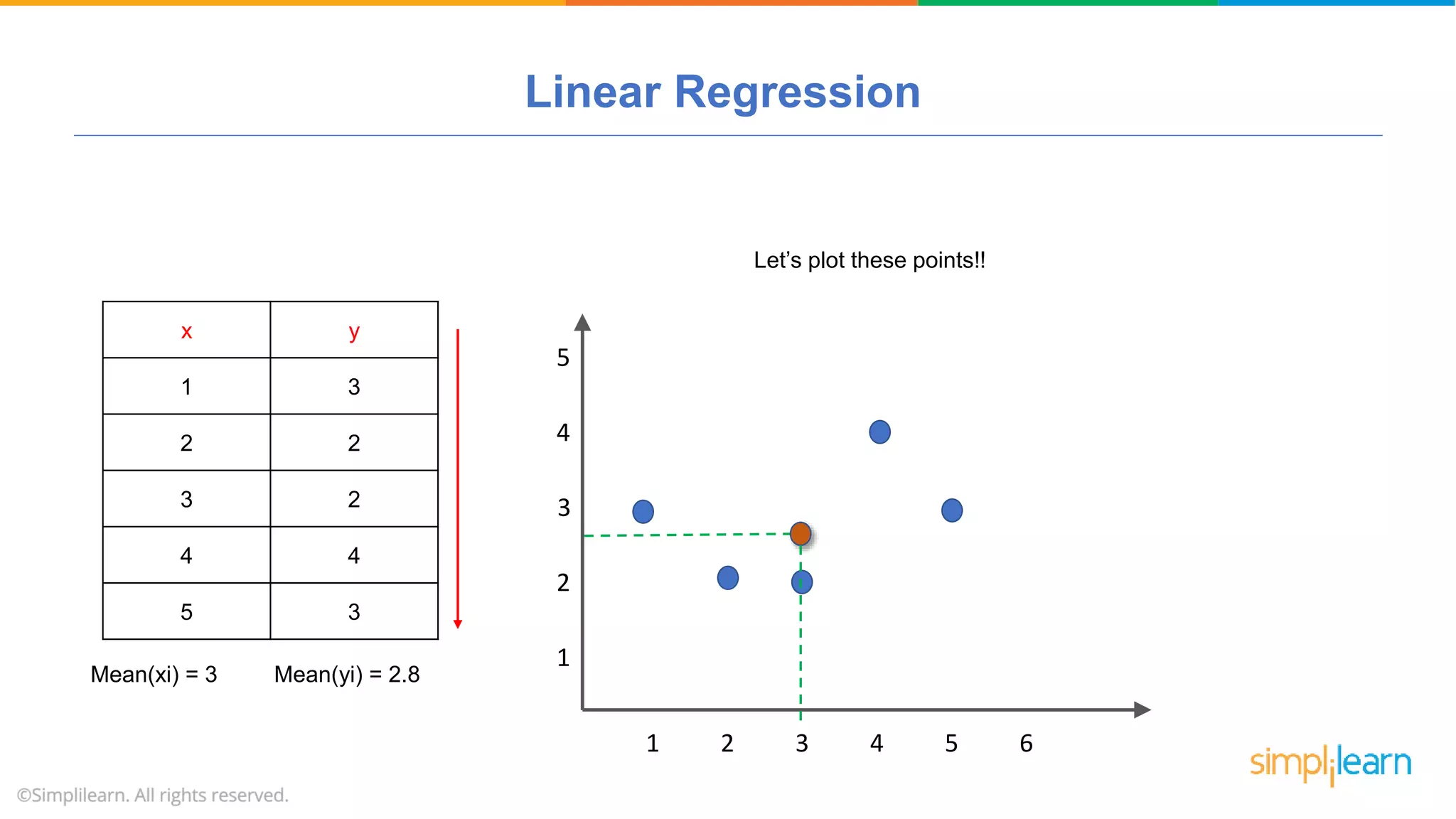
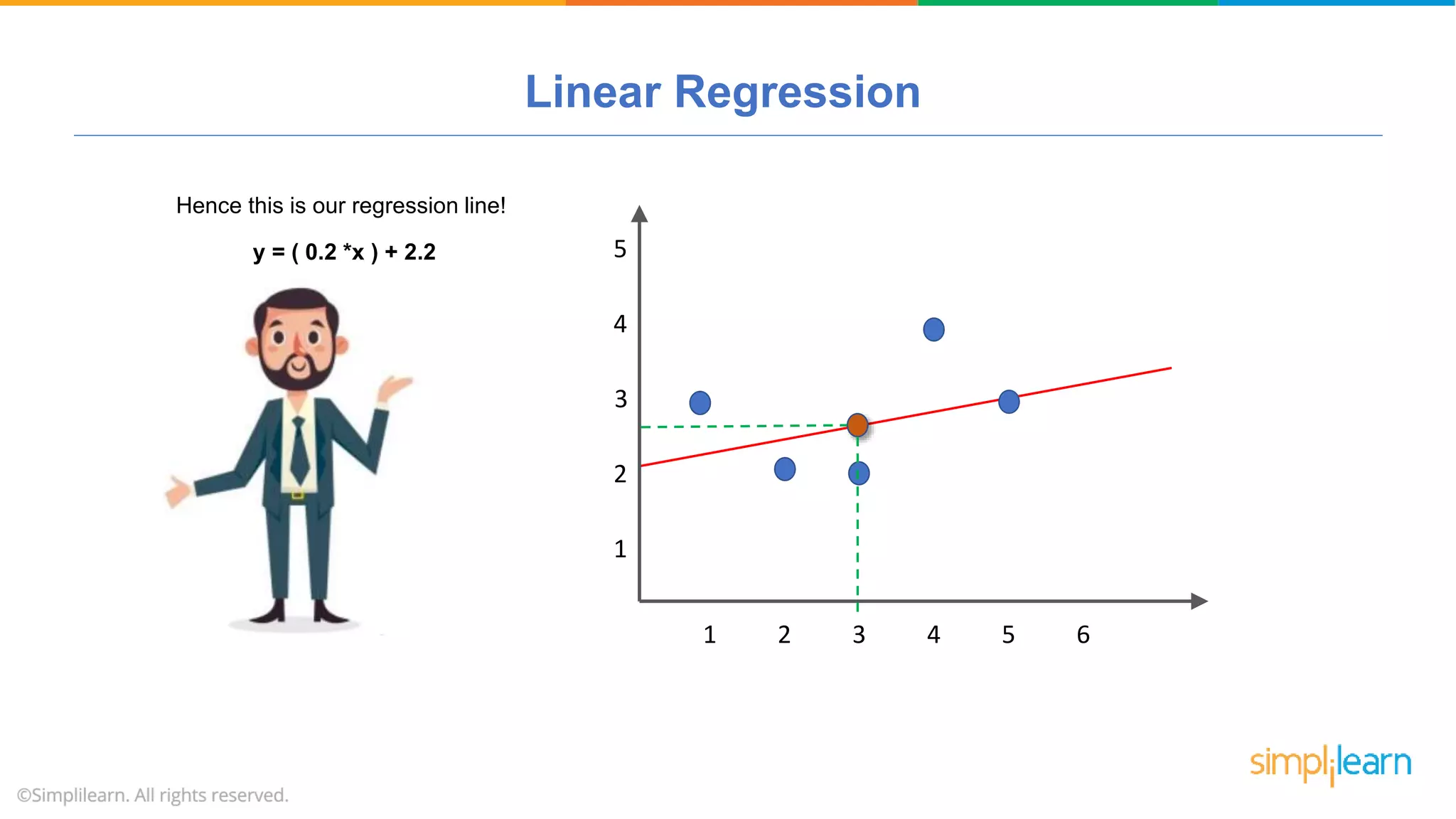
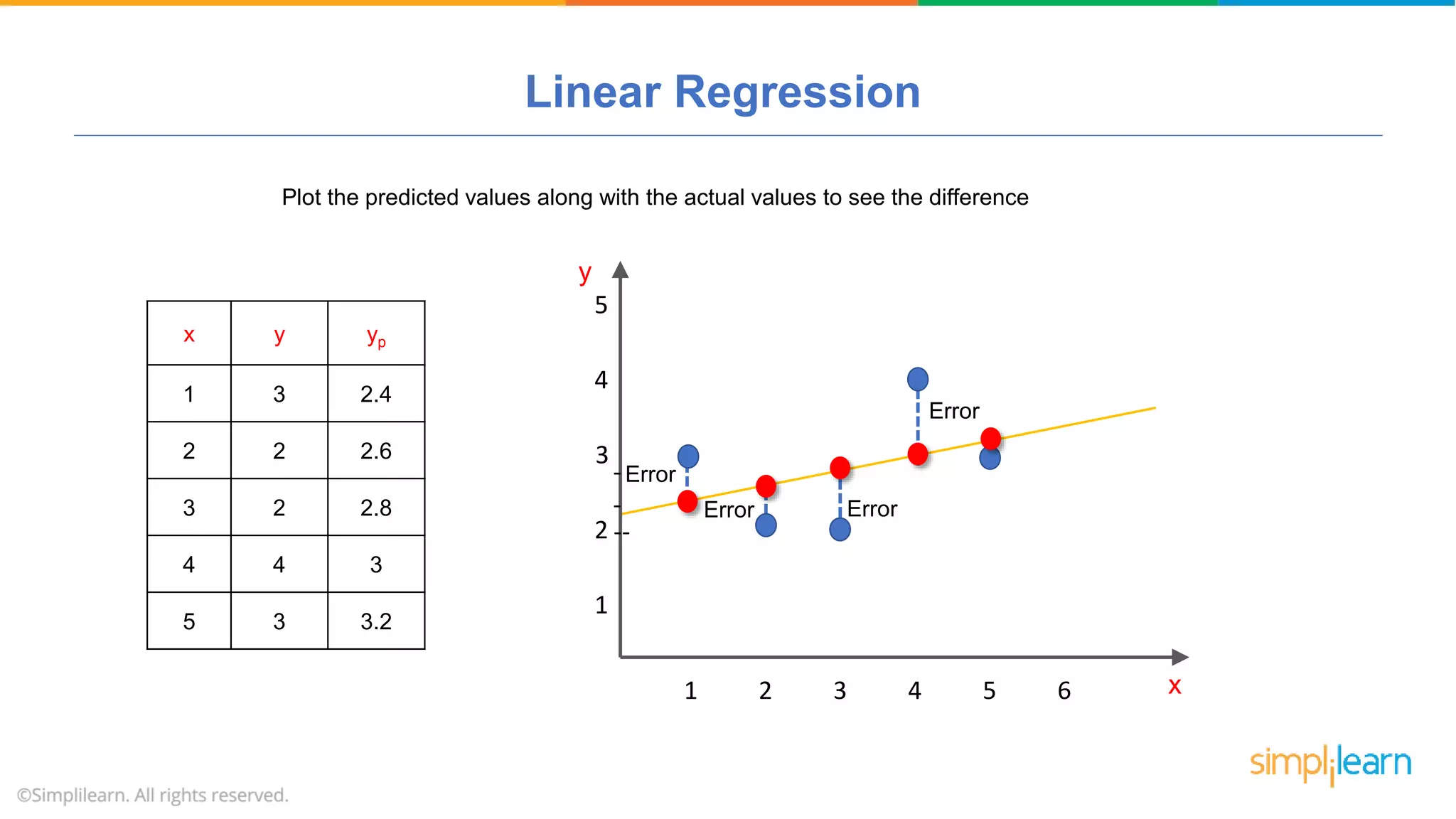
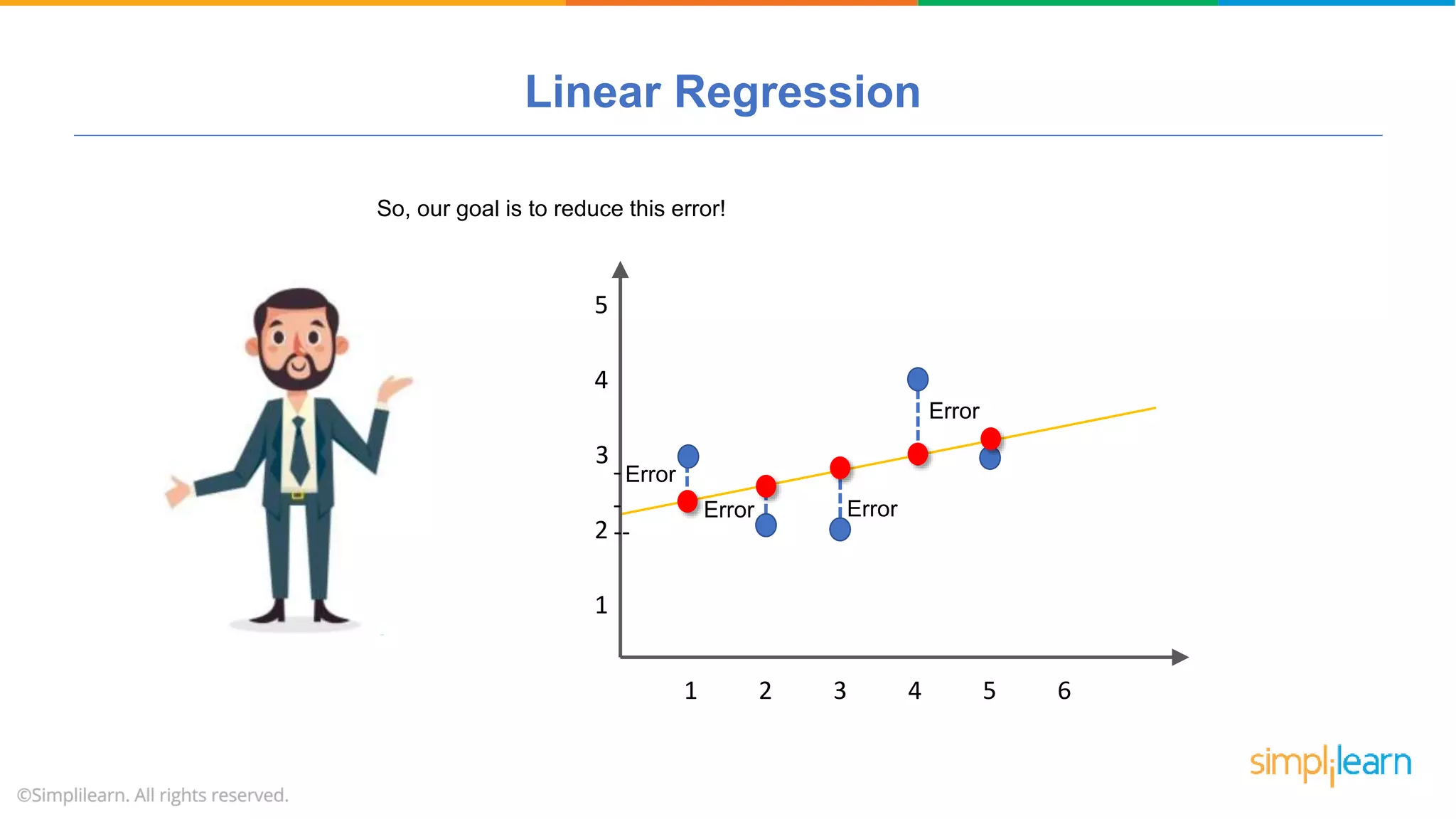
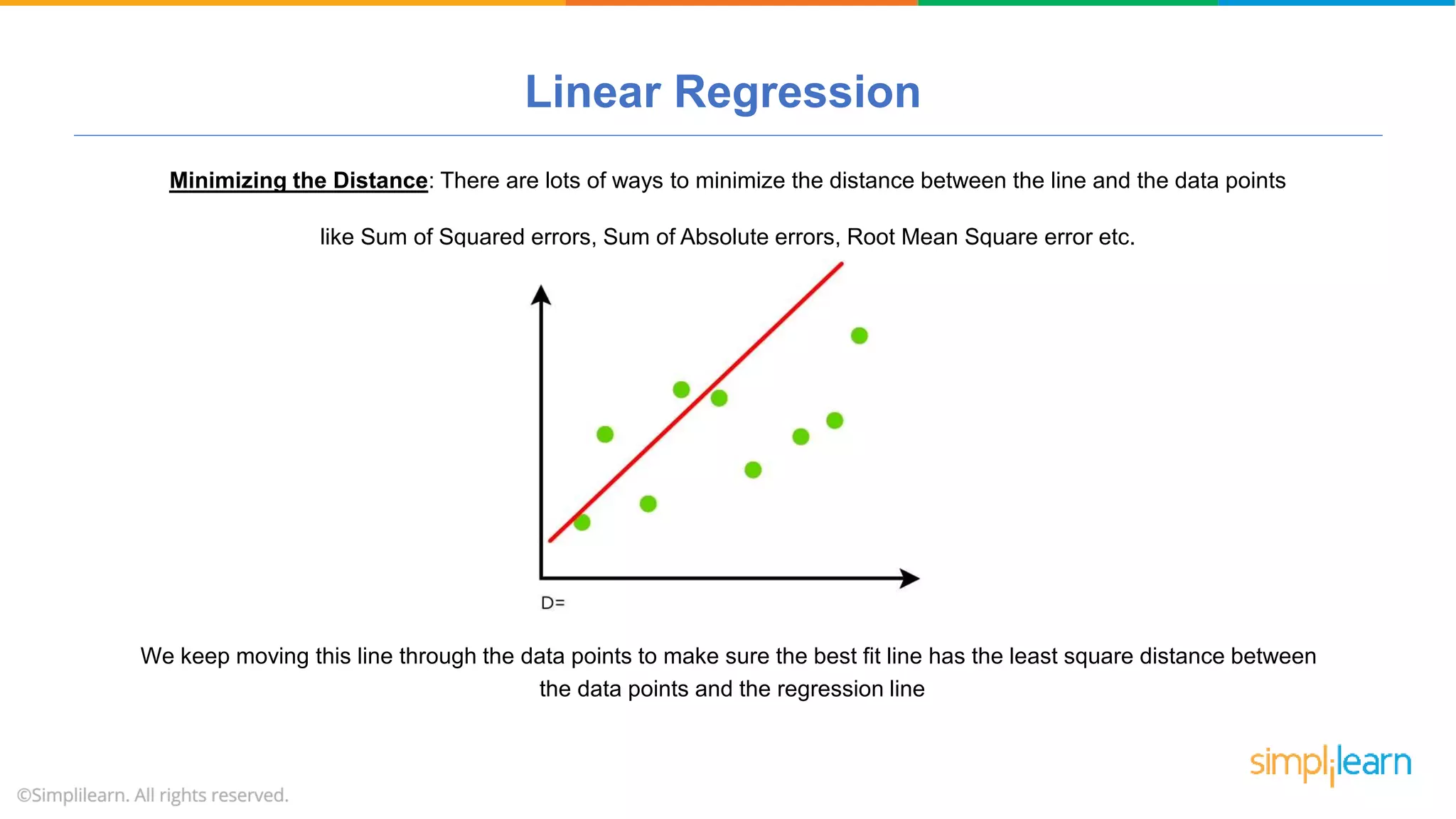
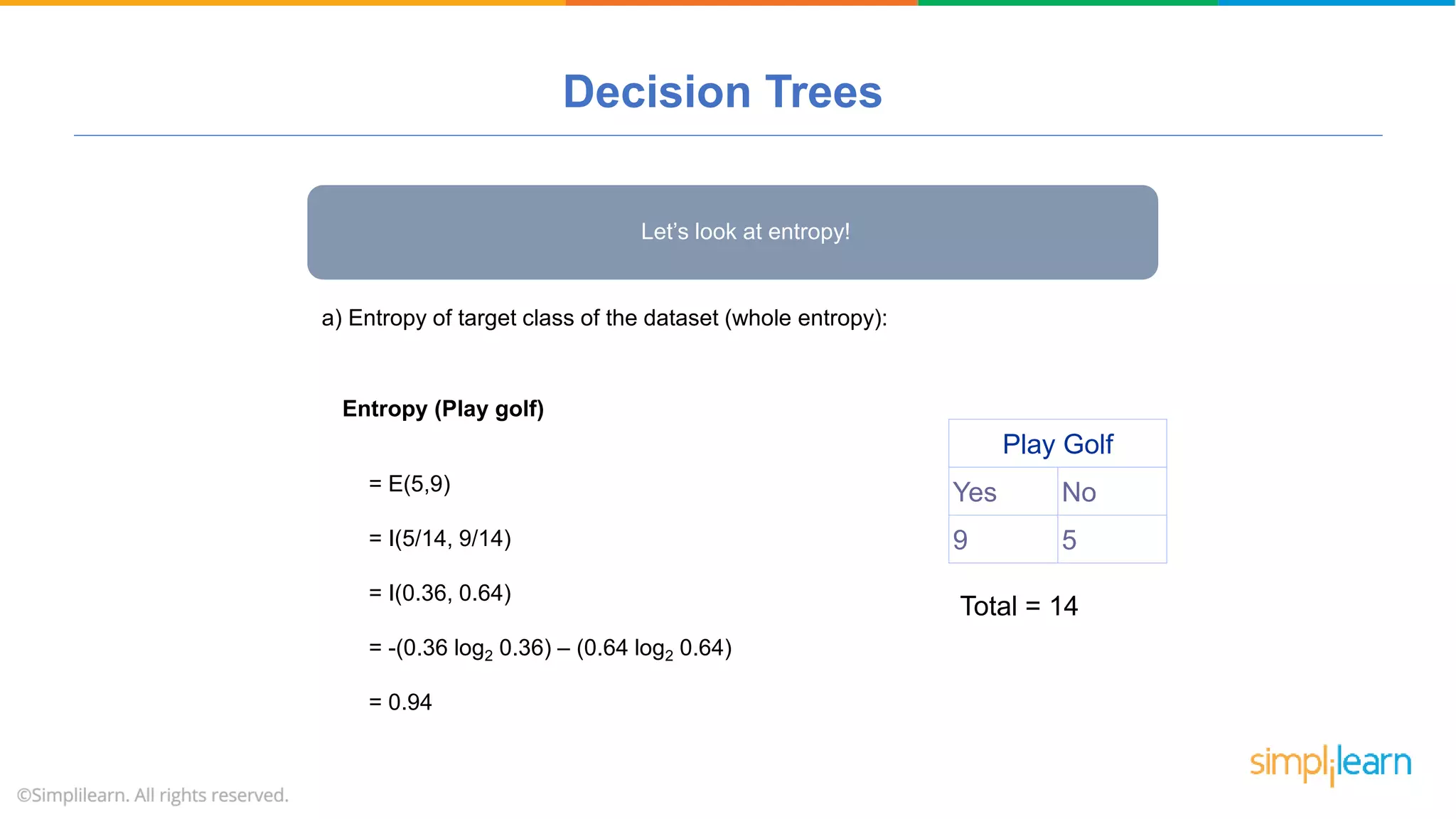
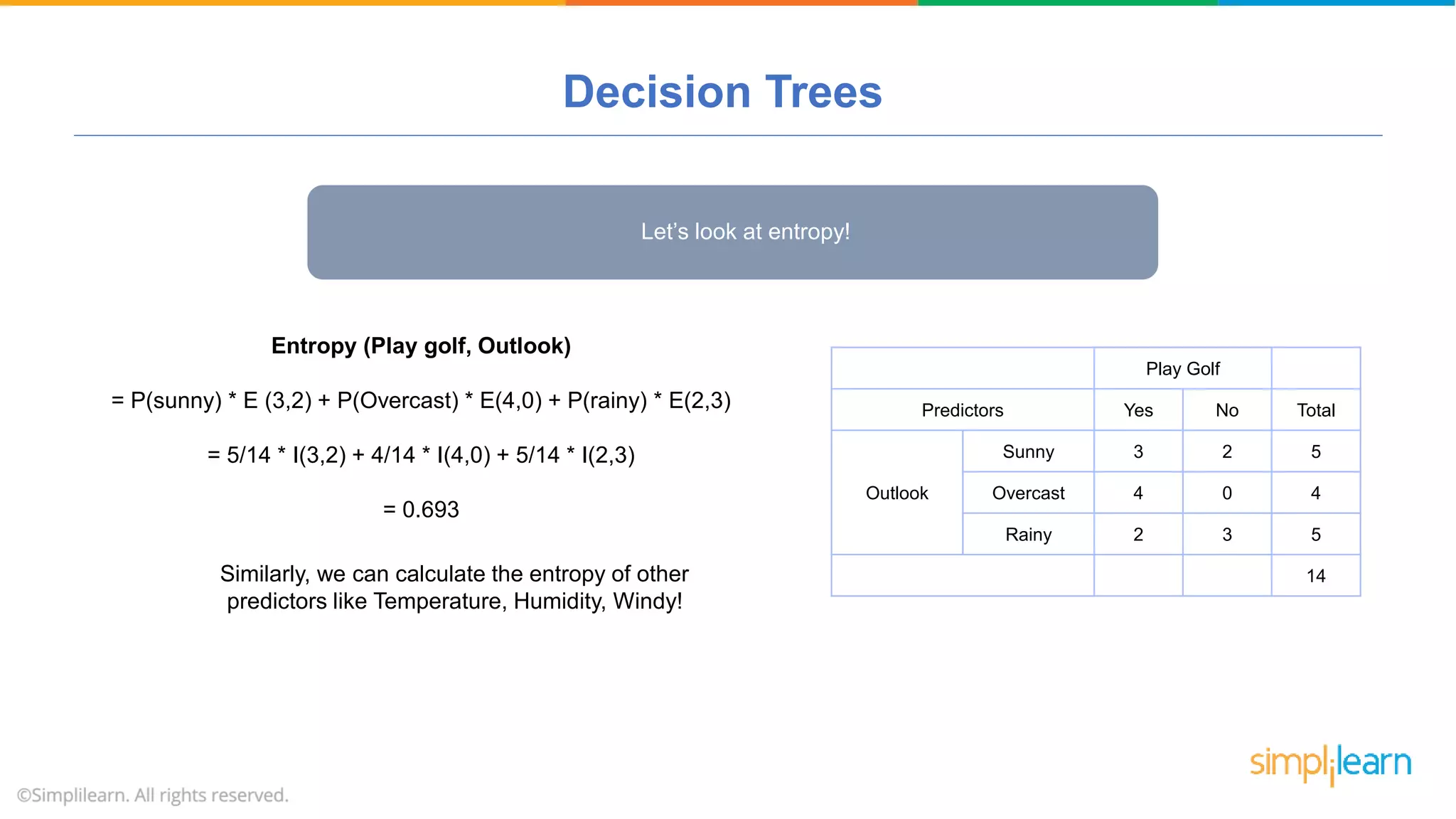
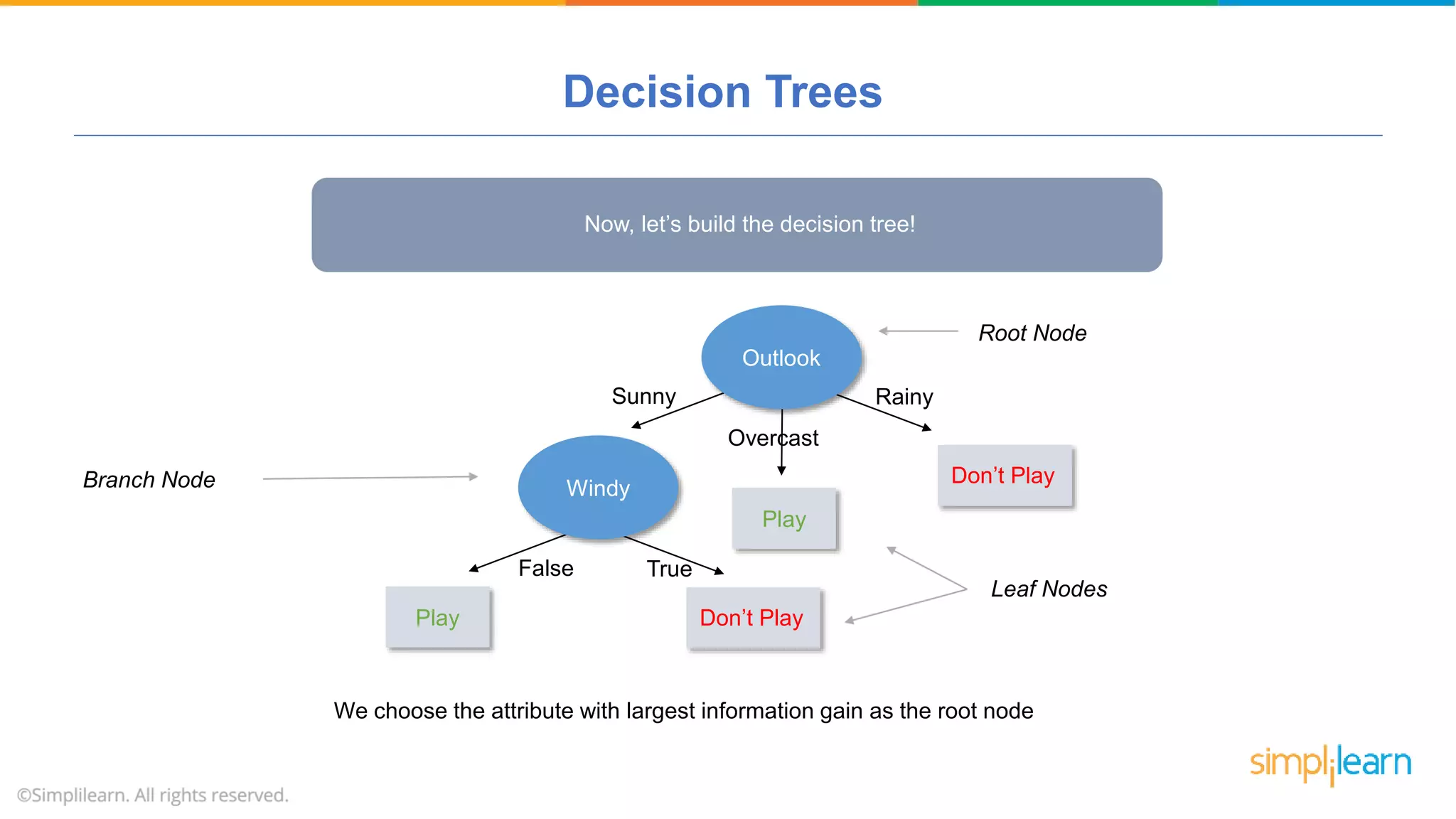
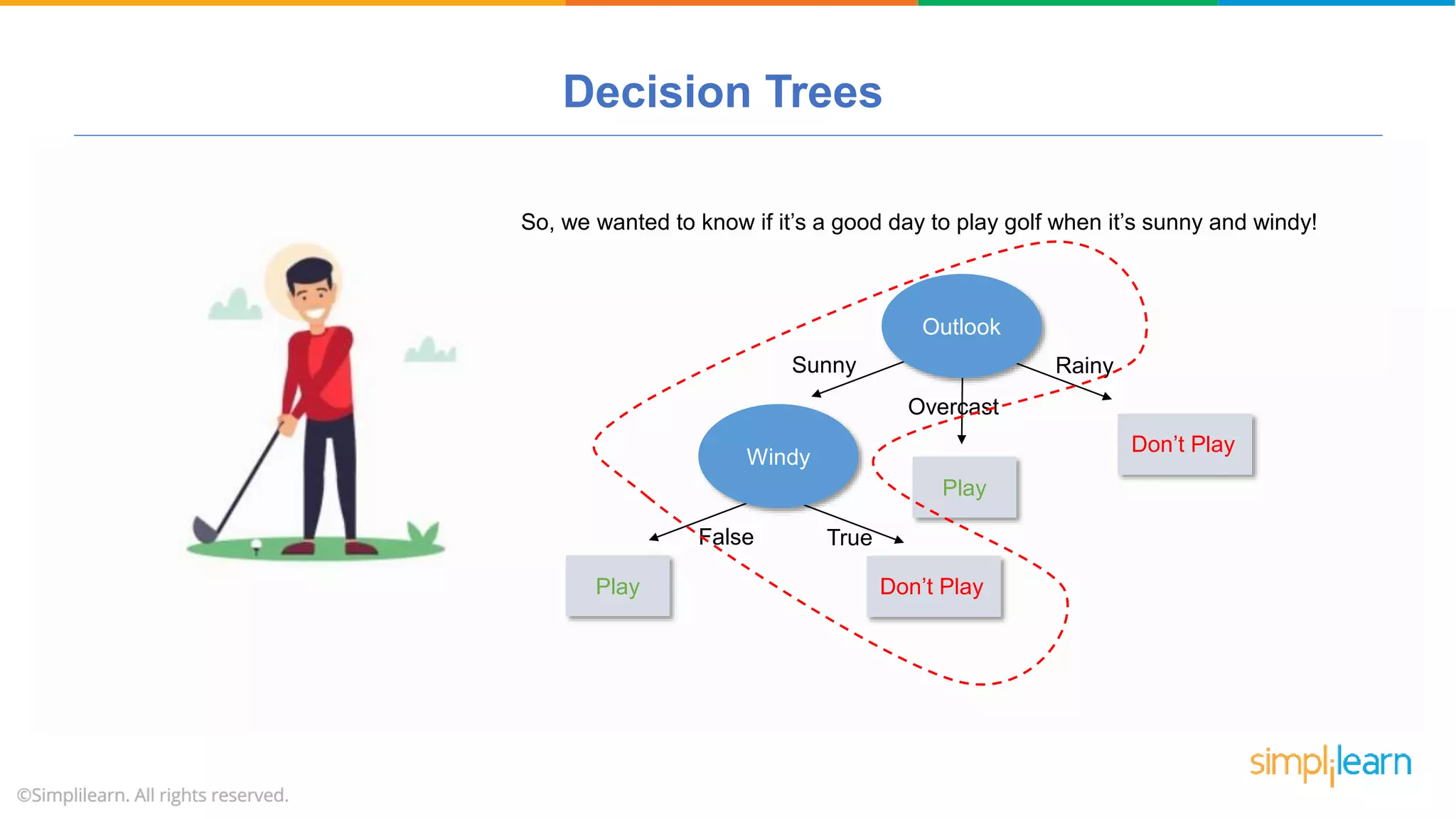
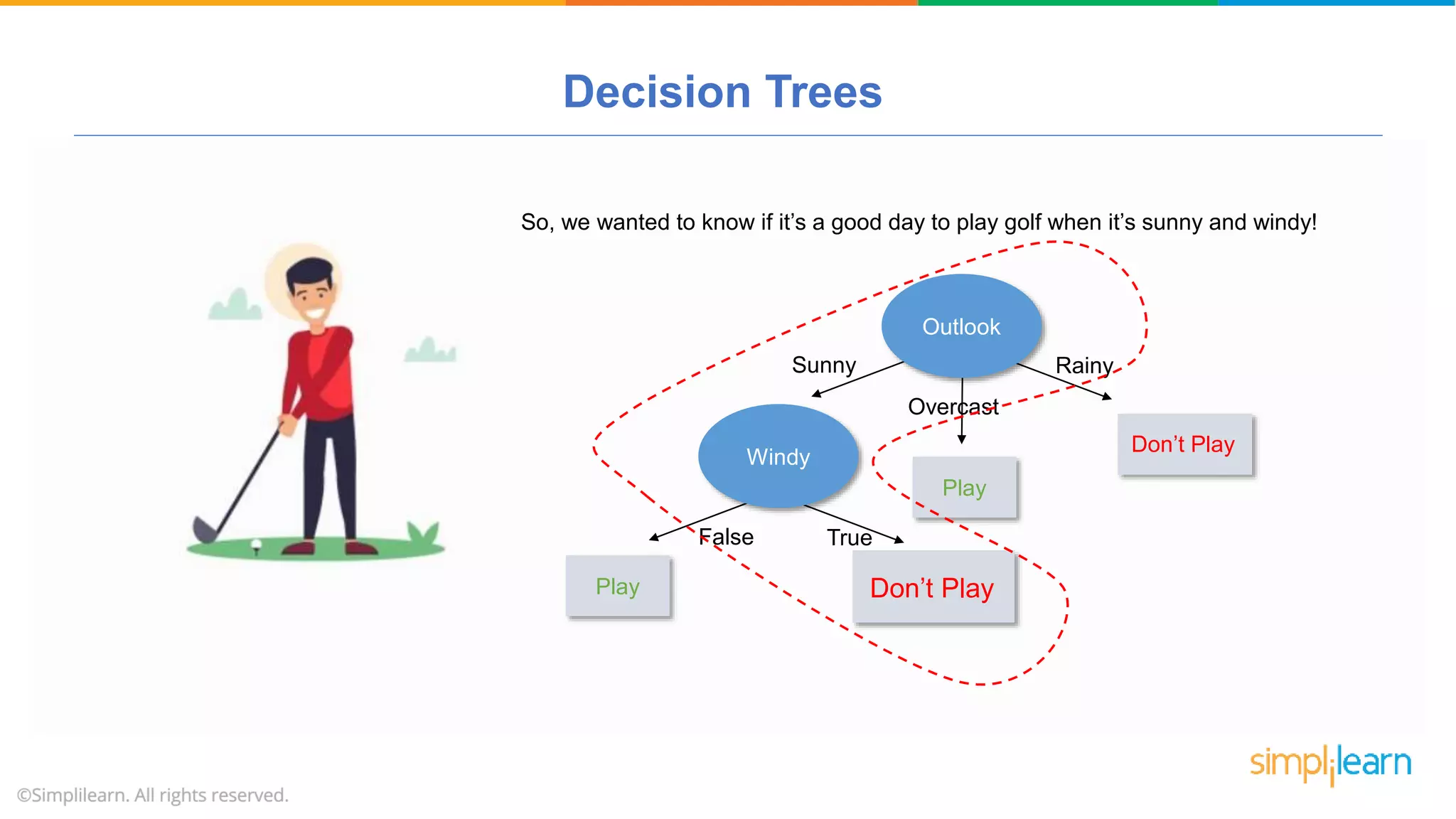
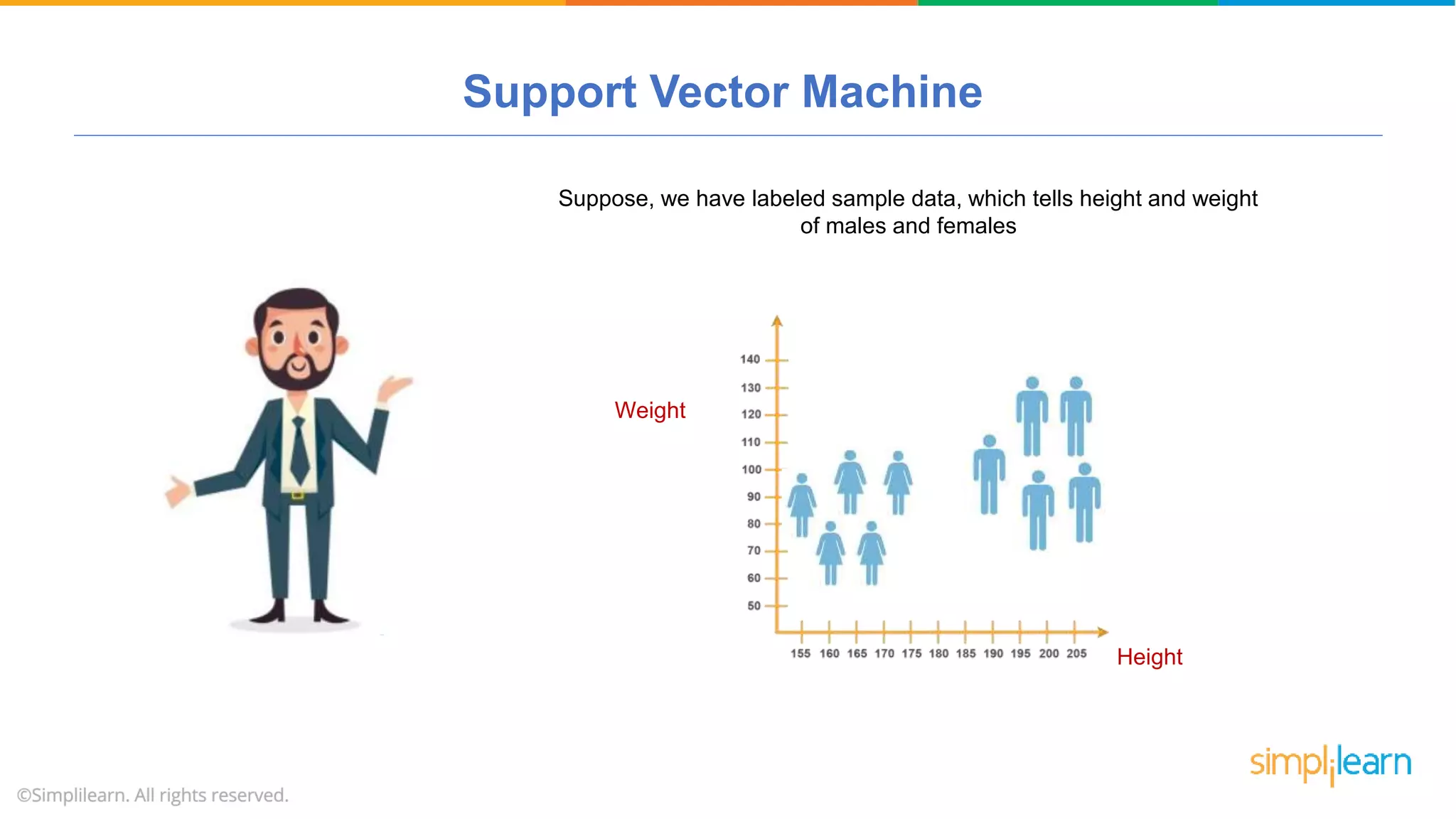
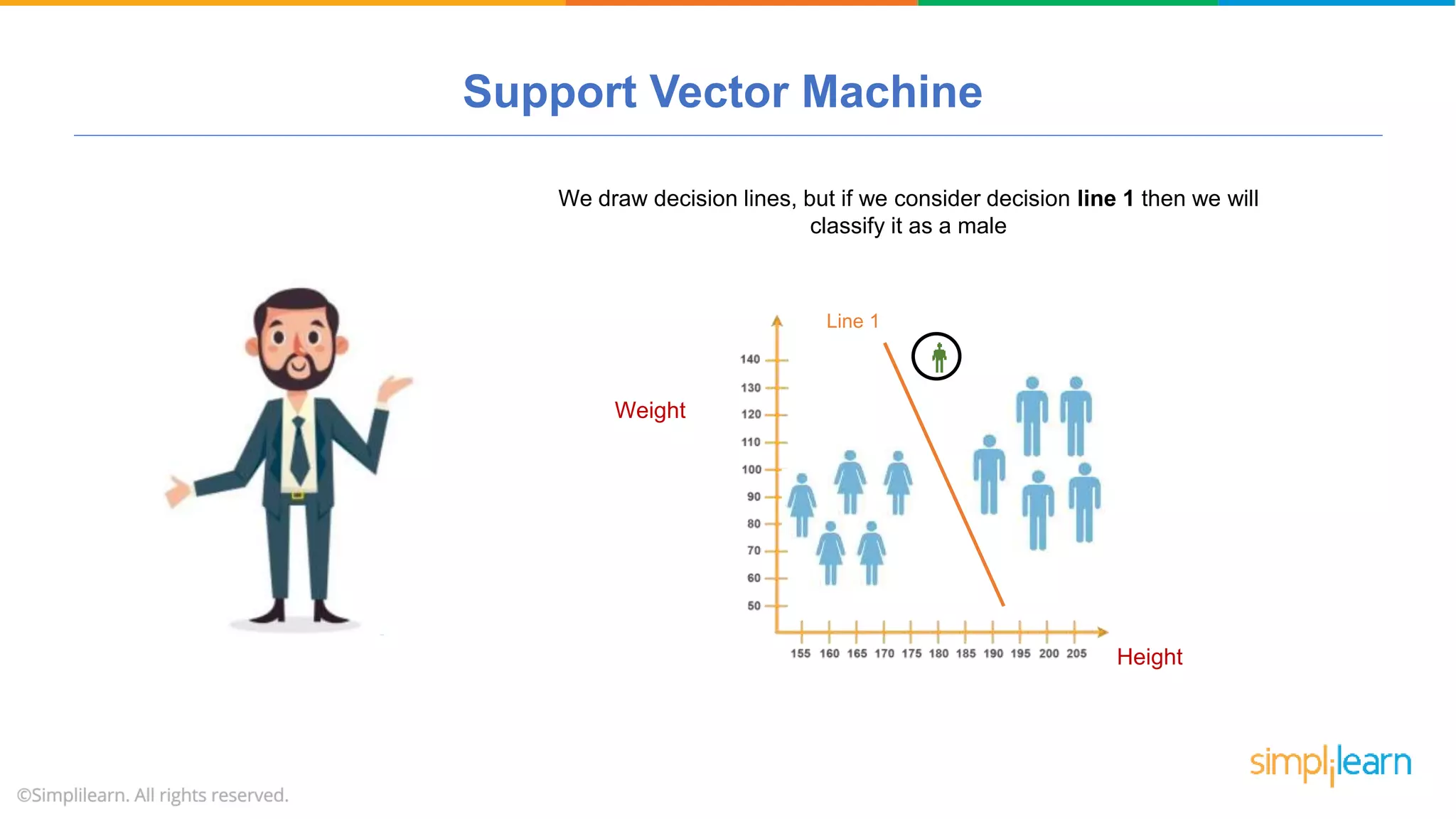
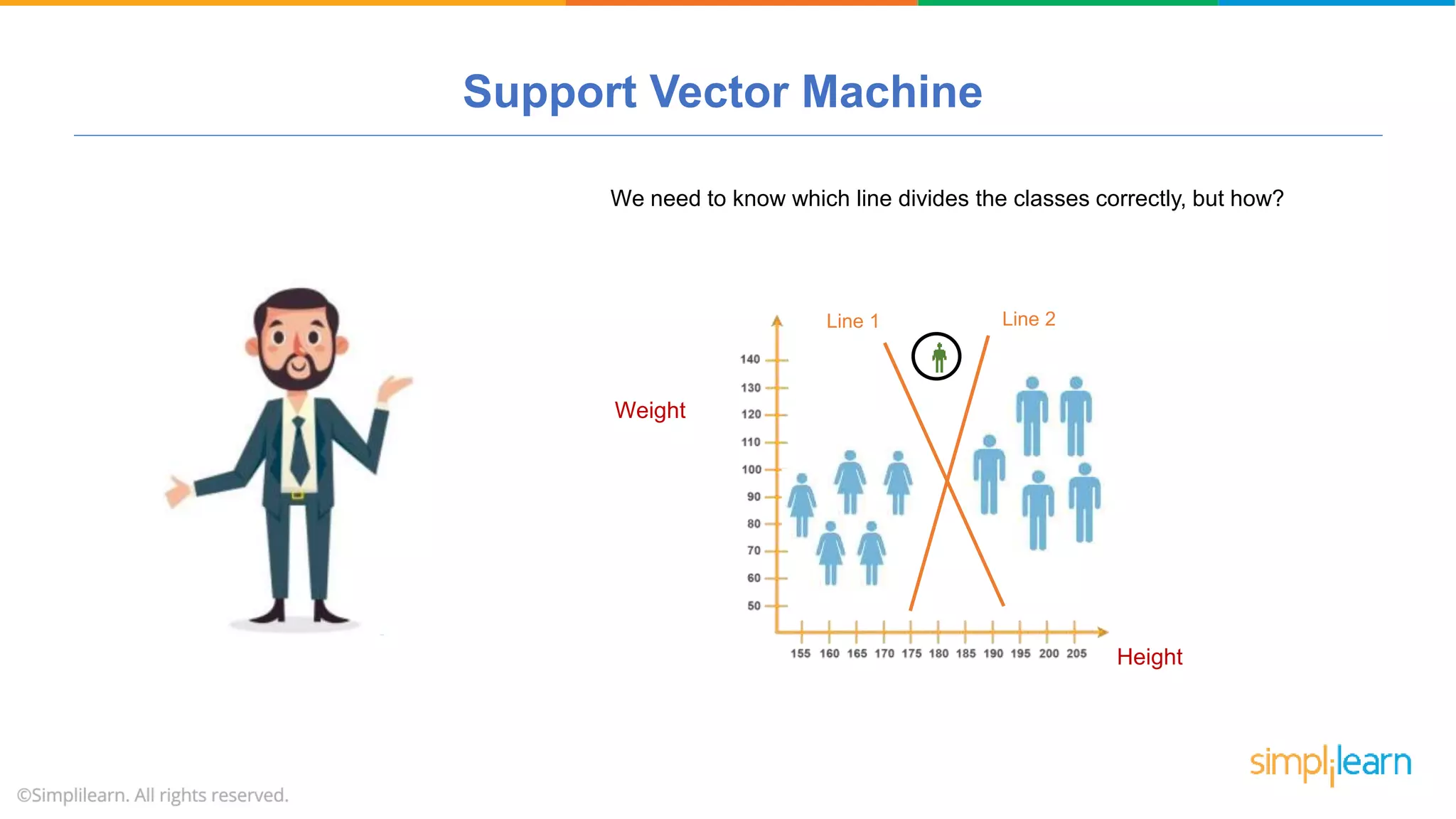
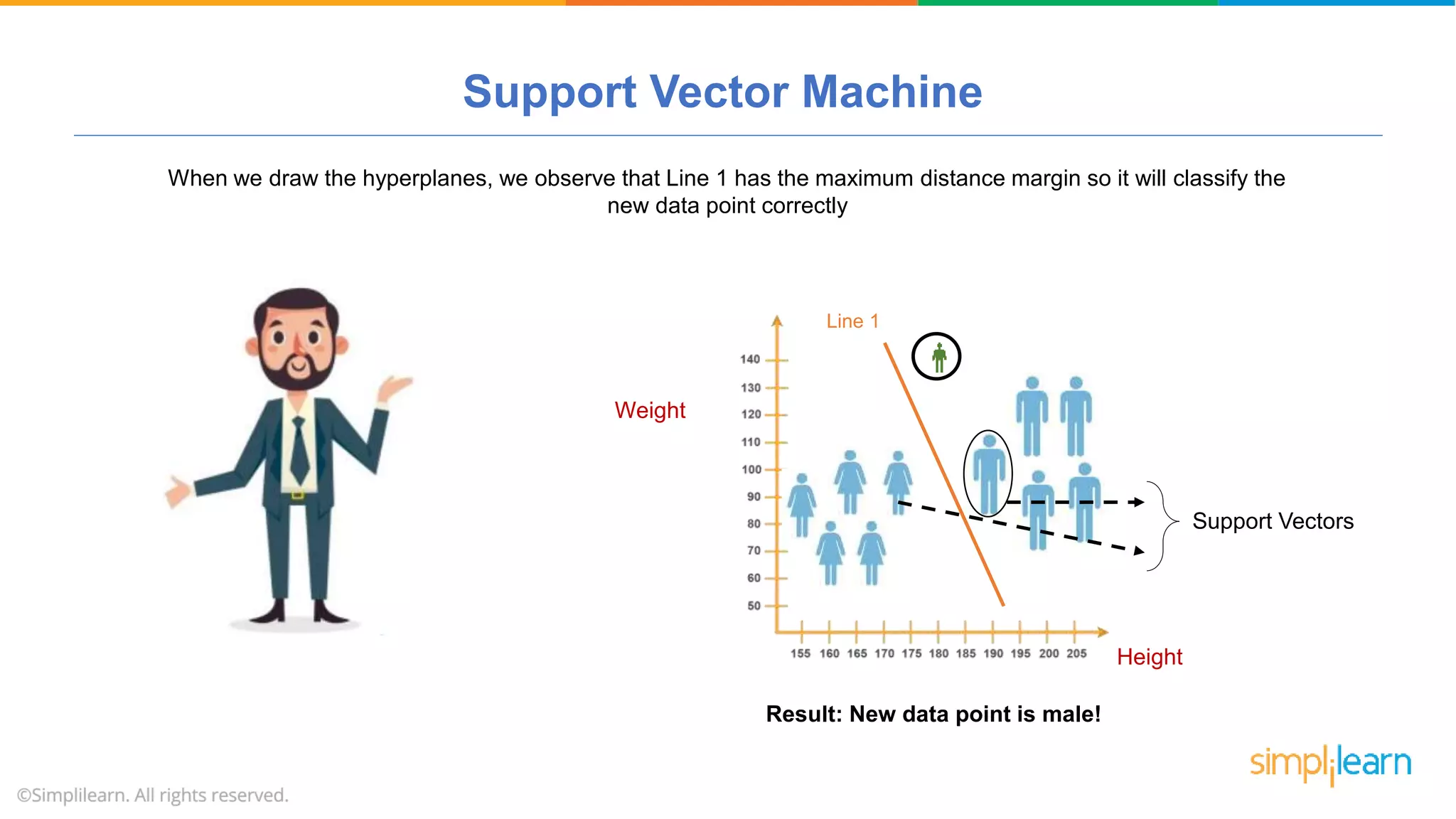
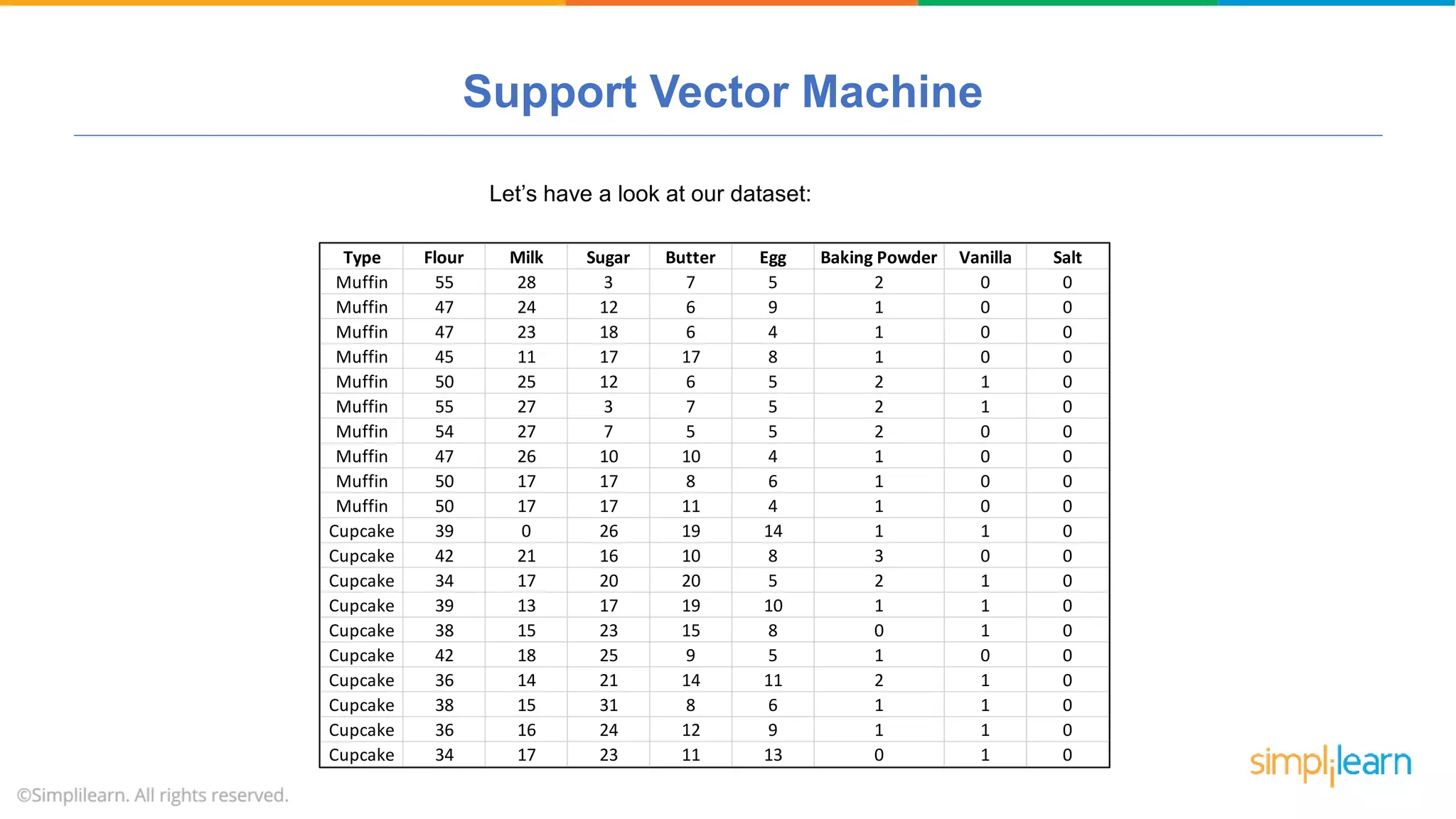
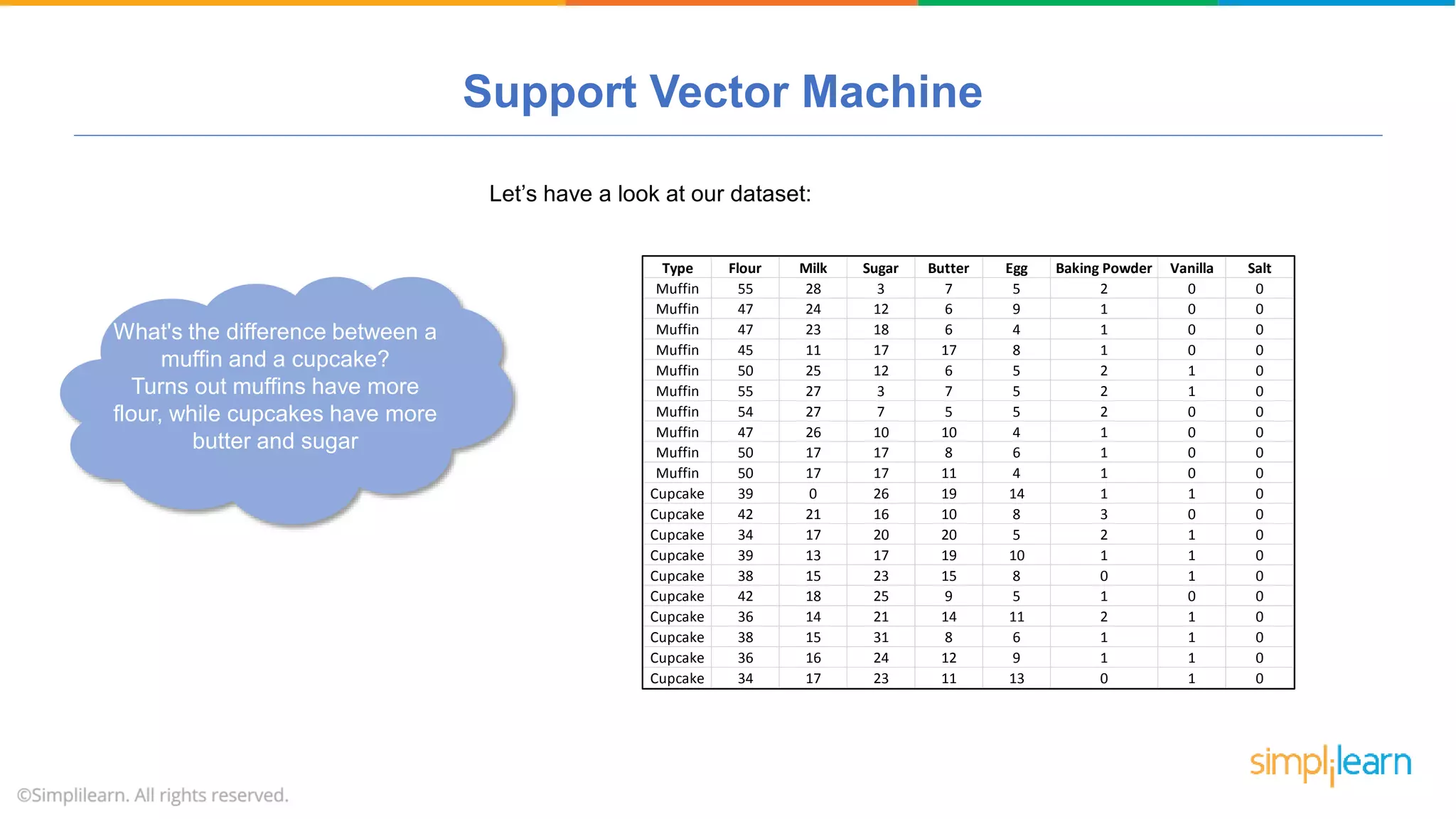
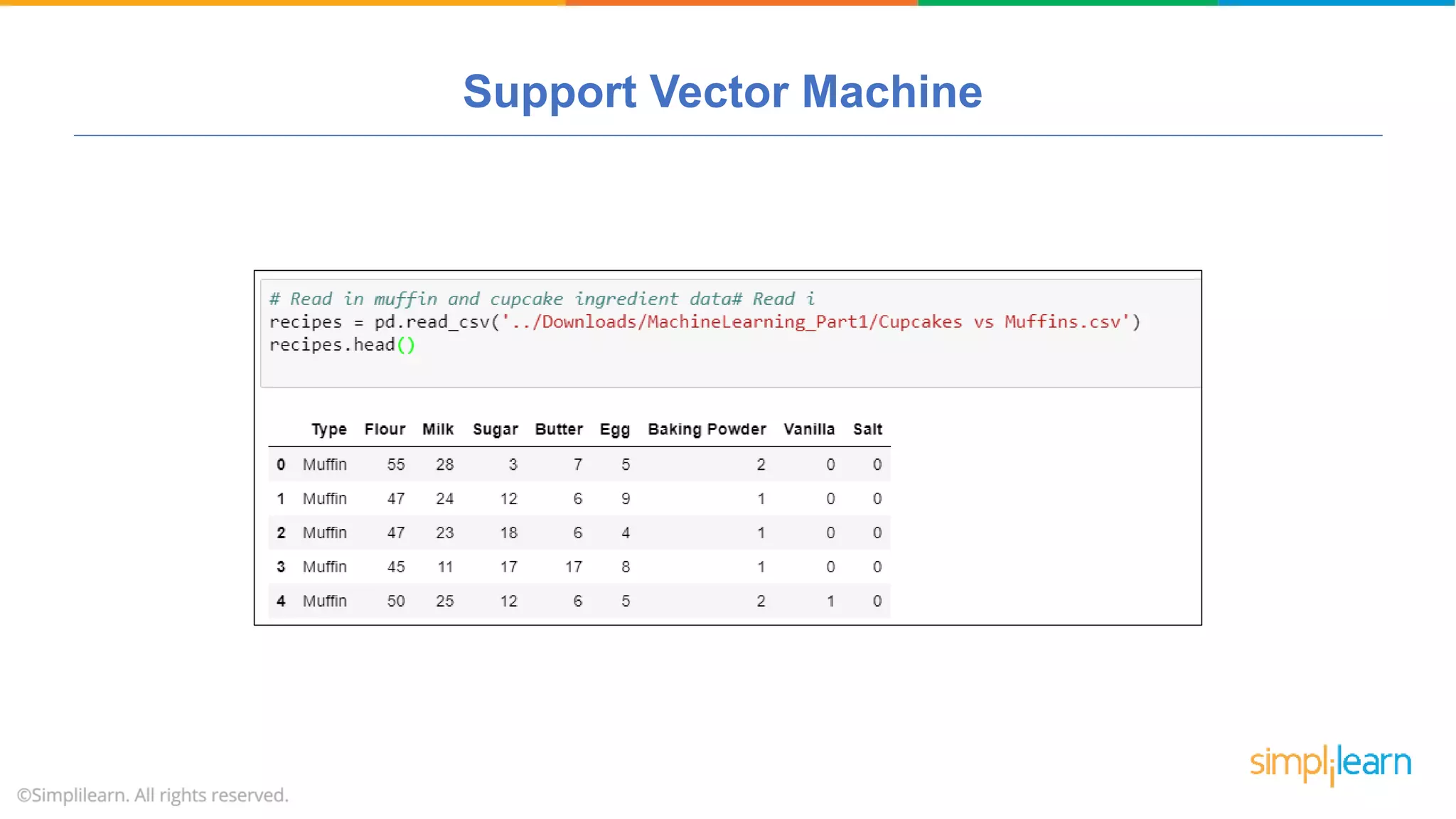
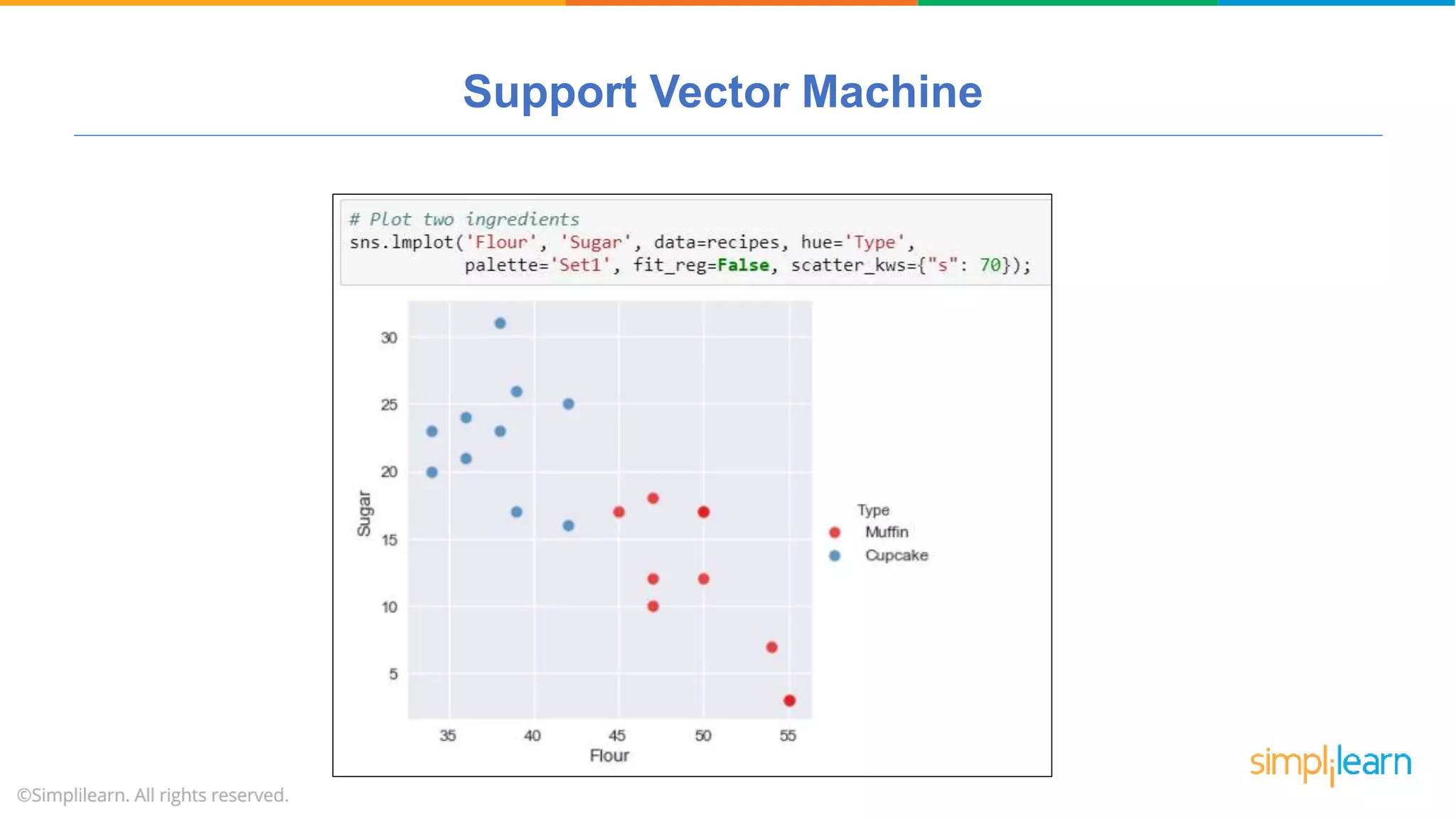
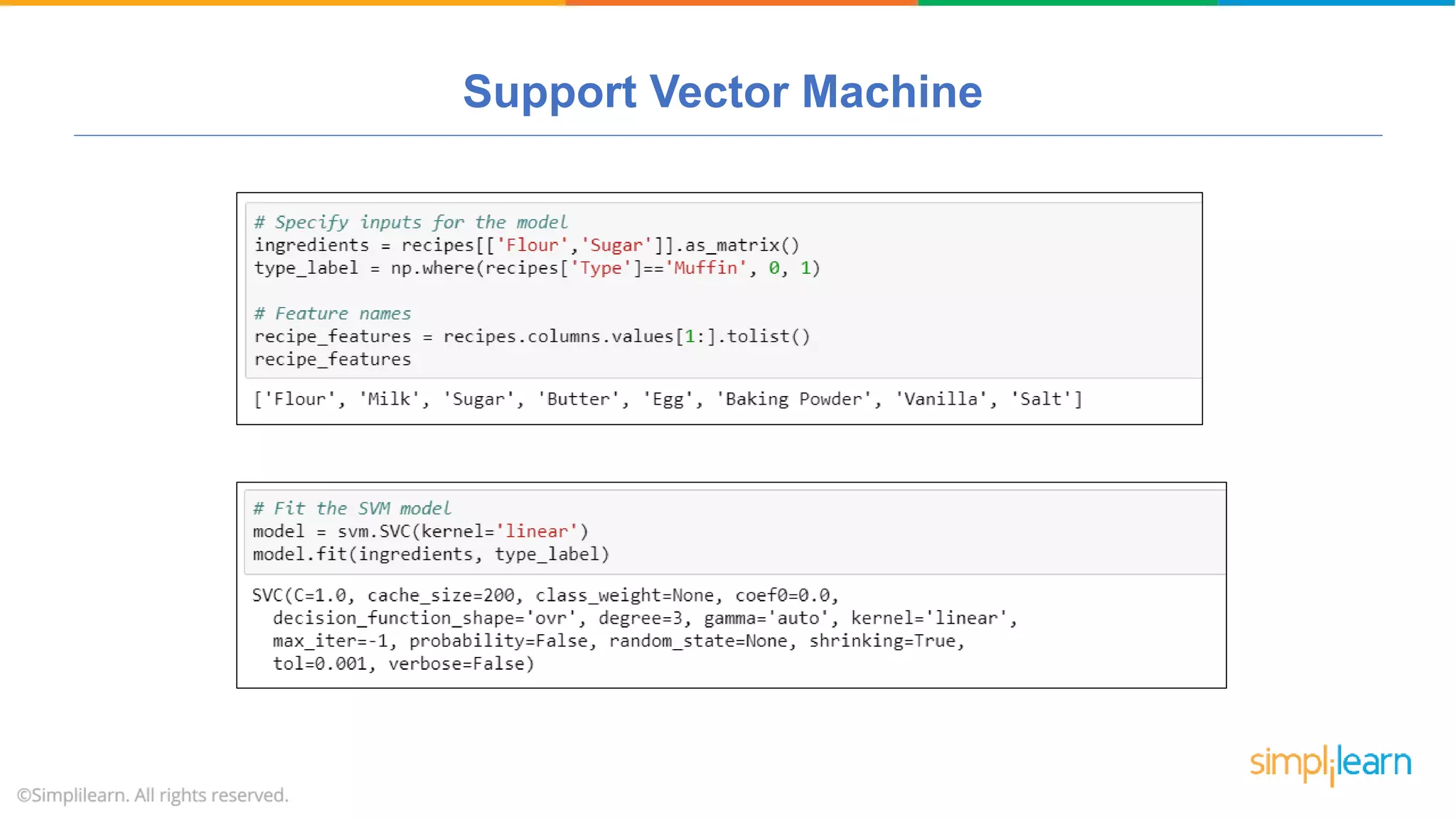
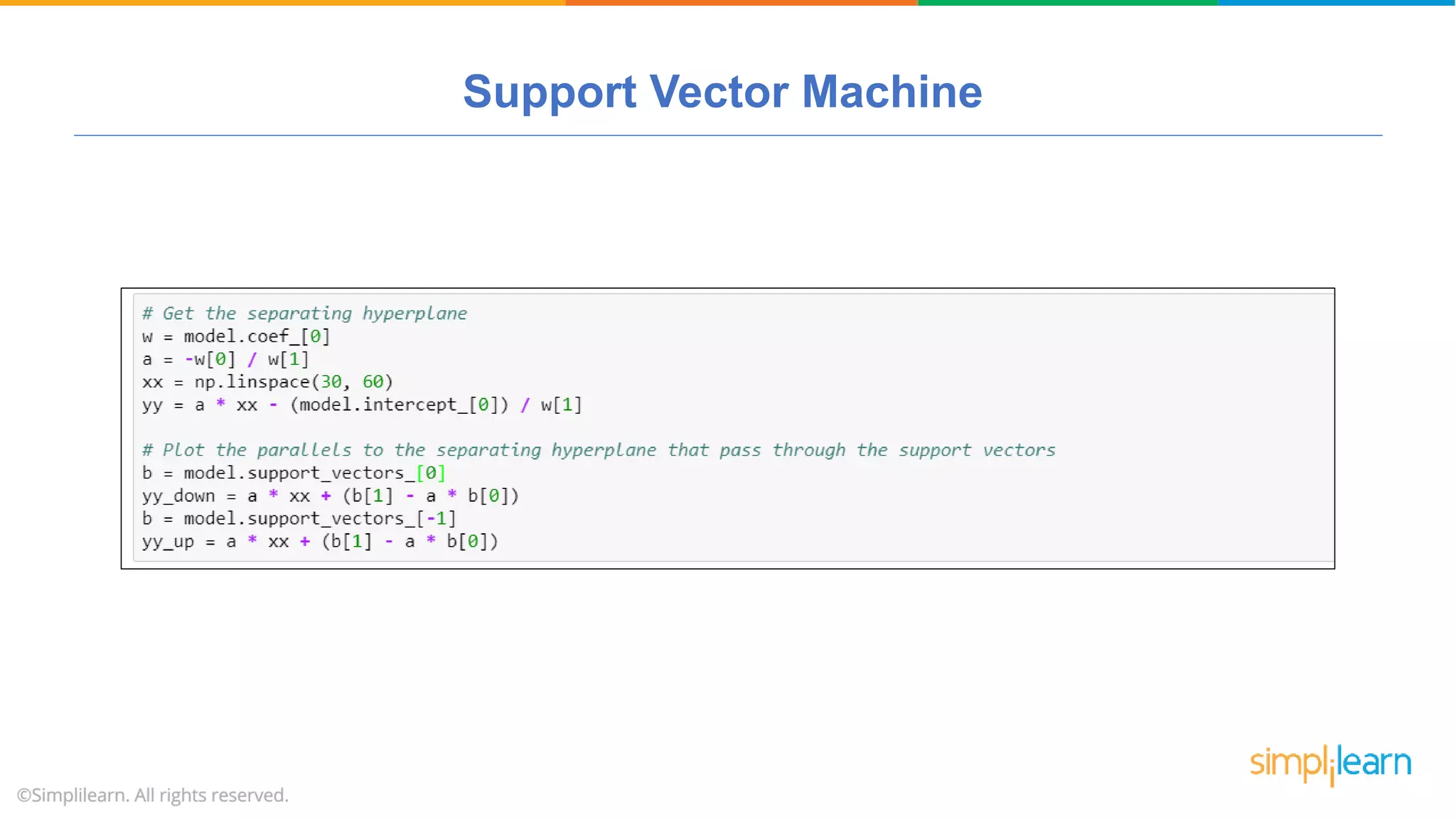
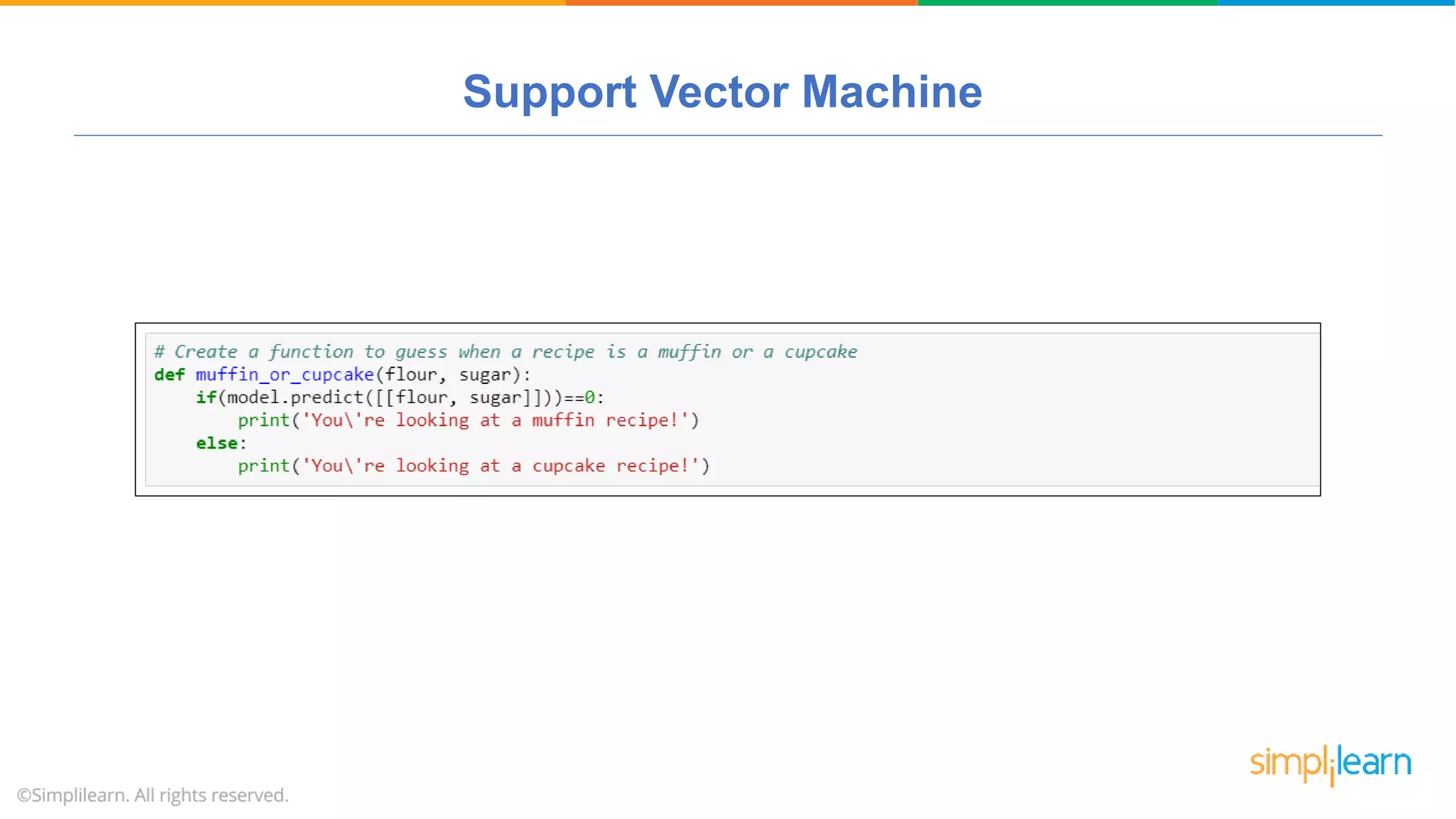
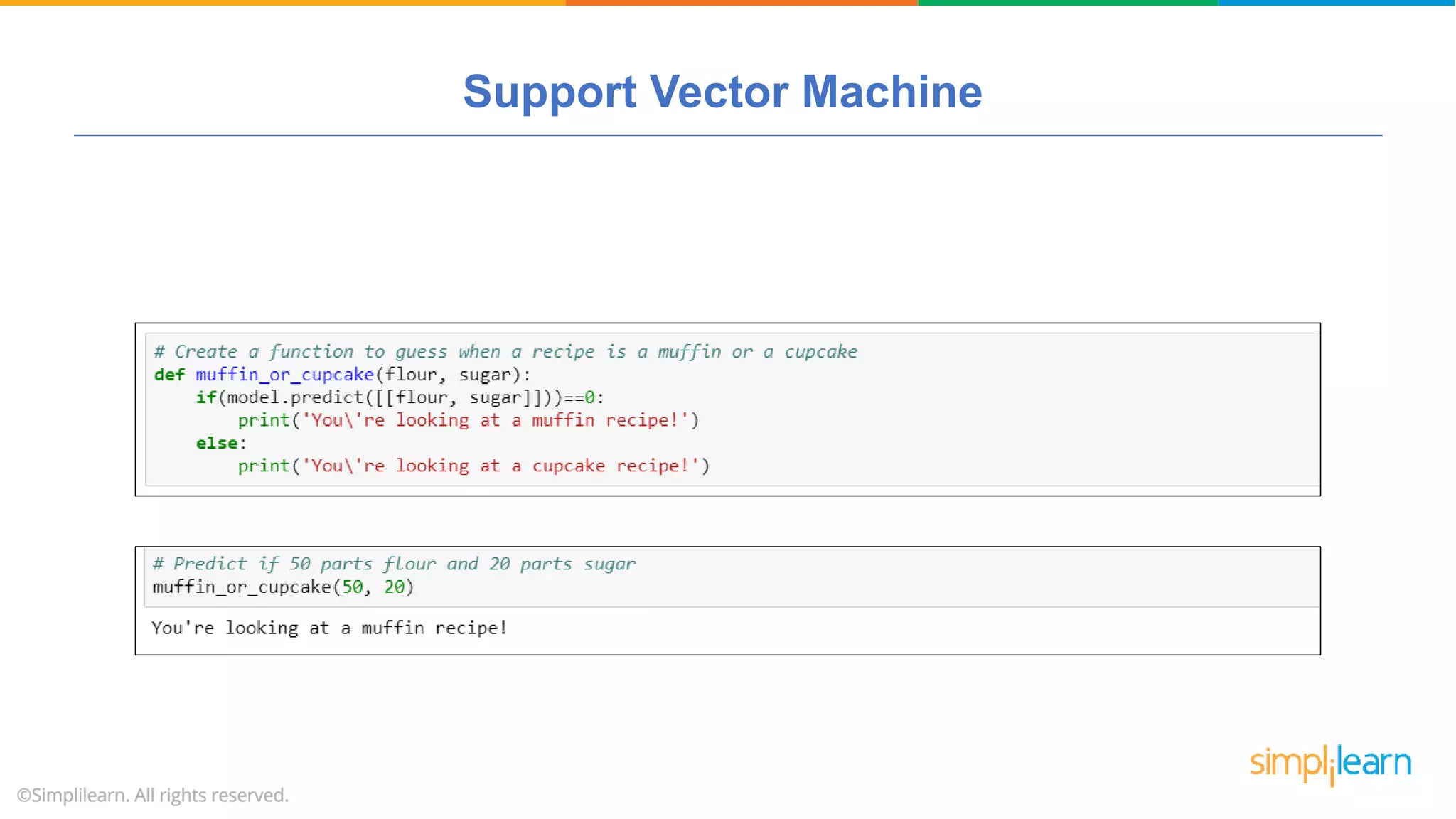
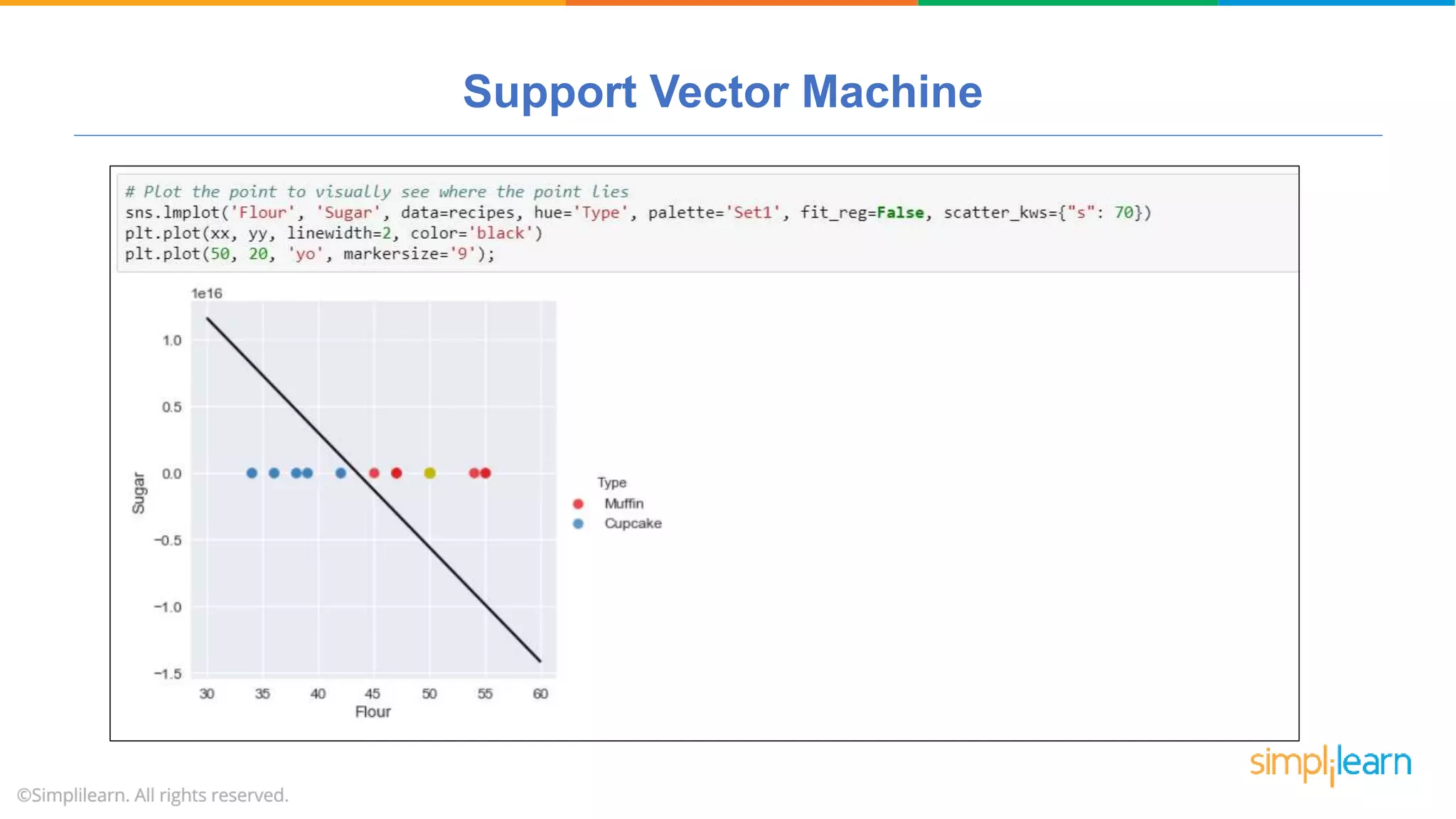
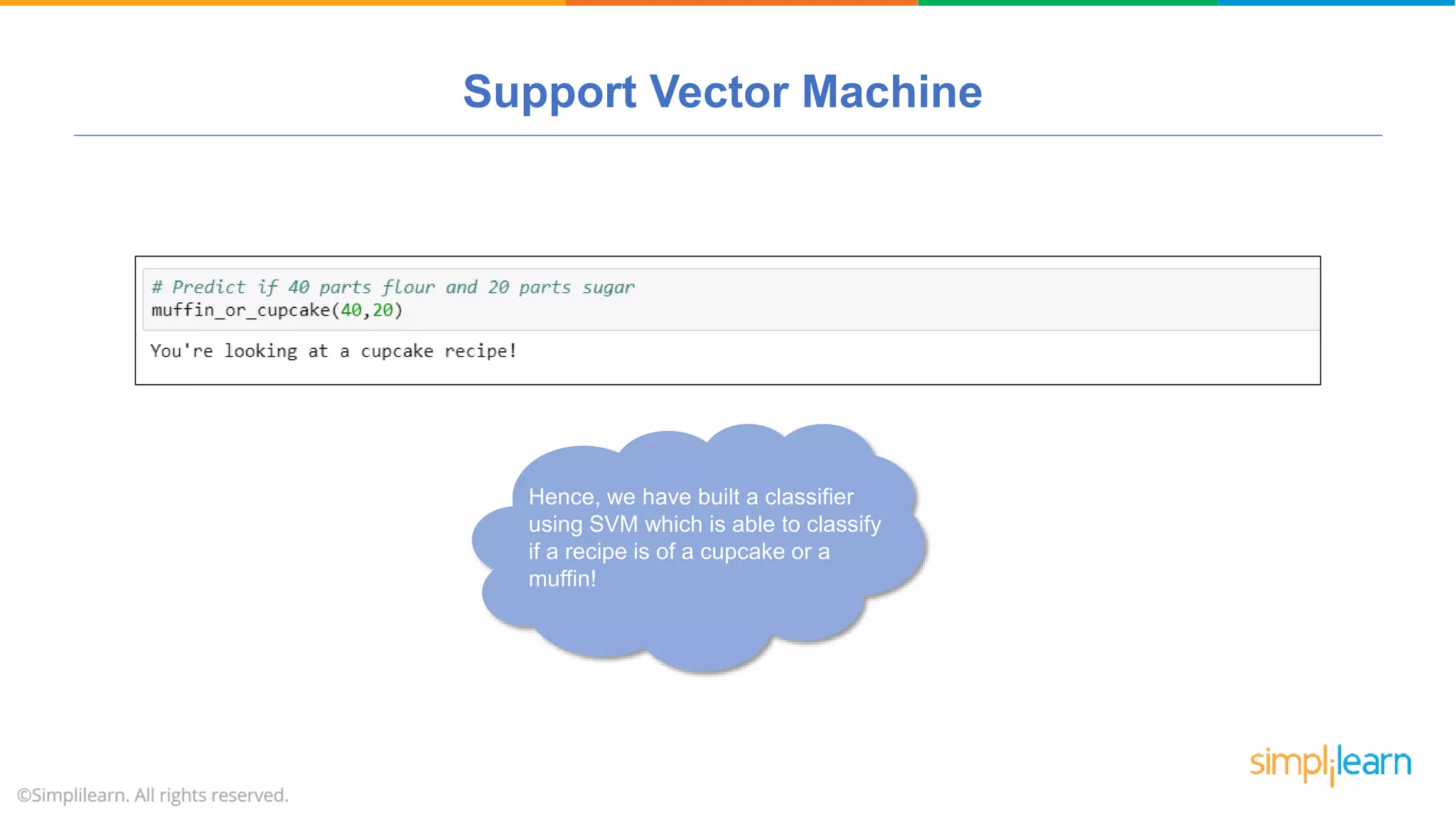
The document provides a comprehensive tutorial on machine learning, covering its definition, types (supervised, unsupervised, and reinforcement learning), and various algorithms (linear regression, decision trees, and support vector machines). It also includes practical use cases, such as classifying recipes and detecting anomalies, along with explanations of key concepts like entropy and information gain in decision trees. Overall, it emphasizes the significance of machine learning in real-world applications and the mechanics behind different learning models.