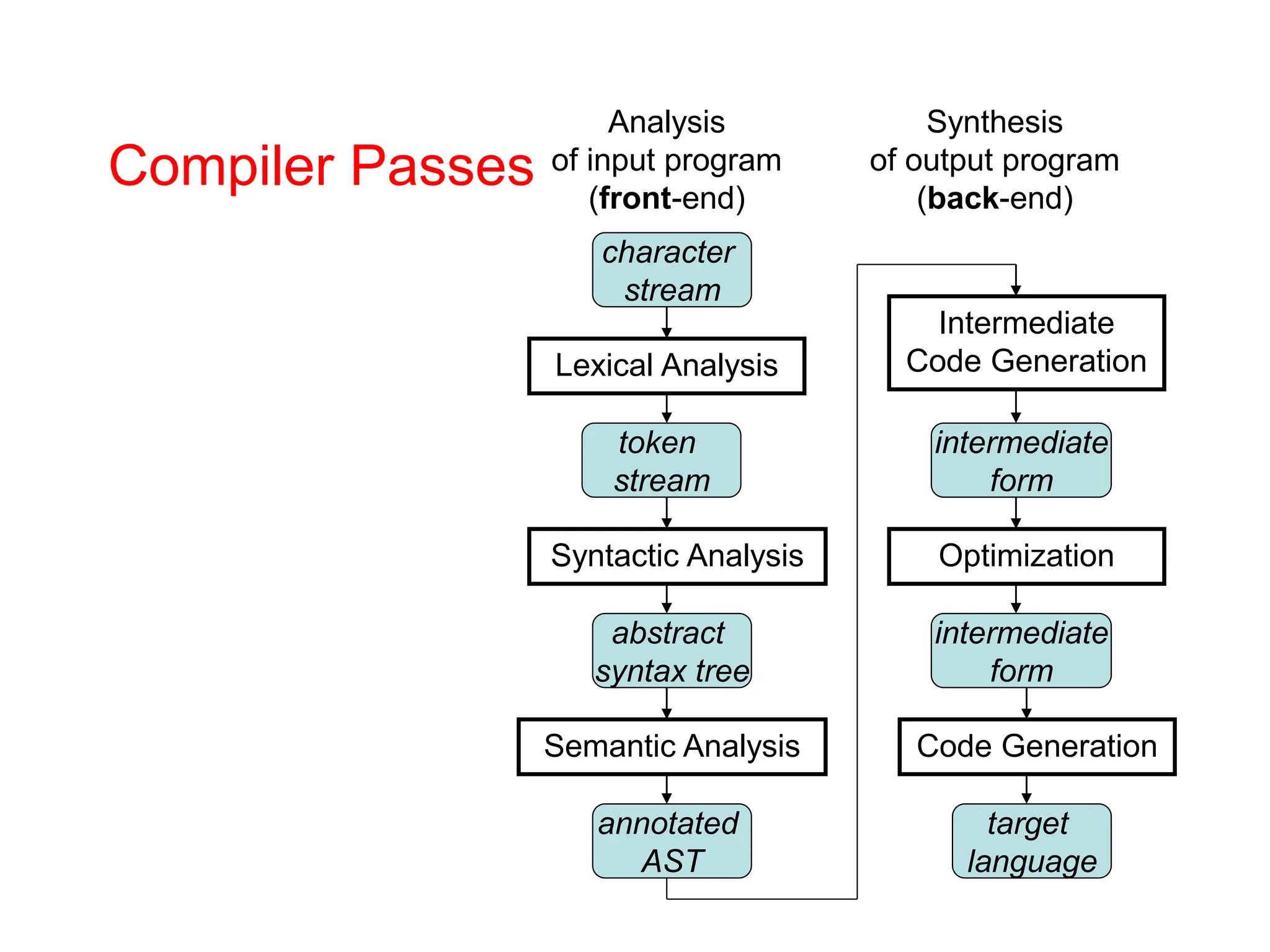
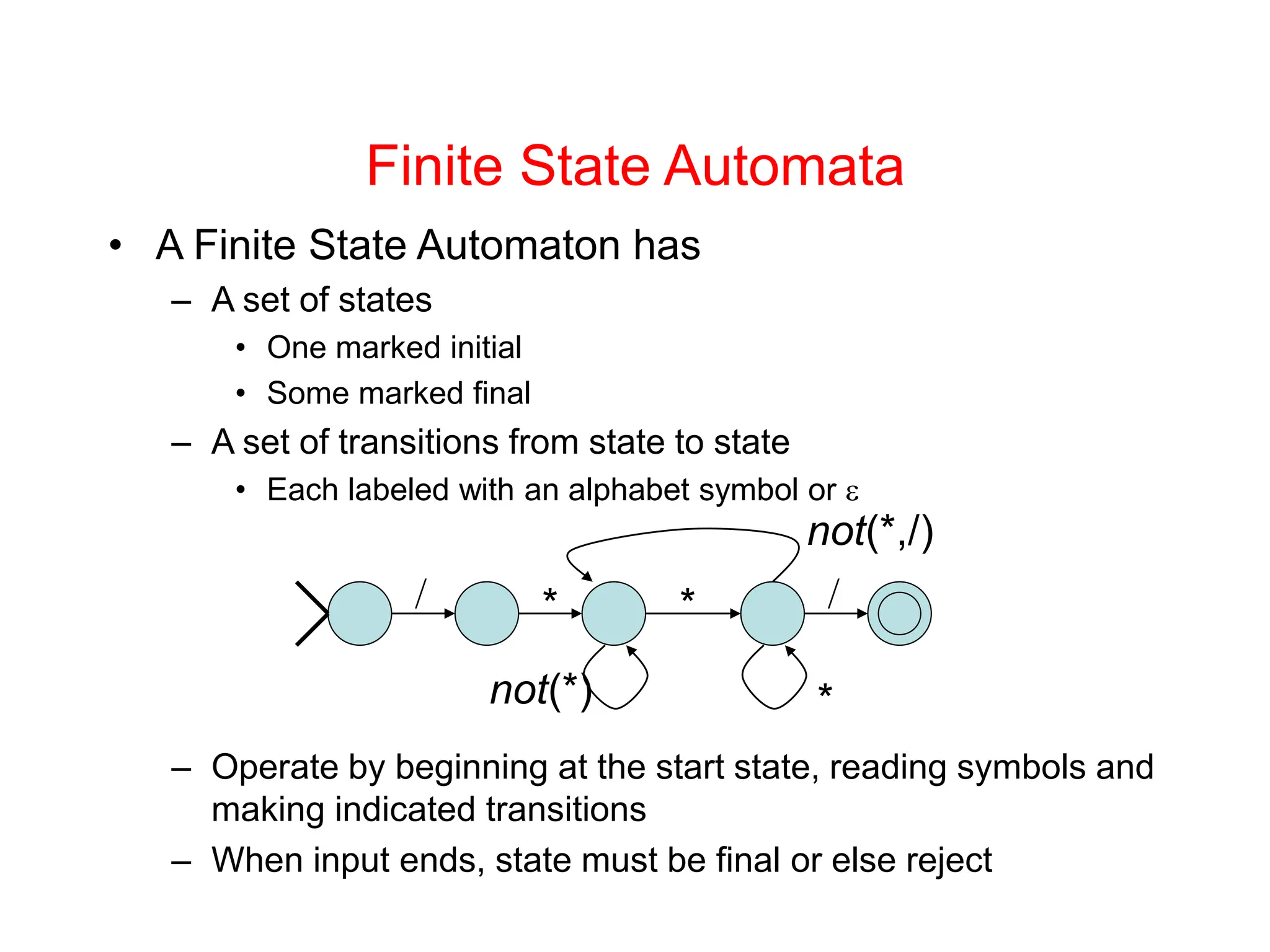
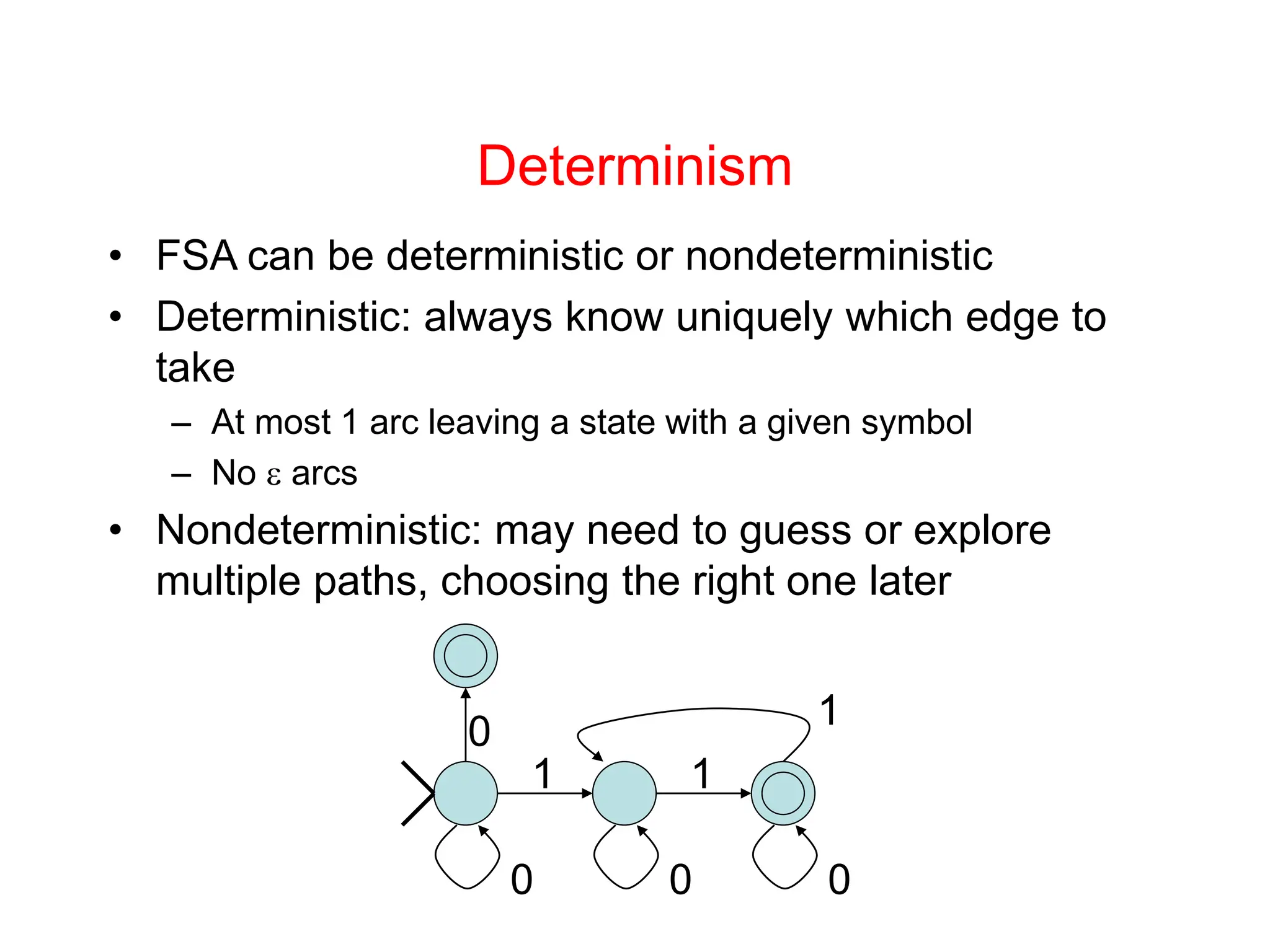
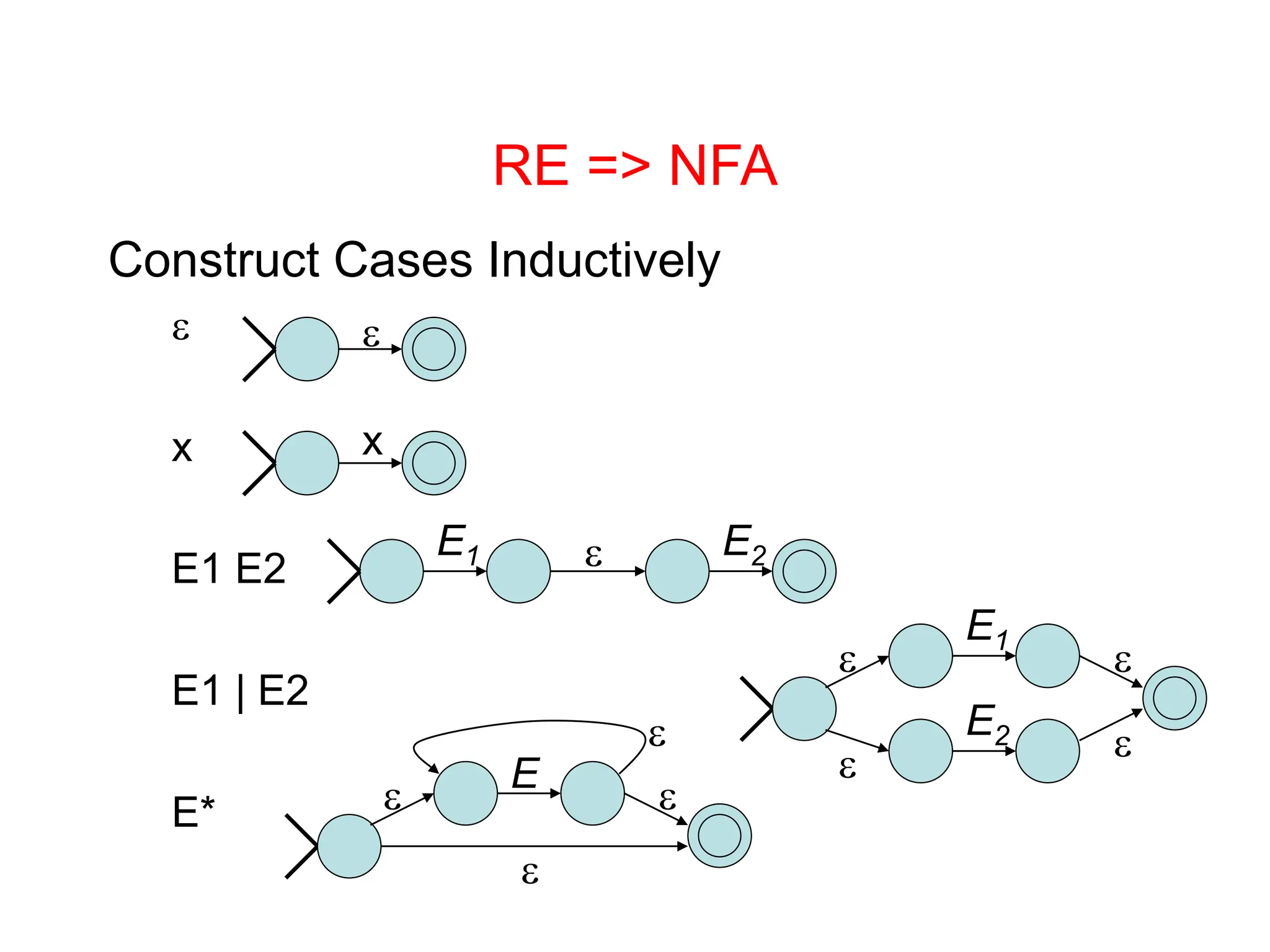
Lexical analysis is the first phase of compilation where the character stream is converted to tokens. It must be fast. It separates concerns by having a scanner handle tokenization and a parser handle syntax trees. Regular expressions are used to specify patterns for tokens. A regular expression specification can be converted to a finite state automaton and then to a deterministic finite automaton to build a scanner that efficiently recognizes tokens.








![Notational Conveniences • E+ means 1 or more occurrences of E • Ek means exactly k occurrences of E • [E] means 0 or 1 occurrences of E • {E} means E* • not(x) means any character in alphabet by x • not(E) means any strings from alphabet except those in E • E1-E2 means any string matching E1 that’s not in E2 • There is no additional expressive power here](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-10-2048.jpg)

![Using REs to Specify Tokens Identifiers ident ::= letter ( digit | letter)* Integer constants integer ::= digit+ sign ::= + | - signed_int ::= [sign] integer Real numbers real ::= signed_int [fraction] [exponent] fraction ::= . digit+ exponent ::= (E | e) signed_int](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-12-2048.jpg)


![RE Specification of initial MiniJava Lex Program ::= (Token | Whitespace)* Token ::= ID | Integer | ReservedWord | Operator | Delimiter ID ::= Letter (Letter | Digit)* Letter ::= a | ... | z | A | ... | Z Digit ::= 0 | ... | 9 Integer ::= Digit+ ReservedWord::= class | public | static | extends | void | int | boolean | if | else | while|return|true|false| this | new | String | main | System.out.println Operator ::= + | - | * | / | < | <= | >= | > | == | != | && | ! Delimiter ::= ; | . | , | = | ( | ) | { | } | [ | ]](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-15-2048.jpg)



![Subset Construction Given NFA with states and transitions – label all NFA states uniquely Create start state of DFA – label it with the set of NFA states that can be reached by transitions, i.e. w/o consuming input – Process the start state To process a DFA state S with label [S1,…,Sn] For each symbol x in the alphabet: – Compute the set T of NFA states S1,…,Sn by an x transition followed by any number of transitions – If T not empty • If a DFA state has T as a label add an x transition from S to T • Otherwise create a new DFA state T and add an x transition S to T A DFA state is final iff at least one of the NFA states is](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-23-2048.jpg)

![DFA => code [continued] • Option 2: use tool to generate table driven parser – Rows: states of DFA – Columns: input characters – Entries: action • Go to next state • Accept token, go to start state • Error • Pros – Convenient – Exactly matches specification, if tool generated • Cons – “Magic” – Table lookups may be slower than direct code, but switch implementation is a possible revision](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-25-2048.jpg)



![jflex Token Specifications Helper definitions for character classes and regular expressions letter = [a-zA-Z] eol = [rn] Simple) token definitions are of the form: regexp { Java stmt } regexp can be (at least): • a string literal in double-quotes, e.g. "class", "<=" • a reference to a named helper, in braces, e.g. {letter} • a character list or range,in square brackets,e.g.[a-zA-Z] • a negated character list or range, e.g. [^rn] • . (which matches any single character) • regexp regexp,regexp|regexp,regexp*,regexp+, regexp?, (regexp)](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-29-2048.jpg)
![jflex Tokens [Continued] Java stmt (the accept action) is typically: • return symbol(sym.CLASS); for a simple token • return symbol(sym.CLASS,yytext()); for a token with extra data based on the lexeme stringyytext() • empty for whitespace](https://image.slidesharecdn.com/lex-231216075048-ec350ea5/75/Lexical-analysis-syntax-analysis-semantic-analysis-Ppt-30-2048.jpg)