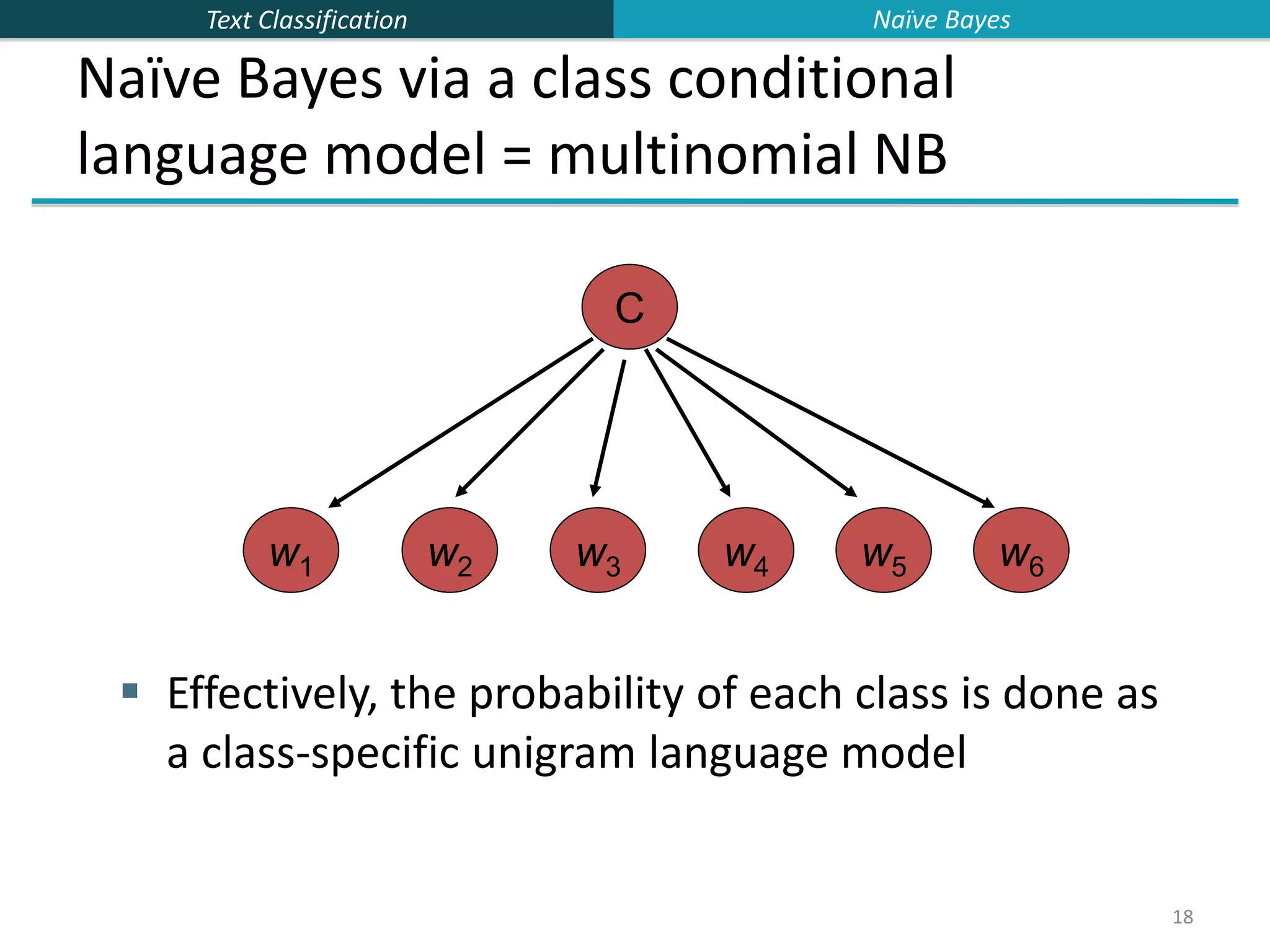
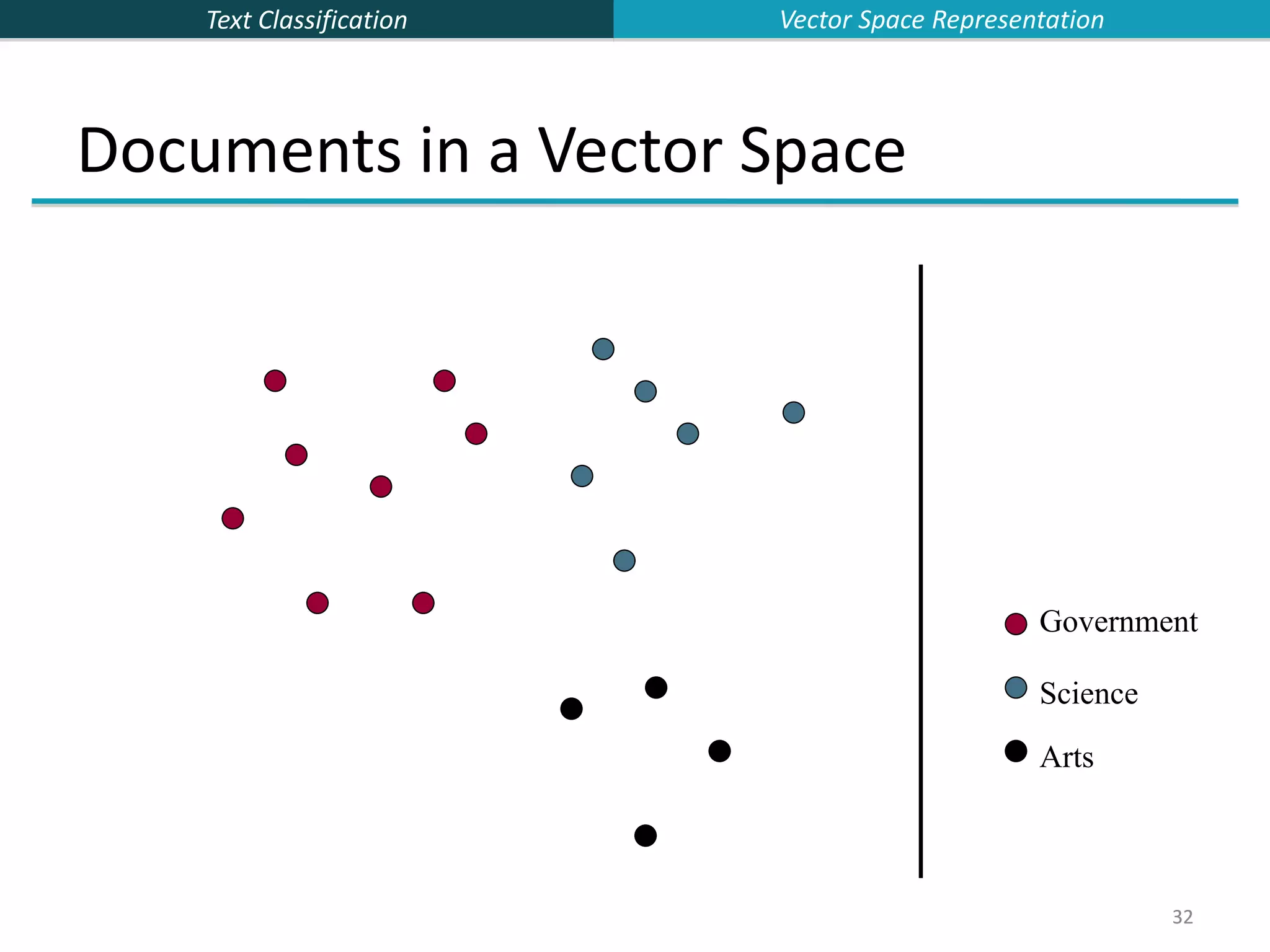
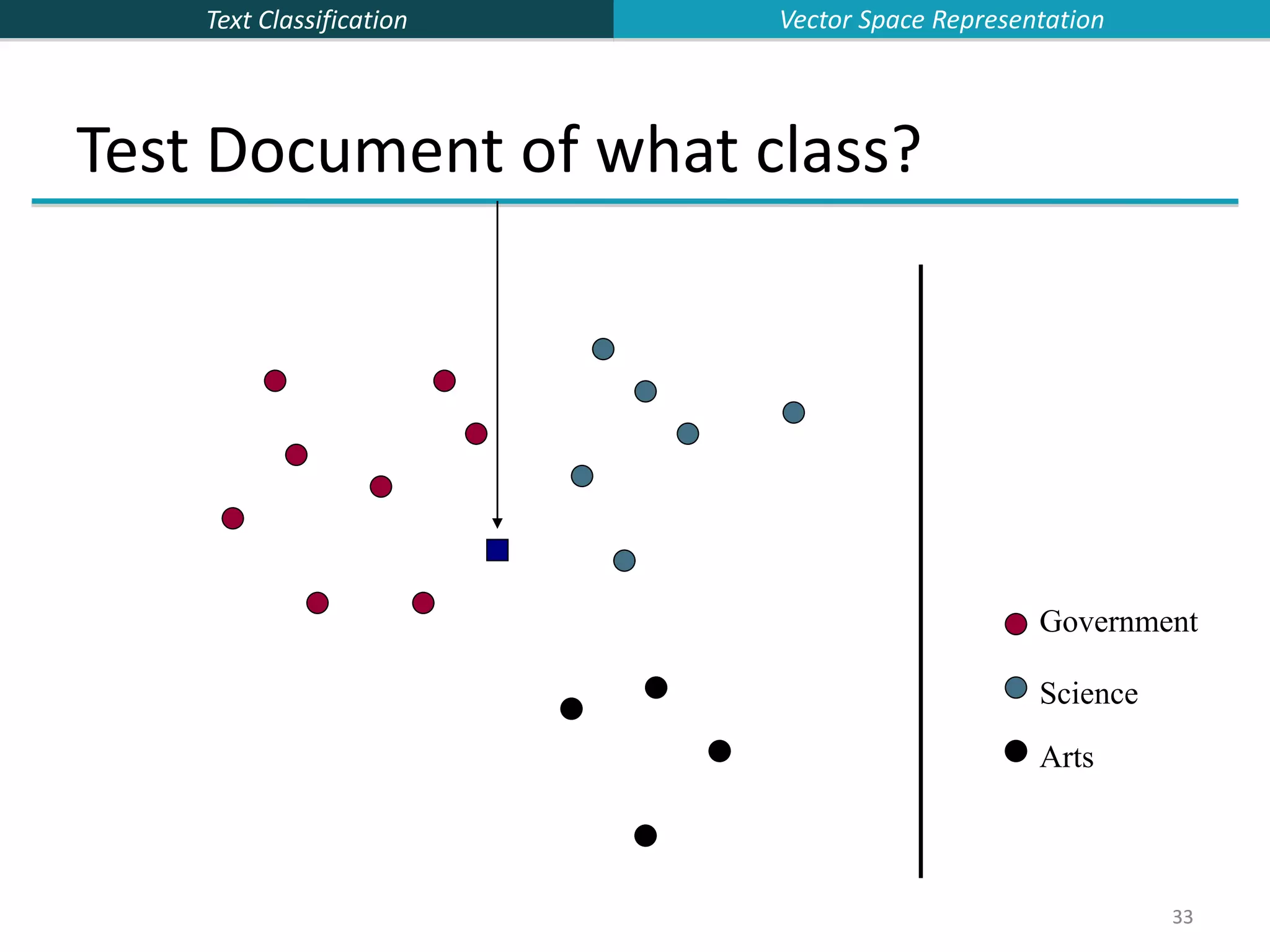
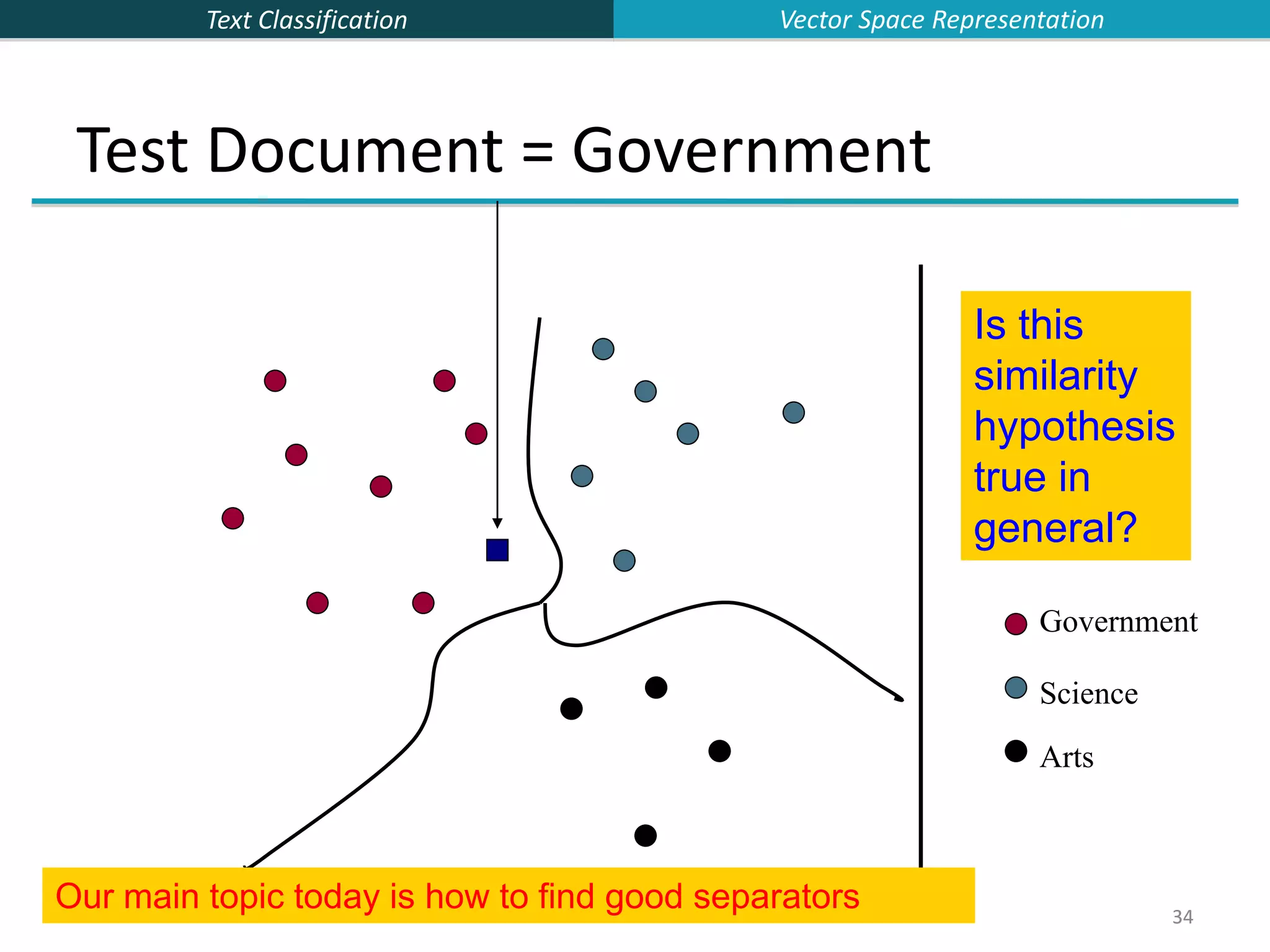
This document provides an overview of text classification and the Naive Bayes algorithm for text classification. It begins by defining text classification and giving examples like spam filtering and document classification. It then explains supervised classification and the goal of learning a classifier from labeled training data. The document spends several slides explaining the Naive Bayes algorithm for text classification, including the Naive Bayes assumption of conditional independence between features. It discusses parameter estimation and smoothing techniques to avoid overfitting. Finally, it compares the multivariate Bernoulli and multinomial Naive Bayes models for text classification.


















![Text Classification 23 Underflow Prevention: using logs Multiplying lots of probabilities, which are between 0 and 1 by definition, can result in floating-point underflow. Since log(xy) = log(x) + log(y), it is better to perform all computations by summing logs of probabilities rather than multiplying probabilities. Class with highest final un-normalized log probability score is still the most probable. Note that model is now just max of sum of weights… cNB argmax cj C [log P(c j ) log P(xi |c j ) ipositions ] Naïve Bayes](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-23-2048.jpg)
![Text Classification 24 Naive Bayes Classifier Simple interpretation: Each conditional parameter log P(xi|cj) is a weight that indicates how good an indicator xi is for cj. The prior log P(cj) is a weight that indicates the relative frequency of cj. The sum is then a measure of how much evidence there is for the document being in the class. We select the class with the most evidence for it 24 cNB argmax cj C [log P(c j ) log P(xi |c j ) ipositions ] Naïve Bayes](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-24-2048.jpg)














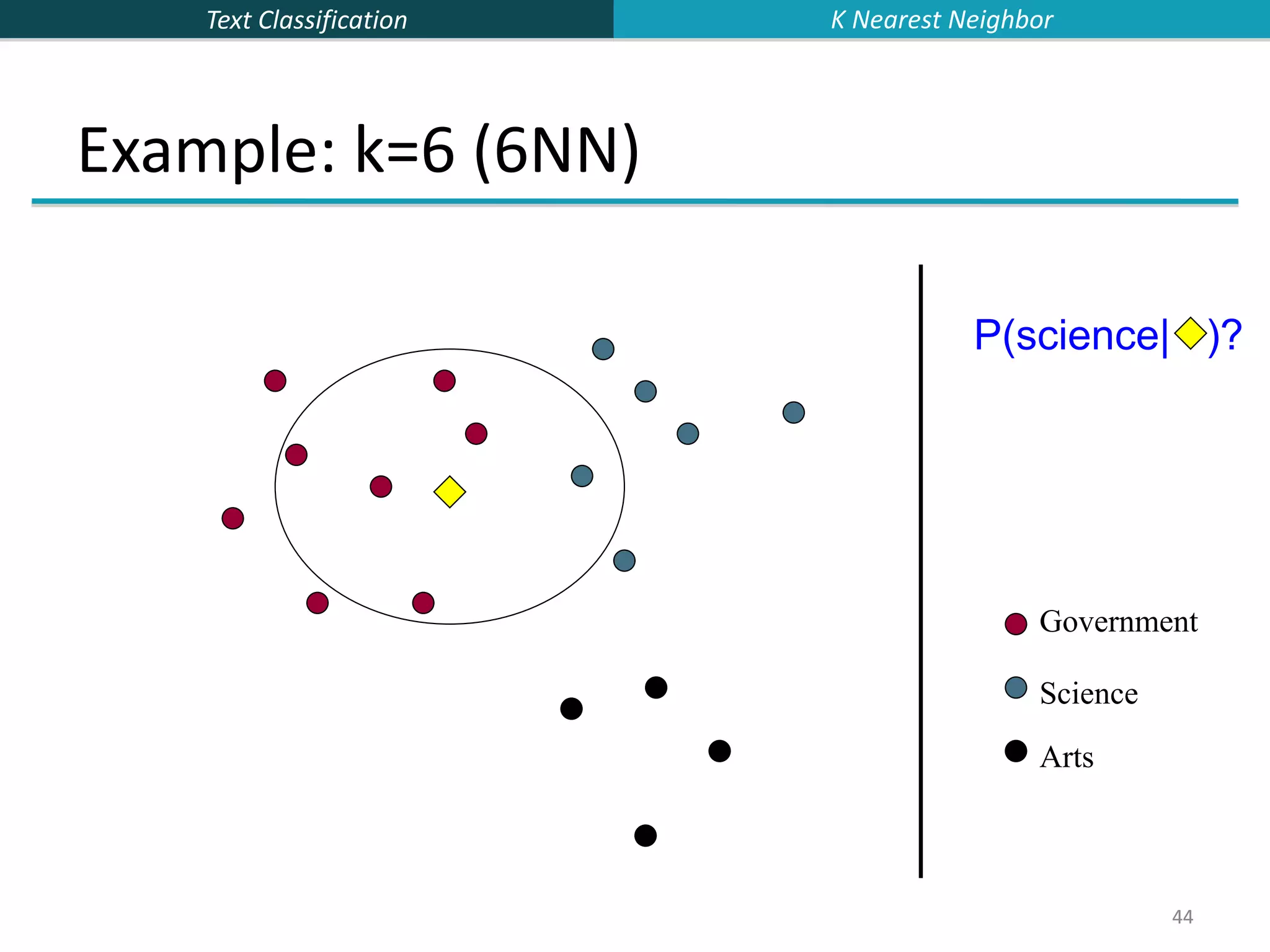
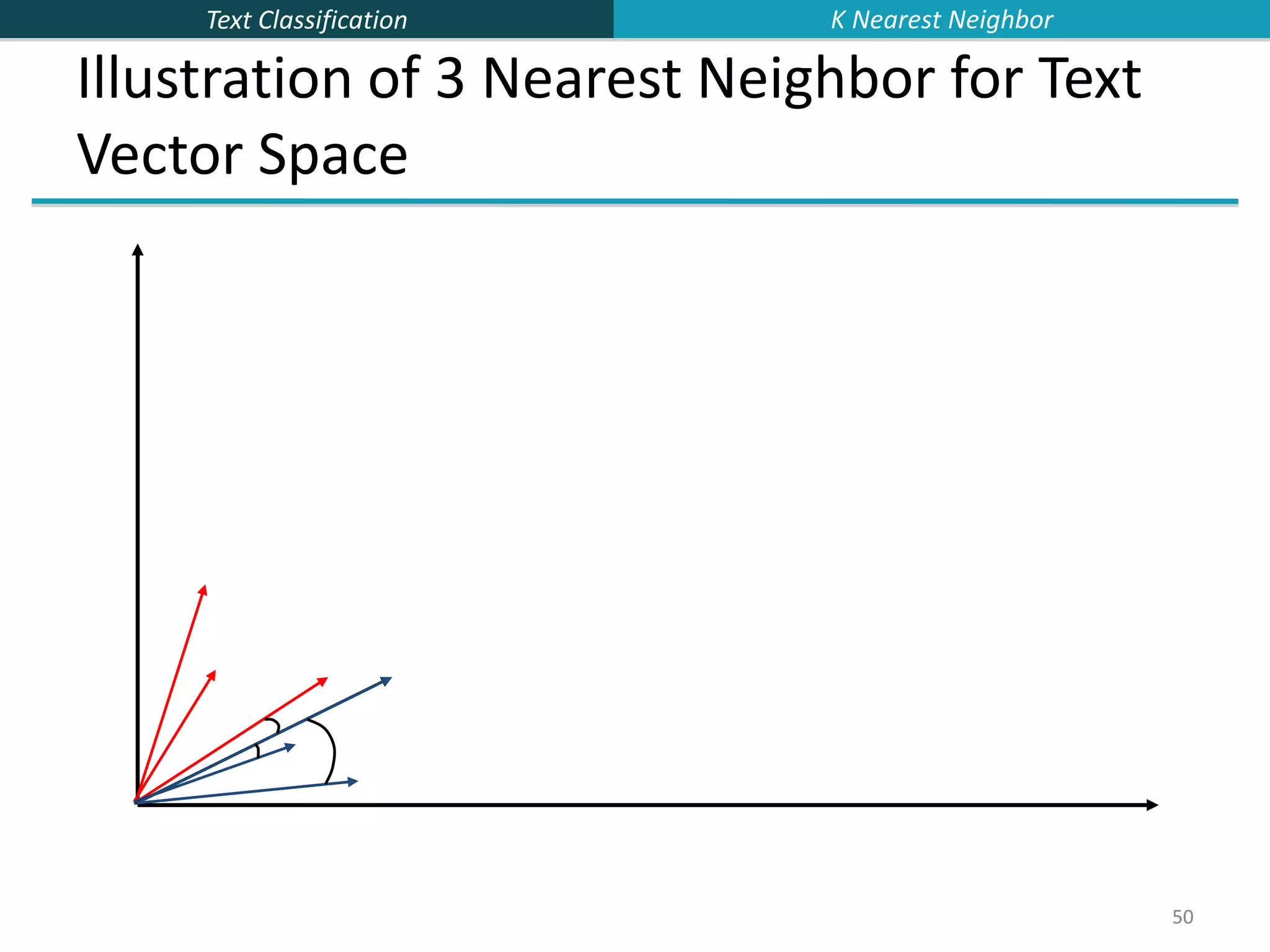
![Text Classification 43 43 k Nearest Neighbor Classification kNN = k Nearest Neighbor To classify a document d into class c: Define k-neighborhood N as k nearest neighbors of d Count number of documents ic in N that belong to c Estimate P(c|d) as ic/k Choose as class argmaxc P(c|d) [ = majority class] K Nearest Neighbor](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-43-2048.jpg)

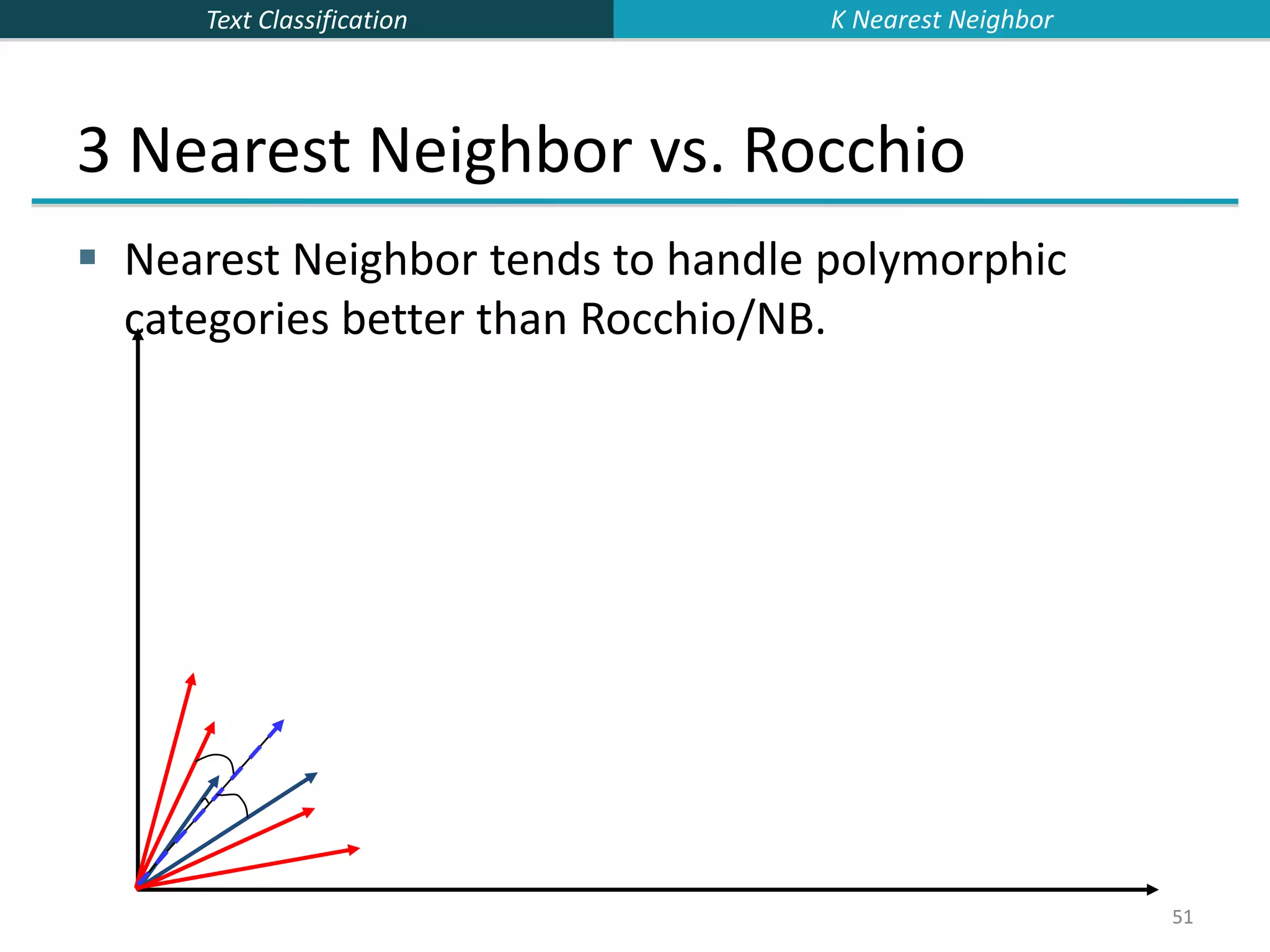
![Text Classification 46 46 kNN Is Close to Optimal Cover and Hart (1967) Asymptotically, the error rate of 1-nearest-neighbor classification is less than twice the Bayes rate [error rate of classifier knowing model that generated data] In particular, asymptotic error rate is 0 if Bayes rate is 0. Assume: query point coincides with a training point. Both query point and training point contribute error → 2 times Bayes rate K Nearest Neighbor](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-46-2048.jpg)









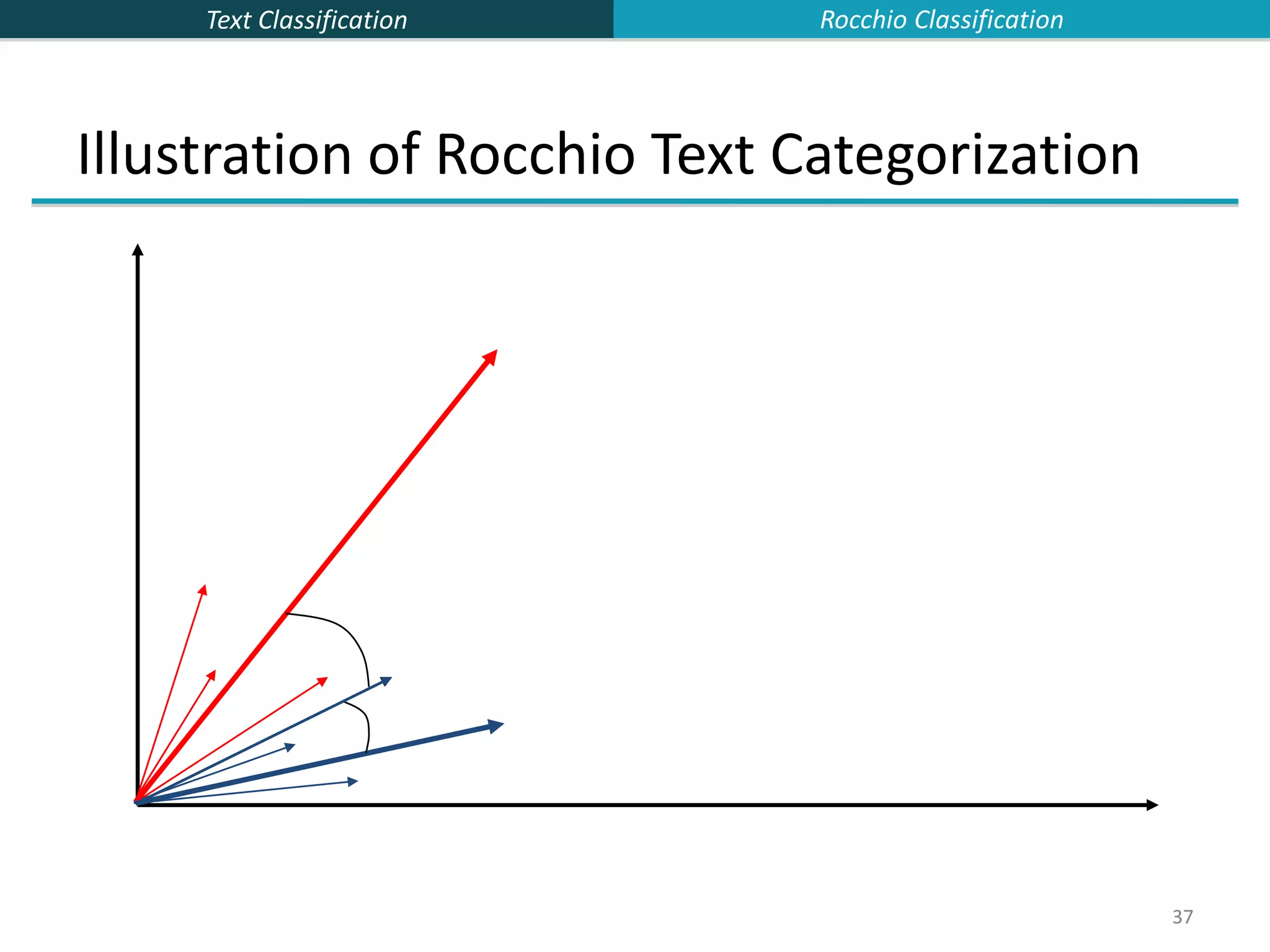
![Text Classification 58 Two-class Rocchio as a linear classifier Line or hyperplane defined by: For Rocchio, set: [Aside for ML/stats people: Rocchio classification is a simplification of the classic Fisher Linear Discriminant where you don’t model the variance (or assume it is spherical).] 58 widi i1 M w (c1) (c2) 0.5 (| (c1) |2 | (c2) |2 ) Linear Vs Nonlinear](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-58-2048.jpg)


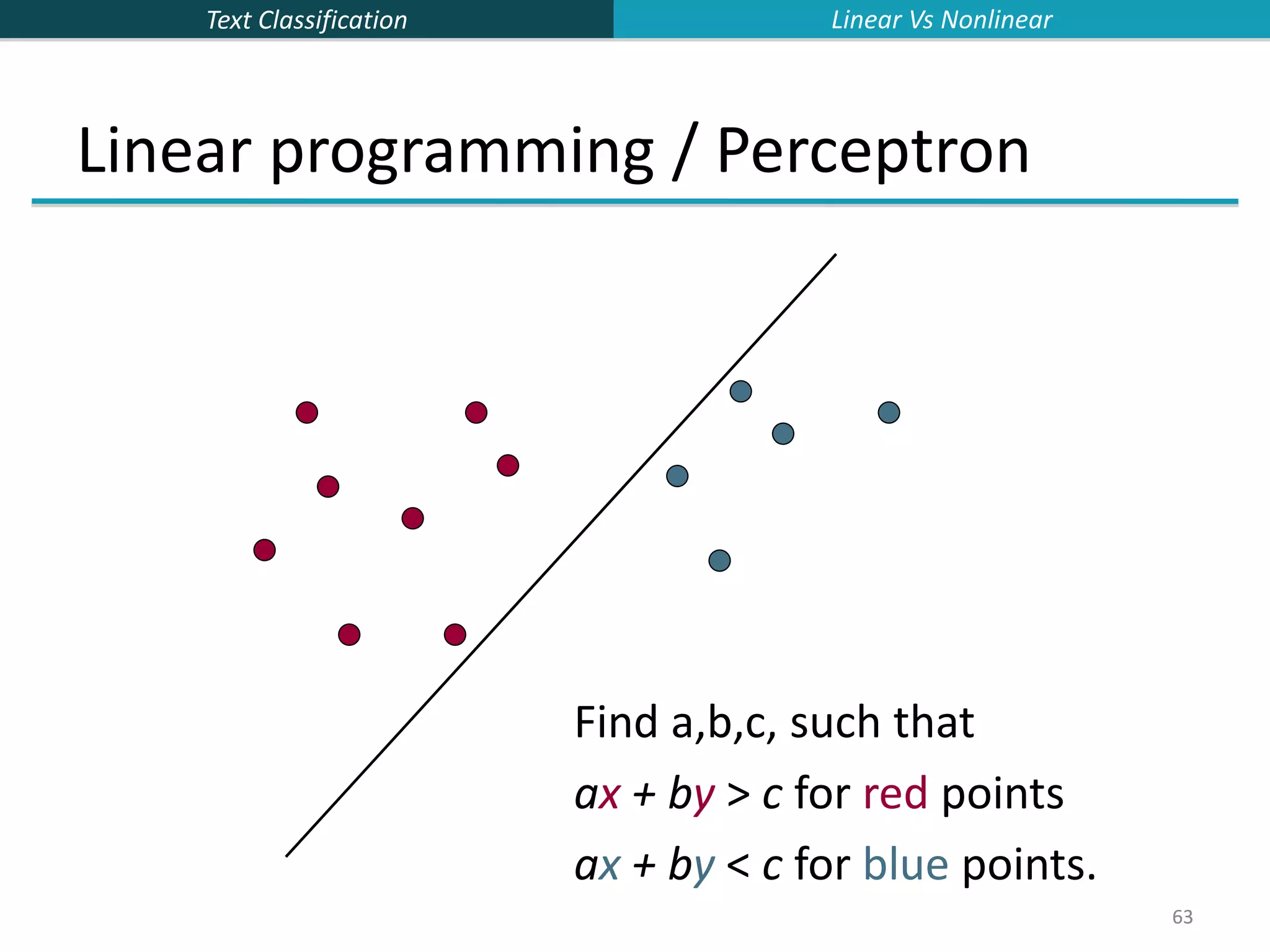
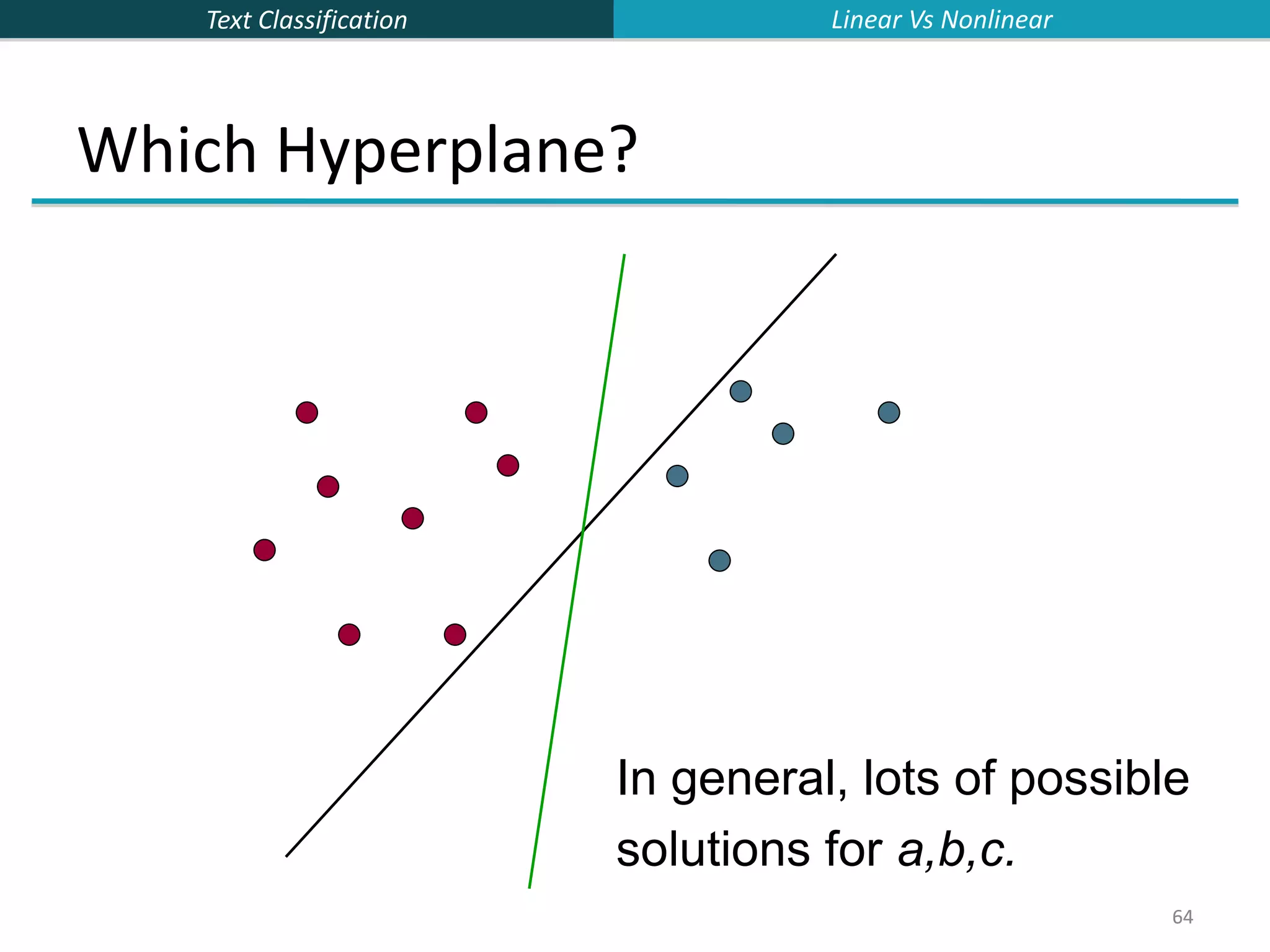
![Text Classification 65 65 Which Hyperplane? Lots of possible solutions for a,b,c. Some methods find a separating hyperplane, but not the optimal one [according to some criterion of expected goodness] E.g., perceptron Most methods find an optimal separating hyperplane Which points should influence optimality? All points Linear/logistic regression Naïve Bayes Only “difficult points” close to decision boundary Support vector machines Linear Vs Nonlinear](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-65-2048.jpg)
![Text Classification 66 66 Linear classifiers: Which Hyperplane? Lots of possible solutions for a, b, c. Some methods find a separating hyperplane, but not the optimal one [according to some criterion of expected goodness] E.g., perceptron Support Vector Machine (SVM) finds an optimal solution. Maximizes the distance between the hyperplane and the “difficult points” close to decision boundary One intuition: if there are no points near the decision surface, then there are no very uncertain classification decisions This line represents the decision boundary: ax + by − c = 0 Support Vector Machine](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-66-2048.jpg)











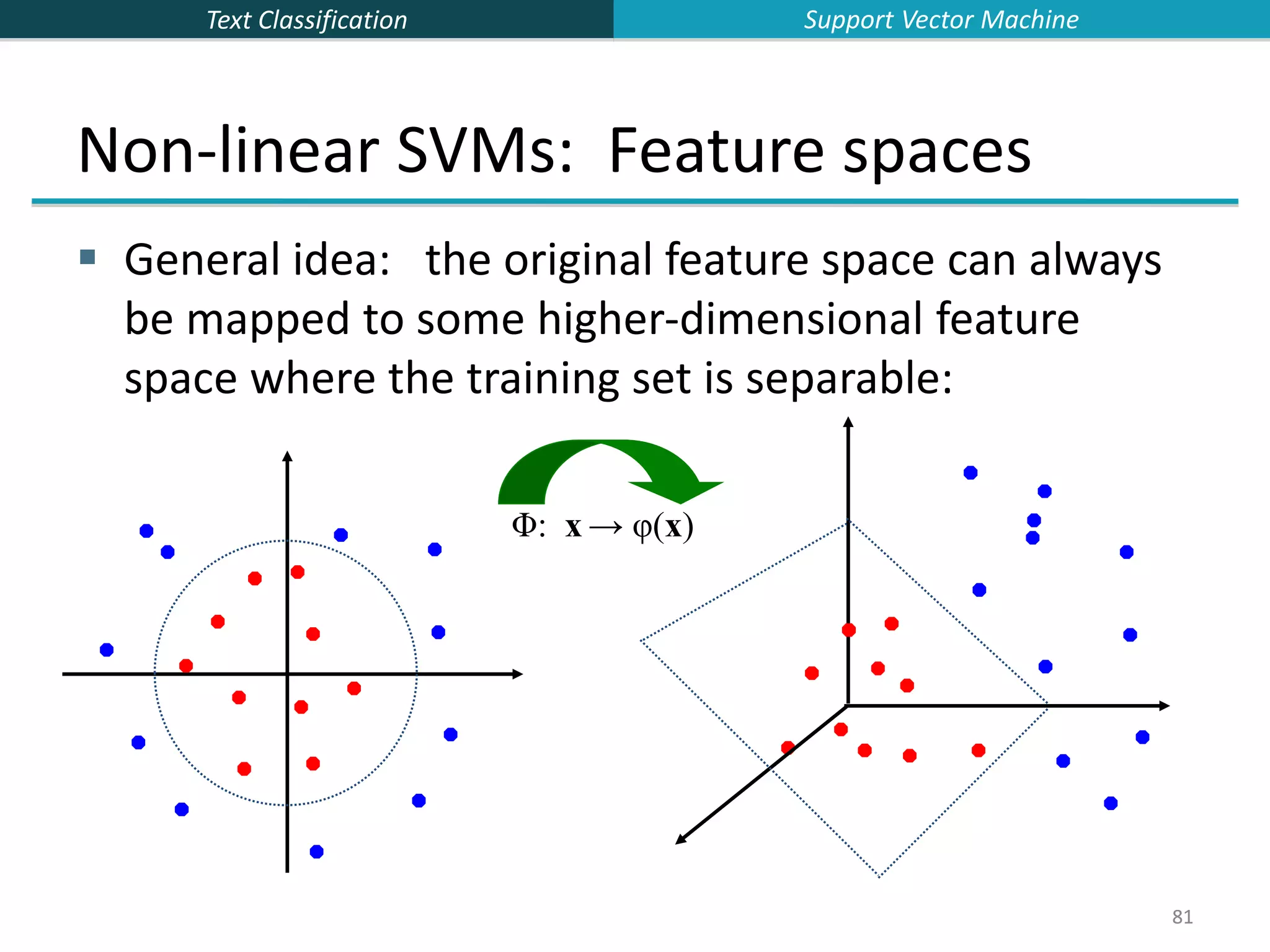
![Text Classification 82 82 The “Kernel Trick” The linear classifier relies on an inner product between vectors K(xi,xj)=xi Txj If every data point is mapped into high-dimensional space via some transformation Φ: x → φ(x), the inner product becomes: K(xi,xj)= φ(xi) Tφ(xj) A kernel function is some function that corresponds to an inner product in some expanded feature space. Example: 2-dimensional vectors x=[x1 x2]; let K(xi,xj)=(1 + xi Txj)2 , Need to show that K(xi,xj)= φ(xi) Tφ(xj): K(xi,xj)=(1 + xi Txj)2 ,= 1+ xi1 2xj1 2 + 2 xi1xj1 xi2xj2+ xi2 2xj2 2 + 2xi1xj1 + 2xi2xj2= = [1 xi1 2 √2 xi1xi2 xi2 2 √2xi1 √2xi2]T [1 xj1 2 √2 xj1xj2 xj2 2 √2xj1 √2xj2] = φ(xi)Tφ(xj) where φ(x) = [1 x1 2 √2 x1x2 x2 2 √2x1 √2x2] Support Vector Machine](https://image.slidesharecdn.com/lecture15-supervised-221224064515-3b75ec9b/75/lecture15-supervised-ppt-82-2048.jpg)