lecture on introduction to Binary Search Tree

lecture on introduction to Binary Search Tree

• 1.
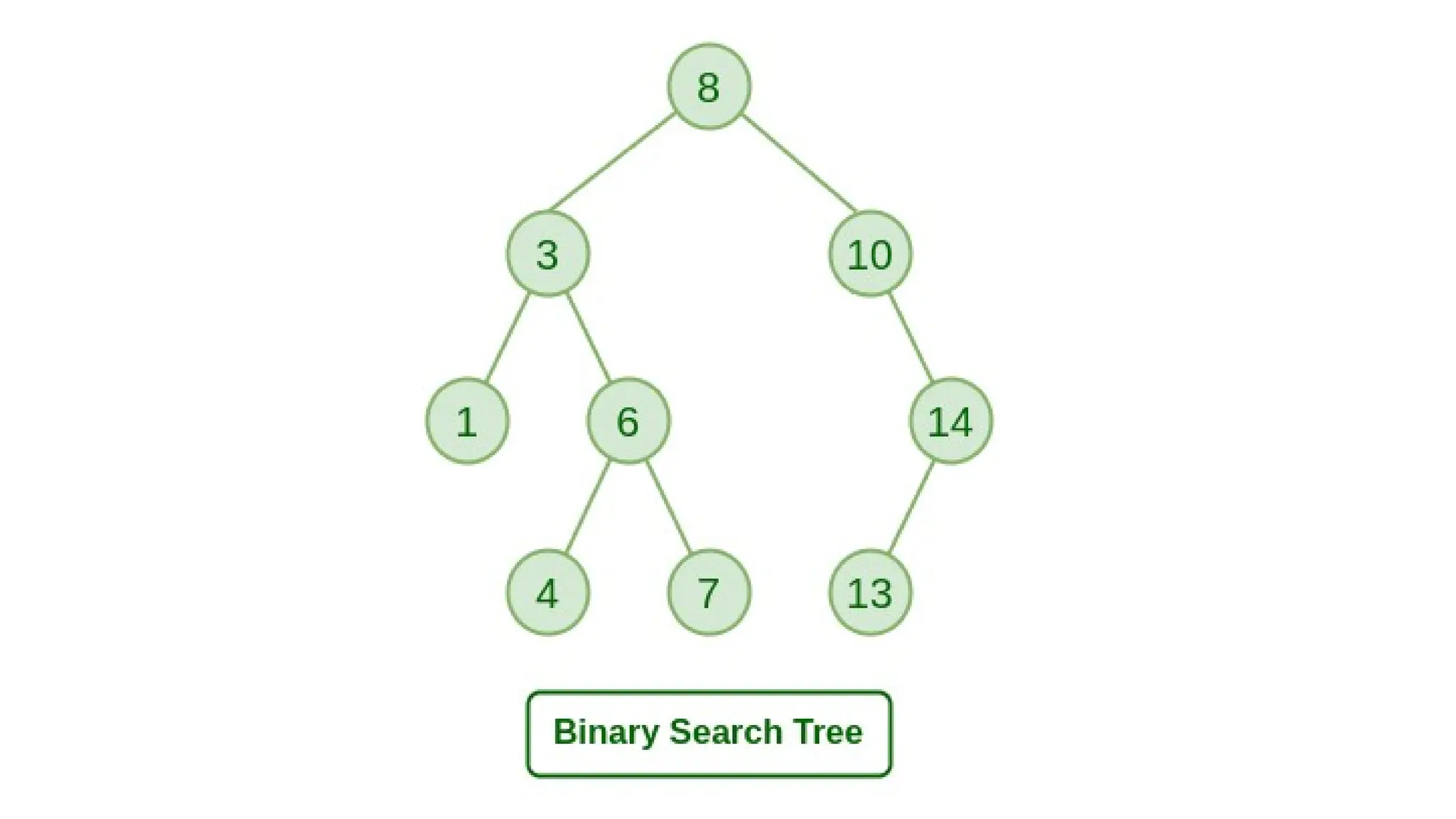
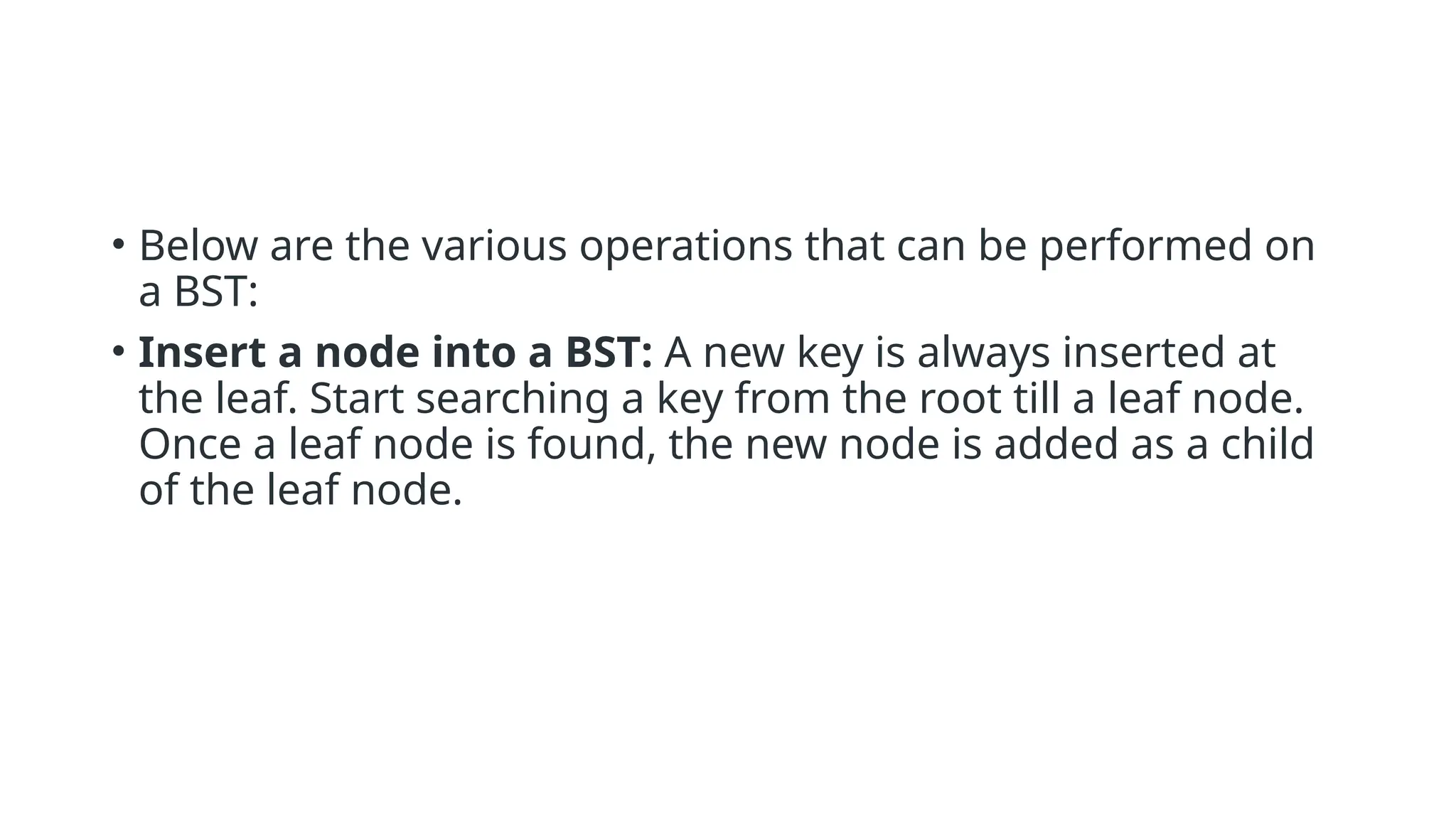
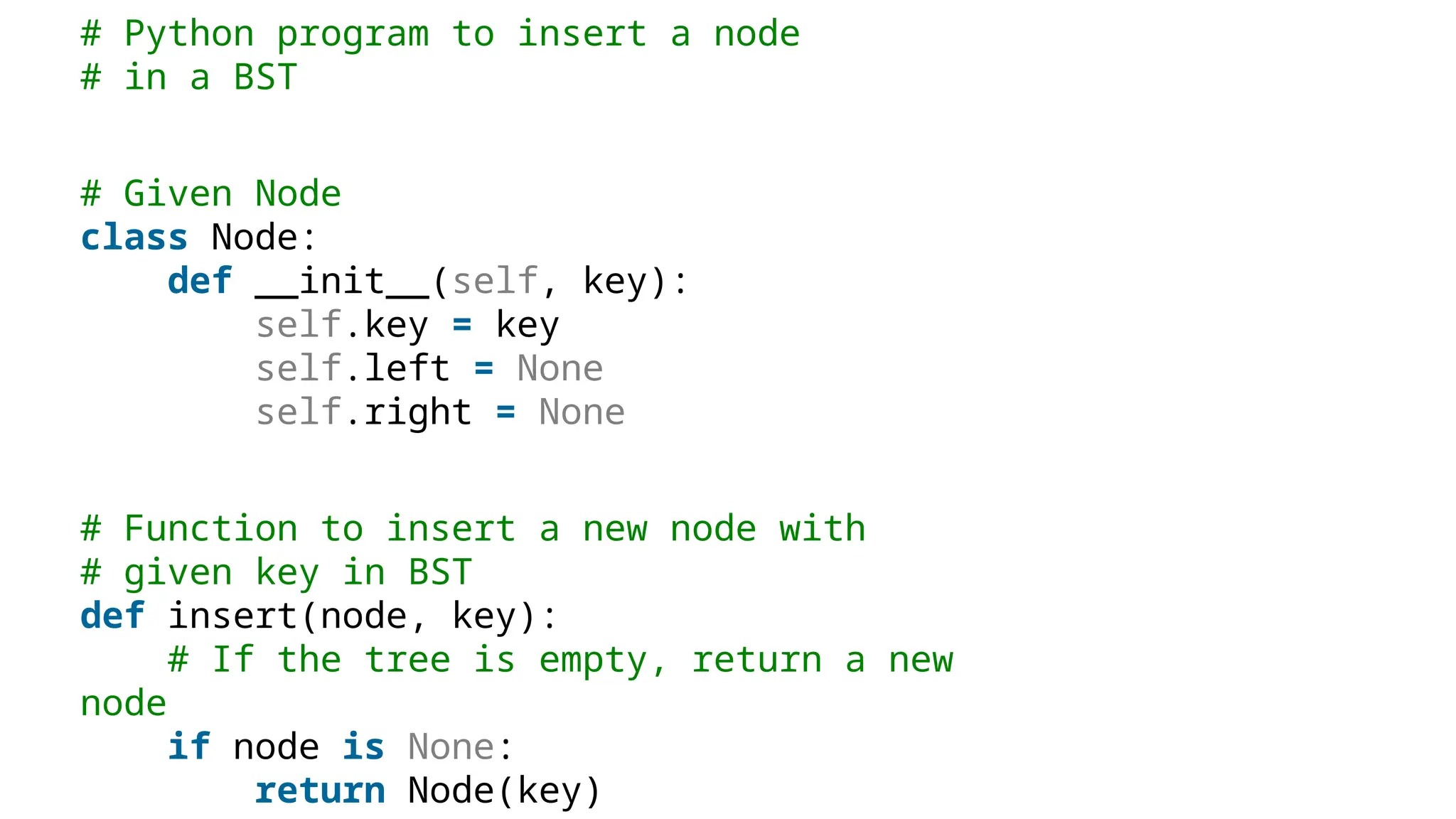
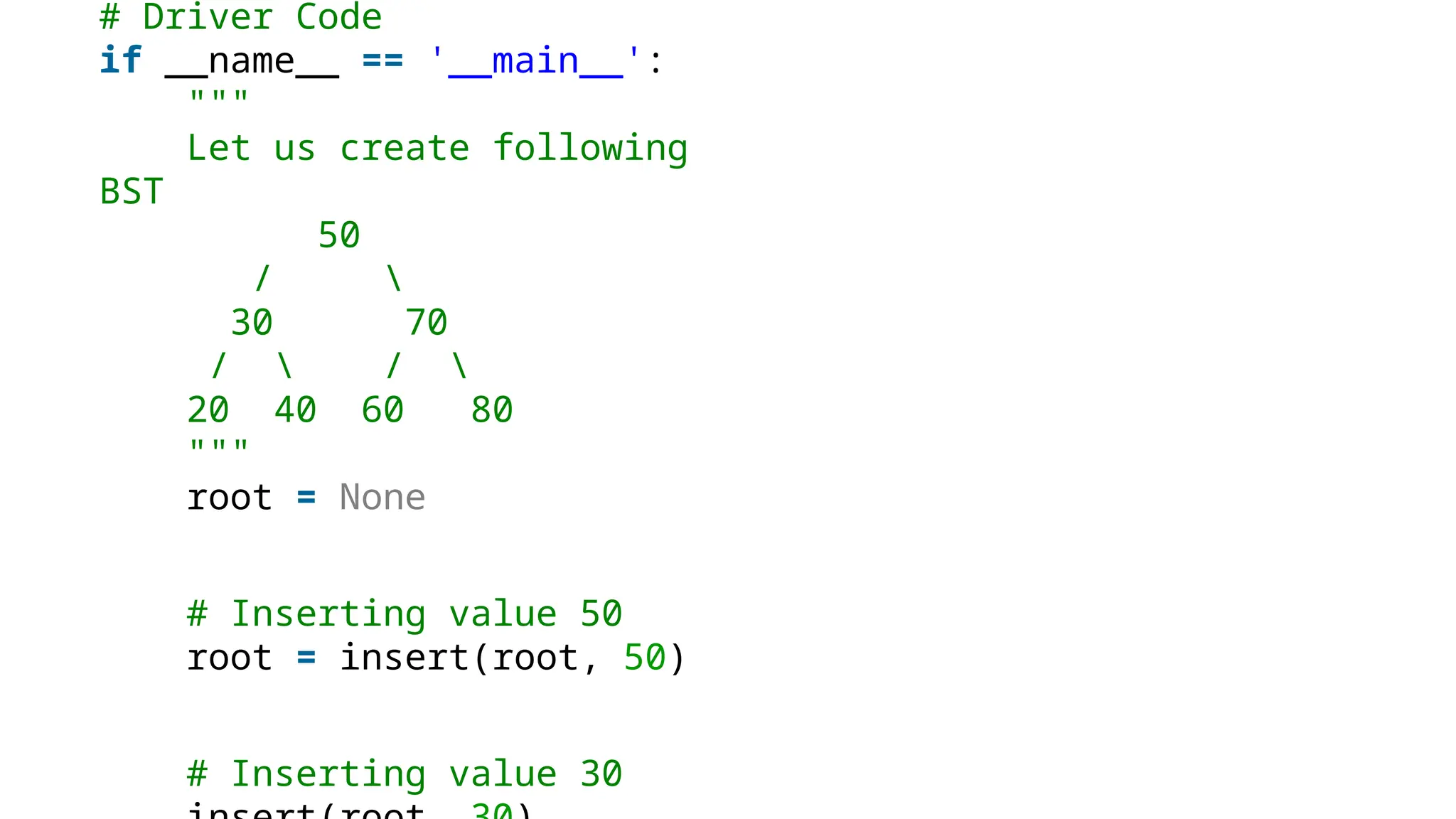
  Binary Search Tree By;Jayf T. Mangansakan, MIS
• 2.
  A Binary SearchTree is a data structure used in computer science for organizing and storing data in a sorted manner. Each node in a Binary Search Tree has at most two children, a left child and a right child, with the left child containing values less than the parent node and the right child containing values greater than the parent node. This hierarchical structure allows for efficient searching, insertion, and deletion operations on the data stored in the tree.
• 4.
  BST is aspecial type of binary tree in which the left child of a node has a value less than the node’s value and the right child has a value greater than the node’s value. This property is called the BST property and it makes it possible to efficiently search, insert, and delete elements in the tree.
• 5.
  The root ofa BST is the node that has the smallest value in the left subtree and the largest value in the right subtree. Each left subtree is a BST with nodes that have smaller values than the root and each right subtree is a BST with nodes that have larger values than the root. BST is a node-based binary tree data structure that has the following properties:
• 6.
  • The leftsubtree of a node contains only nodes with keys lesser than the node’s key. • The right subtree of a node contains only nodes with keys greater than the node’s key. • This means everything to the left of the root is less than the value of the root and everything to the right of the root is greater than the value of the root. Due to this performing, a binary search is very easy. • The left and right subtree each must also be a binary search tree. There must be no duplicate nodes(BST may have duplicate values with different handling approaches)
• 7.
  Handling approach forDuplicate values in the Binary Search tree: • You can not allow the duplicated values at all. • We must follow a consistent process throughout i.e either store duplicate value at the left or store the duplicate value at the right of the root, but be consistent with your approach. • We can keep the counter with the node and if we found the duplicate value, then we can increment the counter
• 8.
  • Below arethe various operations that can be performed on a BST: • Insert a node into a BST: A new key is always inserted at the leaf. Start searching a key from the root till a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
• 9.
  # Python programto insert a node # in a BST # Given Node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key)
• 10.
  # Otherwise, recurdown the tree if key < node.key: node.left = insert(node.left, key) elif key > node.key: node.right = insert(node.right, key) # Return the node pointer return node # Function to do inorder traversal of BST def inorder(root): if root is not None: inorder(root.left) print(root.key, end=" ") inorder(root.right)
• 11.
  # Driver Code if__name__ == '__main__': """ Let us create following BST 50 / 30 70 / / 20 40 60 80 """ root = None # Inserting value 50 root = insert(root, 50) # Inserting value 30
• 12.
  # Inserting value20 insert(root, 20) # Inserting value 40 insert(root, 40) # Inserting value 70 insert(root, 70) # Inserting value 60 insert(root, 60) # Inserting value 80 insert(root, 80) # Print the BST inorder(root)