Downloaded 14 times
Uploaded bynjit-ronbrown
PPT, PDF719 views
Lecture 7(b) derivative as a function
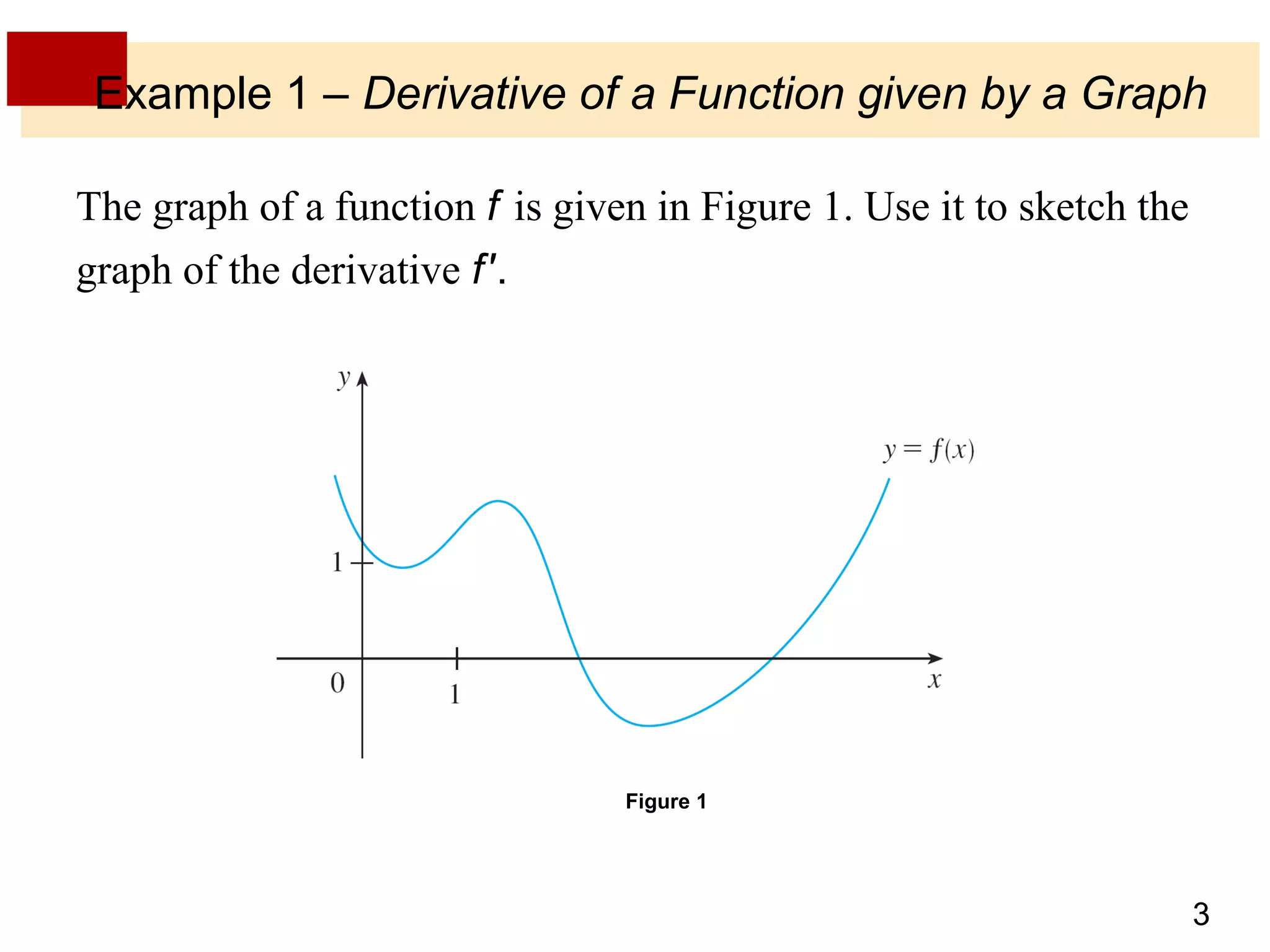
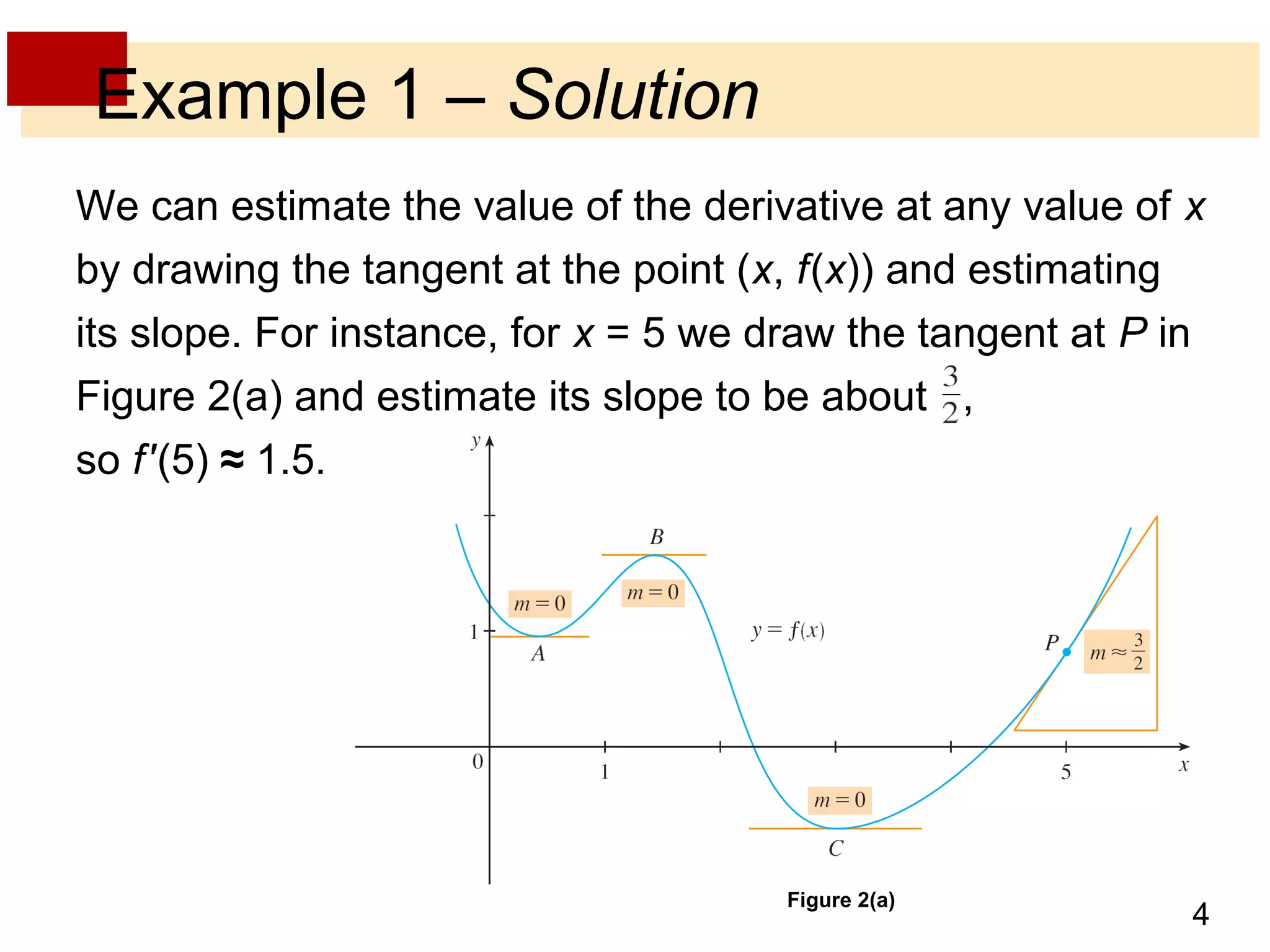
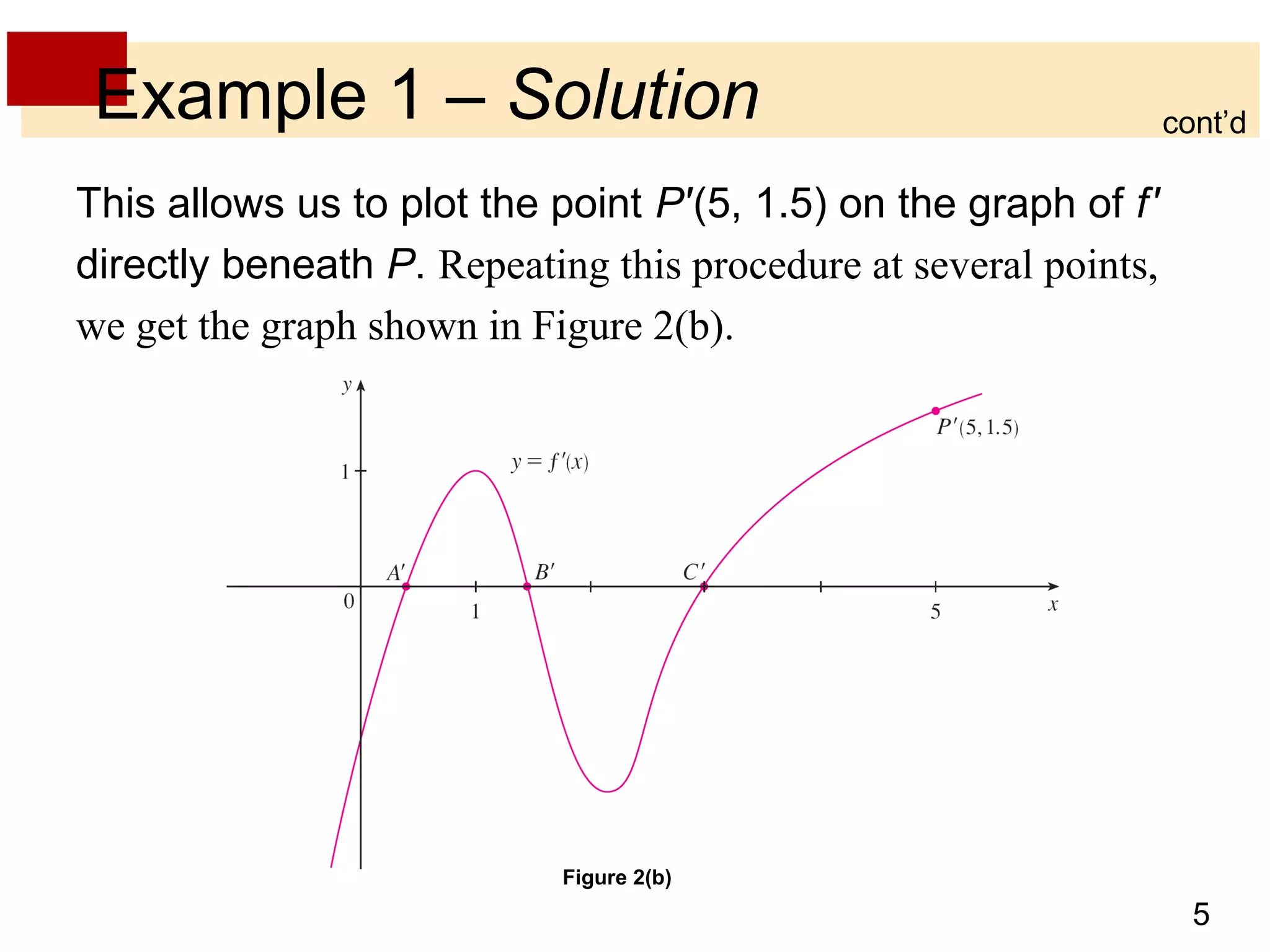
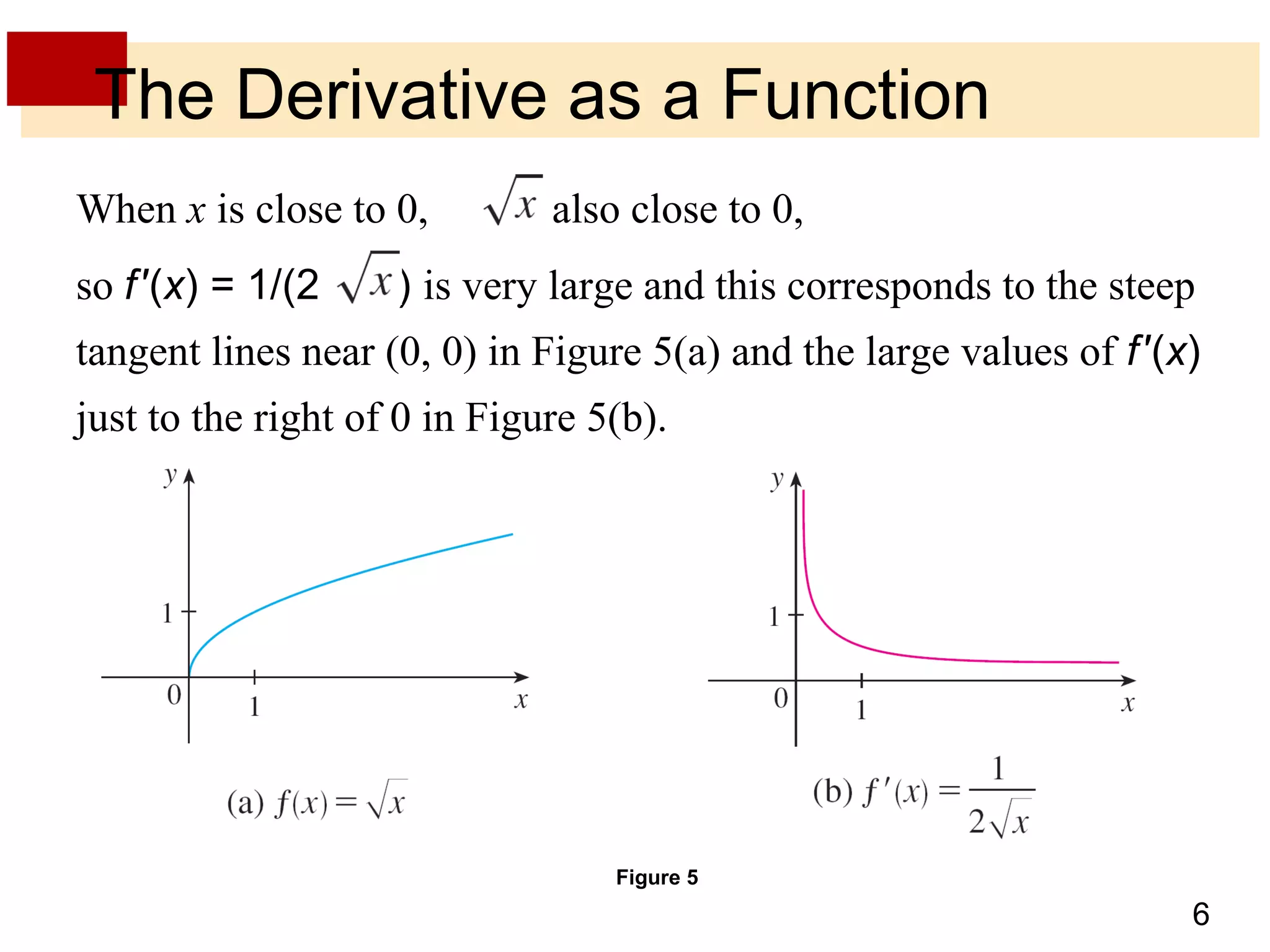
The document discusses the derivative as a function. It explains that the derivative of a function f at a number a can be written as an equation with a as a variable x, yielding the derivative as a function f'(x). It provides an example of using the graph of a function f to sketch the graph of its derivative f' by estimating the slope of tangents at various points on f and plotting corresponding points on f'. The derivative approaches very large values as x approaches 0 if f'(x) = 1/(2√x) and becomes very small as x becomes large, corresponding to flatter tangents on f and a horizontal asymptote for f'. It also discusses other notations for the derivative such as D, d
More Related Content
What's hot
Viewers also liked
Similar to Lecture 7(b) derivative as a function
More from njit-ronbrown
Recently uploaded
Lecture 7(b) derivative as a function
- 1. The Derivative 2.7as a Function
- 2. 2 The Derivativeas a Function We have considered the derivative of a function f at a fixed number a: Here we change our point of view and let the number a vary. If we replace a in Equation 1 by a variable x, we obtain
- 3. Example 1 –Derivative of a Function given by a Graph The graph of a function f is given in Figure 1. Use it to sketch the graph of the derivative f ′. 3 Figure 1
- 4. Example 1 –Solution We can estimate the value of the derivative at any value of x by drawing the tangent at the point (x, f (x)) and estimating its slope. For instance, for x = 5 we draw the tangent at P in Figure 2(a) and estimate its slope to be about , so f ′(5) ≈ 1.5. 4 Figure 2(a)
- 5. 5 Example 1– Solution This allows us to plot the point P ′(5, 1.5) on the graph of f ′ directly beneath P. Repeating this procedure at several points, we get the graph shown in Figure 2(b). Figure 2(b) cont’d
- 6. The Derivative asa Function When x is close to 0, is also close to 0, so f ′(x) = 1/(2 ) is very large and this corresponds to the steep tangent lines near (0, 0) in Figure 5(a) and the large values of f ′(x) just to the right of 0 in Figure 5(b). 6 Figure 5
- 7. 7 The Derivativeas a Function When x is large, f ′(x) is very small and this corresponds to the flatter tangent lines at the far right of the graph of f and the horizontal asymptote of the graph of f ′.
- 8. 8 Other Notations The symbols D and d/dx are called differentiation operators because they indicate the operation of differentiation.
- 9. 9 Other Notations The symbol dy/dx, which was introduced by Leibniz, should not be regarded as a ratio (for the time being); it is simply a synonym for f ′(x). We can rewrite the definition of derivative in Leibniz notation in the form
- 10. 10 Other Notations If we want to indicate the value of a derivative dy/dx in Leibniz notation at a specific number a, we use the notation which is a synonym for f ′(a).