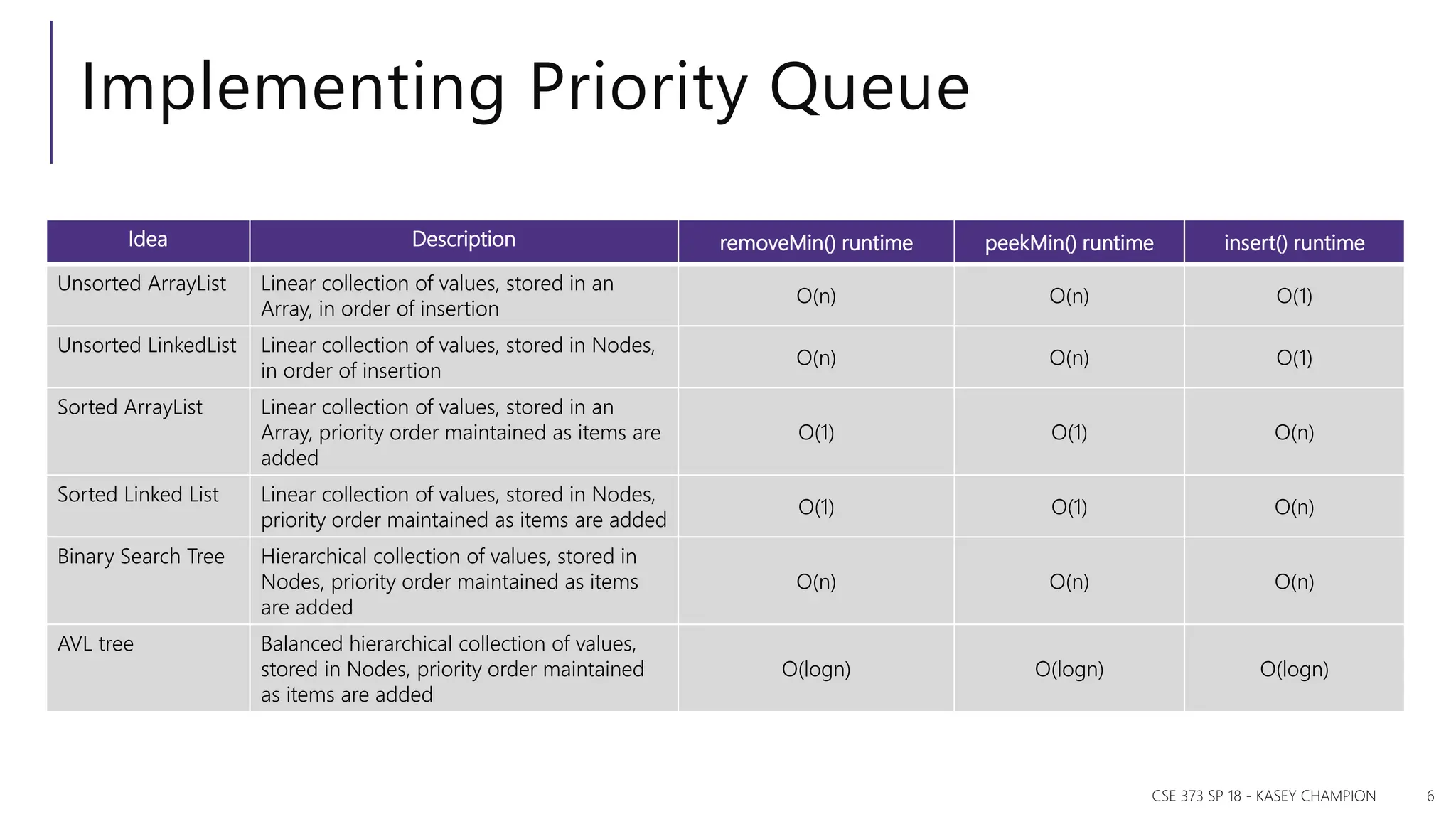
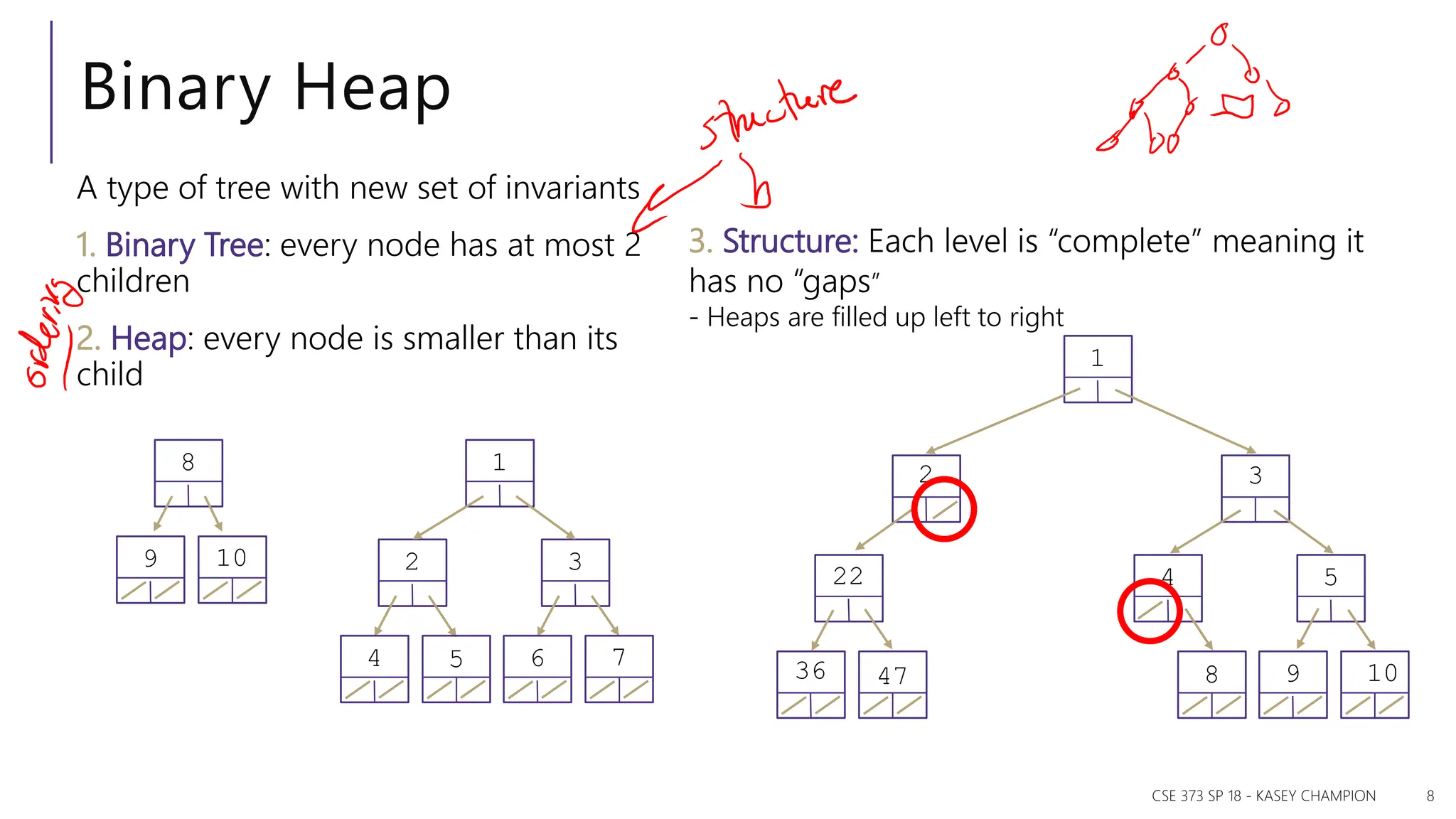
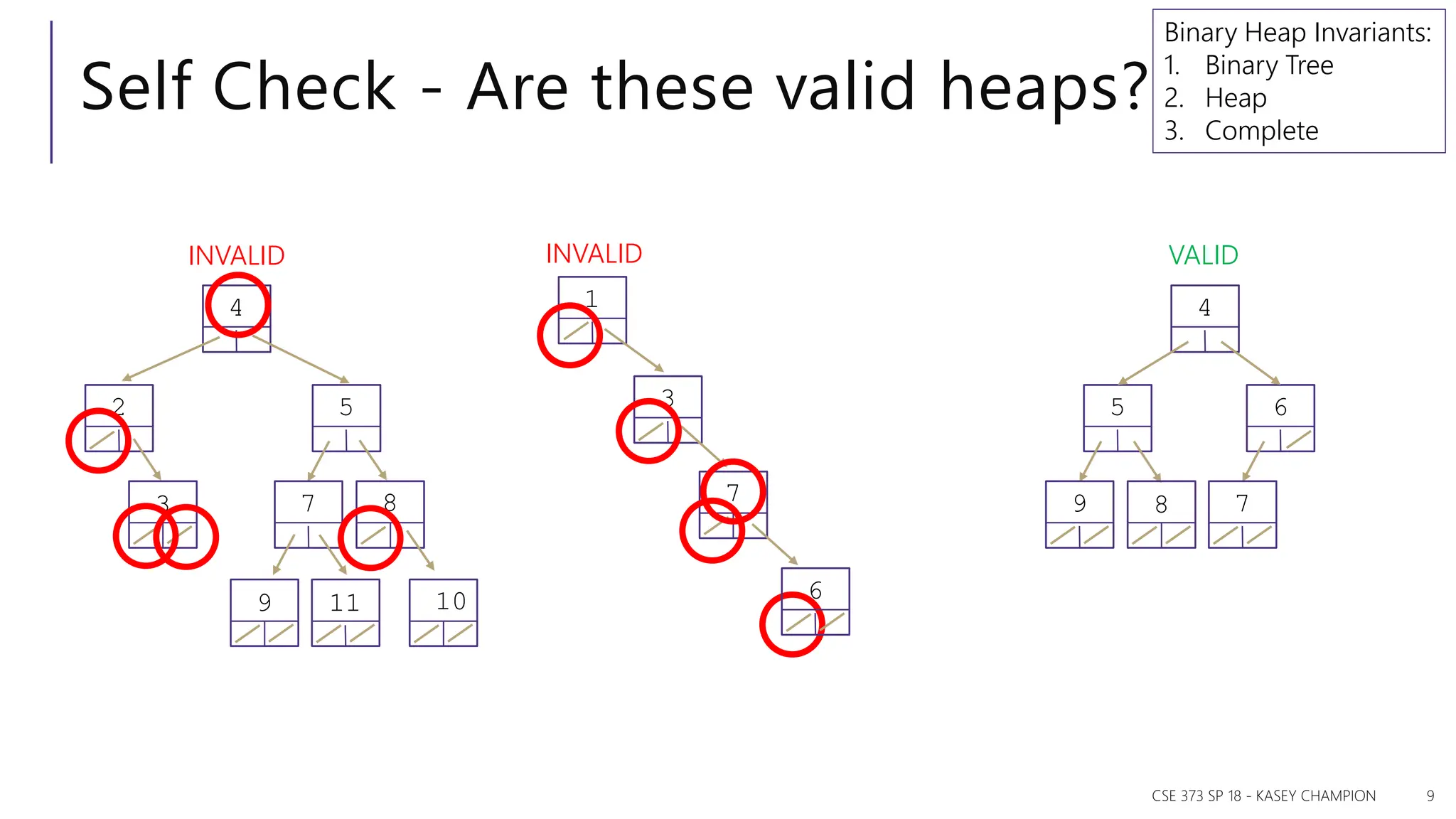
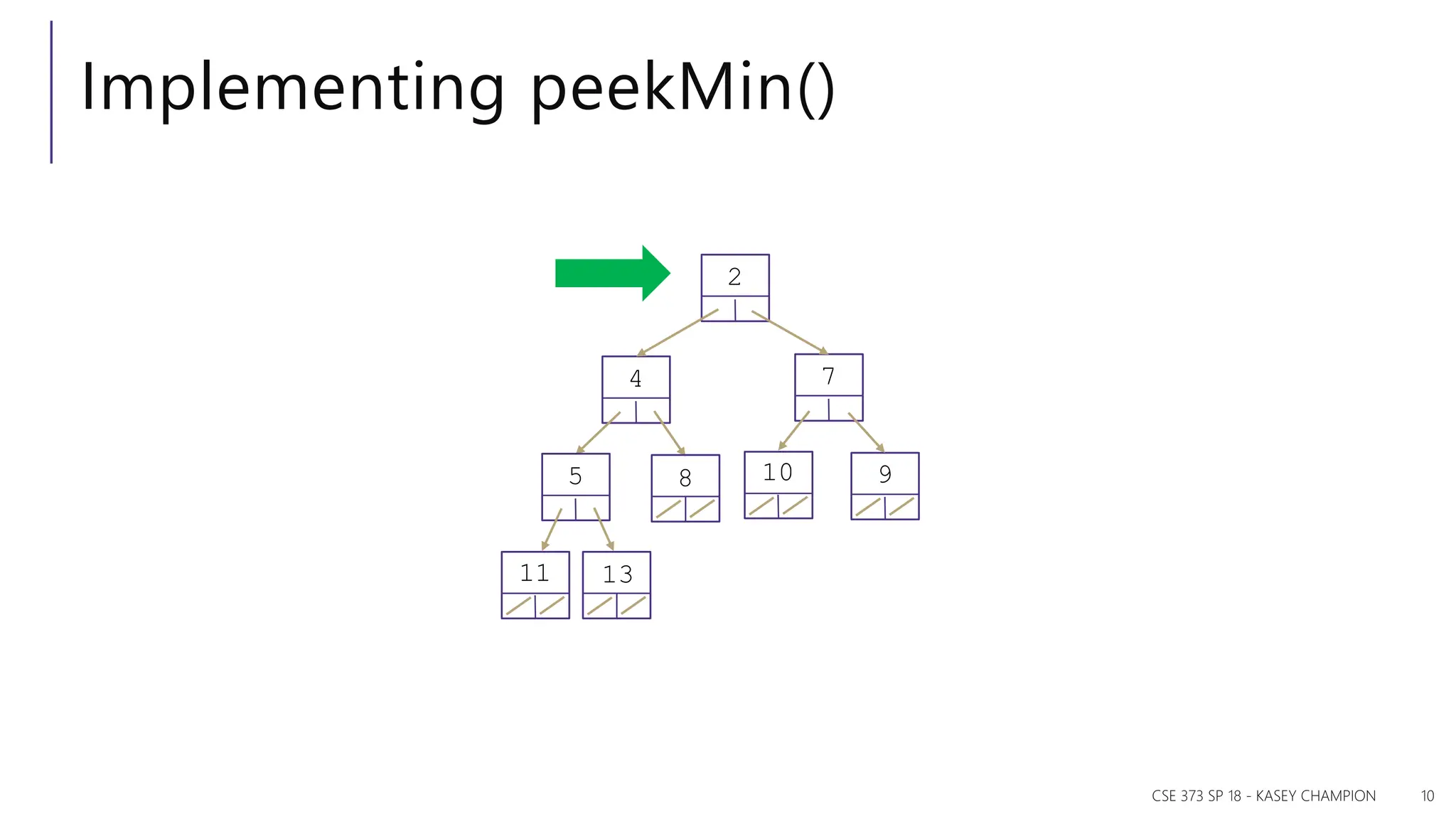
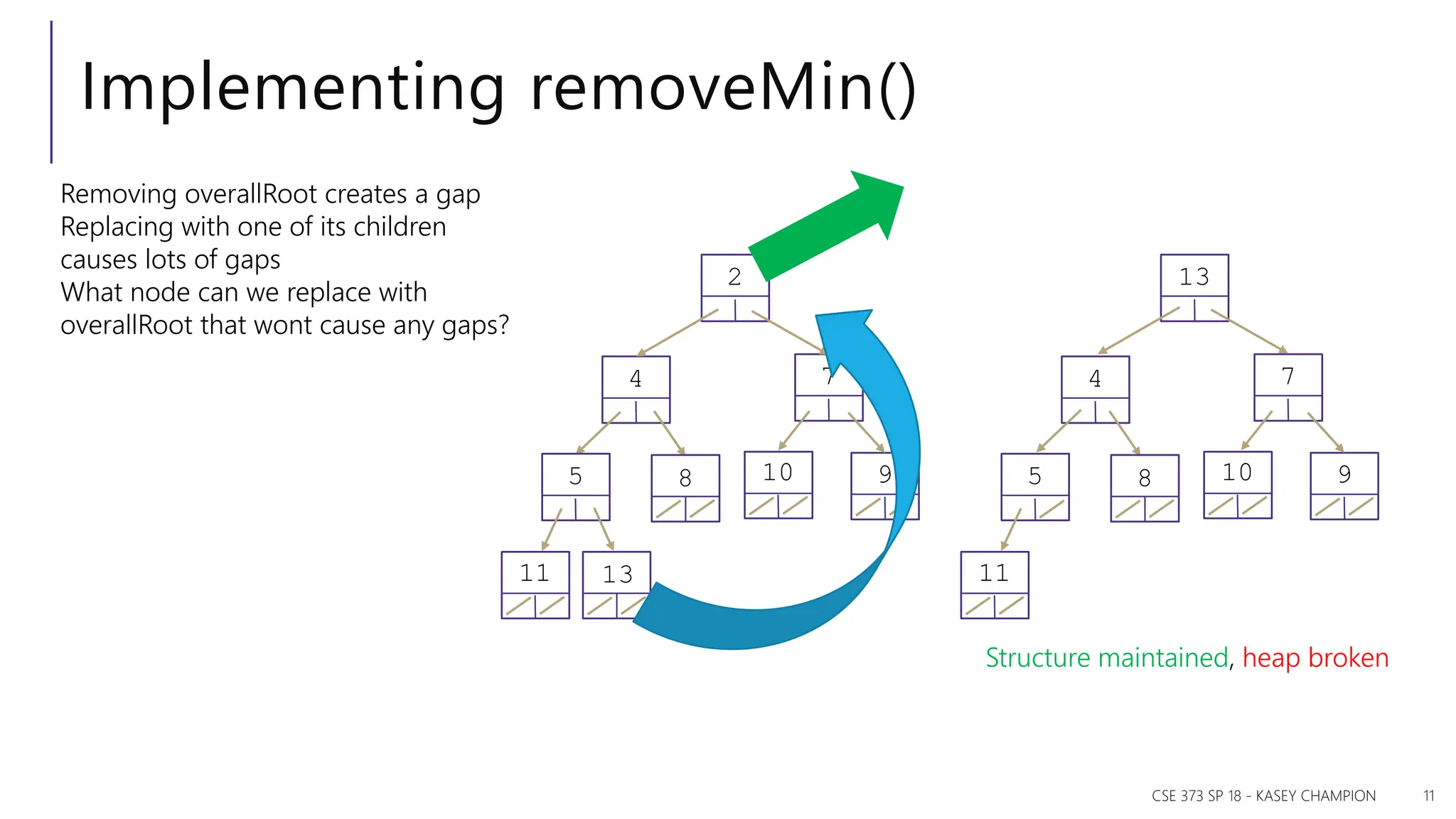
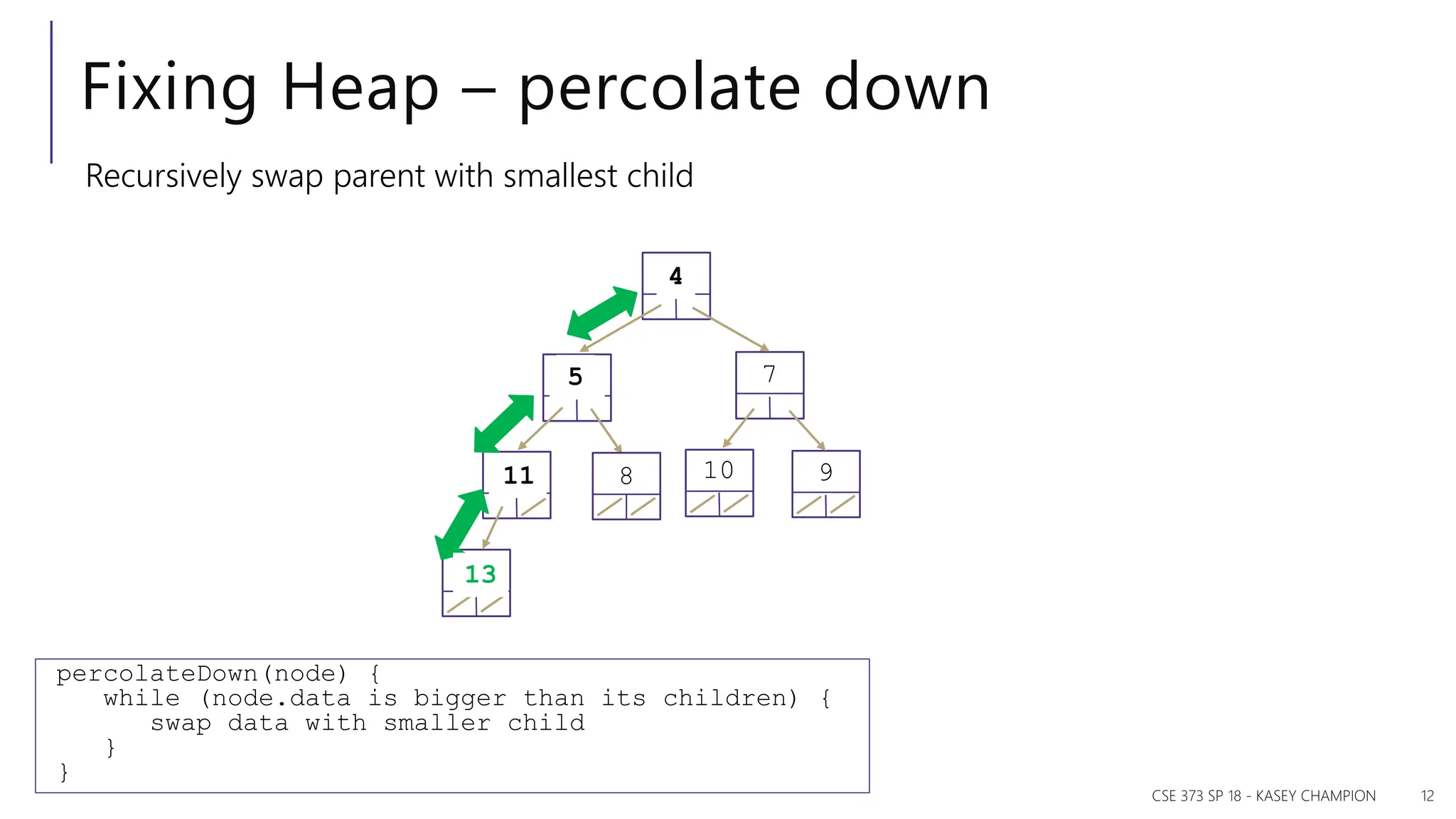
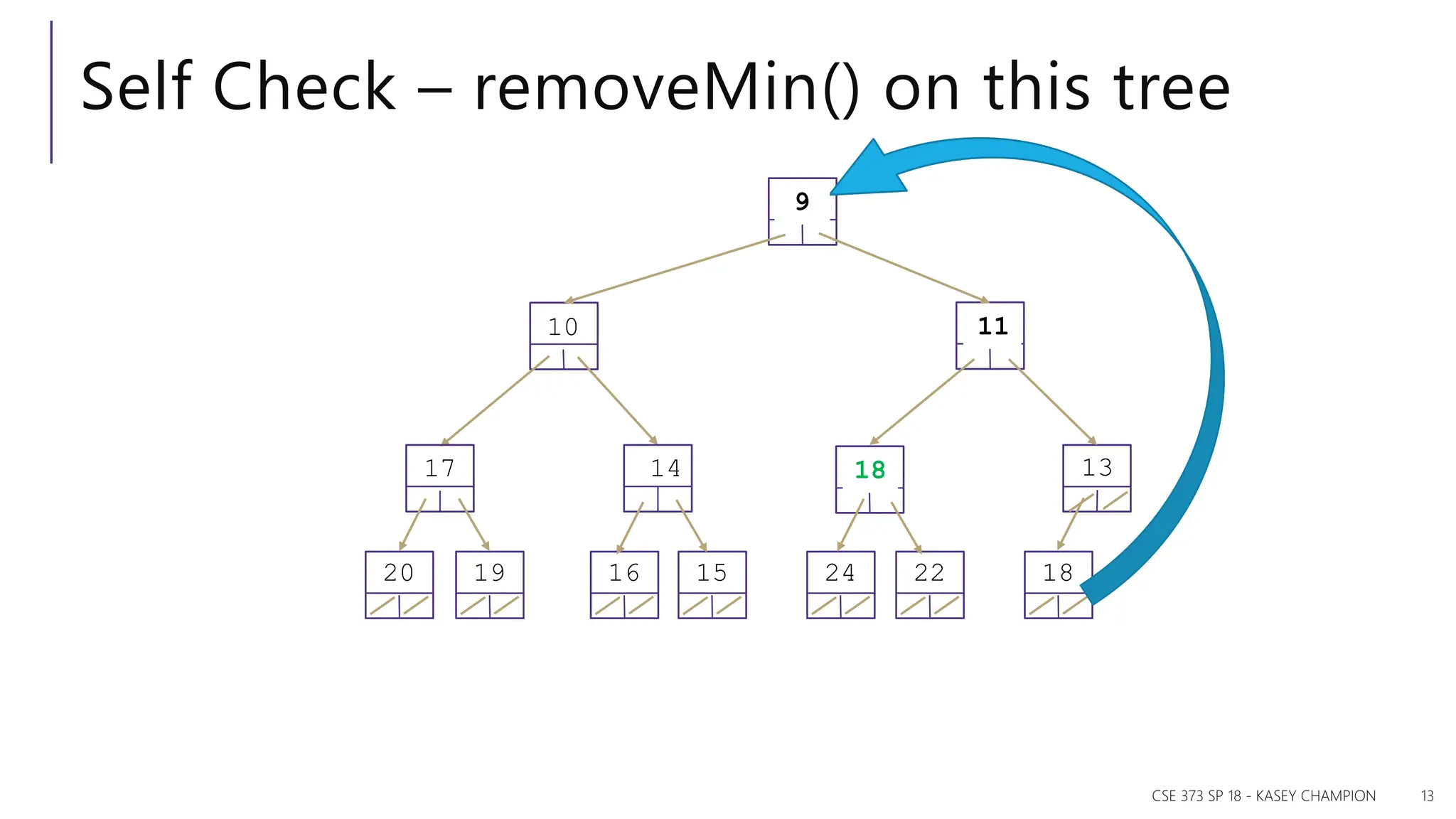
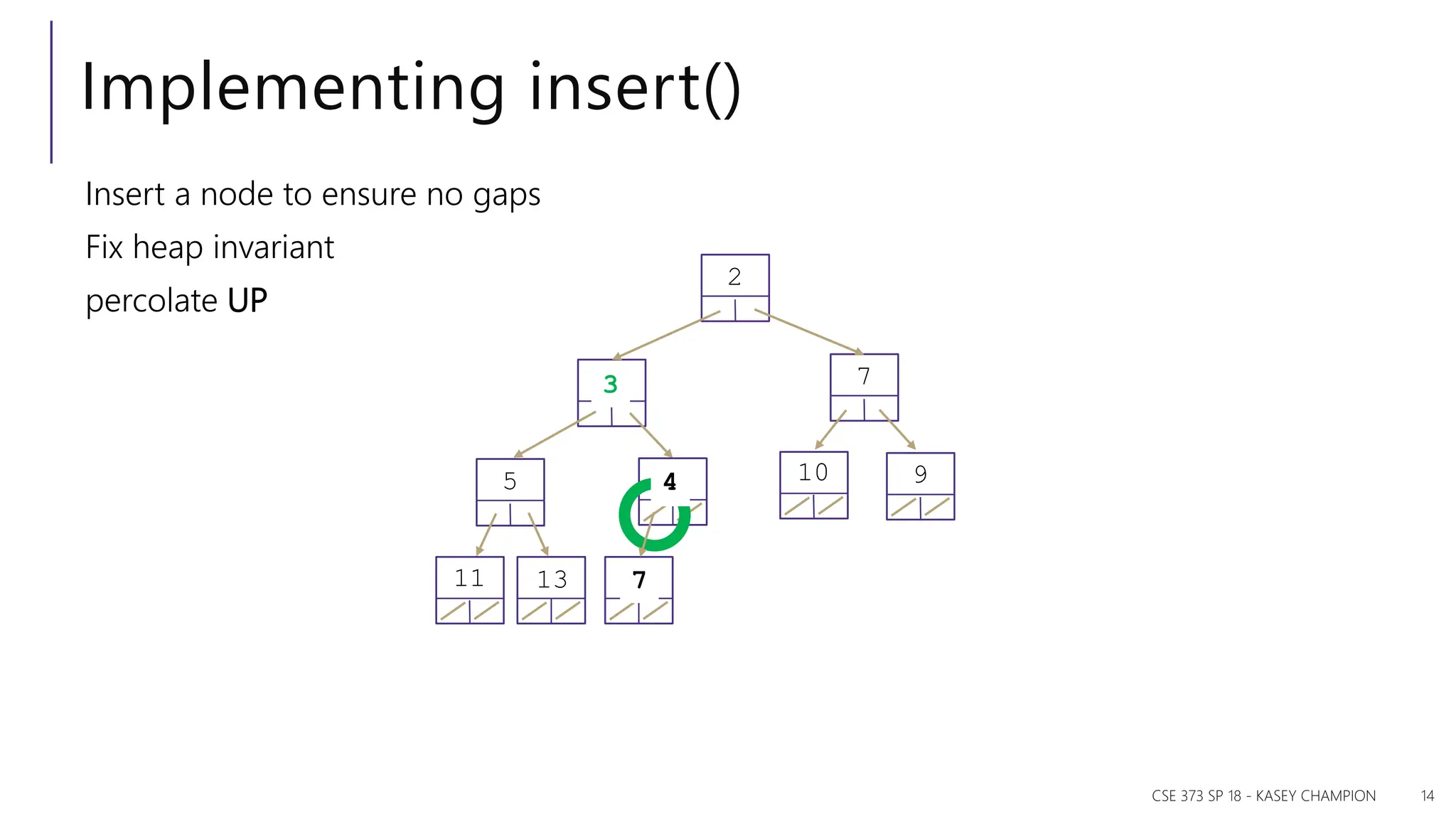
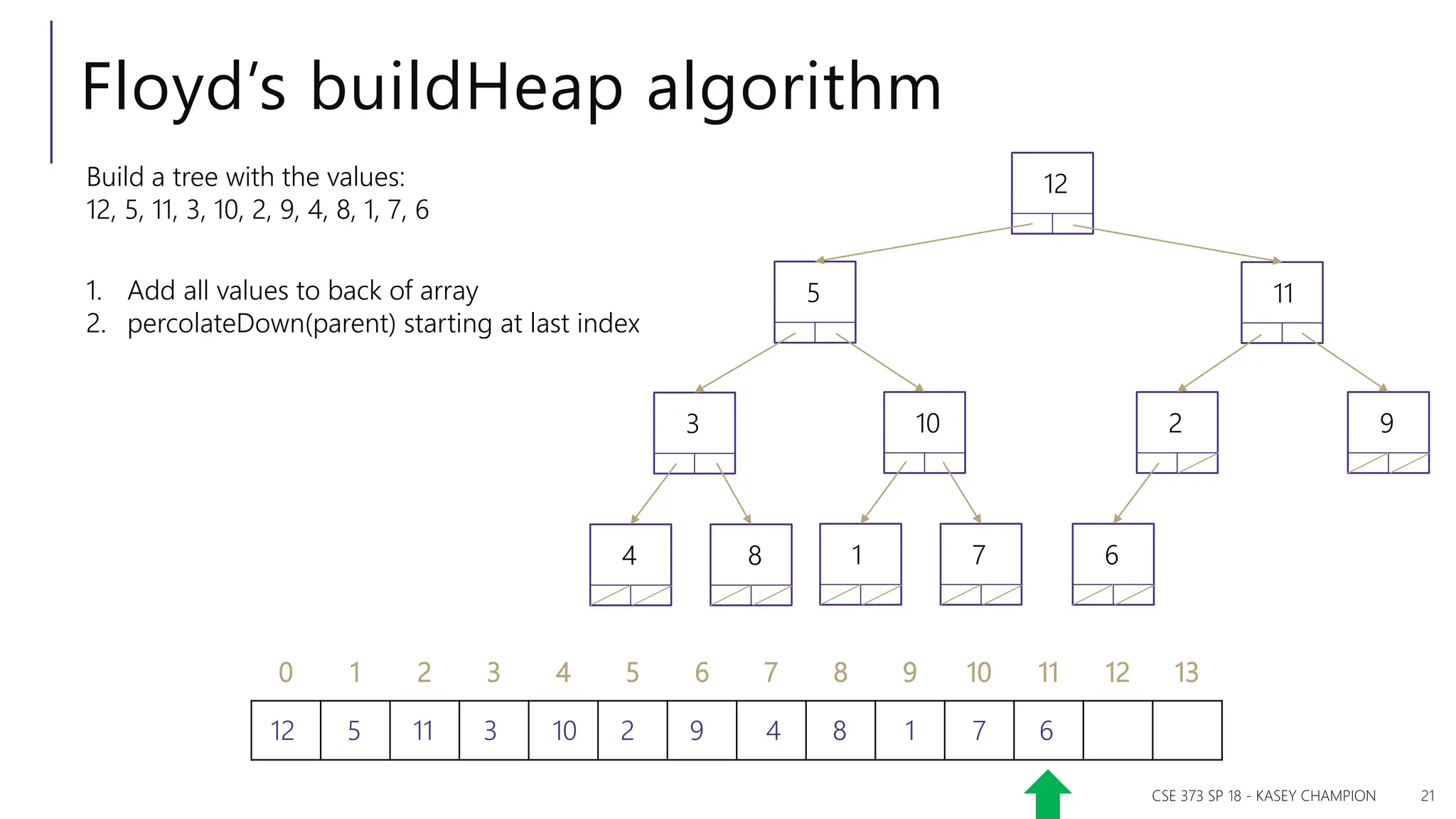
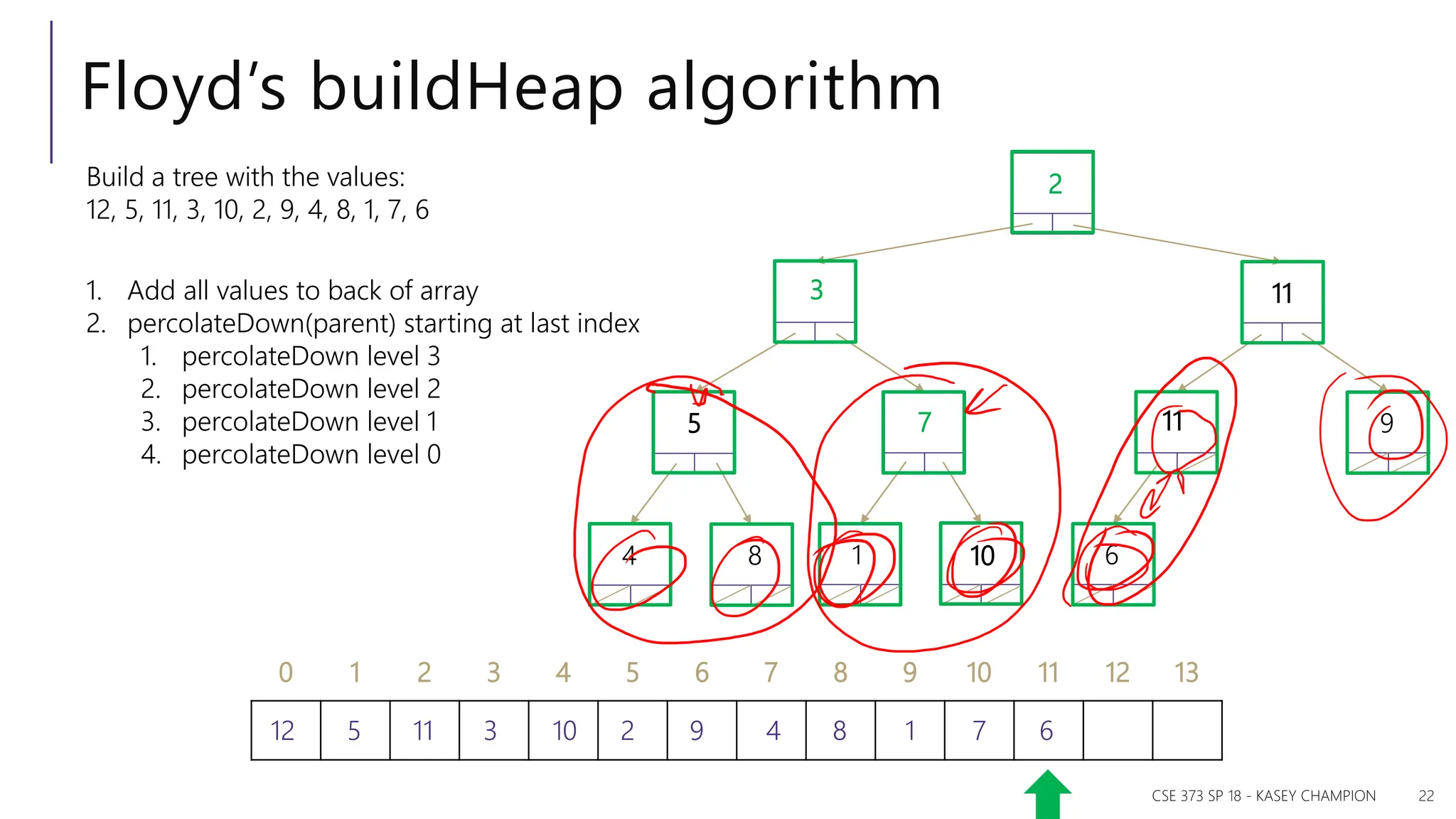
The document discusses priority queues and various data structures used to implement them, including arrays, binary trees, and hash tables. It explains the concept of priority queues, their operations, and different implementations, particularly focusing on binary heaps and their properties. Additionally, it covers the methods for building heaps and using heaps for sorting data efficiently.




![ADT: Priority Queue A Priority Queue models a collection that is not First-In-First-Out (FIFO), but instead most- important-in-first-out. Example: Hospital emergency room. The patient who is most in danger is treated first. Items in a priority queue are comparable, and the comparison determines priority. Often this is done by inserting items as a pair: (item, priority). Operations: insert(item, [priority]) – adds an item to the queue with a given priority deleteMin() – removes and returns the most-important item in the priority queue peekMin() – returns the most-important item in the priority queue without removal (This is a min priority queue. You can also have a max priority queue by swapping min/max.) CSE 373 SU 18 – BEN JONES 5](https://image.slidesharecdn.com/lecture-10-241204123607-60e248a9/75/Introduction-to-the-logic-programing-prolog-5-2048.jpg)








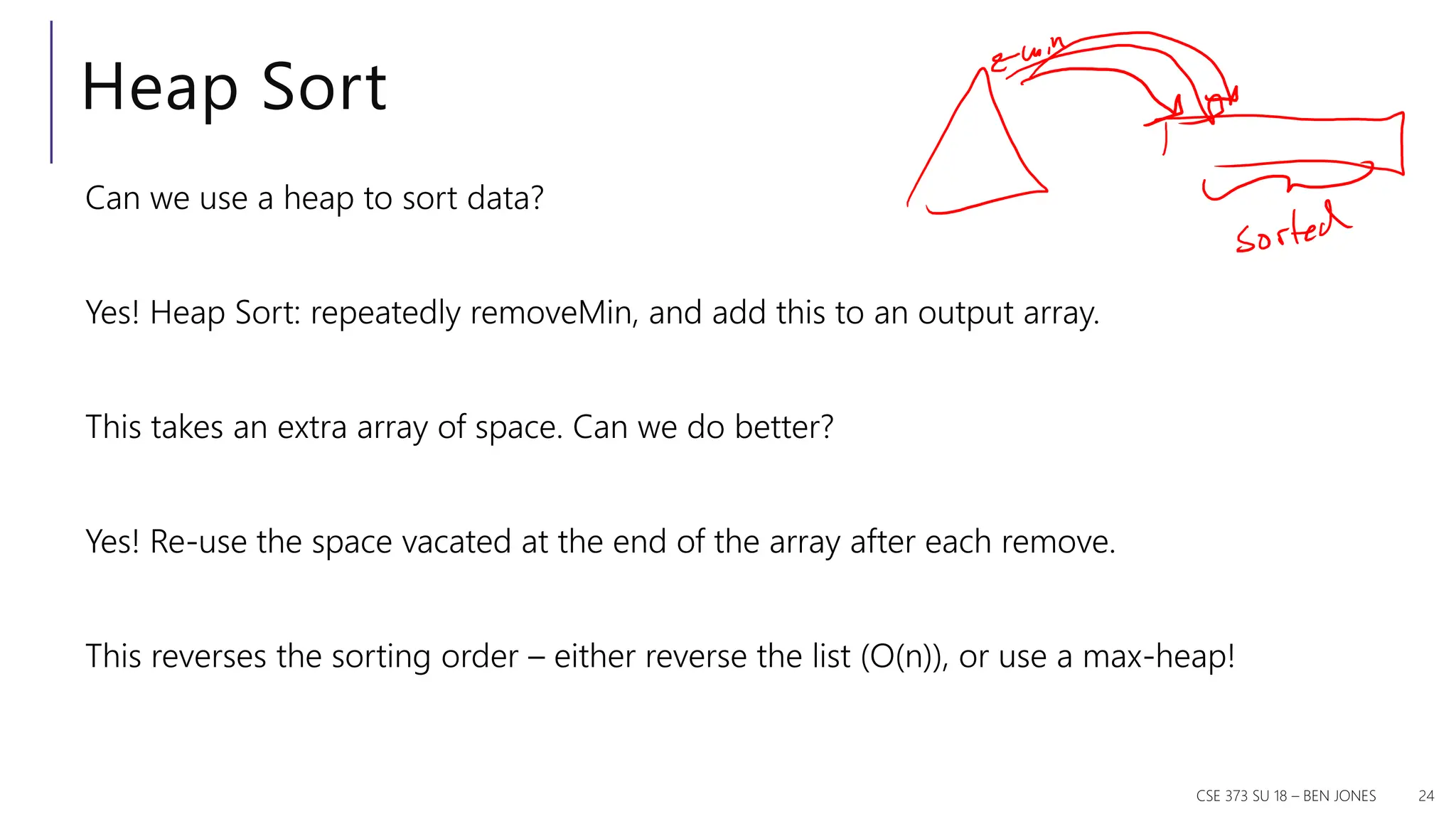
![In Place Heap Sort CSE 373 SP 18 - KASEY CHAMPION 25 public void inPlaceHeapSort(collection) { E[] heap = buildHeap(collection) for (n) output[n – i - 1] = removeMin(heap) } Worst case runtime? Best case runtime? Average runtime? O(nlogn) O(nlogn) O(nlogn) 0 1 2 3 4 5 6 7 8 9 15 17 16 18 20 22 14 4 2 1 Heap Sorted Items Current Item Complication: final array is reversed! - Run reverse afterwards (O(n)) - Use a max heap - Reverse compare function to emulate max heap](https://image.slidesharecdn.com/lecture-10-241204123607-60e248a9/75/Introduction-to-the-logic-programing-prolog-25-2048.jpg)
