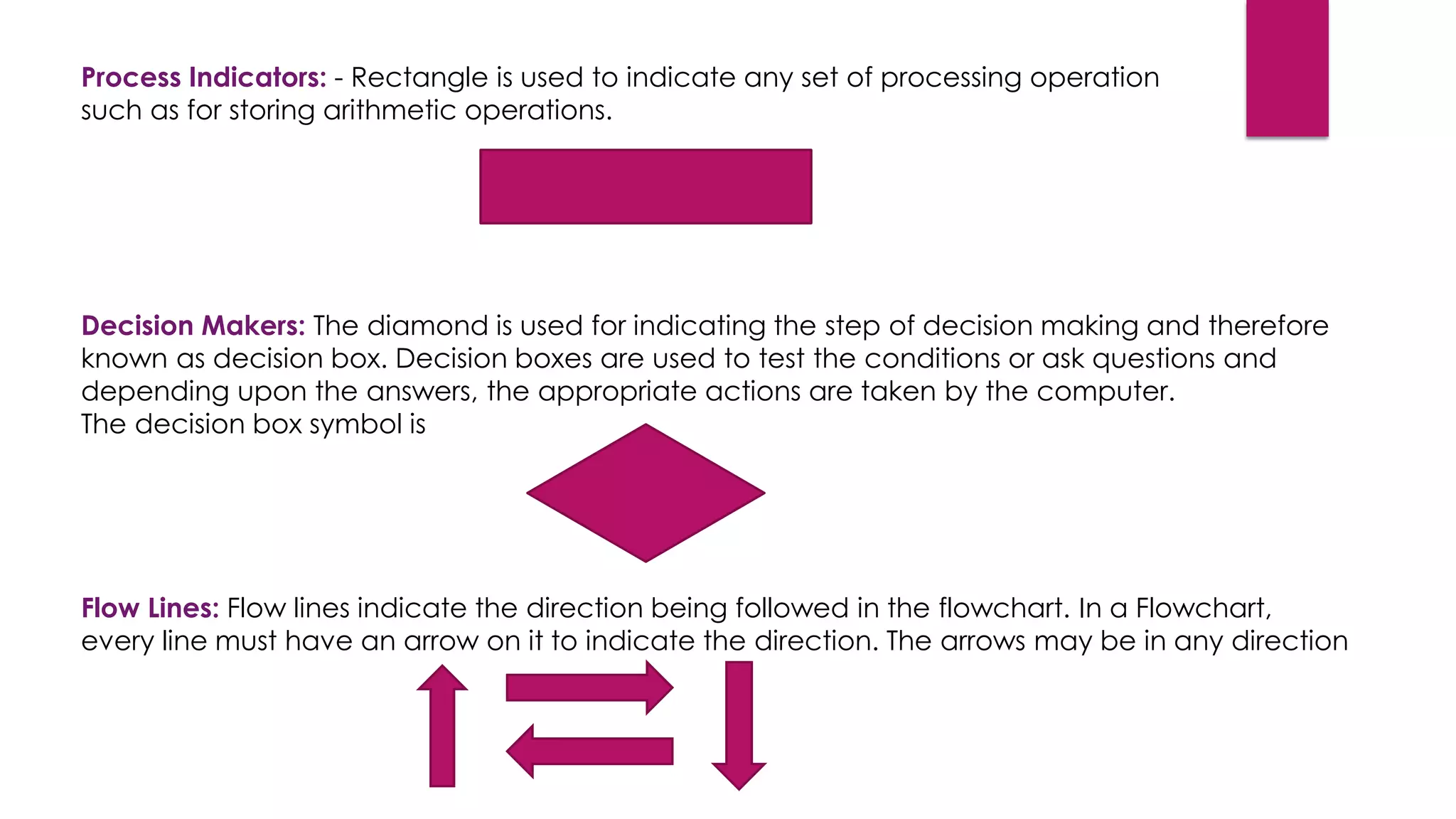
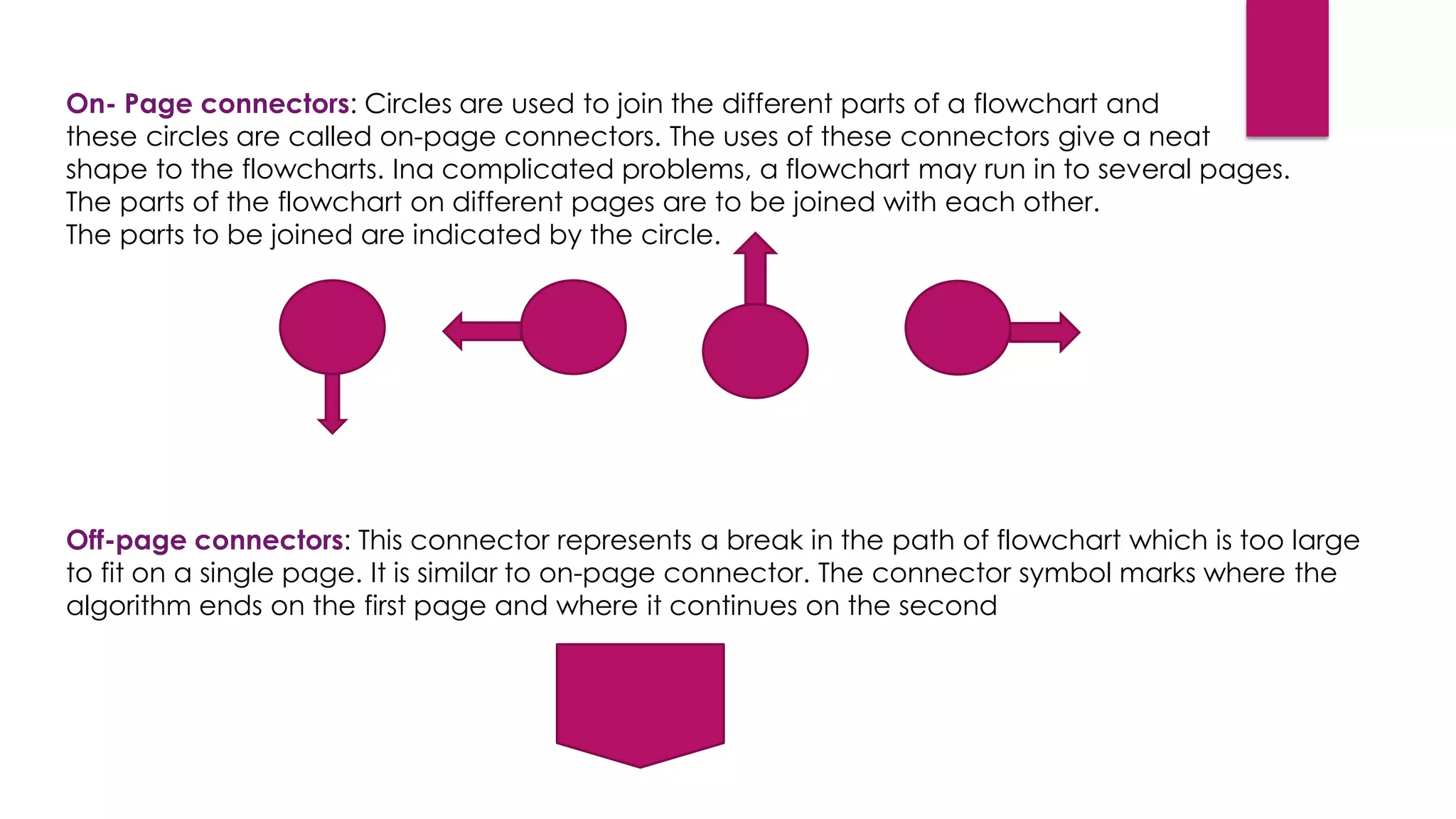
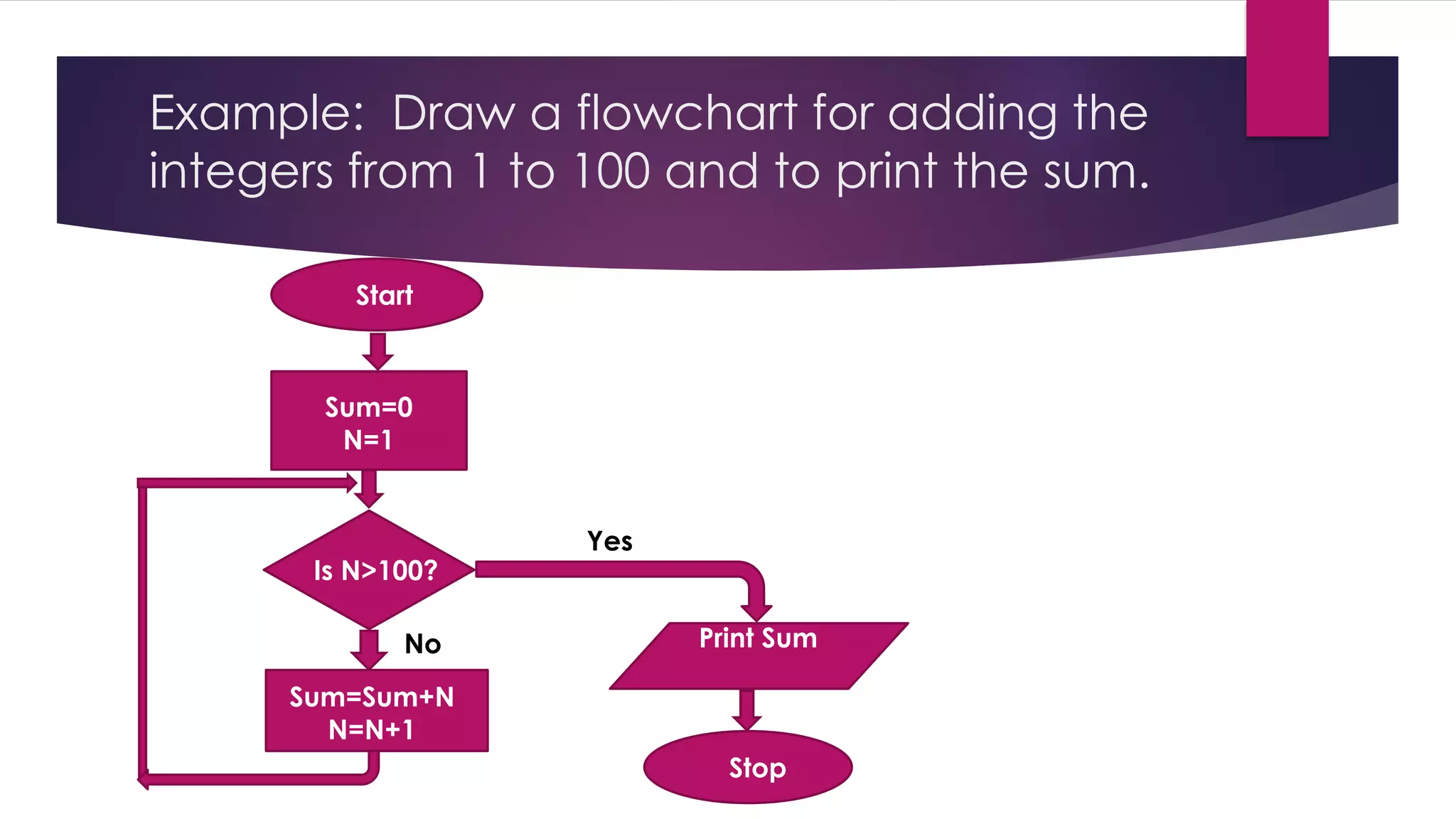
The document discusses algorithms and flowcharts for solving problems. It defines an algorithm as a set of sequential steps to solve a problem and notes that there are various techniques for specifying algorithms, including formally, informally, mathematically, or through graphical flowcharts. The document provides examples of algorithms to solve common problems and explains the properties and steps involved in algorithm development. It also describes flowcharts as a visual representation of an algorithm using standard symbols like ovals, rectangles, and diamonds to indicate starts/stops, processes, and decisions.