Hybrid lwt svd watermarking optimized using metaheuristic algorithms along with encryption for medical image security

Hybrid lwt svd watermarking optimized using metaheuristic algorithms along with encryption for medical image security

• 1.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 DOI : 10.5121/sipij.2015.6106 75 HYBRID LWT- SVD WATERMARKING OPTIMIZED USING METAHEURISTIC ALGORITHMS ALONG WITH ENCRYPTION FOR MEDICAL IMAGE SECURITY Mr. Venugopal Reddy .CH1 , Dr. Siddaiah.P2 1 Professor, Department of ECE, Priyadarshini College of Engineering and Technology, Nellore, A.P, INDIA 2 Professor and Dean, Department of ECE, Principal, University College of Engineering and Technology, Acharya Nagarjuna University, Guntur, A.P, INDIA ABSTRACT Medical image security provides challenges and opportunities, watermarking and encryption of medical images provides the necessary control over the flow of medical information. In this paper a dual security approach is employed .A medical image is considered as watermark and is watermarked inside a natural image. This approach is to wean way the potential attacker by disguising the medical image as a natural image. To further enhance the security the watermarked image is encrypted using encryption algorithms. In this paper a multi–objective optimization approach optimized using different metaheuristic approaches like Genetic Algorithm (GA), Differential Evolution ( DE) and Bacterial Foraging Optimization (BFOA) is proposed. Such optimization helps in preserving the structural integrity of the medical images, which is of utmost importance. The water marking is proposed to be implemented using both Lifted Wavelet Transforms (LWT) and Singular Value Decomposition (SVD) technique. The encryption is done using RSA and AES encryption algorithms. A Graphical User Interface (GUI) which enables the user to have ease of operation in loading the image, watermark it, encrypt it and also retrieve the original image whenever necessary is also designed and presented in this paper. KEYWORDS LWT, SVD, BFOA, GA, DE, AES, RSA, GUI. 1. INTRODUCTION The ever-growing numbers of medical digital images and the need to share them among specialists and hospitals for better and more accurate diagnosis require that patients' privacy be protected. As a result of this, there is a need for medical image watermarking (MIW). However, MIW needs to be performed with special care for two reasons. Firstly, the watermarking procedure cannot compromise the quality of the image. Secondly, confidential patient information embedded within the image should be flawlessly retrievable without risk of error. Due to the advancement of technology, internet has become an indispensable part of life for many people. Information can be sent very quickly by the
• 2.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 76 internet. However, it causes the problems of the information securities and multimedia copyright protections. Therefore, network securities protections have become more important topics. Watermarking is an important technology for these topics. Medical images play a significant role in diagnosis of many diseases. Medical image protection and authentication are becoming increasingly important in an e-Health environment where images are readily distributed over electronic networks. Research has shown that medical image watermarking is a relevant process for enhancing data security, content verification and image fidelity. At the same time, it is necessary to preserve as much original information in the image data as possible, to avoid causing performance loss for human viewers. Security of medical information, derived from strict ethics and legislatives rules, gives rights to the patient and duties to the health professionals. Medical tradition is very strict with the quality of biomedical images, in that it is often not allowed to alter in any way the bit field representing the image (non-destructive). Thus the watermarking method must be reversible, in that the original pixel values must be exactly recovered. This limits significantly the capacity and the number of possible methods. It also constrains to have dedicated routines to automatically suppress and introduce the mark in order to prevent the transmission of unprotected documents. A watermarking method is usually designed depending on an application framework striking a compromise between different requirements: capacity (amount of information that can be embedded), robustness (a fragile watermark will not survive any image processing), privacy (secret knowledge for watermark content access - usually a secret key) and imperceptibility. We can say that the higher the strength of the watermark signal, the more it is robust and/or of higher capacity albeit perceptibility is compromised. Consequently, if it is envisioned to process the image with an information loss, a robust watermark is desirable to authenticate the image origins, while at the same time the watermark should not interfere with the image content interpretation. However each property has its own limitation and conflict with each other. It will be a challenging task to design a good algorithm by coupling both the concept of reversibility and robustness with proper optimization. It is well known that the integrity and confidentiality of medical folders are a critical issue for ethical as well for legal reasons. Classical encryption technology is an important tool that can be used to protect data transmitted over computer networks but it does not solve all digital data protection problems. At the receiver’s side, decrypted content may be subjected to unauthorized use or manipulation[1]. In transform domain watermarking can be performed using DCT (Discrete Cosine Transform) [2] or IWT (Integer Wavelet Transform) [3].Different approaches have been proposed in order to improve the security of medical image transmission using watermarking, which gives one level security. A Tamper Assessment Factor (TAF) of the watermarked image with the physician’s signature and patient diagnosis information embedded into wavelet transform coefficients of the medical images is proposed in [4]. Similarly a novel blind watermarking method with secret key is proposed by embedding Electrocardiograph (ECG) signals in medical images combined with the EZW-based wavelet coder [5]. A blind watermarking scheme using the non-tensor product wavelet filter banks are used for copyright protection is presented in [6]. An efficient watermarking method based on the significant difference of wavelet coefficient quantization is proposed in [7]. A multiple, fragile image authentication scheme is proposed for DICOM images using discrete wavelet transform in [8] in this work multiple watermarks are embedded into wavelet domains, the multiple watermarks serve as reference watermarks. A novel watermarking algorithm based on singular value decomposition (SVD) is proposed in [9]. Both of the D and U components of SVD are explored for embedding the watermark in [10]. To enforce integrity and authenticity several works have been implemented that provides two level security for transmission of medical images. In joint encryption/watermarking [11] method, watermarking and encryption step processes are merged. Joint watermarking/encryption system is slower than simply encrypting the image but it provides reliability control functionalities.
• 3.
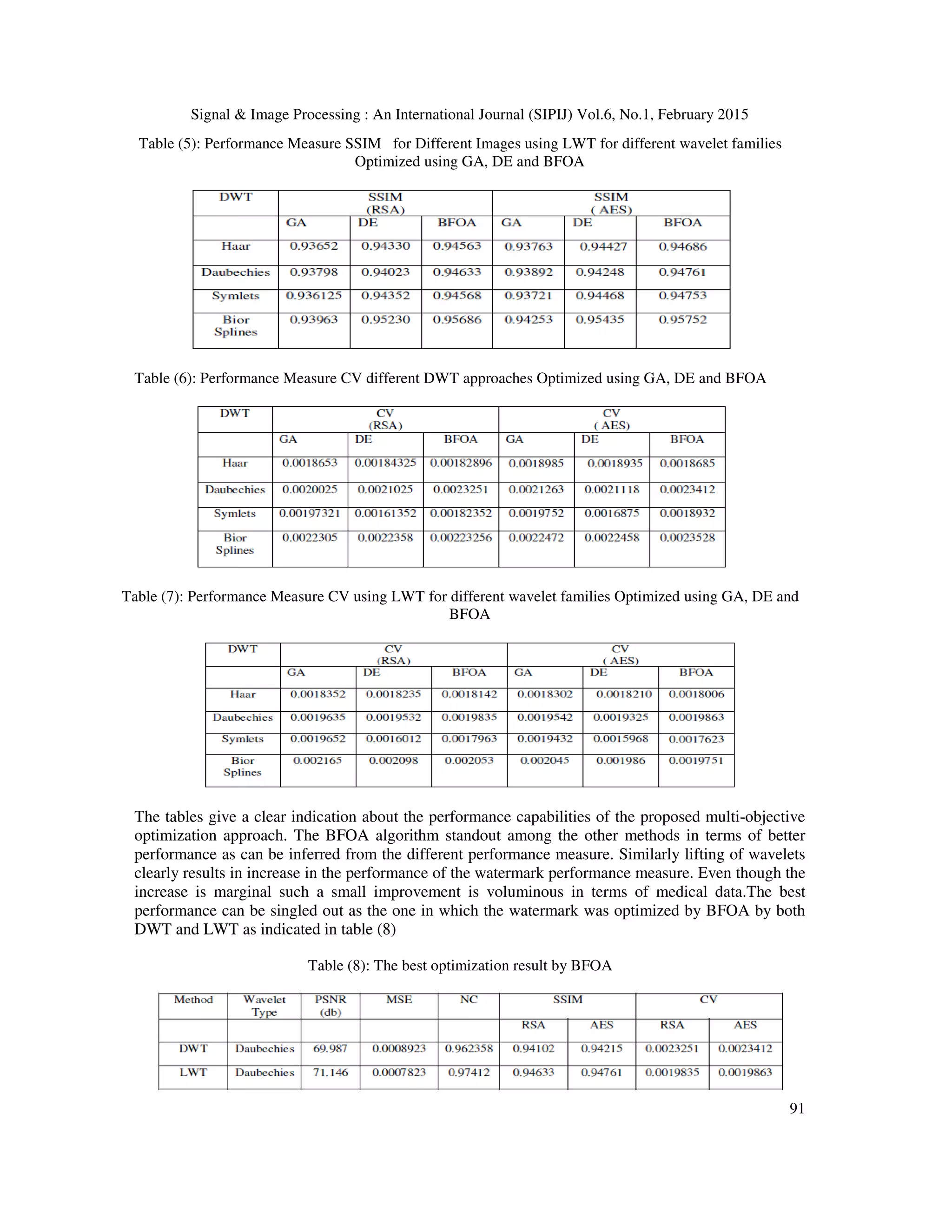
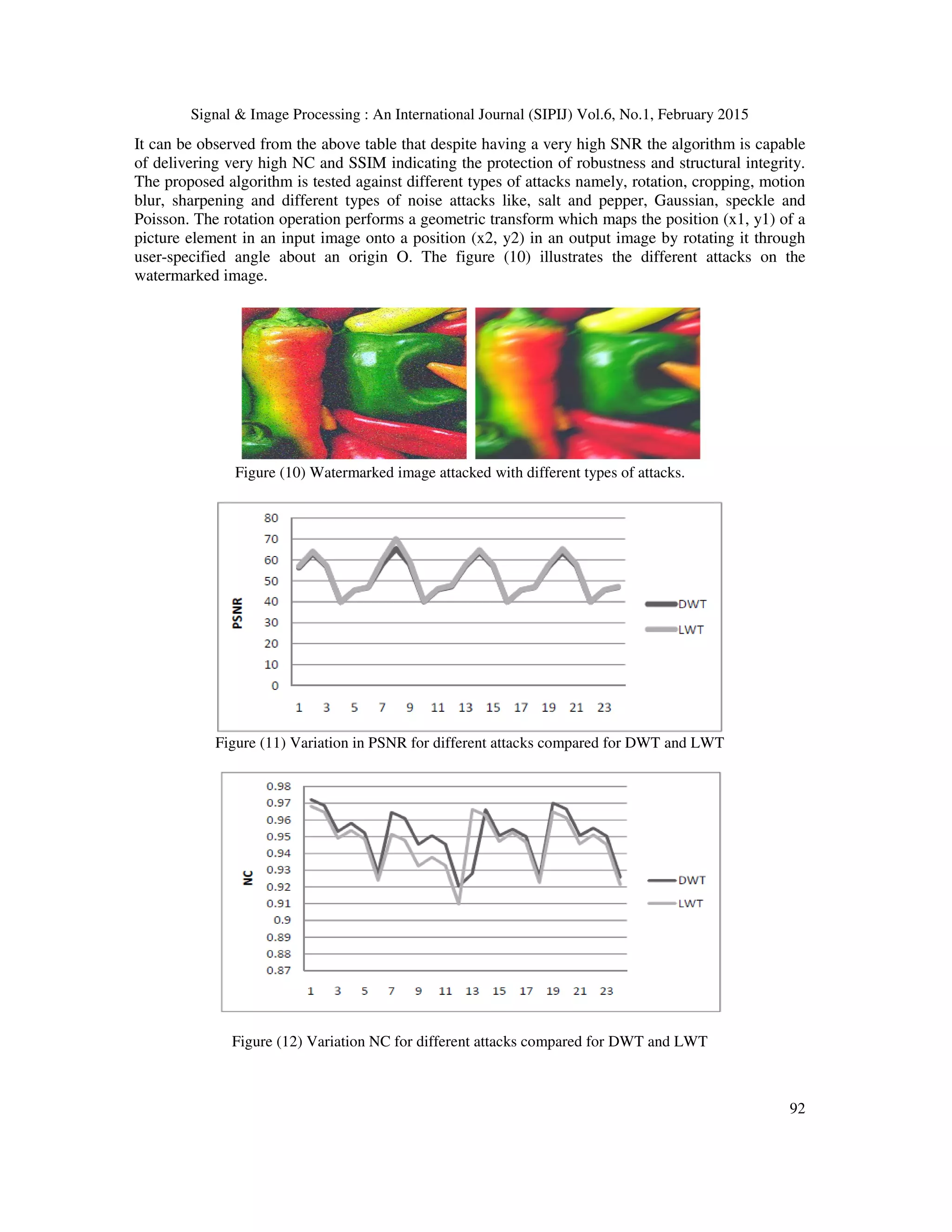
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 77 Watermarking is done by Quantization Index modulation. (QIM) method and AES (Advanced Encryption standard) and RC4 (Rivest cipher 4) algorithms do encryption. A Digital envelope (DE) method to assure data integrity and security that outlines the systematic evaluation, development, and deployment of the DE method for PACS environment is proposed in [12]. A new cryptographic means to improve the trustworthiness of medical images is implemented [13]. A comparative study of AES and RC4 algorithm is done in [14] in the case of AES algorithm, as the key size increases the encryption and decryption time increases, whereas for RC4 it remains almost constant and it is less than AES. Similarly, several methodologies have been proposed for medical image security [15].These methods can detect, whether the medical images are tampered or modified but cannot protect the images from tampering. In this work, the digital watermarking is done by using special symmetric matrices to construct the new nontensor product wavelet filter banks [16] which can capture singularities in all directions. Here, natural image is considered as original image and medical image is taken as watermark to avoid the attacker’s attention toward the medical information. The optimization of watermark through evolutionary approaches has also been researched extensively. A new method for adaptive watermark strength optimization in Discrete Cosine Transform (DCT) domain in which watermark strength is intelligently selected through Genetic Algorithm (GA) is proposed in [17].A novel hybrid PSO, namely (HPSO) to improve the performance of fragile watermarking based DCT which results in enhancing both the quality of the watermarked image and the extracted watermark is implemented in [18]. A novel optimal watermarking scheme based on singular value decomposition (SVD) using differential evolution algorithm (DE) is explained in [19]. Differential evolution (DE) algorithm to balance the tradeoff between robustness and imperceptibility by exploring multiple scaling factors in image watermarking is proposed in [20]. A new improved watermarking scheme is proposed using lifting wavelet transform (LWT) [21] and SVD for medical images. The medical images of patients are watermarked with the image of that particular patient which is extracted at the doctor’s end to identification. Lifting wavelets have distinctive advantage that is explored and is missed in traditional wavelet transform. With lifting wavelets the inverse transformation is undoing the operations of forward transform which reduce the artifacts during transformation. An intelligent reversible watermarking scheme for medical images using Differential Evolution is proposed in [22] and an intelligent reversible watermarking scheme using GA and PSO is proposed in [23]. In this work we have implemented a dual security approach for maintaining the data integrity of the medical images. Watermarking and encryption of watermarked image is proposed. In order to preempt any attack from attacker the medical image is considered as water mark and is embedded in to a natural image. A multi objective optimization approach is proposed to maintain the fidelity of the watermark (medical image) as it contains valuable diagnostic information. This multi -objective approach ensures that there is an optimum tradeoff between robustness, imperceptibility and structural integrity of the watermark. Maintaining the structural integrity of the watermark is necessitated by the fact that most of the diagnostic approaches in medical image consider the morphological factors of the image to divulge precious information about the prognosis of a particular clinical condition. Different performance parameters like Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE), Normalized Coefficient (NC) and Structural Similarity Index (SSIM) is used to frame an objective function. This objective function is optimized using Bacterial Foraging Optimization (BFOA) to choose a particular wavelet in selected wavelet family and scaling factor of the Singular Value Decomposition (SVD). A lifting scheme is further employed to enhance the performance of the selected wavelet family. The medical image security is further enhanced by encrypting the watermarked image using Ron Rivest, Adi Shamir, and Leonard Adleman (RSA) Algorithm and Advanced Encryption Standard (AES) algorithms. Correlation Value (CV) between the watermarked image and the encrypted image is used to measure the efficacy of watermark. The watermarked image is tested for different types of attacks like sharpening, smoothening, rotation , cropping and different
• 4.
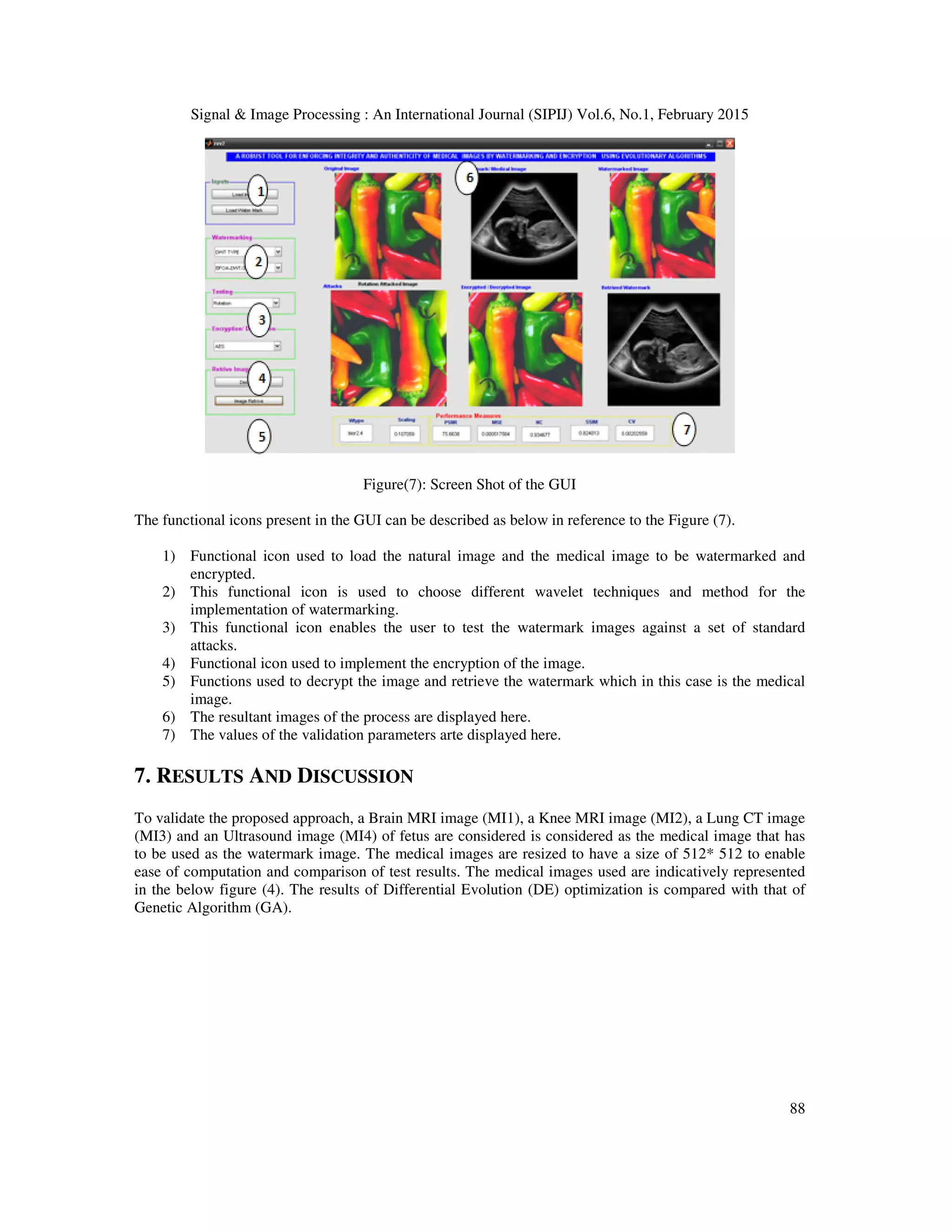
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 78 types of noises which include speckle noise, salt and pepper noise, Gaussian noise and Poisson noise. To enable ease of use and seamless integration of the user a Graphical User Interface (GUI) is designed to automate the process of embedding, encrypting, decrypting and extracting. The tool helps user in analyzing and testing different scenarios and choose the best possible one for a watermarking a given medical image. The performance measures are compared and contrasted with that of the performance measures as achieved by Genetic Algorithm (GA) and Differential Evolution (DE) 2. METHODOLOGIES This work aims at exploiting the features of Lifting Wavelet Transforms (LWT) along with Discrete Wavelet Transforms (DWT) and Singular Value Decomposition (SVD) to provide a robust and imperceptible watermark. Similarly RSA and AES algorithms are used for encrypting the watermarked images to provide an extra layer of security. This section dwells on these concepts and methods used in this research work. 2.1 Discrete Wavelet Transforms The first recorded mention of what we now call a “wavelet” seems to be in 1909, in a thesis by Alfred Haar. The concept of wavelets in its present theoretical form was first proposed by Jean Morlet and the team at the Marseille Theoretical Physics Center working under Alex Grossmann in France. The methods of wavelet analysis have been developed mainly by Y. Meyer and his colleagues, who have ensured the methods’ dissemination. The main algorithm dates back to the work of Stephane Mallat in 1988 [22].In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information (location in time).Thus discrete wavelet transform (DWT) is a linear transformation that operates on a data vector whose length is an integer power of two, transforming it into a numerically different vector of the same length. It is a tool that separates data into different frequency components, and then studies each component with resolution matched to its scale. DWT is computed with a cascade of filters followed by a factor 2 subsampling. Figure (1): Discrete Wavelet Transform tree for two-dimensional image H and L denote high and low-pass filters respectively followed by subsampling. Outputs of these filters are given by equations (1) and (2) [ ] [ ] [ ]1 2j j n a p l n p a n +∞ + =−∞ = −∑ (1)
• 5.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 79 [ ] [ ] [ ]1 2j j n d p h n p a n +∞ + =−∞ = −∑ (2) Elements aj are used for next step (scale) of the transform and elements dj, called wavelet coefficients, determine output of the transform. l[n] and h[n] are coefficients of low and high-pas filters respectively One can assume that on scale j+1 there is only half from number of a and d elements on scale j. This causes that DWT can be done until only two aj elements remain in the analyzed signal. These elements are called scaling function coefficients. The types of wavelets used in this work are described here. Haar wavelet is discontinuous, and resembles a step function. It represents the same wavelet as Daubechies ‘db1’ Ingrid Daubechies, invented what are called compactly supported orthonormal wavelets —The names of the Daubechies family wavelets are written dbN, where N is the order, and db the “surname” of the wavelet. The db1 wavelet, as mentioned above, is the same as Haar wavelet. Biorthogonal family of wavelets exhibits the property of linear phase, which is needed for signal and image reconstruction. By using two wavelets, one for decomposition (on the left side) and the other for reconstruction (on the right side) instead of the same single one, interesting properties are derived. The Symlets are nearly symmetrical wavelets proposed by Daubechies as modifications to the db family. The properties of the two wavelet families are similar. The Wavelets function psi of different wavelet families used in this work are represented in the below figure (3). Figure (2): psi of different wavelet families used in this research work The main feature of DWT that makes it attractive for image processing applications is multiscale representation of function. By using the wavelets, given function can be analyzed at various levels of resolution. The DWT is also invertible and can be orthogonal.DWT involves decomposition of image into frequency channel of constant bandwidth. This causes the similarity of available decomposition at every level. DWT is implemented as multistage transformation. Level wise decomposition is done in multistage transformation. At level 1: Image is decomposed into four sub bands: LL, LH, HL, and HH where LL denotes the coarse level coefficient which is the low frequency part of the image. LH, HL, and HH denote the finest scale wavelet coefficient. The LL sub band can be decomposed further to obtain higher level of decomposition. This decomposition can continues until the desired level of decomposition is achieved for the application. The watermark can also be embedded in the remaining three sub bands to maintain the quality of image as the LL sub band is more sensitive to human eye.
• 6.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 80 2.2 Lifting Wavelet Transforms (LWT) Lifting wavelets come under the category of second generation wavelets that have distinctive advantages over traditional first generation wavelets. The lifting wavelets trim down the computing time and memory requirements as they adopt an in position realization of wavelet transform. Unlike traditional wavelets the computations for lifting wavelets are performed in integer domain rather than real domain. More over the inverse process in lifting wavelets is ruination of the processes performed during the forward transformation. Lifting designs perfect reconstruction filter banks by beginning from the basic nature of the wavelet transform. Wavelet transforms build sparse representations by exploiting the correlation inherent in most real world data. A single lifting step can be described by the following three basic operations: Split — the signal into disjoint components. A common way to do this is to extract the even and odd polyphase components explained in Polyphase Representation. This is also known as the lazy wavelet. Predict — the odd polyphase component based on a linear combination of samples of the even polyphase component. The samples of the odd polyphase component are replaced by the difference between the odd polyphase component and the predicted value. The predict operation is also referred to as the dual lifting step. Update — the even polyphase component based on a linear combination of difference samples obtained from the predict step. The update step is also referred to as the primal lifting step. In practice, a normalization is incorporated for both the primal and dual lifting’s. Figure(3) : one lifting step illustration 2.3 Singular Value Decomposition (SVD) Among the methods to write a matrix as a product of matrices, Singular Value Decomposition (SVD) is a very useful method. Singular Value Decomposition (SVD) is said to be a significant topic in linear algebra by many renowned mathematicians. SVD has many practical and theoretical values; Special feature of SVD is that it can be performed on any real (m, n) matrix. Let’s say we have a matrix A with m rows and n columns, with rank r and r ≤ n ≤ m. Then the A can be factorized into three matrices: Since an image can be represented as a matrix of positive scalar values SVD for any image say A of size ݉ ×݉ is a factorization of the form given by T A USV= (3) [ ]1 2 1, , . . . , , . . . ,r r mU u u u u u+= (4) [ ]1 2 1, , . . . , , . . . ,r r nV v v v v v+= (5)
• 7.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 81 Where U and V are orthogonal matrices in which columns of U are left singular vectors and columns of V are right singular vectors of image A. S is a diagonal matrix of singular values in decreasing order. 1 2 1 0 . . . 0 0 . . . 0 0 . . . 0 0 . . . 0 . . . . . . . . . . . . . . . . . . . . . 0 0 . . . 0 . . . 0 0 0 . . . 0 . . . 0 . . . . . . . . . . . . . . . . . . . . . 0 0 . . . 0 0 . . . 0 0 . . . 0 0 . . . 0 r r n S σ σ σ σ σ +                  =                    (6) The basic idea behind SVD technique of watermarking is to find SVD of image and the altering the singular value to embed the watermark. In Digital watermarking schemes, SVD is used due to its main properties namely a) A small agitation added in the image, does not cause large variation in its singular values. b) The singular value represents intrinsic algebraic image properties. 2.3 Encryption Algorithms Ron Rivest, Adi Shamir, and Leonard Adleman (RSA) Algorithm. RSA is an asymmetric key encryption algorithm [23]. Over 1000 bits long numbers are used. Therefore, it can avoid attacks like brute force, man-in-middle, and so on. RSA algorithm (Zhou et al., 2011) involves the following steps (a) Key (private, public) generation. (b) Encryption is performed using receiver’s public key c) At the receiver’s side decryption is performed using the receiver’s private key [24].Advanced Encryption Standard (AES) was published by NIST (National Institute of Standards and Technology) in 2001[25]. It has 128,192, or 256 bits variable key length. AES encryption is fast and flexible in block ciphers and can be implemented on various platforms. AES (specifies a cryptographic algorithm that can be used to protect electronic data. AES algorithm is a symmetric block cipher, which can encrypt and decrypt the information. In this work 8 rounds and 256 bit key lengths are used. AES Encryption includes the following steps.1. Key Expansion, 2. Initial Round, 3. Nine Rounds, 4. Final Round. Initial round has only added round key operation. Each round has the following steps, a. Substitute Bytes, b. Shift Rows. Mix columns. Add Round Key. In the final round steps a, b, and d are performed, excluding step: c. AES Decryption part a 10 set of reverse rounds are performed to transform encrypted image into the watermarked images using the same encryption key [26]. 3. OPTIMIZATION APPROACHES Evolutionary methods for solving optimization problems have become a very popular research topic in recent years. There are three main processes in all evolutionary algorithms. The first process is the initialization process where the initial population of individuals is randomly generated according to some solution representation. Each solution in the population is then evaluated for fitness value in the second process. The fitness values can be used to calculate the average population fitness or to rank the individual solution within the population for the purpose of selection. The third process is the generation of a new population by perturbation of solutions in the existing population.
• 8.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 82 Initialize Population with Possible solutions Evaluate Fitness in the form of Objective Function Perform watermarking , extract and test image using attacks. Rank the individual solutions Check for stoppin g Criteri Create new population through Selection, Mutation Crossover The optimized wavelet type and scaling factor for SVD Yes NO Start 3.1 Genetic Algorithm Optimization Genetic algorithm (GA) is one of the most widely used artificial intelligent techniques for optimization. GA was first developed by John Holland [27]. The main idea of GA is to mimic the natural selection and the survival of the fittest [27]. In GA, the solutions are represented as chromosomes. The chromosomes are evaluated for fitness values and they are ranked from best to worst based on fitness value. The process to produce new solutions in is accomplished through repeated applications of three genetic operators: selection, crossover, and mutation. First, the better chromosomes are selected to become parents to produce new offspring (new chromosomes) [26]. Once the parent chromosomes are selected, the crossover operator combines the chromosomes of the parents to produce new offspring (perturbation of old solutions). Mutation is a mechanism to inject diversity into the population to avoid stagnation. In addition to the population size and the maximum number of iterations, several decisions on parameters must be made for GA. Crossover method and crossover probability are the second set of decisions to be made In general, these three sets of decisions are set empirically using pilot runs. The flow chart of the Genetic Algorithm is shown in Figure (4). Figure (4): The flow chart of the Genetic Algorithm for the proposed optimization problem In this work Genetic Algorithm (GA) function available in the Matlab optimization tool box is used in the proposed work. The population size is fixed at 20. The elite count used is fixed at 10 % of the population which 2. The selection is based on ranking. The cross over fraction is fixed at 0.2 and the
• 9.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 adaptive feasible mutation function is used. The migration of the population is fixed as forward with a forward fraction of 0.2. The maximum number of generations is fixed at 100. 3.2 Differential Evolution DE was proposed by Storn and Price (1995) for global optimization over continuous search space. Its theoretical framework is simple and requires a relatively few control variables but performs well in convergence. In DE algorithm, a solution is represent with a randomly generated initial population of size N of D the D-dimensional space are commonly represented as real numbers. Again, the concept of solution representation is applied in DE in the same way as it is applied in GA GA is in a new mechanism for generating new solutions. DE generates several solutions with the candidate solution. The population of soluti repeated cycles of three main DE operators operators are not all exactly the same as those with the same names in GA. the generation of trial vector. Consi dimensional vectors. The generation of a trial vector is accomplished by the mutation and crossover operations and can be summarized as follow randomly selected vectors. 2) Create trial vector by the crossover of mutant vector and target vector. Figure (5): The flow chart of Differential Evolution As shown in Figure (5), the first process is the generation of a population of vectors. Each vector in the population is evaluated for fitness value. Each vector takes turns as a candidate or target vector, and for each target vector, a trial vector is formed. The selection process simply chooses between the target vector and trial vector, i.e., the winning vector between the trial vector and the target vector survives into the next round while the losing vector is discarded. observations are made here. First, since a new solution would be selected only if the average fitness of the population would be equal or better from iteration to iteration. Any improvement in the solution is immediately available to be randomly selected to form for the next target vector. This is effect only after all the solutions has completed the iteration. Processing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 adaptive feasible mutation function is used. The migration of the population is fixed as forward with a forward fraction of 0.2. The maximum number of generations is fixed at 100. DE was proposed by Storn and Price (1995) for global optimization over continuous search space. Its theoretical framework is simple and requires a relatively few control variables but performs well in In DE algorithm, a solution is represented by a D-dimensional vector [28]. DE starts with a randomly generated initial population of size N of D-dimensional vectors. In DE, the values in dimensional space are commonly represented as real numbers. Again, the concept of solution on is applied in DE in the same way as it is applied in GA The key difference of DE from GA is in a new mechanism for generating new solutions. DE generates a new solution by combining candidate solution. The population of solutions in DE evolves through repeated cycles of three main DE operators: mutation, crossover, and selection. However, the operators are not all exactly the same as those with the same names in GA. The key process in DE is the generation of trial vector. Consider a candidate or target vector in a population of size N of D he generation of a trial vector is accomplished by the mutation and crossover operations and can be summarized as follows. 1) Create a mutant vector by mutation of three Create trial vector by the crossover of mutant vector and target vector. Figure (5): The flow chart of Differential Evolution As shown in Figure (5), the first process is the generation of a population of new solutions called vectors. Each vector in the population is evaluated for fitness value. Each vector takes turns as a candidate or target vector, and for each target vector, a trial vector is formed. The selection process et vector and trial vector, i.e., the winning vector between the trial vector and the target vector survives into the next round while the losing vector is discarded. observations are made here. First, since a new solution would be selected only if it has better fitness, the average fitness of the population would be equal or better from iteration to iteration. Any improvement in the solution is immediately available to be randomly selected to form a for the next target vector. This is different from GA and PSO where an improvement would take effect only after all the solutions has completed the iteration. Processing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 83 adaptive feasible mutation function is used. The migration of the population is fixed as forward with a DE was proposed by Storn and Price (1995) for global optimization over continuous search space. Its theoretical framework is simple and requires a relatively few control variables but performs well in dimensional vector [28]. DE starts dimensional vectors. In DE, the values in dimensional space are commonly represented as real numbers. Again, the concept of solution The key difference of DE from new solution by combining ons in DE evolves through and selection. However, the The key process in DE is der a candidate or target vector in a population of size N of D- he generation of a trial vector is accomplished by the mutation and crossover Create a mutant vector by mutation of three Create trial vector by the crossover of mutant vector and target vector. new solutions called vectors. Each vector in the population is evaluated for fitness value. Each vector takes turns as a candidate or target vector, and for each target vector, a trial vector is formed. The selection process et vector and trial vector, i.e., the winning vector between the trial vector and the target vector survives into the next round while the losing vector is discarded. Several it has better fitness, the average fitness of the population would be equal or better from iteration to iteration. Any a mutant vector different from GA and PSO where an improvement would take
• 10.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 84 In contrast with GA where parent solutions are selected based on fitness, every solution in DE takes turns to be a target vector (one of the parents), and thus all vectors play a role as one of the parents with certainty. The second parent is the mutant vector which is formed from at least three different vectors. In other words, the trial vector is formed from at least four different vectors and would replace the target vector only if this new vector is better than the target vector; otherwise, it would be abandoned. This replacement takes place immediately without having to wait for the whole population to complete the iteration. This improved vector would then immediately be available for random selection of vectors to form the next mutant vector. In this work Differential Evolution is coded using Matlab. The Parameters used and the settings are mentioned as mentioned below: DEParamsDefault.CR = 0.7; DEParamsDefault.F = 0.8; DEParamsDefault.NP = 30; DEParamsDefault.strategy = 1; DEParamsDefault.minvalstddev = -1; DEParamsDefault.minparamstddev = -1; DEParamsDefault.nofevaliter = 10; DEParamsDefault.nochangeiter = 10; DEParamsDefault.maxiter = inf; DEParamsDefault.maxtime = inf; DEParamsDefault.refreshiter = 10; DEParamsDefault.refreshtime = 60; seconds 3.3 Bacterial Foraging Optimization Swarm intelligence, as an emerging intelligent computing technology, has been the focus of attention of artificial intelligence researchers. In 2002, Passino who was inspired by the social foraging behavior of Escherichia coli, proposed the Bacteria Foraging Optimization Algorithm (BFOA), which has become a new member in the coveted realm of swarm intelligence [29] Since its inception, BFOA has drawn the attention of researchers in different fields of knowledge, in terms of its biological motivation, and elegant structure. The algorithm has been instructed in optimal search by swarm intelligence, which is produced by cooperation and competition among individuals within groups. It has advantages, such as parallel distributed processing, insensitivity to initial value, and global optimization. In the process of foraging, E. coli bacteria undergo four stages, namely, chemotaxis, swarming, reproduction, and elimination and dispersal. In search space, BFOA seek optimum value through the chemotaxis of bacteria, and realize quorum sensing via assemble function between bacterial, and satisfy the evolution rule of the survival of the fittest make use of reproduction operation, and use elimination-dispersal mechanism to avoiding falling into premature convergence[ 29]. The motion patterns that the bacteria will generate in the presence of chemical attractants and repellents are called chemotaxis. For E. coli, this process was simulated by two different moving ways: run or tumble. A Bacterium alternates between these two modes of operation its entire lifetime. The bacterium sometimes tumbles after a tumble or tumbles after a run. This alternation between the two modes will move the bacterium, and this enables it to "search" for nutrients. An interesting group behavior has been observed for several motile species of bacteria including E.coli and S. typhimurium. When a group of E. coli cells is placed in the center of a semisolid agar with a single
• 11.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 85 nutrient chemo-effector, they move out from the center in a traveling ring of cells by moving up the nutrient gradient created by consumption of the nutrient by the group. To achieve this, function to model the cell-to-cell signaling via an attractant and a repellent. The Steps involved in BFOA is as given below. Step 1: Initialization of BFOA parameters. Step 2: Evaluate Fitness in the form of Objective Function. Step 3: Initiate Chemo taxis Tumble / Run Step 4: Check for End of Chemo taxis if yes Go to Step5 otherwise go to Step 2 Step 5: Start Reproduction Step 6: Check if it is end of Reproduction as initiate, if yes go to Step 7 else go to Step 2 Step 7: Initiate Elimination and dispersion Step 8: If end of Elimination and dispersion then go to next Step, or else go to Step 2 Step 9: Provide the Optimized parameters for embedding watermark. BFOA is coded using matlab and the parameters of algorithm used in this research work are as mentioned below. The number of bacteria: 20 Number of chemotactic steps: 10 Limit length of a swim: 4 The number of reproduction steps: 4 The number of elimination-dispersal events: 2 The number of bacteria reproductions: 2 The probability that each bacteria will be eliminated/dispersed: 2 4. PROBLEM FORMULATION FOR MULTI -OBJECTIVE OPTIMIZATION Multi-objective optimization is an appropriate tool for handling different incommensurable objectives with conflicting/ supporting relations or not having any mathematical relation with each other. In this work the multi-objective optimization problem is transformed into a scalar optimization problem with different performance measures represented in it. This kind of scenario is typical of medical images in which it is of foremost importance maintain and preserve the diagnostic information in the medial image. Unlike regular watermarking scheme where in the original image is of importance to the user, in this proposed scheme the watermark (medical image) is of much value to the user. Different performance parameters like Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE), Normalized Coefficient (NC) and Structural Similarity Index (SSIM) is used to frame this multi- objective function Any watermarking scheme should provide robustness, imperceptibility and also should be capable of maintaining the structural integrity of the watermark (medical image). The watermark embedding parameters plays a very crucial role in defining these parameters. In this work the type of wavelet in a particular wavelet family of Discrete Wavelet Transform (DWT) and the scaling factor used in Singular Value Decomposition (SVD) are using the multi-objective optimization function. The fitness function used for this multi-objective optimization is Min {f = (100-PSNR) + (1-NC) + (1-SSIM) + MSE} (7)
• 12.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 86 The Peak Signal to Noise Ratio (PSNR) is used to find the deviation of watermarked and attacked image from the original image. Equation (8) represents the PSNR. In this equation mean squared error (MSE) for two M * N monochrome images f and z and it is given by Equation (9). MaxBits gives the maximum possible pixel value (255) of the image. 2 1010 log MaxBits PSNR X MSE = (8) 1 1 2 0 0 1 (( ( , ) ( , )) M N x y MSE f x y z x y MxN − − = = = −∑∑ (9) Normalized Coefficient (NC) gives a measure of the robustness of watermarking. After extracting the watermark, the normalized correlation coefficient (NC) is computed between the original watermark and the extracted watermark using Equation (10). This is used to judge the existence of the watermark and to measure the correctness of the extracted watermark. j , i j j 2 , 2 i i w(i,j)w (i,j) NC= w(i,j) w (i,j) ∑ ∑ ∑ (10) Where, w and w’ represent the original and extracted watermark, respectively. Structural Similarity Index (SSIM) index is a method for measuring the similarity between embedded and extracted watermark images. The SSIM is measured between two windows X and Y of common size N*N on image using Eq. (11). 1 2 2 2 2 2 1 2 (2 )(2 ) ( , ) ( )( ) x y xy x y x y c c SSIM x y c c µ µ σ µ µ σ σ + + = + + + + (11) A typical flow chart representation of the optimization process is described in the figure below Figure (6): Flow chart of Optimization process used in this work.
• 13.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 87 5. PROPOSED ALGORITHM The water marking is proposed to be implemented using a hybrid approach which encompasses Lifting Wavelet Transforms (LWT) and Singular Value Decomposition (SVD) techniques. The resultant of multi-objective optimization in form type of wavelet in a particular wavelet family of Discrete Wavelet Transform (DWT) and the scaling factor used in Singular Value Decomposition (SVD) is used in the process of embedding and extracting the watermark. In this algorithm, Medical image is taken as the watermark and it is embedded in each block of the Natural image (cover image) by altering the wavelet coefficients of selected DWT sub bands. The steps involved in this process are described below. a) Watermark Embedding and Encryption. Step 1: Obtain the medical image to be embedded and the input natural Step 2: Perform LWT by using the optimized selection of wavelet obtained through optimization approach on the natural image to decompose it into four non- overlapping sub-bands: LL, HL, LH, and HH. Step 3: Apply SVD to ‫ܮܪ‬ sub band i.e.,‫ܸܷܶ݅݅ܵ݅=݅ܣ‬ where ‫ܮܪ=݅ܣ‬ Step 4: Apply SVD to the watermark i.e.,ܹ=ܷ‫ܶݓܸݓܵݓ‬ where ܹ=ܹܽ‫݇ݎܽ݉ݎ݁ݐ‬ Step 5: Modify the singular value of ‫݅ܣ‬ by embedding singular value of ܹ such that ܵ݅‫=ݓ‬ ܵ݅+ߙ×ܵ‫ݓ‬ ,Where ܵ݅‫ݓ‬ is modified singular matrix of ‫݅ܣ‬ and ߙ denotes the scaling factor, is used to control the strength of watermark signal the value of which is optimized through BFOA using the multi objective function. Step 6: Then apply SVD to this modified singular matrix ܵ݅‫ݓ‬ i.e., ܵ݅‫ܶݓ݅ܵ_ܸݓ݅ܵ_ܵݓ݅ܵ_ܷ=ݓ‬ and obtain the modified LWT coefficients, i.e., ‫ܸܶ݅×ݓ݅ܵ_ܵ×ܷ݅=ݓ݅ܣ‬ Step 7: Obtain the watermarked image ‫ݓܣ‬ by applying inverse LWT using one modified and other non modified LWT coefficients. Step 8: Then encrypt the watermarked image with RSA or AES algorithms in the time domain. b) Decryption and Watermark Extraction Step 1: Decrypt the encrypted image to obtain the watermarked image. Step 2: Apply the chosen LWT to decompose the watermarked image ‫ݓܣ‬ in to four sub bands (i.e., ‫݀݊ܽ,ܮܪ,ܪܮ,ܮܮ‬ ‫.)ܪܪ‬ Step 3: Apply SVD to ‫ܮܪ‬ sub band i.e., ‫ܶݓܸ݅ݓ݅ܵݓܷ݅=ݓ݅ܣ‬ , Where ‫ܮܪ=ݓ݅ܣ‬ Compute ܵ‫=∗ݓ‬ (ܵ݅‫,ߙ/)݅ܵ−ݓ‬ where ܵ‫∗ݓ‬ singular matrix of extracted watermark Step 4: Apply SVD to ܵ‫∗ݓ‬ i.e., ܵ‫ܶ∗ݓܵ_ܸ∗ݓܵ_ܵ∗ݓܵ_ܷ=∗ݓ‬ Step 5: Now Compute extracted watermark ܹ∗ i.e., ܹ∗=ܷ‫ܶݓܸ×∗ݓܵ_ܵ×ݓ‬ 6. THE GRAPHICAL USER INTERFACE (GUI) A comprehensive tool capable of performing watermarking and different analysis as required by the user is designed. The tool is proposed to be in the form of a Graphical User Interface (GUI) which enables the user to have ease of operation in loading the image, watermark it, encrypt it and also retrieve the original image whenever necessary. The tool is coded using Matlab Version 7.1 .A Graphical User Interface enable the user to have seamless use and flexibility of operation. The implementation is carried out in a system having Core 2 Duo processor cloaking at a speed of 2 GHz with a RAM of 2GB.
• 14.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 88 Figure(7): Screen Shot of the GUI The functional icons present in the GUI can be described as below in reference to the Figure (7). 1) Functional icon used to load the natural image and the medical image to be watermarked and encrypted. 2) This functional icon is used to choose different wavelet techniques and method for the implementation of watermarking. 3) This functional icon enables the user to test the watermark images against a set of standard attacks. 4) Functional icon used to implement the encryption of the image. 5) Functions used to decrypt the image and retrieve the watermark which in this case is the medical image. 6) The resultant images of the process are displayed here. 7) The values of the validation parameters arte displayed here. 7. RESULTS AND DISCUSSION To validate the proposed approach, a Brain MRI image (MI1), a Knee MRI image (MI2), a Lung CT image (MI3) and an Ultrasound image (MI4) of fetus are considered is considered as the medical image that has to be used as the watermark image. The medical images are resized to have a size of 512* 512 to enable ease of computation and comparison of test results. The medical images used are indicatively represented in the below figure (4). The results of Differential Evolution (DE) optimization is compared with that of Genetic Algorithm (GA).
• 15.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 89 Figure (8): Different Medical Images used in this work. Three standard test images are used as natural images for embedding the watermark. The details of the images are enlisted in the table (1) below. Table (1): Natural Images used for embedding the watermark S.No. Image Name Size ( Pixels) Memory (Kilo Bytes) 1 Image 1 Lena 512*512 443 2 Image 2 Fruits 512*512 169 3 Image 3 Pepper 512*512 31.2 Four different Discrete Wavelet families namely Haar, Daubechies, Symlets and Bior splines are used in this work. RSA and AES encryption algorithms are used for encrypting the watermarked images. The Optimization algorithm Differential Evolution is used for optimization, the process can be initiated through the GUI. The below figure illustrates the steps involved in operation of the method and the tool designed. Figure (9): From Top Left: Natural Inage, Watermark, Watermarked image, Cropped Watermarked image, Encrypted image, Extracted Watermark The encryption algorithm is evaluated on the basis of correlation values. The correlation between two images refers to similarity in them. The correlation value is computed using
• 16.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 90 2 2 2 2 ( ) ( ) ( ) ( ) ( ( )) ( ) ( ( )) E xy E x E y CV E x E x E y E y − = − − (10) Where x and y represents the input and encrypted image The Natural image, Image 3 is taken as a representative image for analysis, and the MRI Knee Image (MI2) is considered to be the watermark. The watermark embedding process is optimized using Bacterial Foraging Optimization (BFOA) and the results presented below are the best of the ten trial runs. The results are also compared against the results of Genetic Algorithm (GA) and Differential Evolution (DE) based optimization. The below tabular column specifies performance of different types of wavelets families and the scalar function as optimized by the proposed approach. Table (2): Performance Measures PSNR, NC, MSE of Different Images using different DWT approaches Optimized using GA, DE and BFOA Table (3): Performance Measures PSNR, NC, MSE of Different Images using LWT for different wavelet families Optimized using GA, DE and BFOA Table (4): Performance Measure SSIM for different DWT approaches Optimized using GA, DE and BFOA
• 17.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 91 Table (5): Performance Measure SSIM for Different Images using LWT for different wavelet families Optimized using GA, DE and BFOA Table (6): Performance Measure CV different DWT approaches Optimized using GA, DE and BFOA Table (7): Performance Measure CV using LWT for different wavelet families Optimized using GA, DE and BFOA The tables give a clear indication about the performance capabilities of the proposed multi-objective optimization approach. The BFOA algorithm standout among the other methods in terms of better performance as can be inferred from the different performance measure. Similarly lifting of wavelets clearly results in increase in the performance of the watermark performance measure. Even though the increase is marginal such a small improvement is voluminous in terms of medical data.The best performance can be singled out as the one in which the watermark was optimized by BFOA by both DWT and LWT as indicated in table (8) Table (8): The best optimization result by BFOA
• 18.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 92 It can be observed from the above table that despite having a very high SNR the algorithm is capable of delivering very high NC and SSIM indicating the protection of robustness and structural integrity. The proposed algorithm is tested against different types of attacks namely, rotation, cropping, motion blur, sharpening and different types of noise attacks like, salt and pepper, Gaussian, speckle and Poisson. The rotation operation performs a geometric transform which maps the position (x1, y1) of a picture element in an input image onto a position (x2, y2) in an output image by rotating it through user-specified angle about an origin O. The figure (10) illustrates the different attacks on the watermarked image. Figure (10) Watermarked image attacked with different types of attacks. Figure (11) Variation in PSNR for different attacks compared for DWT and LWT Figure (12) Variation NC for different attacks compared for DWT and LWT
• 19.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 93 The above figures show the comparison between DWT and LWT for changes in PSNR and NC for different attacks performed for watermarking done using different wavelet families. It can be observed that under attack LWT offer a better PSNR where as DWT offer a better NC performance. The PSNR value and the NC value both continue to be on the higher side, implying the fact that the watermarked image is both imperceptible as well as robust. It can also be observed that the ‘BFOA, gives a better performance when compared to optimization methods. To demonstrate the effect of two typical noises, watermark is subjected to different intensities of attack using these two noises and their influence on imperceptibility and robustness in terms of reduction in PSNR and NC is plotted in the figures (13) and figure (14).Salt and pepper noise with noise density of 0.001, 0.005, 0.01, 0.02, and 0.05 was used for the attack and speckle noise with variance of 0.01, 0.02, 0.04, 0.06, 0.08 and 0.1 was used. The attacks were carried out on image watermarked using the LWT scheme. Figure (13): Reduction in PSNR of the watermarked image with increase in noise density of the salt and pepper noise Figure (14): Reduction in NC of the watermarked image with variance of the speckle noise. 8. CONCLUSION In this paper, a DICOM image security technique based on the reversible watermarking method is proposed, this technique provides system authentication service, image integrity service and patient information confidentiality service; it is reversible because the original medical image can be retrieved at the receiver side without any distortion. The method envisages hiding the medical image in a
• 20.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 94 natural image there by removing the motive for attacking the medical image and disguising it as any ordinary image. Three different objective of analysis are met like choosing the type of wavelet, comparing the performance of DWT and LWT and studying the effect of optimization approaches like GA, DE, and BFOA. The Graphical User Interface provided a strong support in making different analysis.The multi -objective optimization approach has resulted in generation of watermark that is robust and imperceptible. The primary objective of this research is to wean away potential attackers from medical images and present the medical images as embedded in to a natural image. This makes it imperative for the approach to maintain the structural integrity of the watermark as well. The proposed approach is capable of maintaining the structural index as well, making this type of approach more suitable and acceptable for medical images. The LWT method provides a slightly better performance when compared to the DWT method. The Bacterial Foraging Optimization (BFOA) has yielded better results as compared other optimization techniques. Similarly it can also be observed that the Daubechies wavelet family performs better than the other wavelet types. The achieved correlation value shows the effectiveness of the encryption employed. Such a dual security approach can go a long way in maintaining the integrity and authenticity of medical images. Irrespective of the type of wavelet analysis like DWT or LWT it can be conclude that the proposed optimization approach provides high degree of robustness coupled with imperceptibility and at the same time preserves the structural integrity making it high suitable for medical application. REFERENCES [1] C.D. Schou, J. Frost, W.V. Maconachy, "Information Assurance in Biomedical Informatics Systems," IEEE Engineering in Medicine and Biology Magazine, vol. 23, no1, pp. 110–118, 2004. [2] M. Jiansheng, L. Sukang, and Tan Xiaomei, A digital watermarking algorithm based on DCT and DWT, Proceedings of the 2009 International Symposium on Web Information Systems and Applications (WISA ’09) Nanchang, PR China, May 22–24, (2009), pp. 104–107. [3] C. Piao, D. Woo, D. Park, and S. Han, Medical image authentication using hash function and integer Wavelet transform, Congress on Image and Signal Processing, (2008). [4] C.S. Woo, J. Du, and B. Pham, Multiple watermark method for privacy control and tamper detection in medical images, WDIC2005 pages, Australia, February, (2005), pp. 59–64. [5] M. Nambakhsh, A. Ahmadian, and H. Zaidi, A contextual based double watermarking of PET images by Patient ID and ECG Signal, Comput Meth Prog, 104 (2001), 341–353. [6] X. You, L. Du, Y. Cheung, and Q. Chen, A blind watermarking scheme using new nontensor product wavelet filter bank, IEEE Trans On Image Processing, 19 (2010). [7] W. Lin, S. Horng, T. Kao, P. Fan, C. Lee, and Y. Pan, An efficient watermarking method based on significant difference of wavelet coefficient quantization,” IEEE Trans On Multimedia, 10 (2008), 746–757 [8] A. Kannammal and S. Subha Rani, Double watermarking of DICOM medical images using wavelet decomposition technique, Eur J Sci Res (1) (2012), 46–55 [9] R.Z. Liu and T.N. Tan “An SVD-Based Watermarking Scheme for Protecting Rightful Ownership”, IEEE Trans. On Multimedia, Vol. 4, No. 1, pp. 121–128. ,2002. [10] Chin-Chen Chang, Piyu Tsai, Chia-Chen Lin, SVD-based digital image watermarking scheme, Pattern Recognition Letters, Volume 26, Issue 10, 15 July 2005, Pages 1577-1586 [11] D. Bouslimi, G. Coatrieux, M. Cozic, A joint encryption/watermarking systems for verifying the reliability of medical images, IEEE Trans Information Technol Biomed, 16 (2012). [12] F. Cao, H.K. Huang, X.Q. Zhou, Medical image security in HIPAA mandated PACS environment, Comput Med Imaging Graphics 27 (2003), 185–196. [13] L.O.M. Kobayashi, S.S. Furuie, and P.S.L.M. Barreto, Providing Integrity and Authenticity in DICOM Images: A Novel Approach, IEEE TransInform Technol Biomed, 13 (2009). [14] E. Thambiraja, G. Ramesh, and R. Umarani, A survey on various most common encryption techniques, Int J Adv Res Comput Sci Software Eng, 2 (2012), 226–233. [15] W. Puech, J.M. Rodrigues, A new crypto watermarking method for medical images safe transfer, Proc of the 12th European signal processing conference,Vienna, Austria, 2004, 1481–1484. [16] X. You, L. Du, Y. Cheung, and Q. Chen, A blind watermarking scheme using new nontensor product wavelet filter bank, IEEE Trans On Image Processing, 19 (2010). [17] Sikander, B.; Ishtiaq, M.; Jaffar, M.A.; Tariq, M.; Mirza, A.M., "Adaptive Digital Watermarking of Images Using Genetic Algorithm," Information Science and Applications (ICISA), 2010 International Conference on , vol., no., pp.1,8, 21-23 April 2010 [18] Sawsan morkos gharghory “Hybrid Of Particle Swarm Optimization With Evolutionary Operators To Fragile
• 21.
  Signal & ImageProcessing : An International Journal (SIPIJ) Vol.6, No.1, February 2015 95 Image Watermarking Based Dct” international journal of computer science & information technology (ijcsit), vol 3, no 3, june 2011 [19] V. Aslantas , “Optimal SVD based Robust Watermarking using Differential Evolution Algorithm” Proceedings of the World Congress on Engineering 2008 Vol I WCE 2008, July 2 - 4, 2008, London, U.K. [20] Musrrat Ali, Chang Wook Ahn, Millie Pant, “A robust image watermarking technique using SVD and differential evolution in DCT domain”, Optik - International Journal for Light and Electron Optics, Volume 125, Issue 1, January 2014 [21] Sweldens, "The lifting scheme: A construction of second generation wavelets." SIAM Journal on Mathematical Analysis 29.2 (1998): 511-546. [22] Baiying Lei, Ee-Leng Tan, Siping Chen, Dong Ni, Tianfu Wang, Haijun Lei, “Reversible watermarking scheme for medical image based on differential evolution, Expert Systems with Applications”, Volume 41, Issue 7, 1 June 2014, Pages 3178-3188 [23] Talat Naheed, Imran Usman, Tariq M. Khan, Amir H. Dar, Muhammad Farhan Shafique, “Intelligent reversible watermarking technique in medical images using GA and PSO”, Optik - International Journal for Light and Electron Optics, Volume 125, Issue 11, June 2014 [24] Matlab R 2012 a Wavelet Tool Box Reference Manual. [25] PKCS #1 v2.2: RSA Cryptography Standard RSA Laboratories October 27,, 2012. [26] Federal Information Processing Standards Publication 197, Advanced Encryption Standard (AES), November 26, 2001 [27] Matlab R 2012 a Optimization Tool Box Reference Manual. [28] Differential Evolution”A Practical Approach to Global Optimization”Series: Natural Computing Series Price, Kenneth, Storn, Rainer M., Lampinen, Jouni A.2005, XX, 538 p [29] Passino, K.M., "Biomimicry of bacterial foraging for distributed optimization and control," Control Systems, IEEE , vol.22, no.3, pp.52,67, Jun 2002. AUTHORS CH. Venugopal Reddy is working as Professor in the department of ECE, Priyadarshini College of Engineering & Technology, Nellore, affiliated to JNTU Anantapur, A.P. Has more than 13 years of teaching experience. He got his B.Tech(ECE) from K.S.R.M. Engg College, Kadapa, A.P, affiliated to S.V University, Tirupathi, A.P. M.E (Commn.Sys) from Anna University, Chennai. He is presently pursuing Ph.D in the area of Digital Image Water Marking, Acharya Nagarjuna University, Guntur. His research interests are in the areas of Signal Processing, Image Processing and Communications. Dr.P.Siddaiah obtained B.Tech degree in Electronics and Communication Engineering from JNTUA college of Engineering in 1988. He received his M.Tech degree from SV University, Tirupathi. He did his PhD program in JNTU, Hyderabad. He is the chief Investigator for several outstanding projects sponsored by Defense organizations and AICTE, UGC & ISRO. He is currently working as Principal, University College of Engineering and Technology, Acharya Nagarjuna University, Guntur, A.P,India. He has taught a wide variety of courses for UG & PG students and guided several projects. Several members successfully completed their PhD under his guidance. He has published several papers in National and International Journals and Conferences. He is a life member of FIETE, IE, and MISTE.