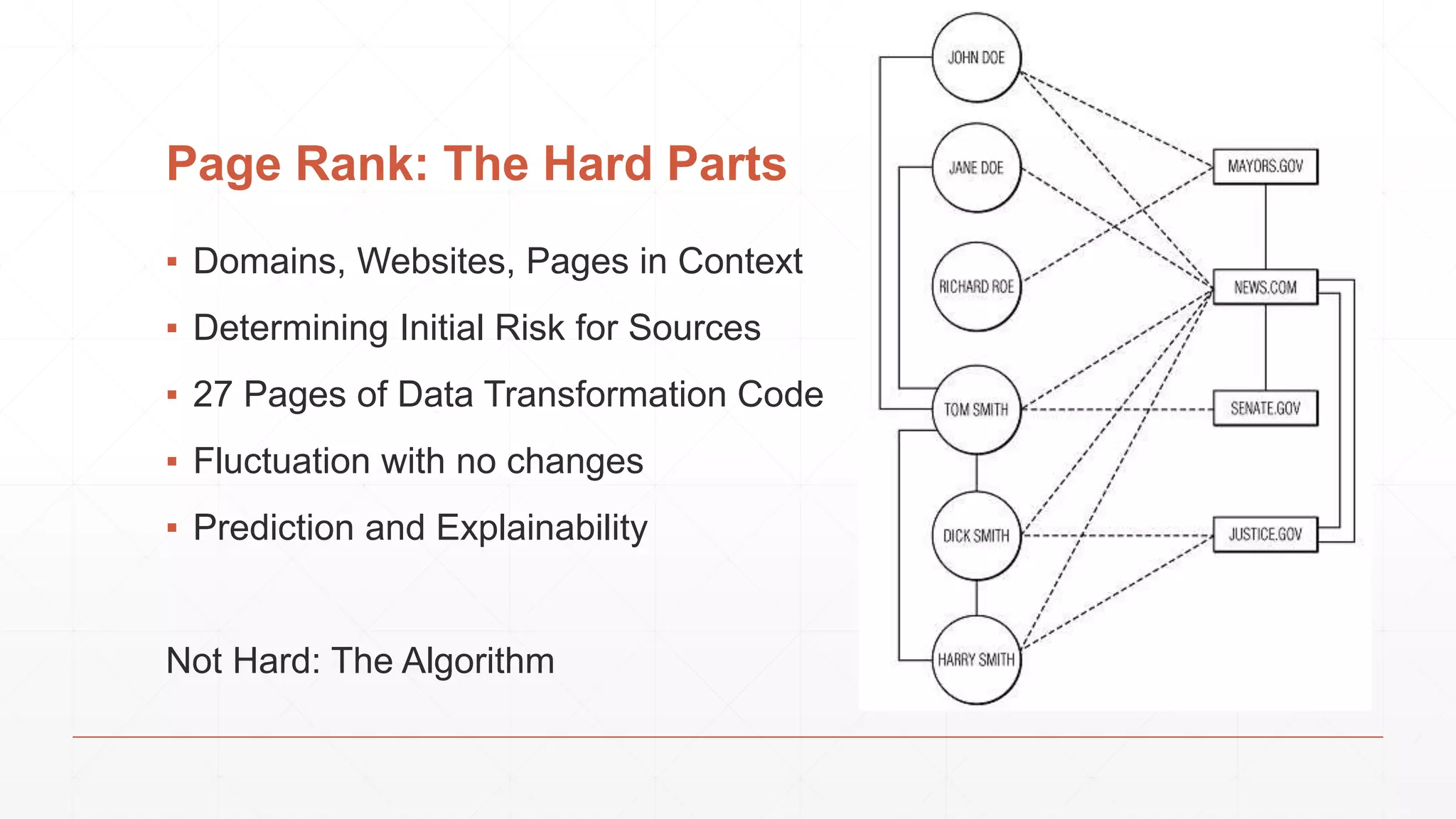
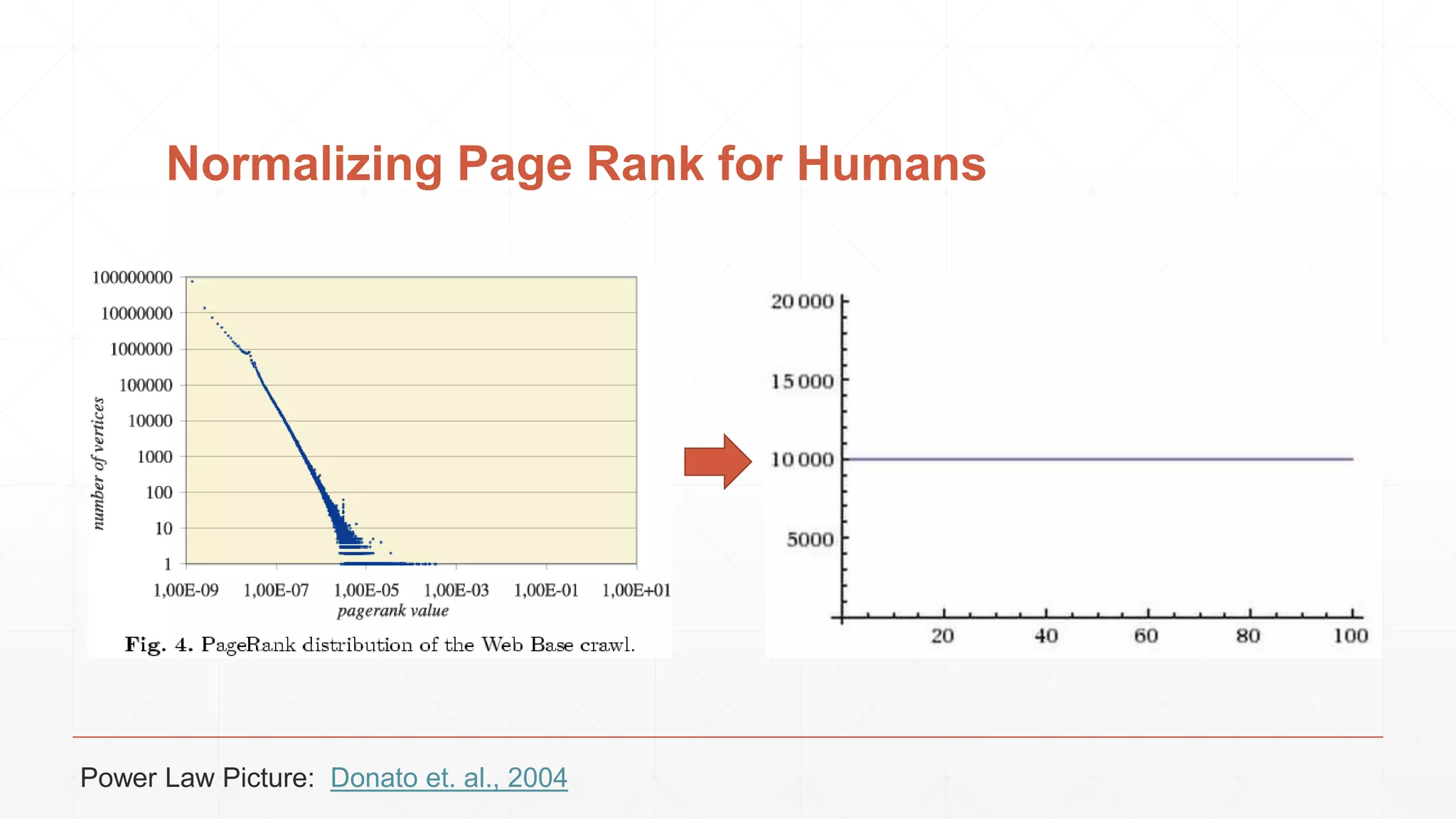
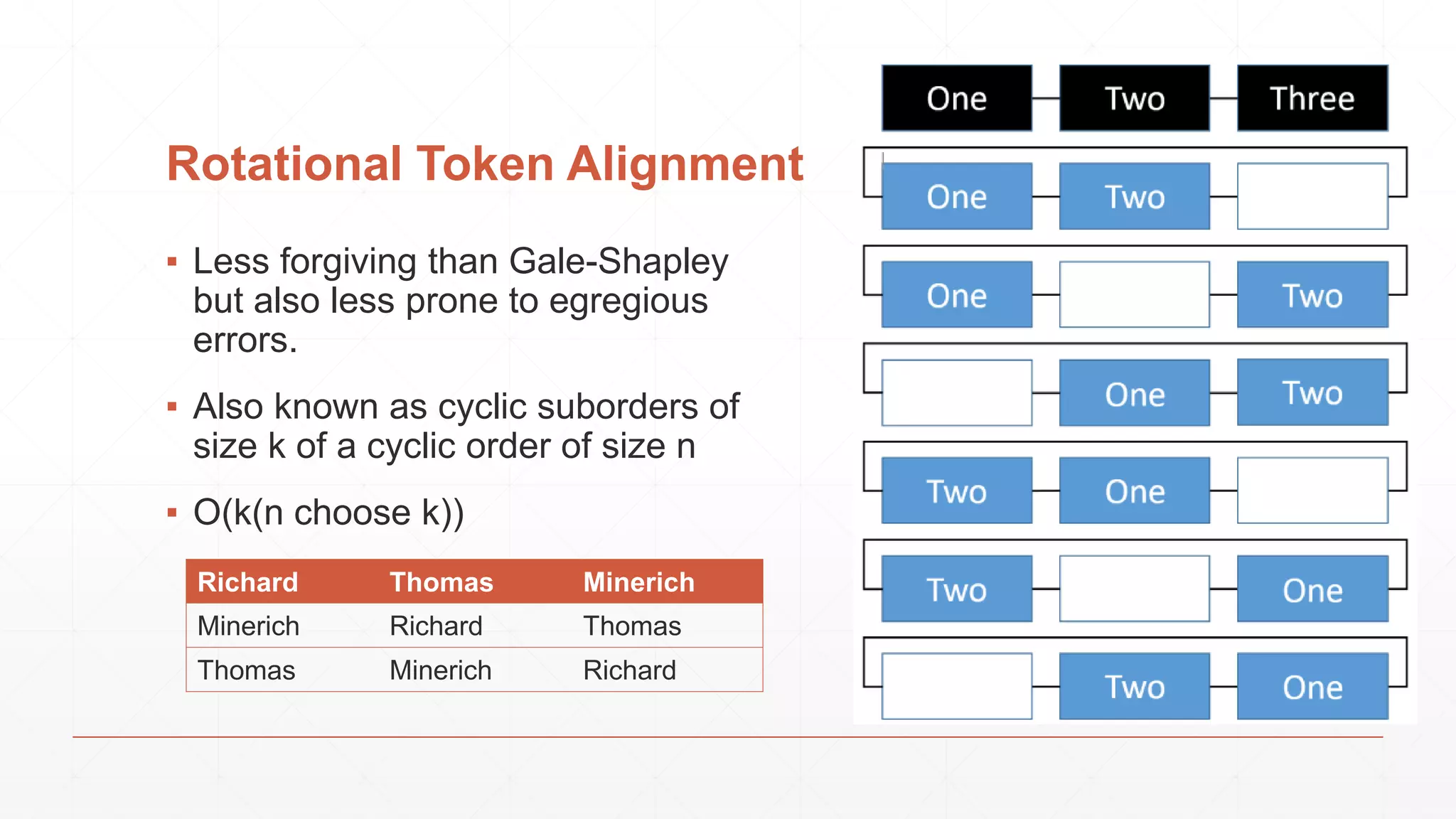
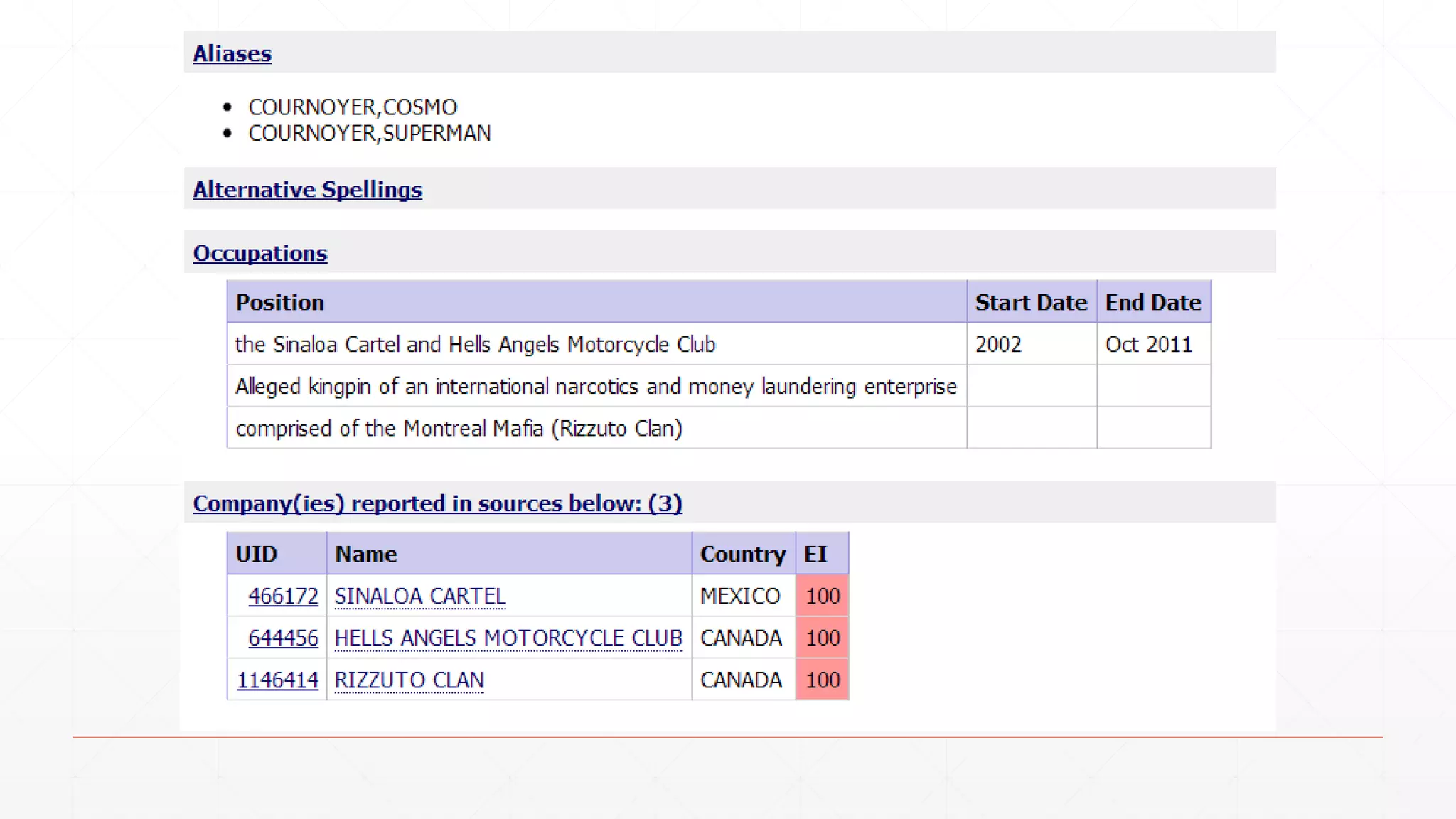
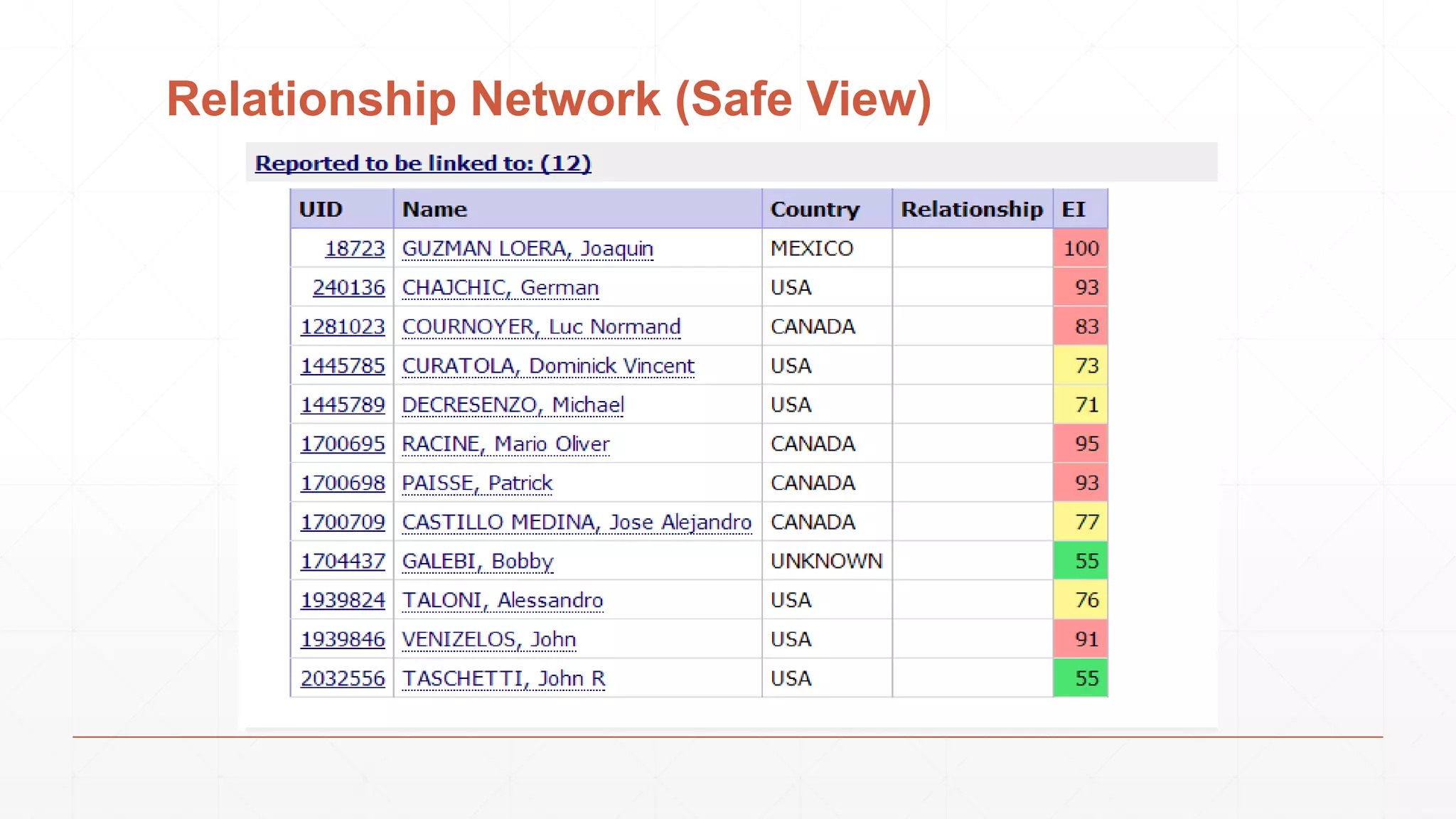
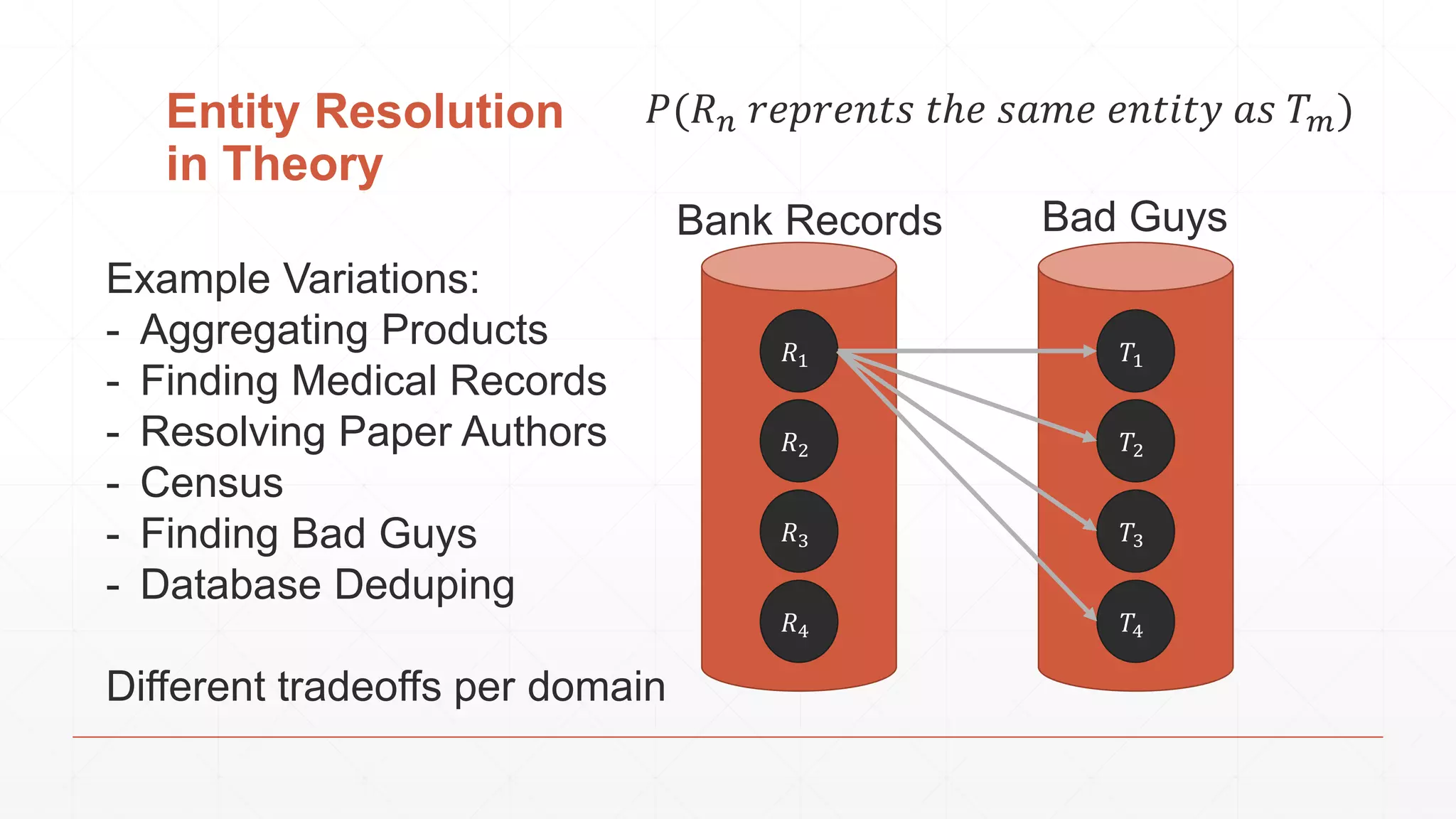
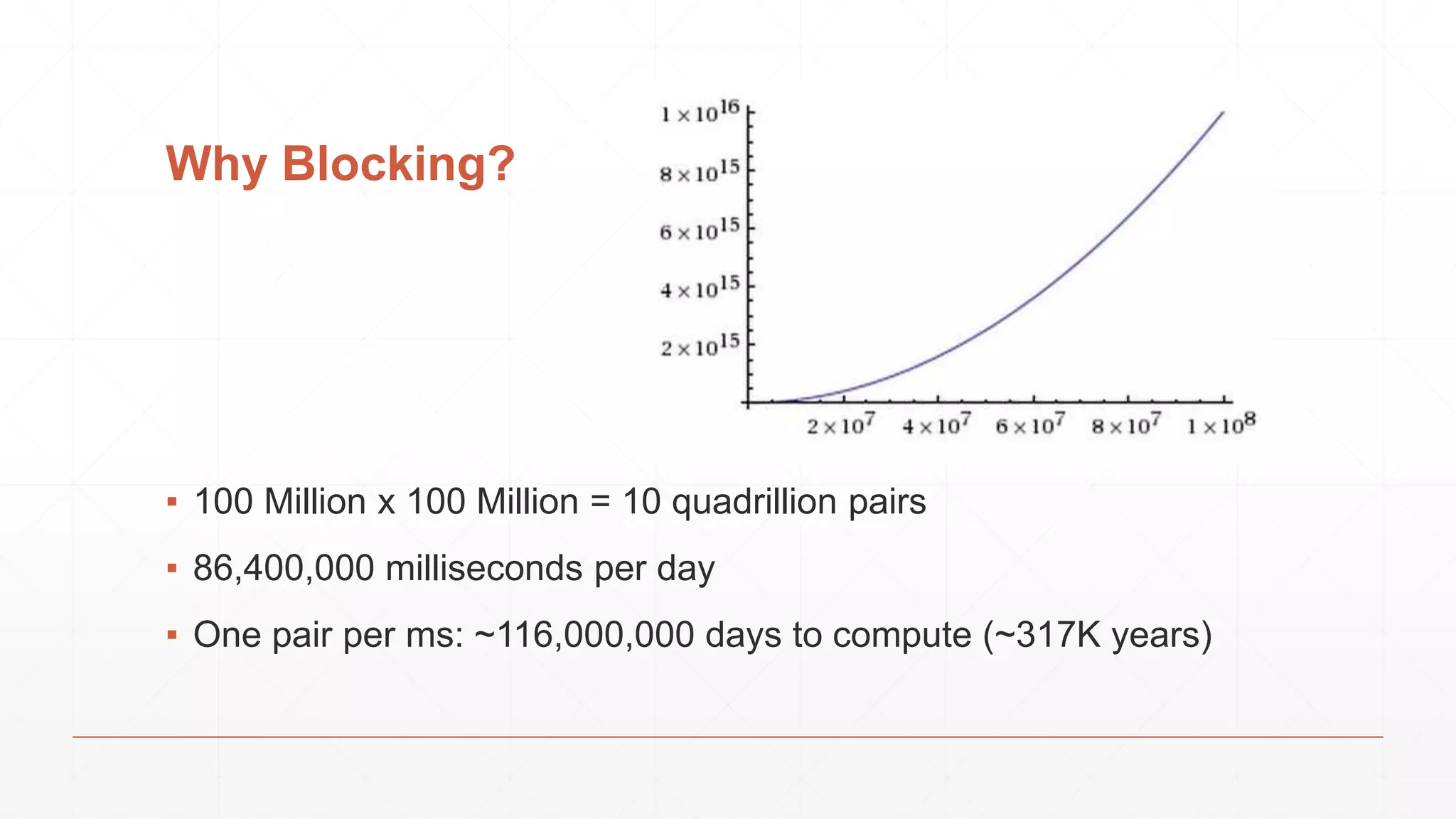
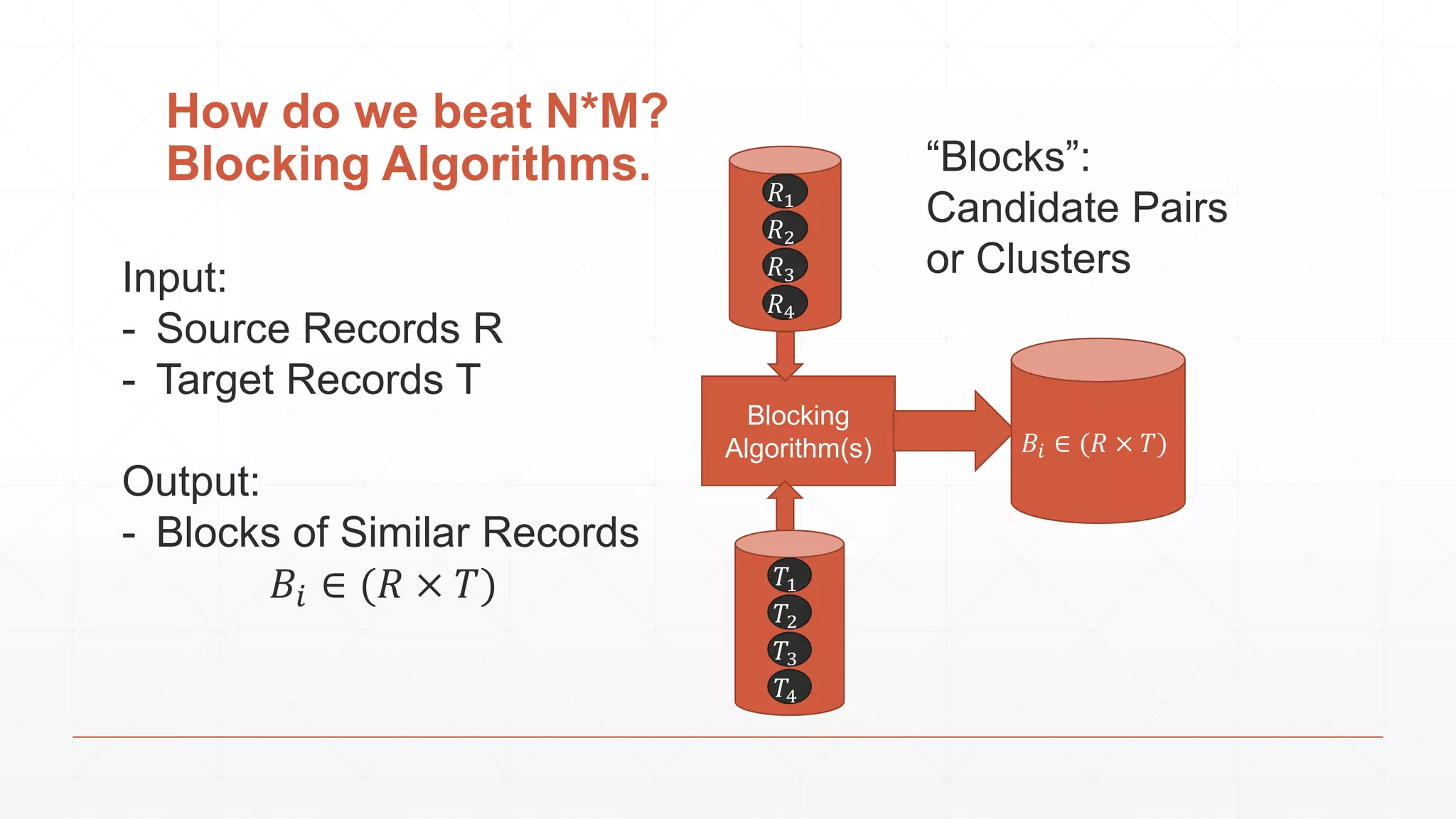
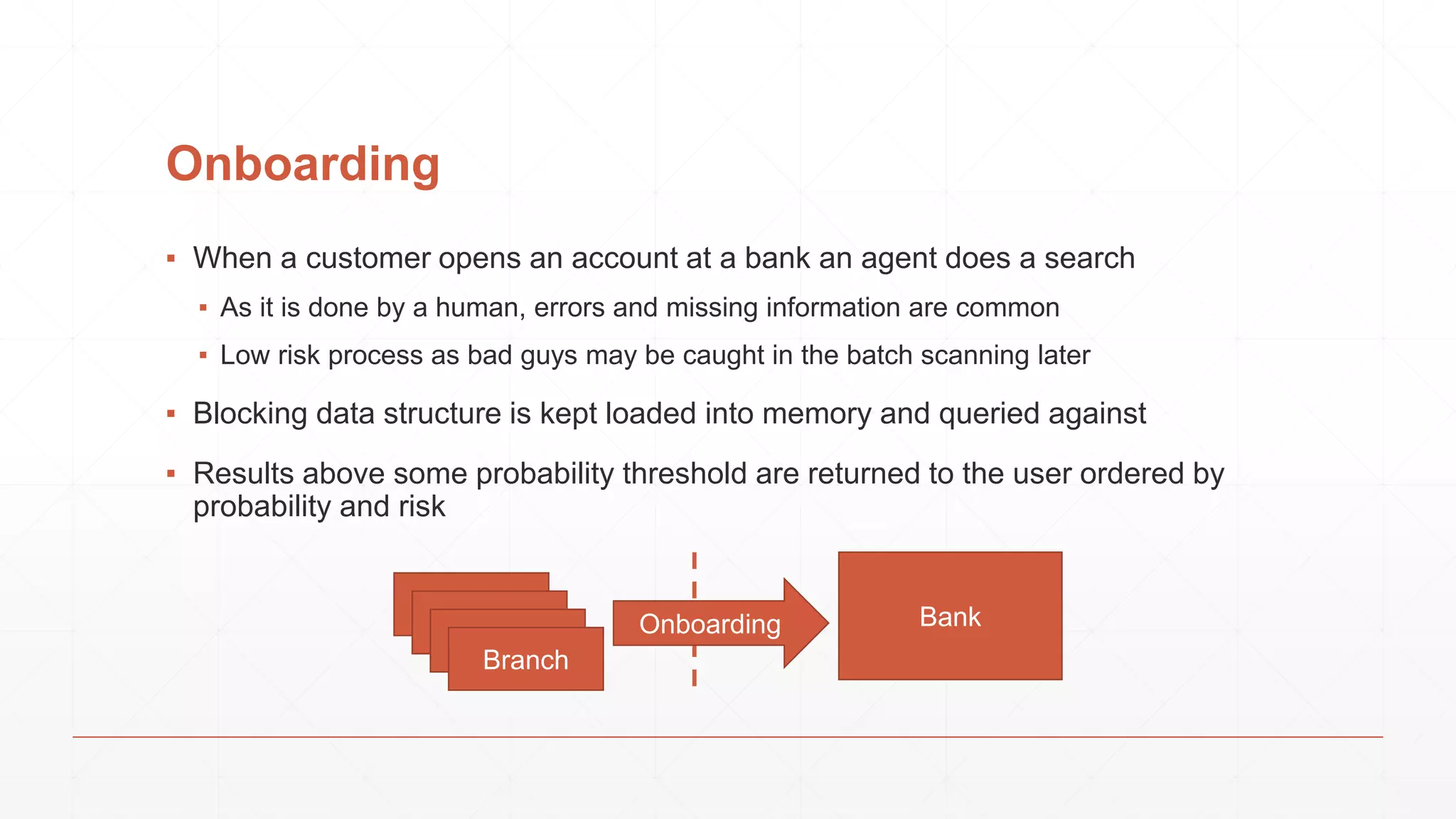
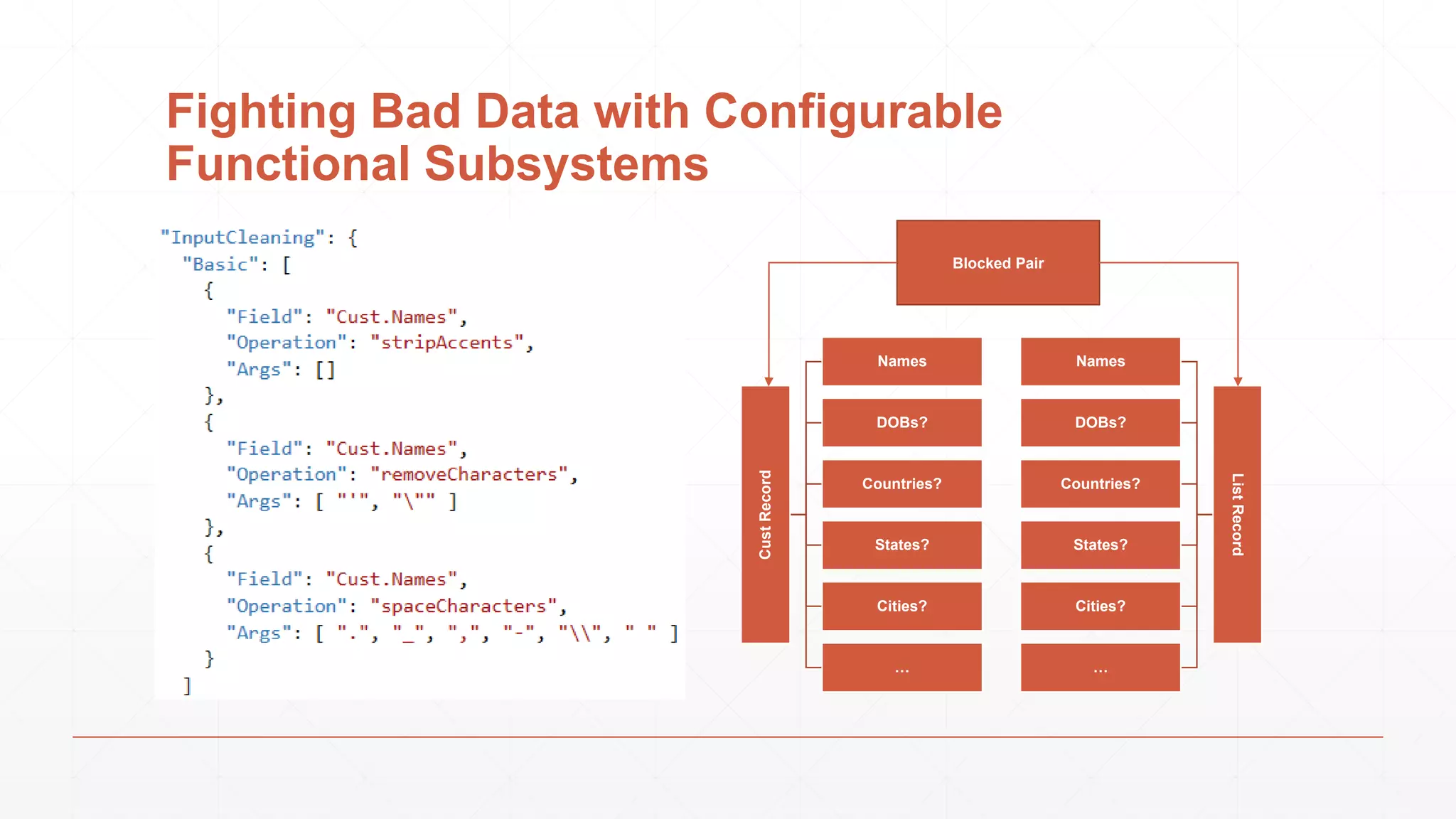
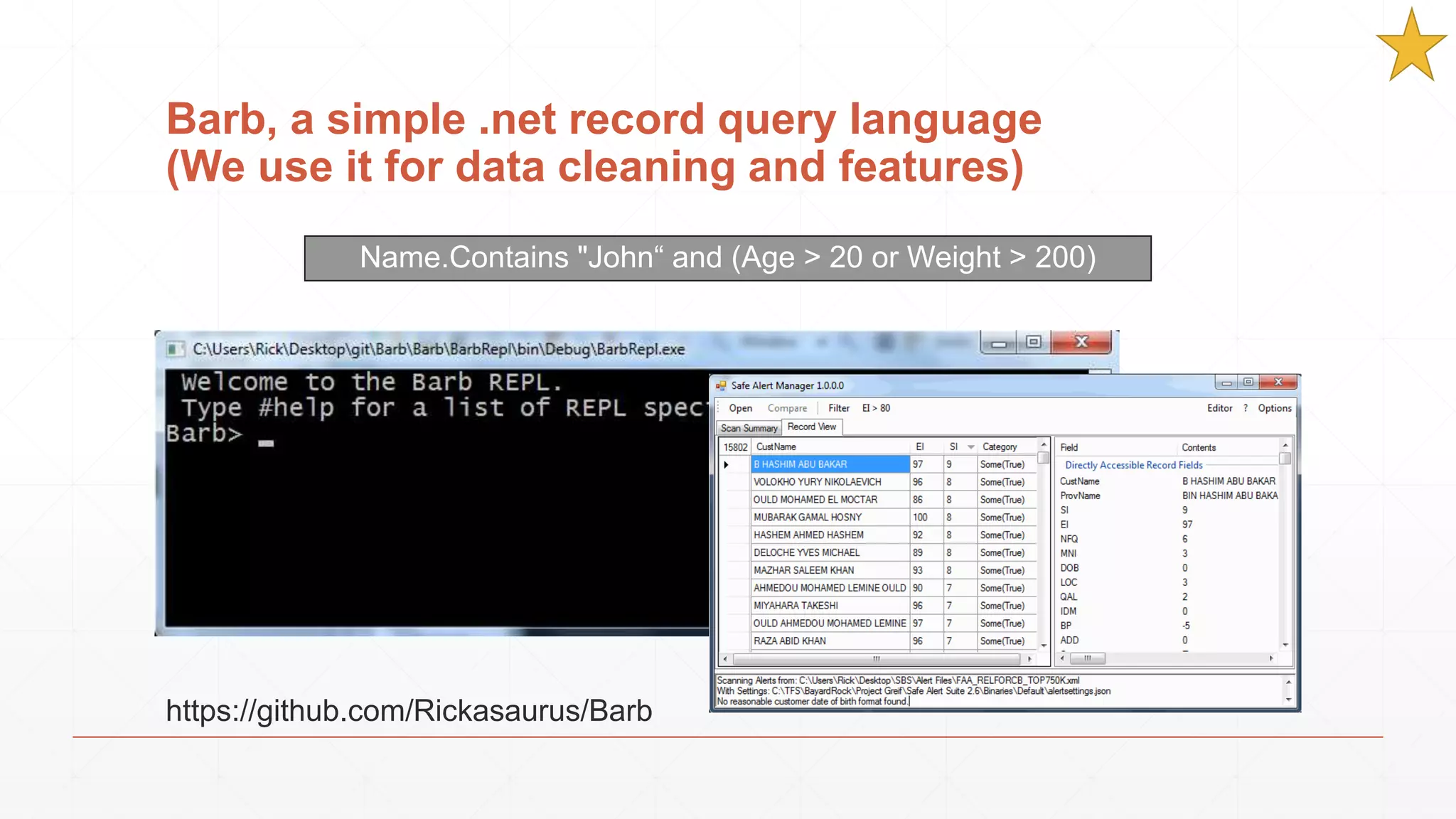
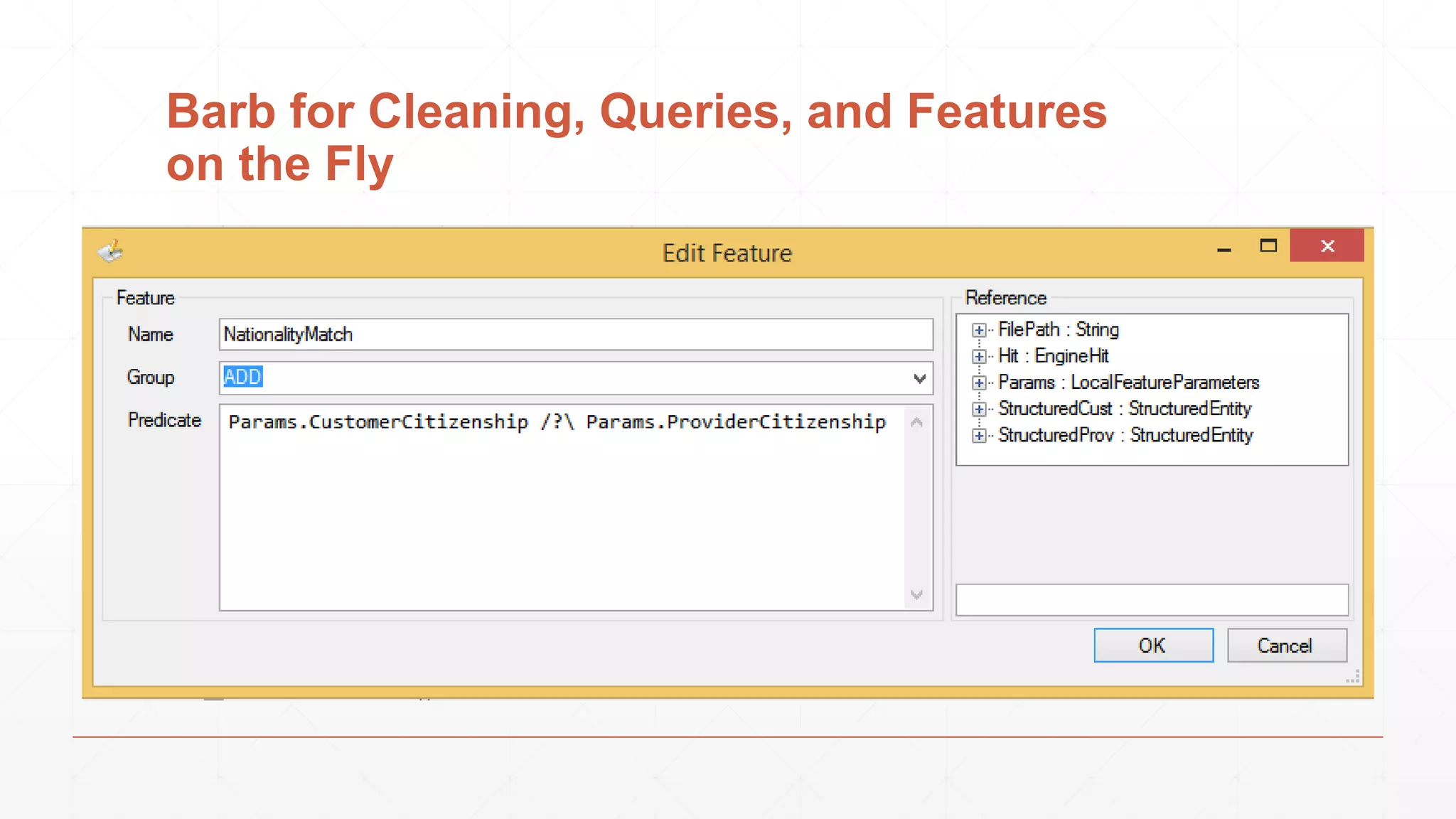
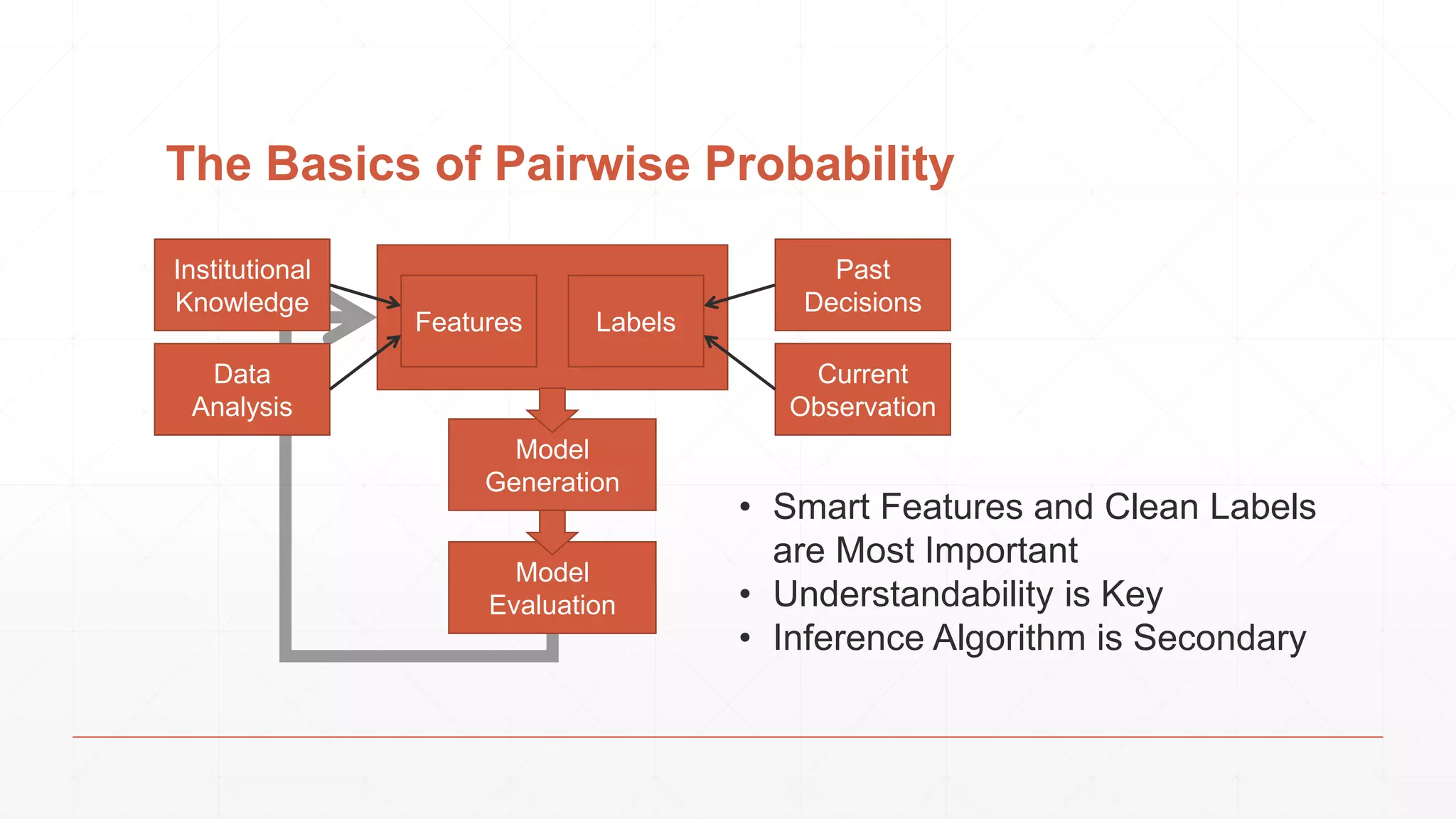
The document discusses techniques in functional programming used for entity resolution to identify money laundering and associated bad actors through customer and bad guy datasets. It highlights methods like blocking, scoring, and risk calculation to efficiently process and correlate large quantities of data while addressing issues like missing or poor-quality data. Additionally, it emphasizes the importance of feature engineering and algorithm choice in enhancing the accuracy of entity matching models.














![Suffix Trees/Arrays Images care of: http://alexbowe.com/fm-index/ Input length: n, Search length: m • Construction in O(n) KS[2003] • Search in O(m) AKO[2004] • Space is 4n Bytes Naively • Compressed Space O(n*H(T)) + o(n) Where T is the input text Newer: Compressed Compact SA How to Introduce Fuzziness?](https://image.slidesharecdn.com/cuny2015b-findingthebadguyswithfunctionalprogramming-151020201950-lva1-app6891/75/How-We-Use-Functional-Programming-to-Find-the-Bad-Guys-28-2048.jpg)




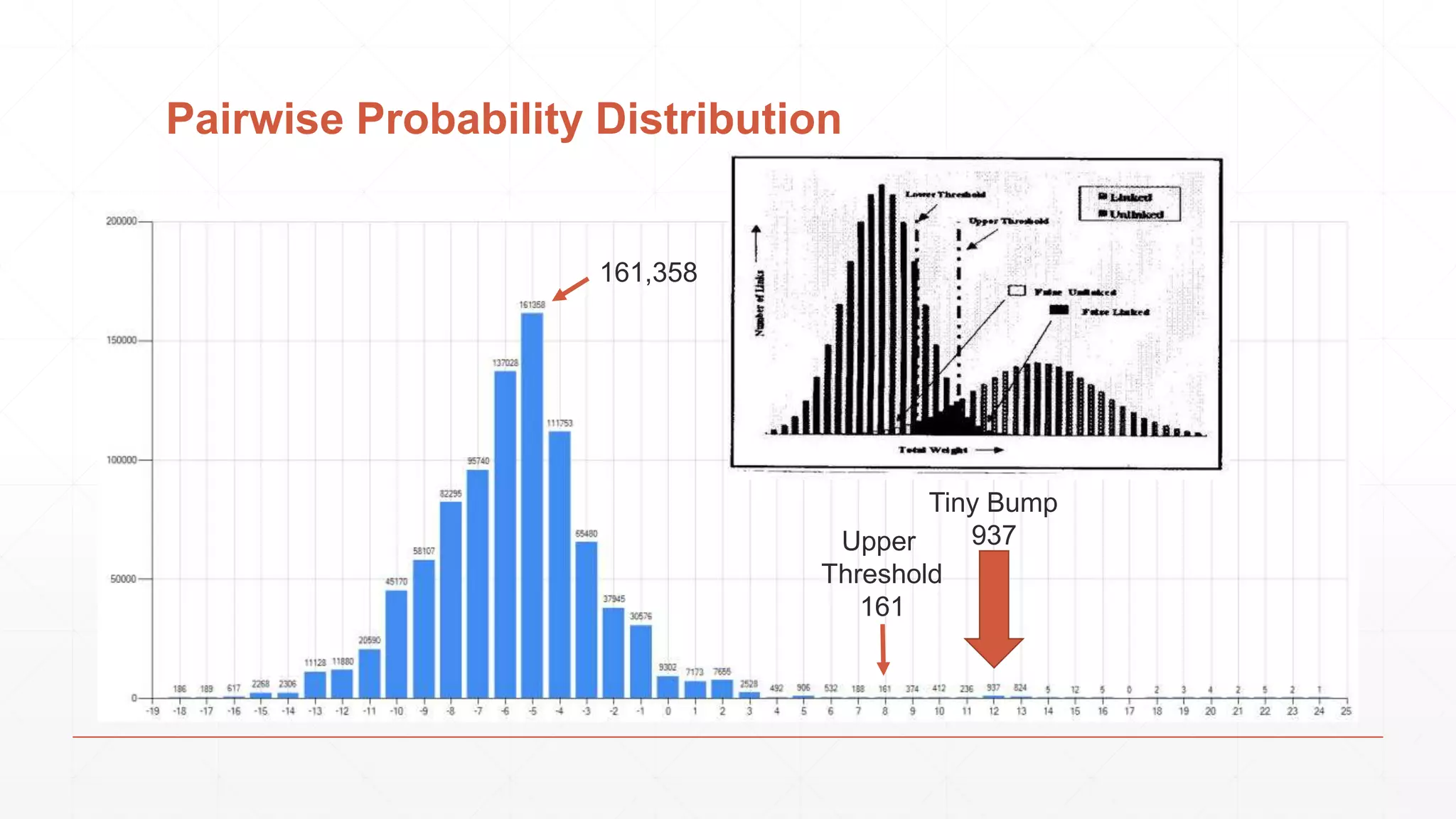
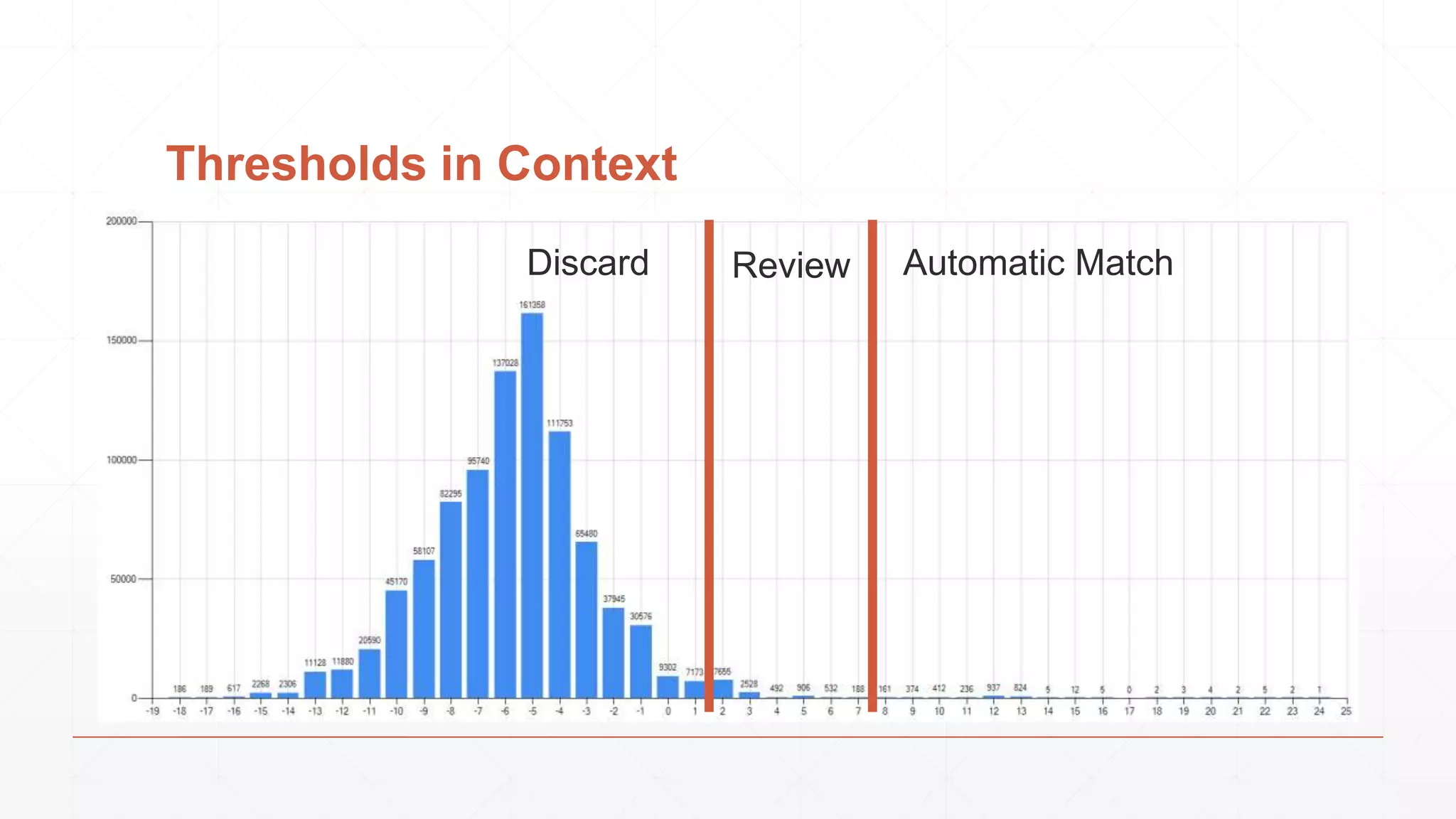
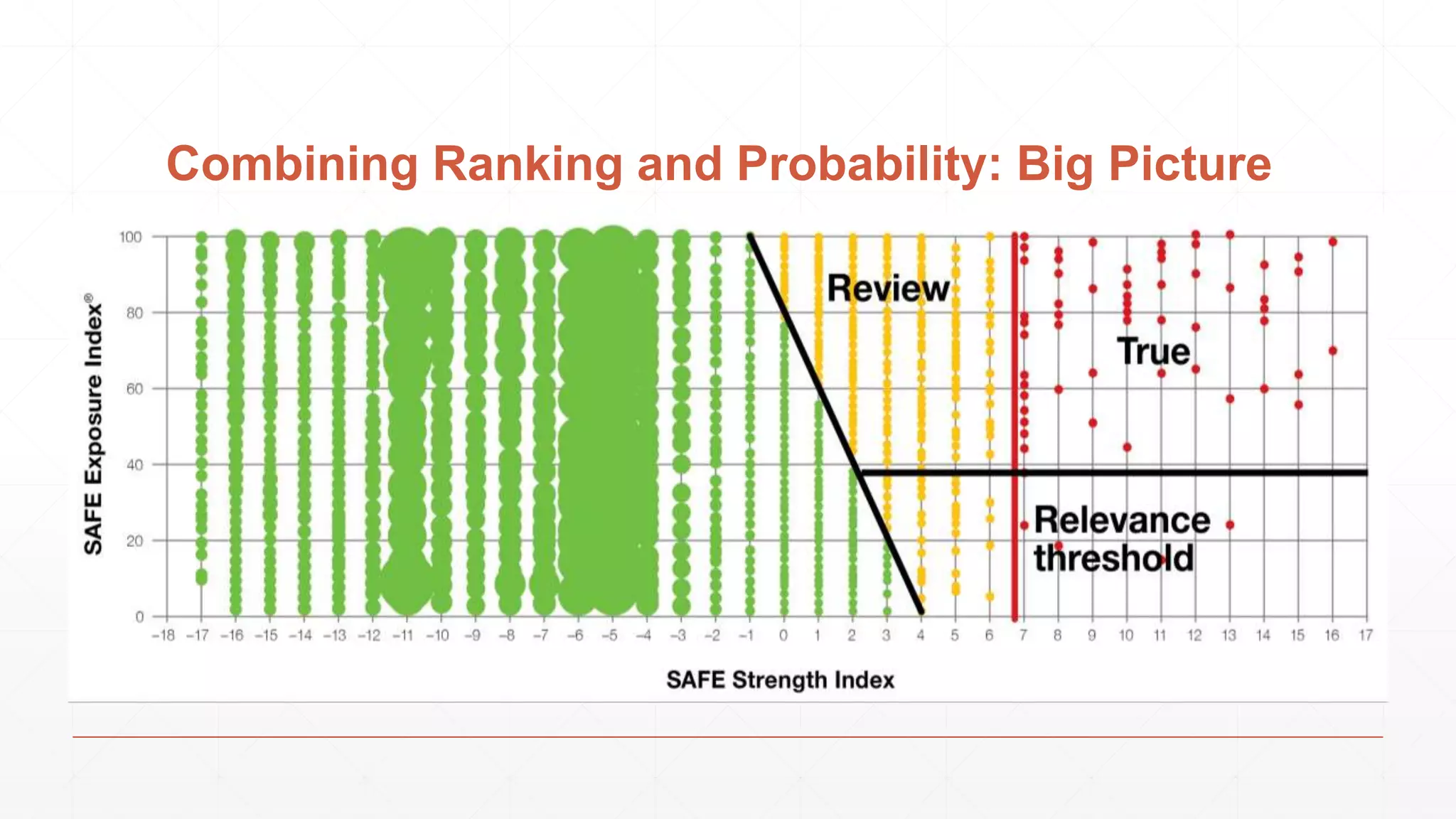
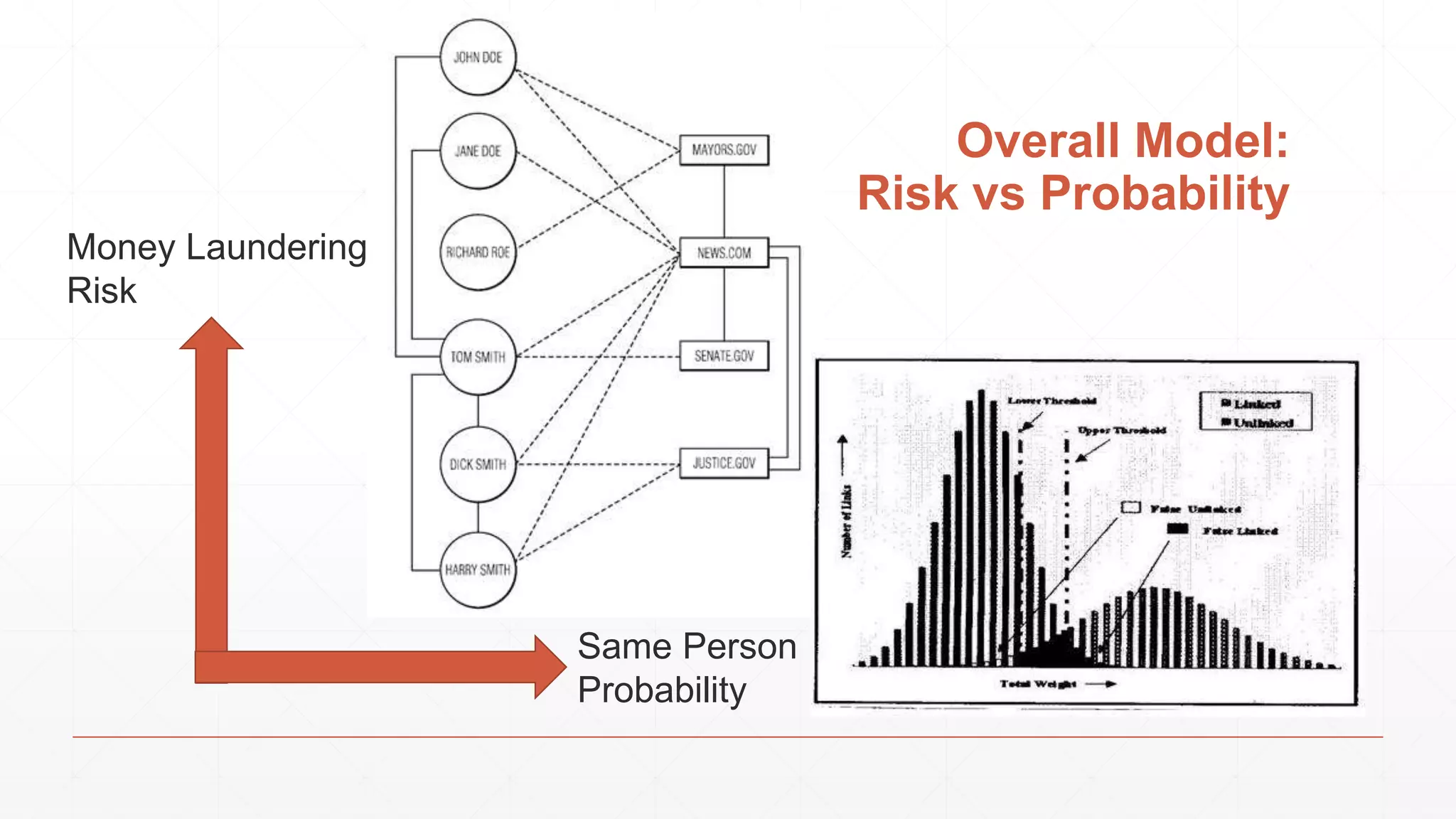
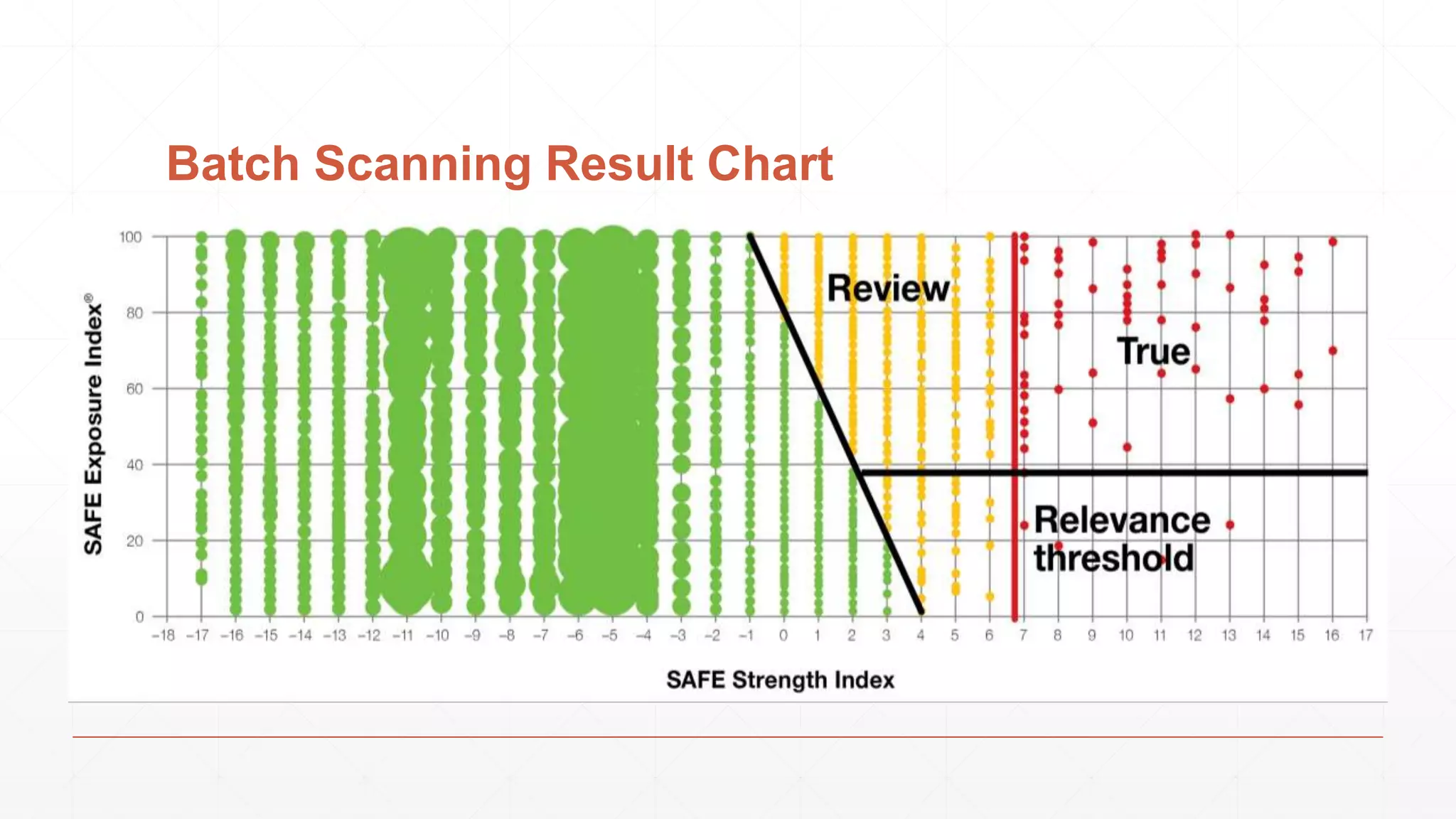
![Simplest: Empirical Summed Similarity ▪ F: feature functions (0 .. m) : (a,b) -> [0, 1] ▪ W: feature weights (0 .. m) : {0+} ▪ 𝑆𝑖𝑚𝑆𝑢𝑚(𝑎, 𝑏) = 𝑖=0 𝑚 𝑓𝑖 𝑤𝑖 Thresholds such that: Match: SimSum(a,b) >= Upper Review: Lower <= SimSum(a,b) <= Upper Discard: SimSum(a,b) <= Lower Image Via: https://www.cs.umd.edu/class/spring2012/cmsc828L/Papers/HerzogEtWires10.pdf](https://image.slidesharecdn.com/cuny2015b-findingthebadguyswithfunctionalprogramming-151020201950-lva1-app6891/75/How-We-Use-Functional-Programming-to-Find-the-Bad-Guys-35-2048.jpg)