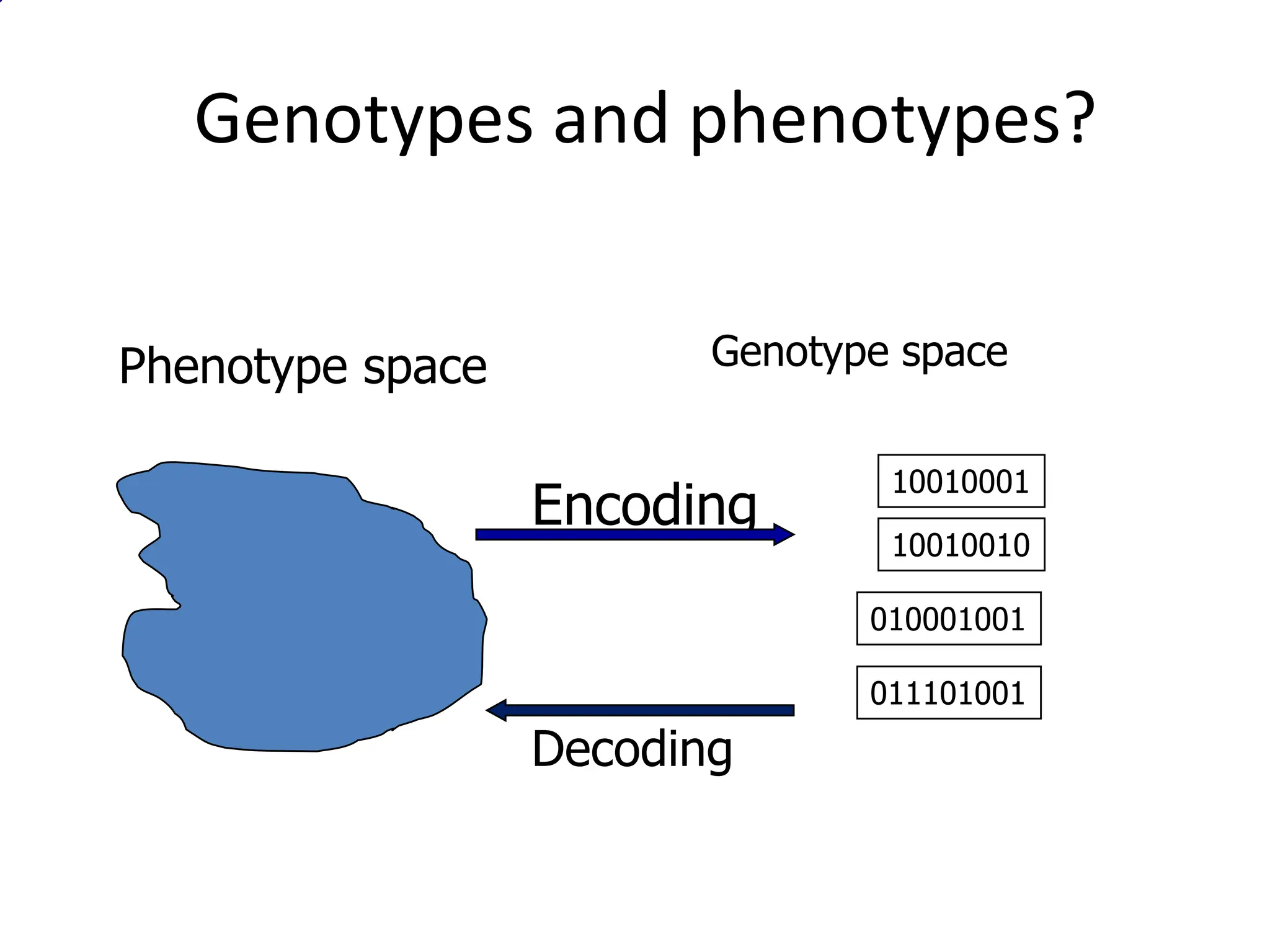
The document discusses genetic algorithms, which are a class of optimization algorithms inspired by biological evolution. It describes the key components of genetic algorithms, including encoding solutions as chromosomes, initializing a population randomly, evaluating fitness, and applying genetic operators like crossover and mutation to produce new generations. The goal is to evolve increasingly fit solutions over many iterations until an optimal or near-optimal solution is found for the given problem.





























![Example: Curve fitting with reproduction operator Consider y = ax2 + bx + c “genes” are a, b, c “chromosome” is the array [a, b, c] What’s the best way to combine two chromosomes into one? We could choose the first half of one and the second half of the other: [a, b, c] We can choose genes randomly: [a, b, c] You could compute “gene averages:” [(a+a)/2, (b+b)/2, (c+c)/2]](https://image.slidesharecdn.com/ga1-240401004116-21b86530/75/generic-optimization-techniques-lecture-slides-31-2048.jpg)
![Example: Curve fitting with reproduction operator Consider y = ax2 + bx + c “genes” are a, b, c “chromosome” is the array [a, b, c] What’s the best way to combine two chromosomes into one? We could choose the first half of one and the second half of the other: [a, b, c] We can choose genes randomly: [a, b, c] You could compute “gene averages:” [(a+a)/2, (b+b)/2, (c+c)/2]](https://image.slidesharecdn.com/ga1-240401004116-21b86530/75/generic-optimization-techniques-lecture-slides-32-2048.jpg)




