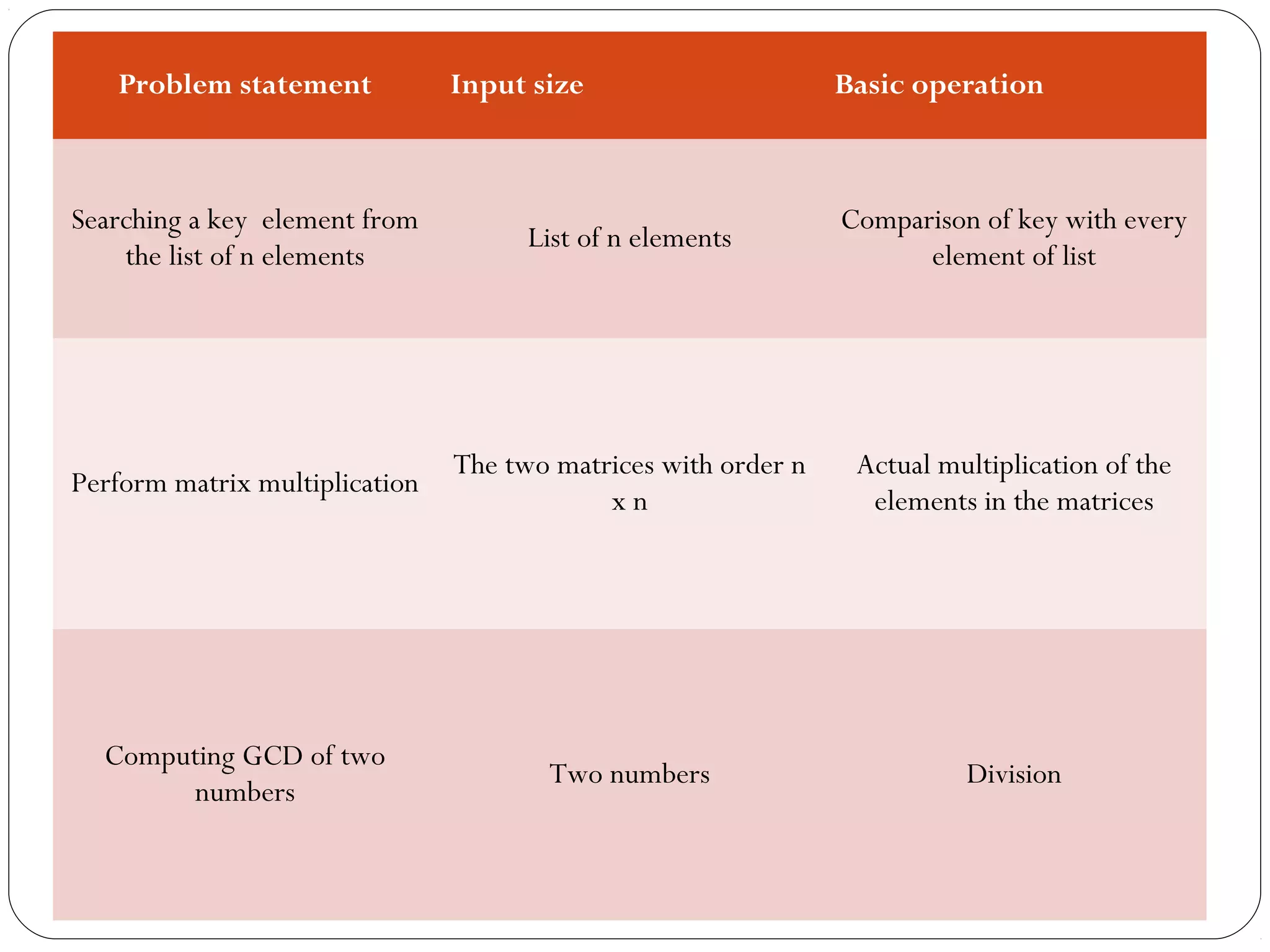
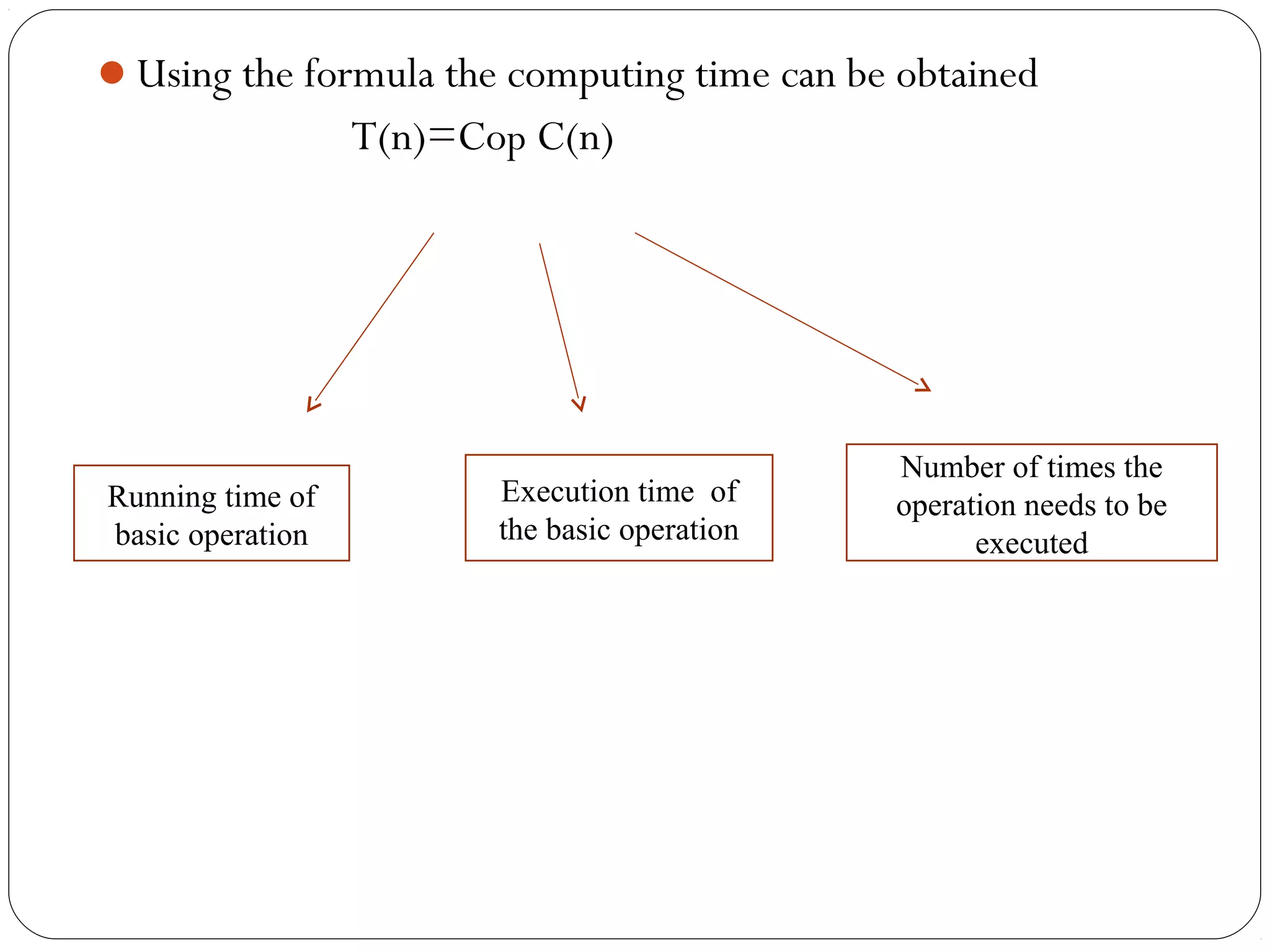
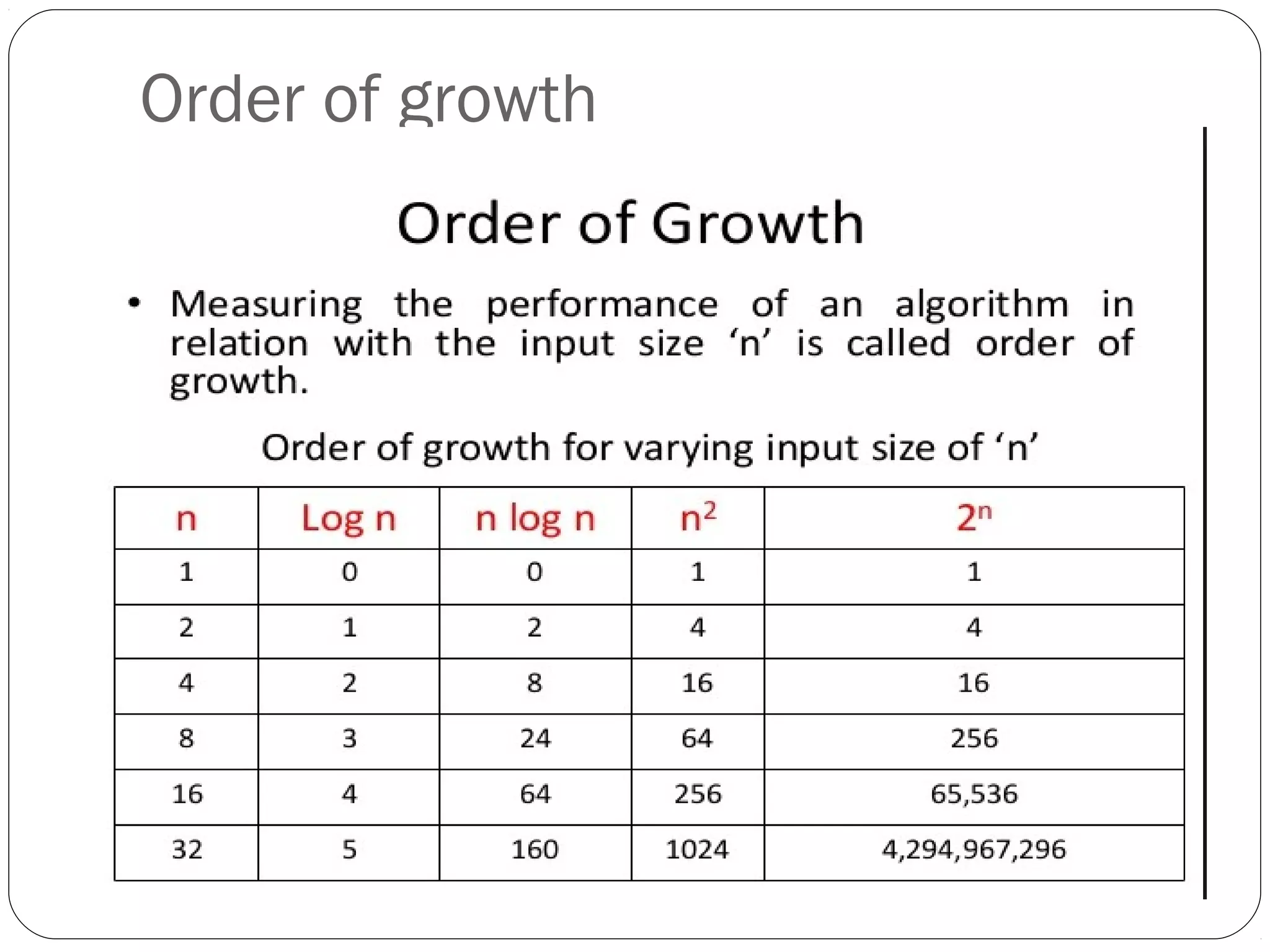
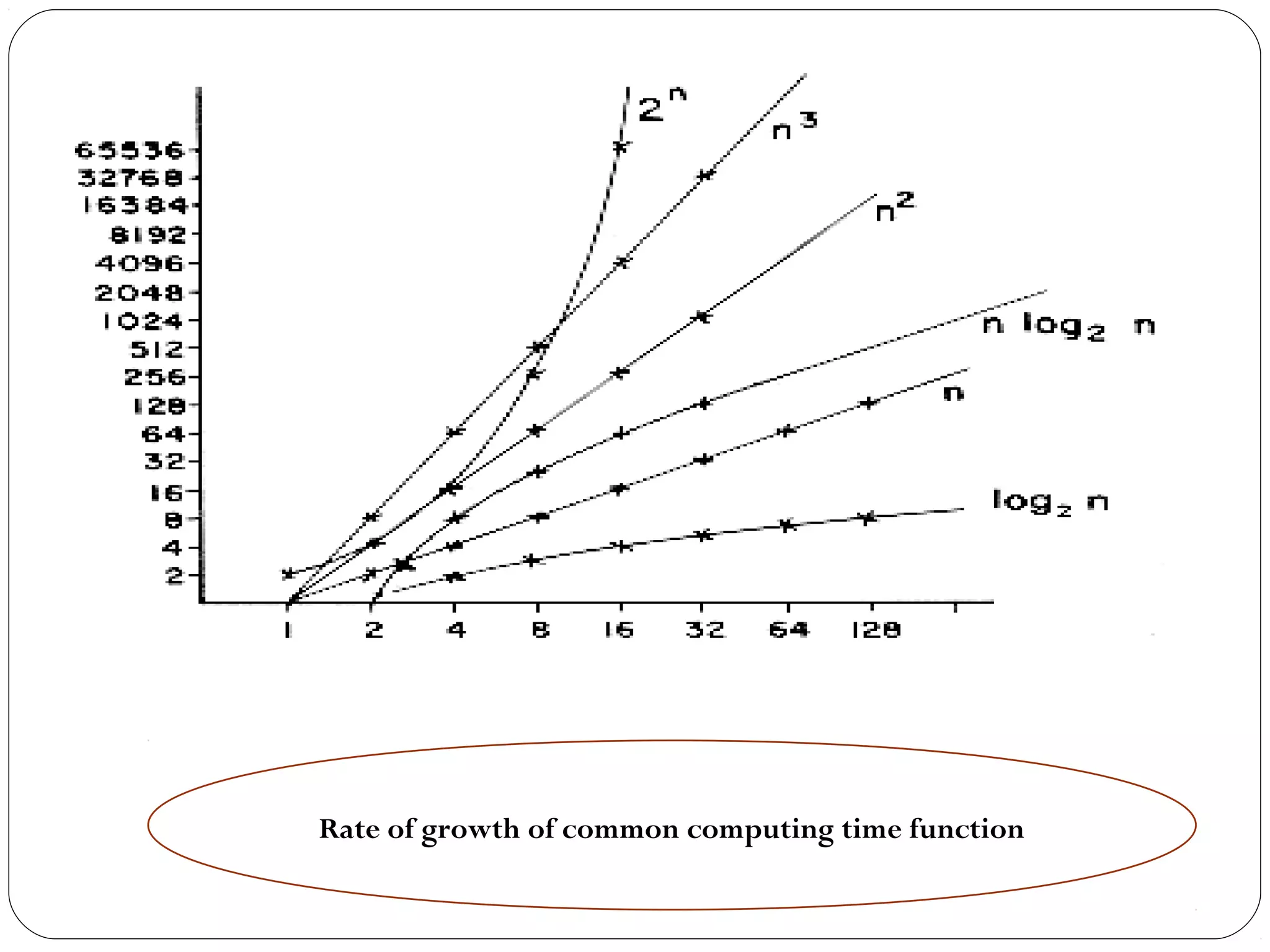
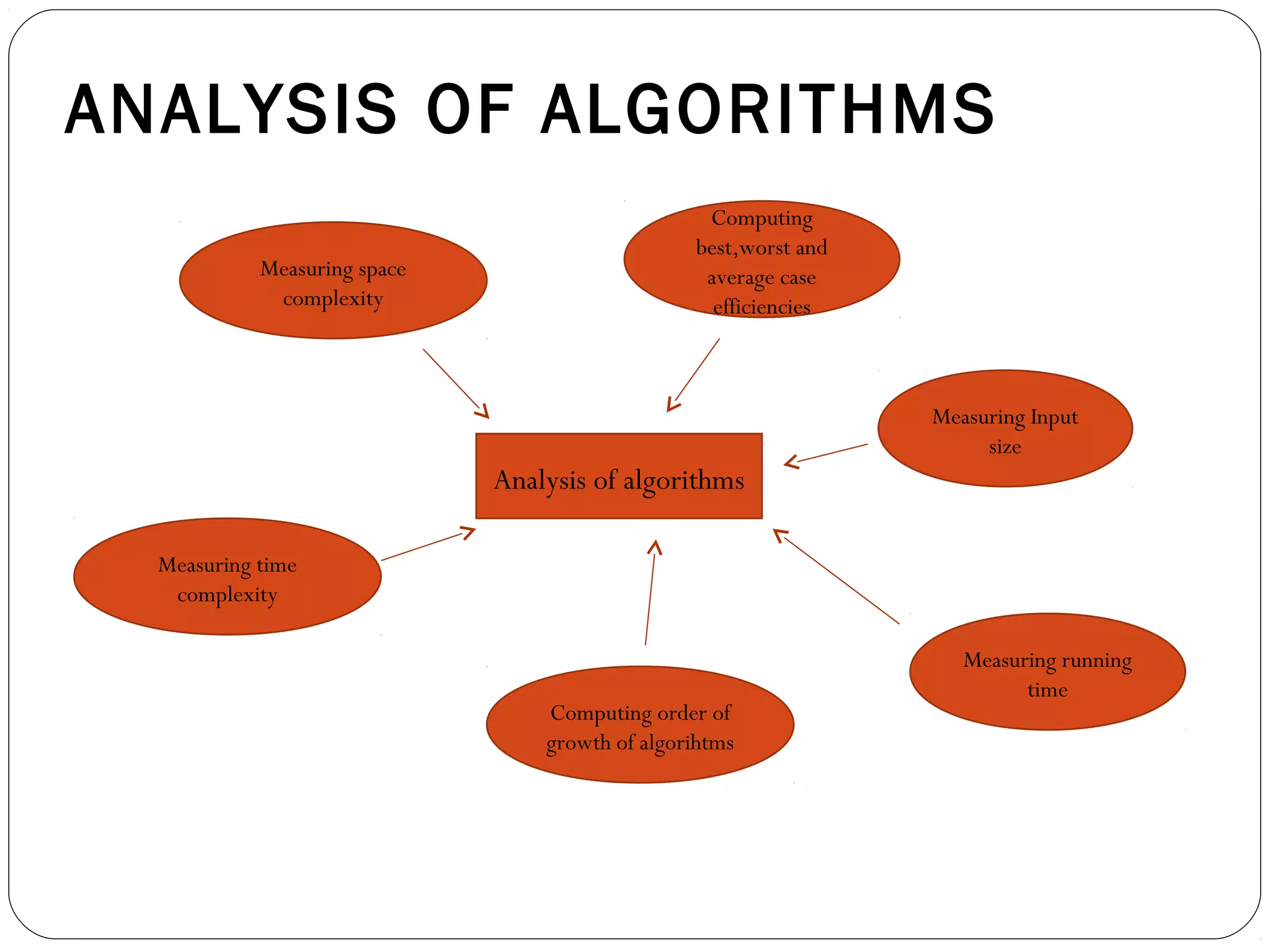
This document discusses analyzing the efficiency of algorithms. It introduces the framework for analyzing algorithms in terms of time and space complexity. Time complexity indicates how fast an algorithm runs, while space complexity measures the memory required. The document outlines steps for analyzing algorithms, including measuring input size, determining the basic operations, calculating frequency counts of operations, and expressing efficiency in Big O notation order of growth. Worst-case, best-case, and average-case time complexities are also discussed.






![For eg: Calculating sum of n numbers For(i=0;i<n;i++) { Sum=sum+a[i]; } Statement Frequency count i=0 1 i<n N+1 i++ n Sum=sum+a[i] n Total 3n+2 Time complexity normally denotes in terms of Oh notation(O). Hence if we neglect the constants then we get the time complexity to be O(n)](https://image.slidesharecdn.com/analysisofframework-180105064913/75/Fundamentals-of-the-Analysis-of-Algorithm-Efficiency-8-2048.jpg)
![Eg: Matrics addition For(i=0;i<n;i++) { for(j=0;j<n;j++) { c[i][j]=a[i][j]+b[i][j] } }](https://image.slidesharecdn.com/analysisofframework-180105064913/75/Fundamentals-of-the-Analysis-of-Algorithm-Efficiency-9-2048.jpg)
![The frequency count is: Statement Frequency count i=0 1 i<n N+1 i++ n j=0 N * 1 = n For Initialization Outer loop of j j<n N * (n+1) =n2 + n times For Outer loop j++ n * n = n2 C[i][j]=a[i][j]+b[i][j] n * n = n2 Total 3n2 +4n+2 O(n2 )](https://image.slidesharecdn.com/analysisofframework-180105064913/75/Fundamentals-of-the-Analysis-of-Algorithm-Efficiency-10-2048.jpg)