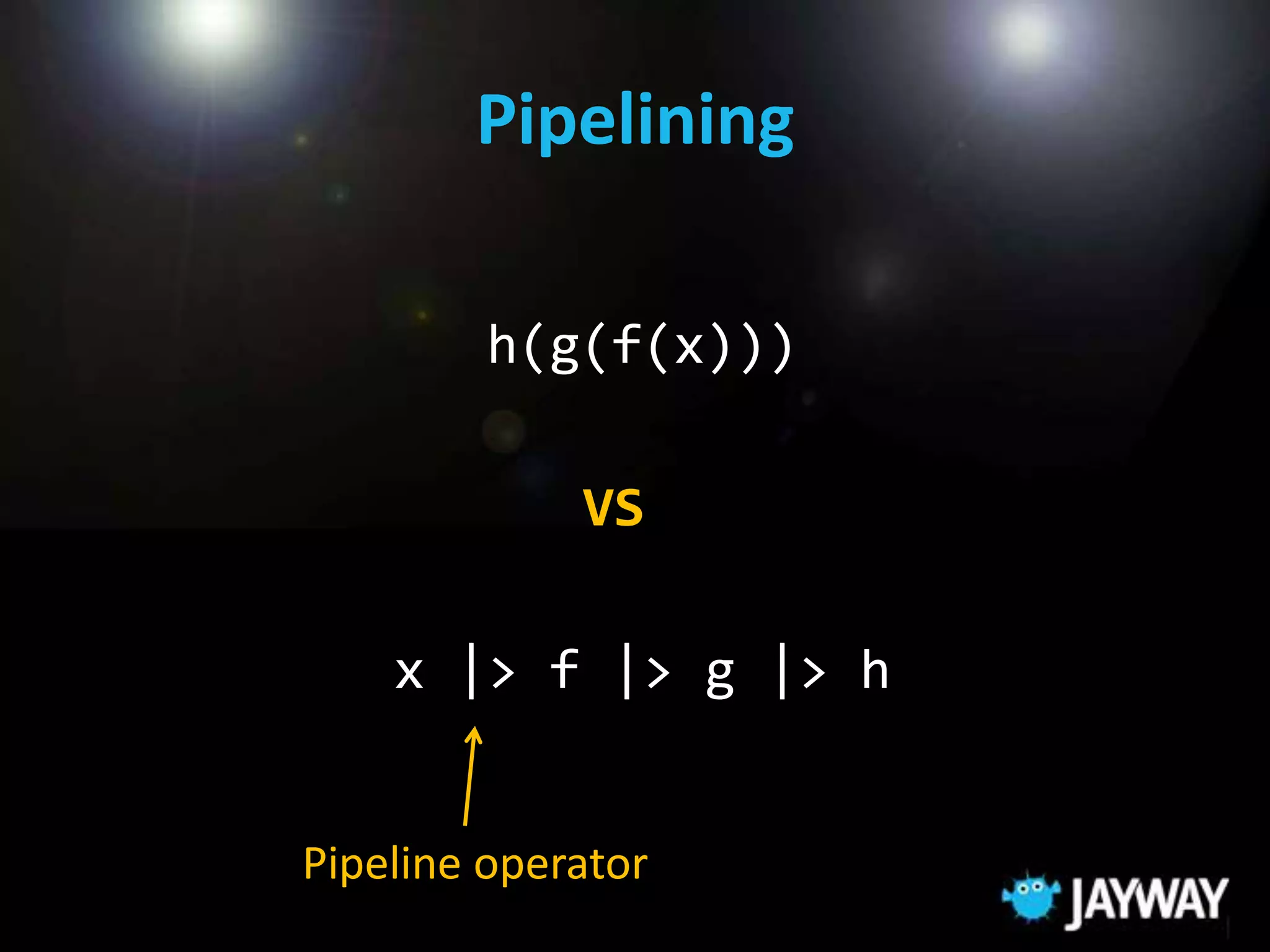
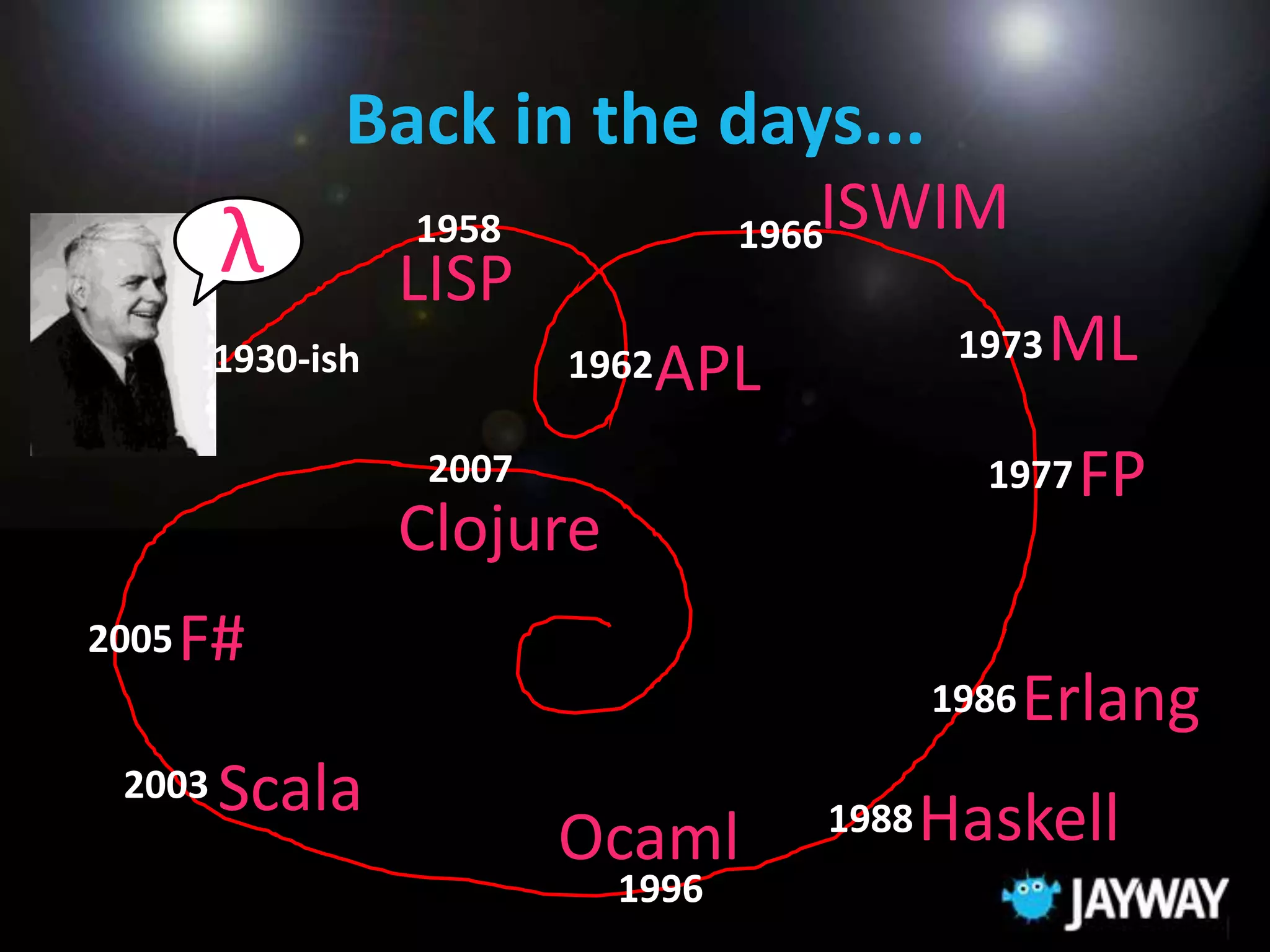
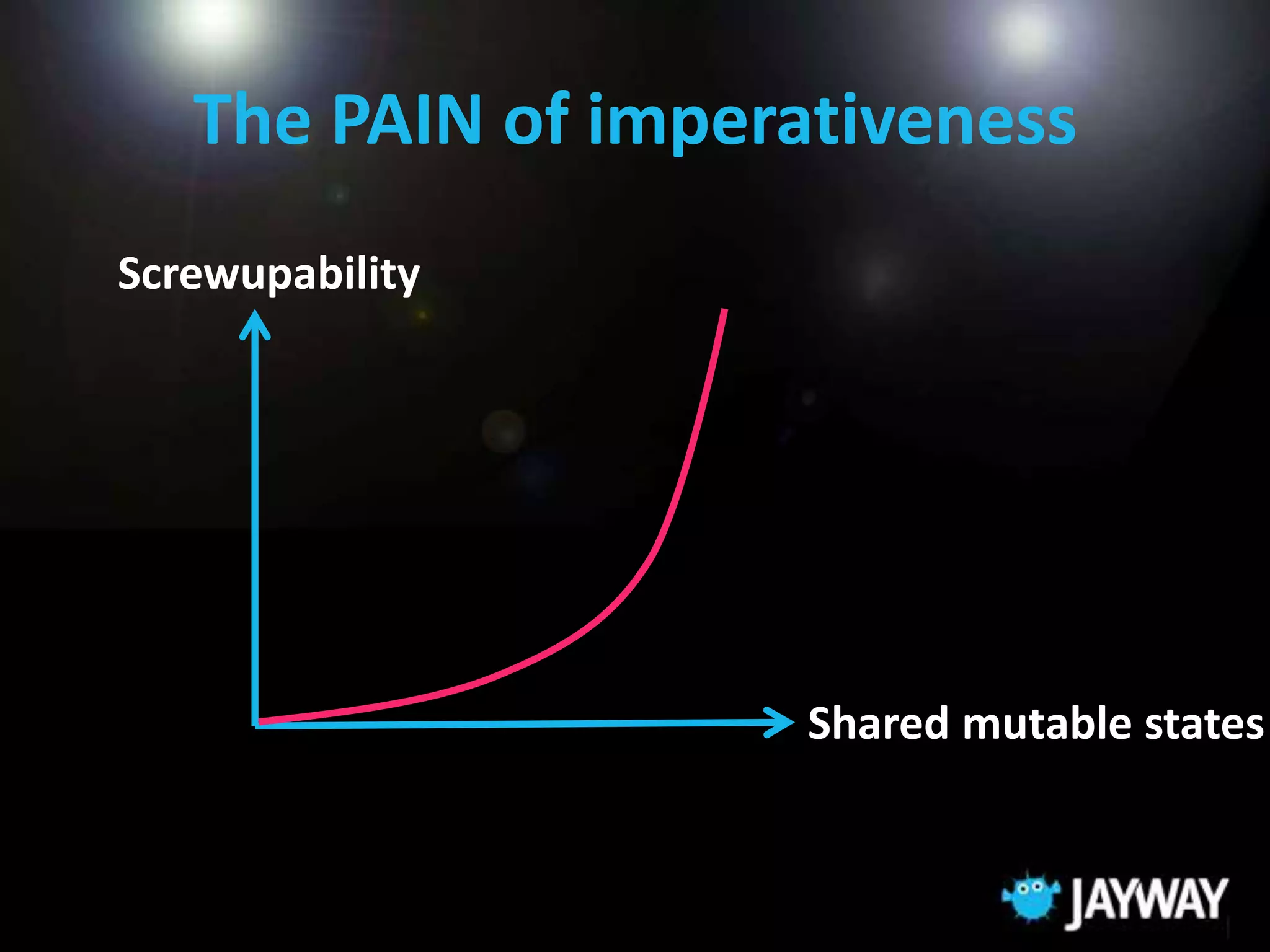
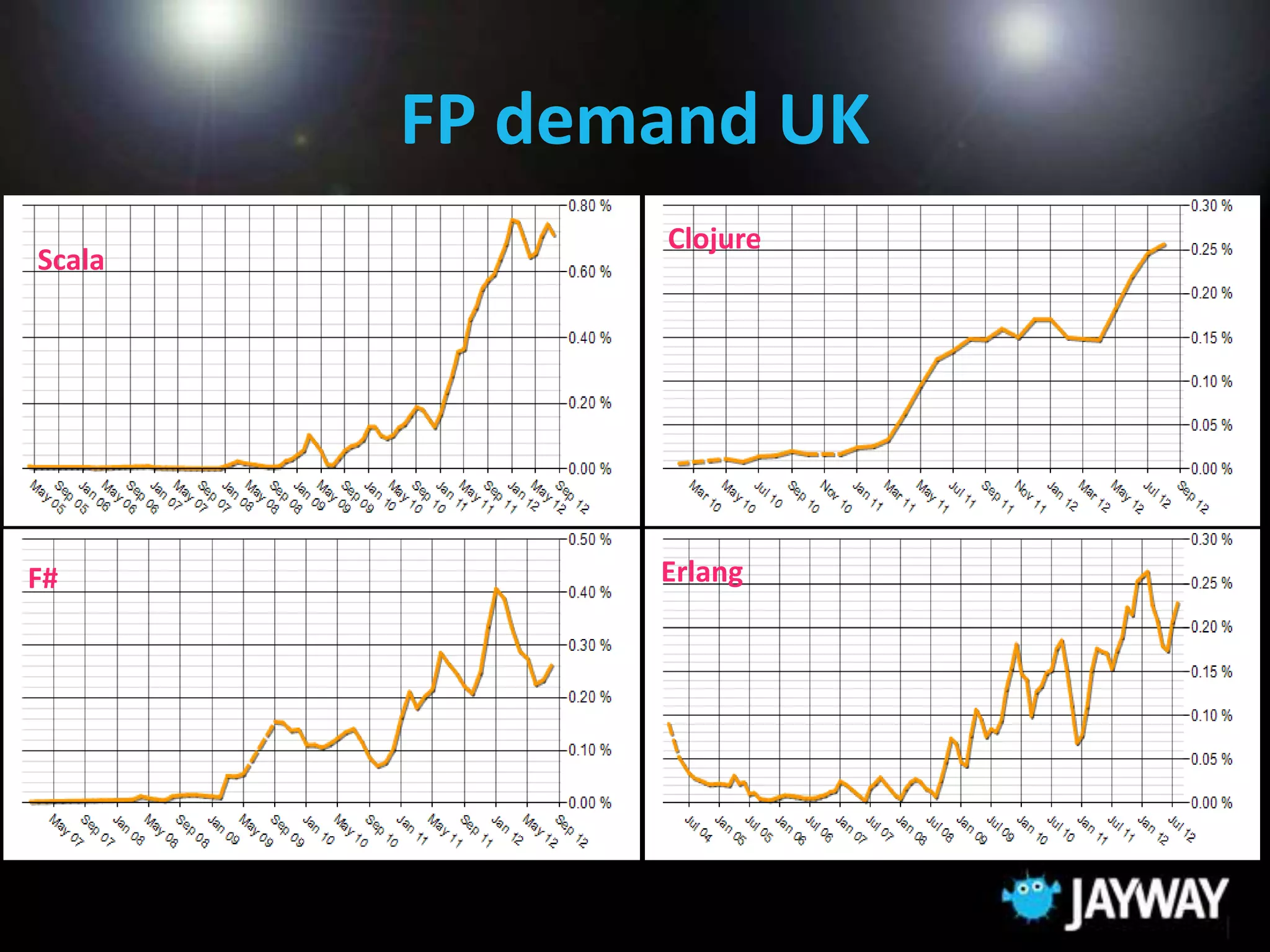
This document provides an overview of functional programming and the F# language. It discusses the benefits of functional programming such as focusing on logic over control flow and side effects. It introduces concepts like declarative programming, immutable data, and higher-order functions. The document also summarizes why F# is a powerful language, as it combines functional, object-oriented, and .NET capabilities. Examples are provided to demonstrate how F# allows writing complex algorithms in a simple, readable way using patterns, functions, and data types.




![Why Functional Programming? let sum lst = foldr (+) lst 0 let product lst = foldr (*) lst 1 let append l1 l2 = foldr cons l1 l2 let length lst = foldr (+) lst 0 let map f lst = foldr (cons << f) lst []](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-7-2048.jpg)












![(Function) values in F# let outer x = let inner y = printfn "outer + inner = %d" (x + y) inner 21 let rec sum list = match list with | [] -> 0 | head::tail -> head + sum tail](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-21-2048.jpg)
![Pattern matching let rec merge l1 l2 = Parallel pattern match l1, l2 with OR pattern | [], xs | xs, [] -> xs | x::xs', (y::_ as ys) when x <= y -> x::merge xs' ys | xs, y::ys' -> y::merge xs ys' Named pattern Guarded pattern](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-22-2048.jpg)






![F# data types - List let l1 = ["a"; "list"; "of"; "strings"] let l2 = "a"::"consed"::"list"::[] let l3 = [1..42] let l4 = [for i in l3 -> i*i]](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-30-2048.jpg)
![Higher-order functions let rec double l = match l with | [] -> List.empty | h::t -> h*2::double t](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-31-2048.jpg)
![Higher-order functions let rec length (l:string list) = match l with | [] -> List.empty | h::t -> h.Length::length t](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-32-2048.jpg)
![Higher-order functions let rec map f l = match l with | [] -> List.empty | h::t -> f(h)::map t](https://image.slidesharecdn.com/functionalprogramminginfsharp-120914132401-phpapp02/75/Functional-programming-in-f-sharp-33-2048.jpg)