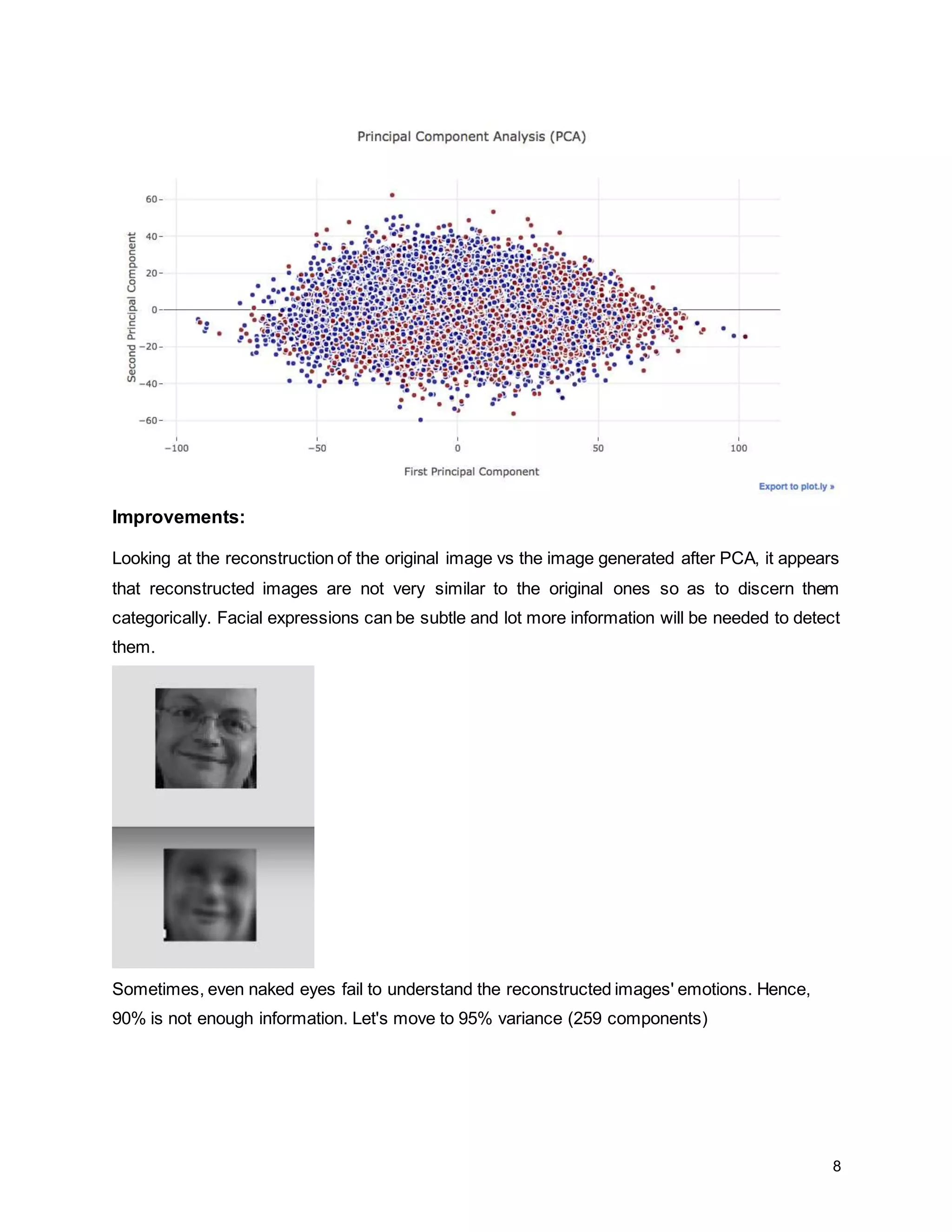
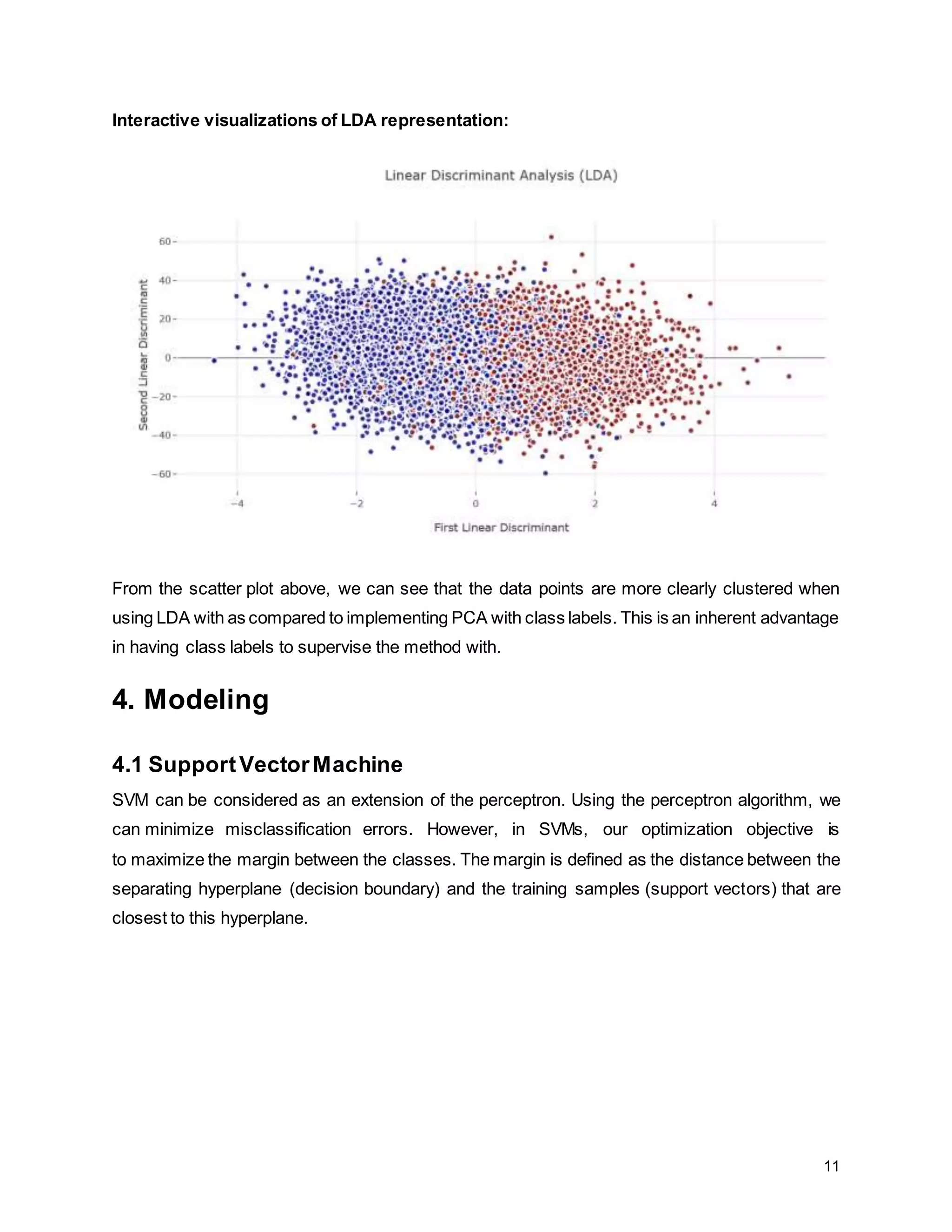
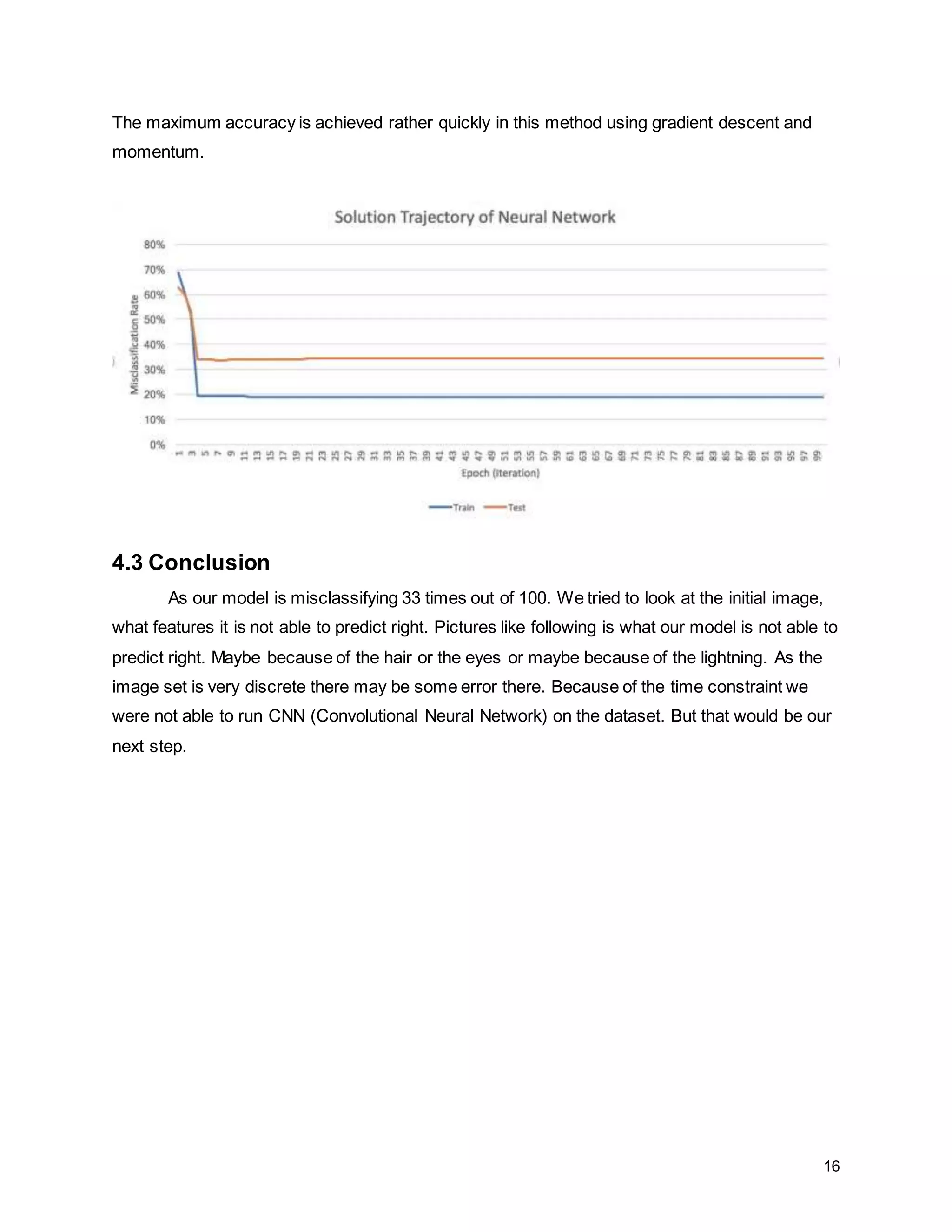
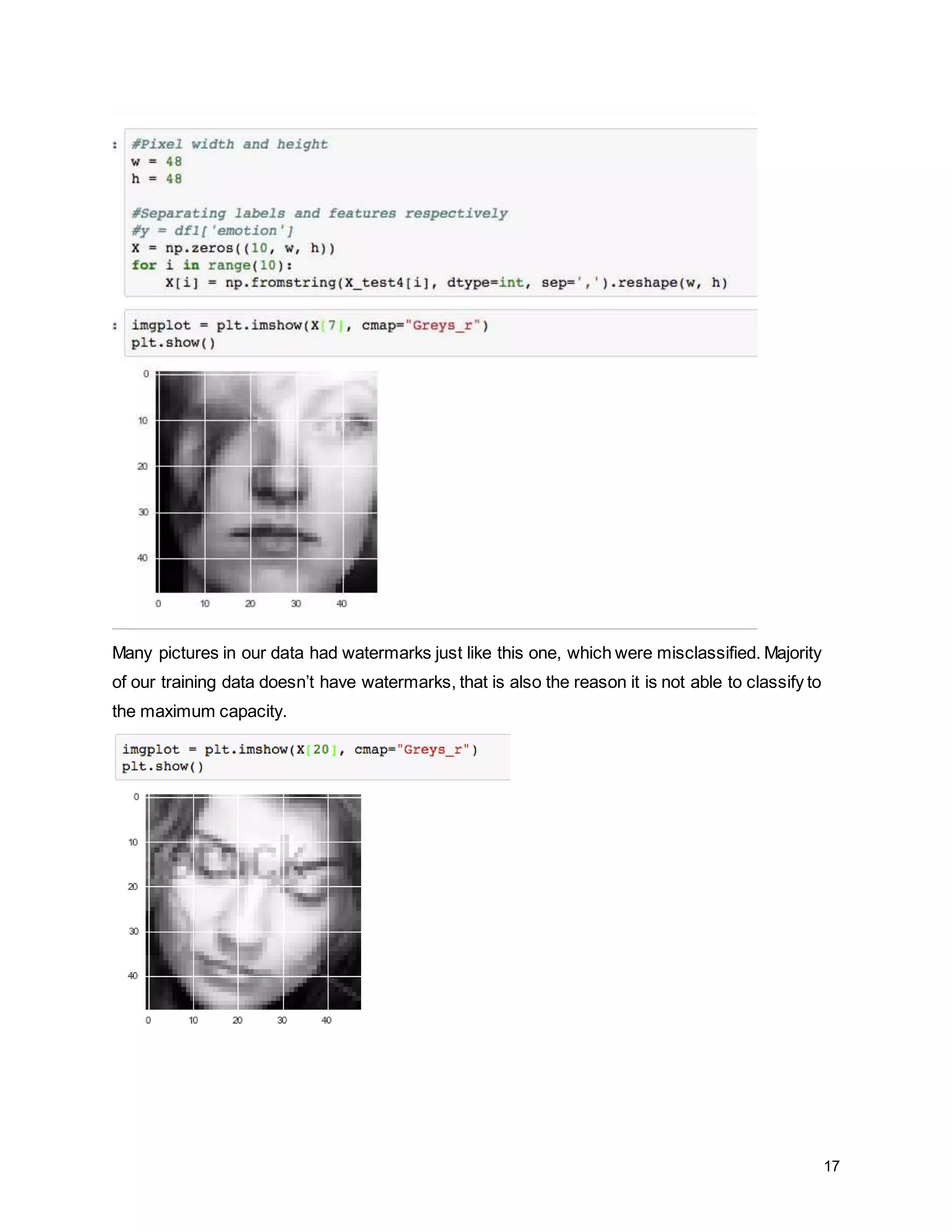
The report details a project focused on facial expression recognition using data science and Python, specifically employing convolutional neural networks (CNN) to classify images as 'happy' or 'sad'. It discusses dataset characteristics, preprocessing methods, dimensionality reduction techniques such as PCA and LDA, and evaluates the performance of machine learning models including support vector machines and neural networks. Future improvements are suggested to include the implementation of CNNs for enhanced classification accuracy.