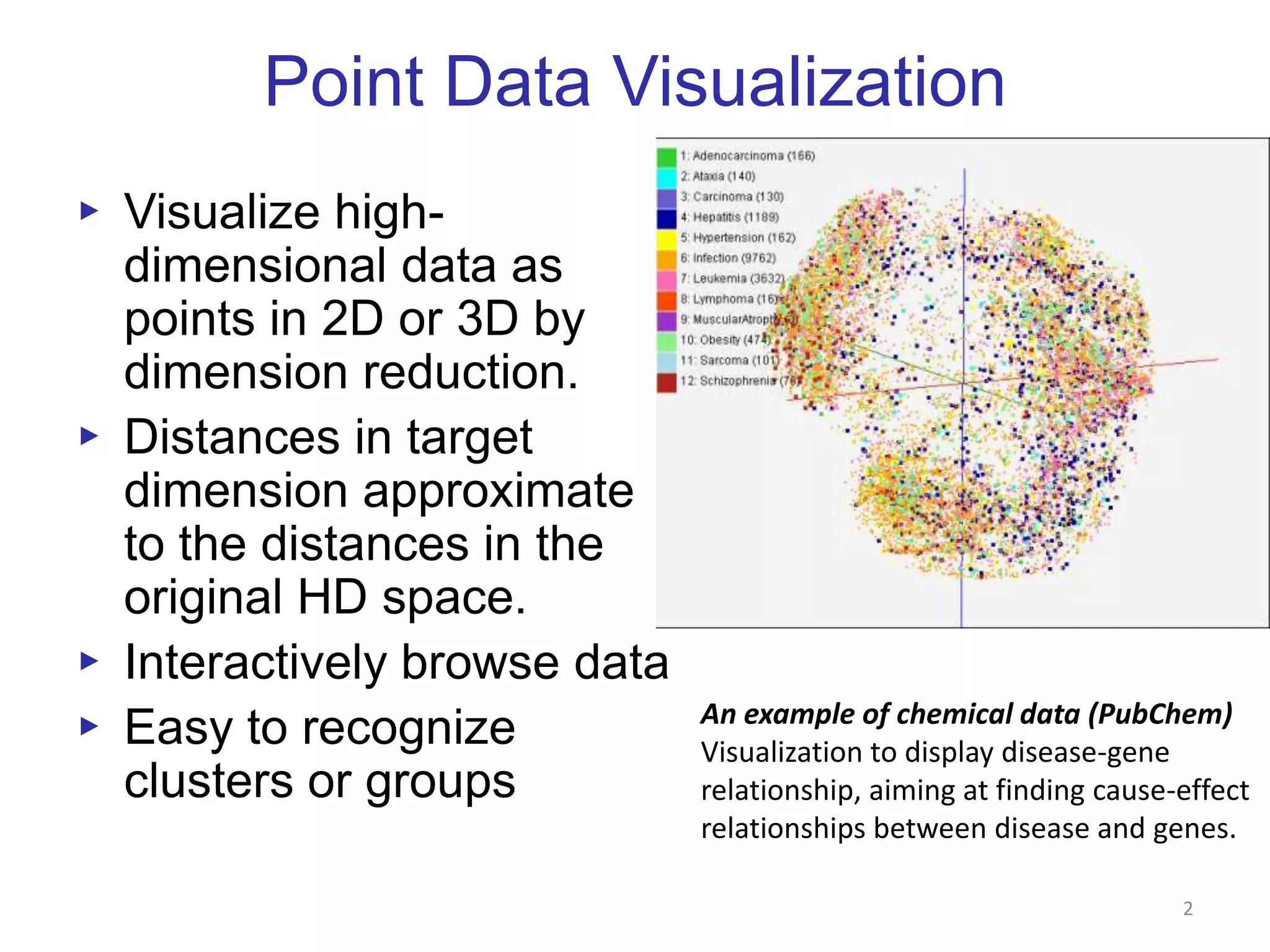
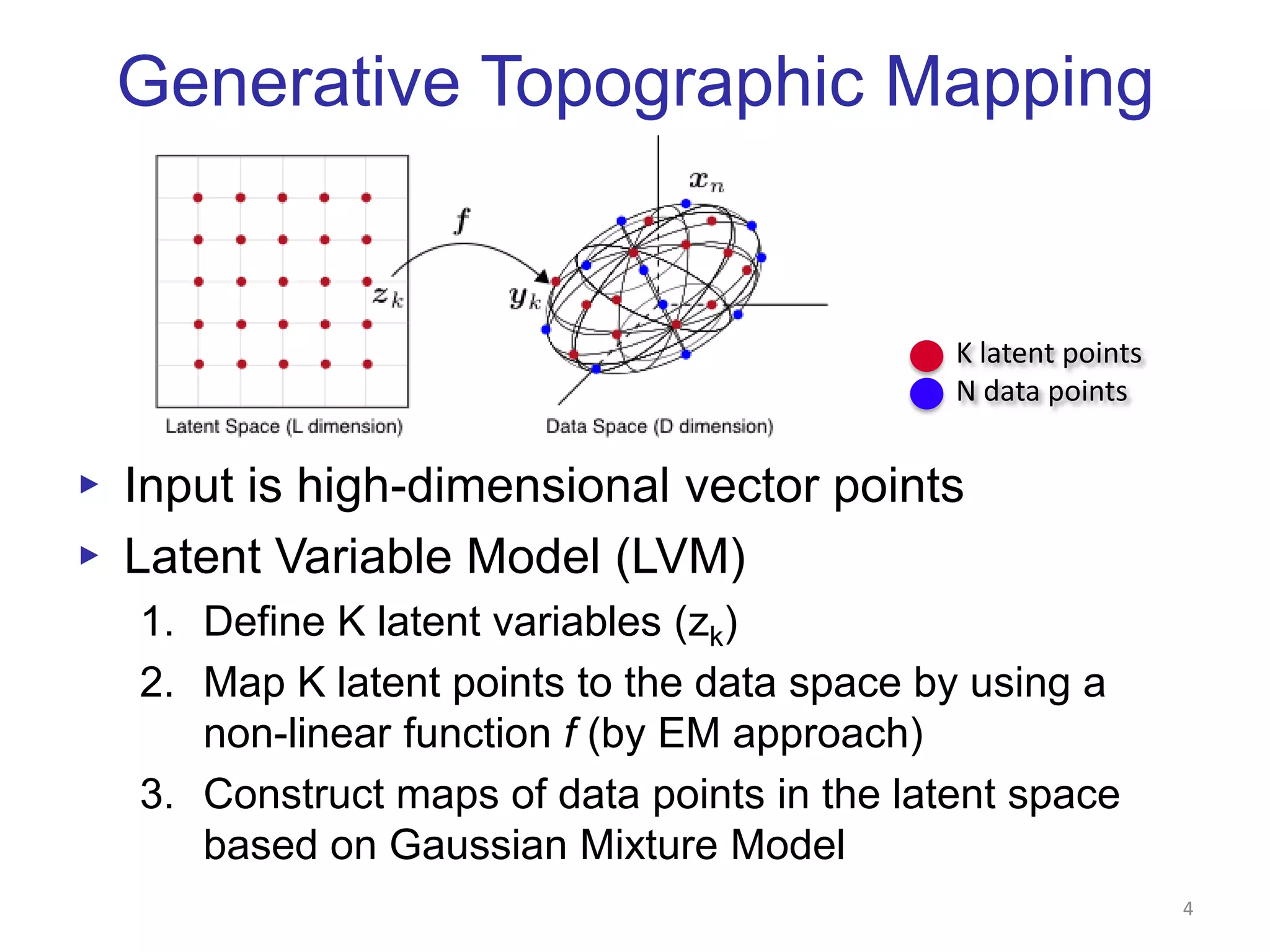
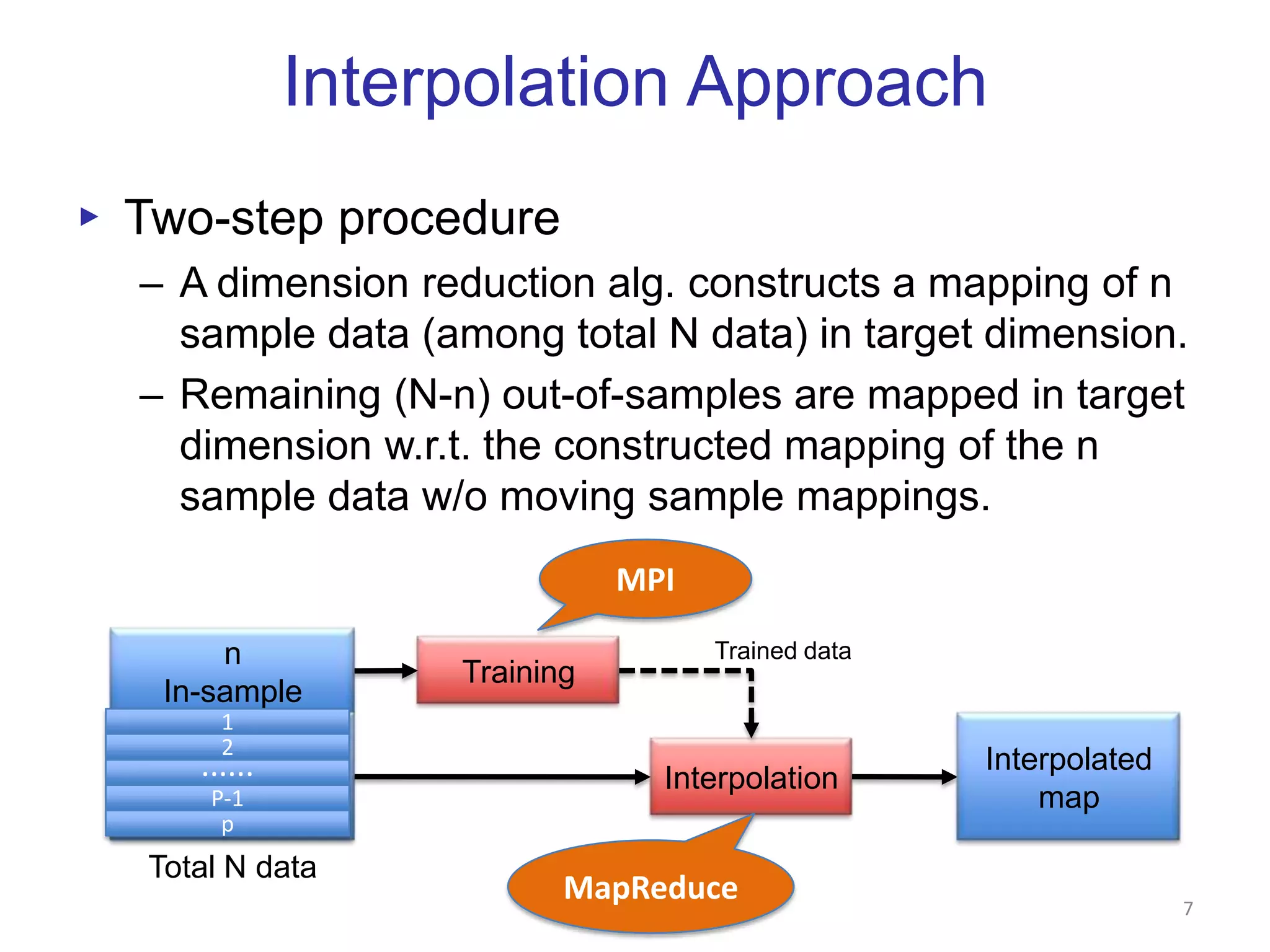
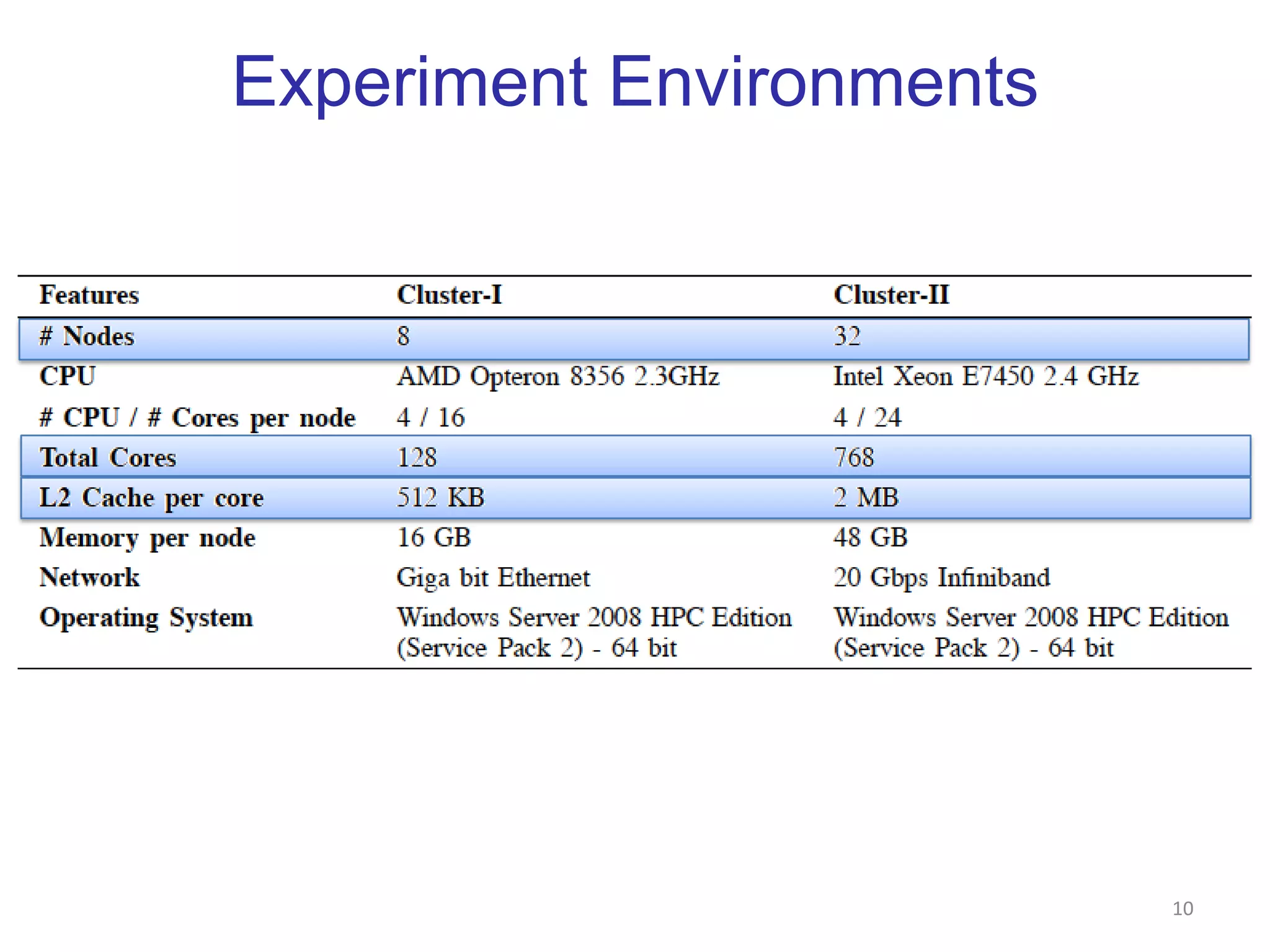
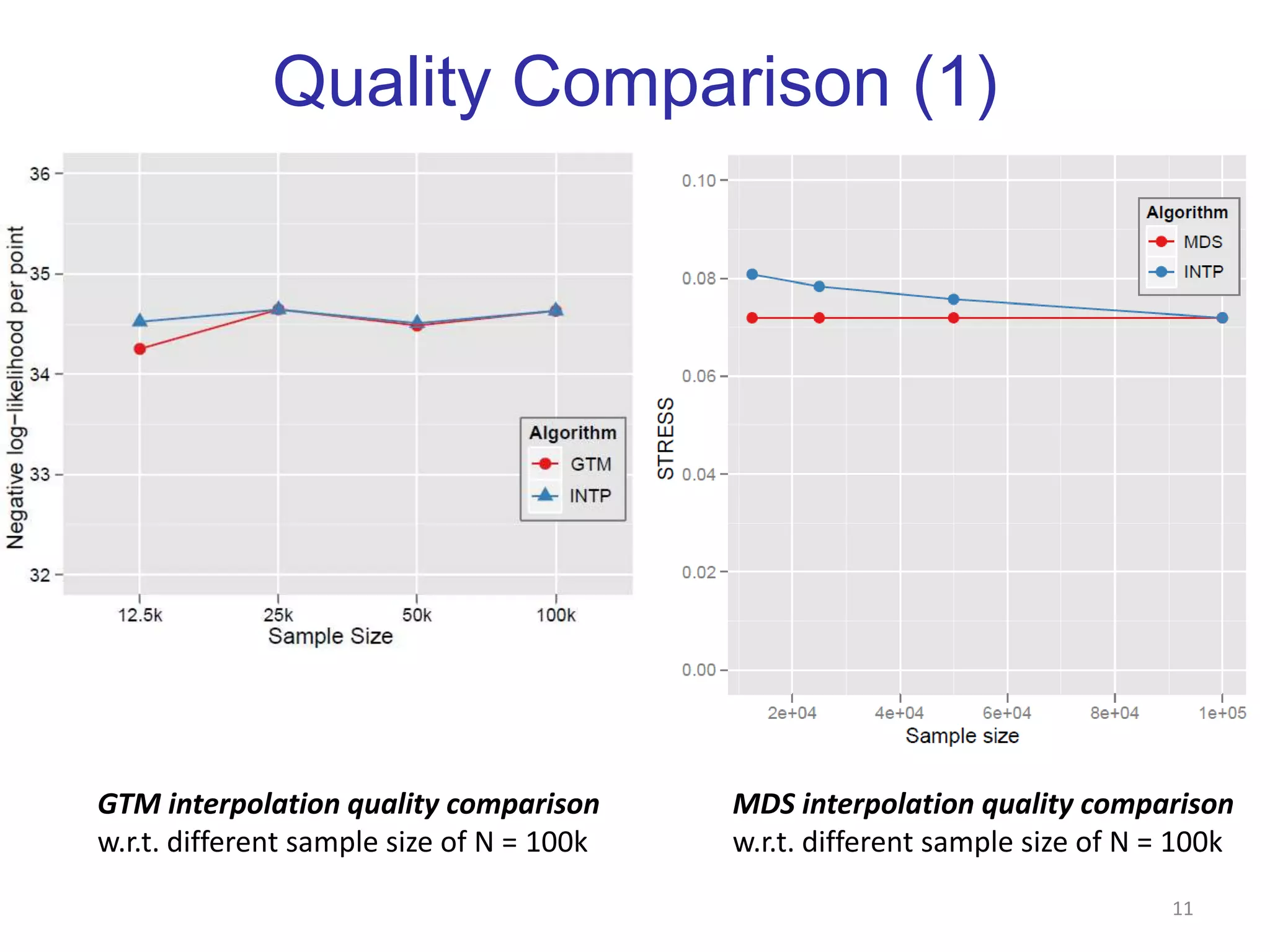
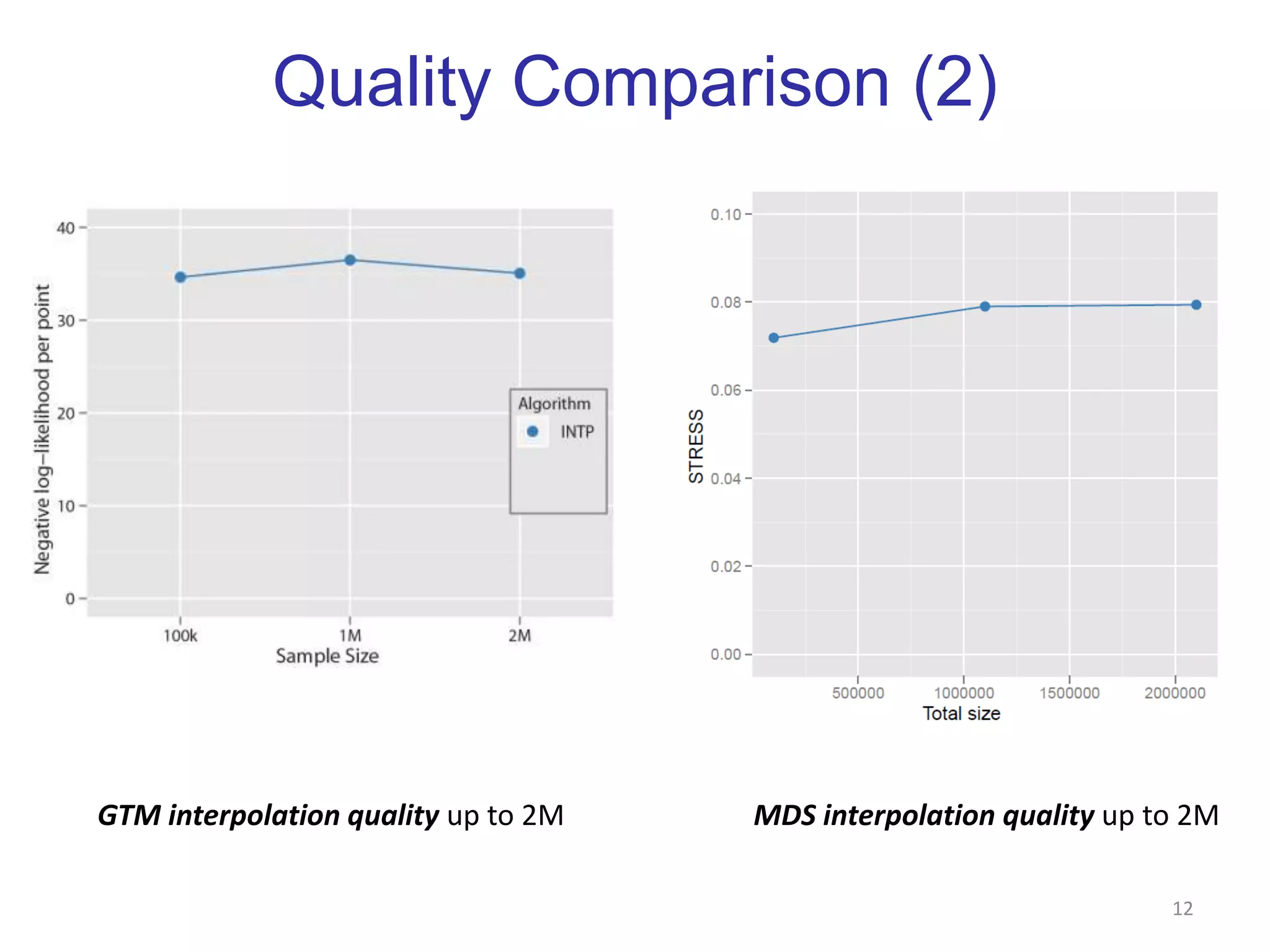
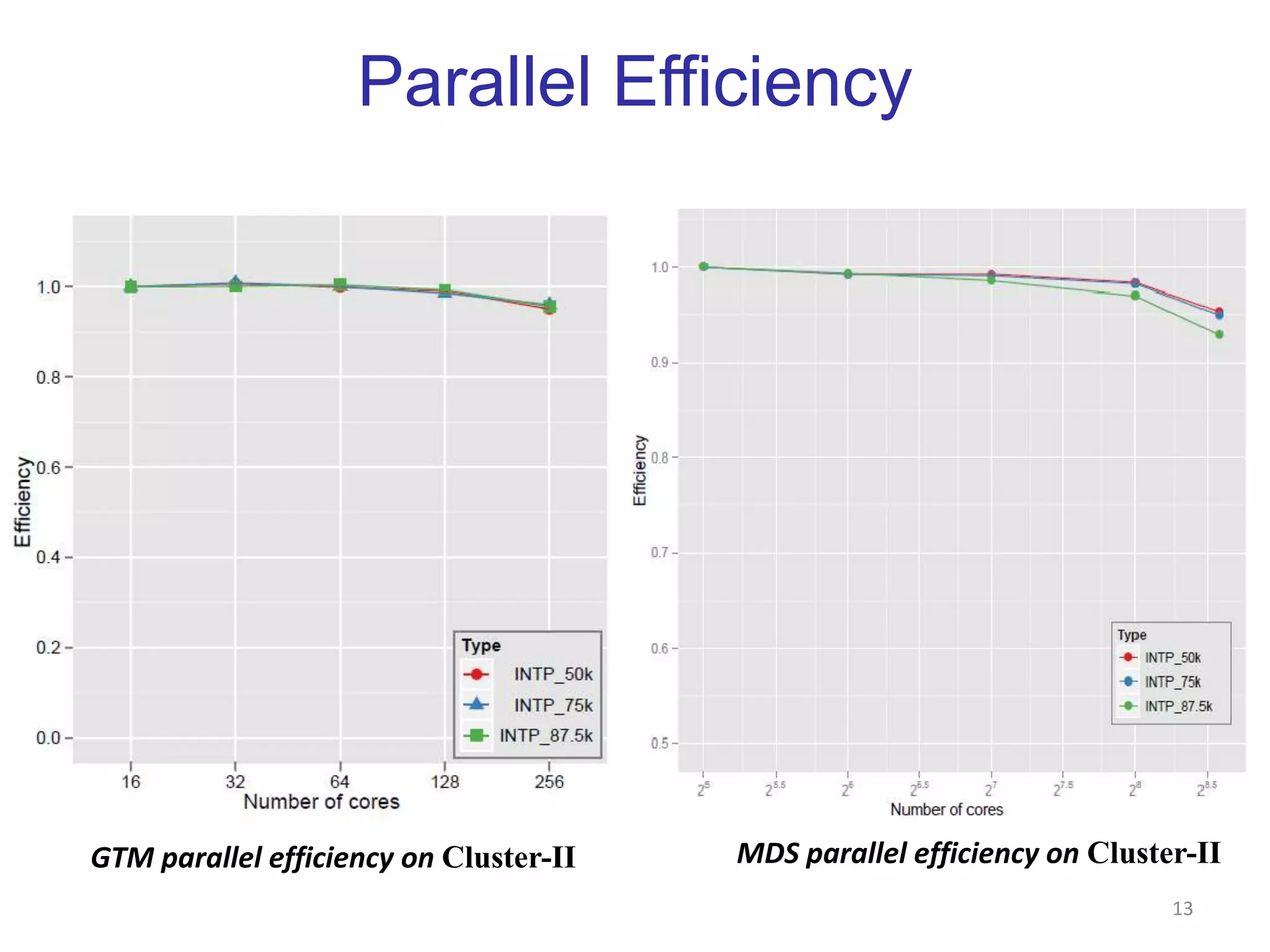
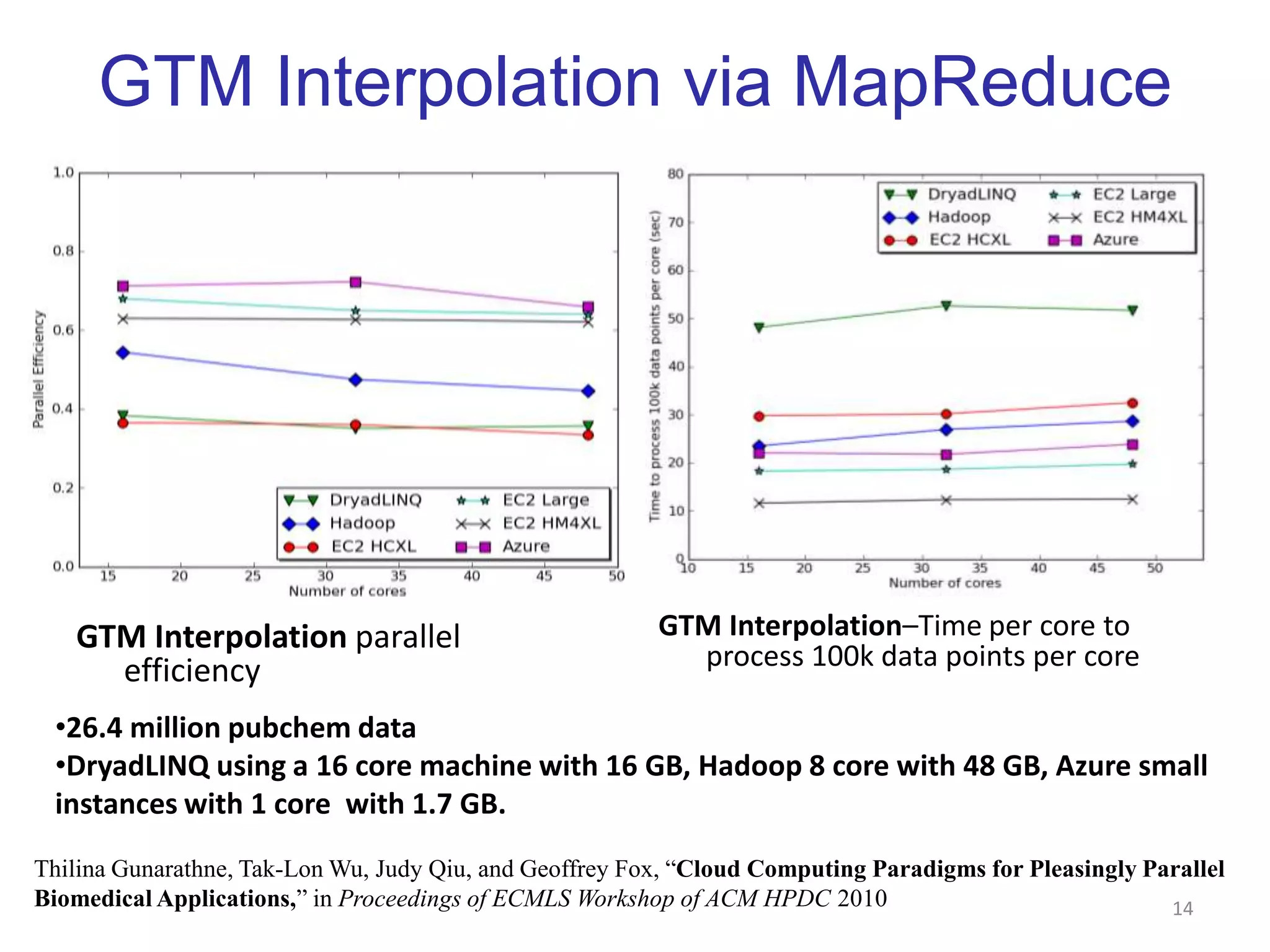
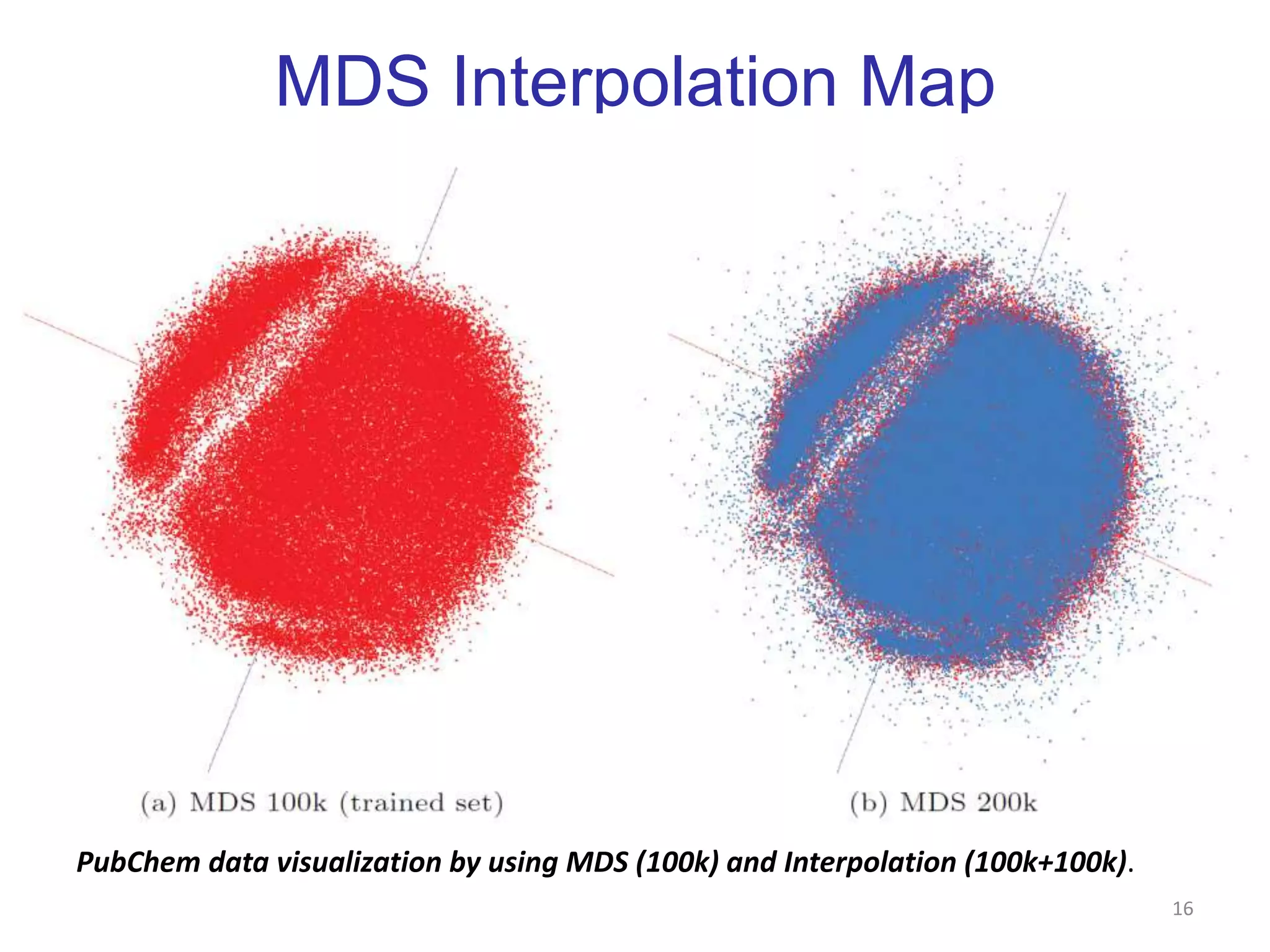
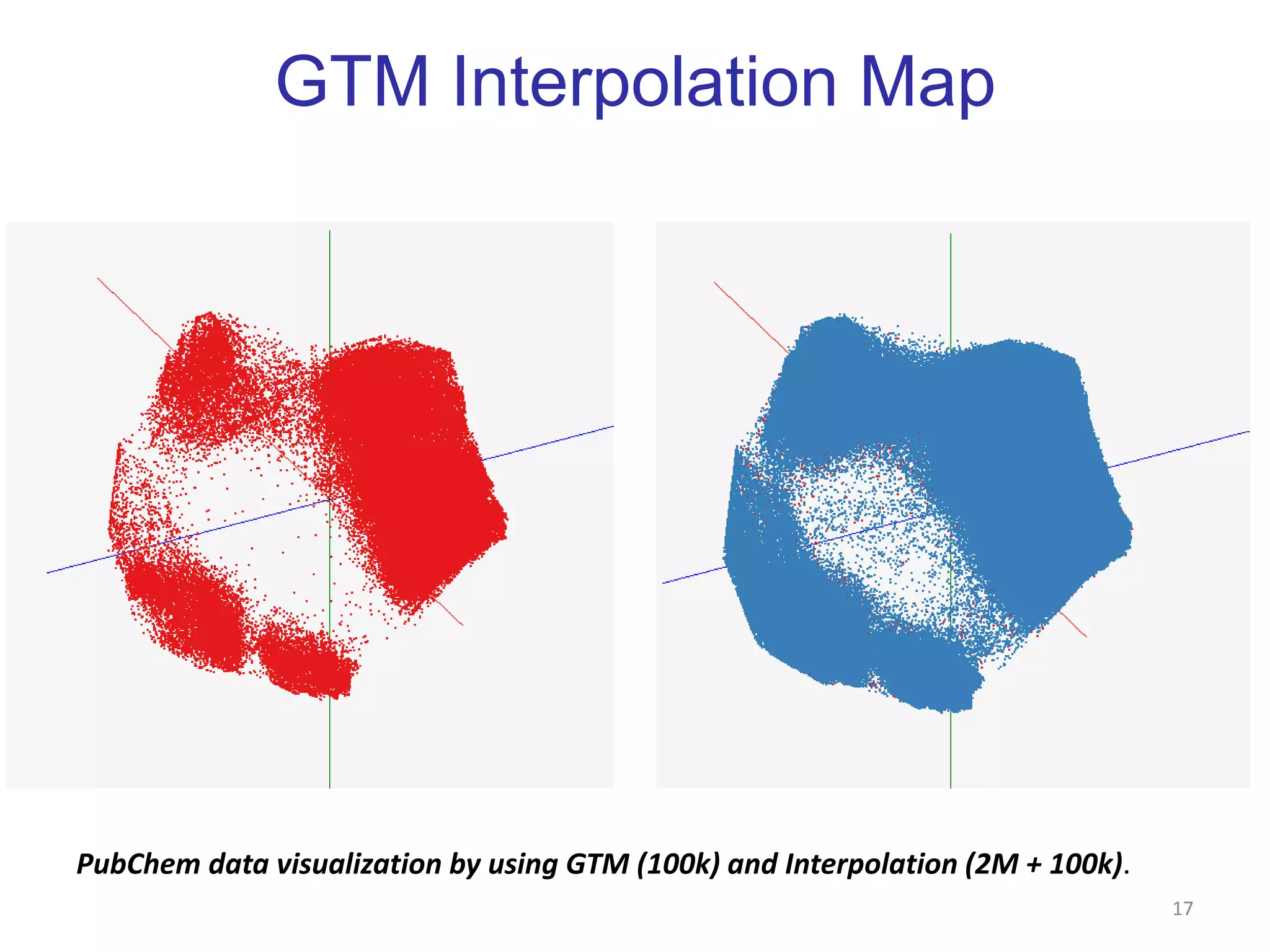
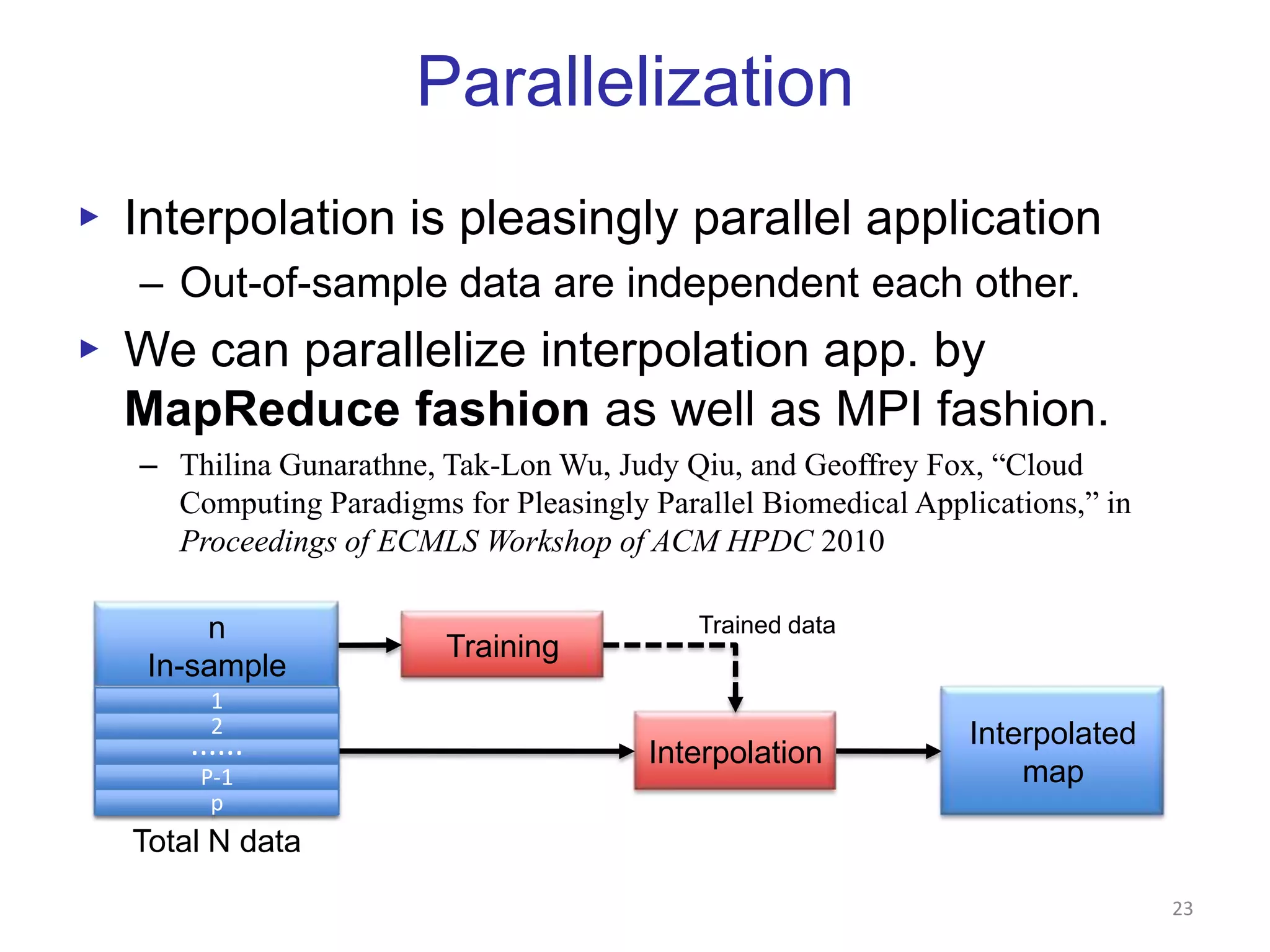
This document discusses dimension reduction techniques for visualizing large, high-dimensional data. It presents multidimensional scaling (MDS) and generative topographic mapping (GTM) for this task. To address challenges of data size, an interpolation approach is introduced that maps new data points based on a reduced set of sample points. Experimental results show MDS and GTM interpolation can efficiently visualize millions of data points in 2-3 dimensions with reasonable quality compared to processing all points directly.