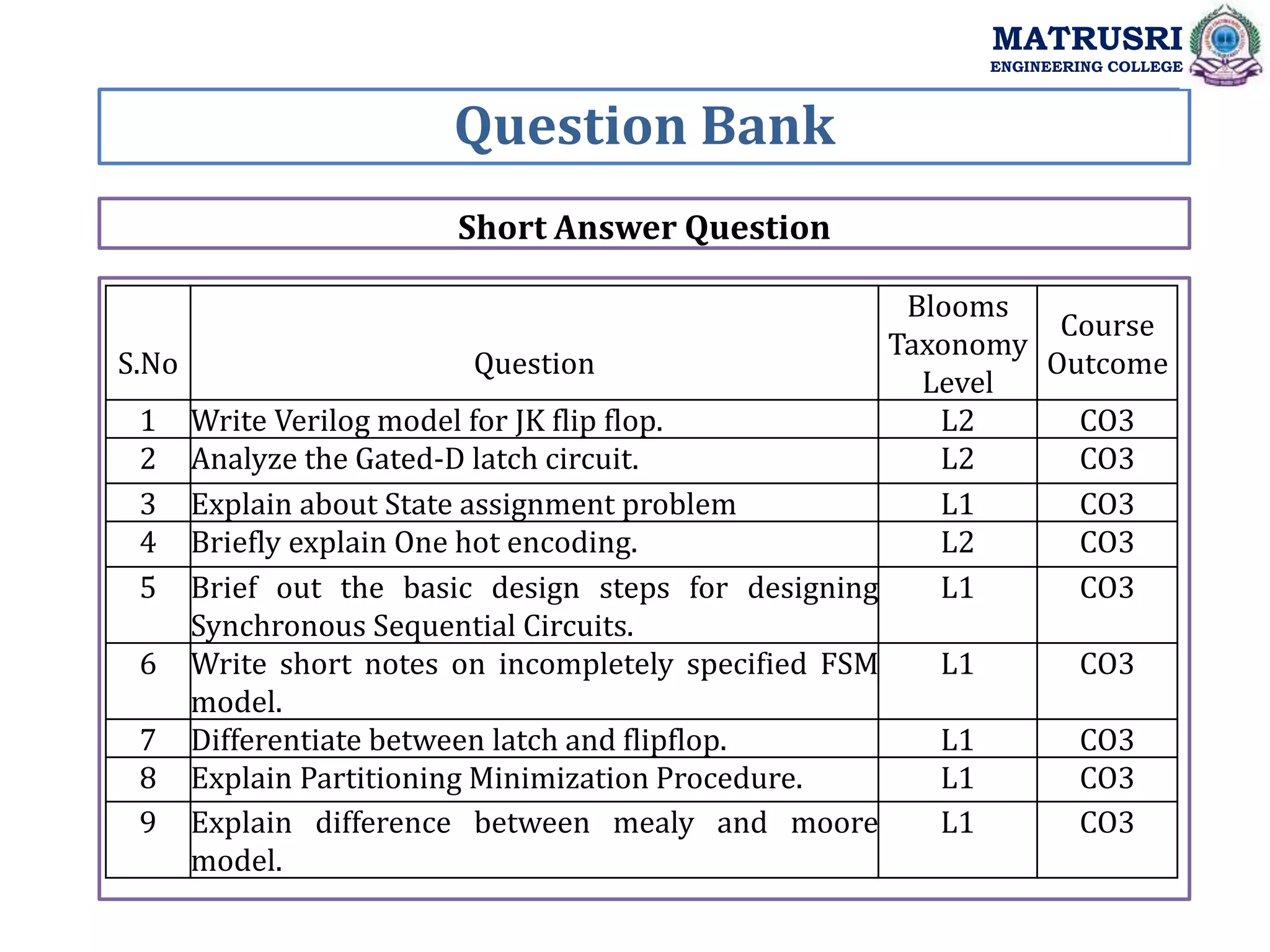
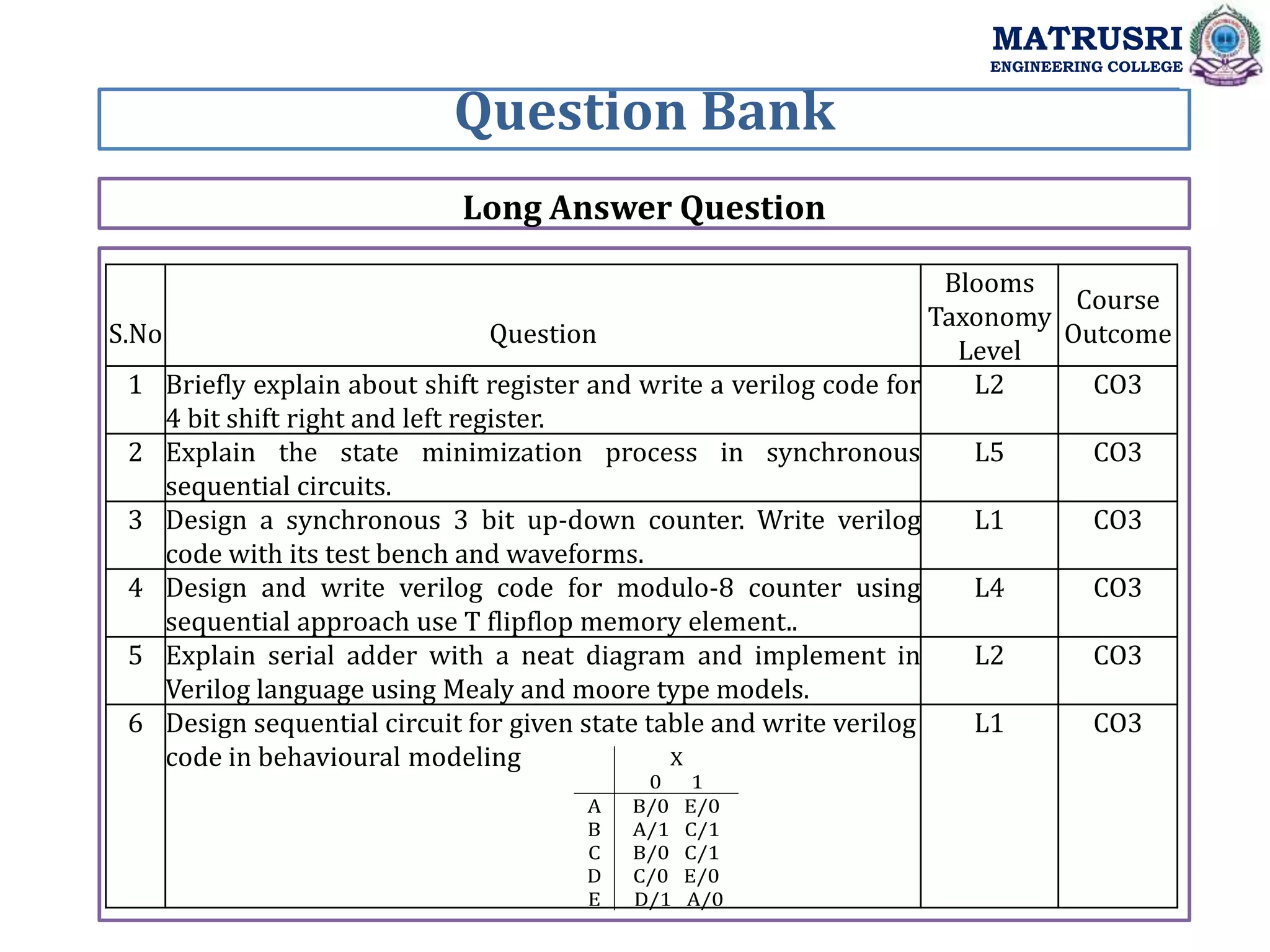
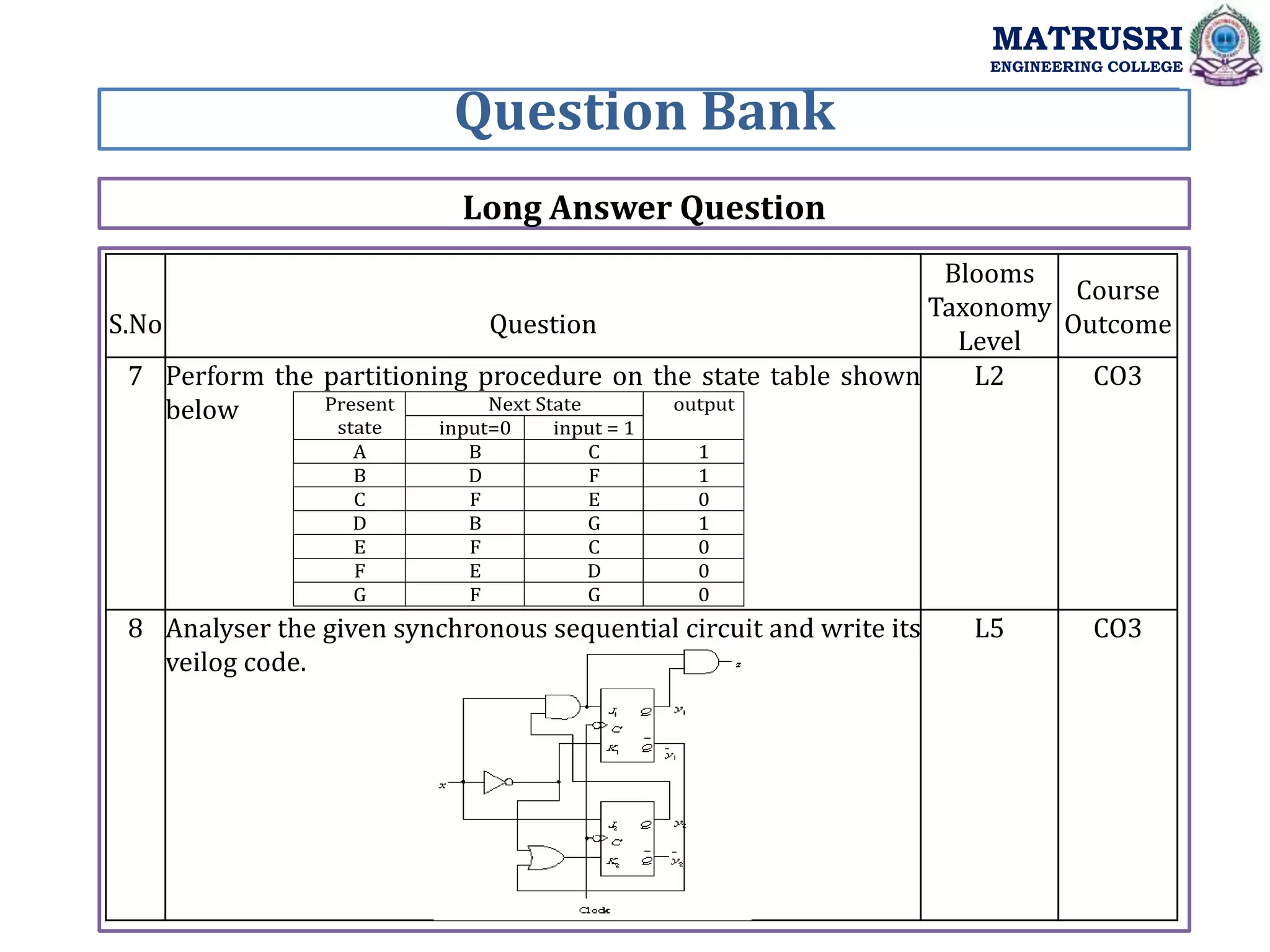
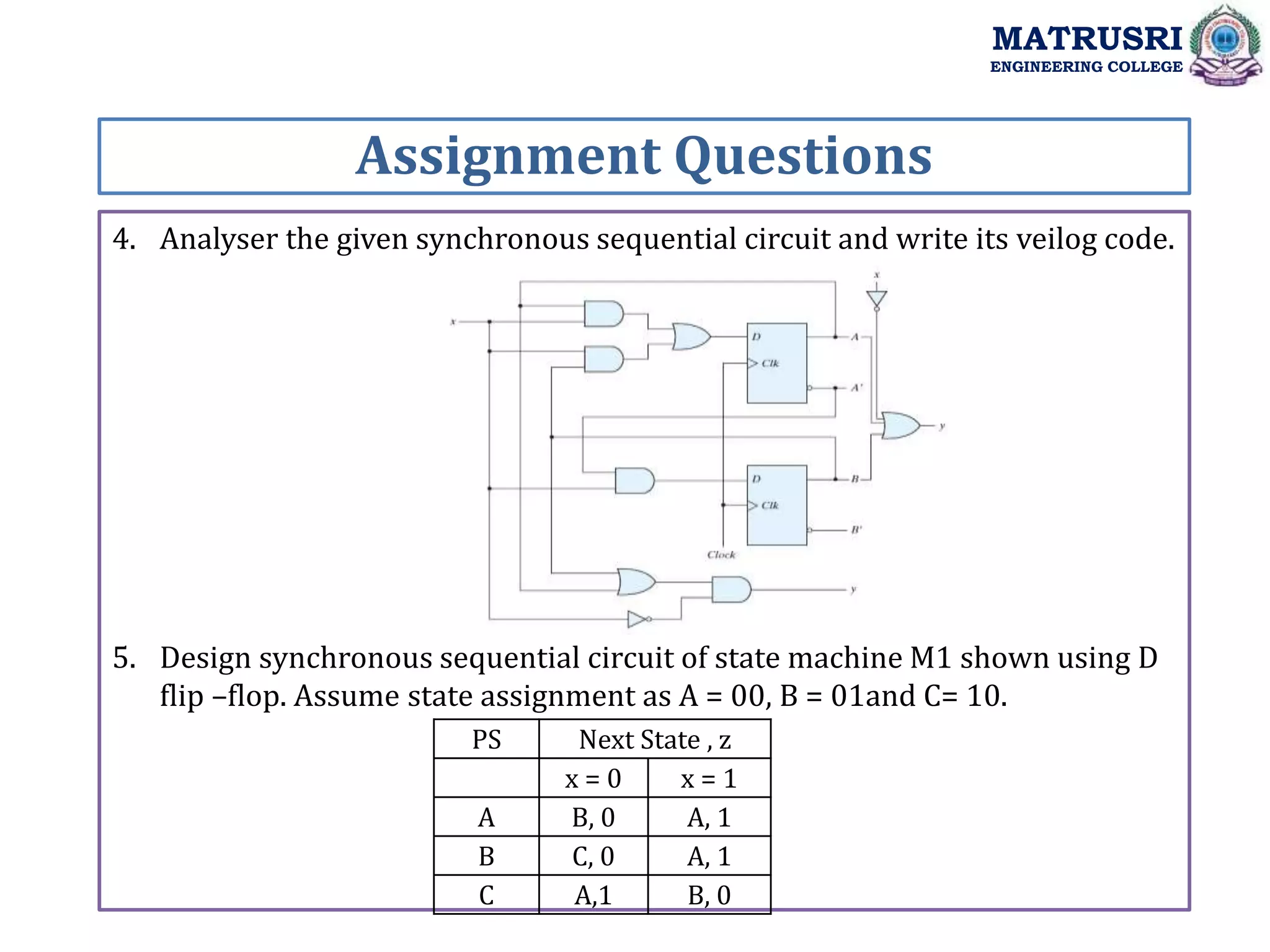
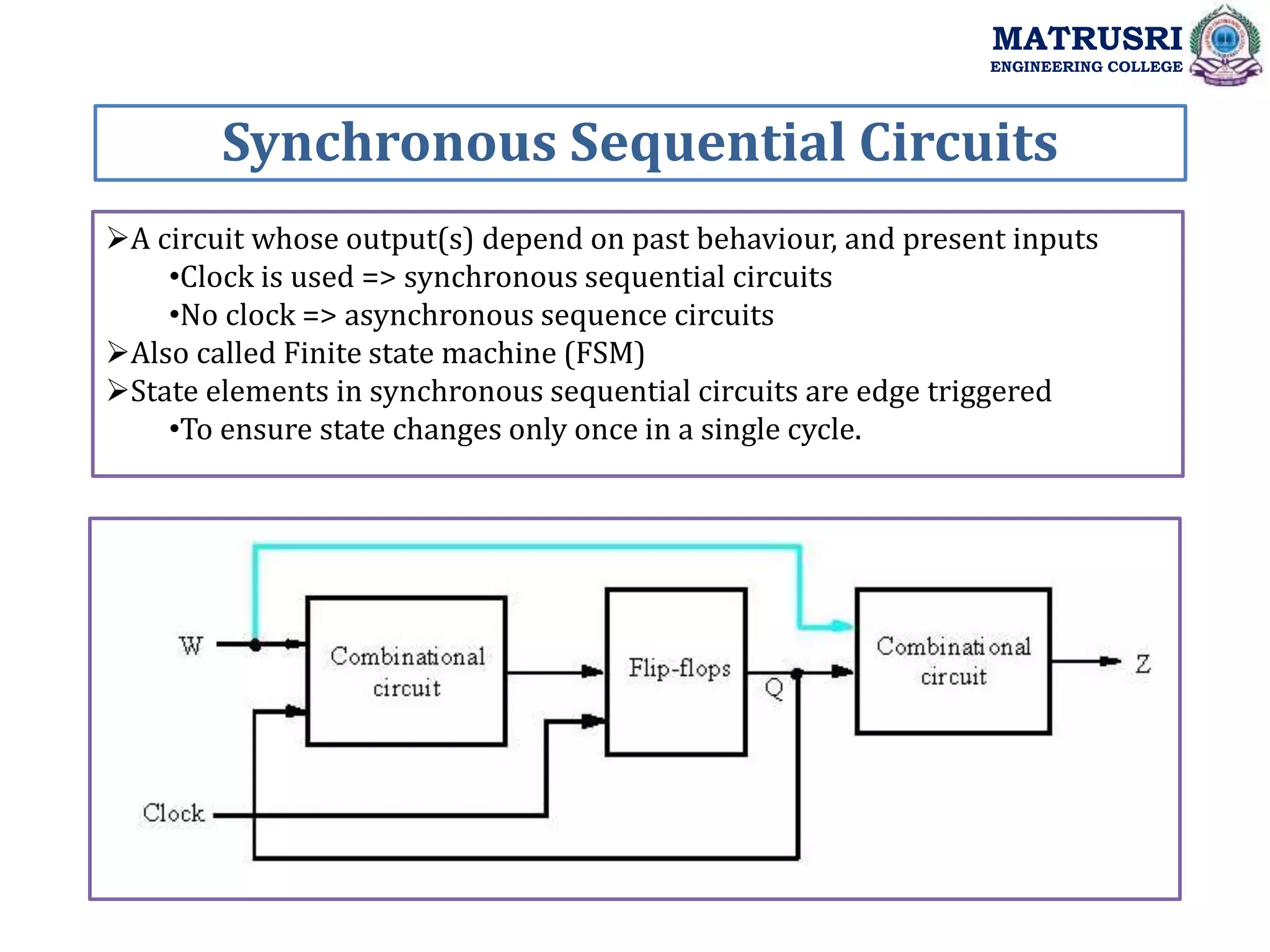
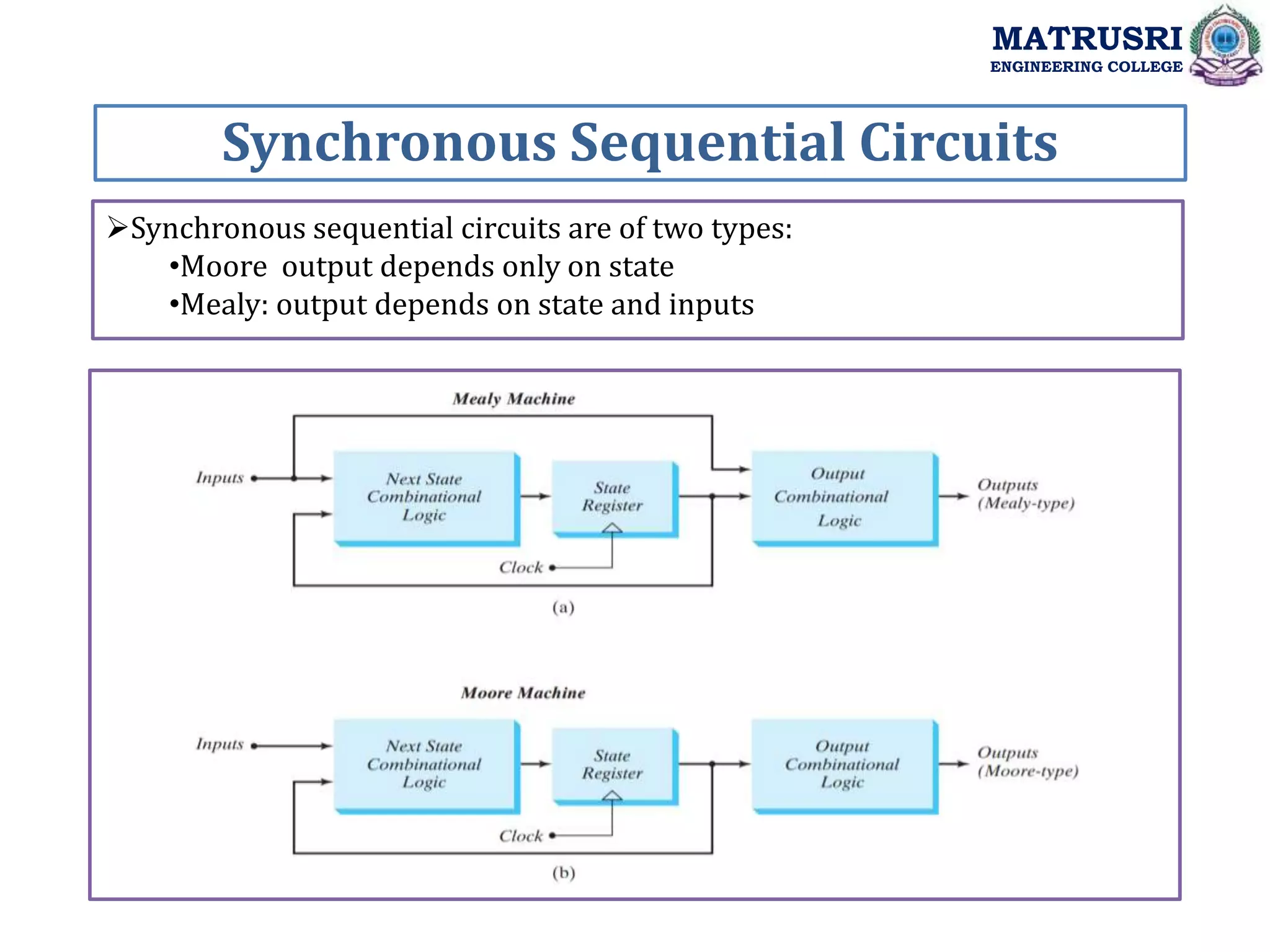
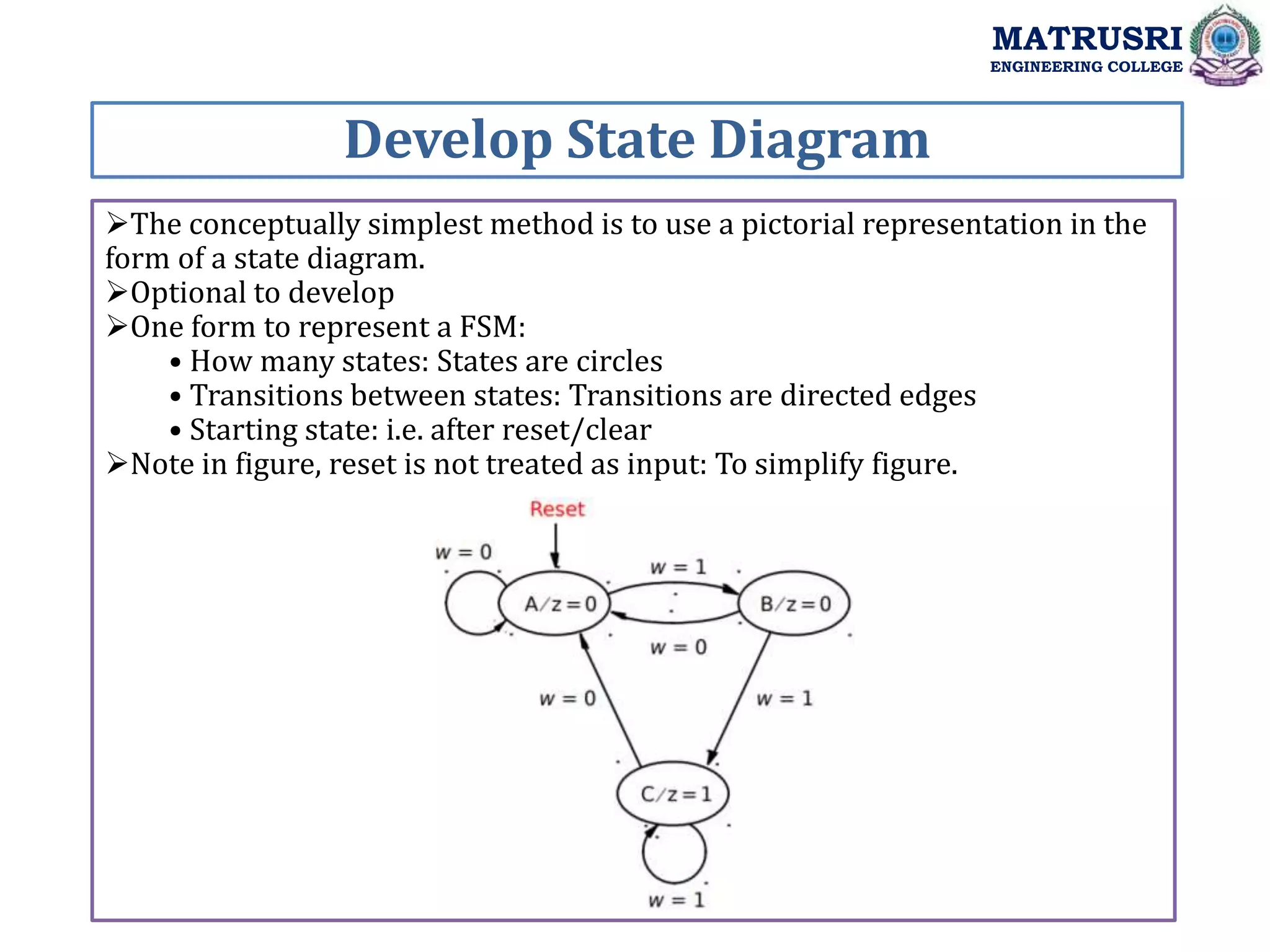
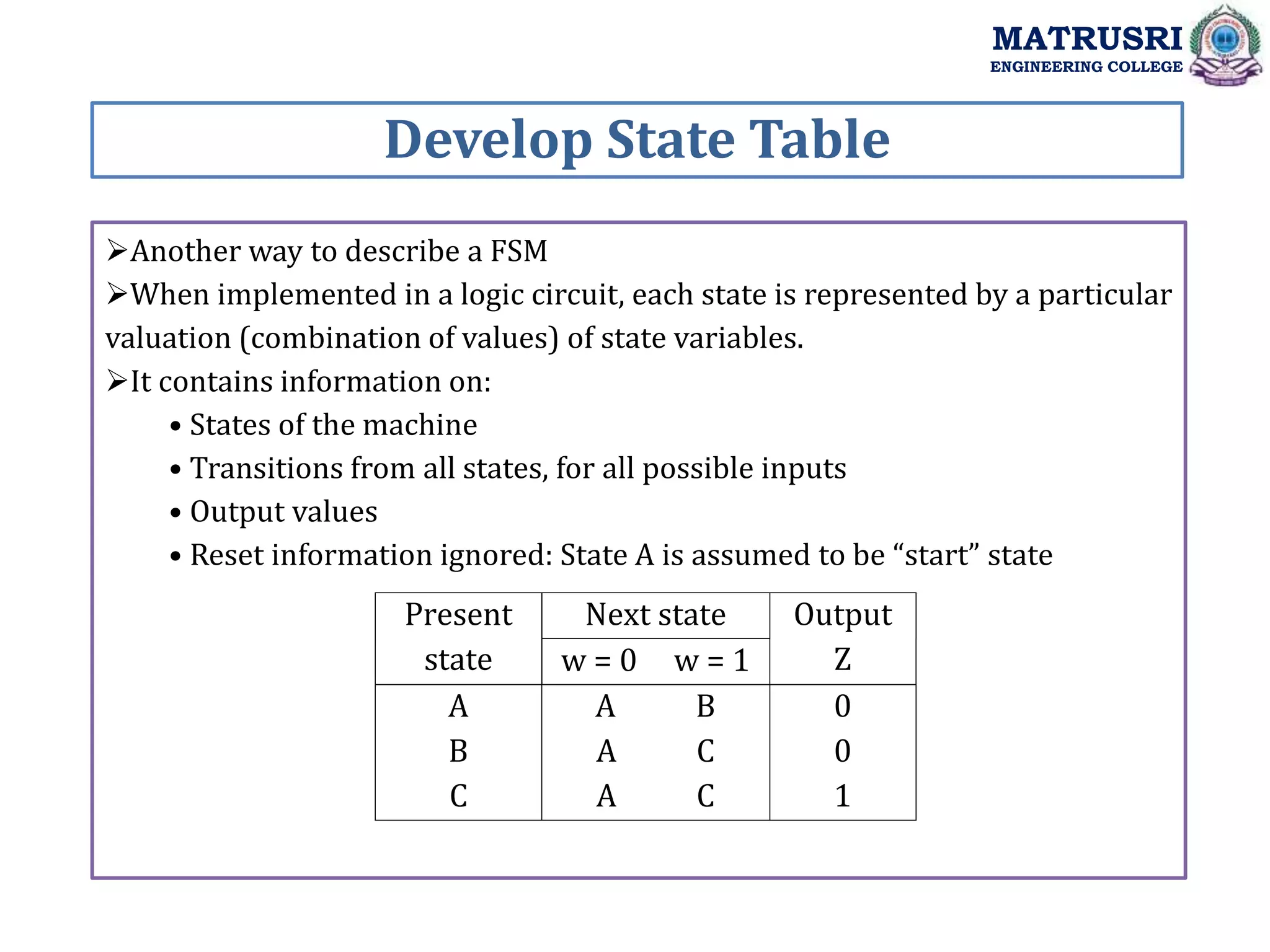
The document outlines the curriculum for a course on Digital System Design with Verilog at Matrusri Engineering College, focusing on synchronous sequential circuits and finite state machines. It details various modules such as latches, flip-flops, counters, and shift registers, along with their testing methods and FSM design procedures. Students are expected to design and implement sequential logic circuits using Verilog, culminating in the development of both Moore and Mealy state models.








![Counter MATRUSRI ENGINEERING COLLEGE module updowncount ( R, clk, L, E, updwn, Q ); parameter n = 8; input [n-1]R; input clk, L, E, updwn; output [n-1] Q; reg [n-1]Q; integer direction; always @(posedge clk) begin if (updwn) direction = 1; else direction = −1; if (L) Q <= R; else if (E) Q <= Q + direction; end endmodule Testbench: module updowncounttest_v; reg clk, L, E, updwn; reg [n-1]R wire [n-1:0] Q; Updowncount uut(R, clk, L, E, updwn, Q); always #5 clk= ~clk; initial begin #400 $finish; end initial begin L=1;clk=1;updwn=0; R=8’o23;E=1; #10 L=0; #150 L=1; #20 L=0; updwn=1; end endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-13-2048.jpg)
![Shift Register MATRUSRI ENGINEERING COLLEGE Right Shift: module shift4 (R, L, w, Clock, Q); input [3:0] R; input L, w, Clock; output reg [3:0] Q; always @(posedge Clock) if (L) Q <= R; else Q[3:0]={w, Q[3: 1]}; endmodule Left Shift: module shift4 (R, L, w, Clock, Q); input [3:0] R; input L, w, Clock; output reg[3:0] Q; always @(posedge Clock) if (L) Q <= R; else Q[3:0]={Q[2: 0],w}; endmodule Testbench: module shift4_tst_v; reg L,w,Clock; reg [3:0]R; wire [3:0]Q; shift4 uut(R, L, w, Clock, Q); initial begin R = 4’b1011; L = 1; w = 1; #20; L = 0; end always #5 Clock = ~ Clock; endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-14-2048.jpg)
![Shift Register MATRUSRI ENGINEERING COLLEGE Serial In Serial Out: module shift (C, SI, SO); input C,SI; output SO; reg [7:0] tmp; always @(posedge C) begin tmp = tmp << 1; tmp[0] = SI; end assign SO = tmp[7]; endmodule Parallel In Parallel Out: module pipo(pin, clk, reset, pout); input [3:0] pin; input clk, reset; output reg [3:0] pout; always @ (posedgeclk or posedge reset) begin if (reset) pout <= 4'b0000; else pout <= pin; end endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-15-2048.jpg)
![Shift Register MATRUSRI ENGINEERING COLLEGE Parallel In Serial Out: module Shiftregister_PISO( Clk, Parallel_In,load, Serial_Out); input Clk,load; input [3:0]Parallel_In; output reg Serial_Out; reg [3:0]tmp; always @(posedge Clk) begin if(load) tmp<=Parallel_In; else begin Serial_Out<=tmp[3]; tmp<={tmp[2:0],1'b0}; end end endmodule Serial In Parallel Out: module ShiftRegister_SIPO(Clk, SI, PO); input Clk,SI; output [7:0] PO; reg [7:0] tmp; always @(posedge Clk) begin tmp = {tmp[6:0], SI}; end assign PO = tmp; endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-16-2048.jpg)






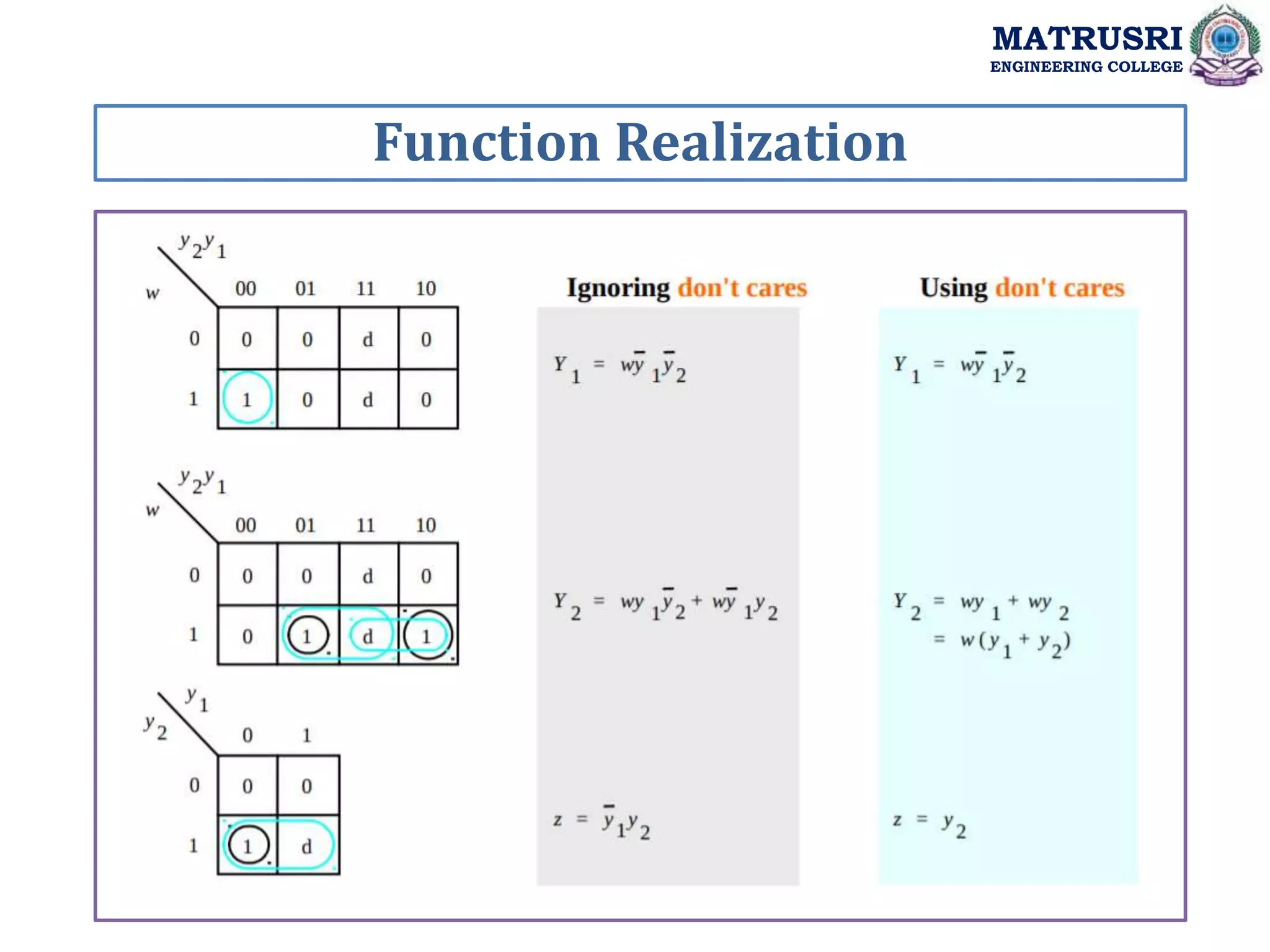
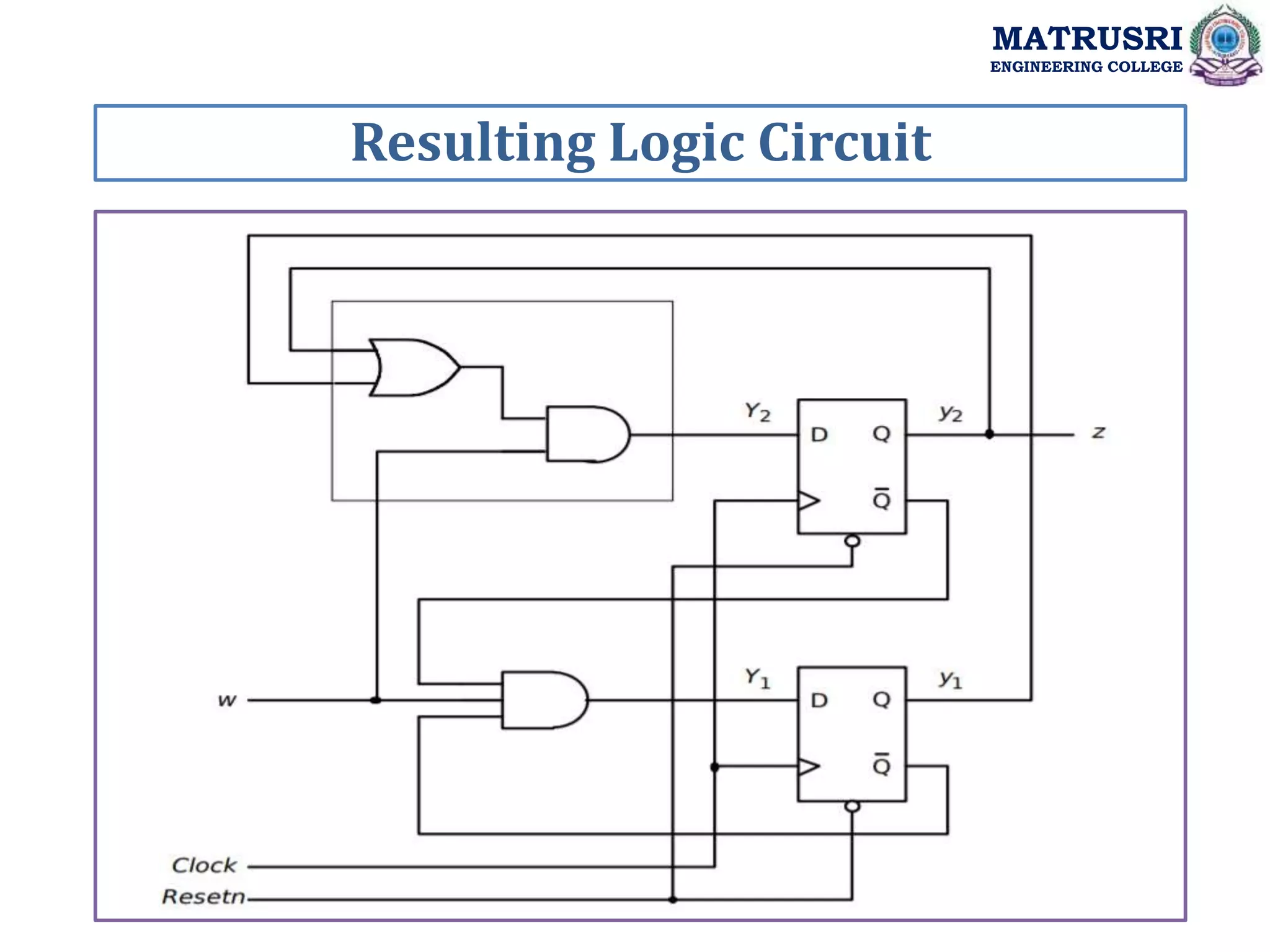
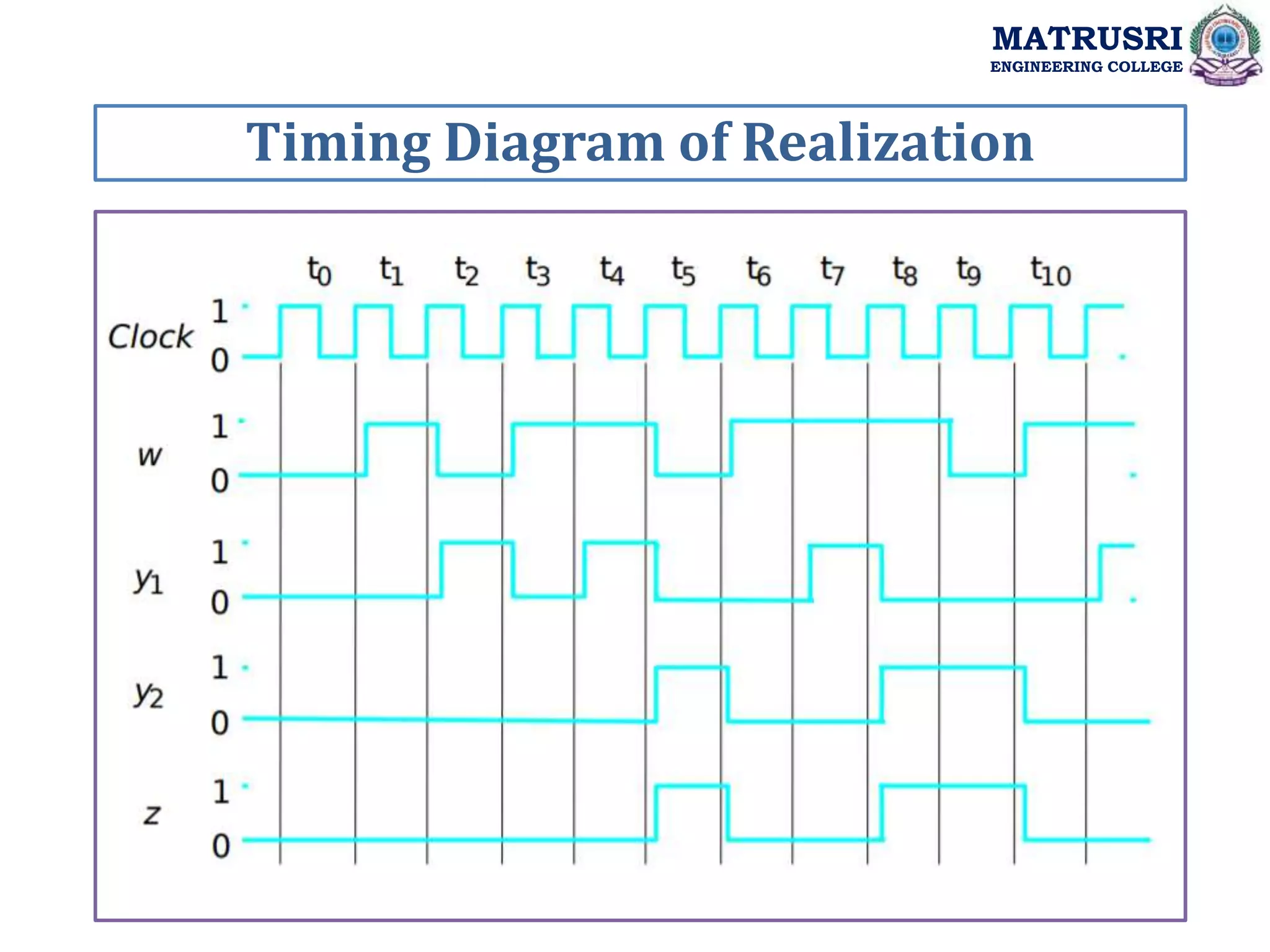
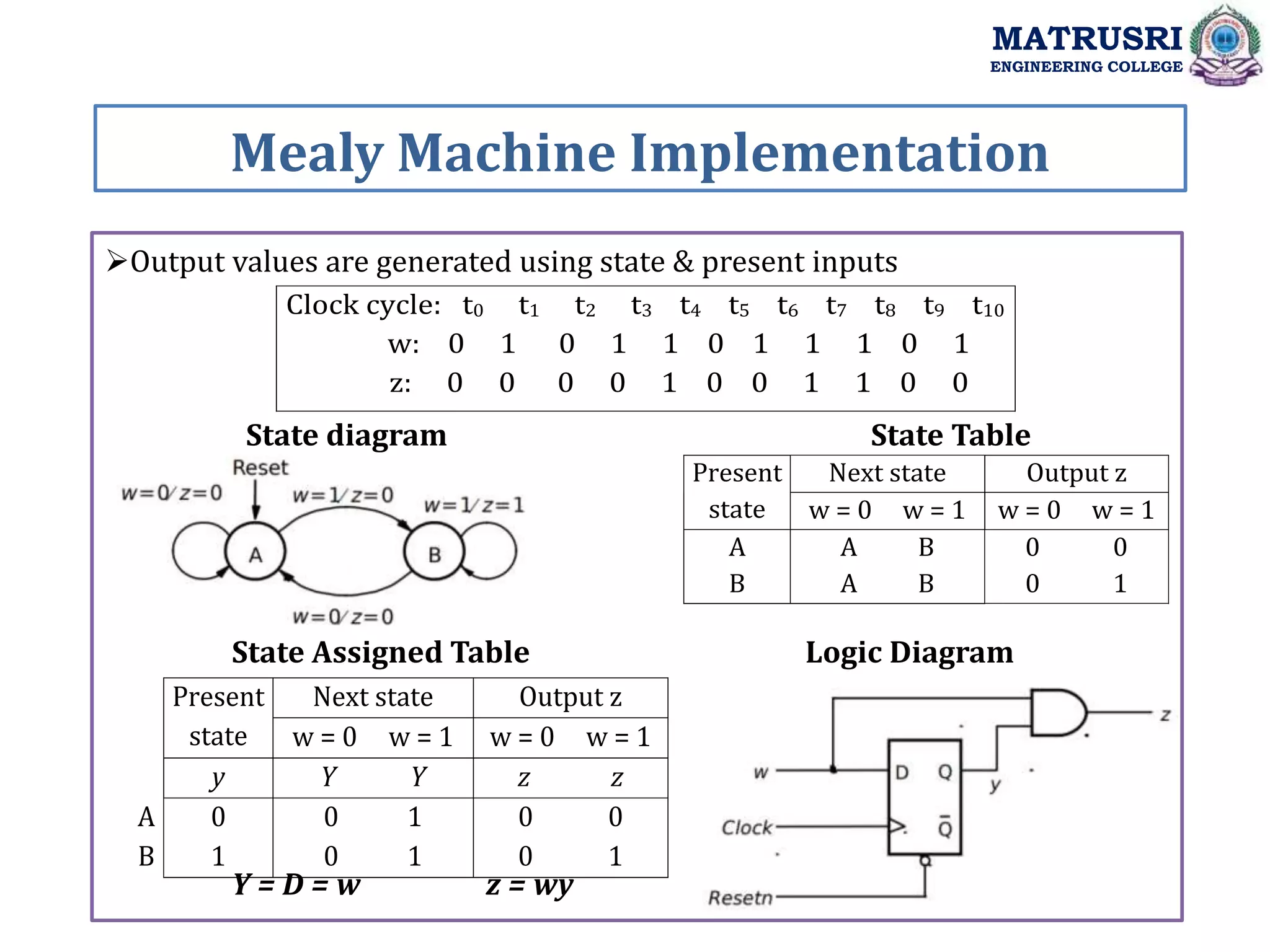
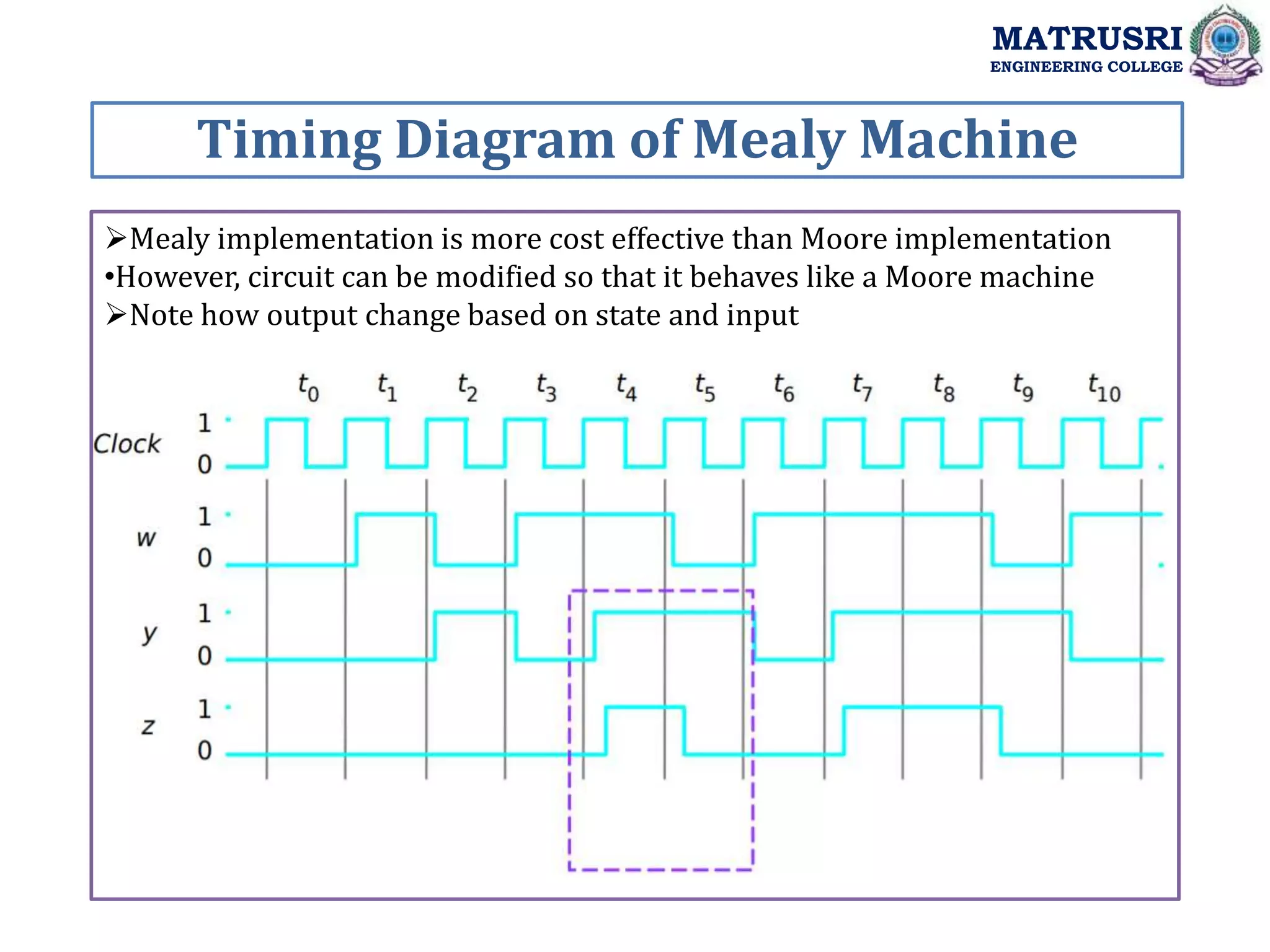



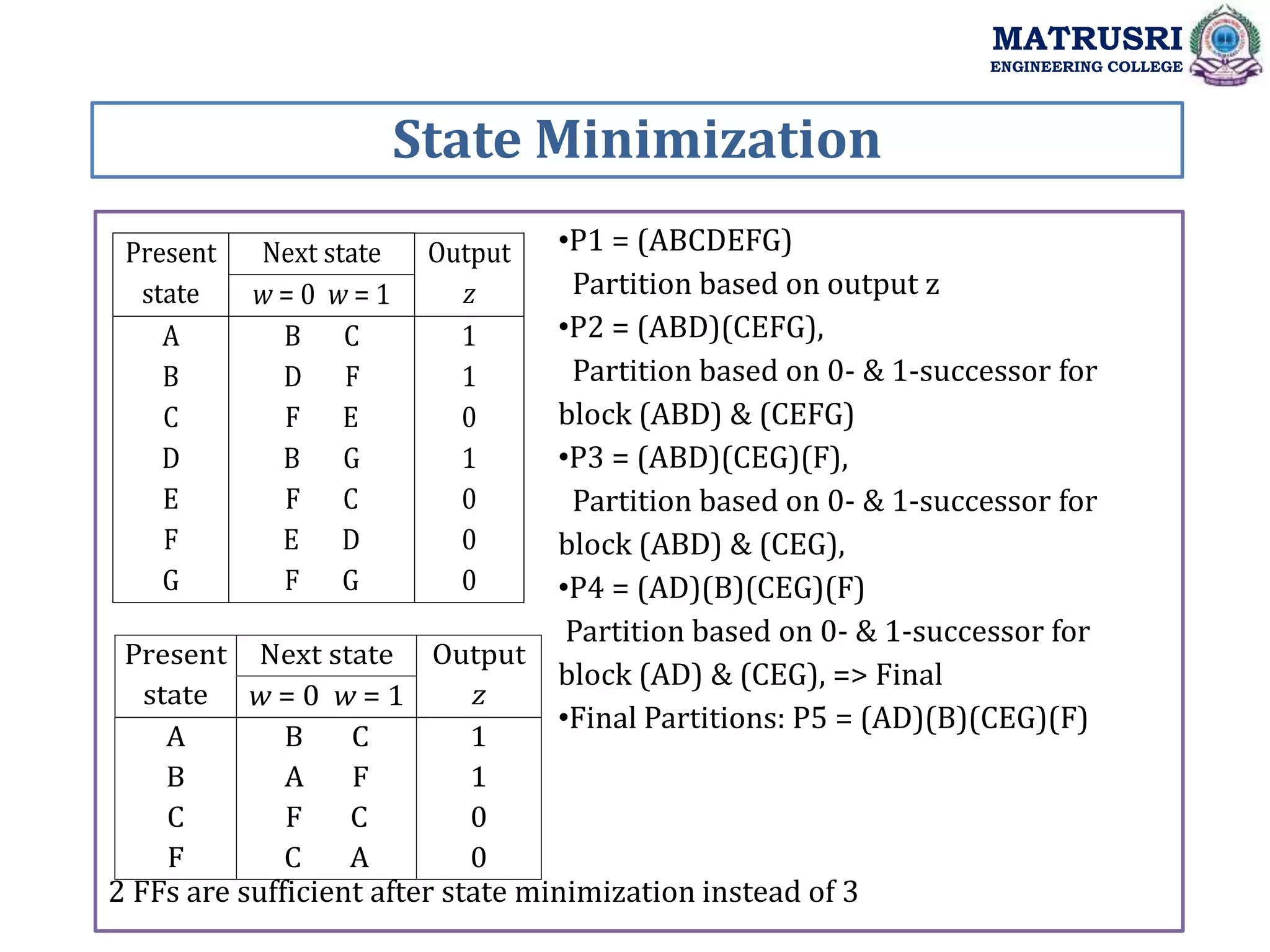



![module simple (Clock, Resetn, w, z); input Clock, Resetn, w; output z; reg [2:1] y, Y; parameter [2:1] A = 2'b00, B = 2'b01, C = 2'b10; always @(w or y) case (y) A: if (w) Y = B; else Y = A; B: if (w) Y = C; else Y = A; C: if (w) Y = C; else Y = A; default: Y = 2'bxx; endcase always @(negedge Resetn or posedge Clock) if (Resetn == 0) y <= A; else y <= Y; assign z = (y == C); endmodule Moore FSM Model MATRUSRI ENGINEERING COLLEGE](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-39-2048.jpg)



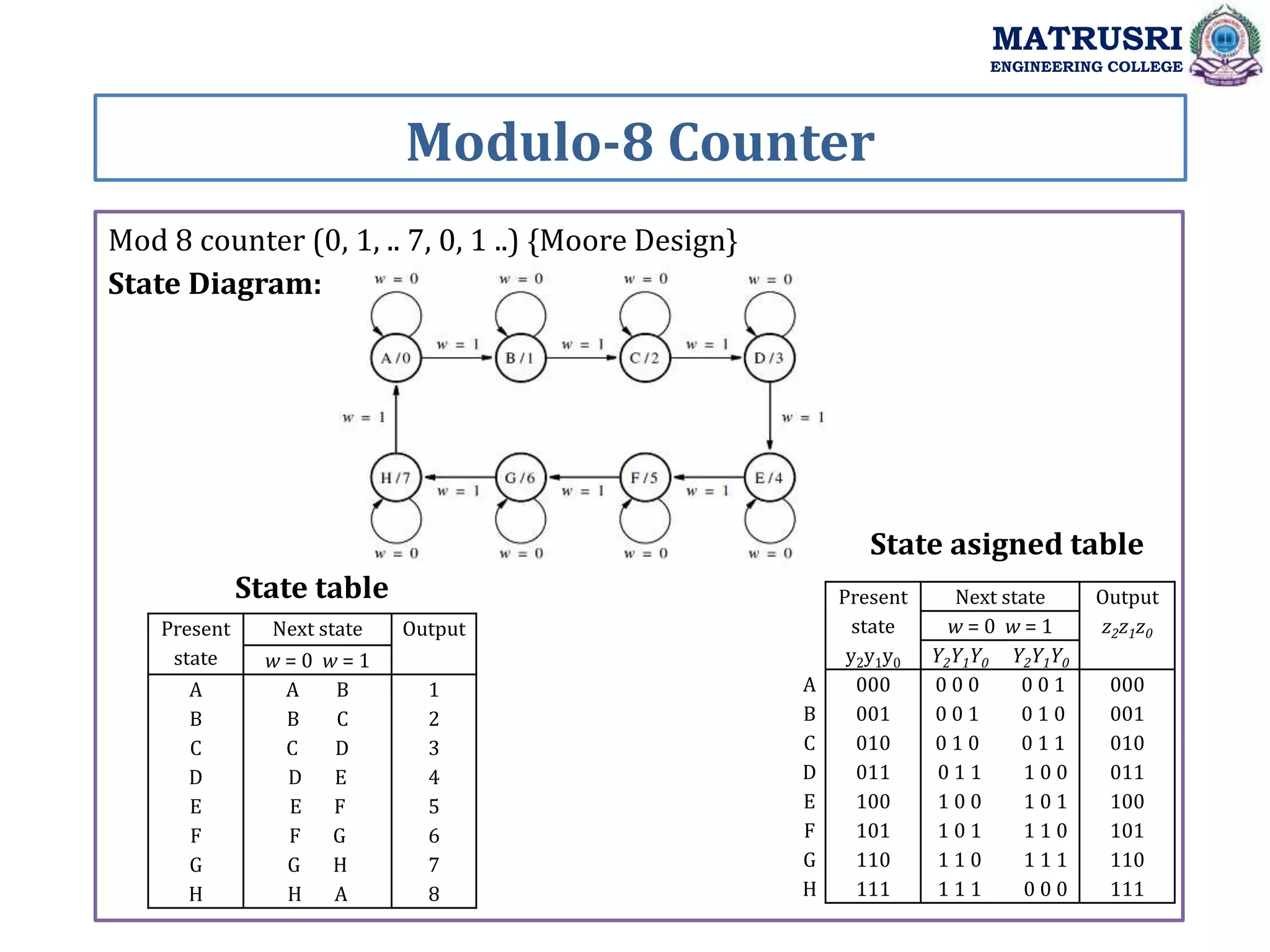
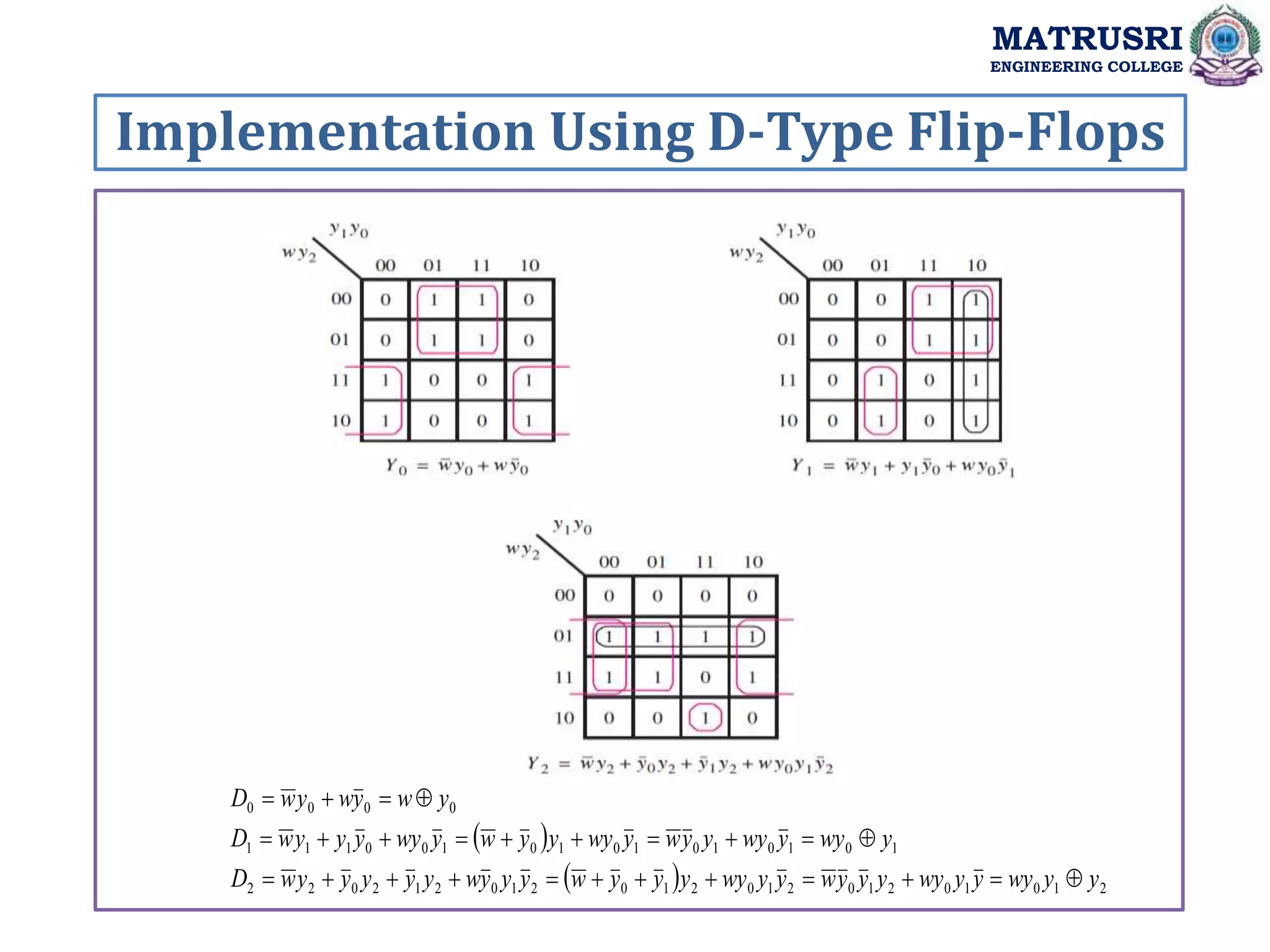
![Verilog Implementation MATRUSRI ENGINEERING COLLEGE module updowncount ( q, reset, s, clk,m ); output reg [2:0]q; input reset, clk; always@(posedge clk) begin if(reset==1) q<=0; else case(m) 0: q=q+1; 1: q=q-1; endcase end endmodule Testbench: module updowncounttest_v; reg reset,clk,m; wire [2:0] q; updowncountuut( .q(q),.reset(reset),.s(s),.clk(clk),.m(m) ); always #5 clk= ~clk; initial begin #400 $finish; end initial begin reset=1;clk=1; m=0; #10 reset=0; #150 reset=1; #20 reset=0; m=1; end endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-48-2048.jpg)








![module serialadder (A, B, Reset, Clock, Sum); input [3:0] A, B; input Reset, Clock; output wire [3:0] Sum; reg [3:0] Count; reg s, y, Y; wire [3:0] QA, QB; wire Run; parameter G = 1'b0, H = 1'b1; shift shift_A (A, Reset, 1'b1, 1'b0, Clock, QA); shift shift_B (B, Reset, 1'b1, 1'b0, Clock, QB); shift shift_S (4'b0, Reset, Run, s, Clock, Sum); always @(QA, QB, y) case (y) G: begin s = QA[0]^QB[0]; if (QA[0] & QB[0]) Y = H; else Y = G; end Verilog Code MATRUSRI ENGINEERING COLLEGE H: begin s = QA[0]~^QB[0]; if (~QA[0] & ~QB[0]) Y = G; else Y = H; end default: Y = G; endcase always @(posedge Clock) if (Reset) y <= G; else y <= Y; always @(posedge Clock) if (Reset) Count = 4; else if (Run) Count = Count-1; assign Run =|Count; endmodule](https://image.slidesharecdn.com/dsdunitiii-220726083717-e657ea86/75/Digital-System-Design-Synchronous-Sequential-Circuits-61-2048.jpg)