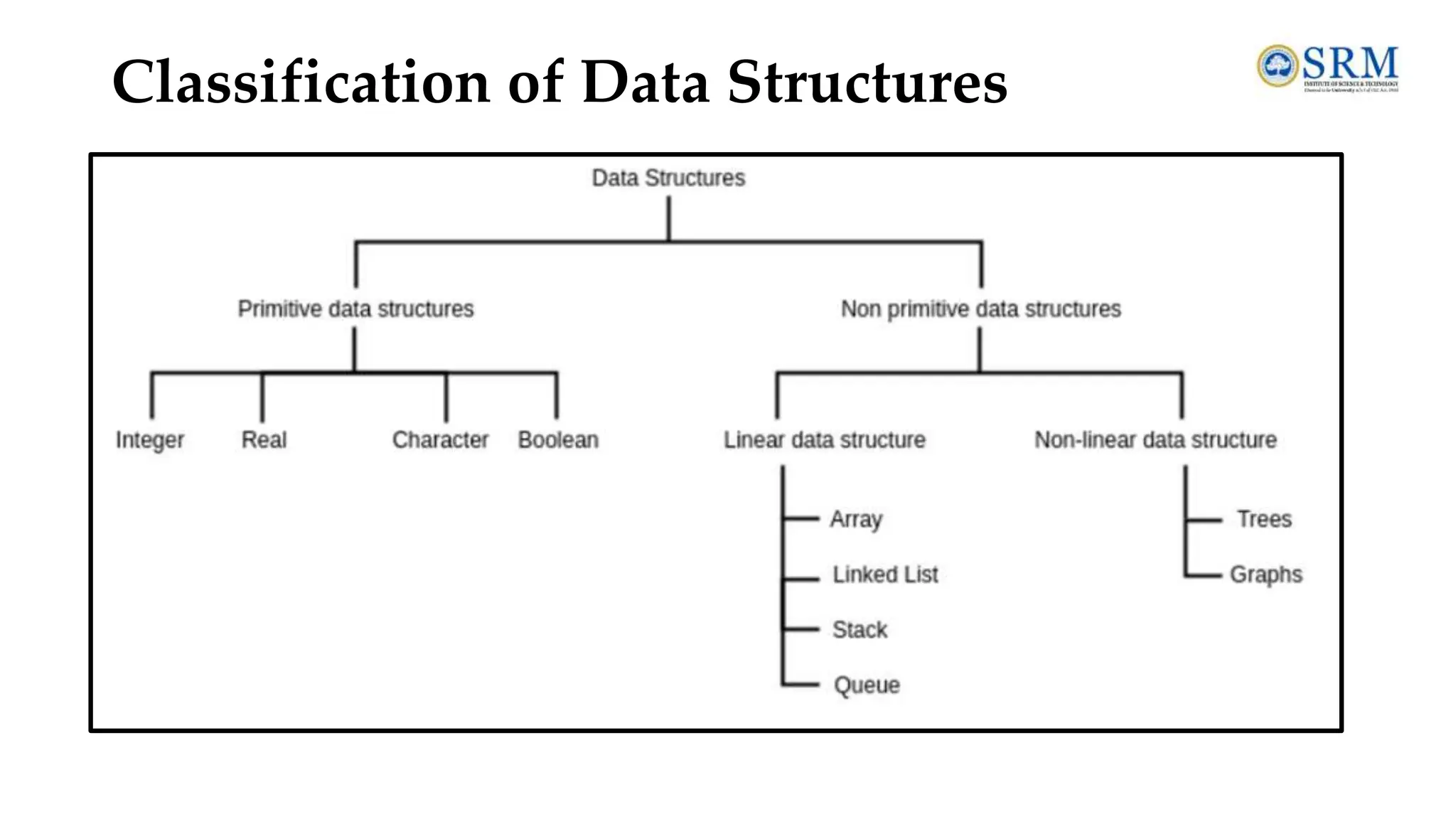
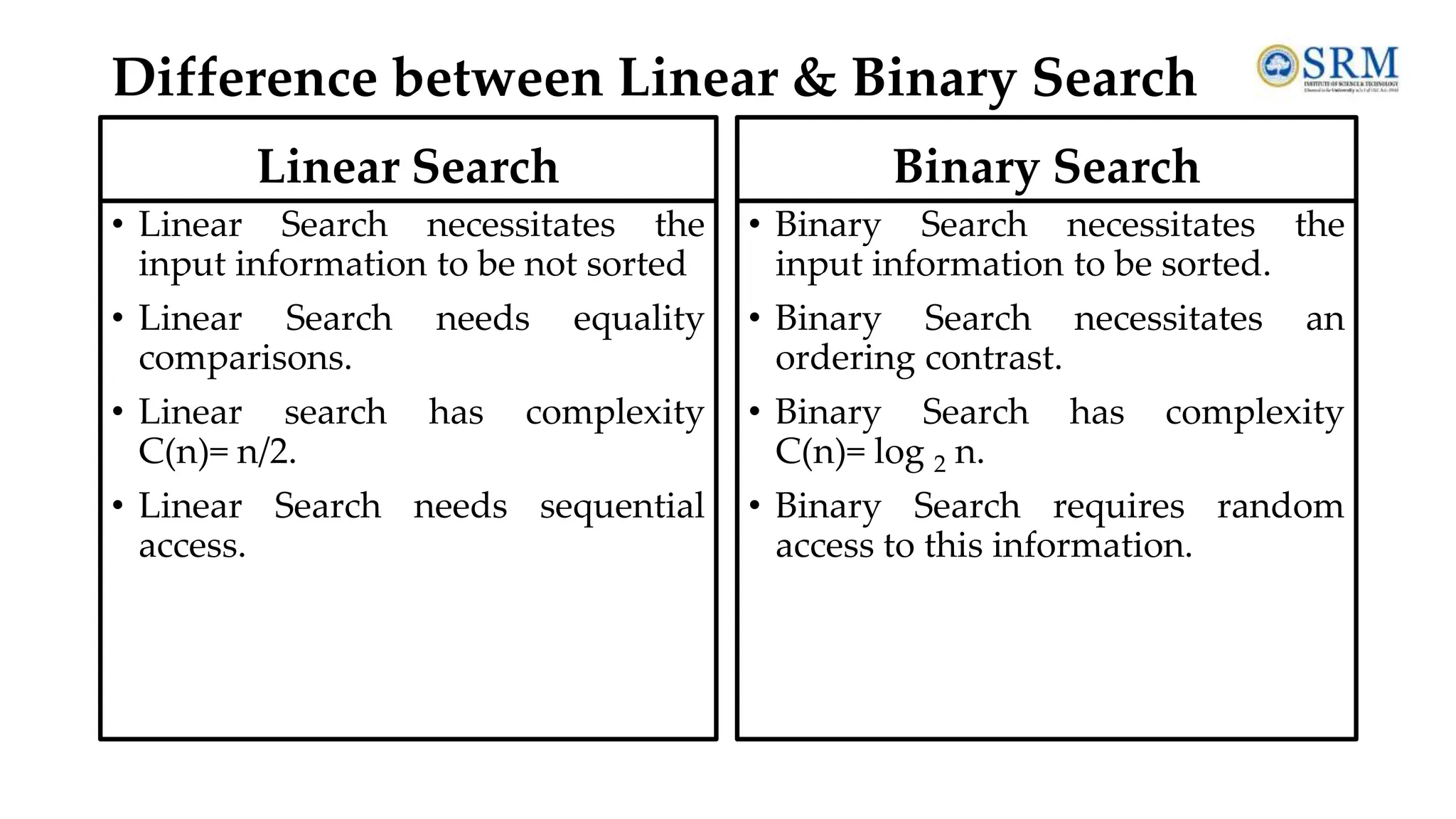
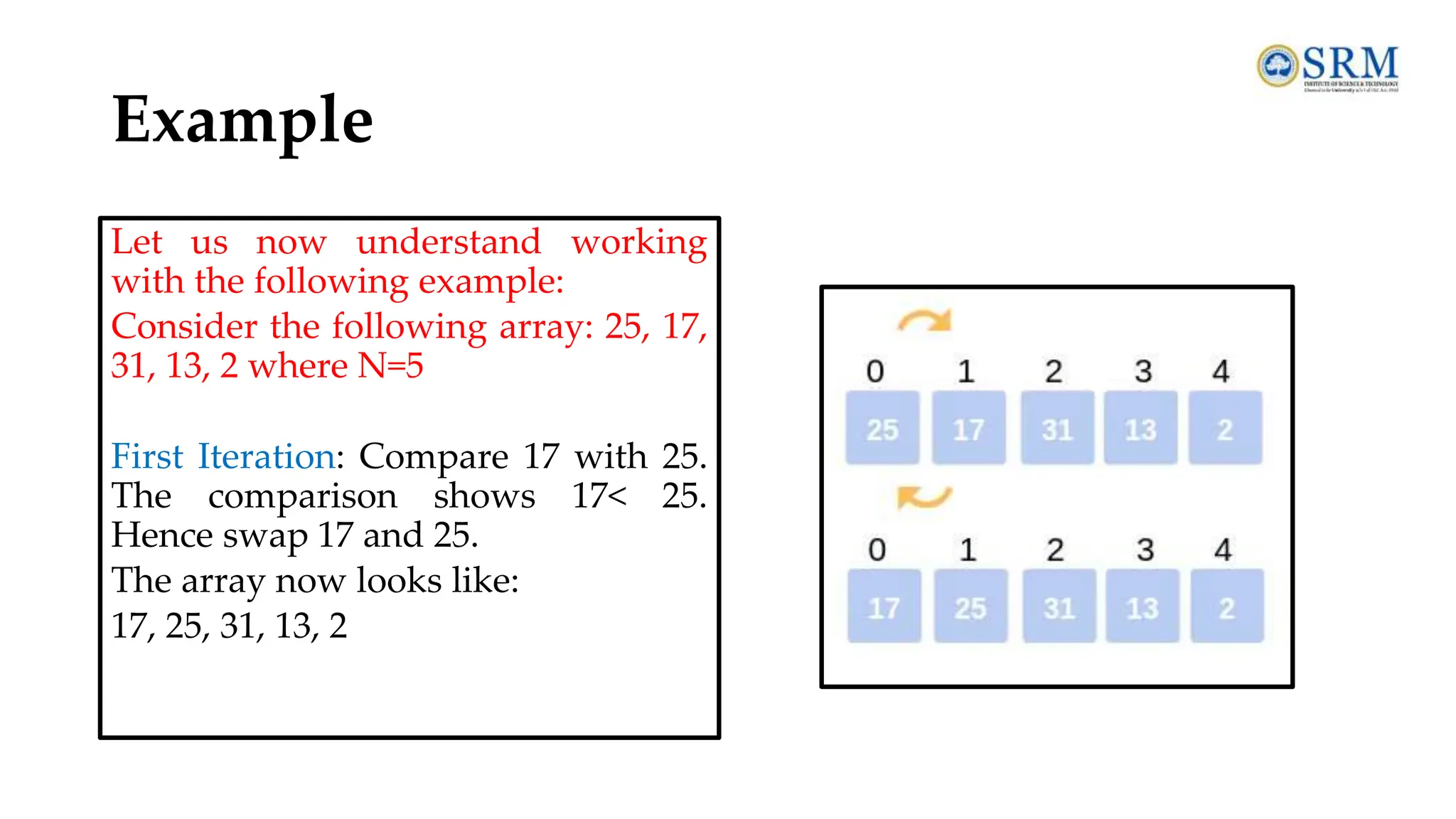
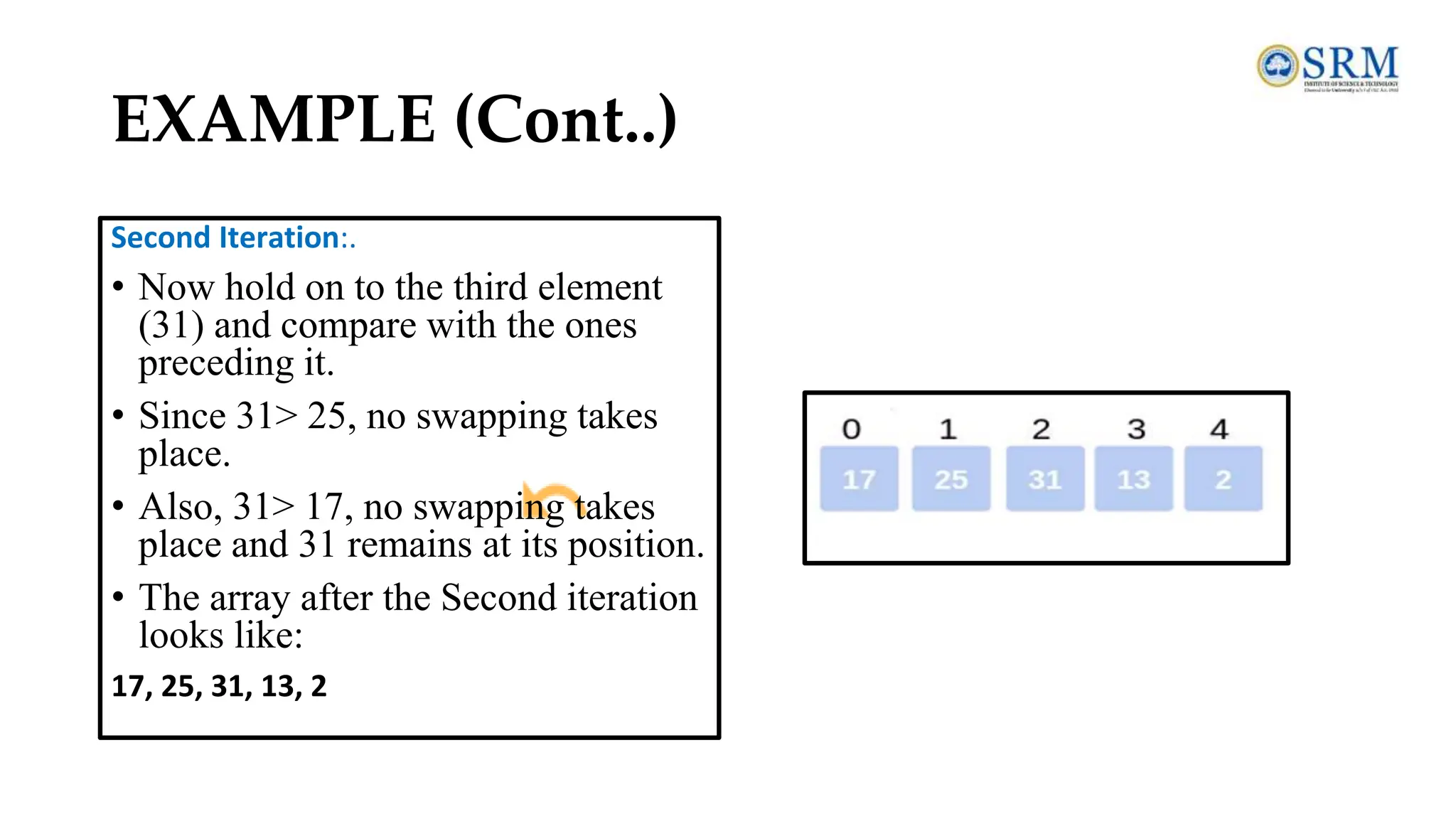
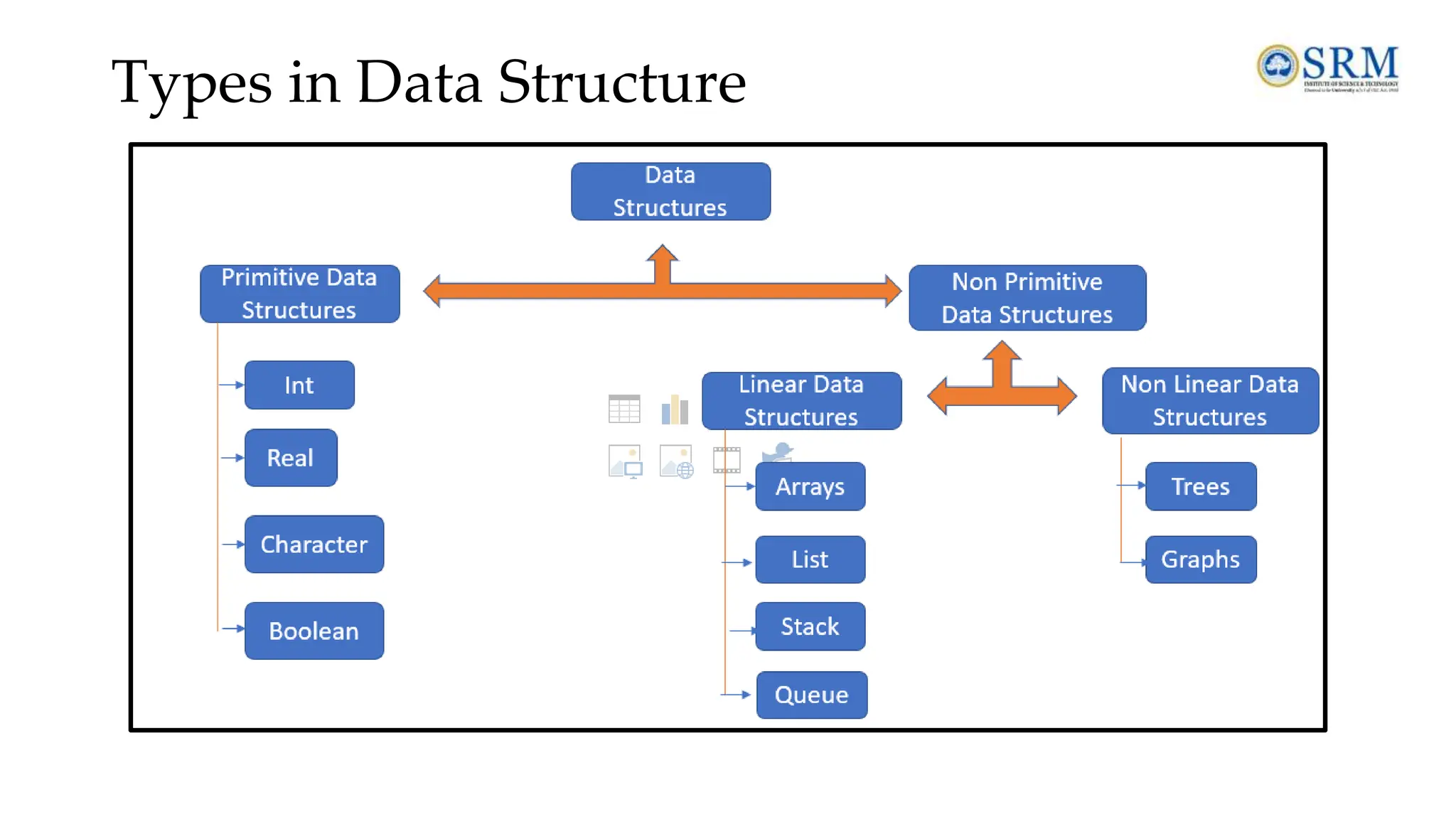
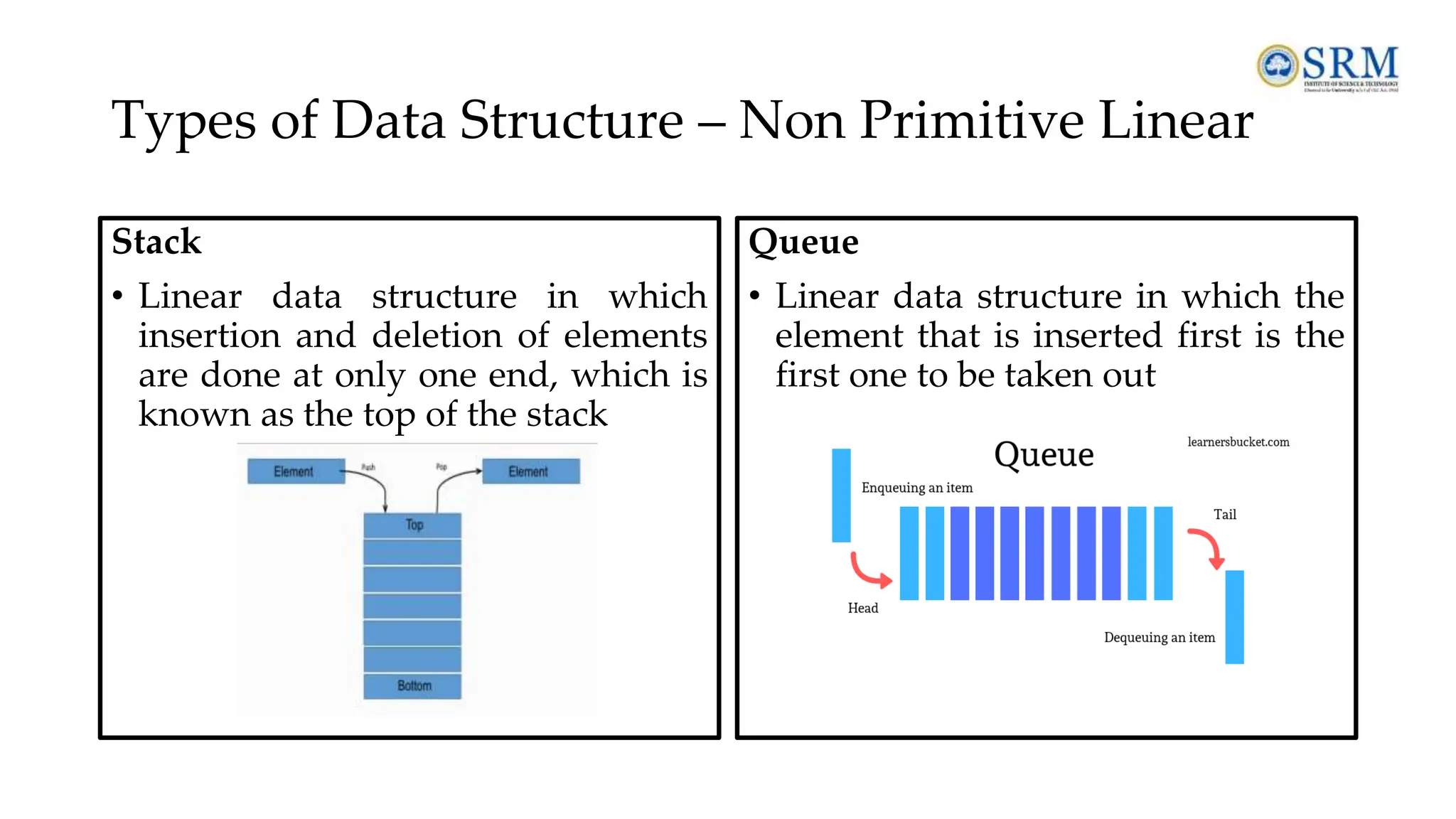
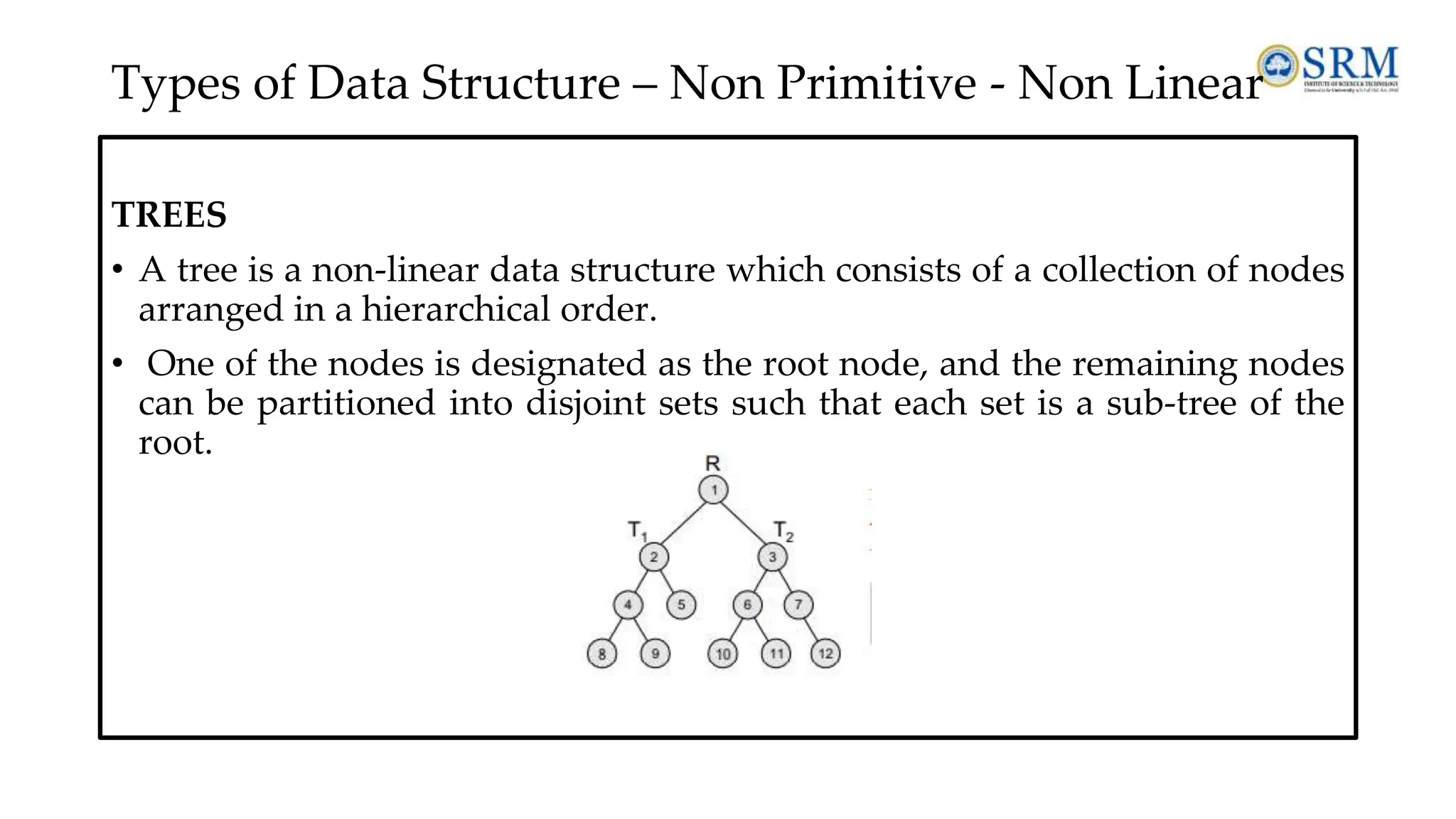
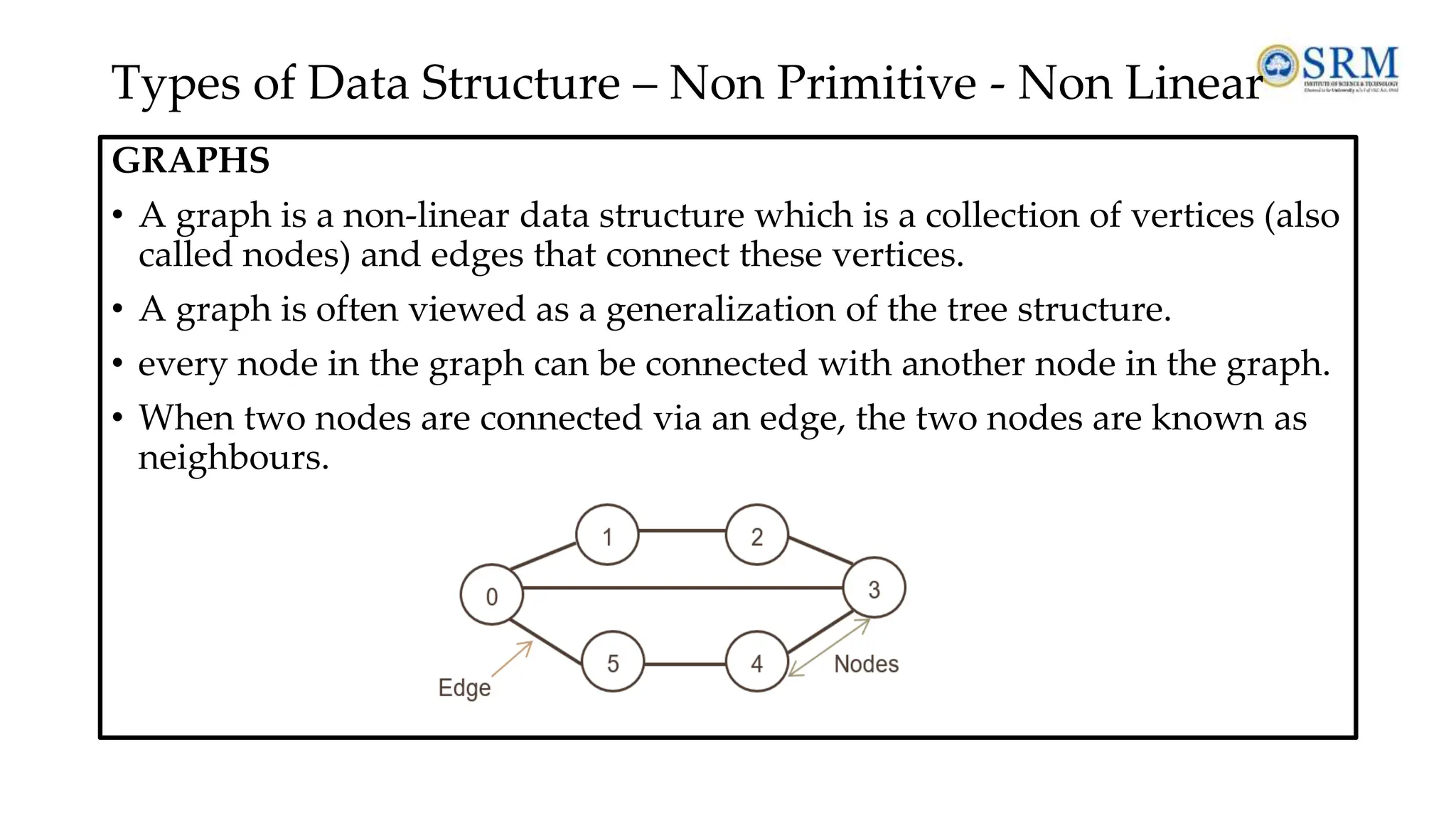
The document provides a comprehensive overview of data structures and algorithms, covering essential topics such as definitions, types of data structures, operations, abstract data types, and searching and sorting algorithms. It emphasizes the importance of efficient data organization and manipulation in computer science, detailing linear and non-linear data structures, their operations, and the complexities of various searching techniques like linear and binary search. Additionally, it includes examples and operations associated with algorithms, alongside review questions for better understanding.





































![Algorithm for Binary Search • In Step 1, we initialize the value of variables, BEG, END, and POS. • In Step 2, a while loop is executed until BEG is less than or equal to END. • In Step 3, the value of MID is calculated. • In Step 4, we check if the array value at MID is equal to VAL. If a match is found, then the value of POS is printed and the algorithm exits. If a match is not found, and if the value of A[MID] is greater than VAL, the value of END is modified, otherwise if A[MID] is greater than VAL, then the value of BEG is altered. • In Step 5, if the value of POS = –1, then VAL is not present in the array and an appropriate message is printed on the screen before the algorithm exits.](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-39-2048.jpg)











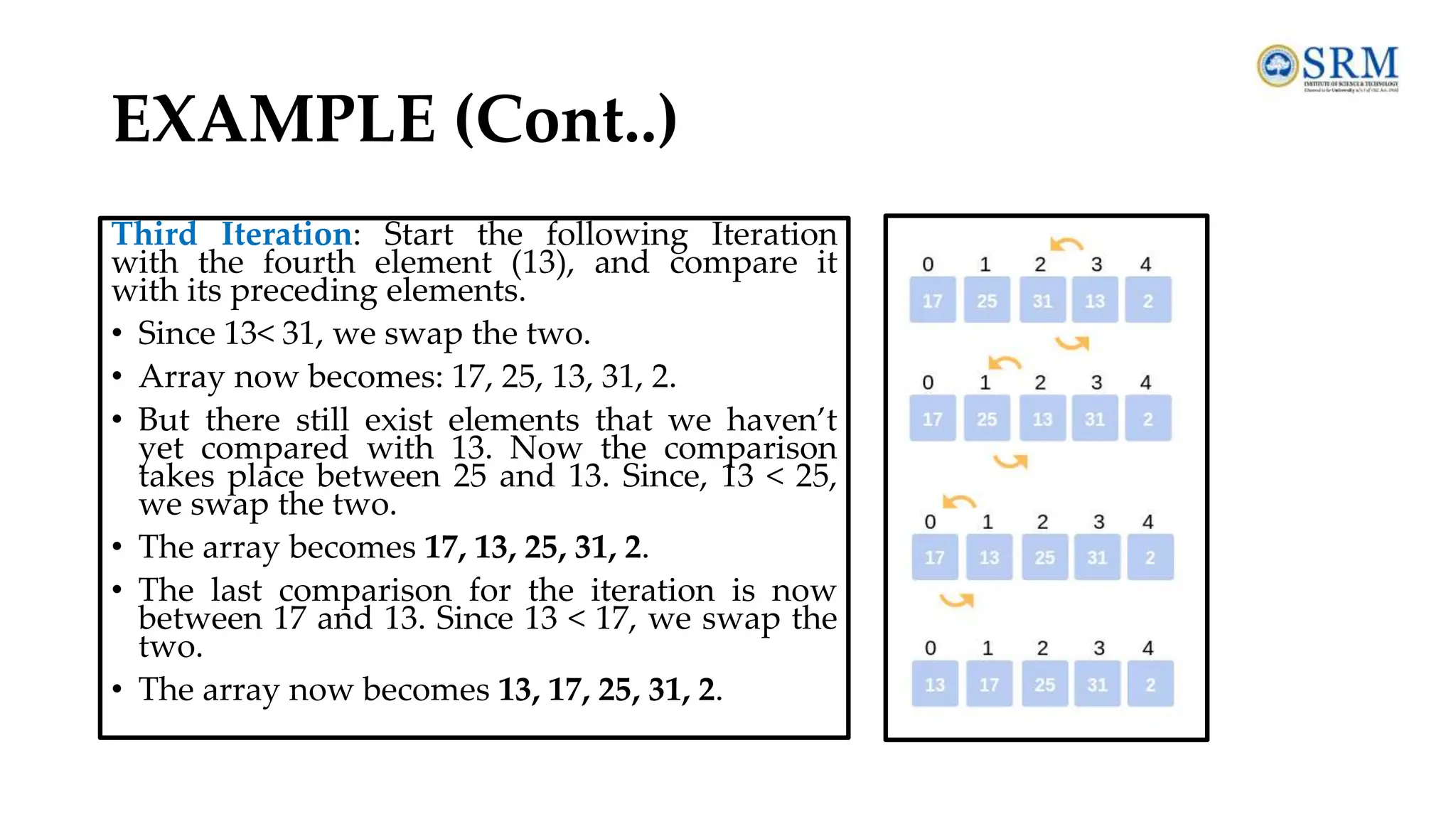
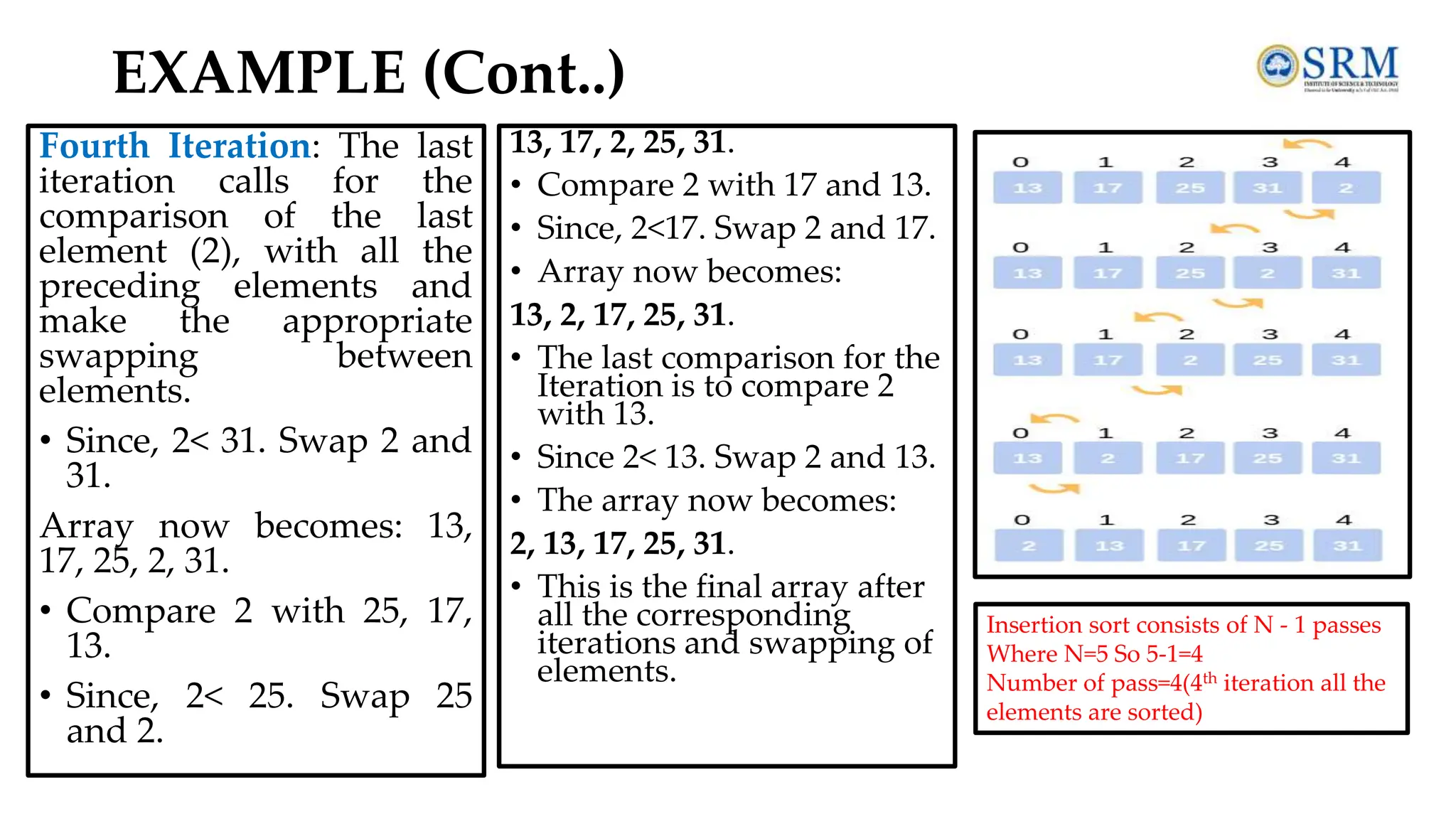
![INSERTION SORT • Insertion sorts works by taking elements from the list one by one and inserting them in their current position into a new sorted list. • Insertion sort consists of N - 1 passes, where N is the number of elements to be sorted. • The ith pass of insertion sort will insert the ith element A[i] into its rightful place among A[1], A[2] to A[i - 1]. After doing this insertion the records occupying A[1]....A[i] are in sorted order. Pseudo code INSERTION-SORT(A) for i = 1 to n key ← A [i] j ← i – 1 while j > = 0 and A[j] > key A[j+1] ← A[j] j ← j – 1 End while A[j+1] ← key End for](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-52-2048.jpg)












![Example 4 #include <stdio.h> int main() { int n, i, sum = 0; scanf("%d", &n); int arr[n]; for(i = 0; i < n; i++) { scanf("%d", &arr[i]); sum = sum + arr[i]; } printf("%d", sum); } Space Complexity: • The array consists of n integer elements. • So, the space occupied by the array is 4 * n. Also we have integer variables such as n, i and sum. Assuming 4 bytes for each variable, the total space occupied by the program is 4n + 12 bytes. • Since the highest order of n in the equation 4n + 12 is n, so the space complexity is O(n) or linear.](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-69-2048.jpg)





![int sum(int A[], int n) { int sum = 0, i; for(i = 0; i < n; i++) sum = sum + A[i]; return sum; } • In above calculation Cost is the amount of computer time required for a single operation in each line. • Repetition is the amount of computer time required by each operation for all its repetitions. • Total is the amount of computer time required by each operation to execute. So above code requires '4n+4' Units of computer time to complete the task. Here the exact time is not fixed. And it changes based on the n value. If we increase the n value then the time required also increases linearly. Totally it takes '4n+4' units of time to complete its execution Example 2](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-75-2048.jpg)















































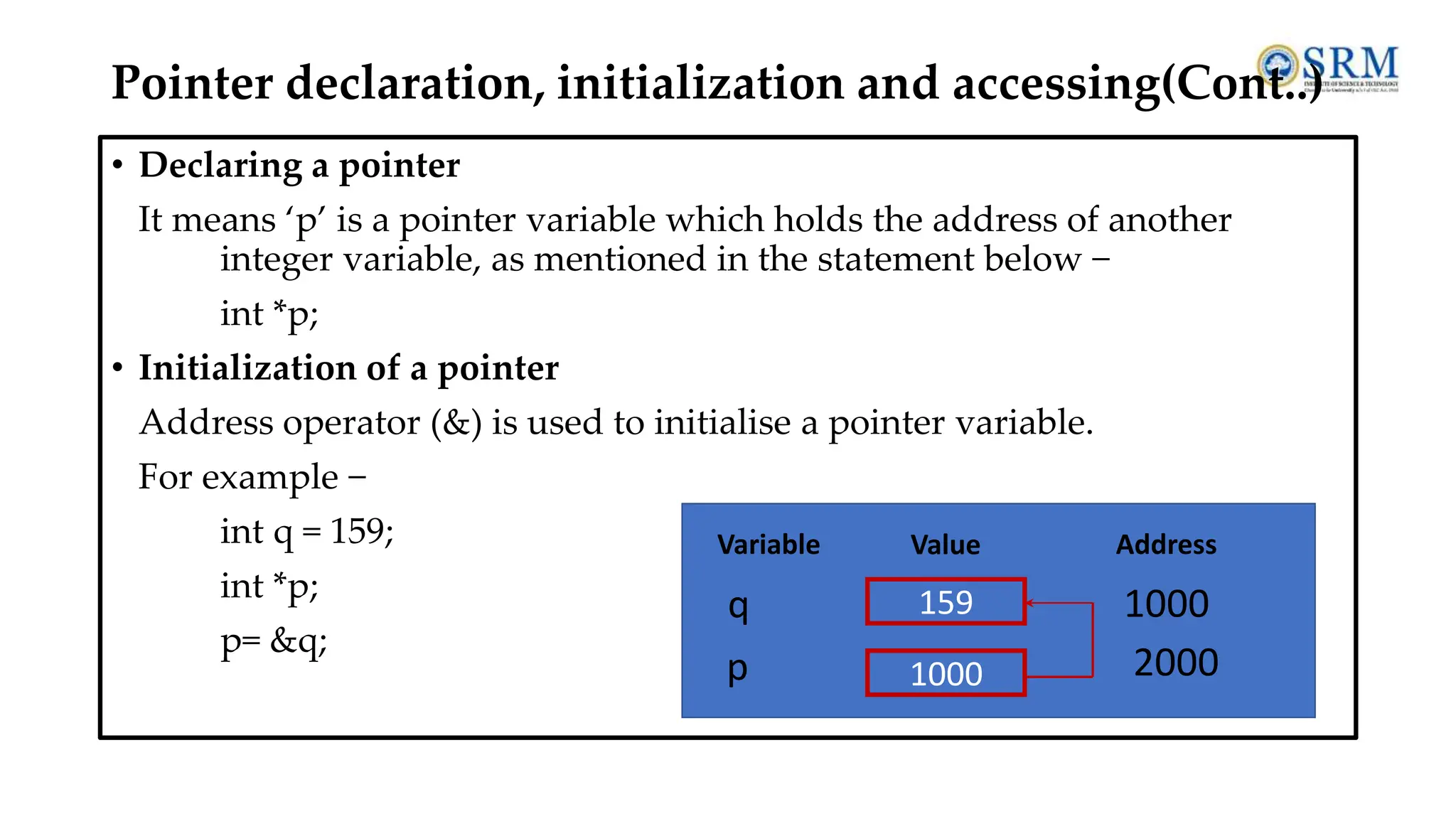


![⮚The compiler allocates Continuous memory locations for all the elements of the array. ⮚The base address = first element address (index 0) of the array. ⮚Syntax: data_type (var_name)[size_of_array] • For Example − int a [5] = {10, 20,30,40,50}; ⮚Elements • The five elements are stored as follows − Pointers and one-dimensional arrays Elements a[0] a[1] a[2] a[3] a[4] Values 10 20 30 40 50 Address 1000 1004 1008 1012 1016 Base Address a=&a[0]=1000 //Declaration int *p; int my_arr[] = {11, 22, 33, 44, 55}; p = my_arr;](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-132-2048.jpg)
![• If ‘p’ is declared as integer pointer, then, an array ‘a’ can be pointed by the following assignment − p = a; (or) p = &a[0]; • Every value of 'a' is accessed by using p++ to move from one element to another element. When a pointer is incremented, its value is increased by the size of the data type that it points to. This length is called the "scale factor". • The relationship between ‘p’ and 'a' is explained below P = &a[0] = 1000 P+1 = &a[1] = 1004 P+2 = &a[2] = 1008 P+3 = &a[3] = 1012 P+4 = &a[4] = 1016 Pointers and one-dimensional arrays (Cont)](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-133-2048.jpg)
![• Address of an element is calculated using its index and the scale factor of the data type. An example to explain this is given herewith. • Address of a[3] = base address + (3* scale factor of int) = 1000 + (3*4) = 1000 +12 = 1012 • Pointers can be used to access array elements instead of using array indexing. • *(p+3) gives the value of a[3]. • a[i] = *(p+i) Pointers and one-dimensional arrays (Cont..)](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-134-2048.jpg)
![•Following is the C program for pointers and one-dimensional arrays − #include<stdio.h> main ( ) { int a[5]; int *p,i; printf ("Enter 5 lements"); for (i=0; i<5; i++) scanf ("%d", &a[i]); p = &a[0]; printf ("Elements of the array are"); for (i=0; i<5; i++) printf("%d", *(p+i)); } Output When the above program is executed, it produces the following result − Enter 5 elements : 10 20 30 40 50 Elements of the array are : 10 20 30 40 50 Example Program](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-135-2048.jpg)
![POINTER ARRAYS Syntax: data_type (*var_name)[size_of_array] •Example: int (*arr_ptr)[5], *a_ptr, arr[5][5] ={{10,20,30,23,12}, {15,25,35,33,88}, {45,25,77,57,54}, {65,34,67,33,99}, {44,45,55,44,65}}; arr_ptr= & arr; a_ptr= & arr; arr_ptr++; a_ptr++; Example Program 1020 10 1024 20 1028 30 1032 23 1036 12 1040 15 1044 25 1048 35 1052 33 1056 88 1060 45 1064 25 1068 77 1072 57 1076 54 1080 65 1084 34 1088 67 1092 33 1096 99 1100 44 1104 45 1108 55 1112 44 1116 65 arr_ptr a_ptr](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-136-2048.jpg)
![Example Program : 1D array using Pointer #include<stdio.h> int main() { int array[5]; int i,sum=0; int *ptr; printf("nEnter array elements (5 integer values):"); for(i=0;i<5;i++) scanf("%d",&array[i]); /* array is equal to base address * array = &array[0] */ ptr = array; for(i=0;i<5;i++) { //*ptr refers to the value at addresssum = sum + *ptr; ptr++; } printf("nThe sum is: %d",sum); } Output Enter array elements (5 integer values): 1 2 3 4 5 The sum is: 15](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-137-2048.jpg)

![Pointers and two-dimensional arrays • Memory allocation for a two-dimensional array is as follows − int a[3] [3] = {1,2,3,4,5,6,7,8,9}; 1 2 3 4 5 6 7 8 9 0 1 2 0 1 2 Row 1-> 1 2 3 a[0][0] a[0][1] a[0][2] 1000 1004 1008 Row 2-> 4 5 6 a[1][0] a[1][1] a[1][2] 1012 1016 1020 Row 1-> 7 8 9 a[2][0] a[2][1] a[2][2] 1024 1028 1032 Base Address=1000=&a[0][0]](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-139-2048.jpg)
![Pointers and two-dimensional arrays • Assigning Base Address to pointer int *p p=&a[0][0] (or) p=a Pointer is used to access the elements of 2-dimensional array as follows a[i][j]=*(p+j *columnsize+j) a[1] [2] = *(1000 + 1*3+2) = *(1000 + 3+2) = *(1000 + 5*4) // 4 is Scale factor = * (1000+20) = *(1020) a[1] [2] = 6](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-140-2048.jpg)
![Example Program #include<stdio.h> main ( ) { int a[3] [3], i,j; int *p; clrscr ( ); printf ("Enter elements of 2D array"); for (i=0; i<3; i++) { for (j=0; j<3; j++) { scanf ("%d", &a[i] [j]); } } p = &a[0] [0]; printf ("elements of 2d array are"); for (i=0; i<3; i++) { for (j=0; j<3; j++) { printf ("%d t", *(p+i*3+j)); } printf ("n"); } getch ( ); } Output When the above program is executed, it produces the following result − enter elements of 2D array 1 2 3 4 5 6 7 8 9 Elements of 2D array are 1 2 3 4 5 6 7 8 9](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-141-2048.jpg)



![Declaration of Structures Syntax: struct struct_Name • { • <data-type> member_name; • <data-type> member_name; • … • } list of variables; Example: Structure to hold student details struct Student { int regNo; char name[25]; int english, science, maths; } stud;](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-145-2048.jpg)
![Declaration of Structures Syntax: struct struct_Name { <data-type> member_name; <data-type> member_name; … }; struct struct_Name struct_var; struct Student { int regNo; char name[25]; int english, science, maths; }; struct Student stud;](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-146-2048.jpg)

![Accessing and Updating Structures struct Student { int regNo; char name[25]; int english, science, maths; }; struct Student stud; scanf(“%d %s %d %d %d”,&stud.regNo, stud.name, &stud.english,&stud.science, &stud.maths); printf("Register number =% dn",stud.Regno); printf("Name %s",stud.name); stud.english= stud.english +10; stud.science++; //Accessing member Regno //Accessing member name //Updating member english](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-148-2048.jpg)
![Nested Structures struct Student { int regNo; char name[25]; struct marks { int english, science, maths; } } Amar; Amar.regNo; Amar.marks.english ; Amar.marks.science ; Amar.marks.maths; struct Student { int regNo; char name[25]; struct m marks; } Amar; struct m { int english; int science; int maths; }; struct Student { int regNo; char name[25]; struct {int english, science, maths } marks; } Amar;](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-149-2048.jpg)
![Example Program #include <stdio.h> #include <string.h> struct Books { char title[50]; char author[50]; char subject[100]; int book_id; }; /* book 1 specification */ strcpy( Book1.title, "C Programming"); strcpy( Book1.author, "Nuha Ali"); strcpy( Book1.subject, "C Programming Tutorial"); Book1.book_id = 6495407 int main( ) { struct Books Book1; /* Declare Book1 of type Book */ struct Books Book2; /* Declare Book2 of type Book */](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-150-2048.jpg)

![Example Program #include<stdio.h> struct student { char name[20]; int id; float marks; }; void main() { struct student s1,s2,s3; int dummy; printf("Enter the name, id, and marks of student 1 "); scanf("%s %d %f",s1.name,&s1.id,&s1.marks); scanf("%c",&dummy); printf("Enter the name, id, and marks of student 2 "); scanf("%s %d %f",s2.name,&s2.id,&s2.marks); scanf("%c",&dummy); printf("Enter the name, id, and marks of student 3 "); scanf("%s %d %f",s3.name,&s3.id,&s3.marks); scanf("%c",&dummy); printf("Printing the details....n"); printf("%s %d %fn",s1.name,s1.id,s1.marks); printf("%s %d %fn",s2.name,s2.id,s2.marks); printf("%s %d %fn",s3.name,s3.id,s3.marks); }](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-152-2048.jpg)


![Array of Structures struct Student { int regNo; char name[25]; int english, science, maths; }; struct Student stud[10]; scanf(“%d%s%d%d%d”,&stud[1].regNo,stud[1].name,&stud[1].english,&stu d[1].science, &stud[1].maths); printf("Register number = %dn",stud[1].Regno); printf("Name %s",stud[1].name); stud.[1]english= stud[0].english +10; stud[1].science++; //Accessing member Regno //Accessing member name //Updating member english](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-155-2048.jpg)
![Example Program #include<stdio.h> #include <string.h> struct student{ int rollno; char name[10]; }; int main() { int i; struct student st[5]; printf("Enter Records of 5 students"); for(i=0;i<5;i++){ printf("nEnter Rollno:"); scanf("%d",&st[i].rollno); printf("nEnter Name:"); scanf("%s",&st[i].name); } printf("nStudent Information List:"); for(i=0;i<5;i++){ printf("nRollno:%d, Name:%s",st[i].rollno,st[i].name); } return 0; }](https://image.slidesharecdn.com/dsa-unit1-240719140228-426d5465/75/Data-structure-and-algorithms-unit-1-pdf-SRM-156-2048.jpg)

