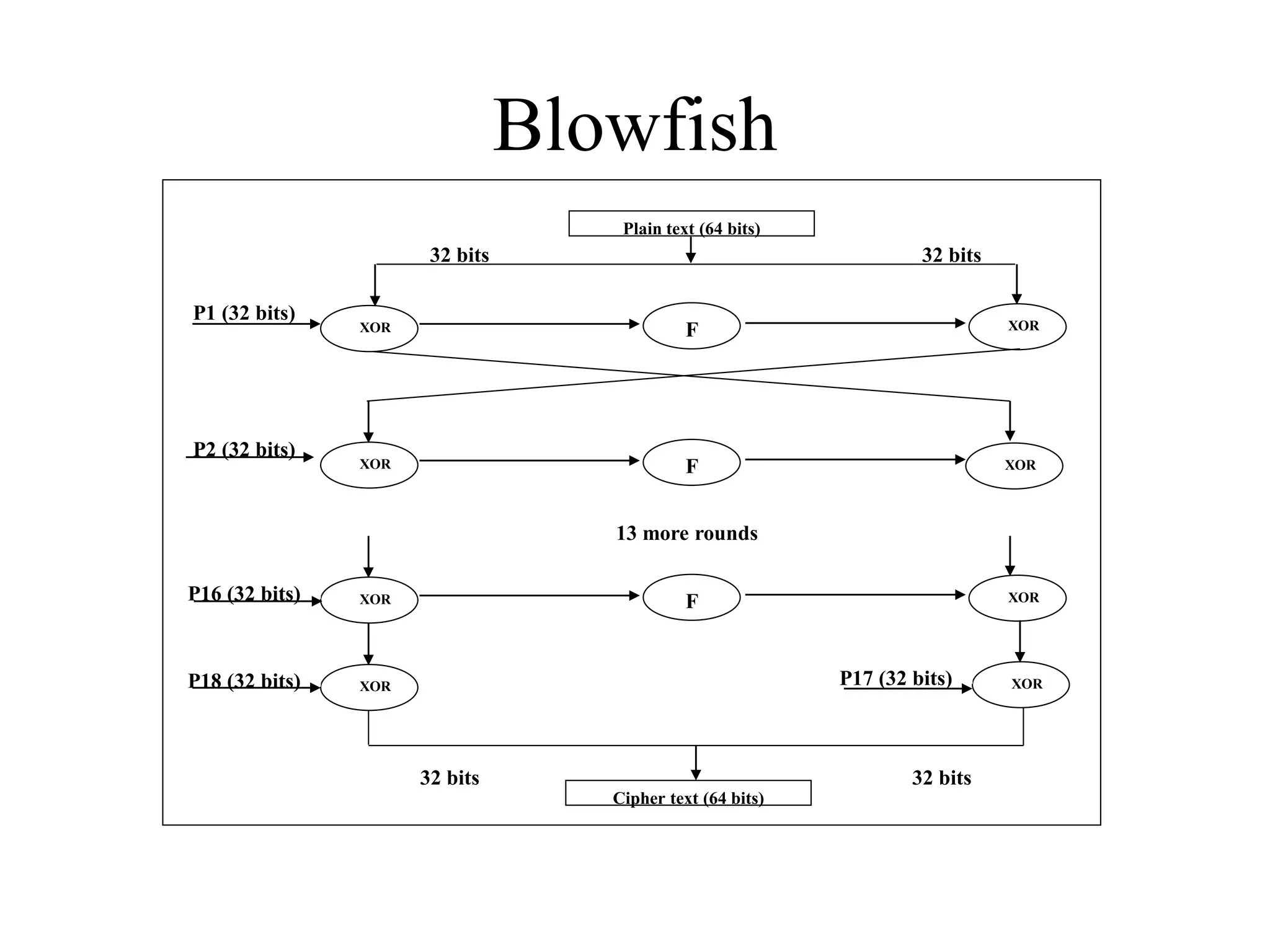
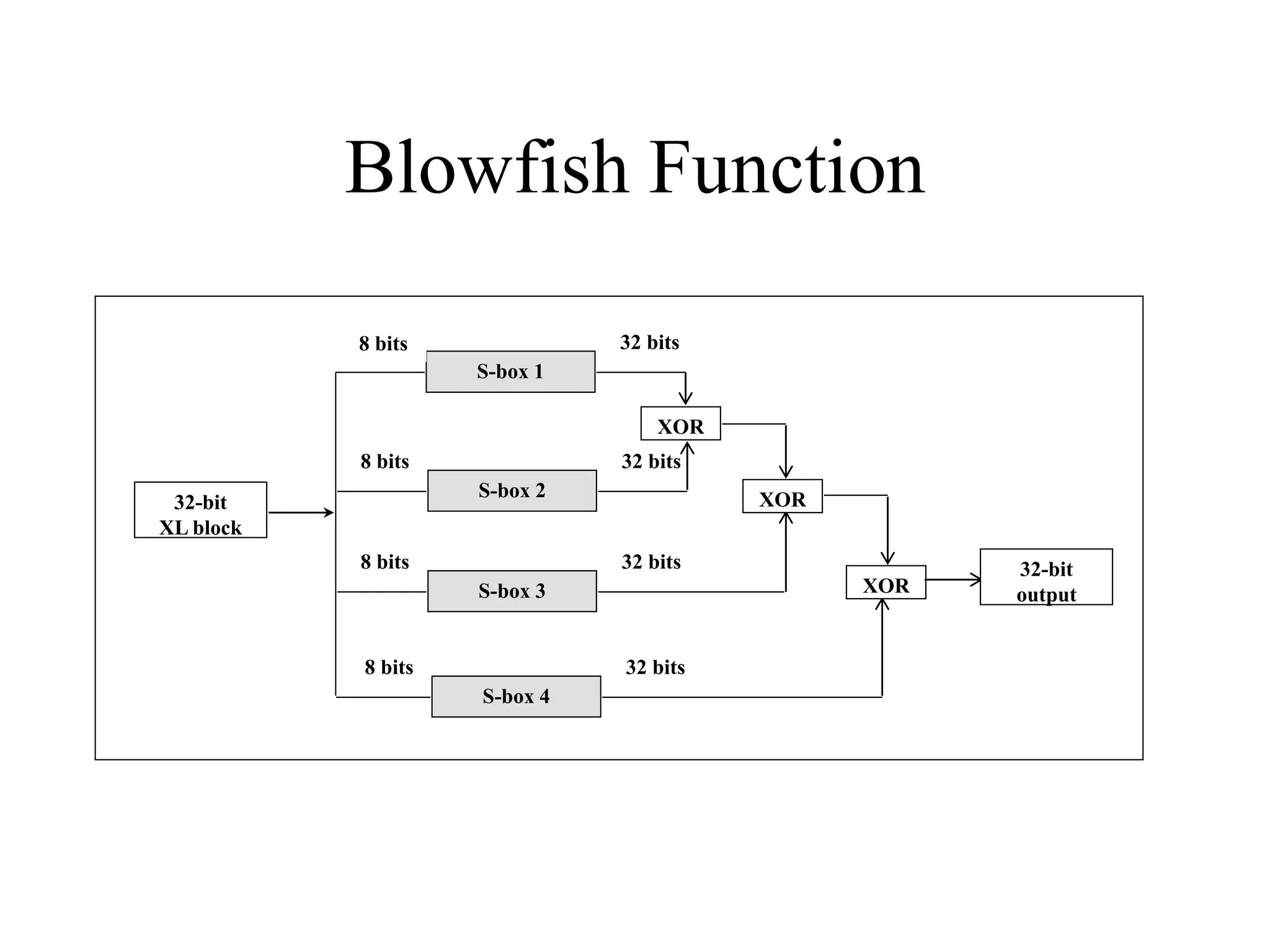
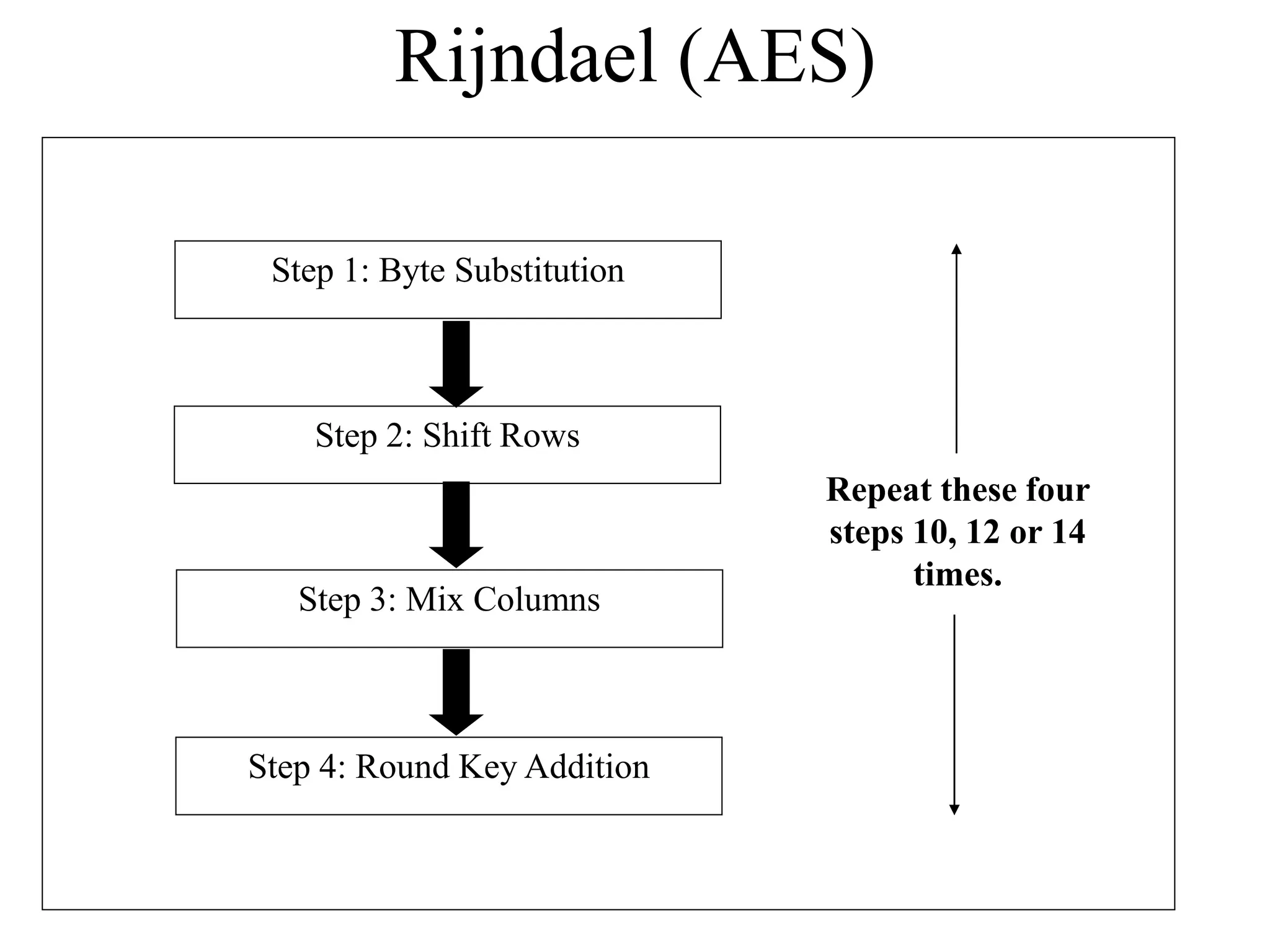
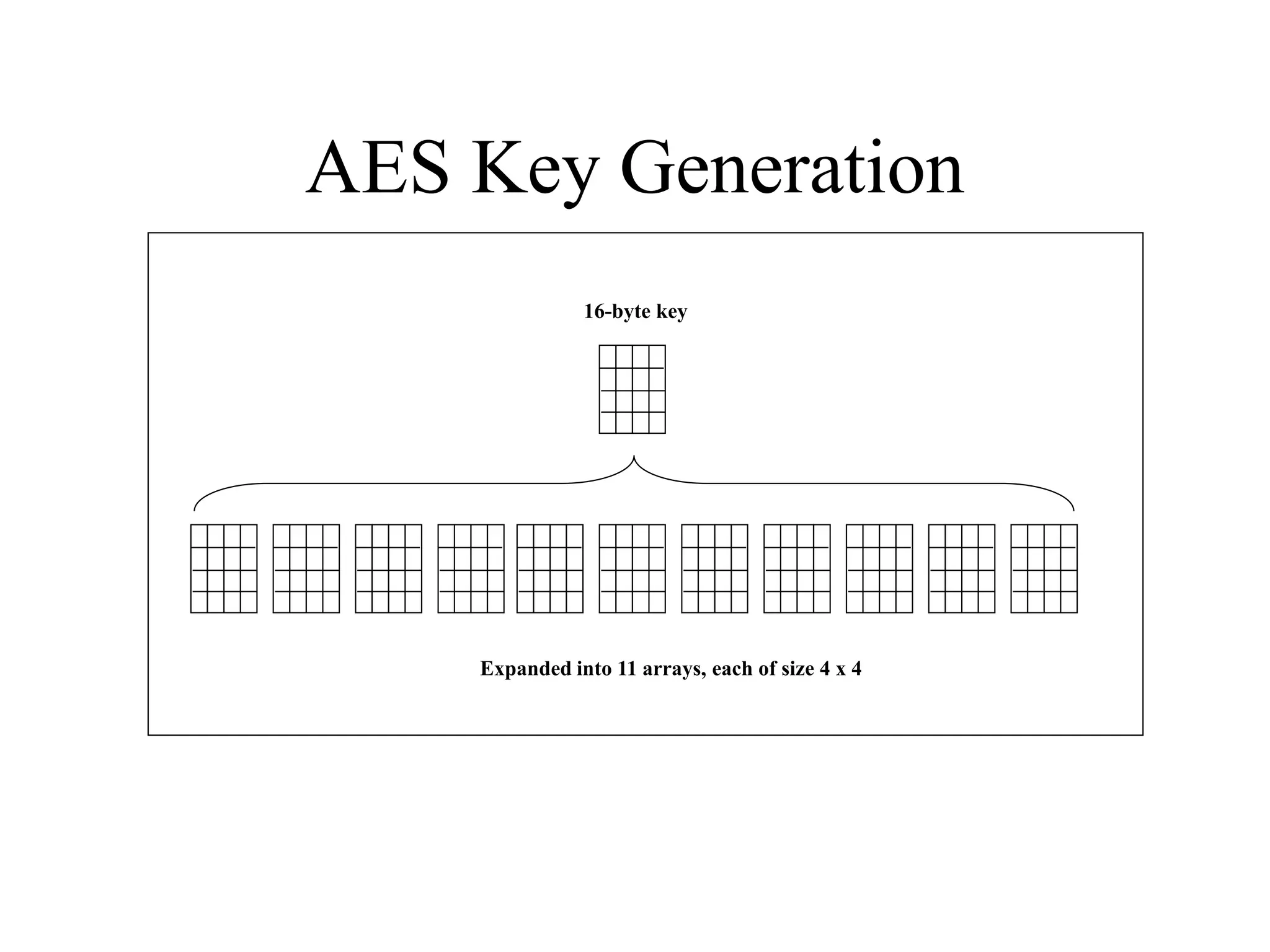
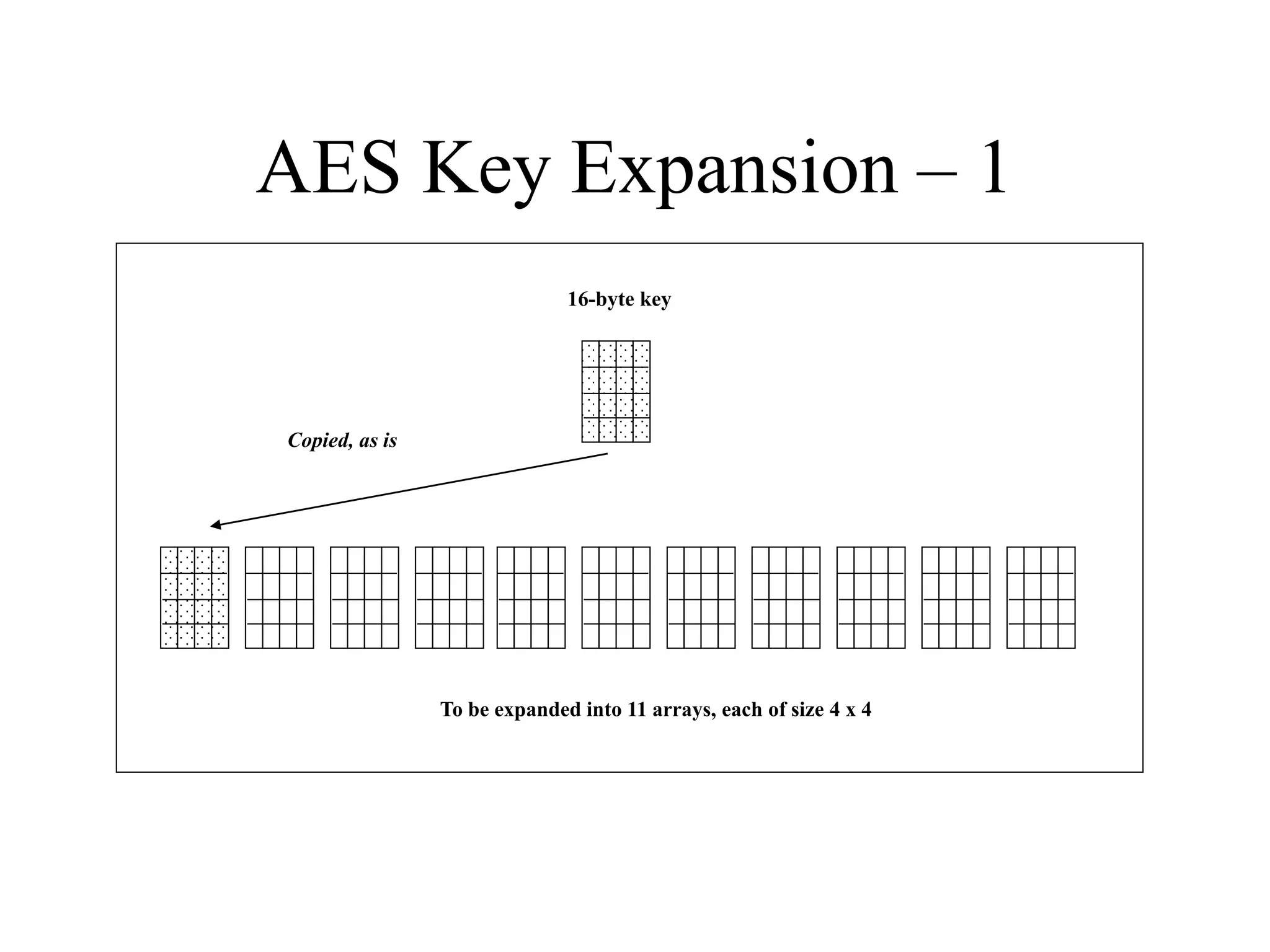
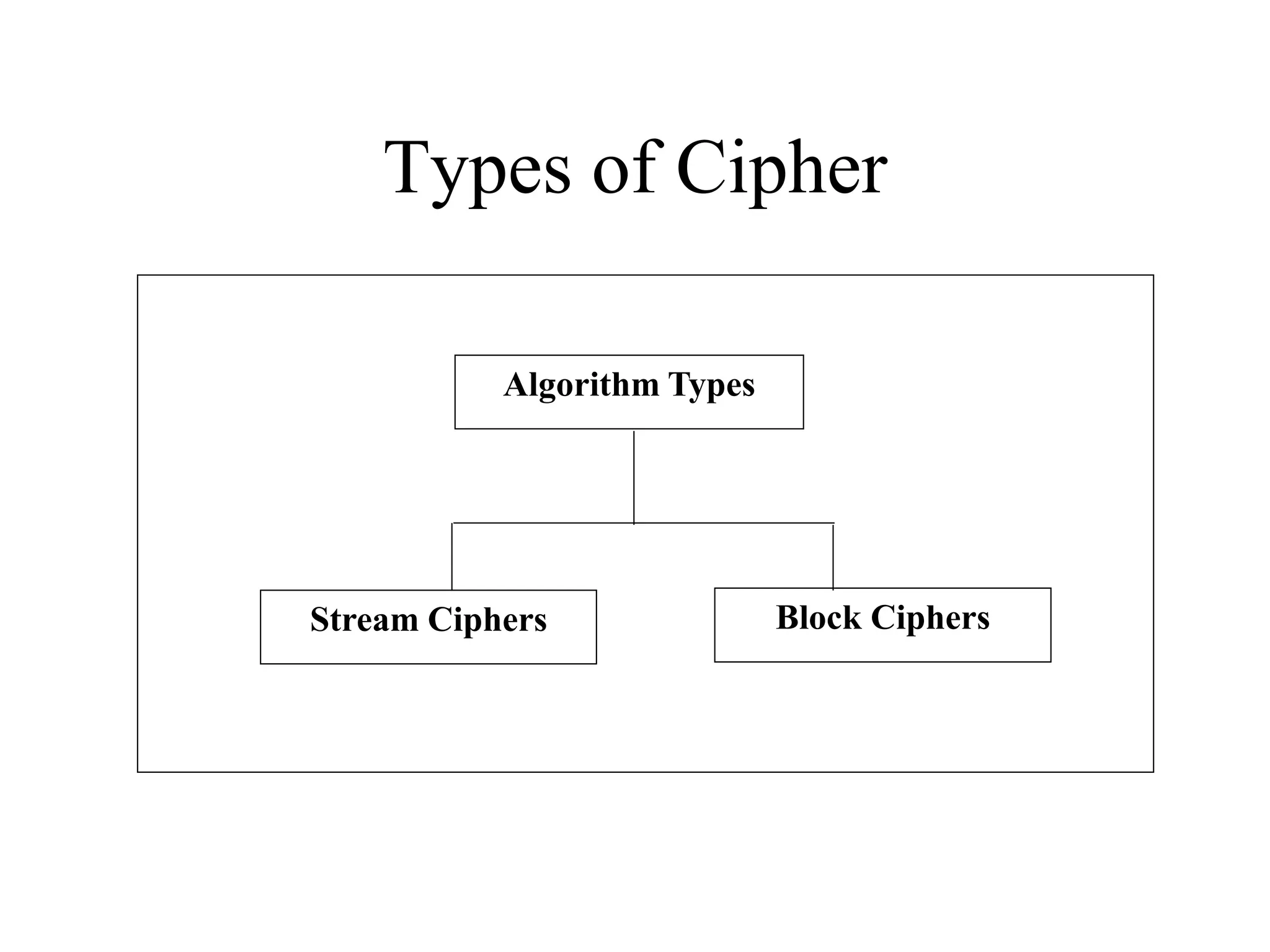
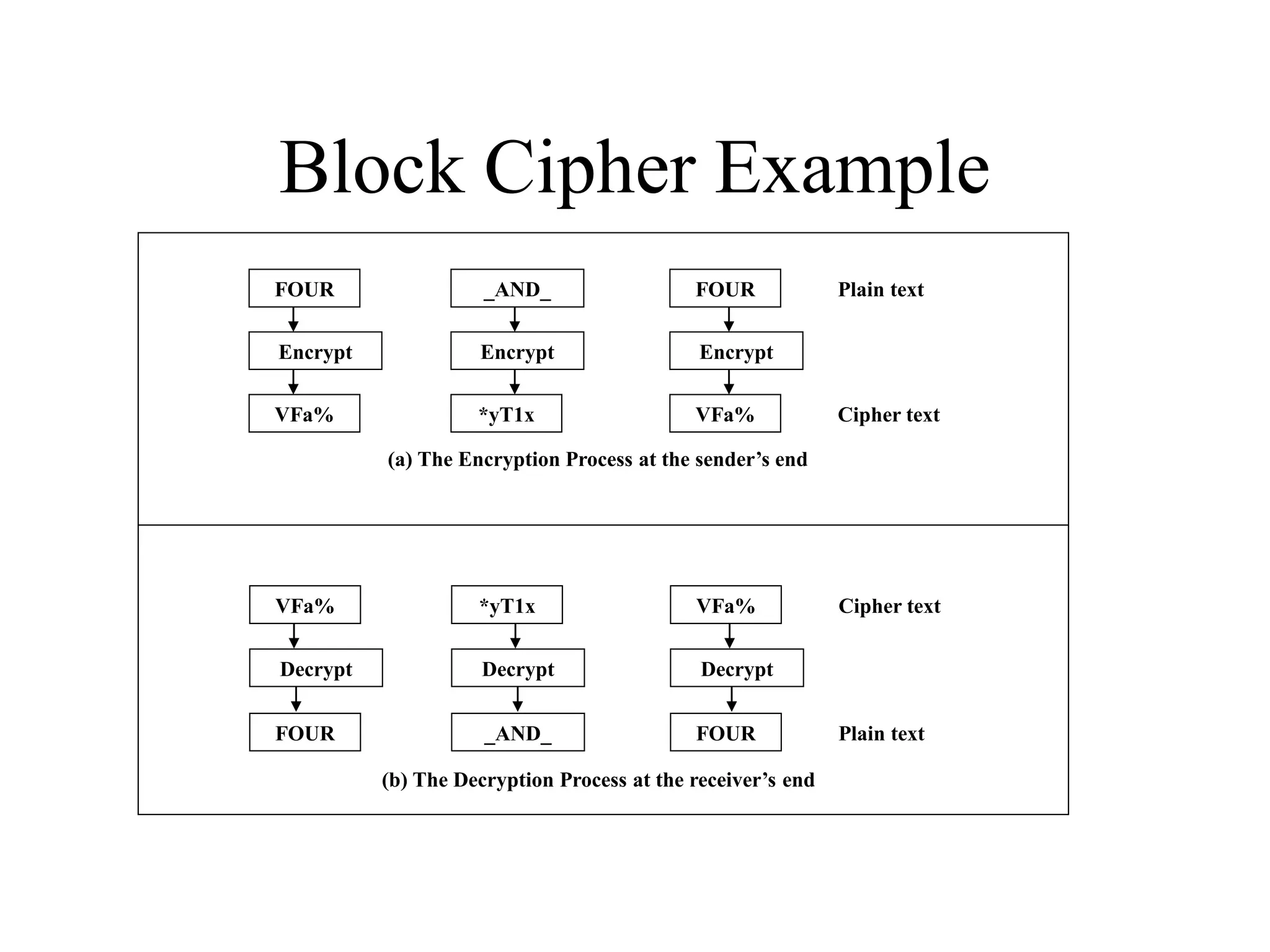
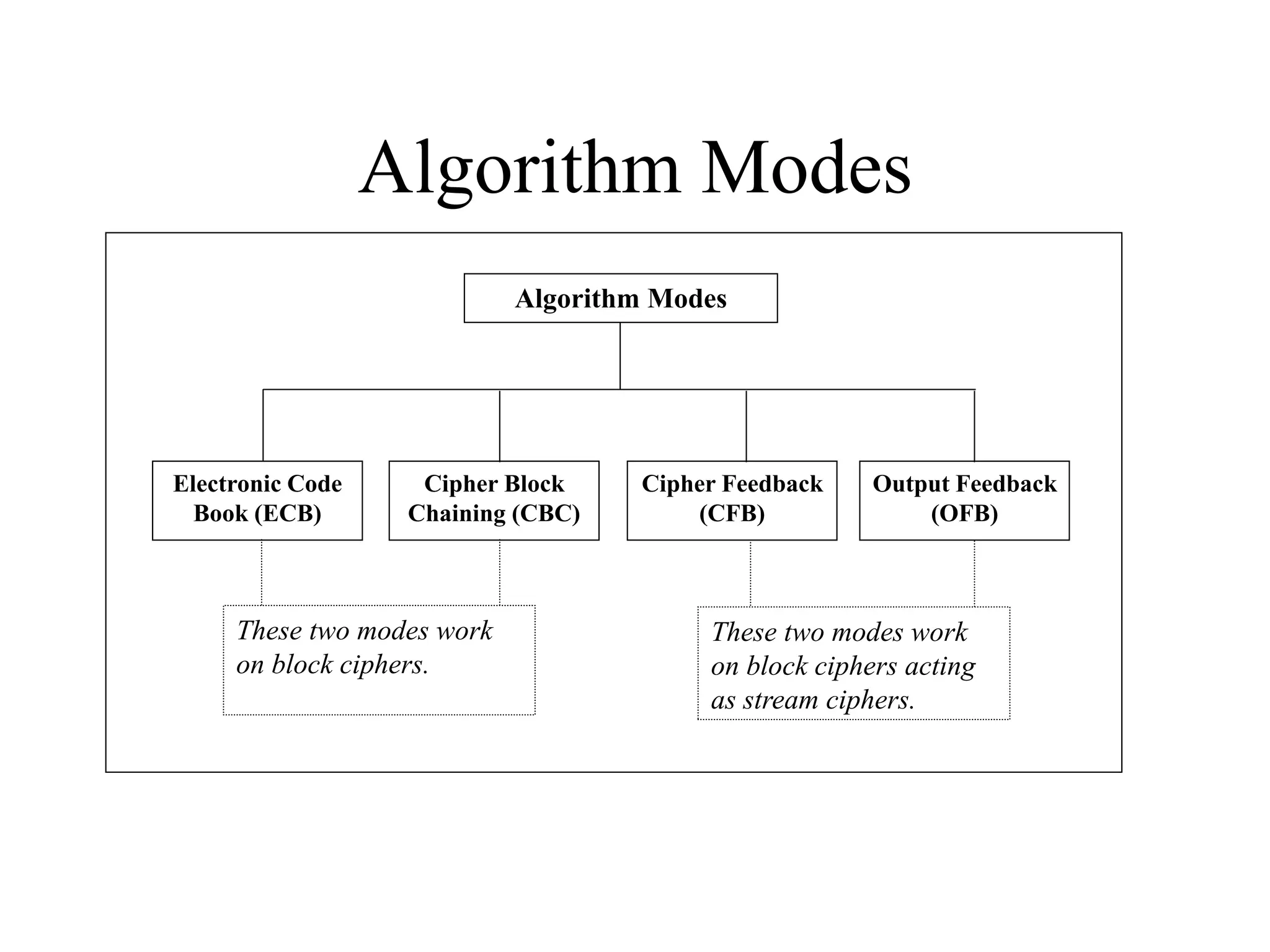
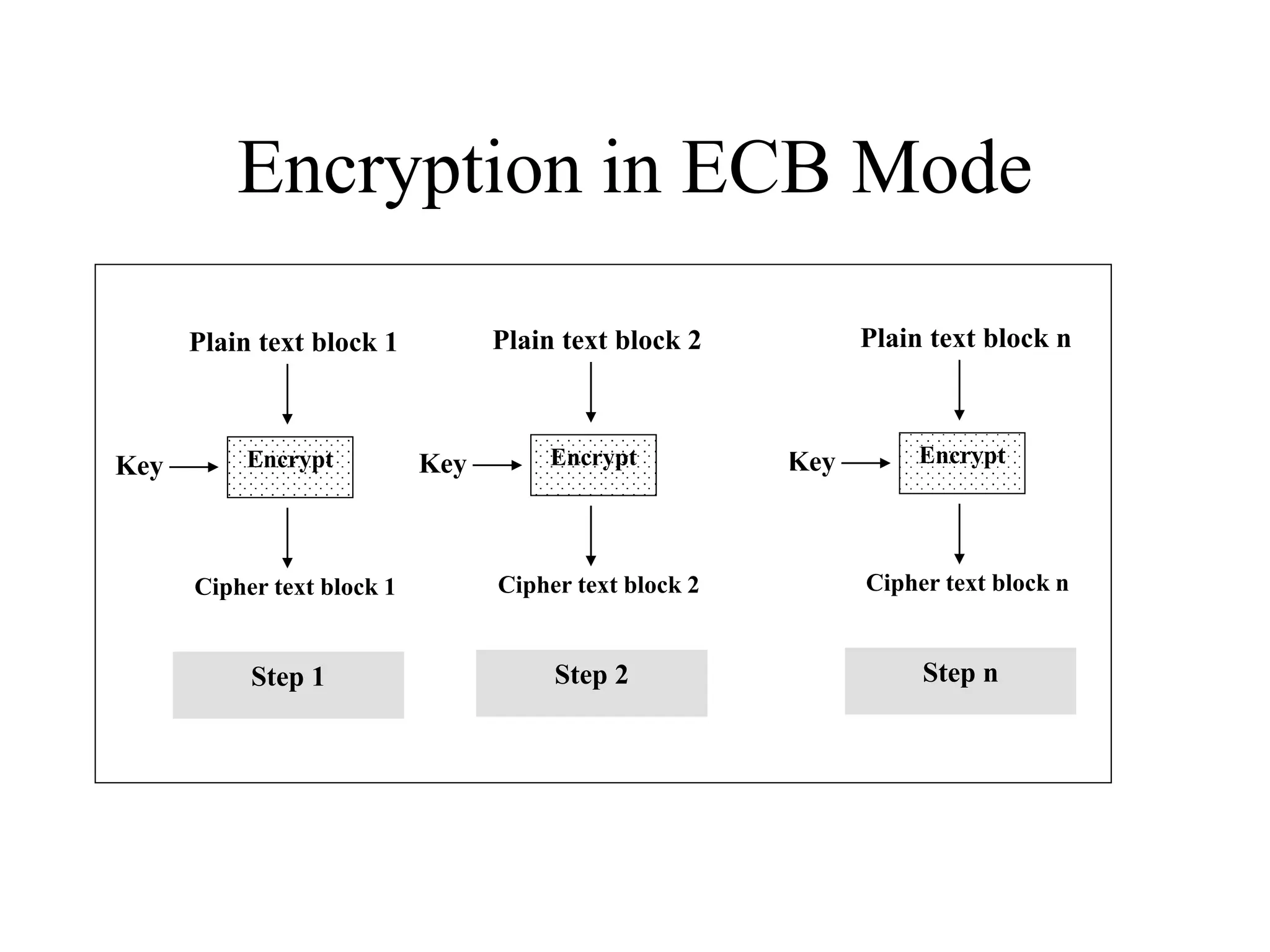
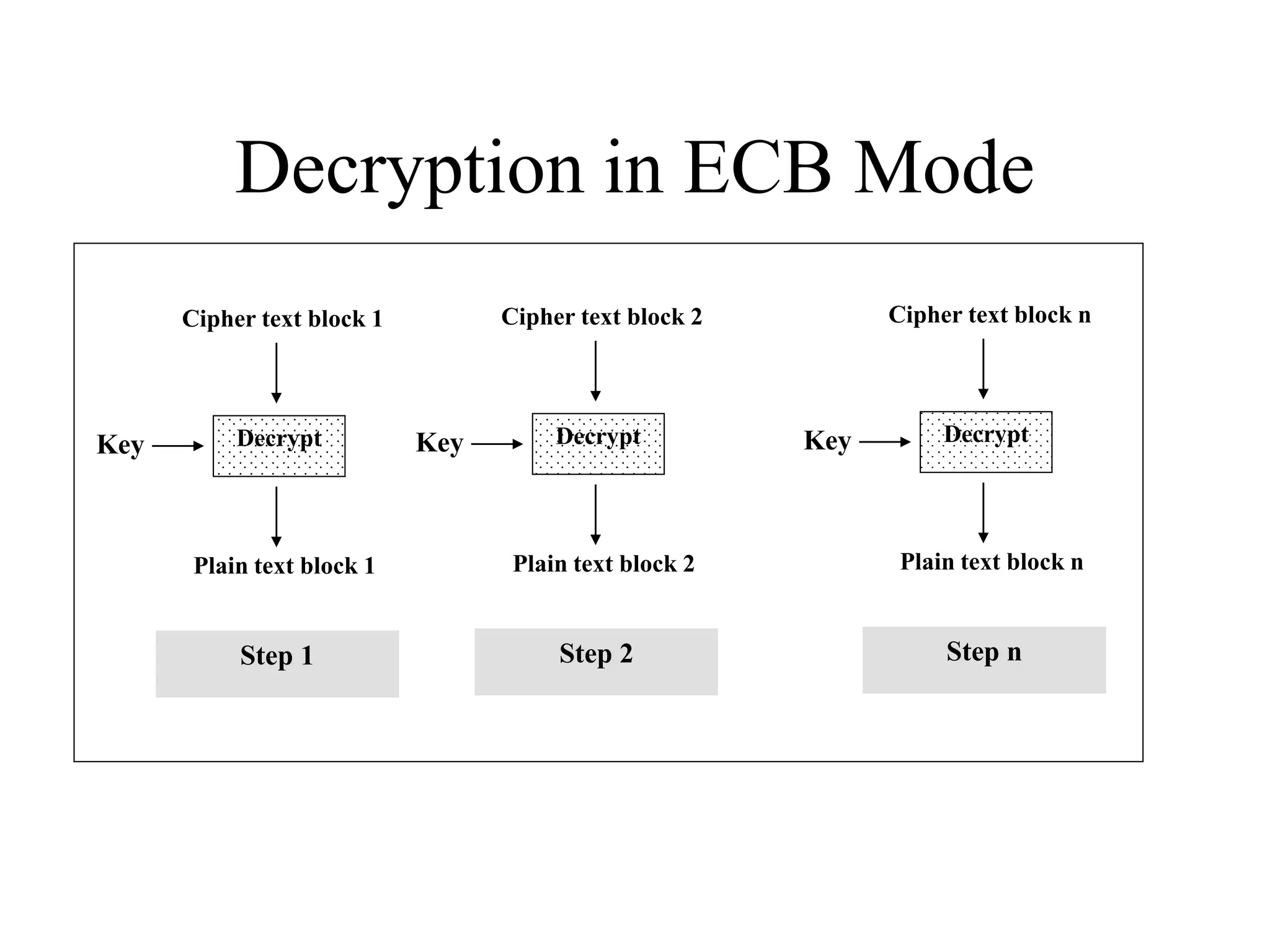
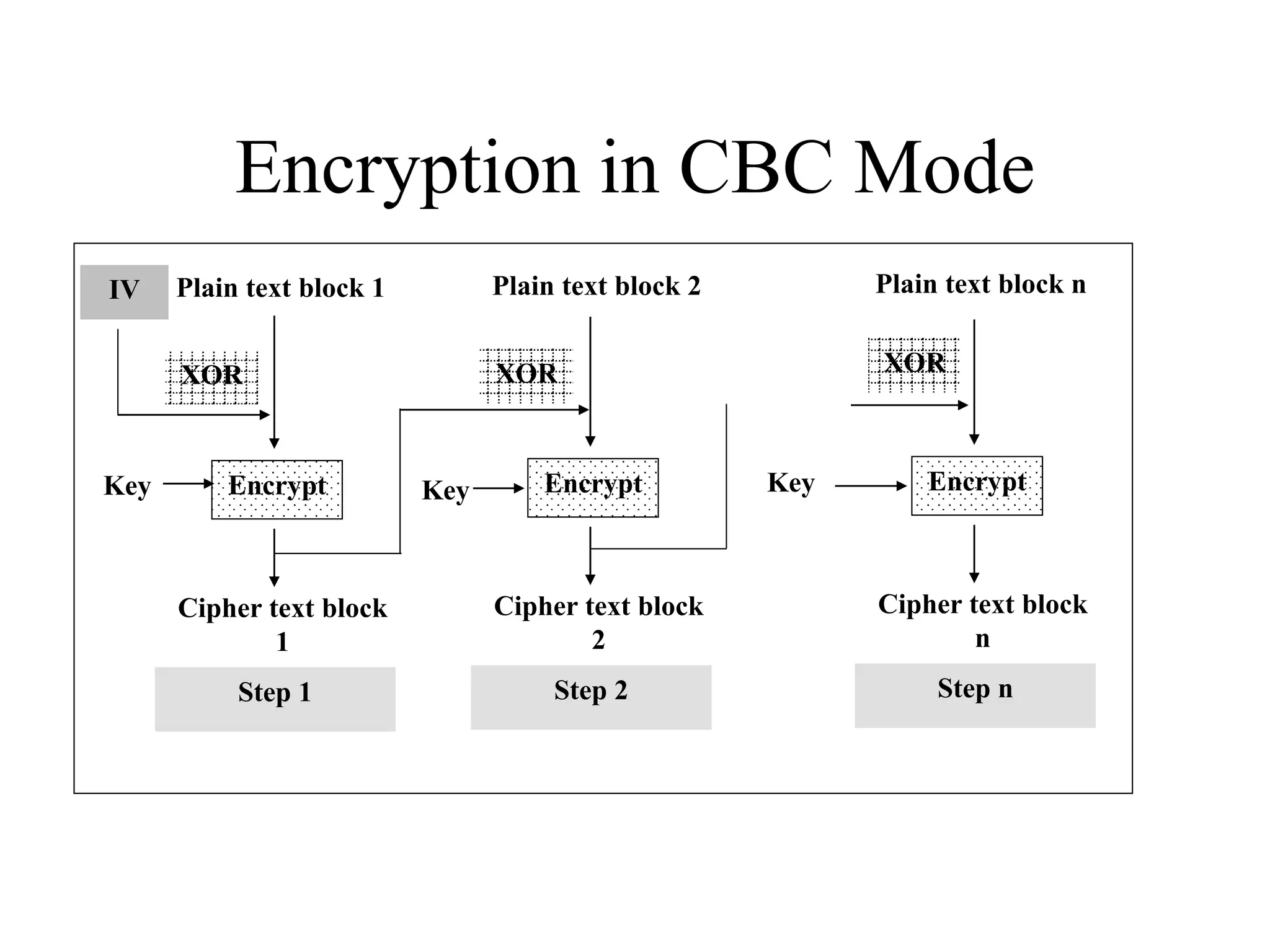
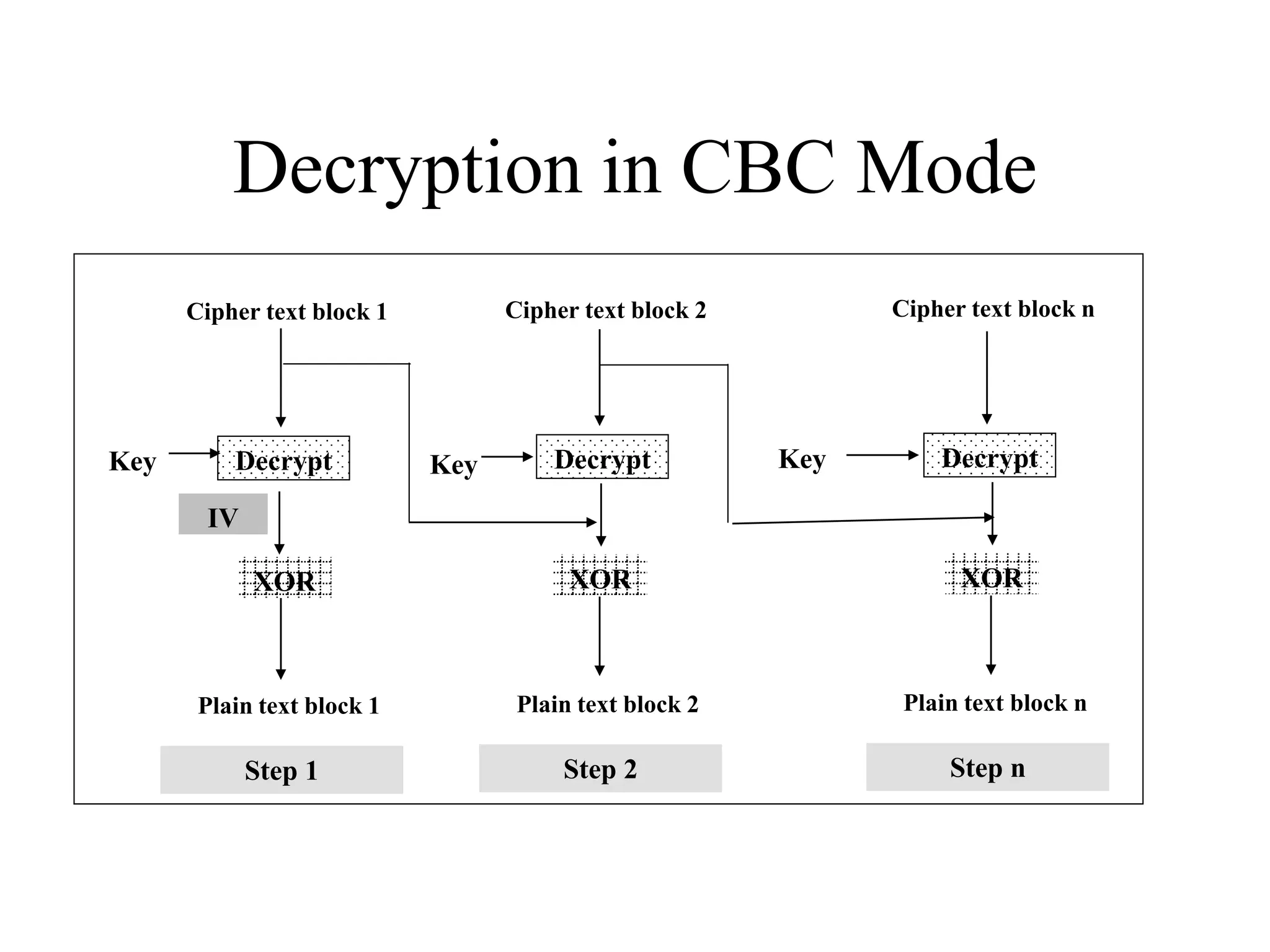
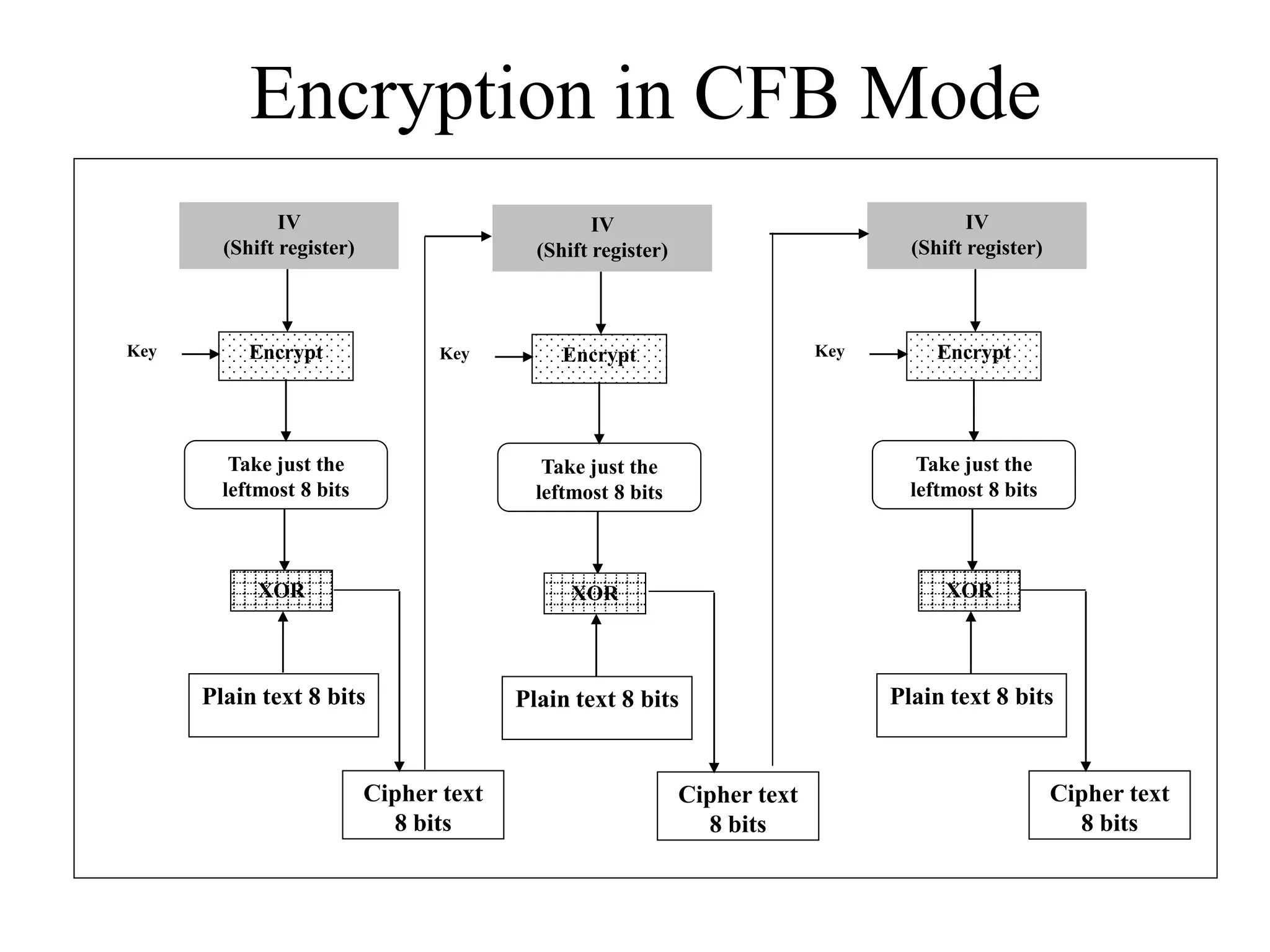
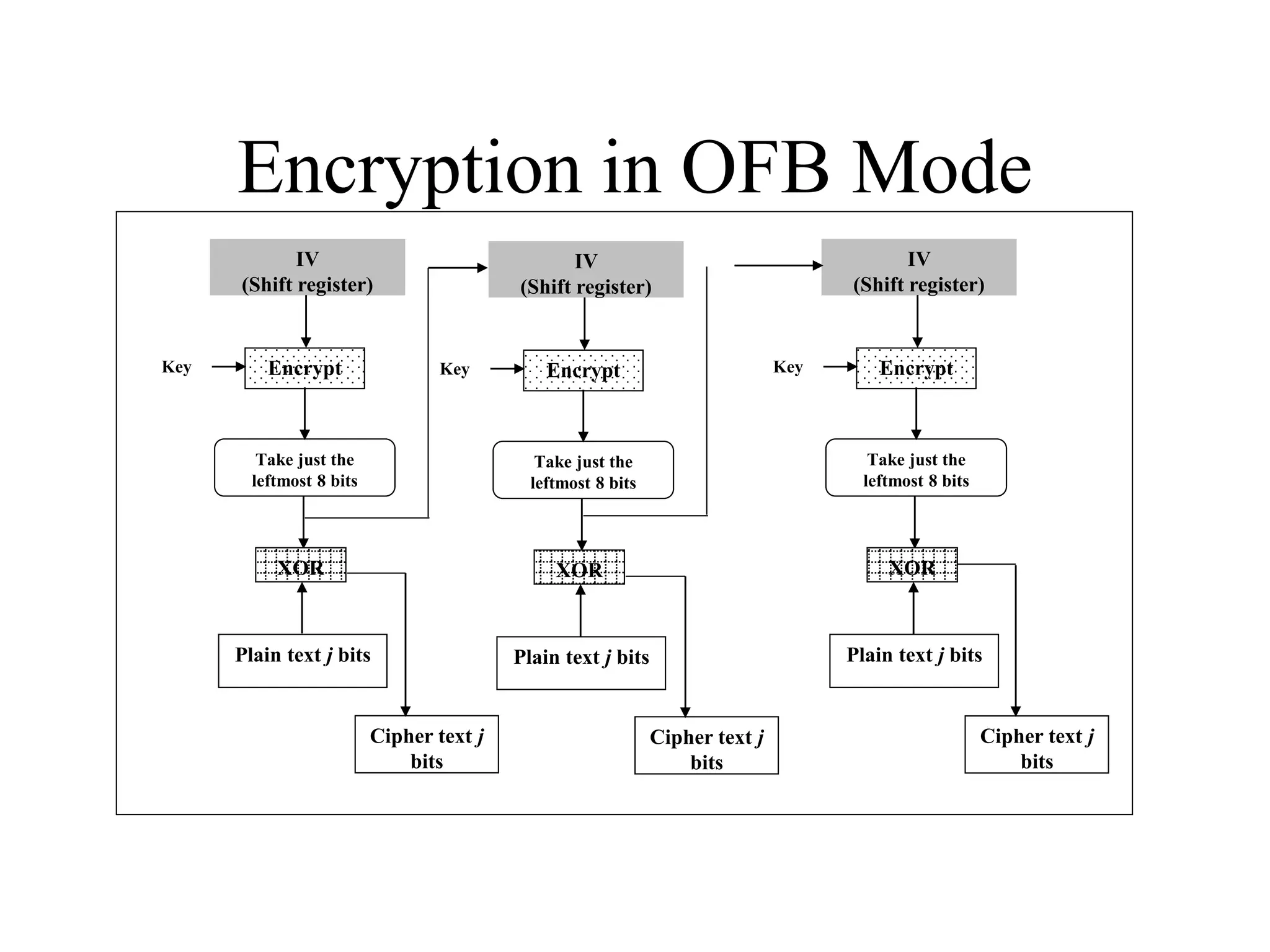
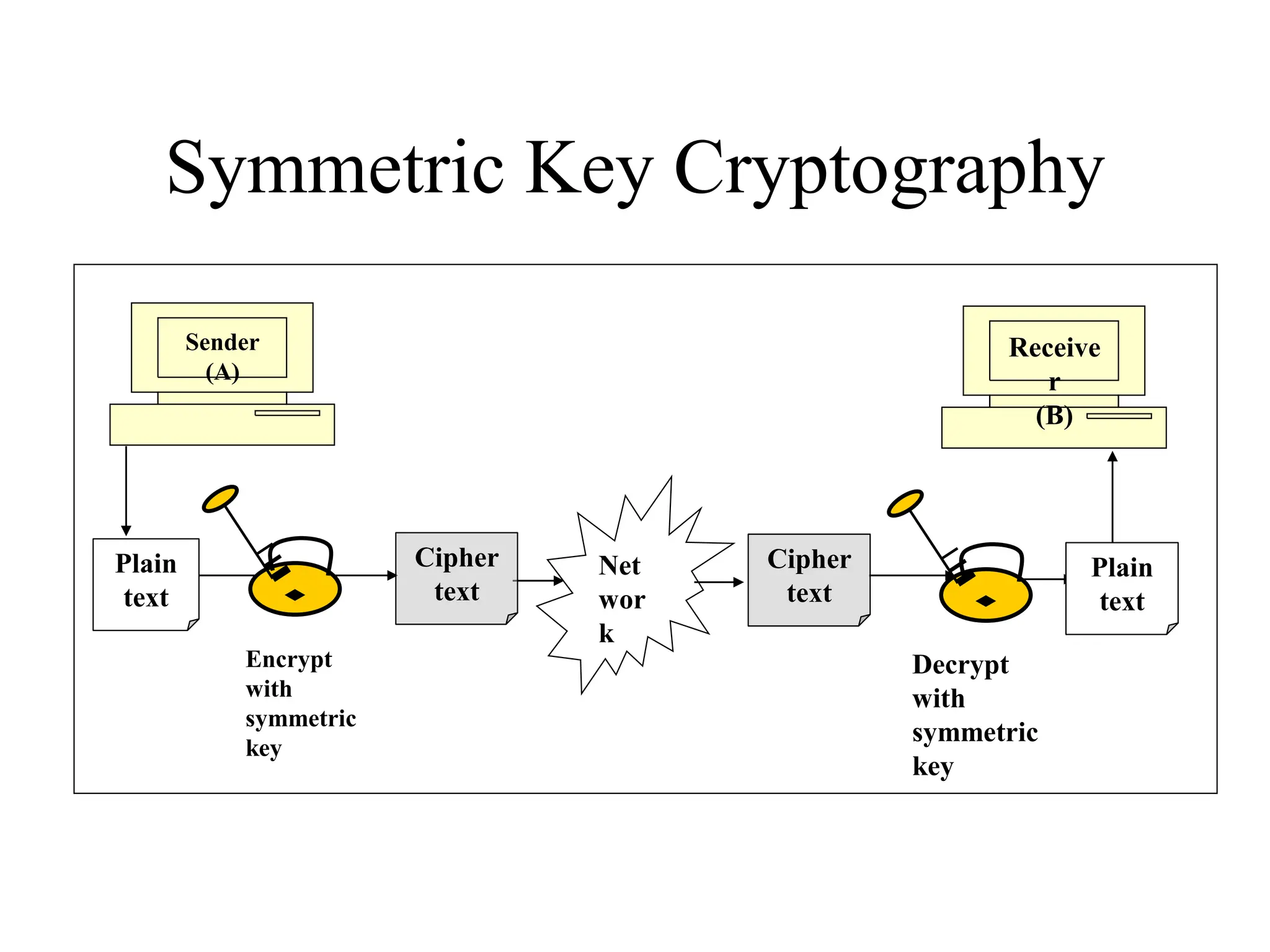
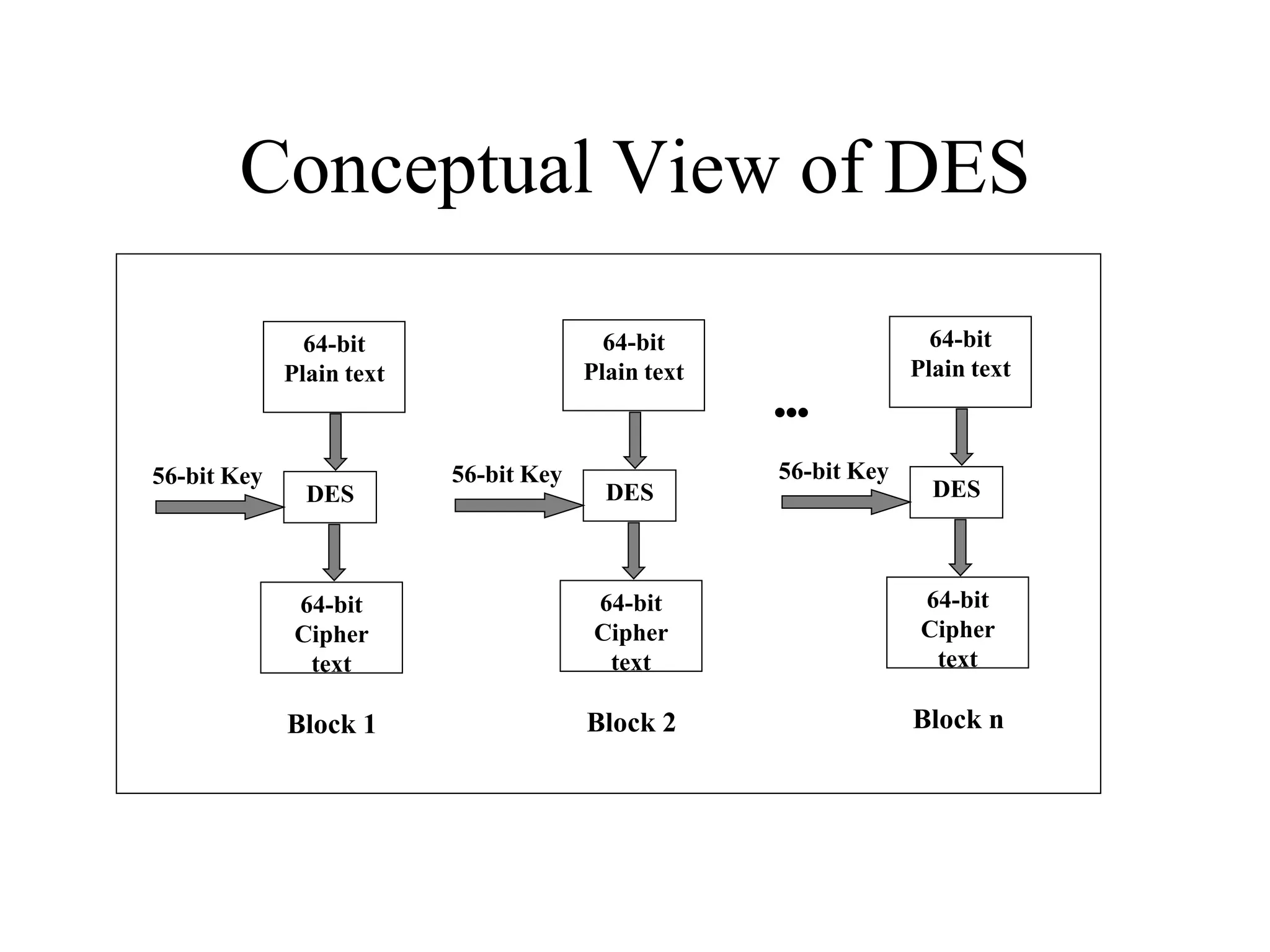
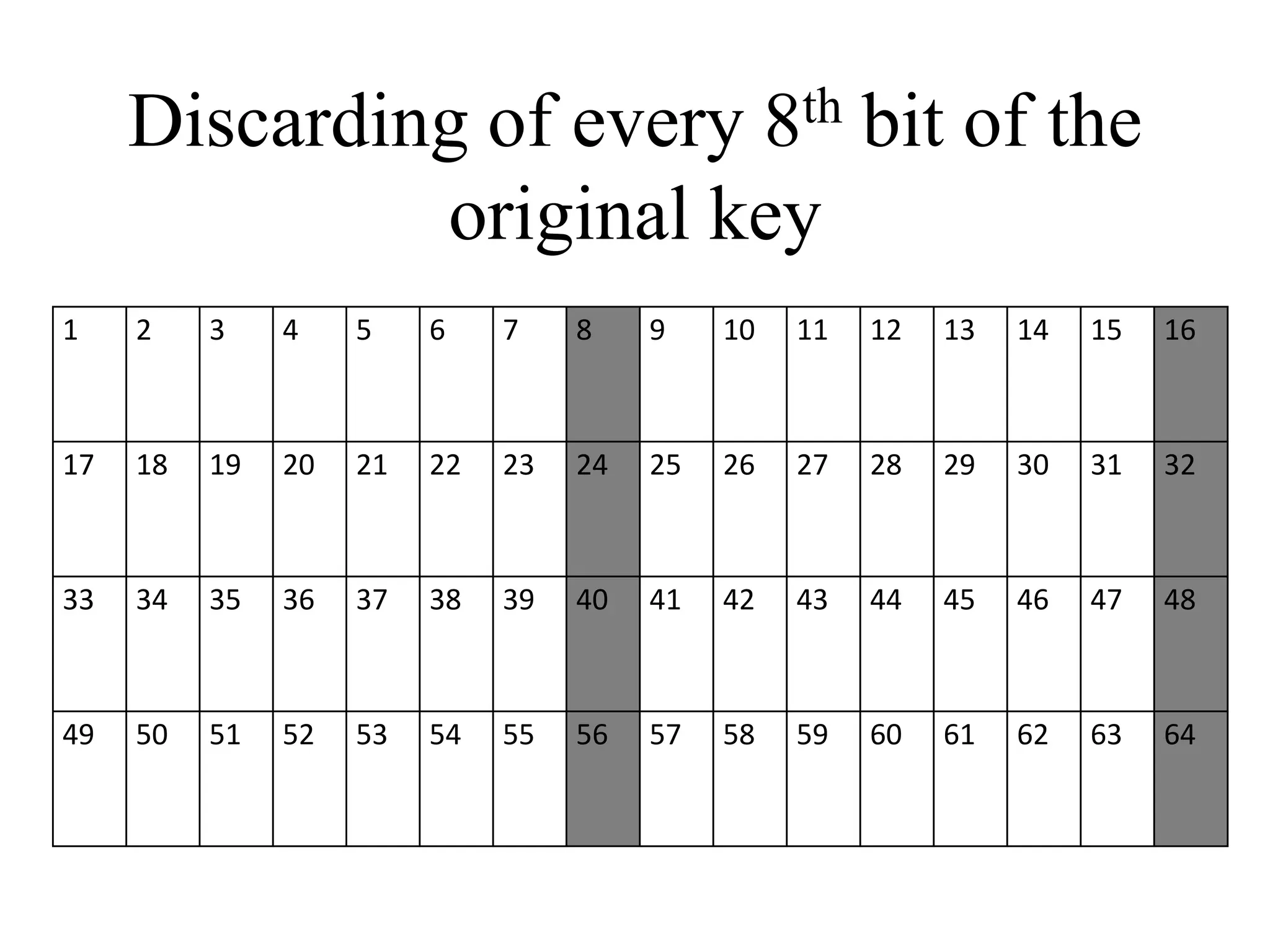
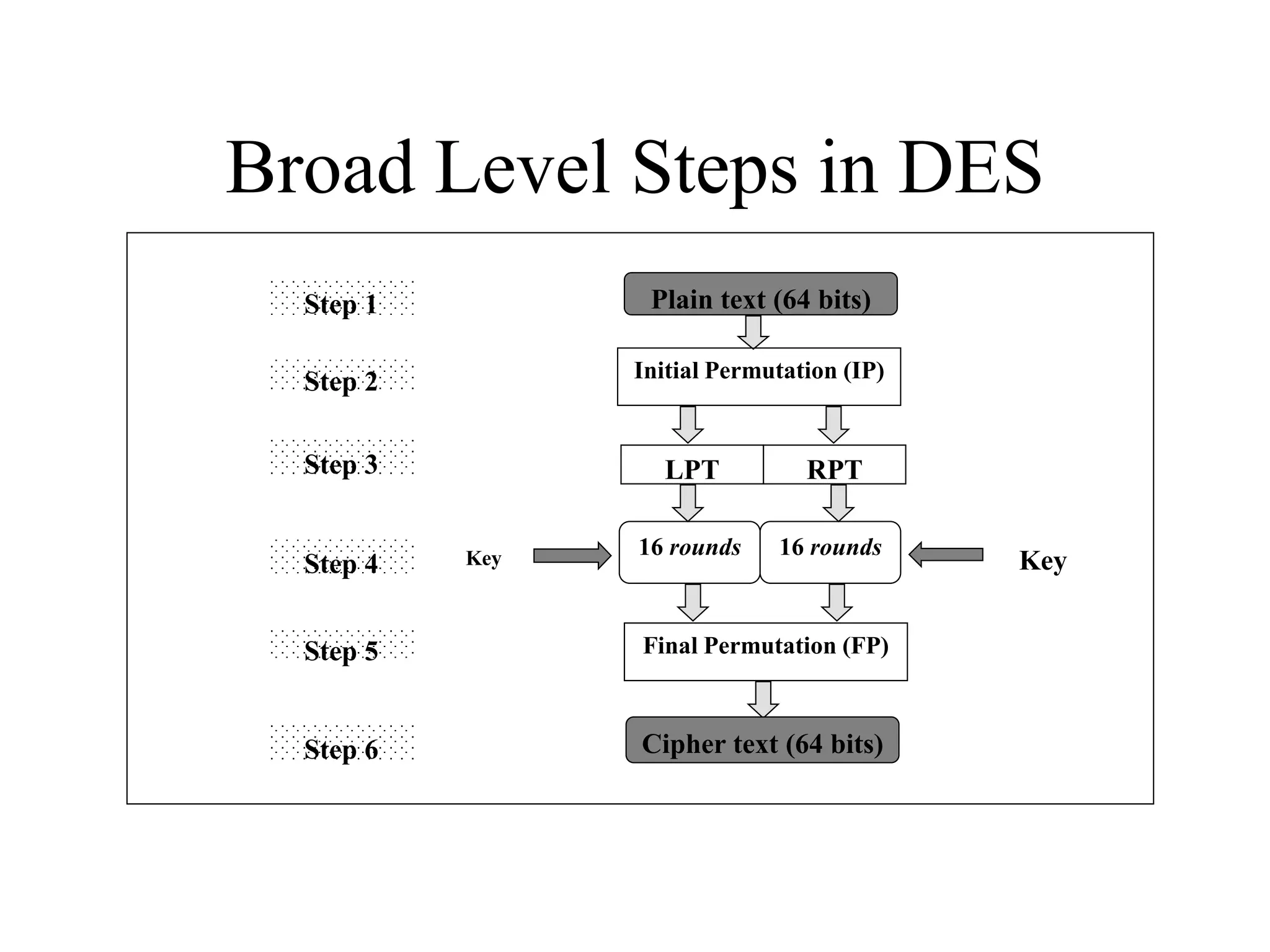
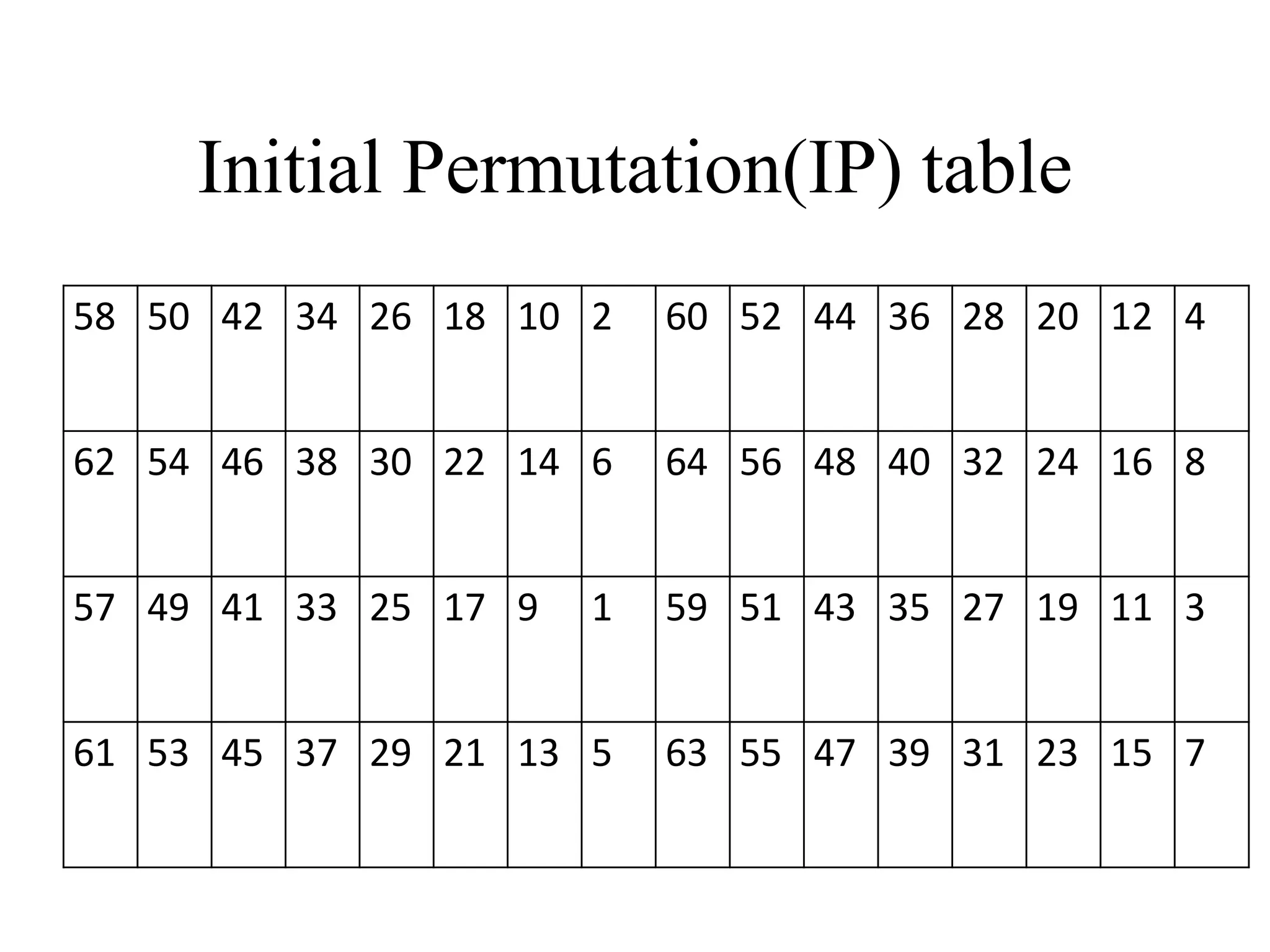
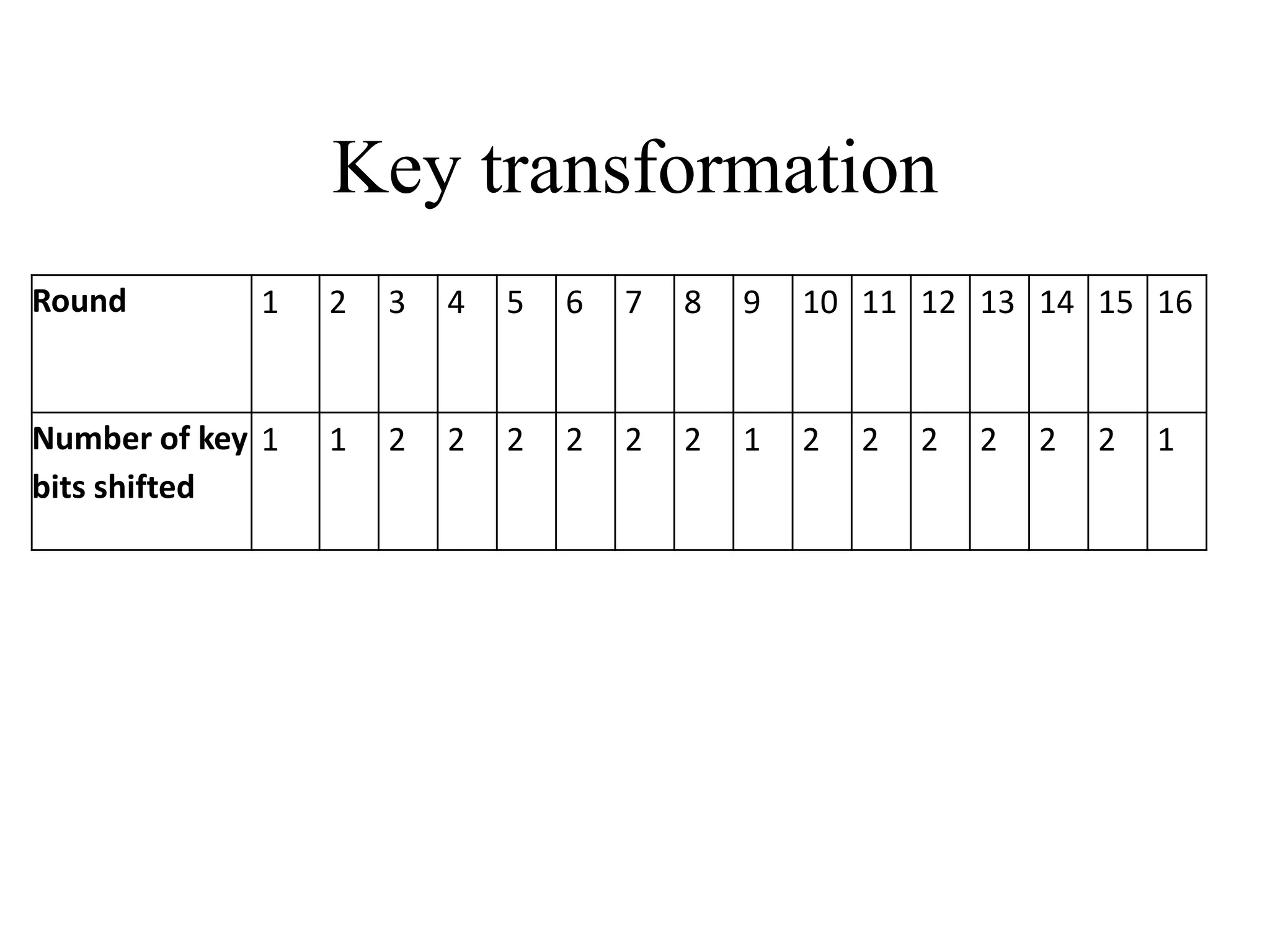
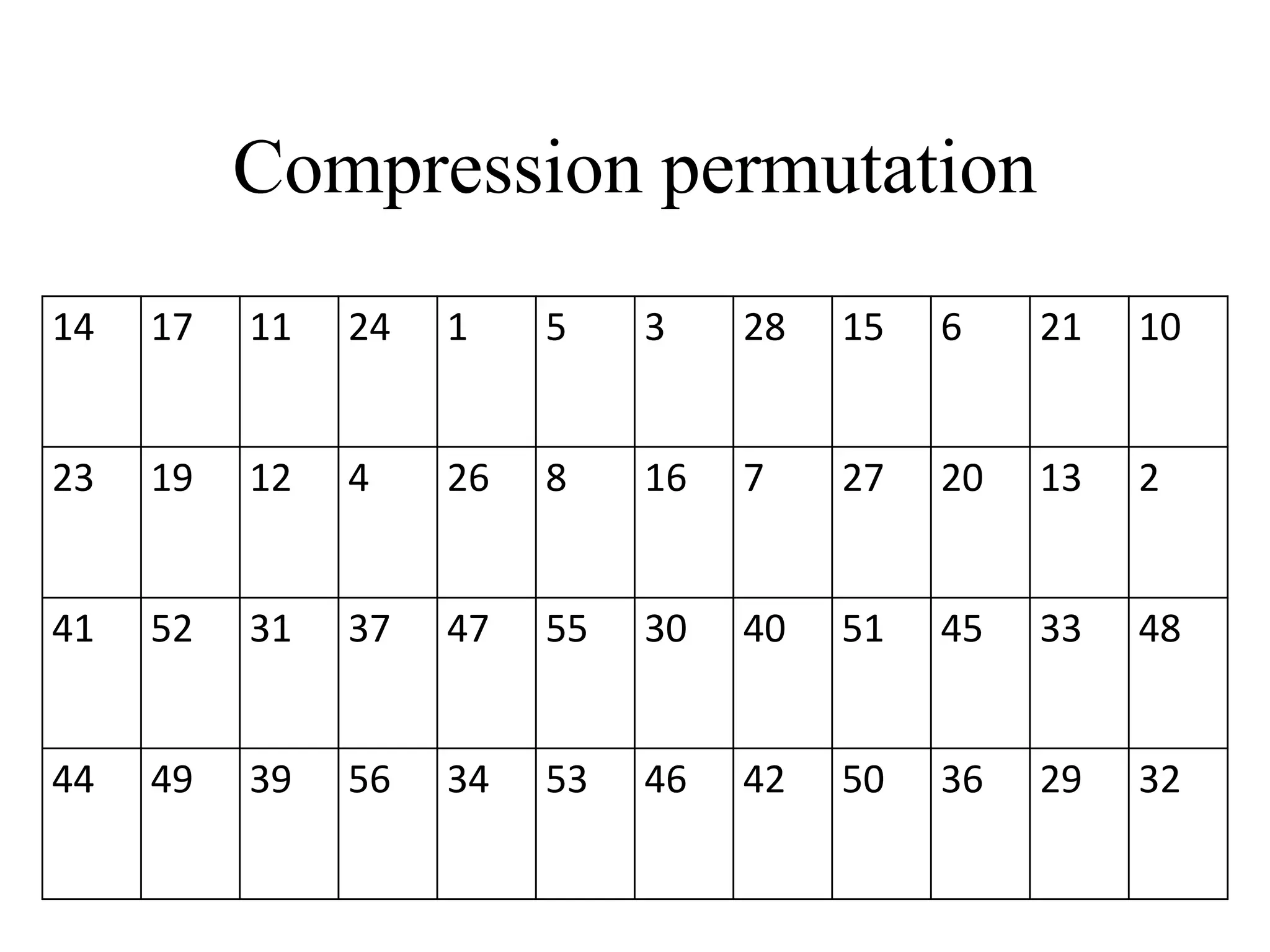
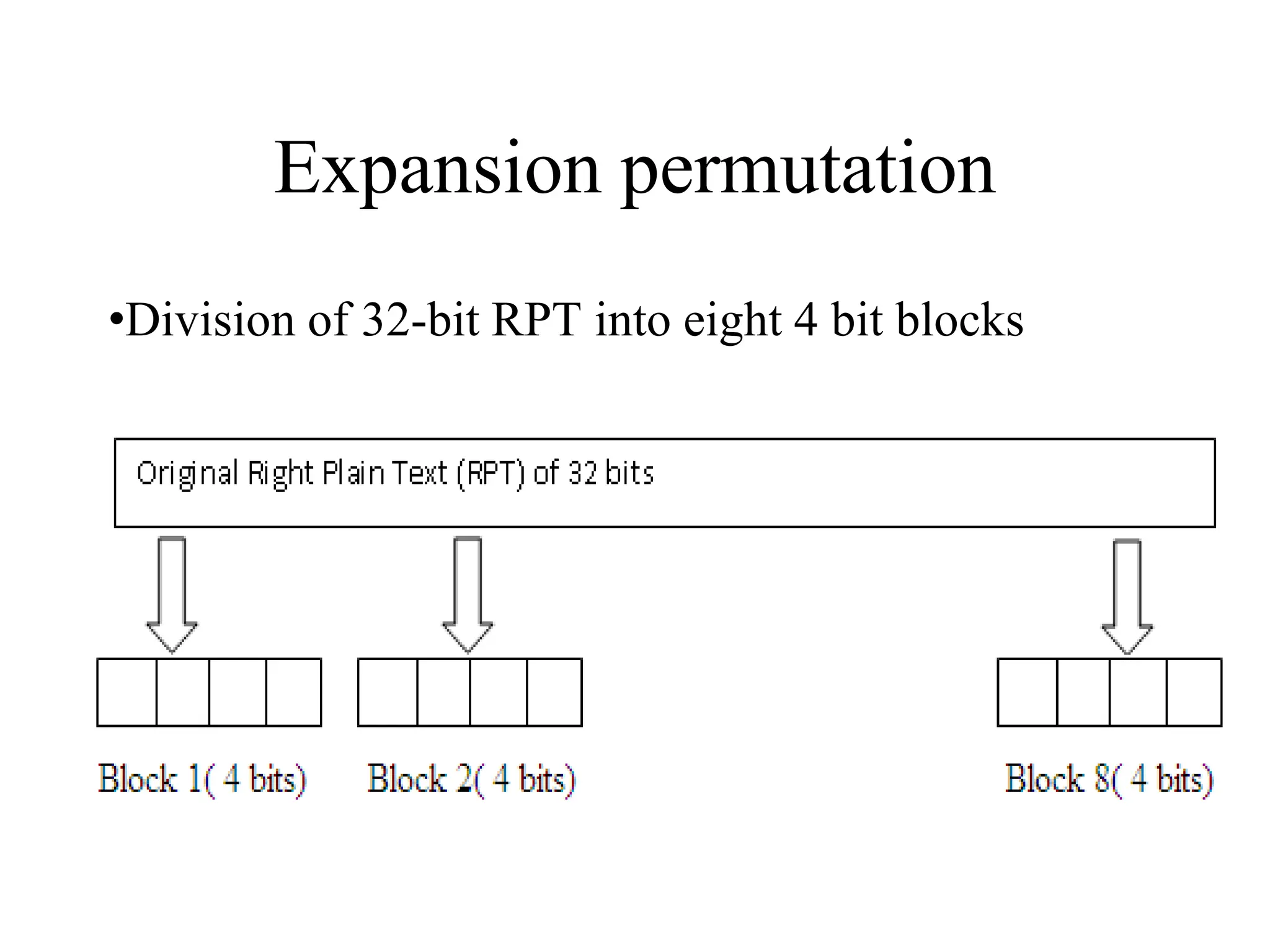
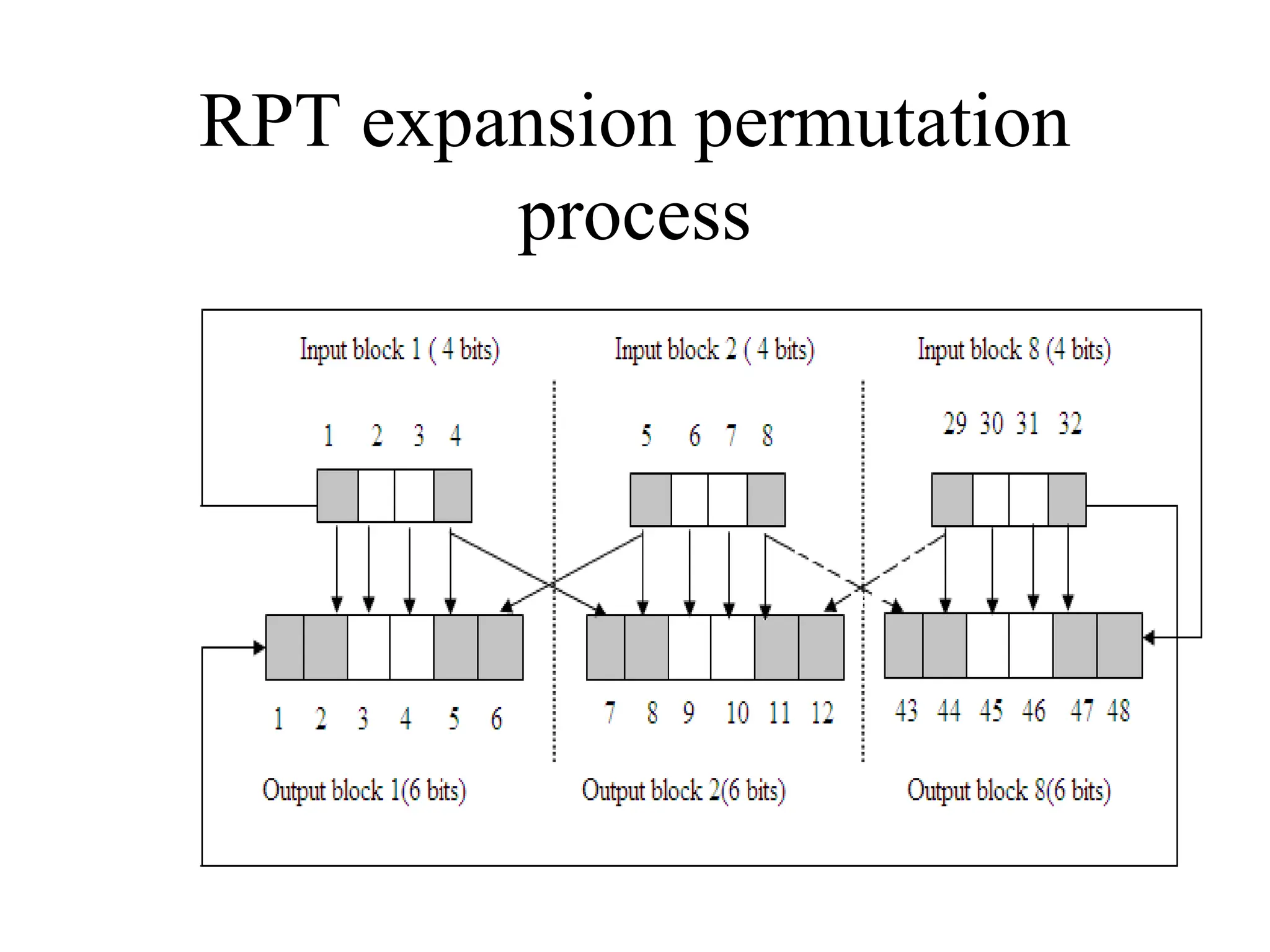
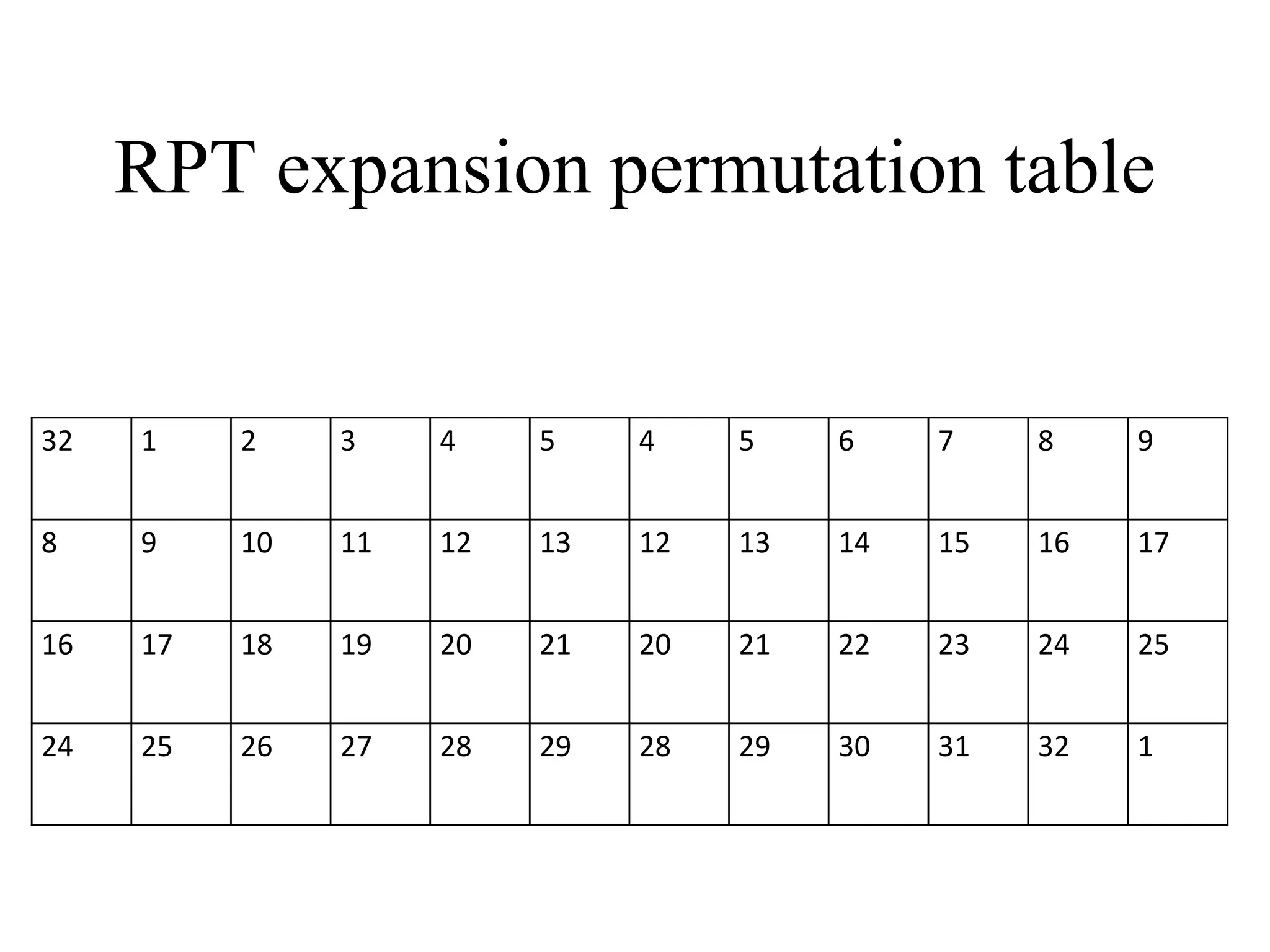
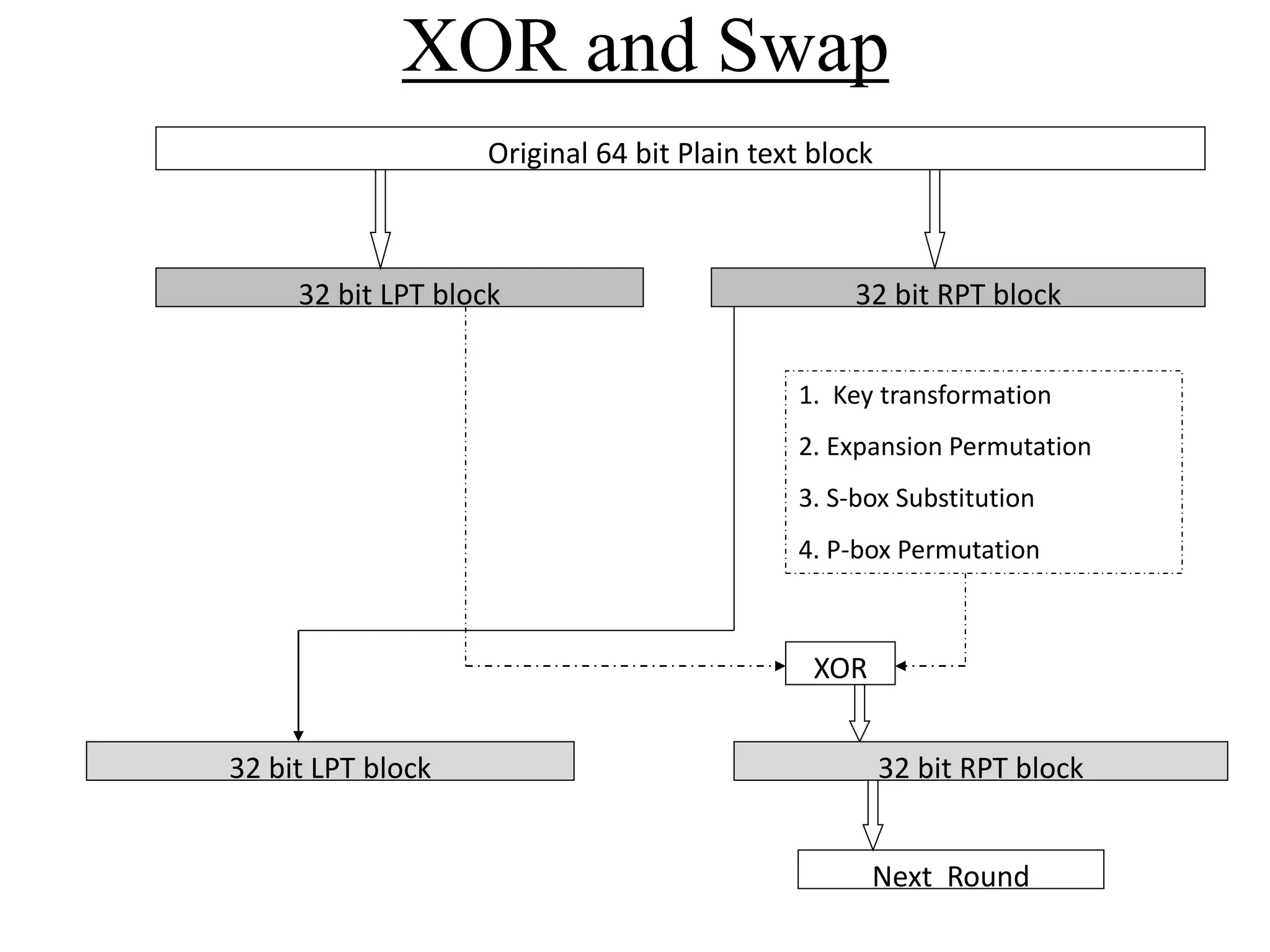
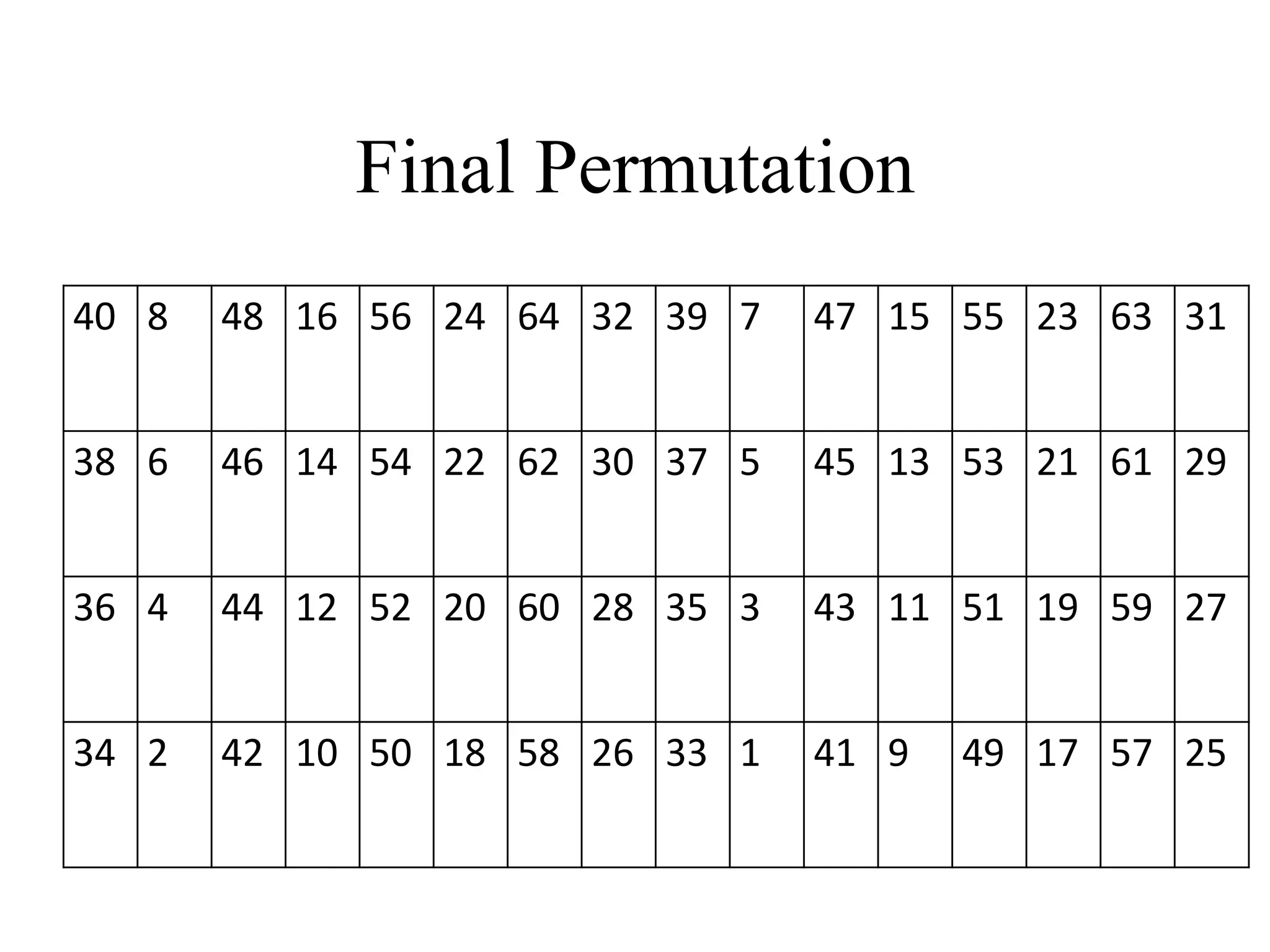
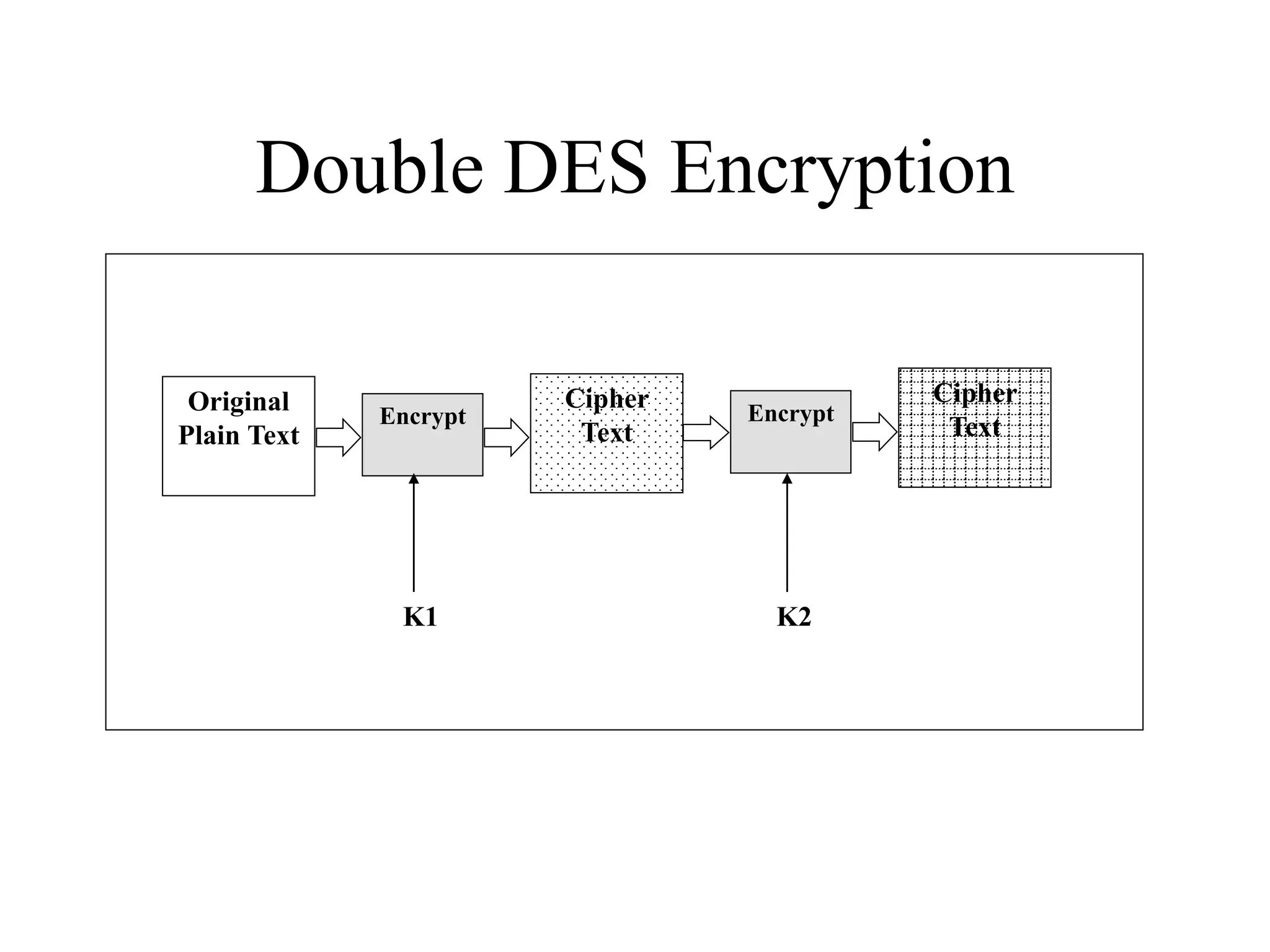
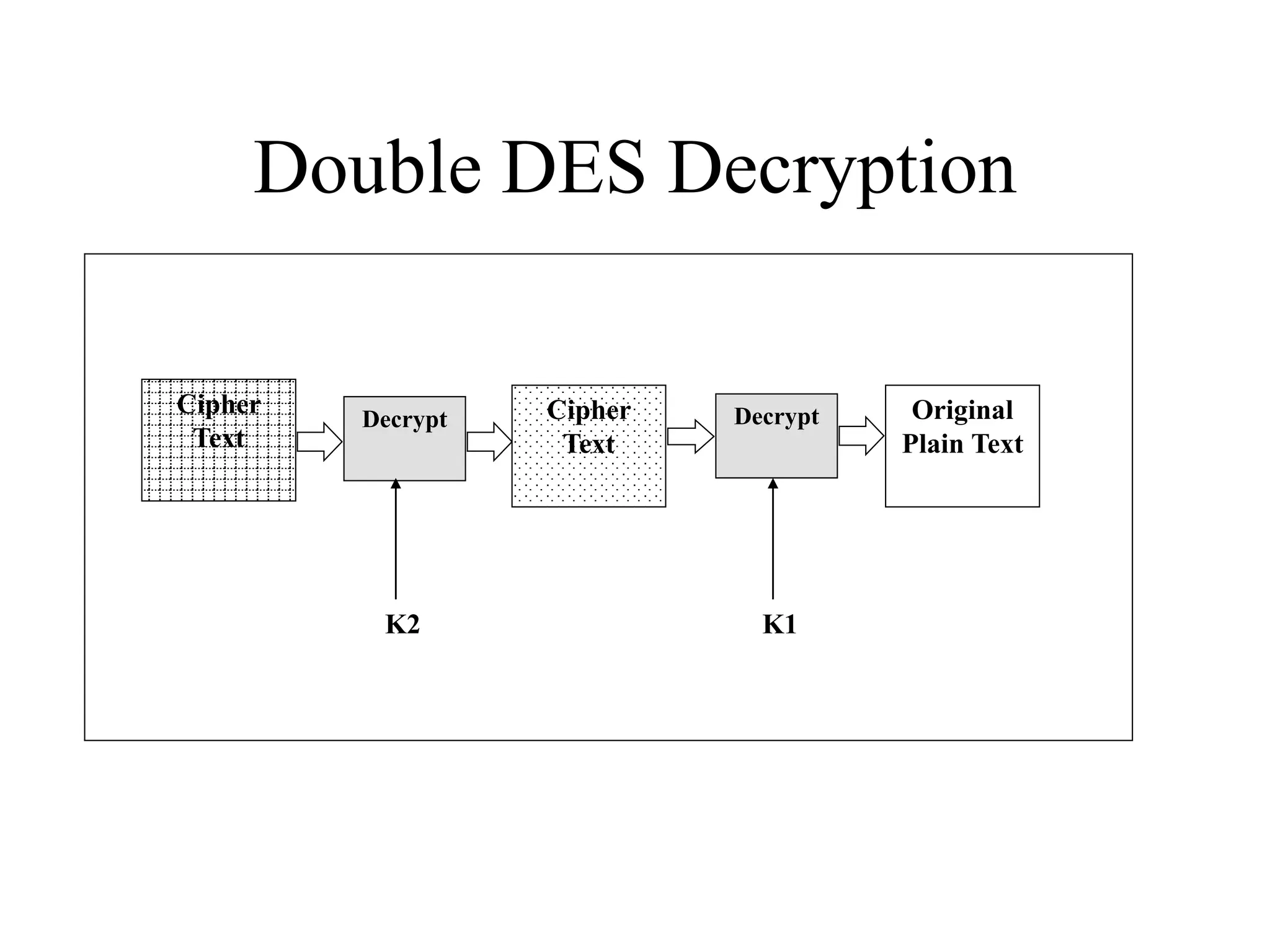
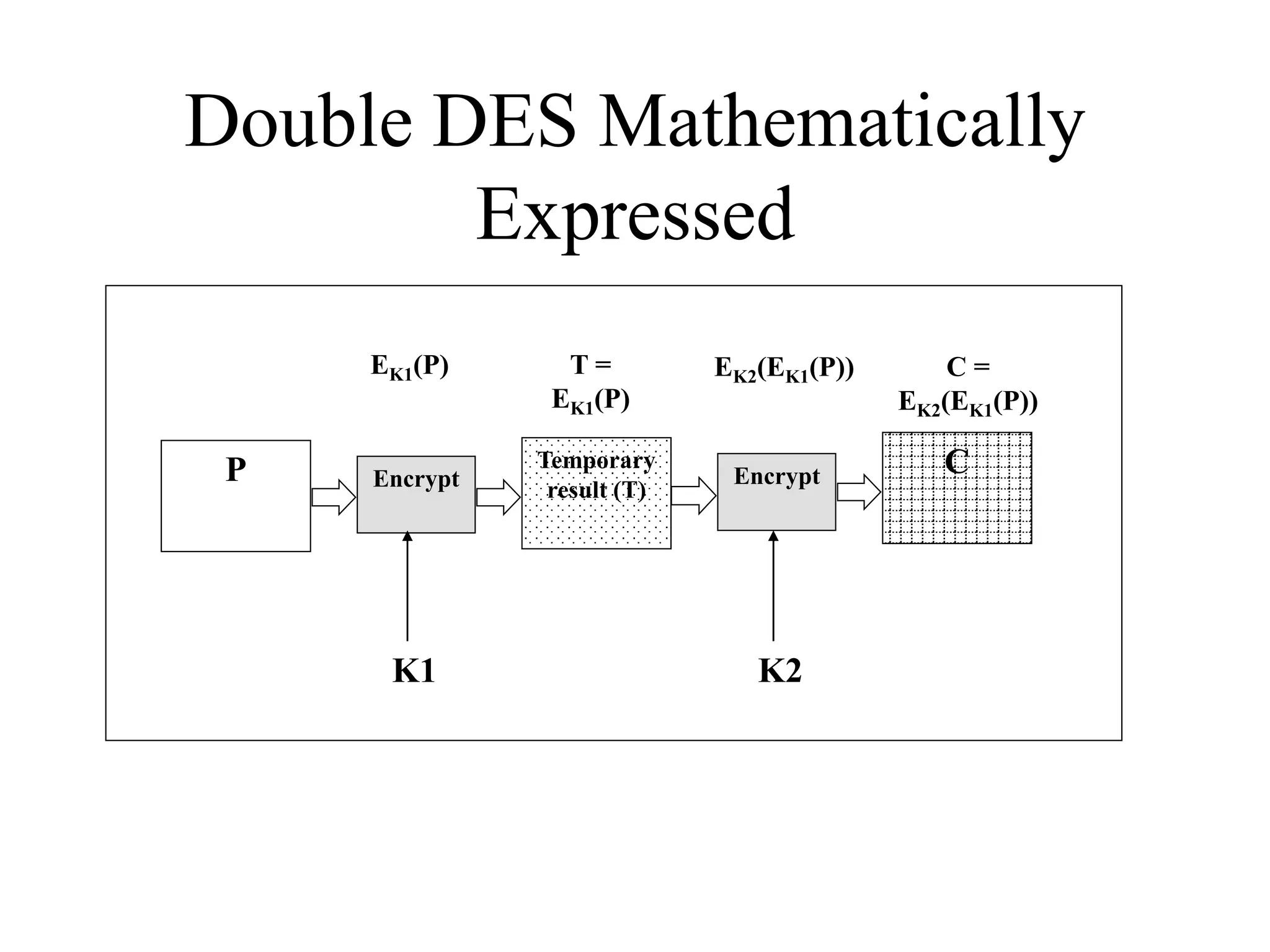
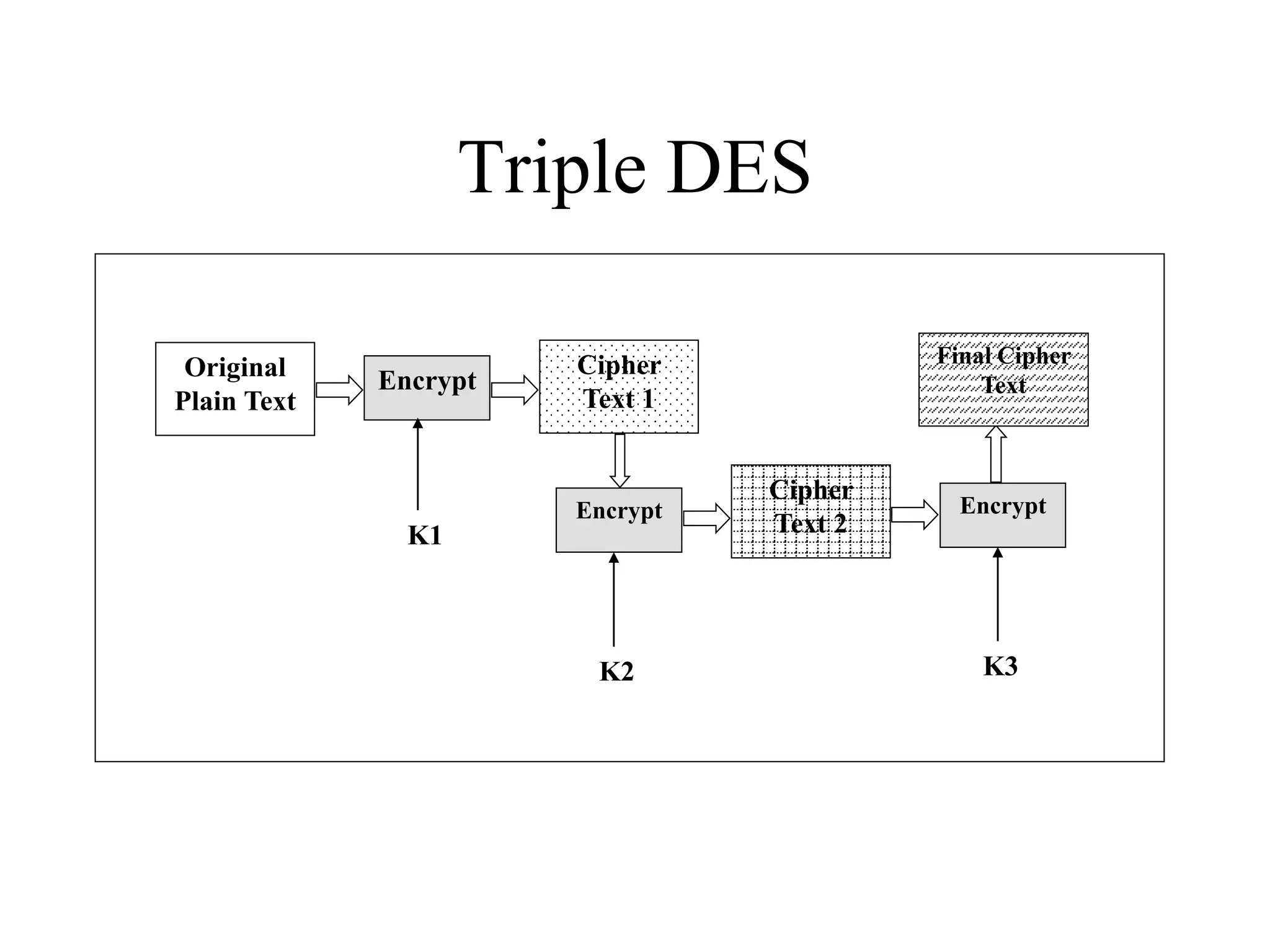
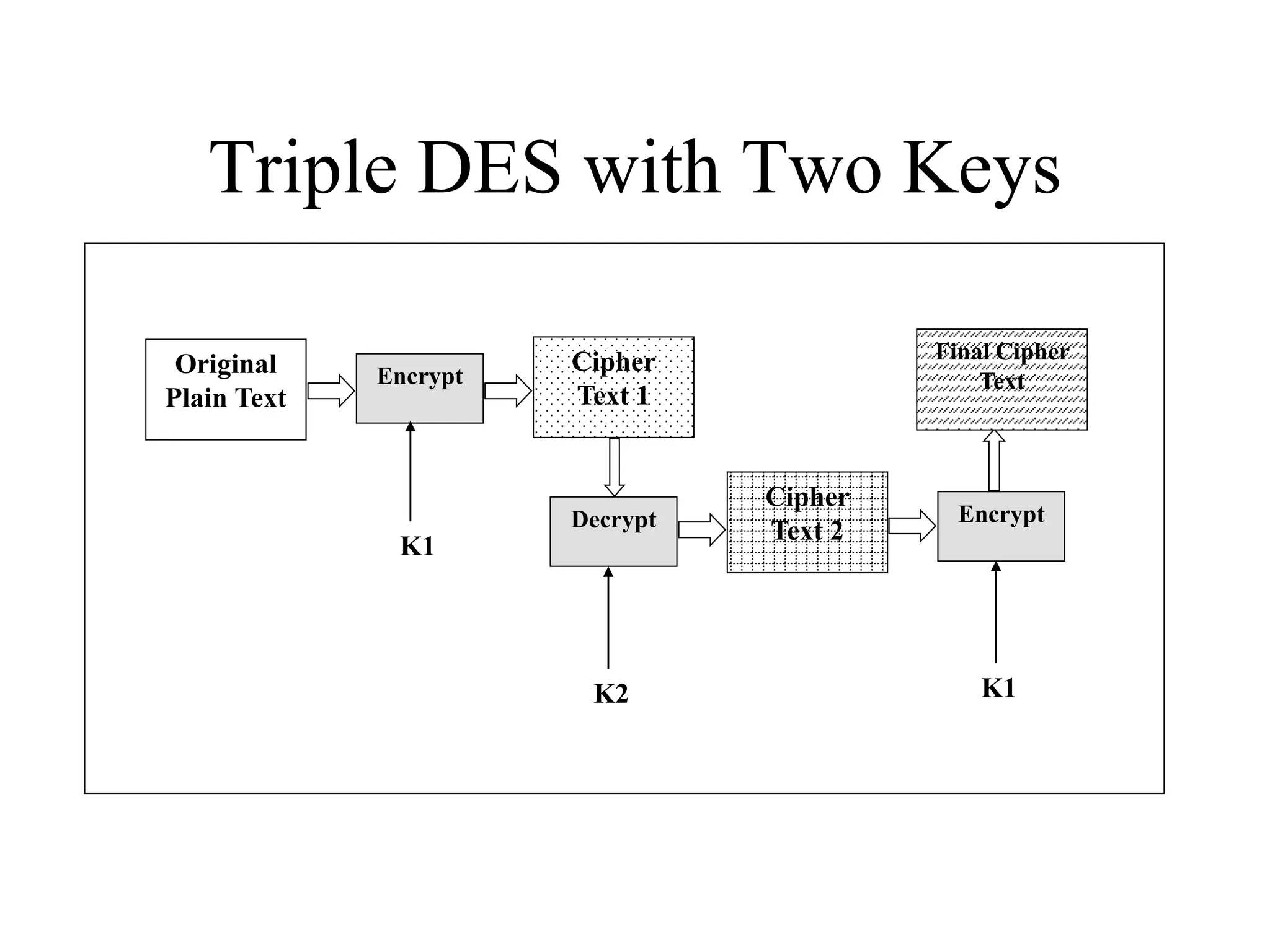
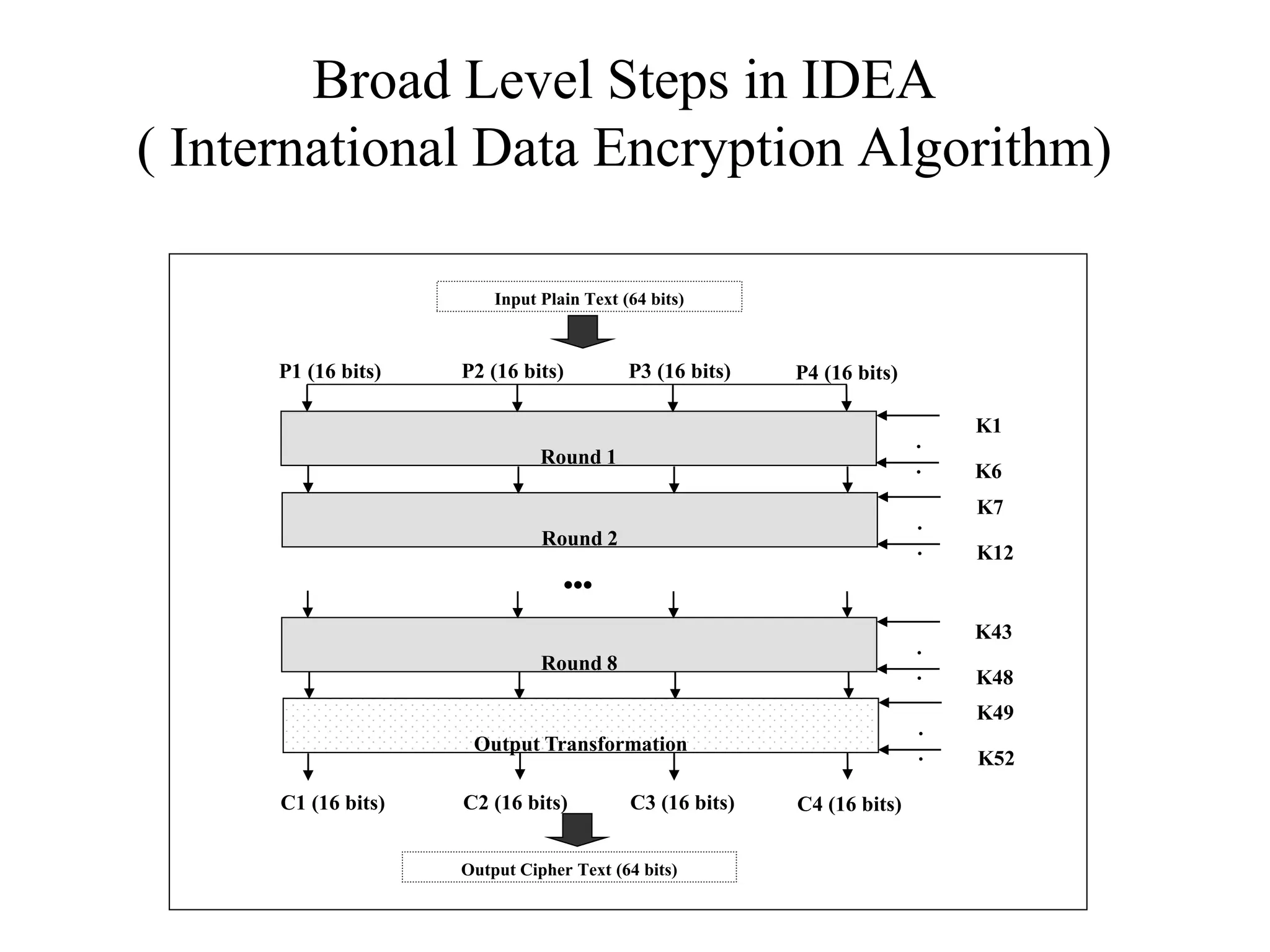
The document discusses various computer-based symmetric key cryptographic algorithms and ciphers. It describes the basic mechanisms of stream ciphers and block ciphers, providing examples of each. It then explains several popular symmetric key algorithms in more detail, including DES, Triple DES, IDEA, Blowfish, RC5, and Rijndael (AES). For each algorithm, it outlines the basic encryption/decryption process and key aspects of the algorithm such as round structure, key scheduling, and substitution and permutation operations.








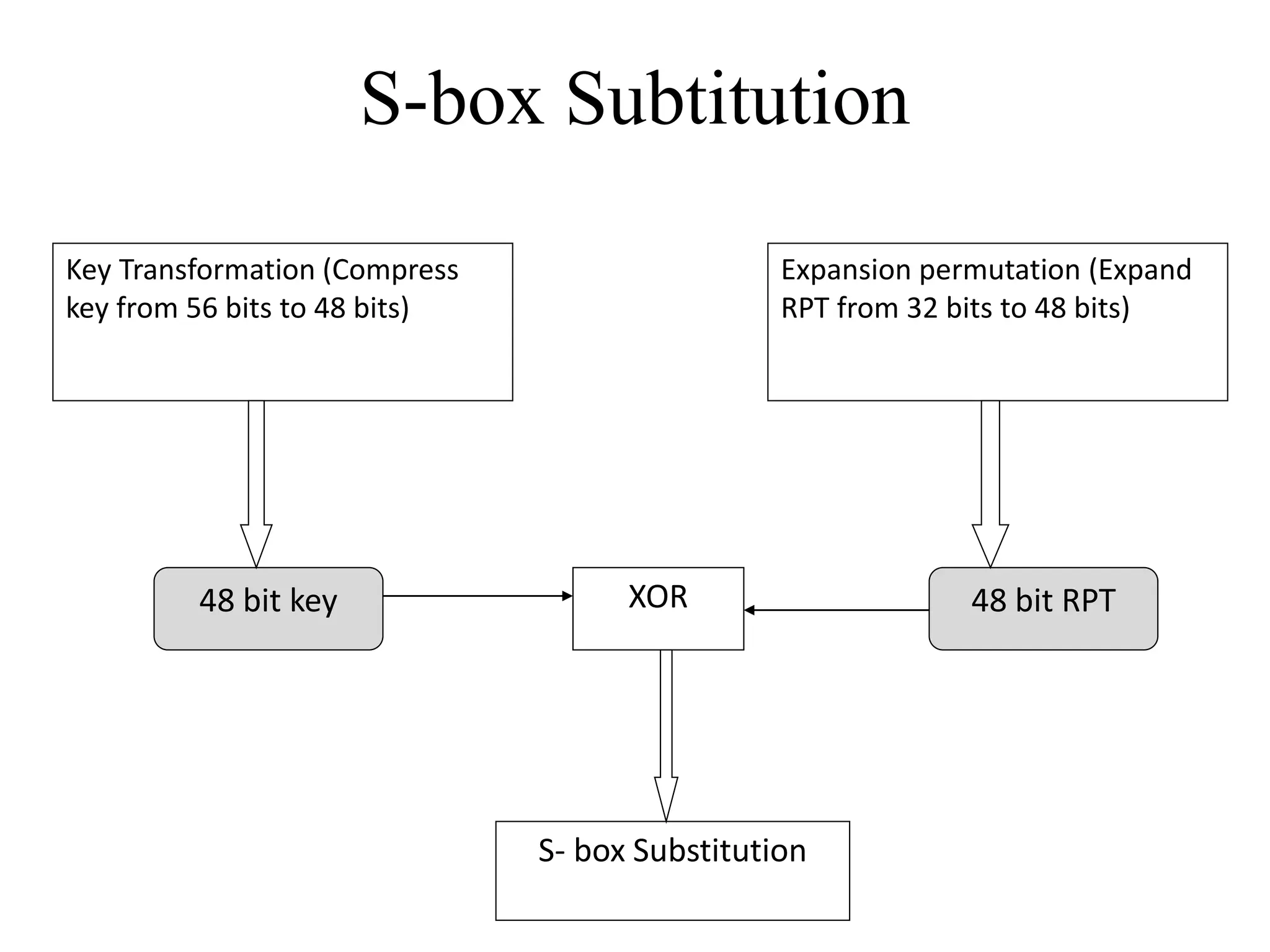
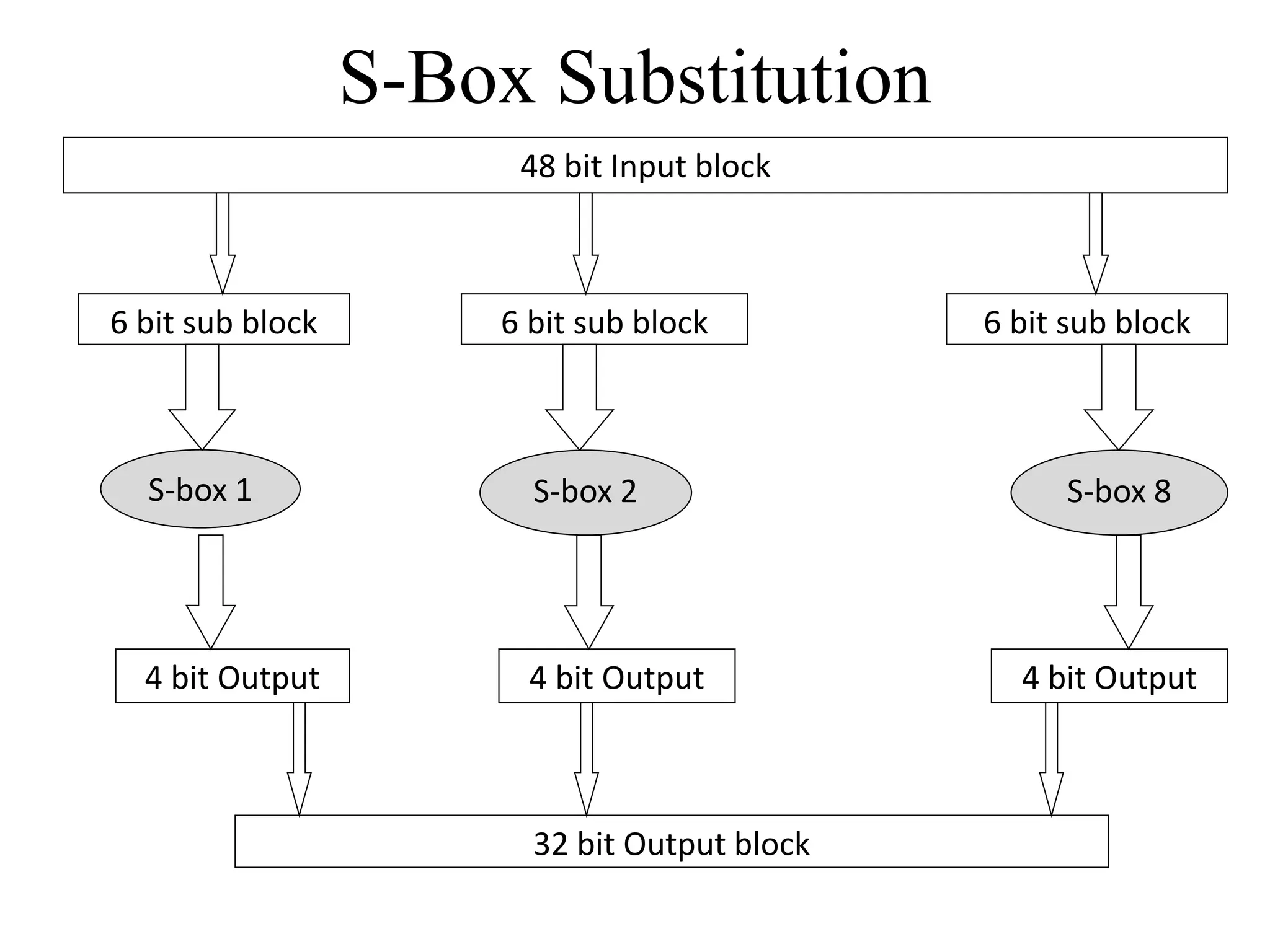
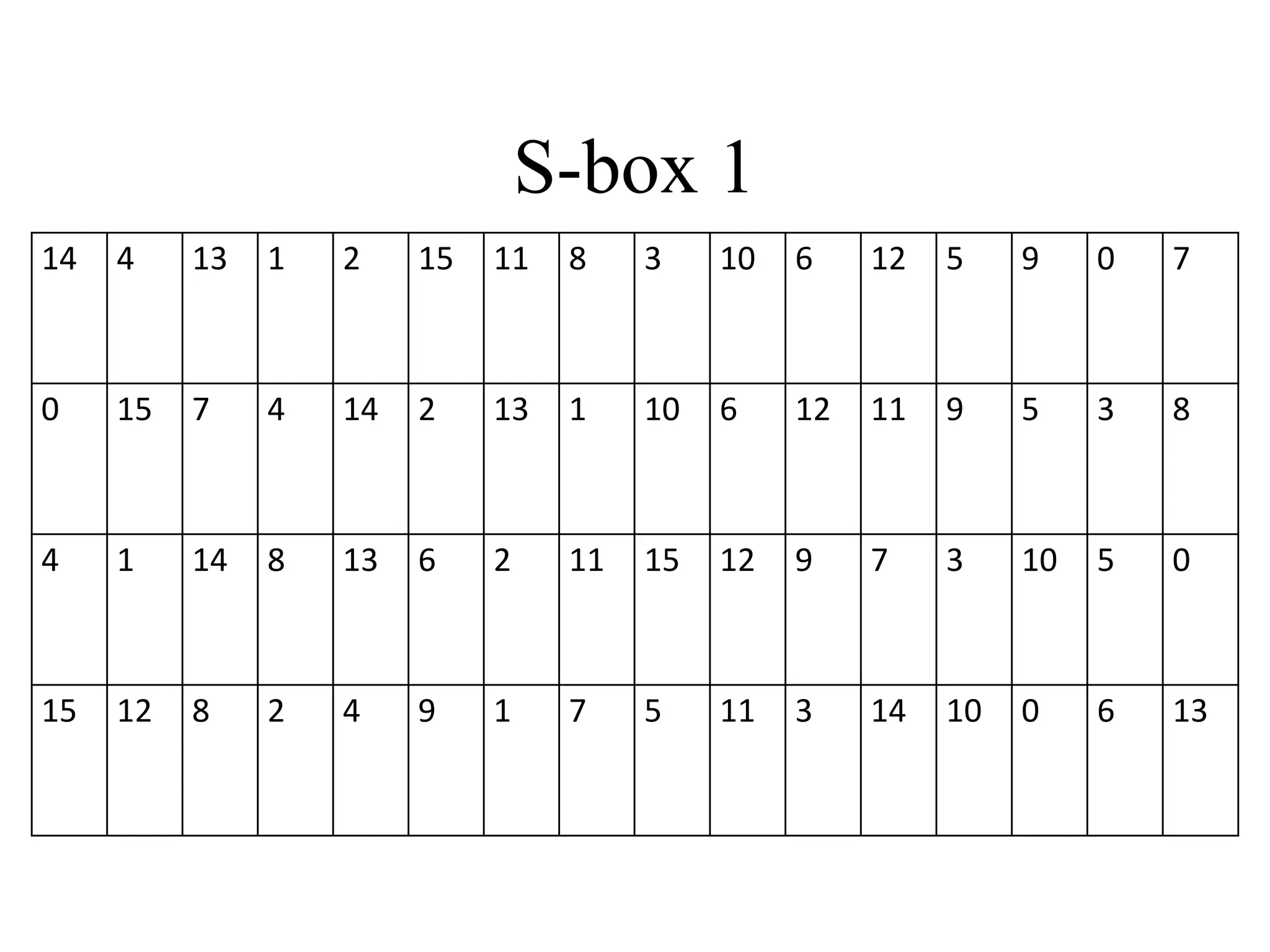
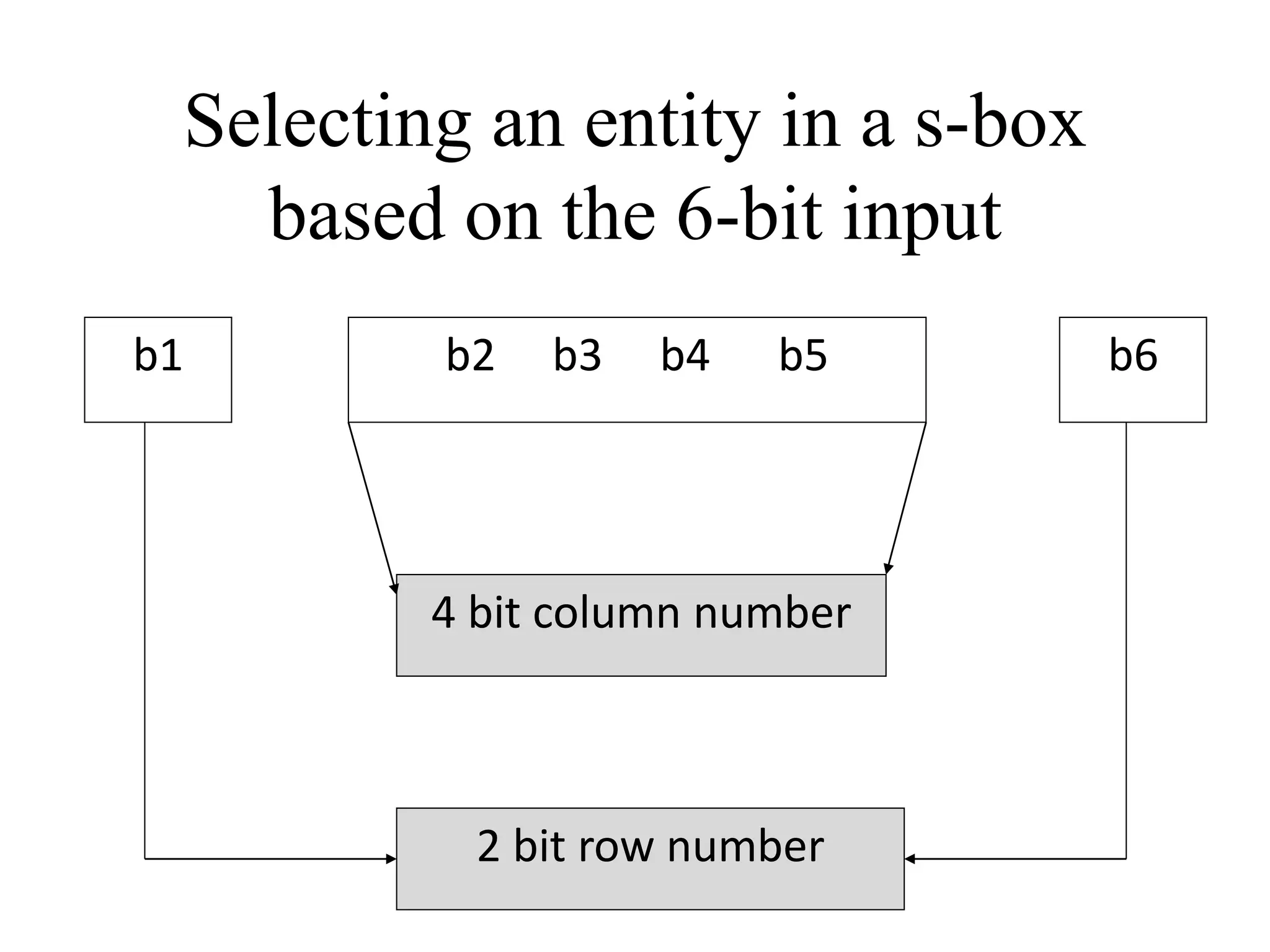






![Encryption using RC5 First, divide the original plain text into two blocks of equal size. Call them as A and B. Add A and S[0] to produce C. Add B and S[1] to produce D. 1. XOR C and D to produce E. 4. XOR D and F to produce G. 2. Circular-left shift E by D bits. 3. Add E and S[2i] to produce F. 5. Circular-left shift G by F bits. 6. Add G and S[2i + 1] to produce H. Increment i by 1. Check: Is i > r? Stop Yes No Note: First perform all the left-hand side steps, and then come to the right hand side steps, as indicated by the step numbers. Call F as C (i.e. C = F) Call H as D (i.e. D = H)](https://image.slidesharecdn.com/chapter03-240306061112-270e9ef0/75/Cryptography-Symmetric-Key-Algorithm-CSE-47-2048.jpg)
![RC5 Encryption A = A + S[0] B = B + S[1] For i = 1 to r A = ((A XOR B) <<< B) + S[2i] B = ((B XOR A) <<< A) + S[2i + 1] Next i](https://image.slidesharecdn.com/chapter03-240306061112-270e9ef0/75/Cryptography-Symmetric-Key-Algorithm-CSE-48-2048.jpg)
![RC5 Decryption For i = r to 1 step –1 (i.e. decrement i each time by 1) B = ((B – S[2i + 1]) >>> A) XOR A A = ((A – S[2i]) >>> B) XOR B Next i B = B – S[1] A = A – S[0]](https://image.slidesharecdn.com/chapter03-240306061112-270e9ef0/75/Cryptography-Symmetric-Key-Algorithm-CSE-49-2048.jpg)