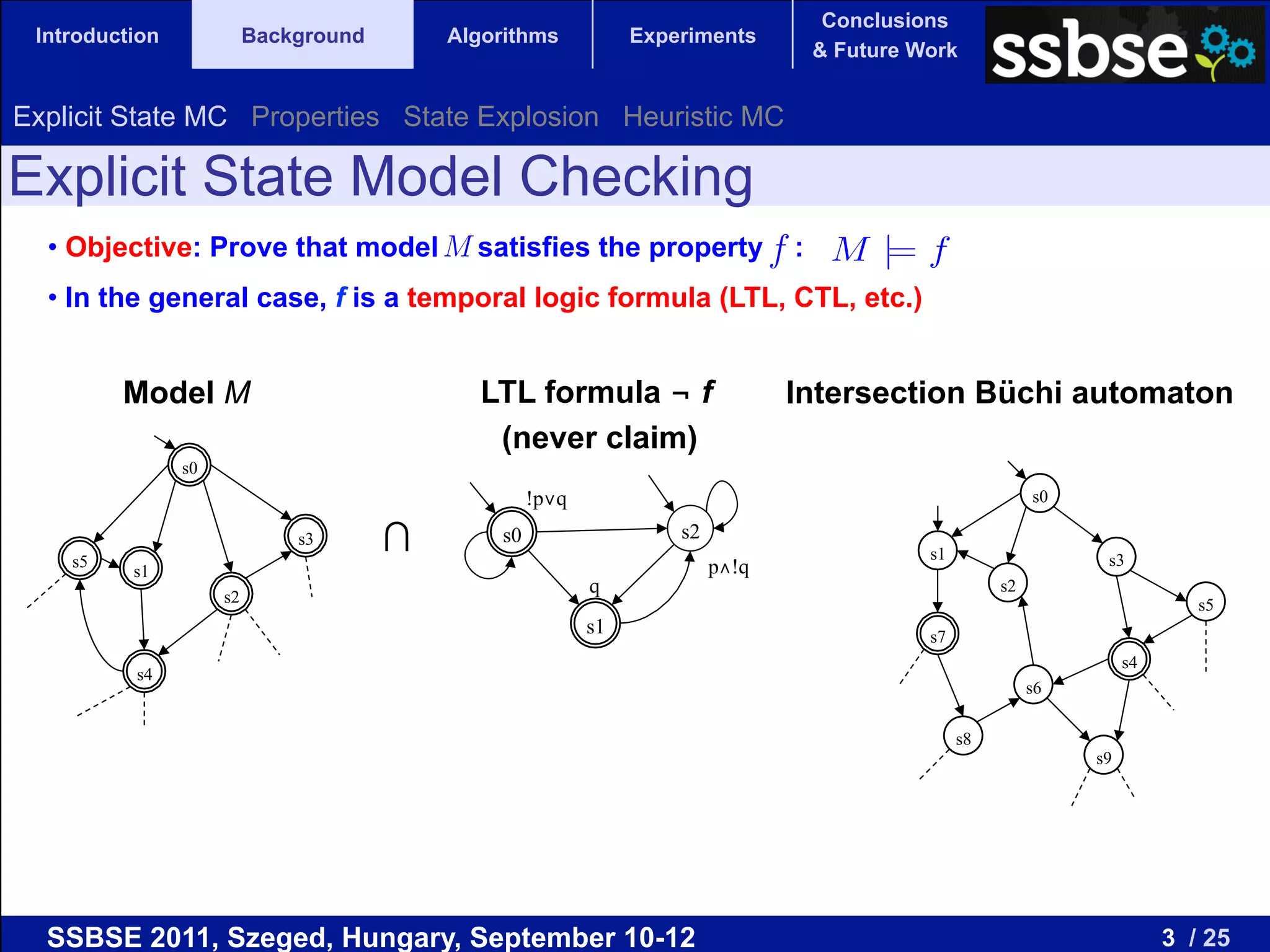
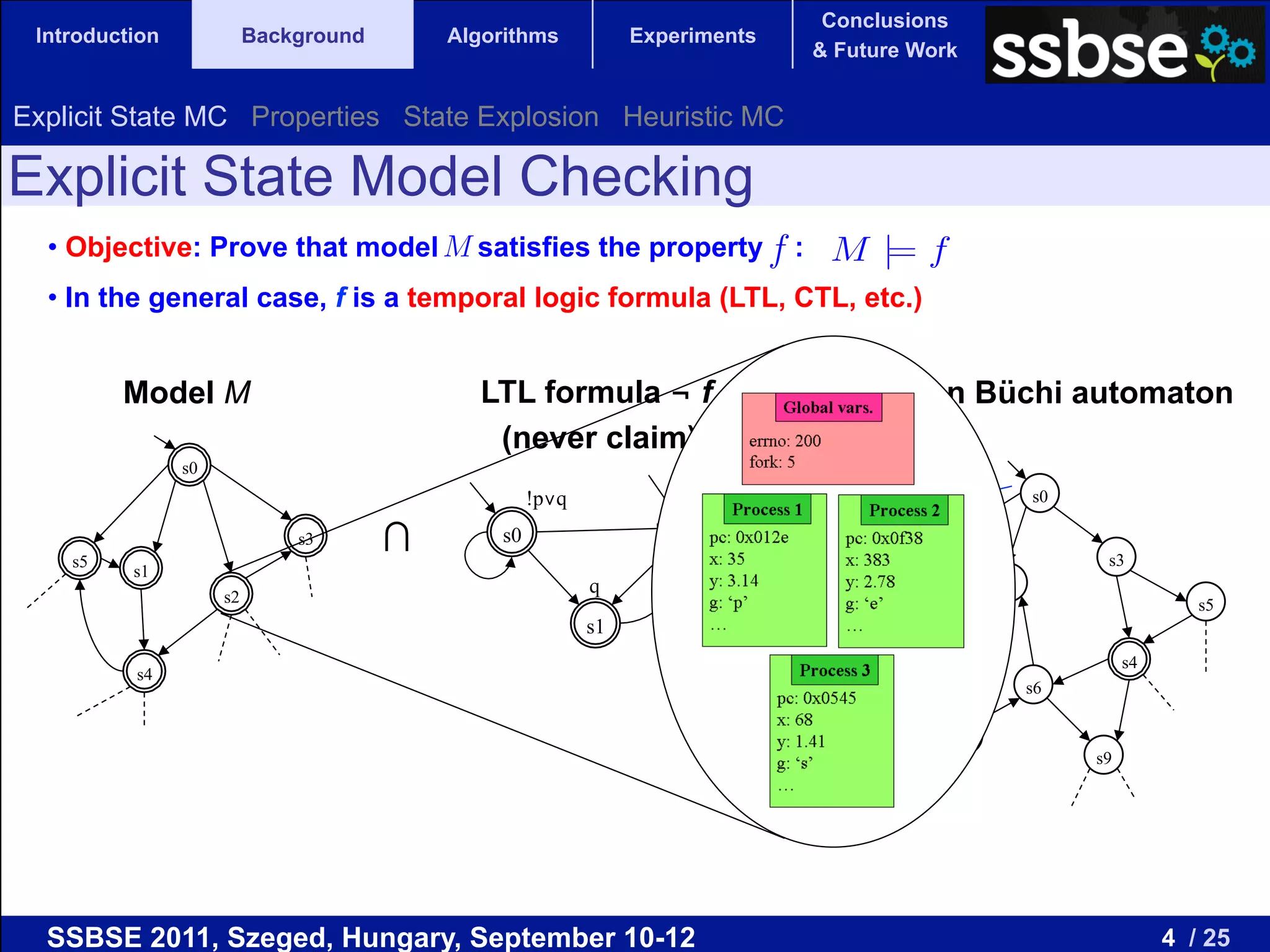
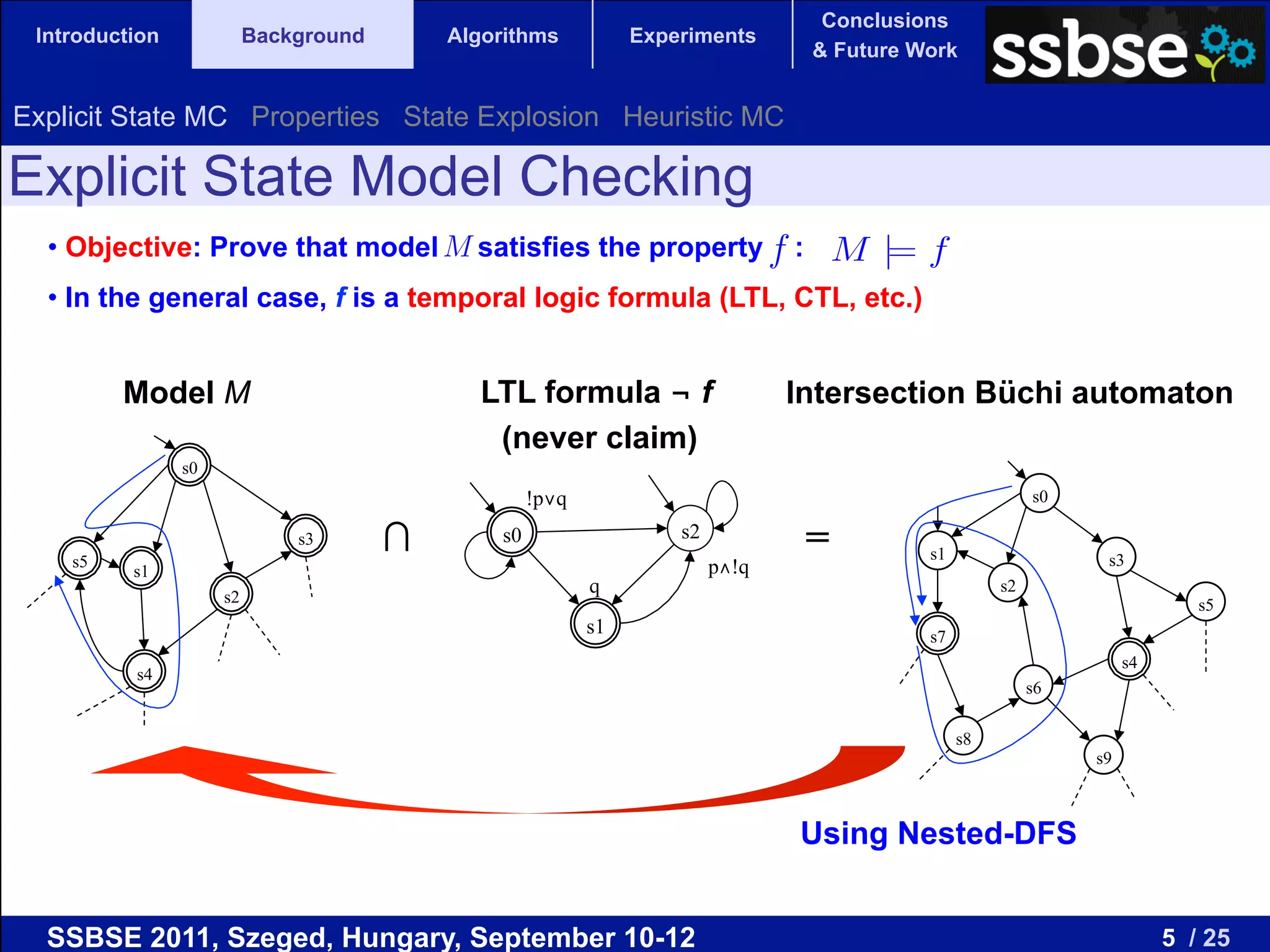
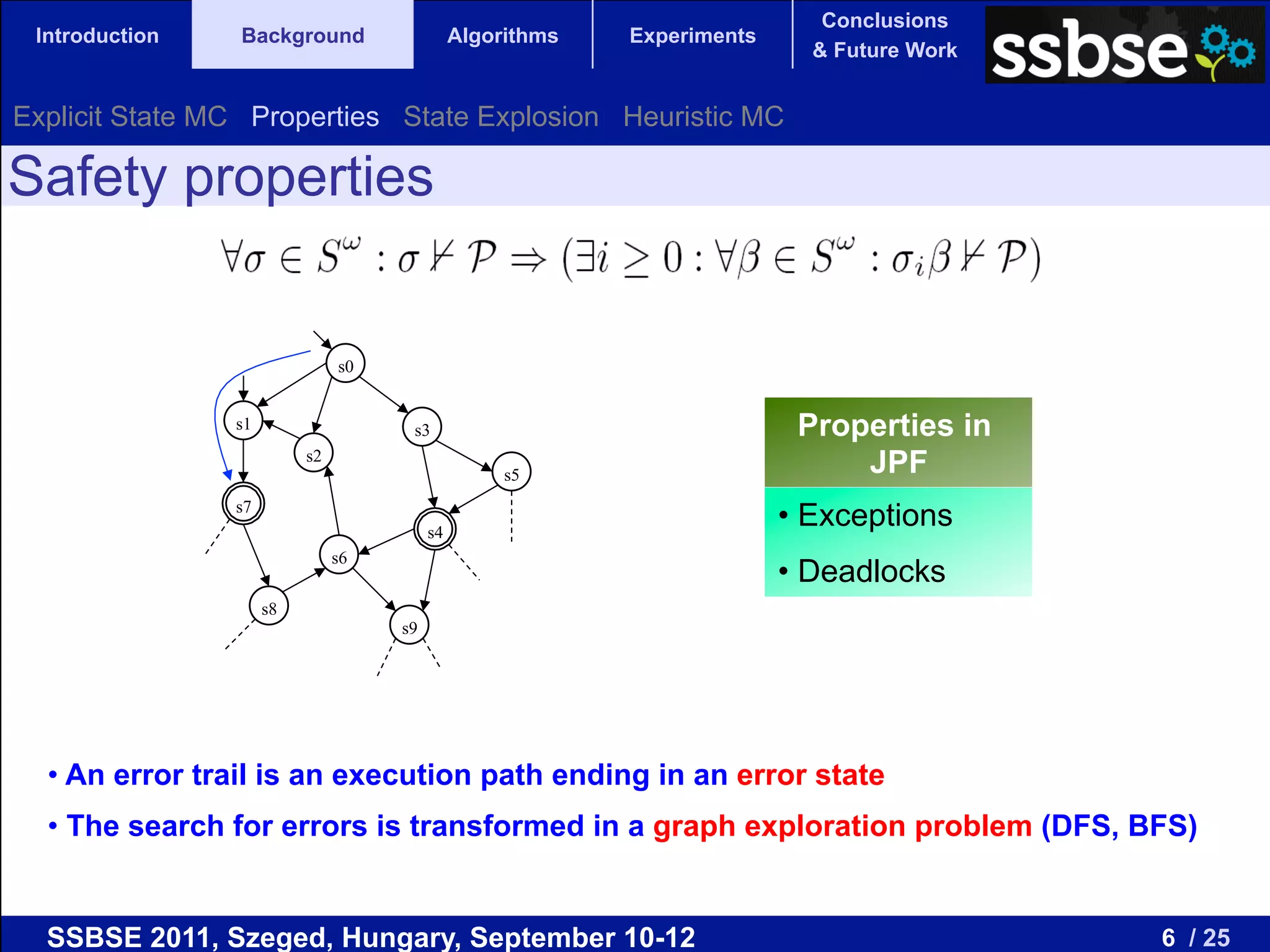
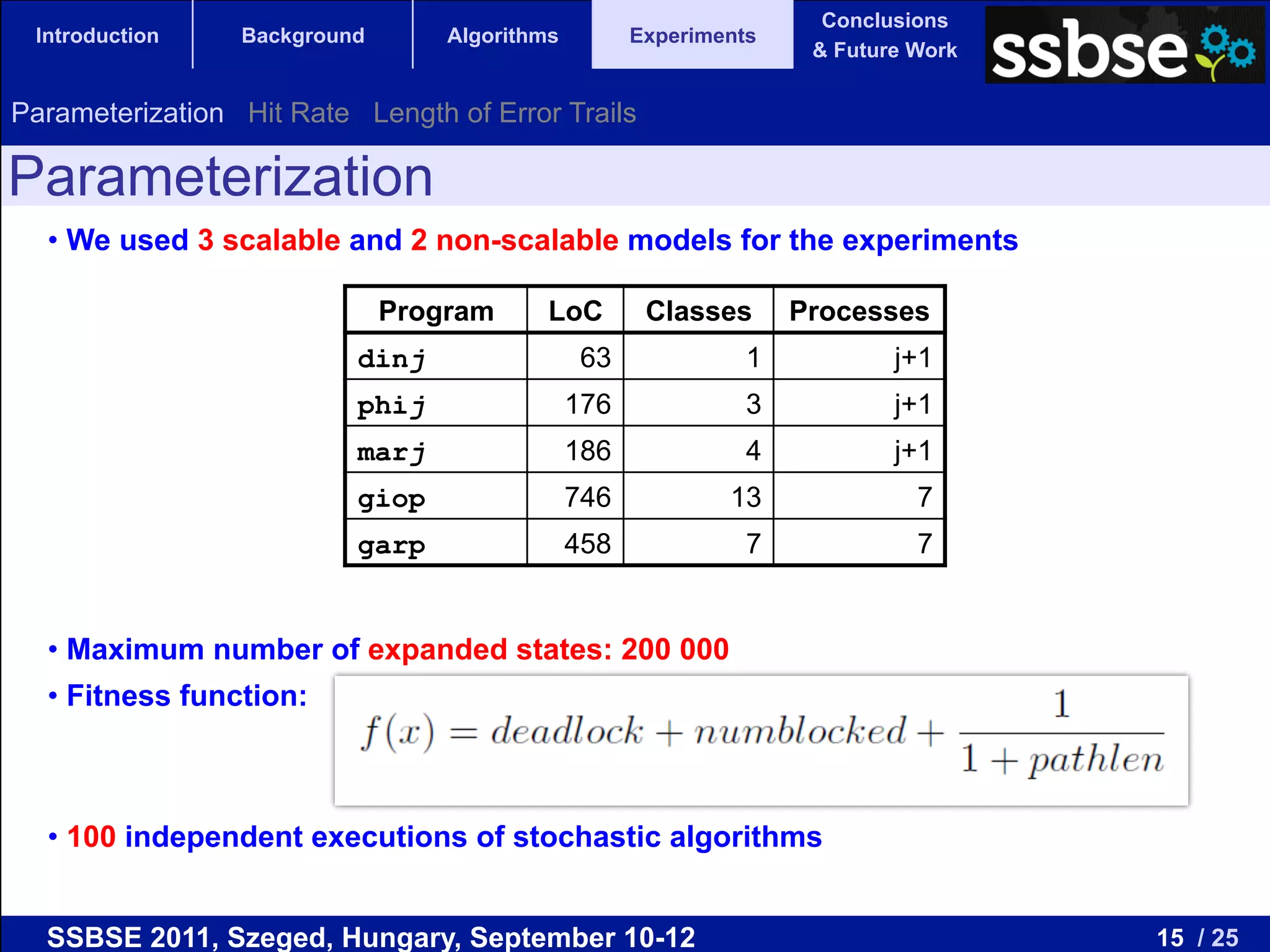
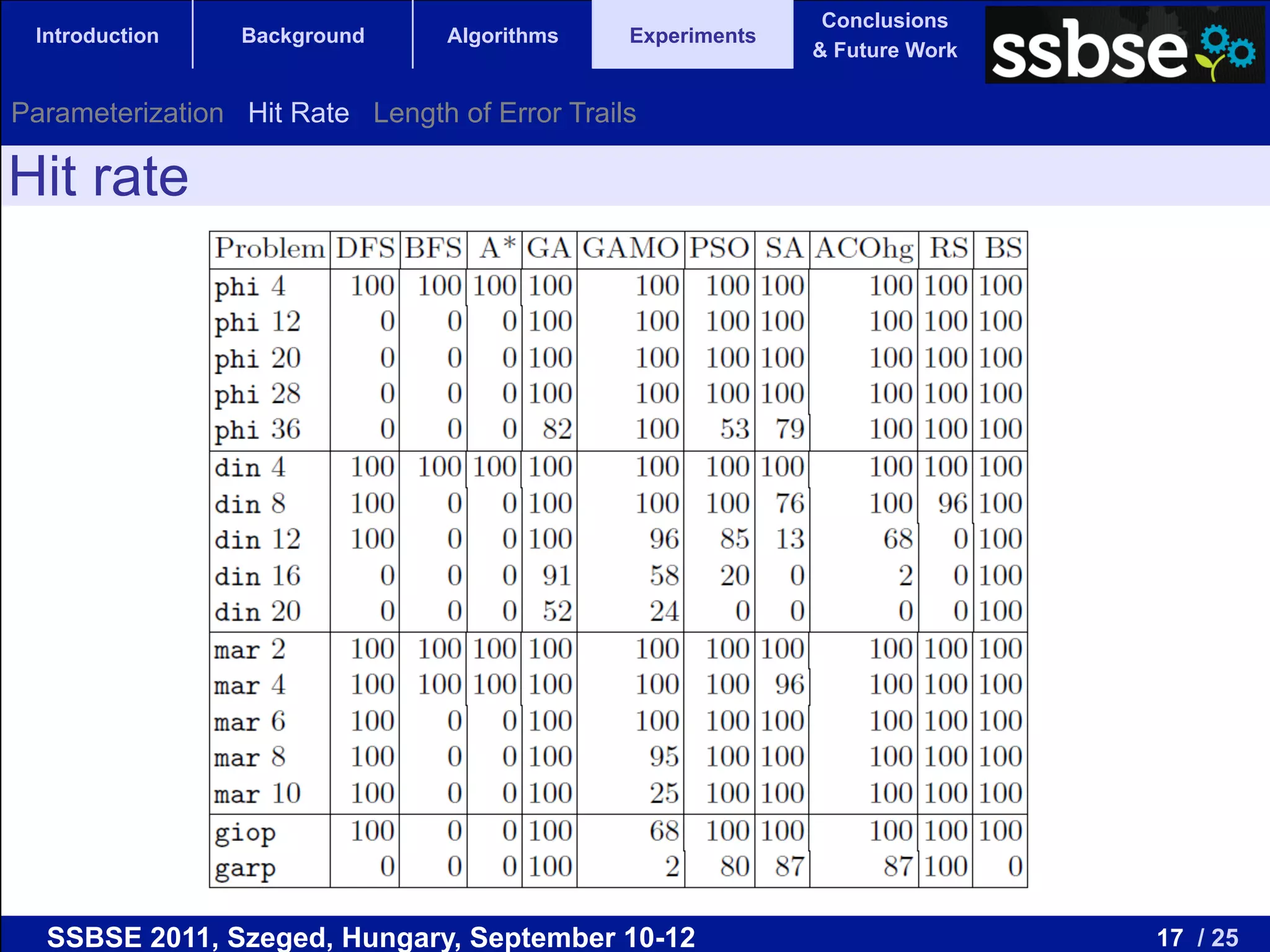
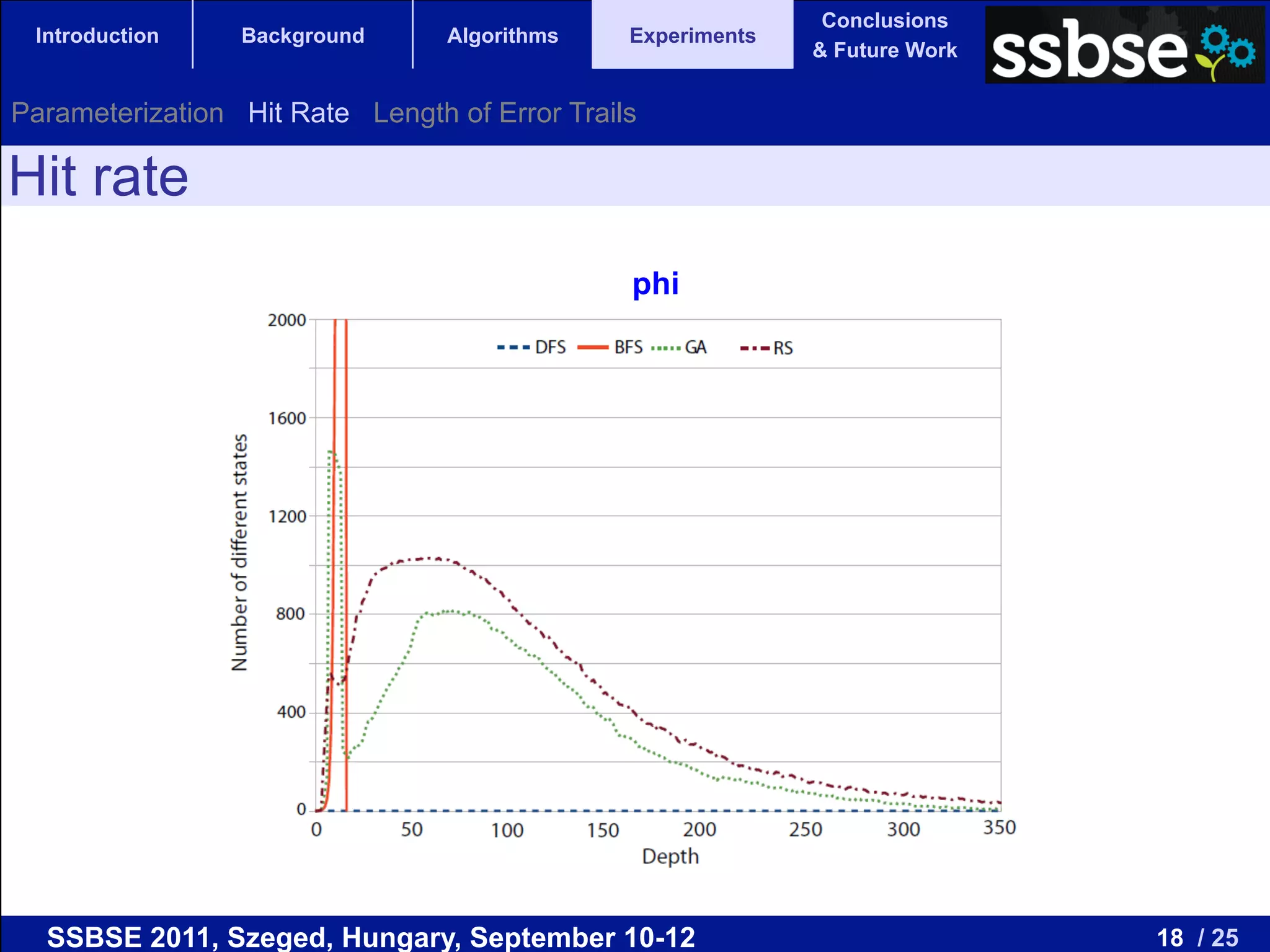
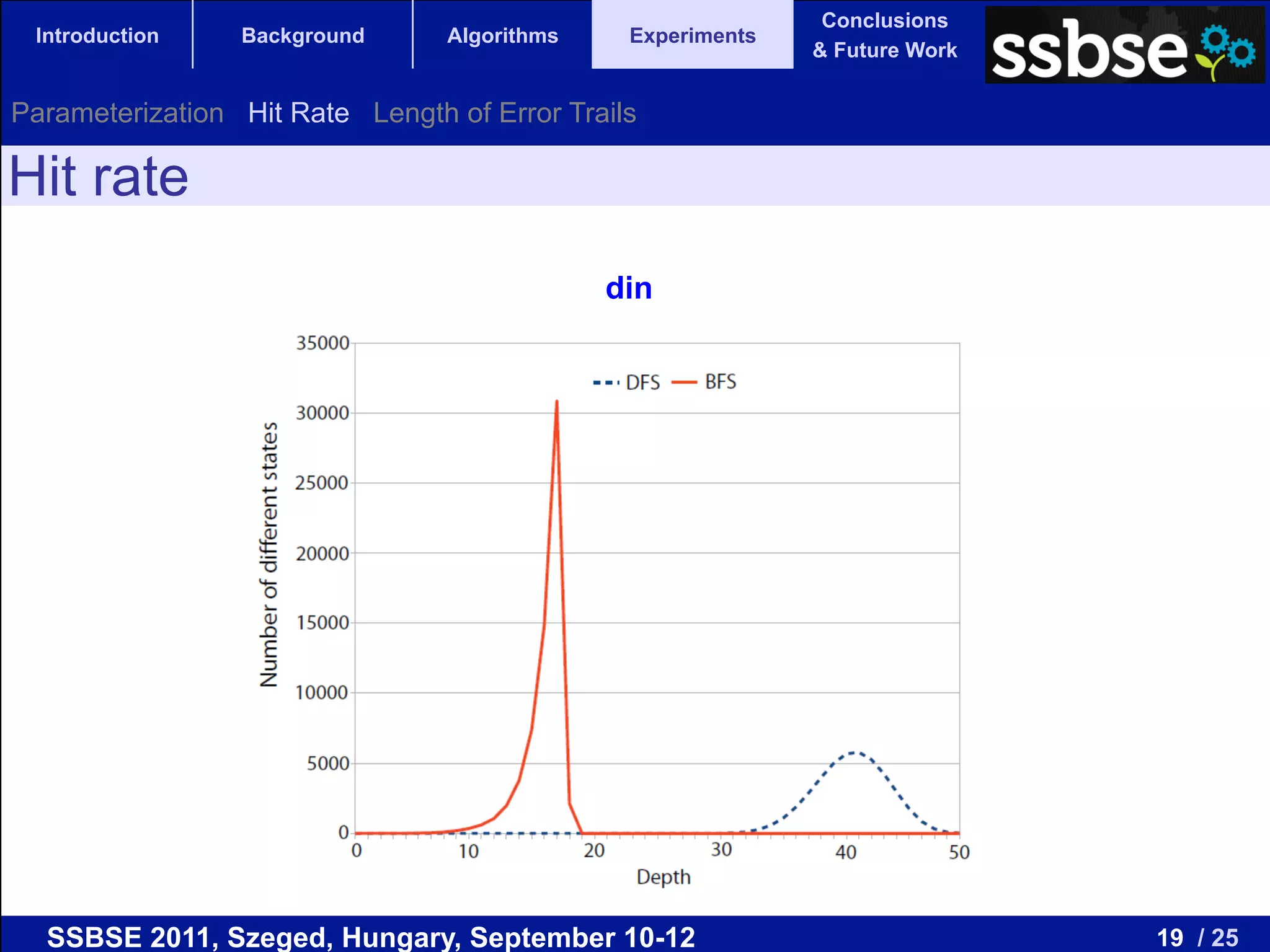
The document compares various metaheuristic algorithms and classical methods for error detection in concurrent Java programs, highlighting the complexity of proving the correctness of such systems. It concludes that metaheuristic approaches, particularly beam search, are more effective than traditional algorithms in finding errors and suggests future work on guided and hybrid algorithms. The discussion includes the challenges of state explosion in model checking and the potential for developing stochastic, complete algorithms to improve error detection efficiency.