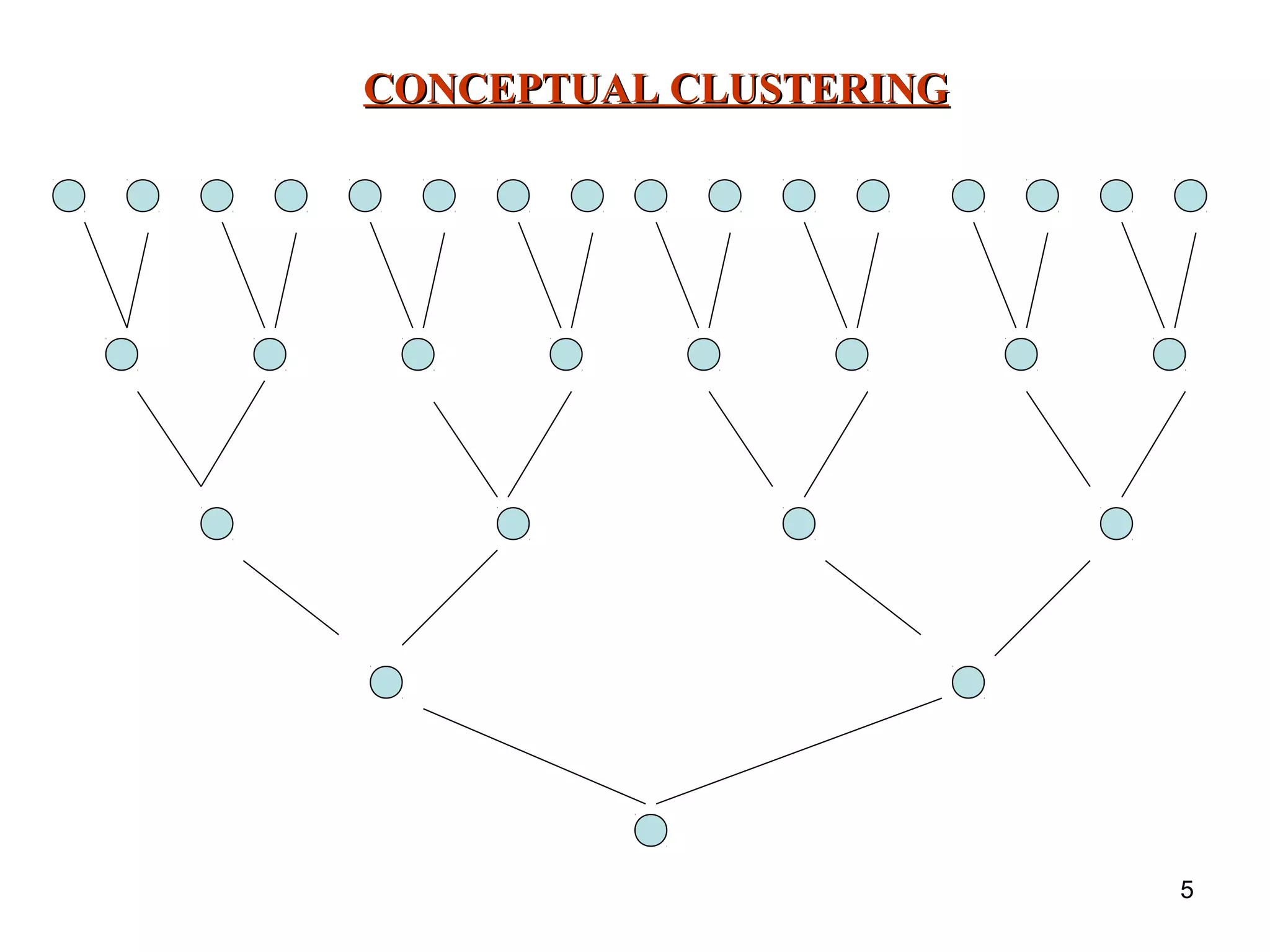
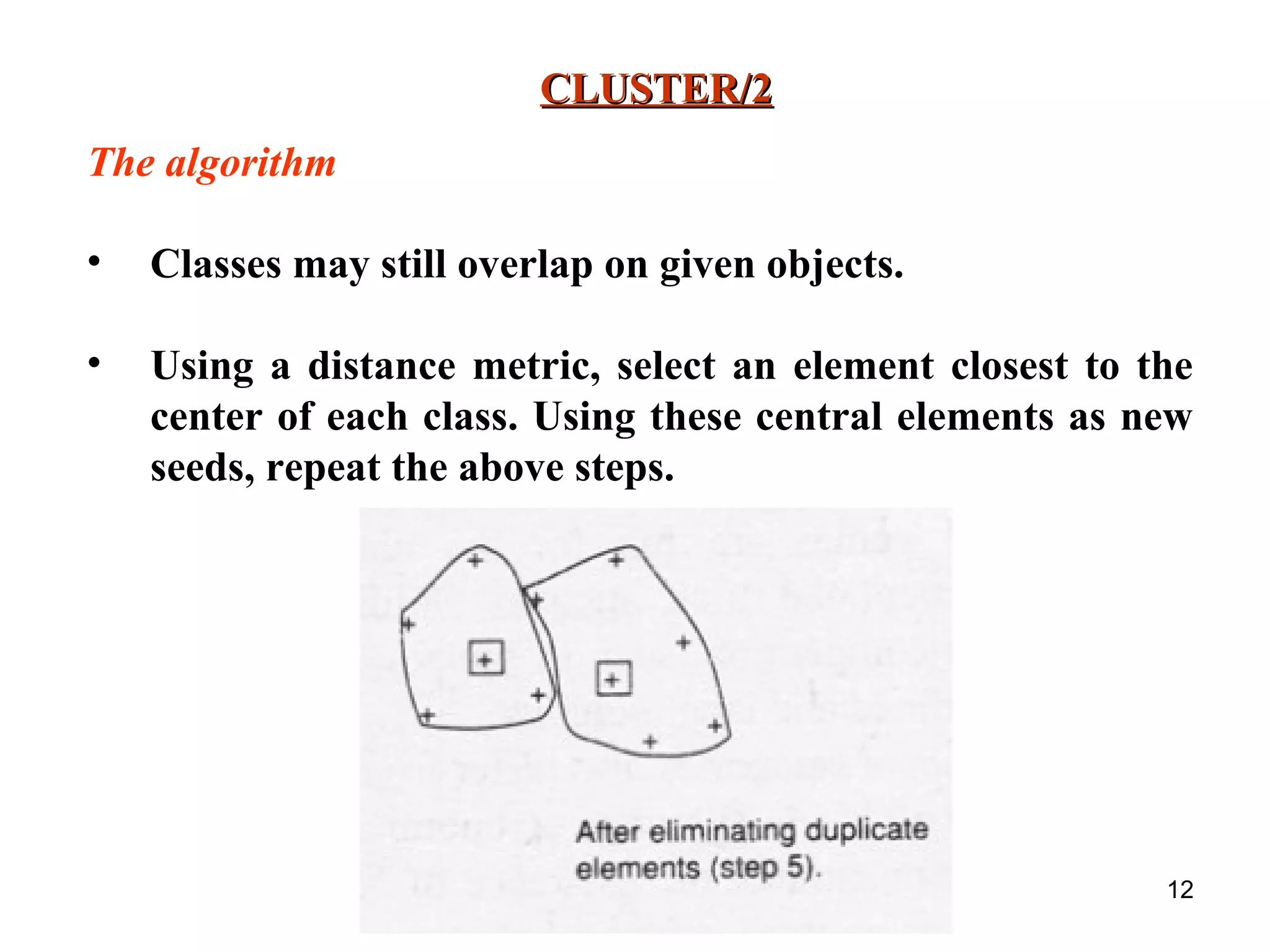
The document discusses unsupervised learning and conceptual clustering techniques for organizing unclassified data into meaningful categories without predefined labels. It describes various clustering algorithms, particularly numeric taxonomy and the Cluster/2 algorithm, which utilizes distance metrics to form classes based on feature similarities. The process involves selecting seed objects, generating general and specific descriptions for categories, and iteratively refining clusters until satisfactory classifications are achieved.