Downloaded 15 times
Uploaded byMegha Sharma
Classification Algorithm.
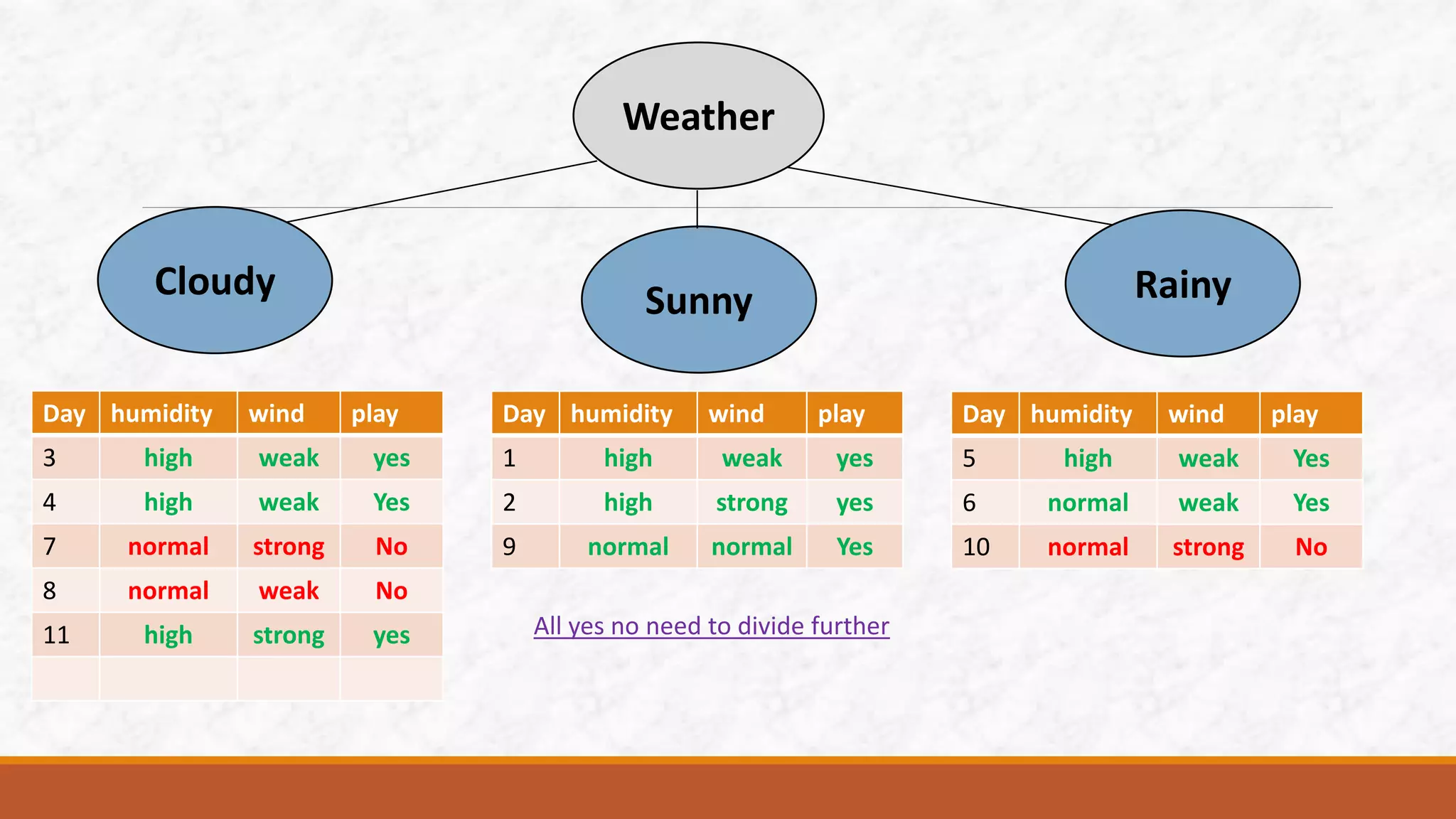
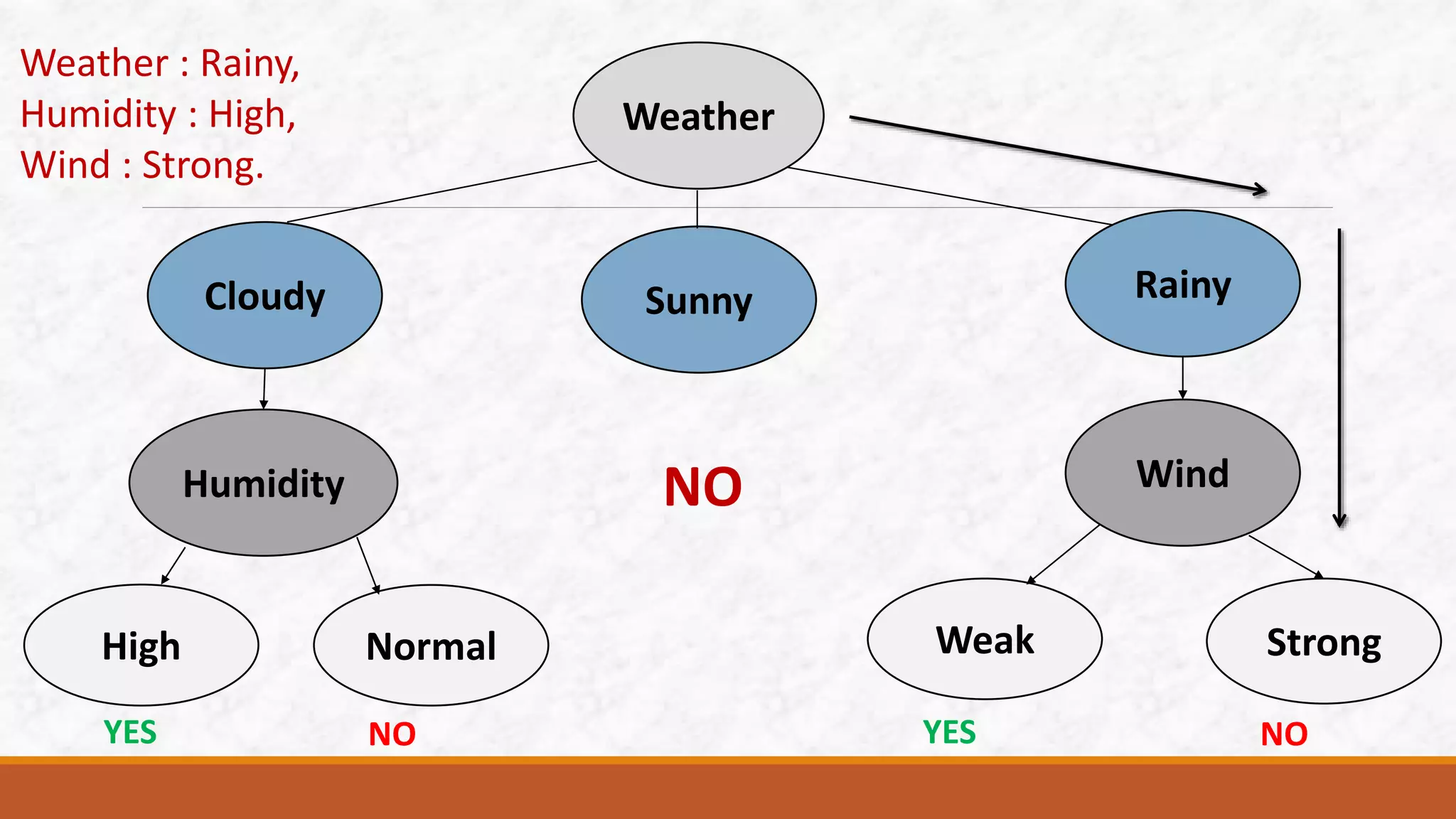
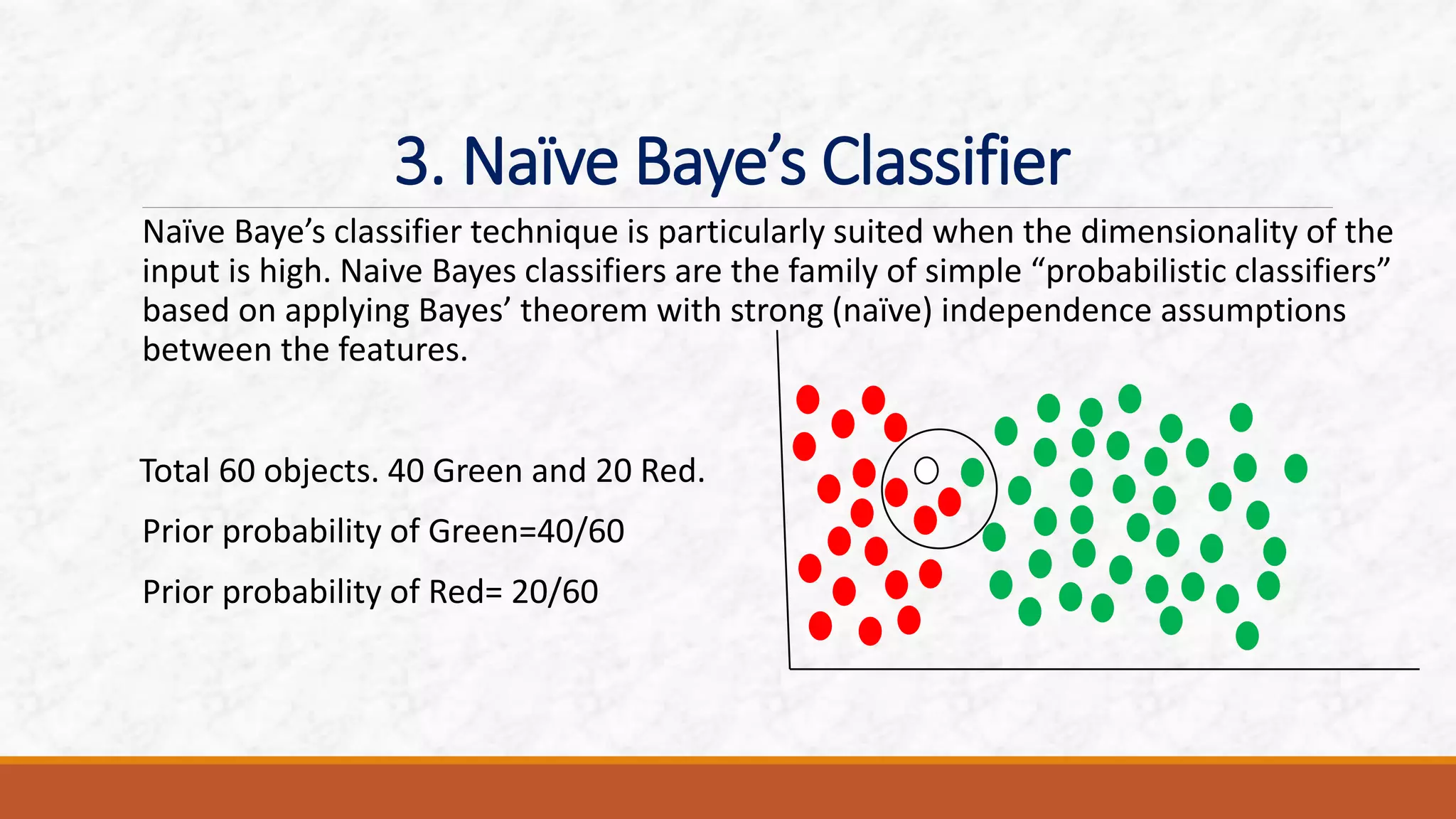
This document discusses various classification algorithms including k-nearest neighbors, decision trees, naive Bayes classifier, and logistic regression. It provides examples of how each algorithm works. For k-nearest neighbors, it shows how an unknown data point would be classified based on its nearest neighbors. For decision trees, it illustrates how a tree is built by splitting the data into subsets at each node until pure subsets are reached. It also provides an example decision tree to predict whether Amit will play cricket. For naive Bayes, it gives an example of calculating the probability of cancer given a patient is a smoker.
Classification Algorithm.
- 1.
- 2. BUSINESS INTELLIGENCE CLASSIFICATION ALGORITHMS Mrs.Megha Sharma M.Sc. Computer Science. B.Ed.
- 3. K-Nearest Neighbours Decision trees NaiveBaye’s Classifier Logistic Regression Artificial Neural Network Support Vector Machines
- 4. 1. K-Nearest Neighbour K-Nearest algorithm classifies data sets based on their similarity with neighbours. It works in a very simple way by taking into account the distance from known data point. After we gather the ‘k’ neighbours , we simply take the majority and classify the unknown data into that category. Class A: Class B: Unknown data : When k=3 Data point belongs to class B
- 5. 2. Decision Trees Adecision tree represents classification. Decision trees predict the future based on the previous learning and input data sets. It taken multiple input values and returns back the probable output with the single value which is considered as a decision. A decision tree starts with a single node, which branches into possible outcomes. Each of those outcomes lead to additional nodes, which branch off into other possibilities. Algorithm: 1. Begin the tree with the root node 2. Split into subsets. 3. If subset is pure (all yes or all no) stop the process. Else go to step 1 and repeat the process until we get pure subset.
- 6. E.g. We wantto predict whether Amit will play cricket or not? Weather : Rainy, Humidity : high, Wind : Strong. Day Weather Humidity wind Play 1 Sunny high weak yes 2 Sunny high strong yes 3 Cloudy high weak yes 4 Cloudy high weak Yes 5 Rainy high weak Yes 6 Rainy normal weak Yes 7 Cloudy normal strong No 8 Cloudy normal weak No 9 Sunny normal normal Yes 10 rainy normal strong No 11 Cloudy high strong yes
- 7. Weather Rainy Cloudy Sunny Day humiditywind play 3 high weak yes 4 high weak Yes 7 normal strong No 8 normal weak No 11 high strong yes Day humidity wind play 1 high weak yes 2 high strong yes 9 normal normal Yes Day humidity wind play 5 high weak Yes 6 normal weak Yes 10 normal strong No All yes no need to divide further
- 8. Weather Rainy Cloudy Sunny High Humidity Normal Strong Weak Wind YESNO YES NO Weather : Rainy, Humidity : High, Wind : Strong. NO
- 9. Concept of Probability Probabilityis a measure of the likelihood of an event to occur. P(A) = Number of favorable outcomes to A Total number of outcomes Number of red balls= 6 Number of Blue balls= 4 Total no of balls= 10 P(R): The probability of selecting a red ball is = 6/10 P(B): The probability of selecting a blue ball is = 4/10
- 10. Box-A Box-B Conditional Probability Box A1 Red 4 Blue Total 5 Box B 3 Red 2 Blue Total 5 Total 4 Red 6 Blue 10 P(R) = 4/10 P (B)= 6/10 Probability of getting red ball if ball is drawn from Box A. P(R|A) = 1/5 Similarly Probability of getting red ball if ball is drawn compulsorily from box B. P(R|B)= 3/5
- 11. Bayesian Methods Thomas Bayes,a statistician had given a probabilistic theory known as Baye’s theorem for probability , which describe the probability of an event or occurrence, based on prior knowledge of events and expected outcome. Baye’s Formula: P(A|B) = P (B|A) P(A) P(B) • Where P(A) and P(B) , are prior probabilities or observed probabilities independent of each other. • P(A|B), is conditional probability (posterior probability), the likelihood of event A occurring given that B is True. • P(B|A), is conditional probability (posterior probability), the likelihood of event B occurring given that A is True.
- 12. Example: Finding out apatient probability of having cancer disease. Let say “smoking test” is the test for diagnosing disease. 10% of Patients have cancer : P(A) = 0.1. 5% of Patient is a smoker: P(B) = 0.05. Among those patients diagnosed with cancer , 7% are smokers i.e. P(B|A) . Using Bayes theorem we can find the probability of having cancer if the patient is smoker. P(A|B) = (0.07* 0.1)/ 0.05 = 0.14 If the patient is a smoker, their chances of having cancer is 14%
- 13. 3. Naïve Baye’sClassifier Naïve Baye’s classifier technique is particularly suited when the dimensionality of the input is high. Naive Bayes classifiers are the family of simple “probabilistic classifiers” based on applying Bayes’ theorem with strong (naïve) independence assumptions between the features. Total 60 objects. 40 Green and 20 Red. Prior probability of Green=40/60 Prior probability of Red= 20/60
- 14. Continue… Probability of Xgiven Green = 1/40 Probability of X given Red=3/20 Posterior probability of X being Green : prior probability of Green * Likelihood of X given Green 4/6 x 1/40 =1/60 Posterior probability of X being Red : prior probability of Red * Likelihood of X given Red 2/6 x 3/20 = 1/20 Finally we classify X as ‘Red’ since its class membership achieves the largest posterior probability.
- 15. Thanks For Watching. NextTopic : Classification Algorithms Part-II.
- 16. About the Channel Thischannel helps you to prepare for BSc IT and BSc computer science subjects. In this channel we will learn Business Intelligence , A.I., Digital Electronics, Internet OF Things Python programming , Data-Structure etc. Which is useful for upcoming university exams. Gmail: omega.teched@gmail.com Social Media Handles: omega.teched megha_with OMega TechEd