(chapter 3) A Concise and Practical Introduction to Programming Algorithms in Java

1A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Frank NIELSEN nielsen@lix.polytechnique.fr A Concise and Practical Introduction to Programming Algorithms in Java Chapter 3: Functions and recursivity

2A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen So far... Executive review Lecture 1: Java=Typed compiled programming language Variables: Type var; (boolean, int, long, float, double) Assignment: var=Expression; (with type checking) Expression: Operand1 Operator Operand2 (+-*/%) Instruction (;) & comments // or /* */

3A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen So far... Executive review Lecture 2: Program workflow (blocks/branching/loops) Determine the set of instructions at runtime Blocks: sequence of instructions { } Branching condition: if predicate B1 else B2 (switch case break) Loops: while, do, for and escaping break Numerical precisions: finite-precision arithmetic (absurd results, loose of associativity, etc.)

4A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Meaning of a function in mathematics ? ● Source (X) and target (Y) domains ● A map that associates to elements of X elements of Y ● An element of X is associated at most once to a member of Y ● The mapping gives always the same result (deterministic/no randomness) ● Functions of several variables may be built blockwise... ...using Cartesian product of spaces

5A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Meaning of functions for computing ? ● A portion of a program processing data and returning a result ●A function not returning a result is also called a procedure ●A function has typed parameters as arguments ●A function usually yields the same result for a given set of arguments (except for side-effects or use of pseudo-randomness) ● A function needs to be declared first before calling it elsewhere TypeF F(Type1 arg1, Type2 arg2, ..., TypeN argN) { TypeF result; block of instructions; return result; }

6A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen class INF311{ public static typeF F(type1 arg1, ..., typeN argN) { // Description Block of instructions; } ... } ● This kind of function is also called a static method ● Functions must be defined inside classes ● A function not returning a result has type void (also known as a procedure) Declaring functions in Java

7A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Defining the body of a function in Java Class INF311{ public static typeF F(type1 arg1, ..., typeN argN) { // Description Block of instructions; } } Body of a function ● Body should contain an instruction return to indicate the result ● If branching structures are used (if or switch) , a return should be written for all different branches. Otherwise we get acompiler error!

8A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Defining the body of a function in Java class INF311{ public static typeF F(type1 arg1, ..., typeN argN) { // Description Block of instructions; } } Body of a function Body should contain an instruction return to indicate the result If branching structures are used (if or switch) , then a return should be written for all different branches. ... Otherwise we get a compiler error! (why? => not type safe!)

10A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen A few examples of basic functions class FuncDecl{ public static int square(int x) {return x*x;} public static boolean isOdd(int p) {if ((p%2)==0) return false; else return true;} public static double distance(double x, double y) {if (x>y) return x-y; else return y-x;} public static void display(double x, double y) {System.out.println("("+x+","+y+")"); return; // return void } public static void main (String[] args) { ... } }

11A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen class FuncDecl{ public static int square(int x){...} public static boolean isOdd(int p) {...} public static double distance(double x, double y) {...} public static void display(double x, double y) {...} public static void main (String[] args) { display(3,2); display(square(2),distance(5,9)); int p=123124345; if (isOdd(p)) System.out.println("p is odd"); else System.out.println("p is even"); } } A few examples of basic functions

13A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen ● Modularity (ease of presentation) ● Code re-use (program once, re-use many times!) -> library (API) ● Ease certification of correctness and test routines. Benefits of using functions

17A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Calling functions: Inner Mechanism TypeF result=F(param1, param2, ..., paramN); param1, ..., paramN should be of the same types as the ones declared in the function A function call can be used inside an expression, or even as a parameter of another function (nested calls) Example: F1(F2(x),F3(x)) Assignment's rule checks at compile time for type equivalence: System.out.println(IsPrime(23121971)); double dist=distance(u,v); Beyond the scope of the function's class, we need to put the function' class with a dot. Requires the function to be public. Math.cos(x); TD2.factorial(n); TC.lireInt();

18A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Revisiting IsPrime: measuring time We repeat this computation 1000 times to measure the elapsed time Function call in class TC: TC.demarrerChrono(); Function call in class TC: TC.tempsChrono();

19A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Potential side effects of functions: Static variables (effet de bord) ● Function that might modify/alterate the environment For example: ... displaying a value ... But also modify a variable of the base class ● A class variable is declared inside the class scope, ...not in function bodies ● Class variables are declared using the keyword static

20A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Side effects of functions: Static variables CountingCounting number ofnumber of function callsfunction calls Declaration of class variable static int classvar;

21A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Function: Signature and overloading signature of a function = ordered sequence of parameter types Two functions with different signatures can bear the same name (since the compiler can distinguish them!) static double plusone(...) int double String

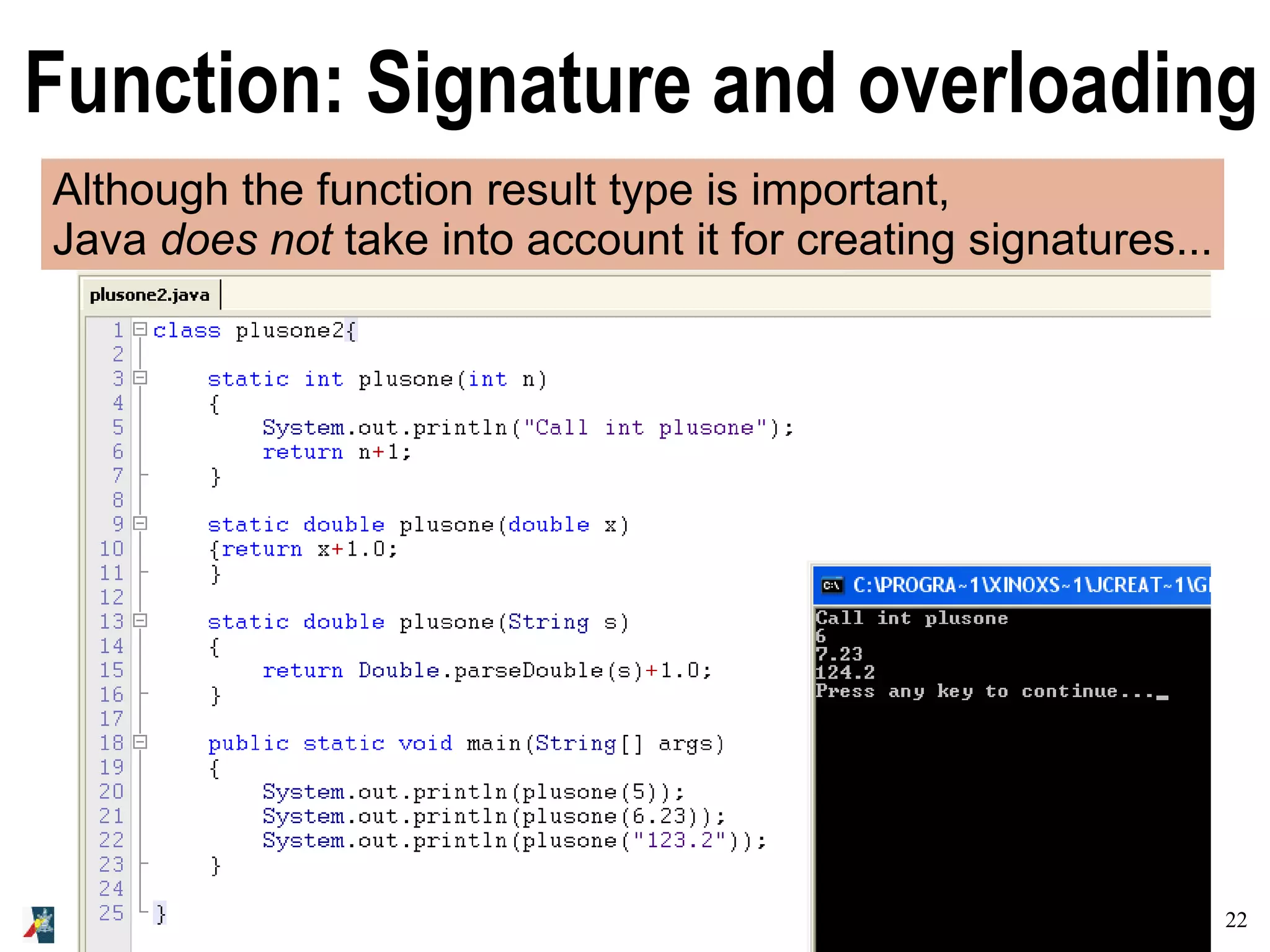
22A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Although the function result type is important, Java does not take into account it for creating signatures... Function: Signature and overloading

23A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Function: Signature and overloading static int plusone (int n) static double plusone(int n) !!! COMPILATION ERROR !!! class SignatureError{ public static int plusone(int n) {return n+1;} public static double plusone(int n) {return n+1.0;} public static void main(String args[]) {} } C:JSignature.java:6: plusone(int) is already defined in SignatureError static double plusone(int n)

24A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Executing functions in Java ● Work place of the function is created when the function is called ● ... and destroyed once it is executed (value returned) ● Parameter values are equal to the results of the expressions ● Function parameters are allocated in memory reserved for the function ● If a parameter is modified inside the function body, it remains unchanged in the calling function. public static void main(String args[])

25A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Executing functions in Java Memory (stack) Memory for main Memory for Increment Memory for plusone As soon as we exit this function, k takes its original value of (5) passage par valeur

27A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Principle of recursion A beautiful principle of computing ! Loosely speaking, ... ...the inverse of inductivism in mathematics ● A function that calls itself... ● ...not forever, so that there should be stopping states... ● ...Function parameters should tend to the ones that do not ...require recursion to finalize the computation... But all this is an informal glimpse of recursion (self-structure)

29A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Population growth: Newly born pair of M/F rabbits are put in a field. Newly born rabbits take a month to become mature, after which time ... They produce a new pair of baby rabbits every month Q.: How many pairs will there be in subsequent years? Example: Fibonacci numbers Leonard de Pise (1170- 1245) 1, 1, 2, 3, 5, 8, 13, 21, 34, 55......

30A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Example: Fibonacci numbers Leonard de Pise Much better algorithms at.... http://fr.wikipedia.org/wiki/Suite_de_Fibonacci

31A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Understanding a recursive function recursive function called: ● Allocation of memory for local variables ● Stack operations to compute ● ... Call the function with other parameters, if required ● Process operations that remains on the stack int fibo(int n) {int x,y; if(n <= 1) return 1; x=fibo(n-1); y=fibo(n-2); return x+y;} x=fibo(2) y=fibo(1) return x+y fibo(3) Recursive calls

32A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen x=fibo(2) y=fibo(1) return x+y x=fibo(1) y=fibo(0) return x+y return 1; fibo(3) fibo(2) fibo(1) Understanding a recursive function

33A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen x=fibo(2) y=fibo(1) return x+y x=1 y=fibo(0) return x+y return 0; fibo(3) fibo(2) fibo(0) Understanding a recursive function

36A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen x=1 y=1 return x+y fibo(3)=2 As we can see, there is a lot of redundant work here. -> Very inefficient algorithm. Can cause stack overflow if the #recursive calls... ...become too large 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, .. Understanding a recursive function

38A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Recursion: Halting problem When does a recursive program terminate? The arguments always decrease and there is always a stopping criterion

40A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Does not always halt because we may never reach terminal case (n=0) for odd numbers Recursion: Halting problem Do we always reach that terminal state?

42A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Syracuse problem and termination conjecture Conjectured to halt (computer simulation helps intuition but does not give a full proof) Recursion: Halting problem

43A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen There is provably no algorithm that can take as input a program (binary string) and return true if and only if this program halts. http://en.wikipedia.org/wiki/Halting_problem Halting problem: Computer Science Proof skipped

44A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Terminal recursion Does not put function calls on the stack (thus avoid stack overflow) What happens if we call Factorial(100) ? Recursive calls are alwaysof the form return f(...); ->No instruction (computation) after the function (Factorial is not terminal since return n*f(n-1); ) if (n<=1) return 1; else return n*f(n-1);

45A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen factorial with terminal recursion Arguments plays the role of accumulators What happens if we call Factorial(100) ?

46A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Terminal Recursion: Revisiting Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ... accum ulator

47A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Recursivity and Nature Drawing fractal curves and motifs Koch's snowflake Fractals: ● Patterns that are present at different scales ● The curve at stage n is defined recursively... ....from the curve at stage n-1

48A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Fractal: Sierpinski motif Generation 1 Generation 2 Generation 3 Generation 4 Generation 5 The recursive pattern is given by a simple rewritting rule: Replace a triangle by 3 triangles defined by the... midpoints of the edges of the source triangle Waclaw Sierpinski (1882-1969) Polish mathematician

49A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen Sierpinski curve (2D pyramid) http://www.enseignement.polytechnique.fr/profs/informatique/Philippe.Chassignet/MACLIB/Java/maclib_java.html

(chapter 3) A Concise and Practical Introduction to Programming Algorithms in Java

More Related Content

What's hot

Viewers also liked

Similar to (chapter 3) A Concise and Practical Introduction to Programming Algorithms in Java

Recently uploaded

(chapter 3) A Concise and Practical Introduction to Programming Algorithms in Java