Downloaded 286 times
Uploaded byShab Bi
Binary expression tree
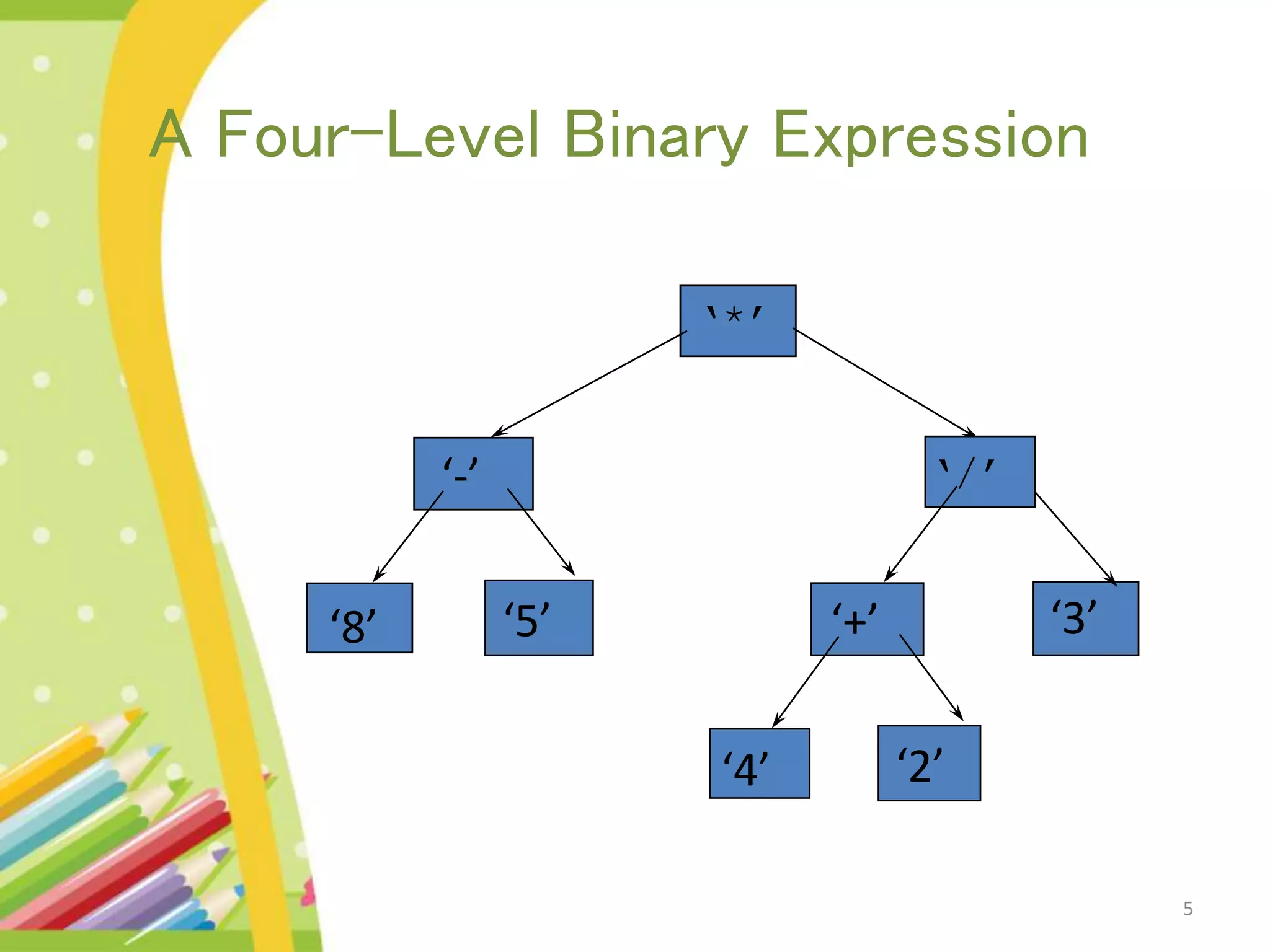
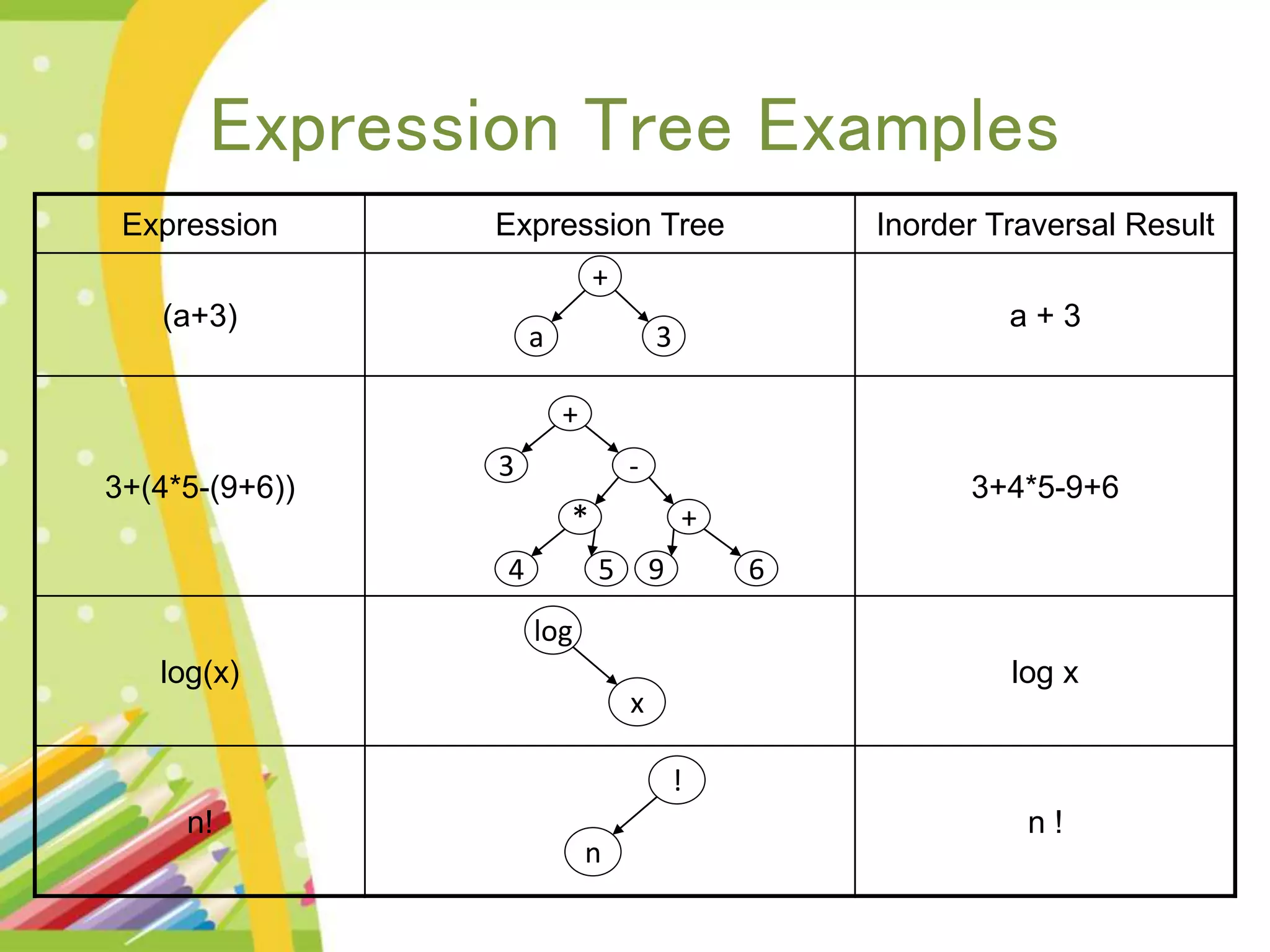
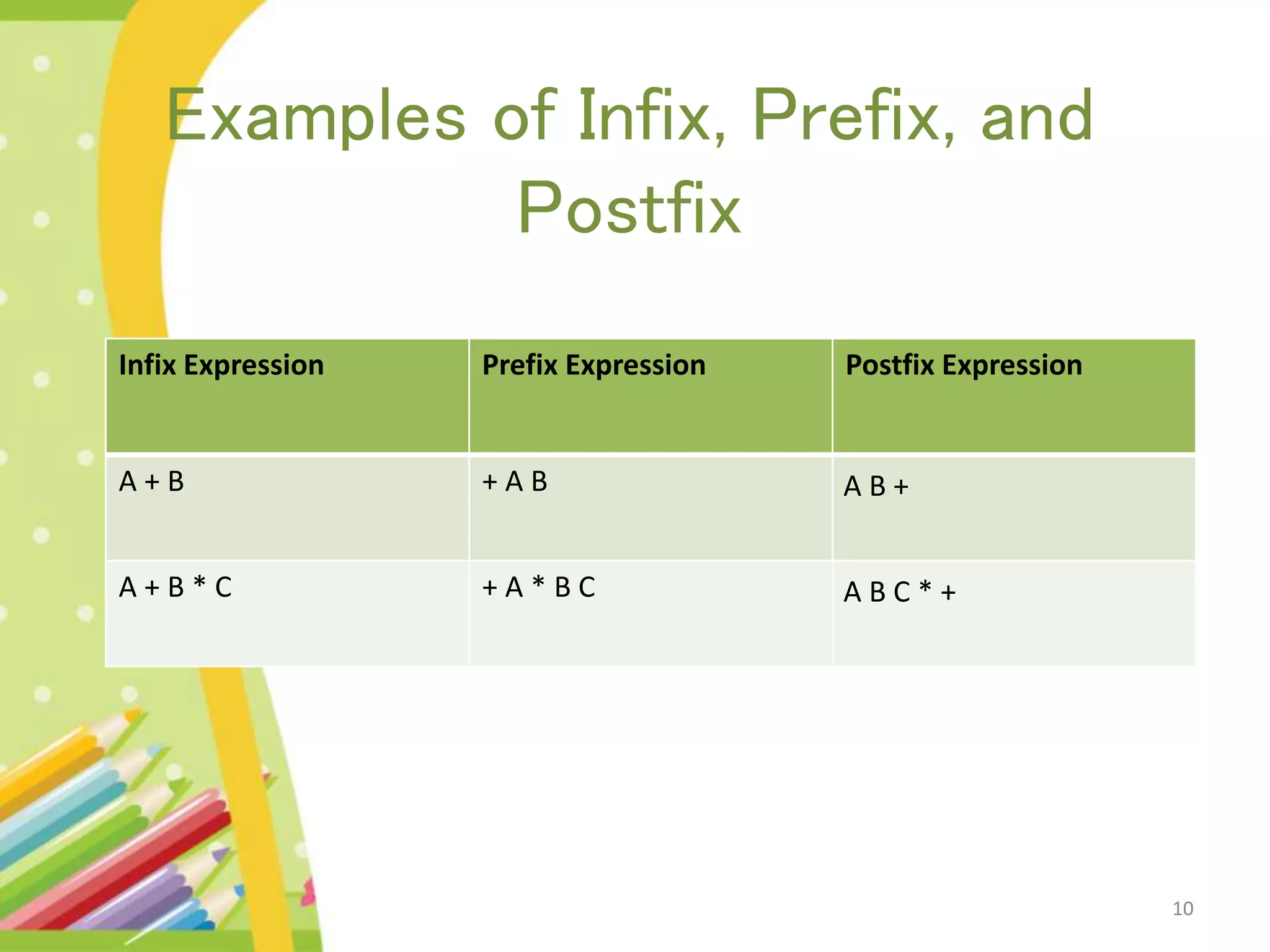
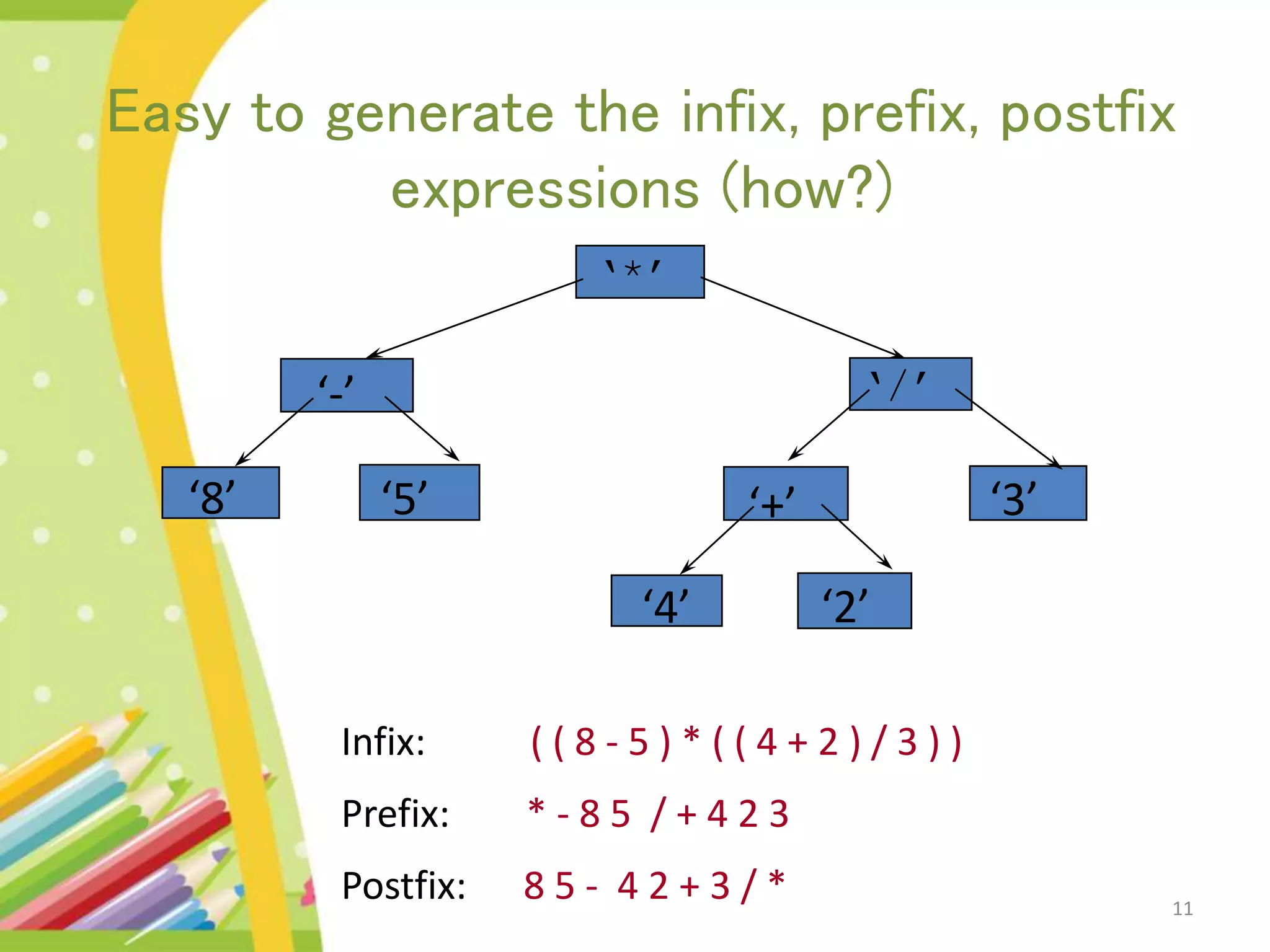
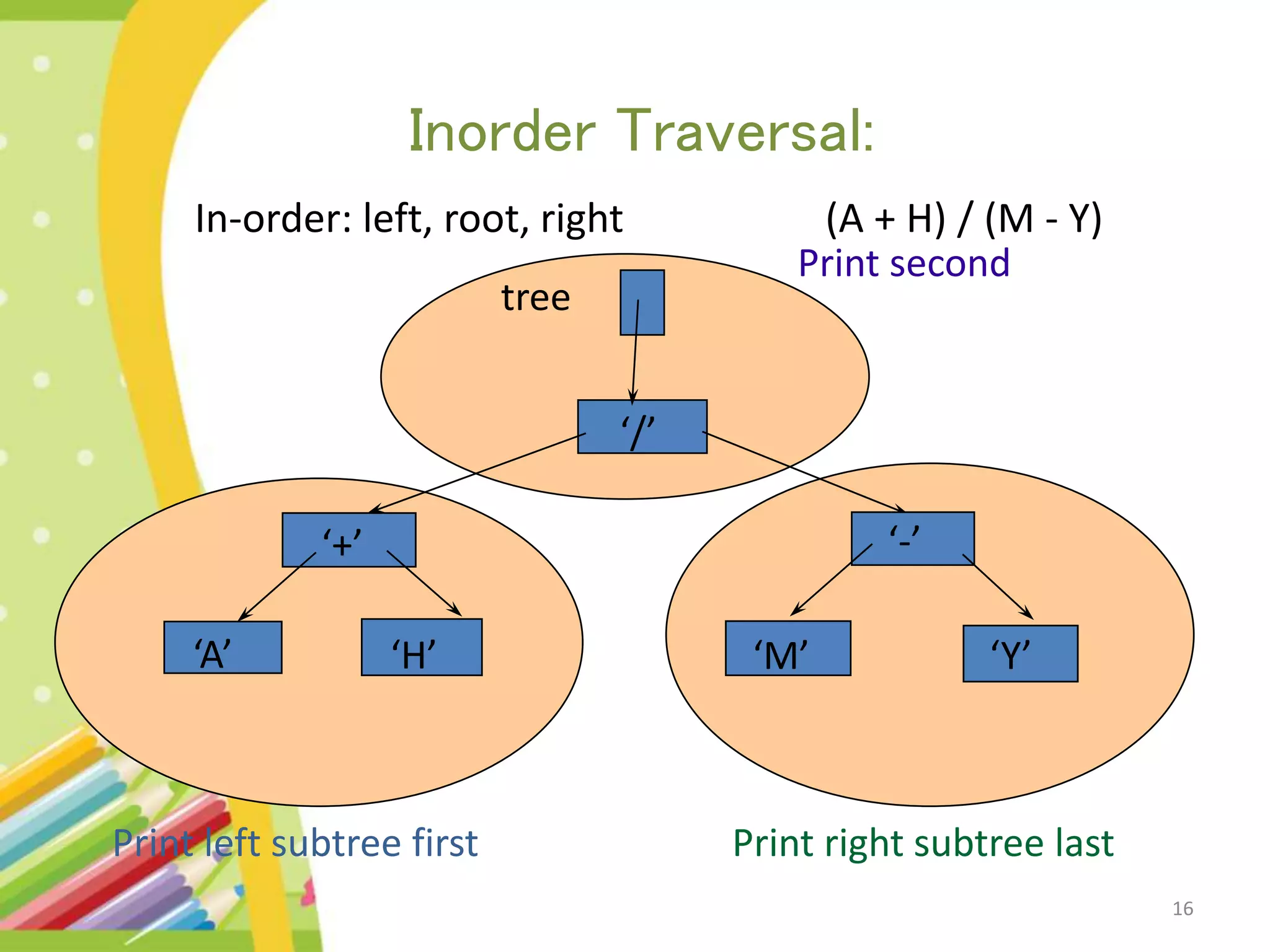
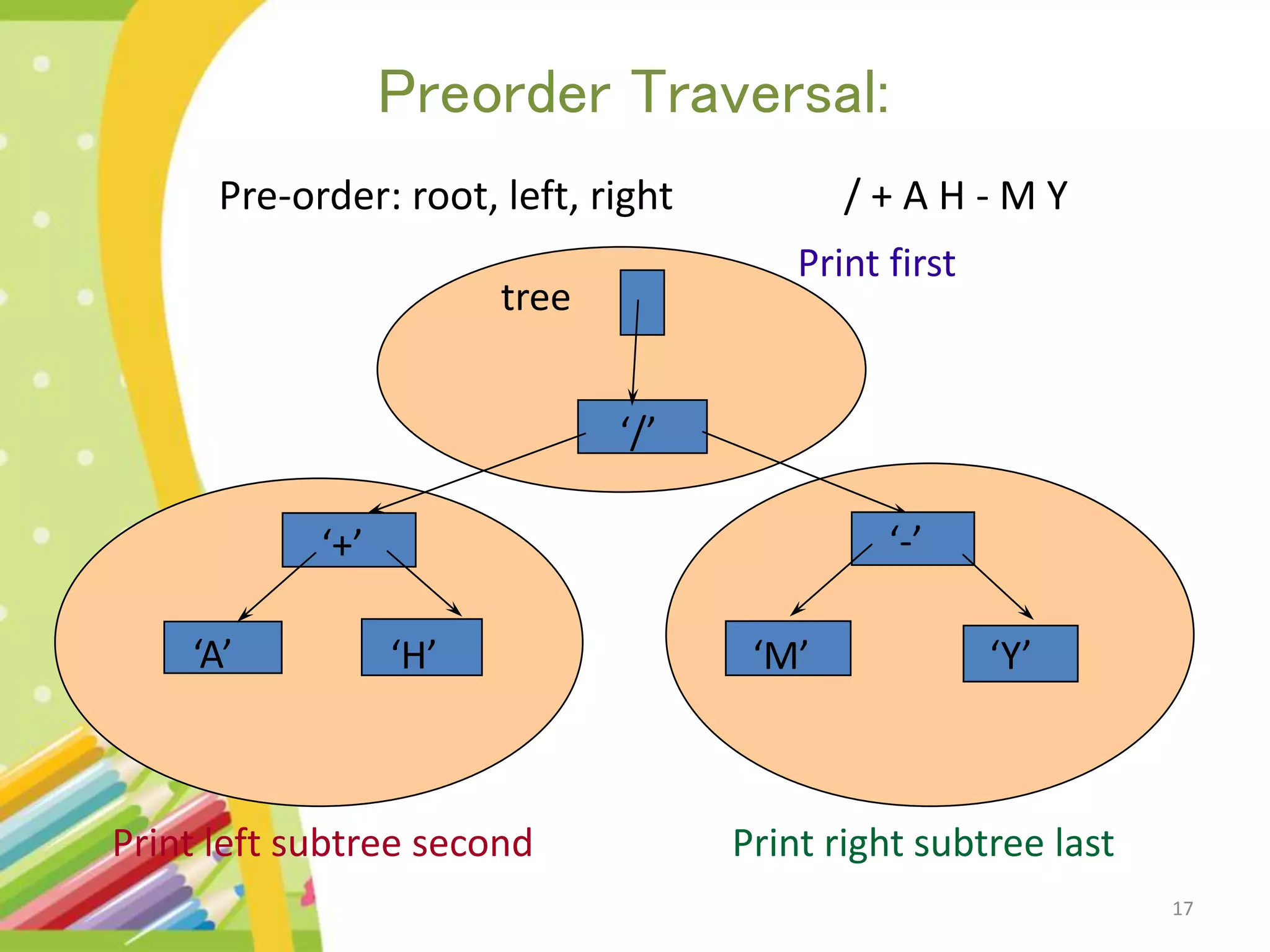
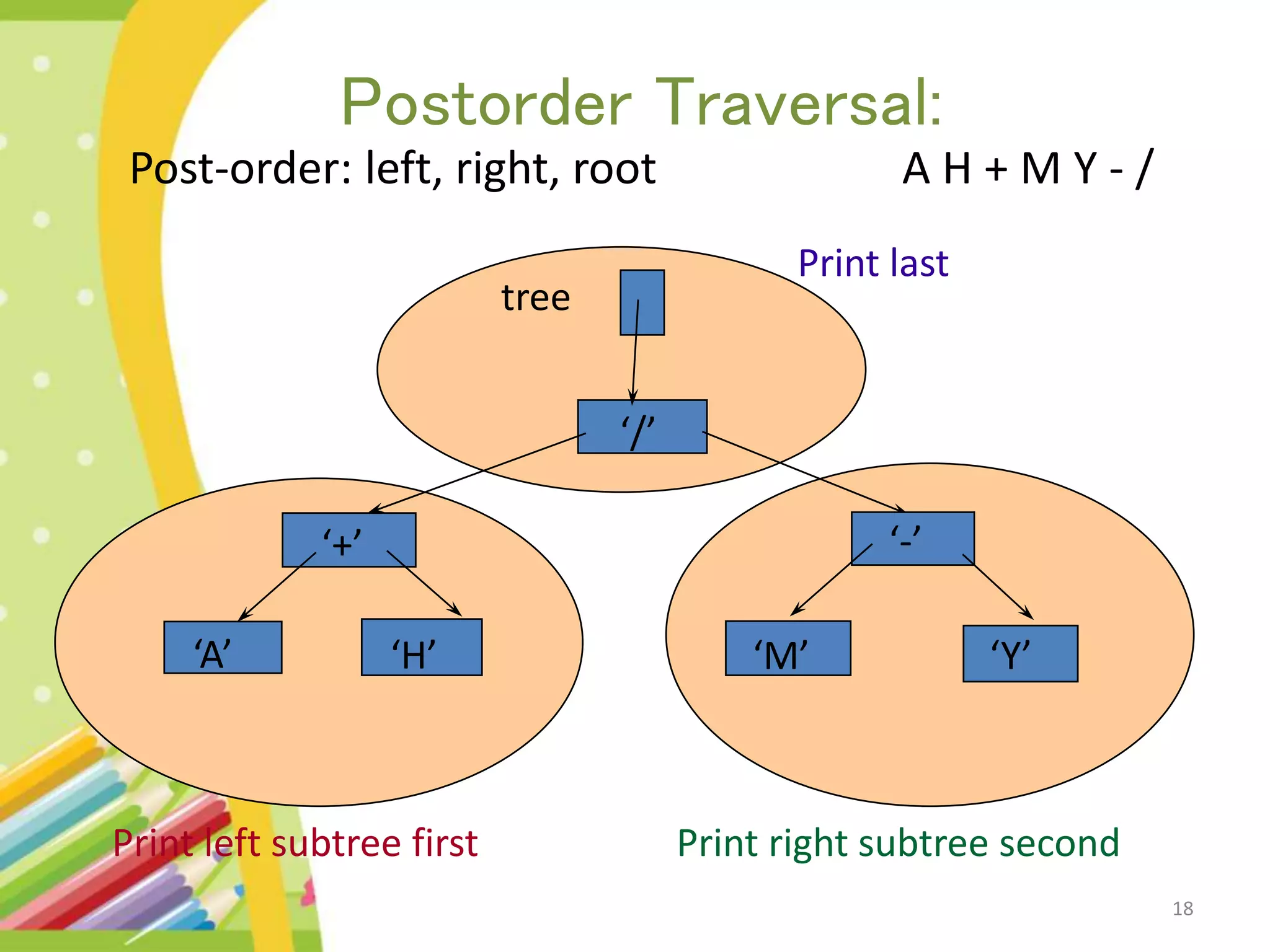
The document discusses binary expression trees, which are a type of binary tree used to represent arithmetic expressions. A binary expression tree has operands as leaf nodes and operators as internal nodes. The left and right subtrees of each operator node represent subexpressions that must be evaluated before applying the operator. The document provides examples of binary expression trees and discusses traversing them using inorder, preorder, and postorder traversals. Algorithms are presented for building a binary expression tree from a prefix notation expression and for evaluating an expression by scanning it and using operator and value stacks.
Binary expression tree
- 1. Data Structures Presentation By: AmnaIqbal Amna Muzzafar Asma Iqbal Faiza Zahid Maryam Tariq Sumaira Shabana kausar Shamsa Tahseen Fatima Zeerak
- 2. 2 An application ofbinary trees Binary Expression Trees
- 3. 3 A special kindof binary tree in which: • The leaves of a binary expression tree are operands, such as constants or variable names , and the other nodes contain operators • Each leaf node contains a single operand • Each nonleaf node contains a single binary operator • The left and right subtrees of an operator node represent subexpressions that must be evaluated before applying the operator at the root of the subtree. A Binary Expression Tree is . . .
- 4. 4 A Binary ExpressionTree What value does it have? ( 4 + 2 ) * 3 = 18 ‘*’ ‘+’ ‘4’ ‘3’ ‘2’
- 5. 5 A Four-Level BinaryExpression ‘*’ ‘-’ ‘8’ ‘5’ ‘/’ ‘+’ ‘4’ ‘3’ ‘2’
- 6. Expression Tree Examples InorderTraversal ResultExpression TreeExpression a + 3(a+3) 3+4*5-9+63+(4*5-(9+6)) log xlog(x) n !n! + 3a + -3 * 54 + 69 log x ! n
- 7. Infix Expressions • Whenyou write an arithmetic expression such as B * C, the form of the expression provides you with information so that you can interpret it correctly. In this case we know that the variable B is being multiplied by the variable C since the multiplication operator * appears between them in the expression This type of notation is referred to as infix since the operator is in between the two operands that it is working on. 7
- 8. Prefix Expressions • Prefixexpression notation requires that all operators precede the two operands that they work on. • A + B * C would be written as +A*BC in prefix. The multiplication operator comes immediately before the operands B and C, denoting that * has precedence over +. The addition operator then appears before the A and the result of the multiplication. 8
- 9. Postfix Expressions • Postfixrequires that its operators come after the corresponding operands. • A + B * C would be written as ABC*+ in postfix. The multiplication operator appears immediately after the B and the C, denoting that * has precedence, with + coming after. 9
- 10. Examples of Infix,Prefix, and Postfix 10 Infix Expression Prefix Expression Postfix Expression A + B + A B A B + A + B * C + A * B C A B C * +
- 11. 11 Easy to generatethe infix, prefix, postfix expressions (how?) Infix: ( ( 8 - 5 ) * ( ( 4 + 2 ) / 3 ) ) Prefix: * - 8 5 / + 4 2 3 Postfix: 8 5 - 4 2 + 3 / * ‘*’ ‘-’ ‘8’ ‘5’ ‘/’ ‘+’ ‘4’ ‘3’ ‘2’
- 12. Infix to Postfixconversion (manual) • An Infix to Postfix manual conversion algorithm is: 1. Completely parenthesize the infix expression according to order of priority you want. 2. Move each operator to its corresponding right parenthesis. 3. Remove all parentheses. • Examples: 3 + 4 * 5 (3 + (4 * 5) ) 3 4 5 * + a / b ^ c – d * e – a * c ^ 3 ^ 4 a b c ^ / d e * a c 3 4 ^ ^ * - - ((a / (b ^ c)) – ((d * e) – (a * (c ^ (3 ^ 4) ) ) ) ) Using normal mathematical operator precedence Not using normal mathematical operator precedence
- 13. 13 Levels Indicate Precedence Thelevels of the nodes in the tree indicate their relative precedence of evaluation (we do not need parentheses to indicate precedence). Each operator has a precedence level. Operators of higher precedence are used before operators of lower precedence Operations at higher levels of the tree are evaluated later than those below them. The operation at the root is always the last operation performed.
- 14. Tree Traversal • Atree traversal is a specific order in which to trace the nodes of a tree. 14
- 15. Types Of TreeTraversal • There are 3 common types of tree traversals. • In-order. • 2. Pre-order. • 3. Post-order. 15
- 16. 16 Inorder Traversal: In-order: left,root, right (A + H) / (M - Y) ‘/’ ‘+’ ‘A’ ‘H’ ‘-’ ‘M’ ‘Y’ tree Print left subtree first Print right subtree last Print second
- 17. 17 Preorder Traversal: Pre-order: root,left, right / + A H - M Y ‘/’ ‘+’ ‘A’ ‘H’ ‘-’ ‘M’ ‘Y’ tree Print left subtree second Print right subtree last Print first
- 18. 18 ‘/’ ‘+’ ‘A’ ‘H’ ‘-’ ‘M’ ‘Y’ tree Printleft subtree first Print right subtree second Print last Postorder Traversal: Post-order: left, right, root A H + M Y - /
- 19. 19 Building a BinaryExpression Tree from an expression in prefix notation • Insert new nodes, each time moving to the left until an operand has been inserted. • Backtrack to the last operator, and put the next node to its right. • Continue in the same pattern.
- 20.
- 21. Algorithm for Expressiontree 1 Scan expression from left to right until end of string 2 If (symbol = operand) P= new node P.data= symbol Push(P) Else Ptr1= Pop() Ptr2= Pop() P= new node P.data= symbol P.Lchild= Ptr2 P.Rchild=Ptr1 Push(P) 3 Exit
- 22. How to scanan expression 1. While there are still tokens to be read in, 1.1 Get the next token. 1.2 If the token is: 1.2.1 A number: push it onto the value stack. 1.2.2 A variable: get its value, and push onto the value stack. 1.2.3 A left parenthesis: push it onto the operator stack. 1.2.4 A right parenthesis: 1 While the thing on top of the operator stack is not a left parenthesis, 1 Pop the operator from the operator stack. 2 Pop the value stack twice, getting two operands. 3 Apply the operator to the operands, in the correct order. 4 Push the result onto the value stack. 2 Pop the left parenthesis from the operator stack, and discard it.
- 23. How to scanan expression 1.2.5 An operator (call it thisOp): 1 While the operator stack is not empty, and the top thing on the operator stack has the same or greater precedence as thisOp, 1 Pop the operator from the operator stack. 2 Pop the value stack twice, getting two operands. 3 Apply the operator to the operands, in the correct order. 4 Push the result onto the value stack. 2 Push thisOp onto the operator stack.
- 24. How to scanan expression 2. While the operator stack is not empty, 1 Pop the operator from the operator stack. 2 Pop the value stack twice, getting two operands. 3 Apply the operator to the operands, in the correct order. 4 Push the result onto the value stack. 3. At this point the operator stack should be empty, and the value stack should have only one value in it, which is the final result