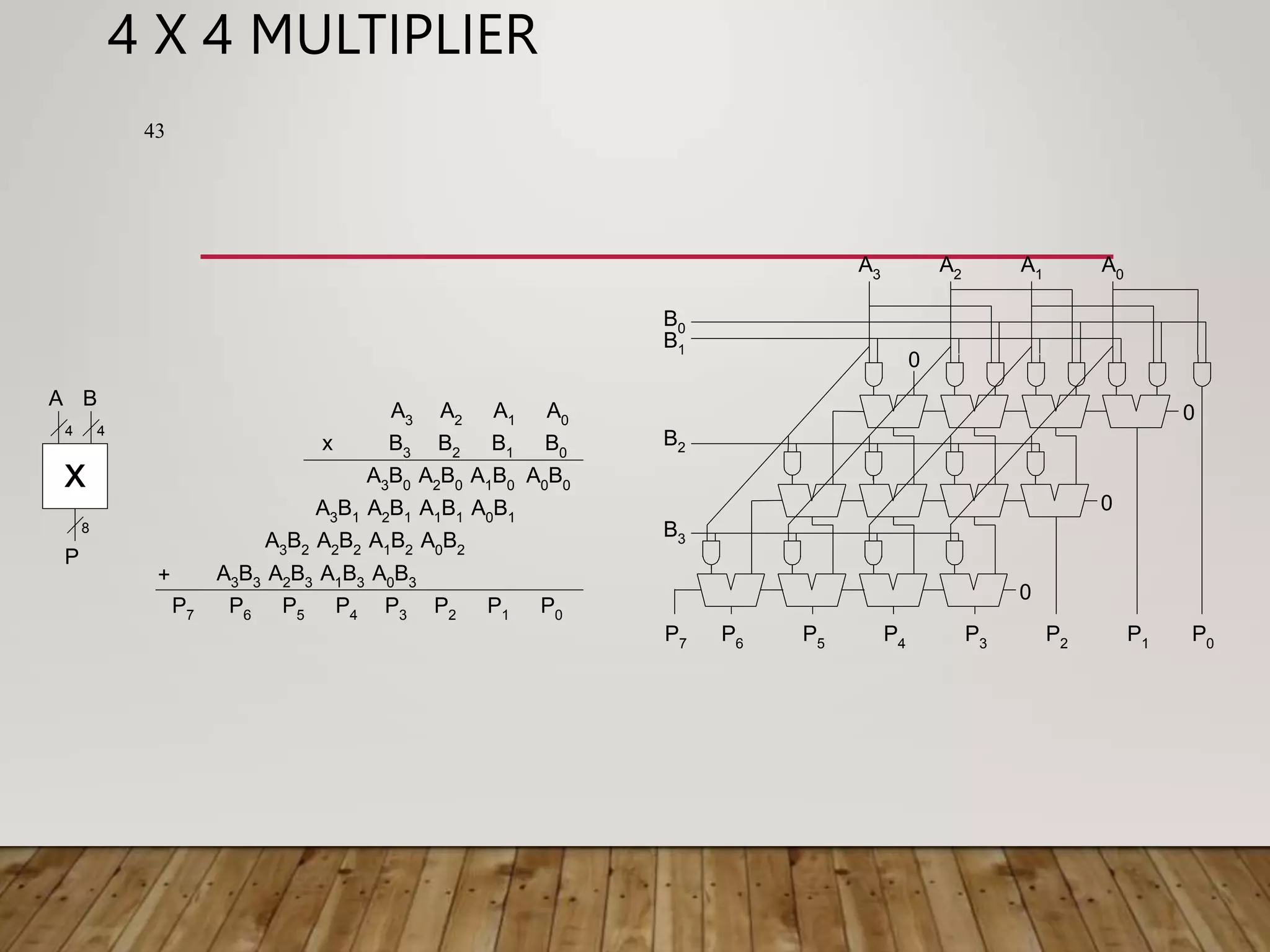
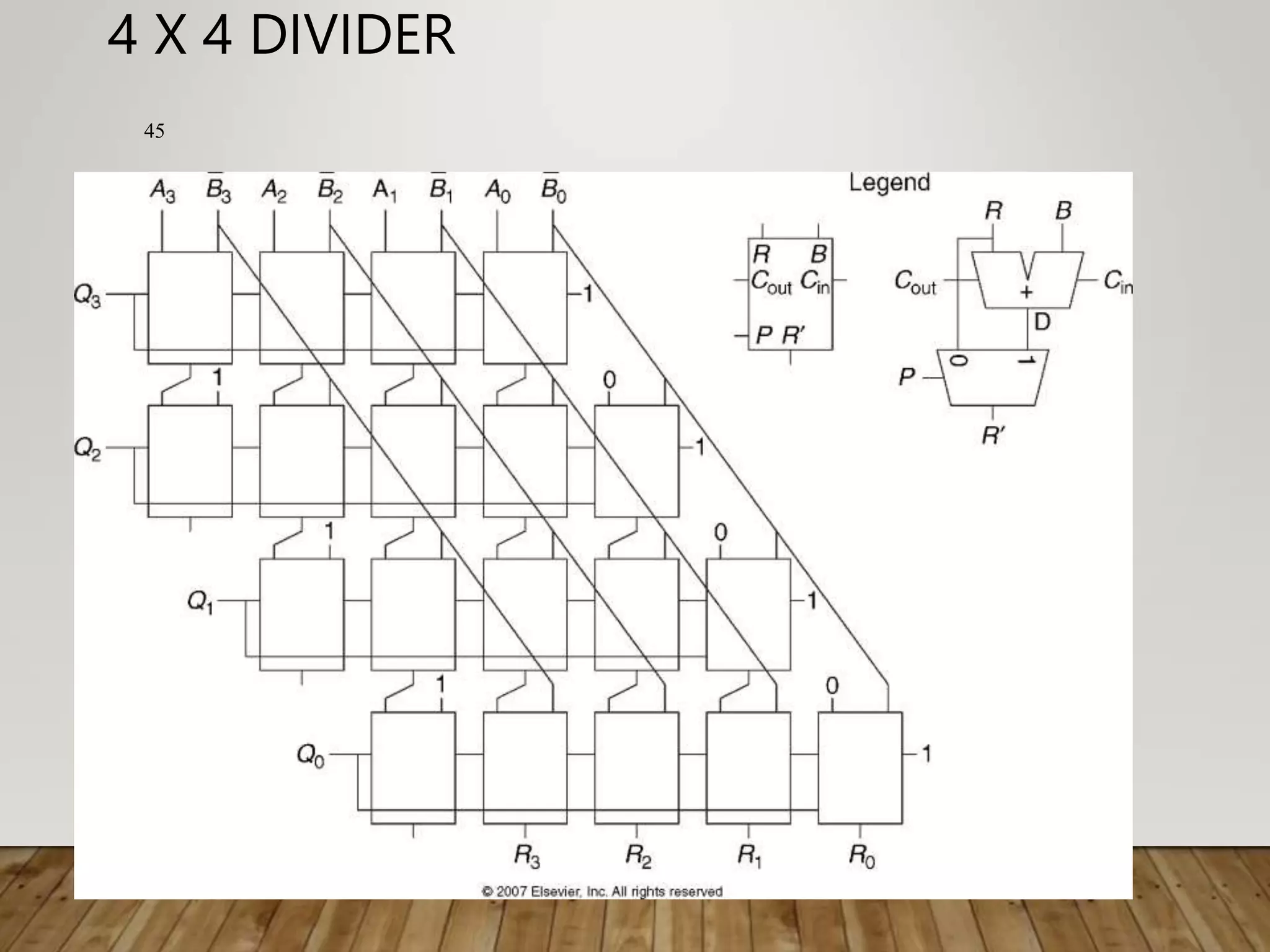
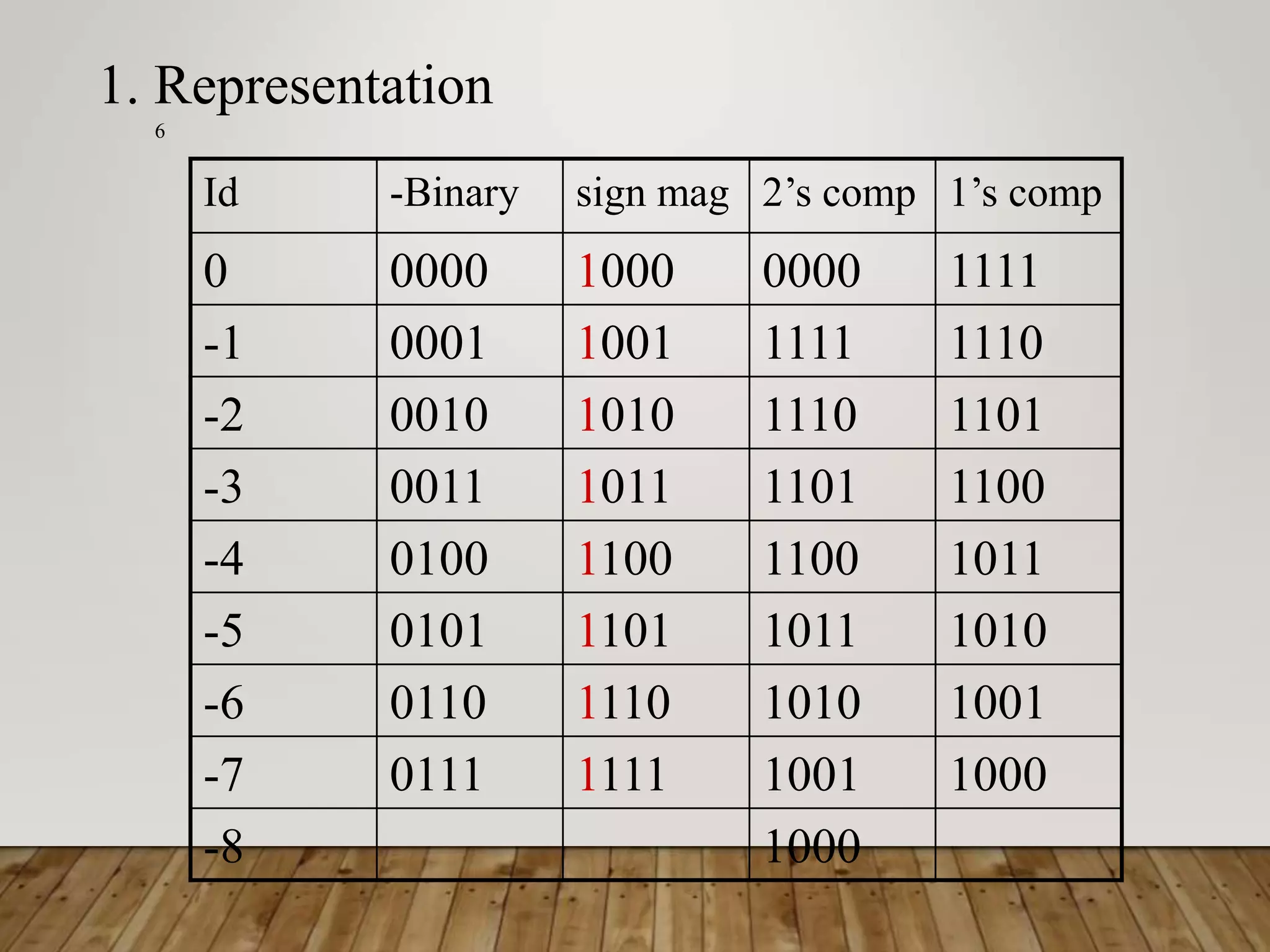
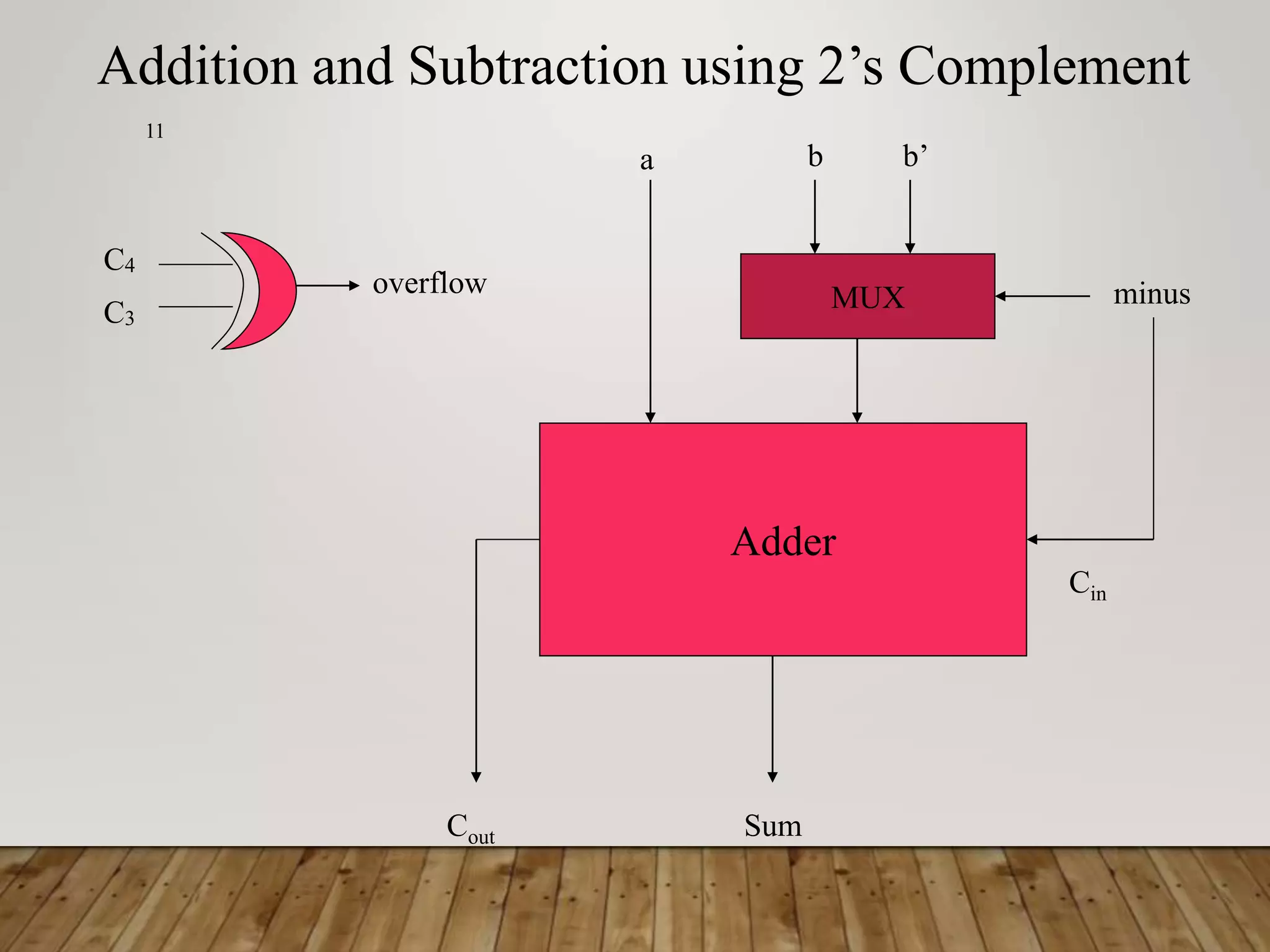
This document summarizes a lecture on standard combinational modules. It discusses representation of numbers using 2's complement and 1's complement, and types of adders including half adders, full adders, ripple-carry adders, carry-lookahead adders, and prefix adders. It provides examples of addition and subtraction using each representation. It also briefly discusses comparators for equality and less than operations.









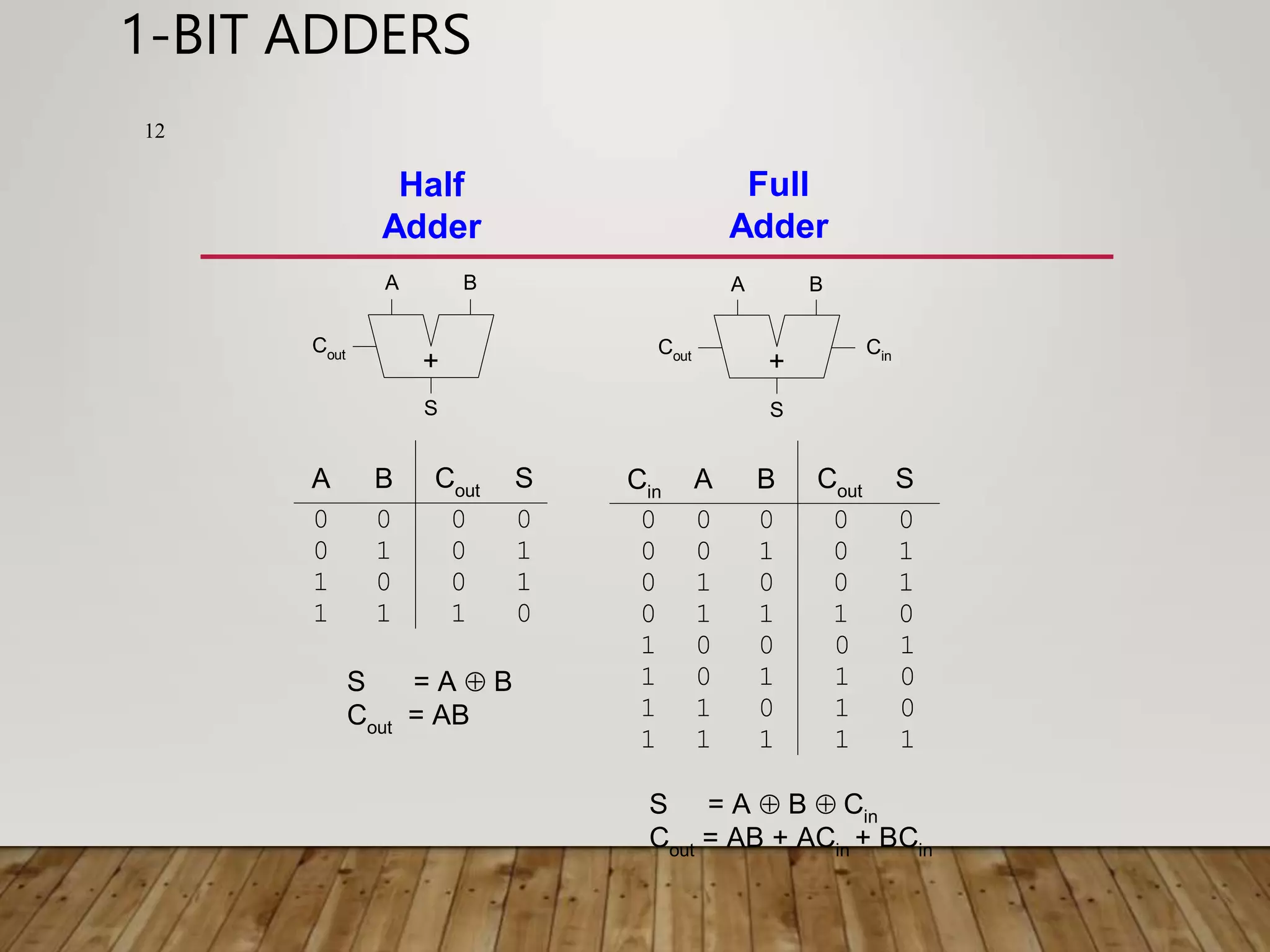
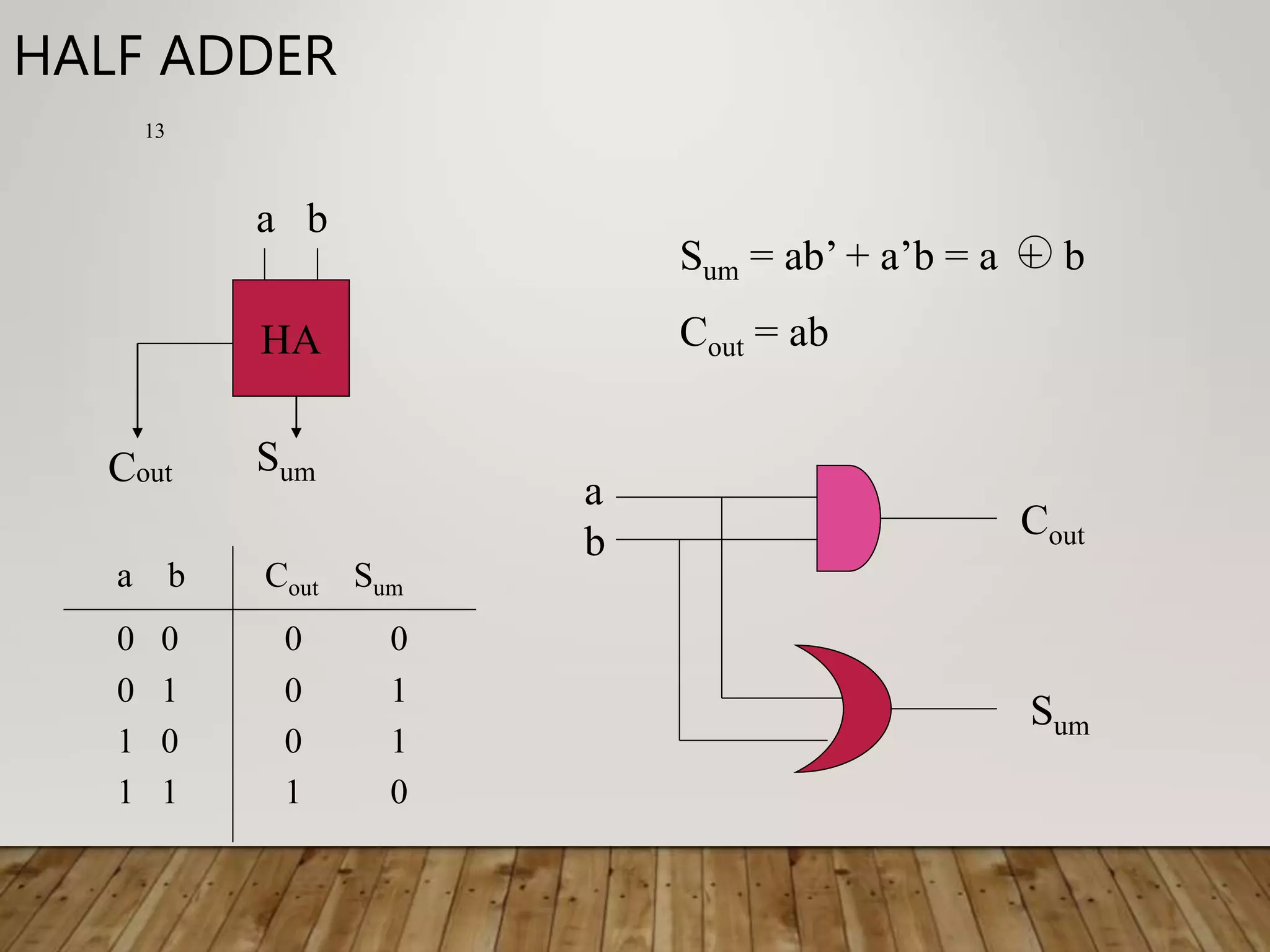
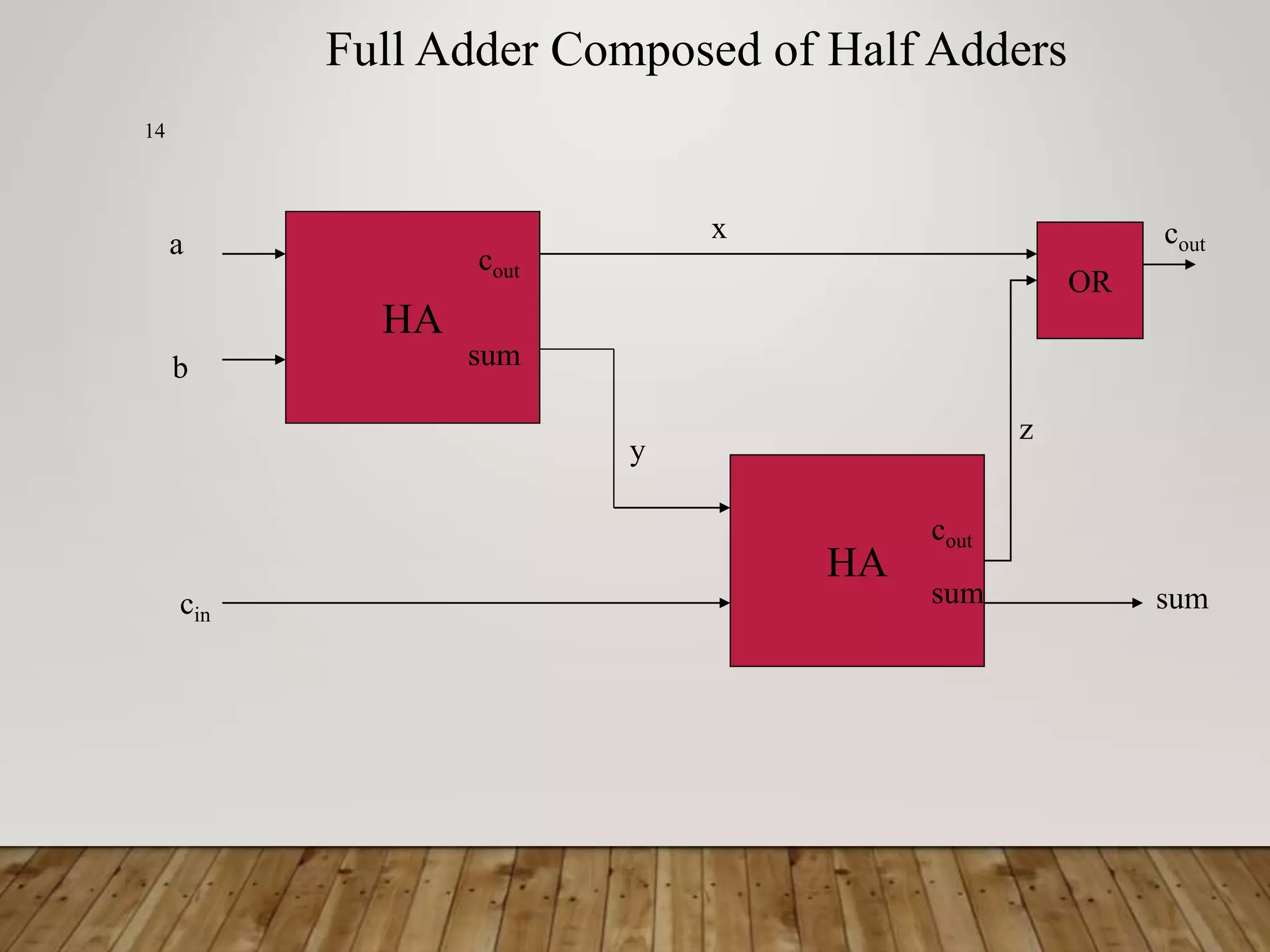
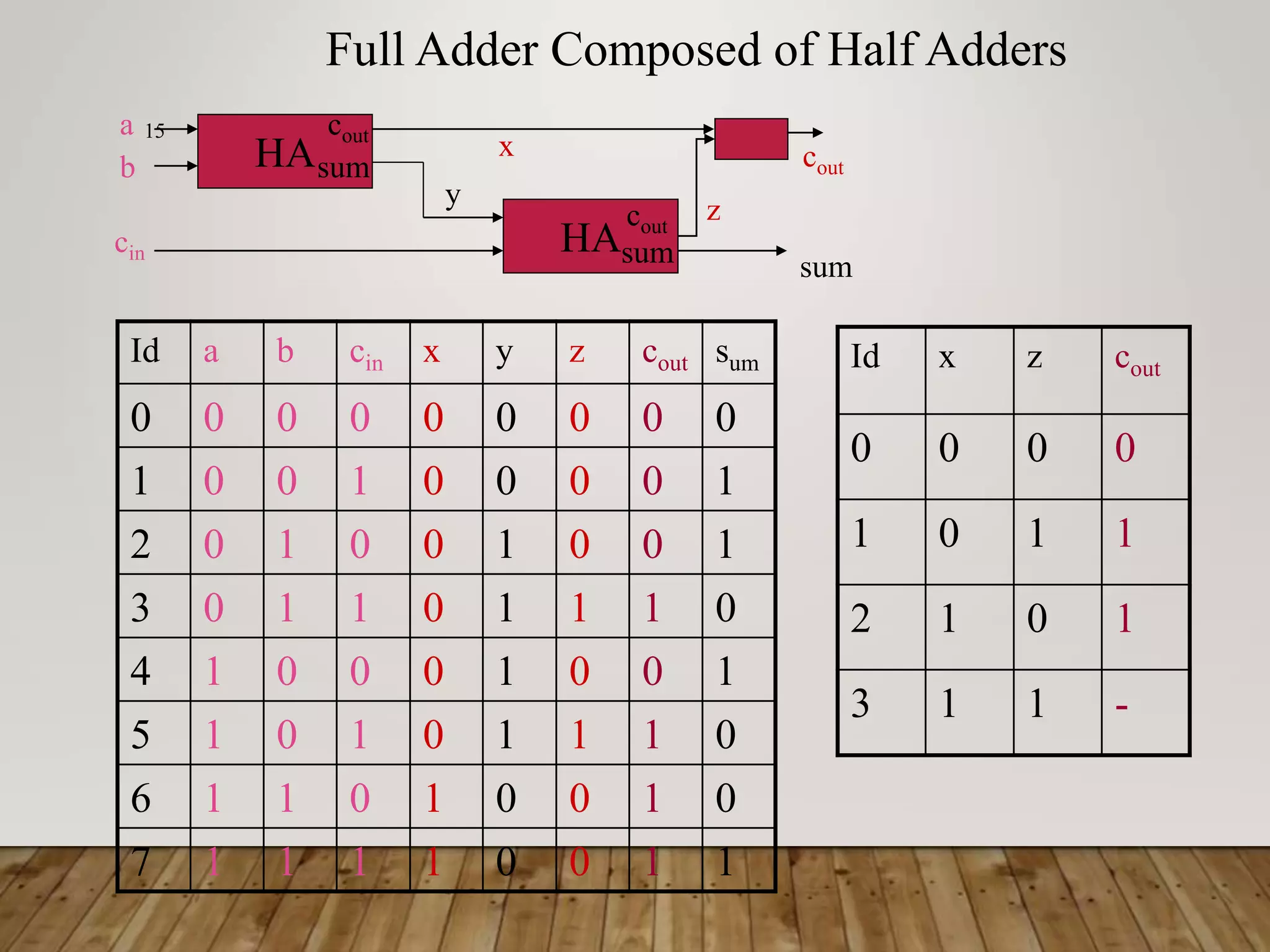




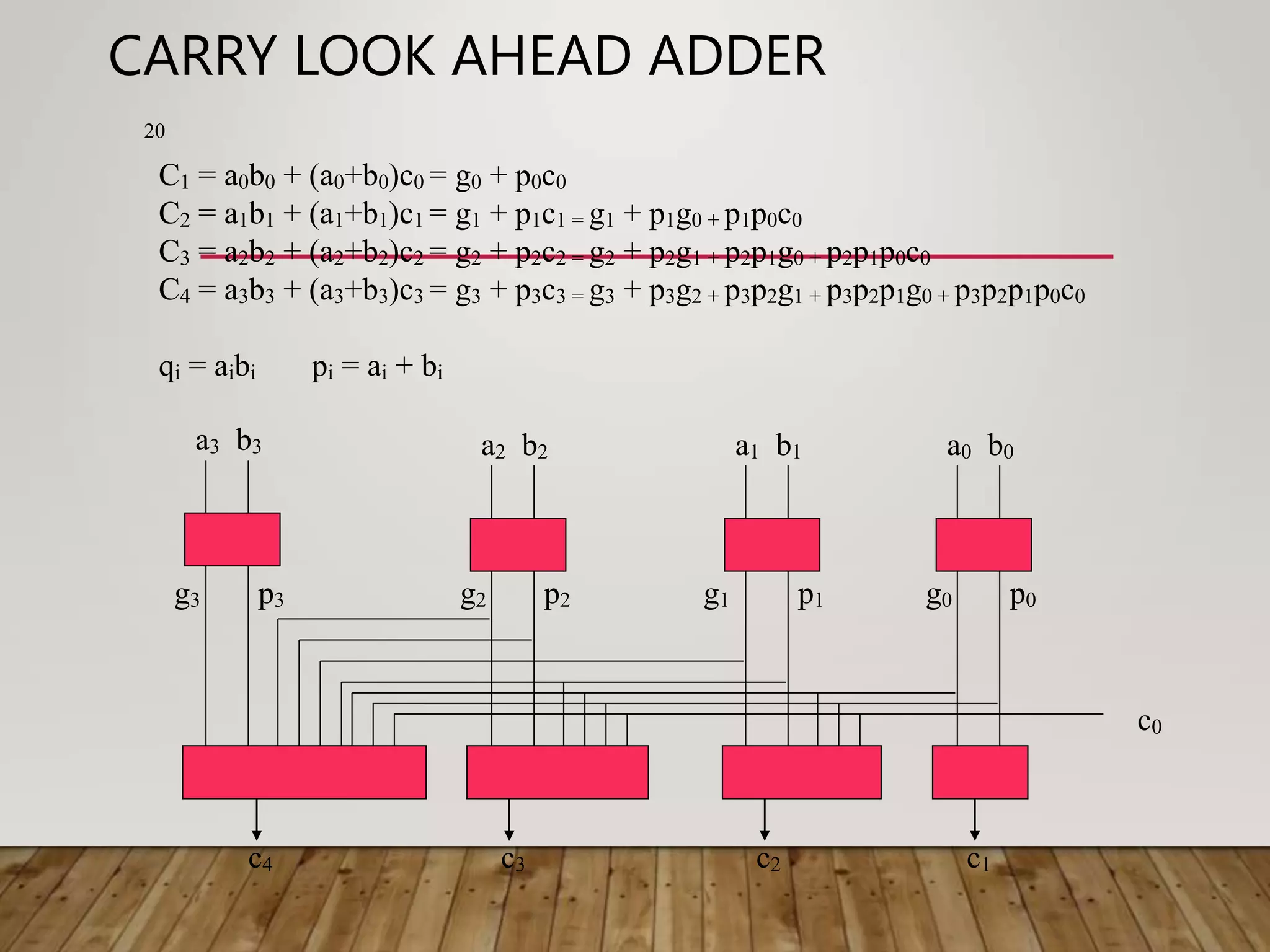

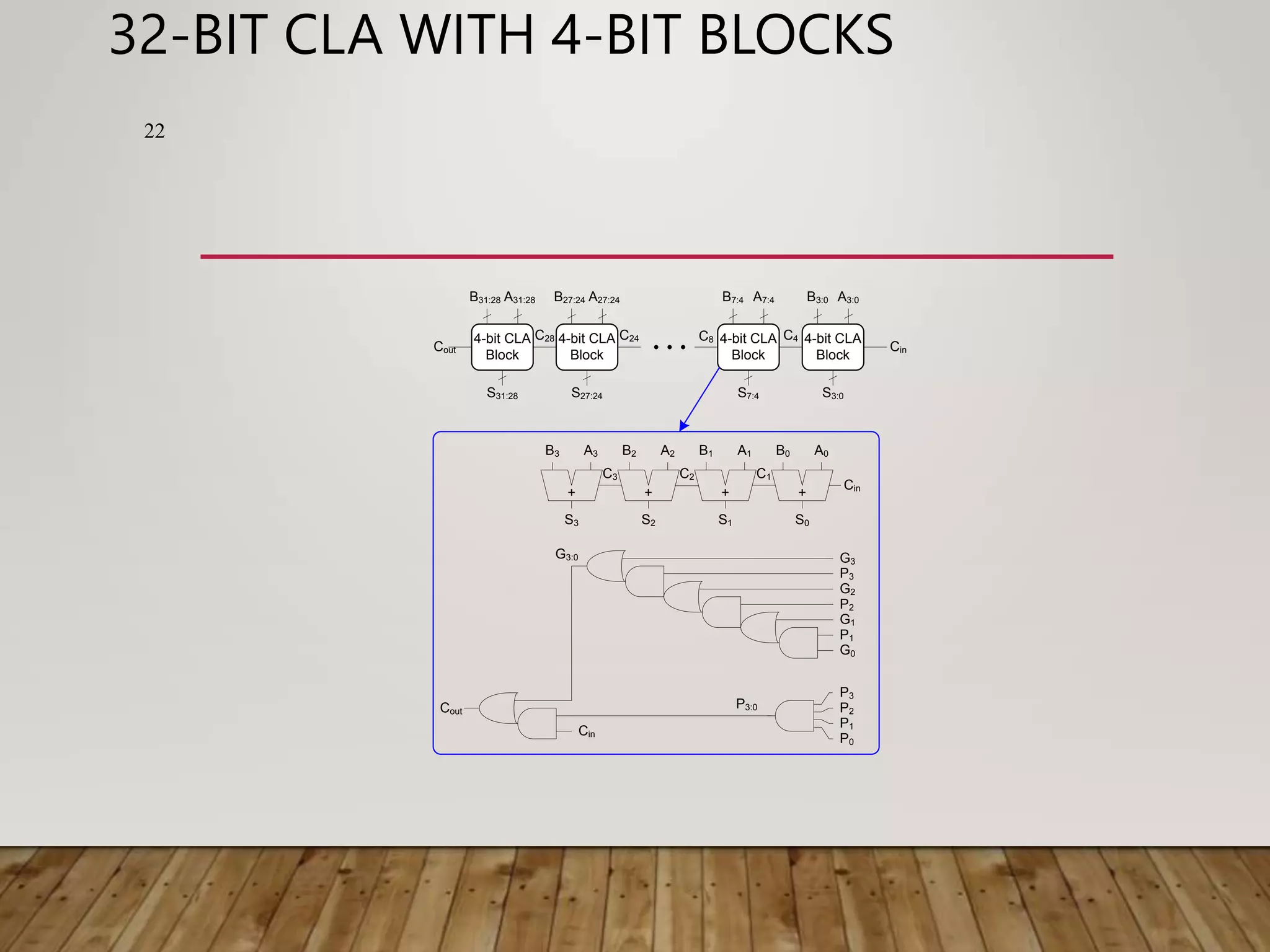




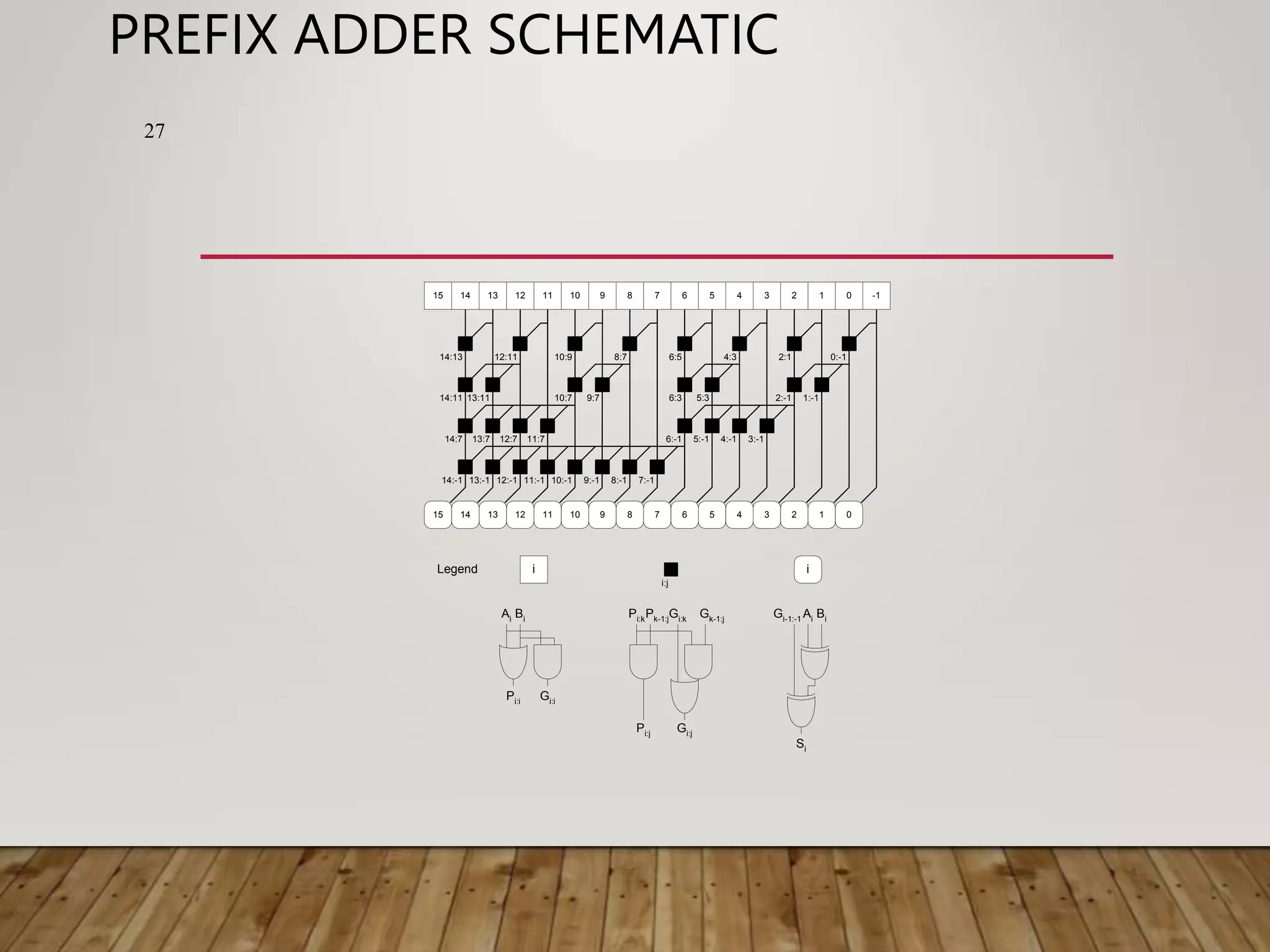


![ADDER DELAY COMPARISONS 30 • Compare the delay of 32-bit ripple-carry, carry- lookahead, and prefix adders. The carry-lookahead adder has 4-bit blocks. Assume that each two-input gate delay is 100 ps and the full adder delay is 300 ps. tripple = NtFA = 32(300 ps) = 9.6 ns tCLA = tpg + tpg_block + (N/k – 1)tAND_OR + ktFA = [100 + 600 + (7)200 + 4(300)] ps = 3.3 ns tPA = tpg + log2N(tpg_prefix ) + tXOR = [100 + log232(200) + 100] ps = 1.2 ns](https://image.slidesharecdn.com/binaryadderdesigncoa-230522141048-75deaab0/75/Binary-Adder-Design-COA-ppt-30-2048.jpg)
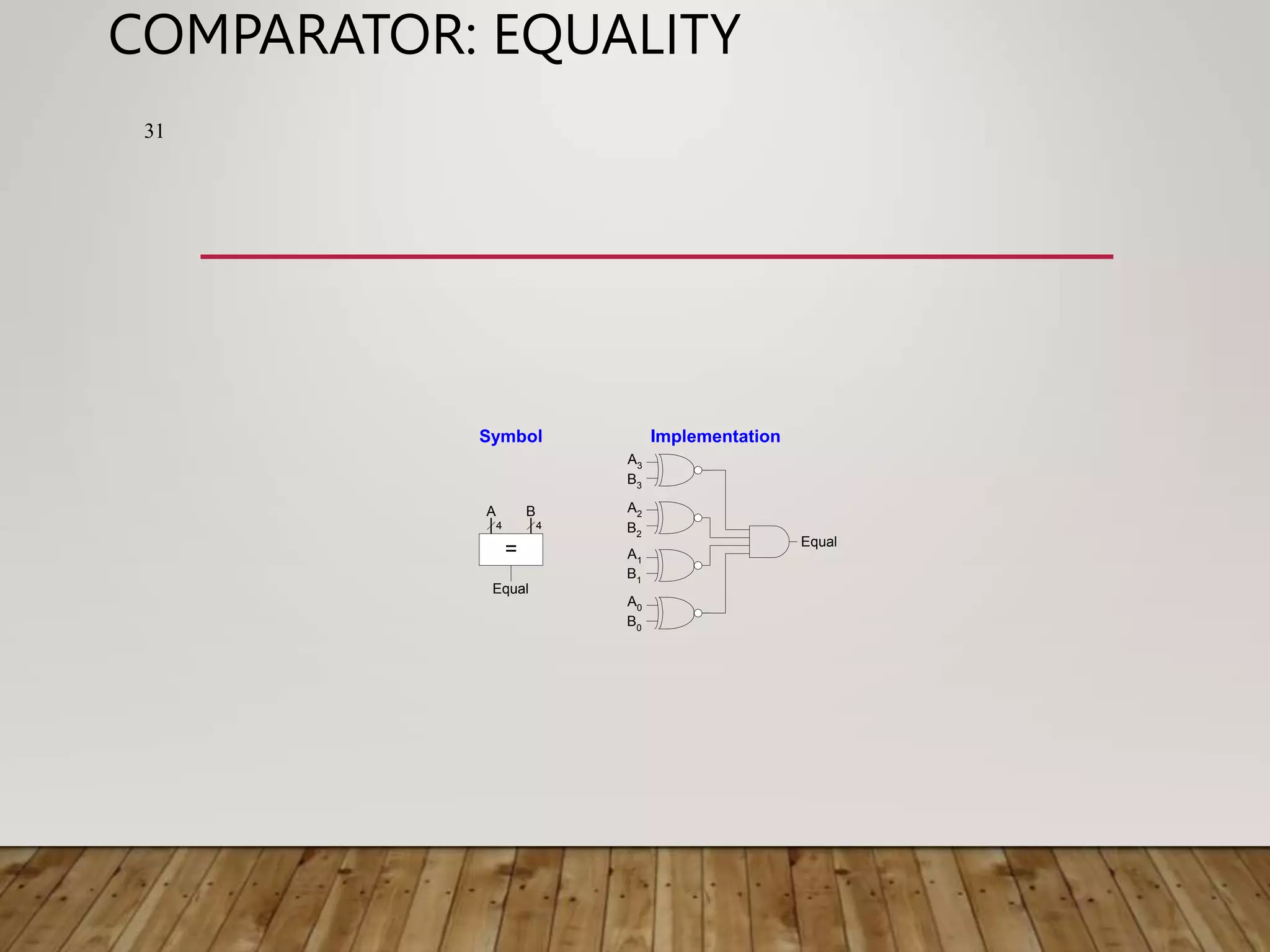
![COMPARATOR: LESS THAN A < B - B A [N-1] N N N 32 • For unsigned numbers](https://image.slidesharecdn.com/binaryadderdesigncoa-230522141048-75deaab0/75/Binary-Adder-Design-COA-ppt-32-2048.jpg)

![ALU DESIGN + 2 0 1 A B Cout Y 3 0 1 F2 F1:0 [N-1] S N N N N N N N N N 2 Zero Extend F2:0 Function 000 A & B 001 A | B 010 A + B 011 not used 100 A & ~B 101 A | ~B 110 A - B 111 SLT 34](https://image.slidesharecdn.com/binaryadderdesigncoa-230522141048-75deaab0/75/Binary-Adder-Design-COA-ppt-34-2048.jpg)
![SET LESS THAN (SLT) EXAMPLE + 2 0 1 A B Cout Y 3 0 1 F2 F1:0 [N-1] S N N N N N N N N N 2 Zero Extend 35 • Configure a 32-bit ALU for the set if less than (SLT) operation. Suppose A = 25 and B = 32.](https://image.slidesharecdn.com/binaryadderdesigncoa-230522141048-75deaab0/75/Binary-Adder-Design-COA-ppt-35-2048.jpg)
![SET LESS THAN (SLT) EXAMPLE + 2 0 1 A B Cout Y 3 0 1 F2 F1:0 [N-1] S N N N N N N N N N 2 Zero Extend 36 • Configure a 32-bit ALU for the set if less than (SLT) operation. Suppose A = 25 and B = 32. – A is less than B, so we expect Y to be the 32-bit representation of 1 (0x00000001). – For SLT, F2:0 = 111. – F2 = 1 configures the adder unit as a subtracter. So 25 - 32 = -7. – The two’s complement representation of -7 has a 1 in the most significant bit, so S31 = 1. – With F1:0 = 11, the final multiplexer selects Y = S31 (zero extended) = 0x00000001.](https://image.slidesharecdn.com/binaryadderdesigncoa-230522141048-75deaab0/75/Binary-Adder-Design-COA-ppt-36-2048.jpg)