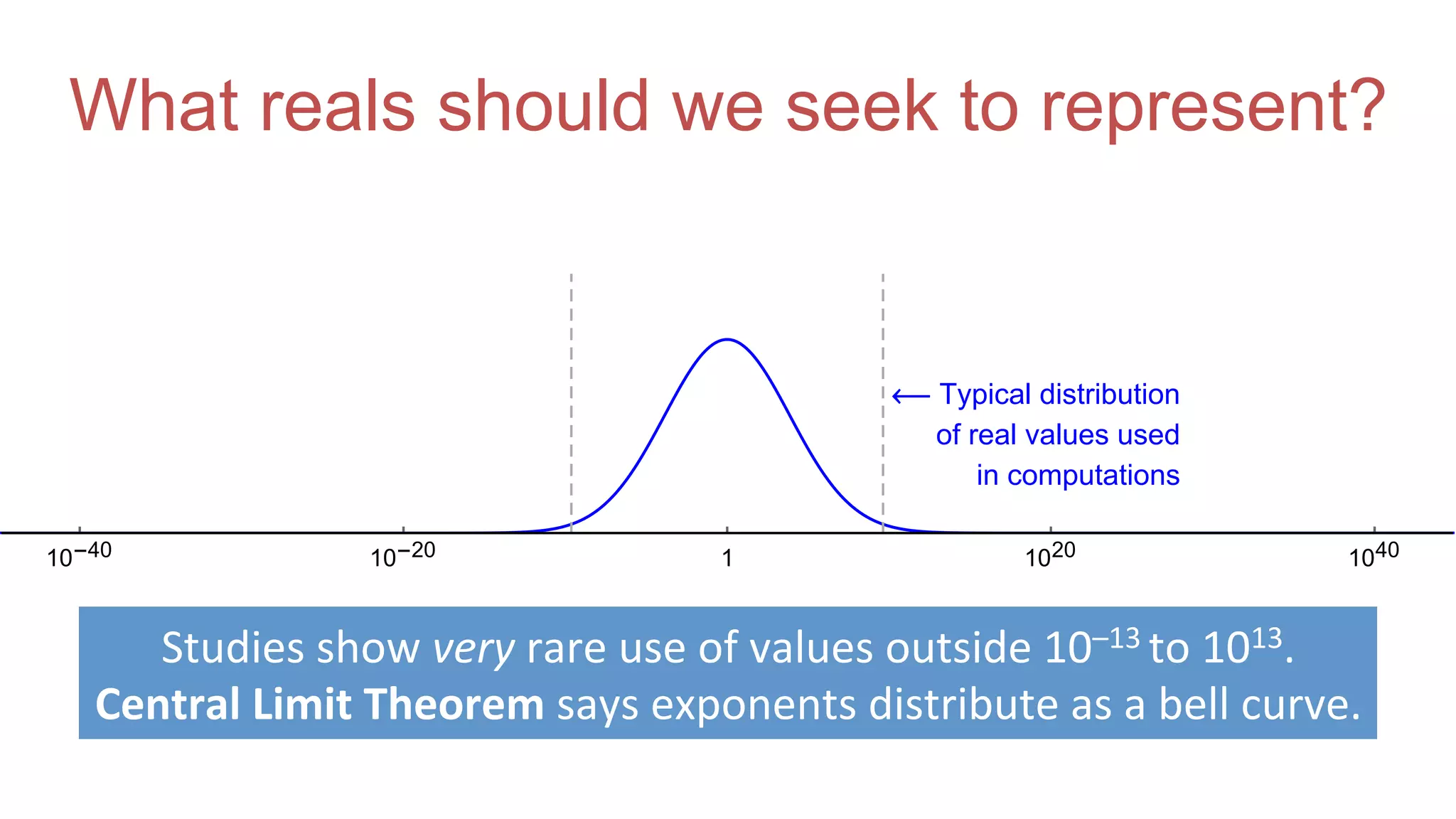
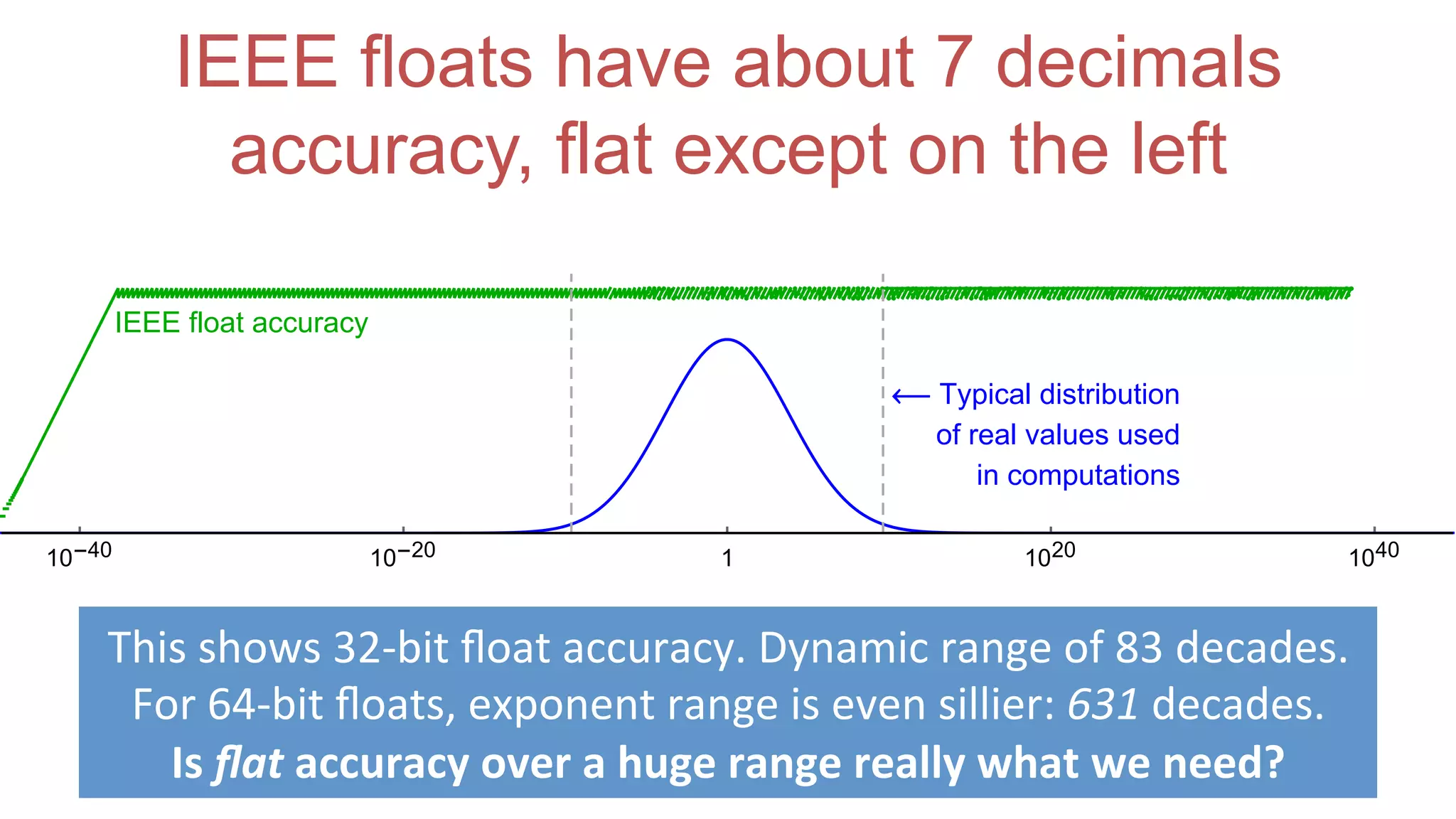
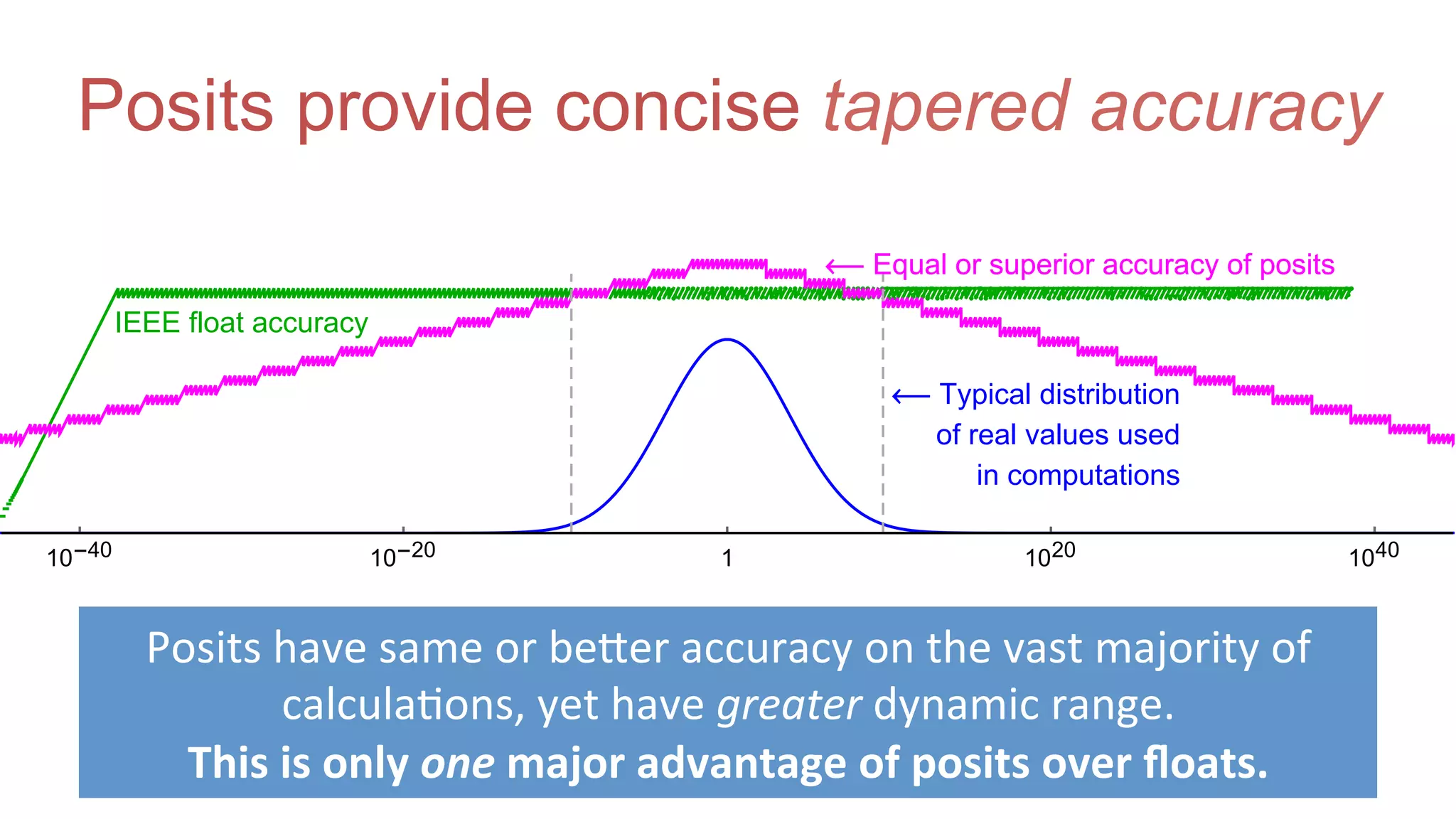
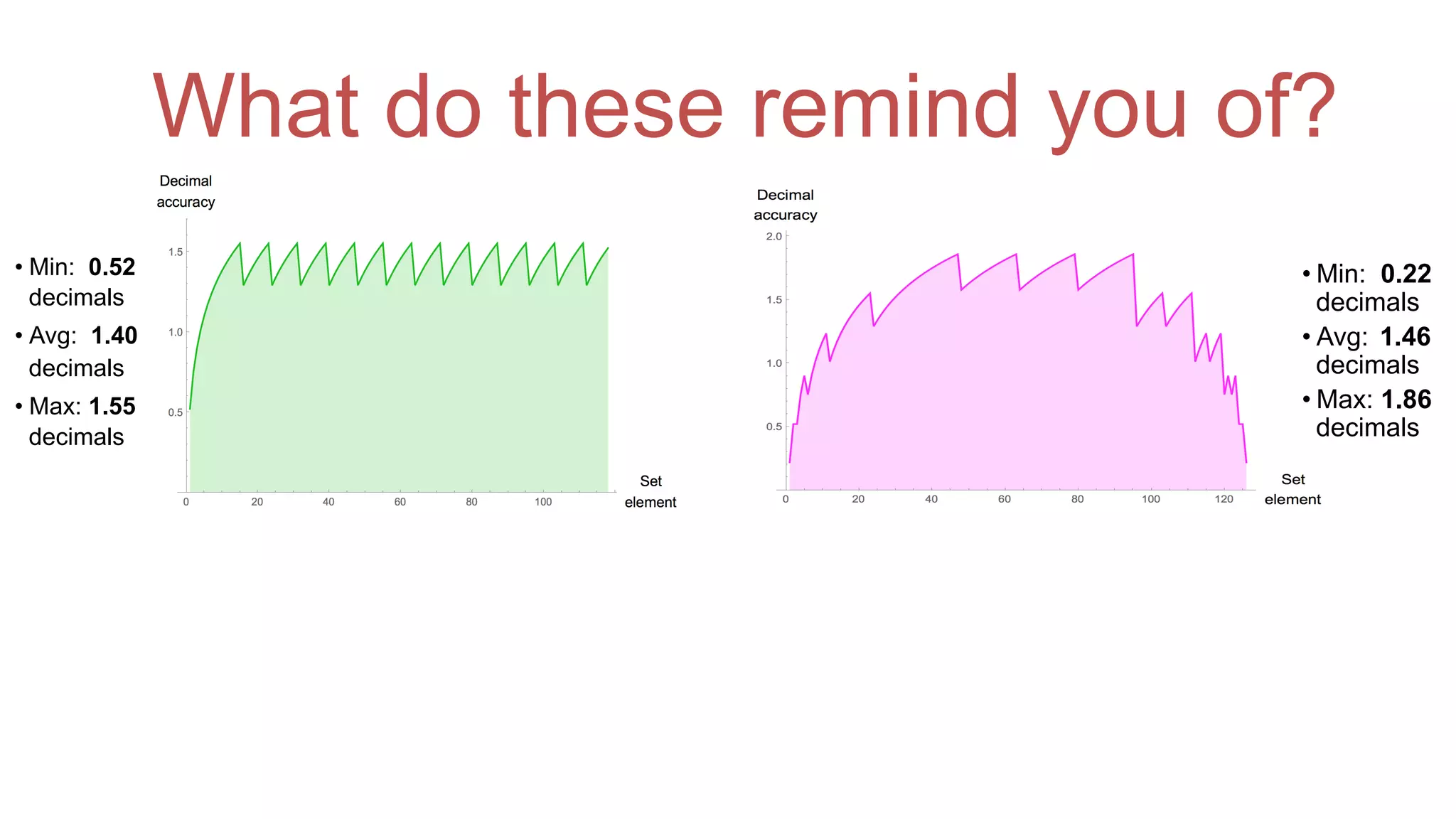
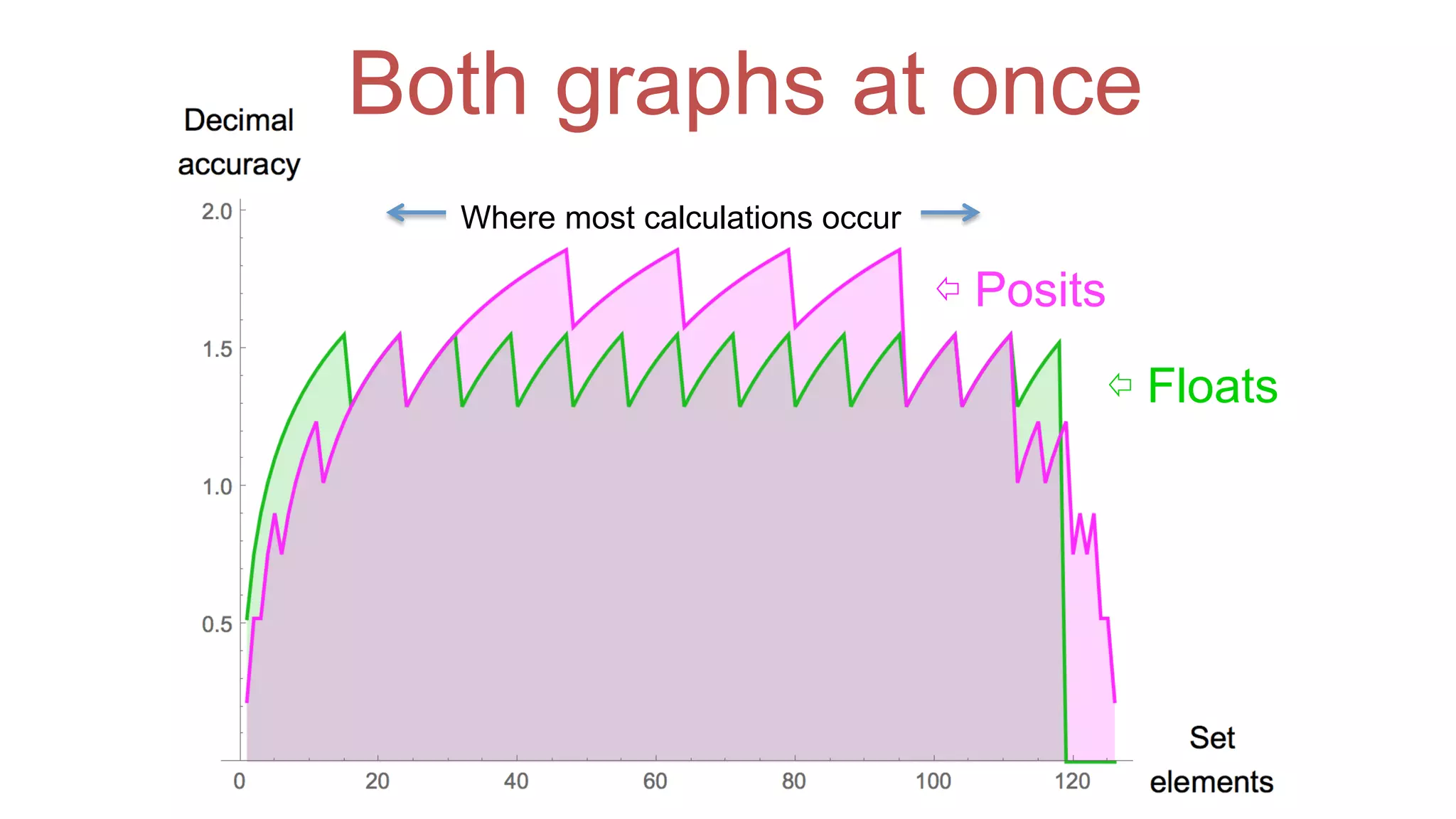
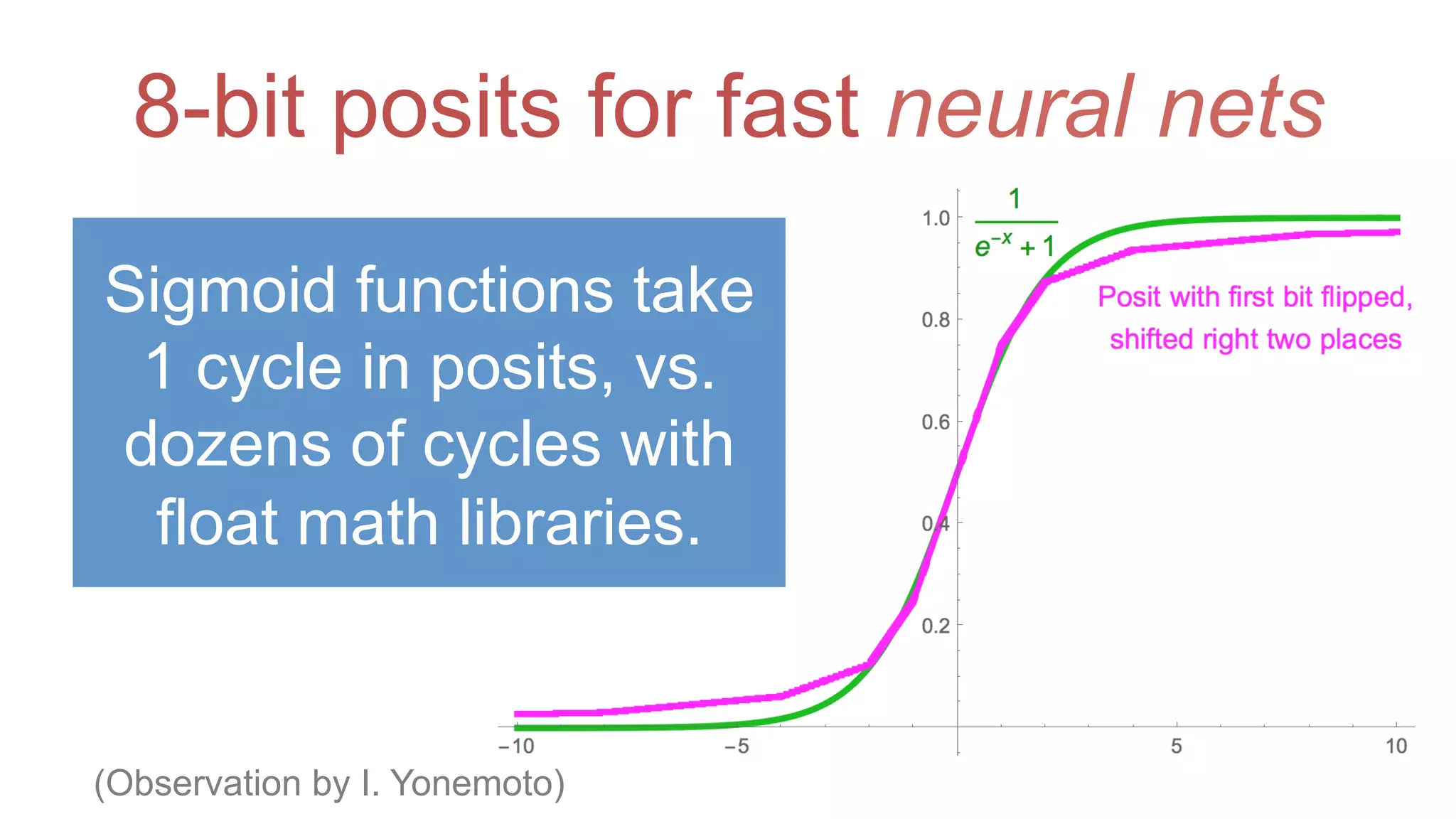
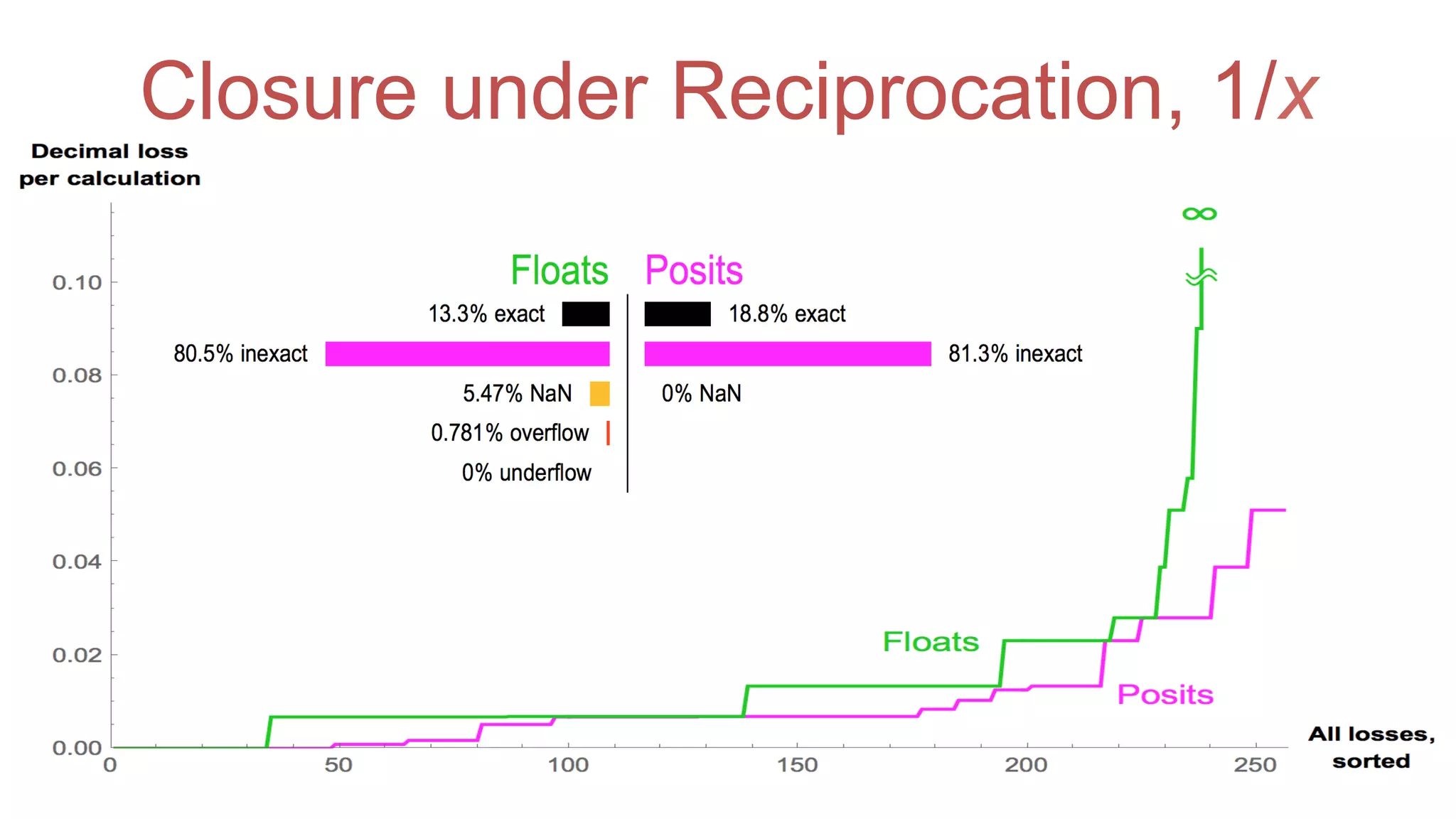
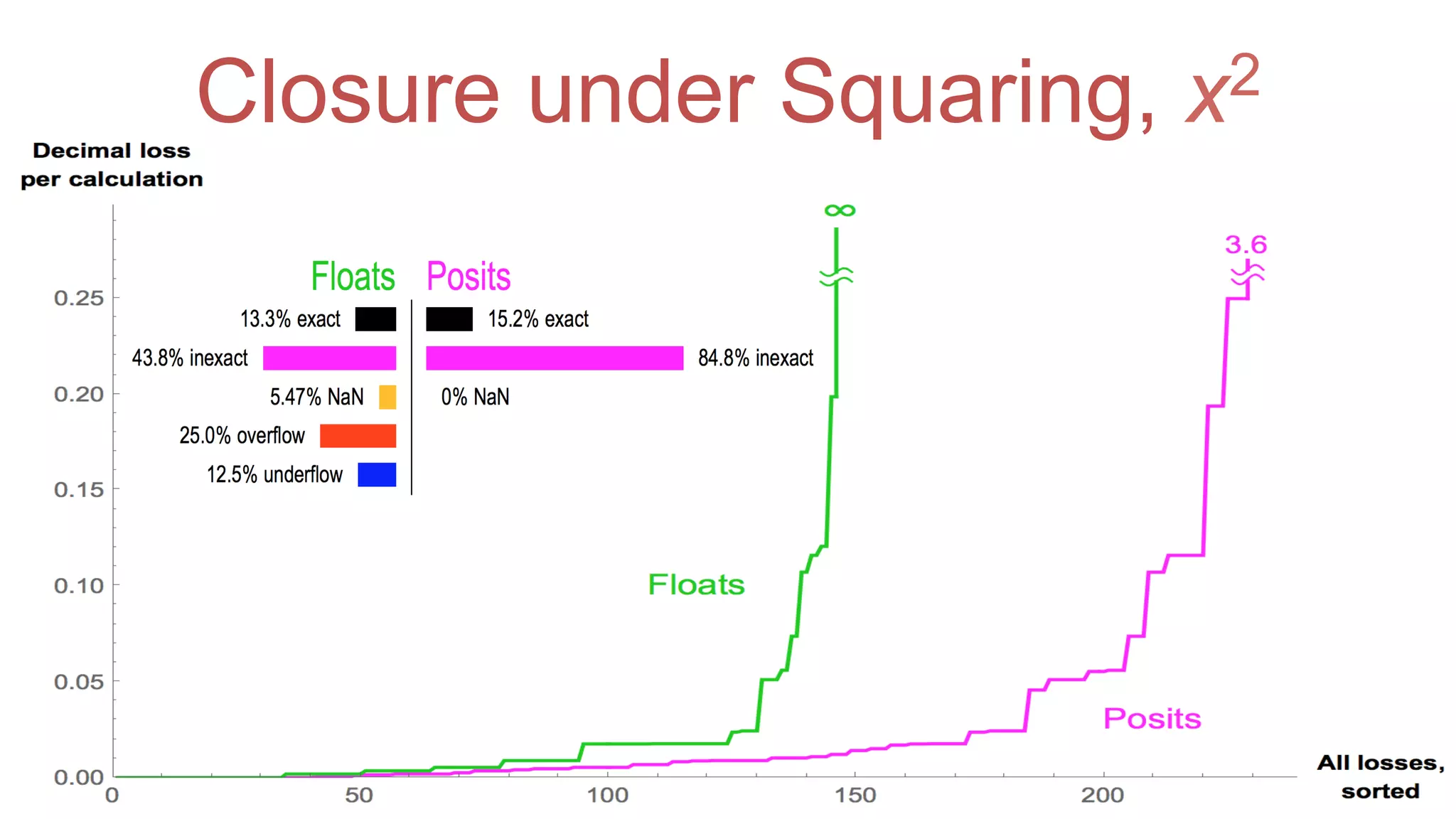
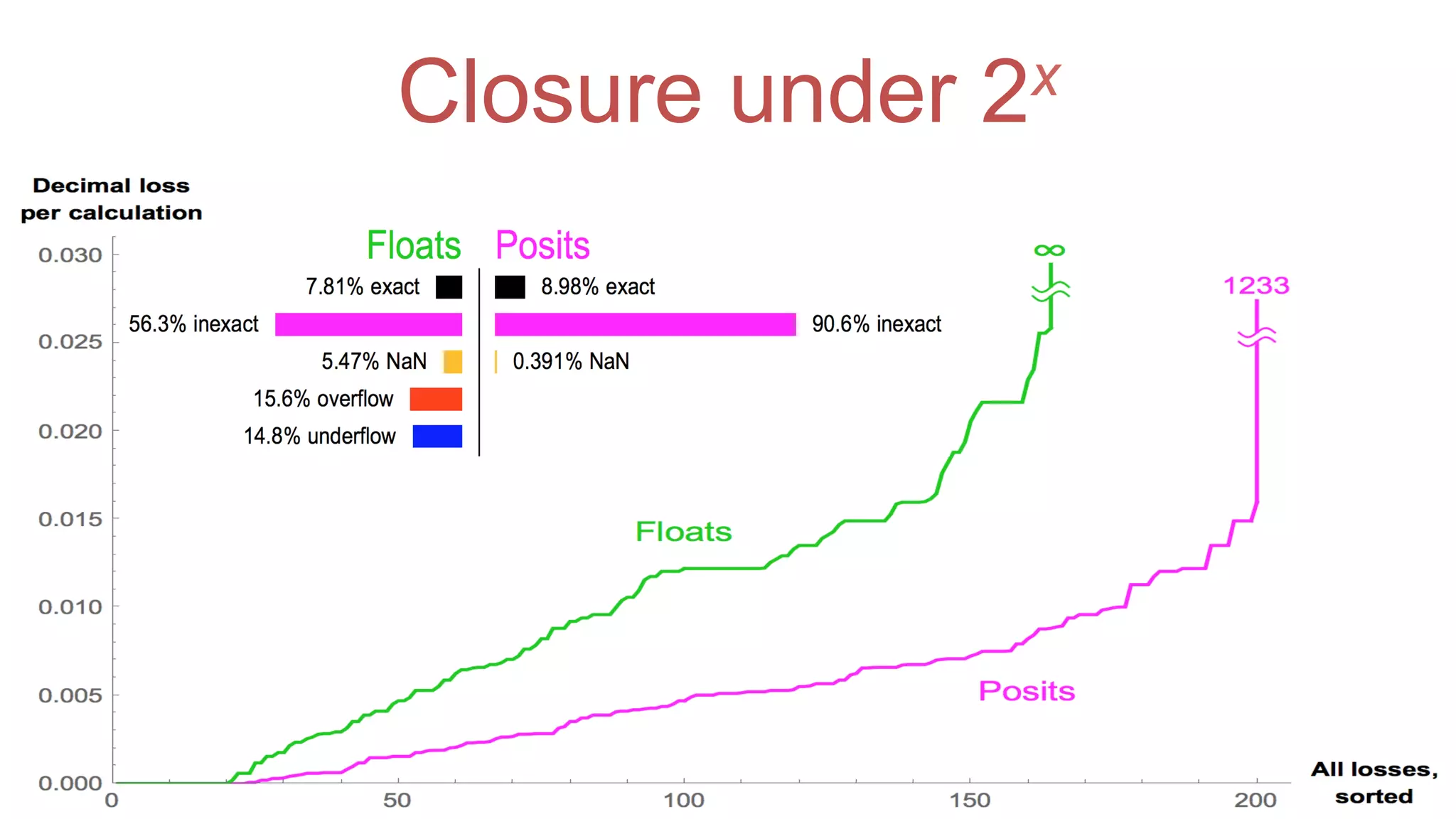
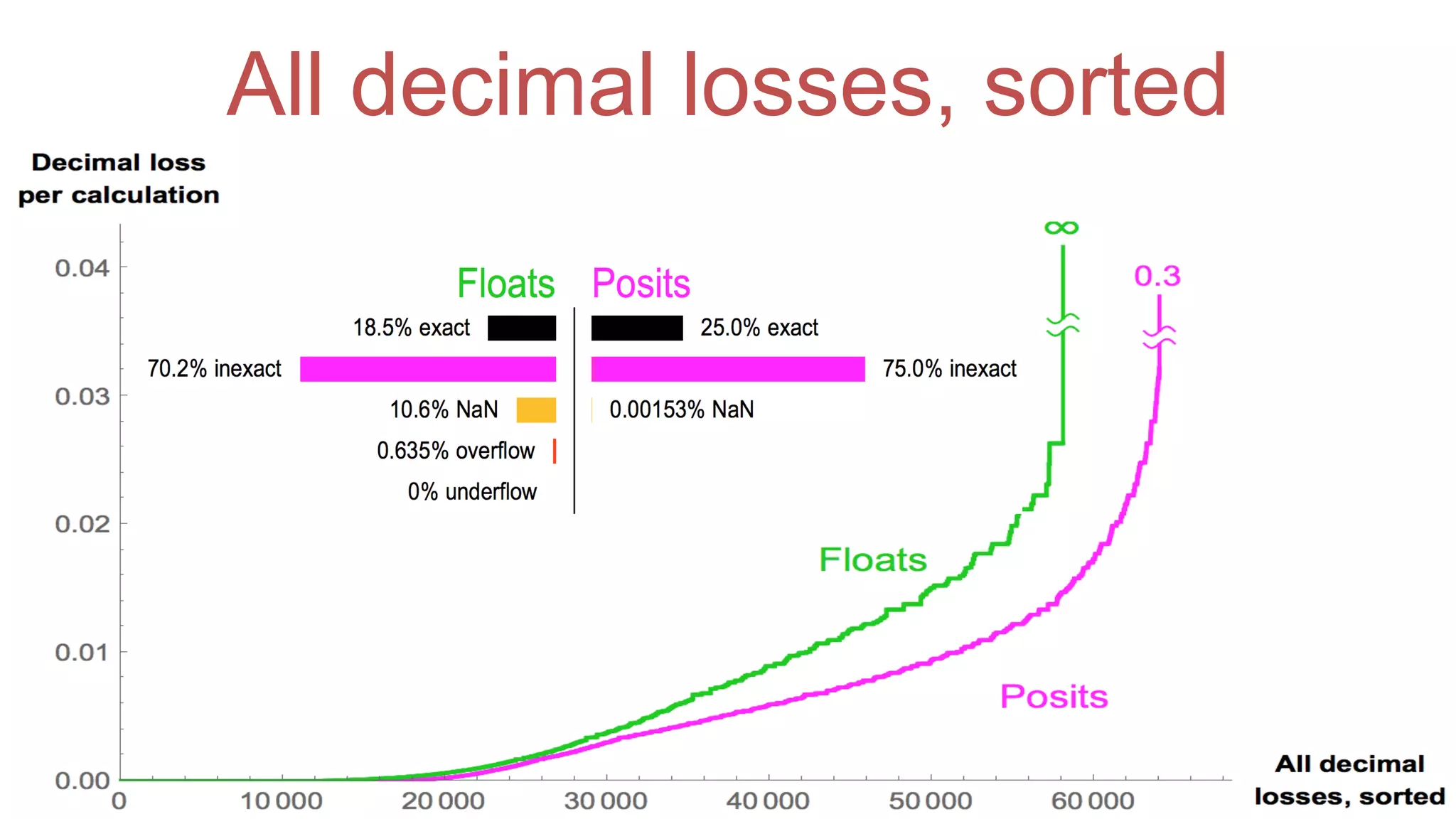
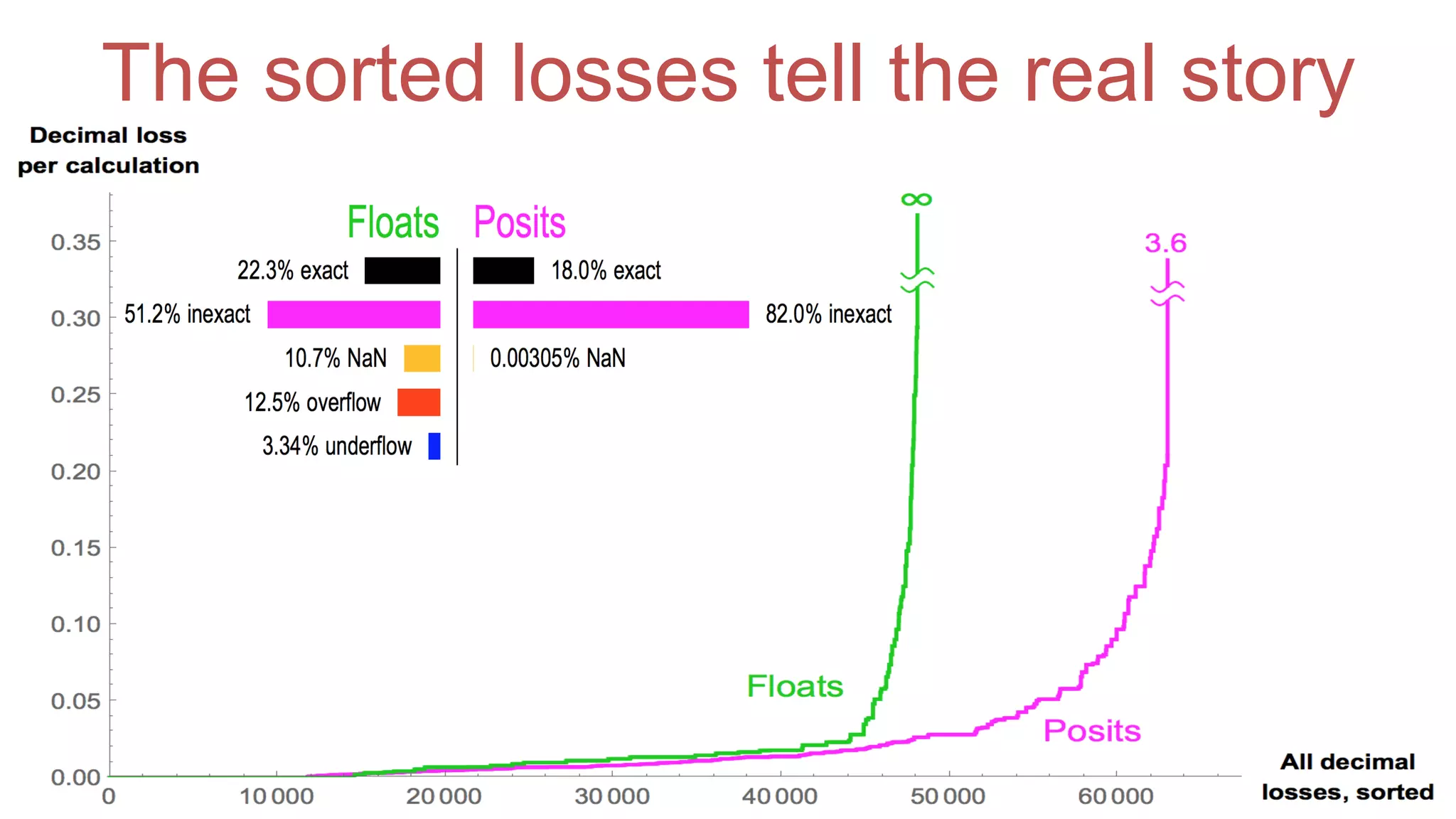
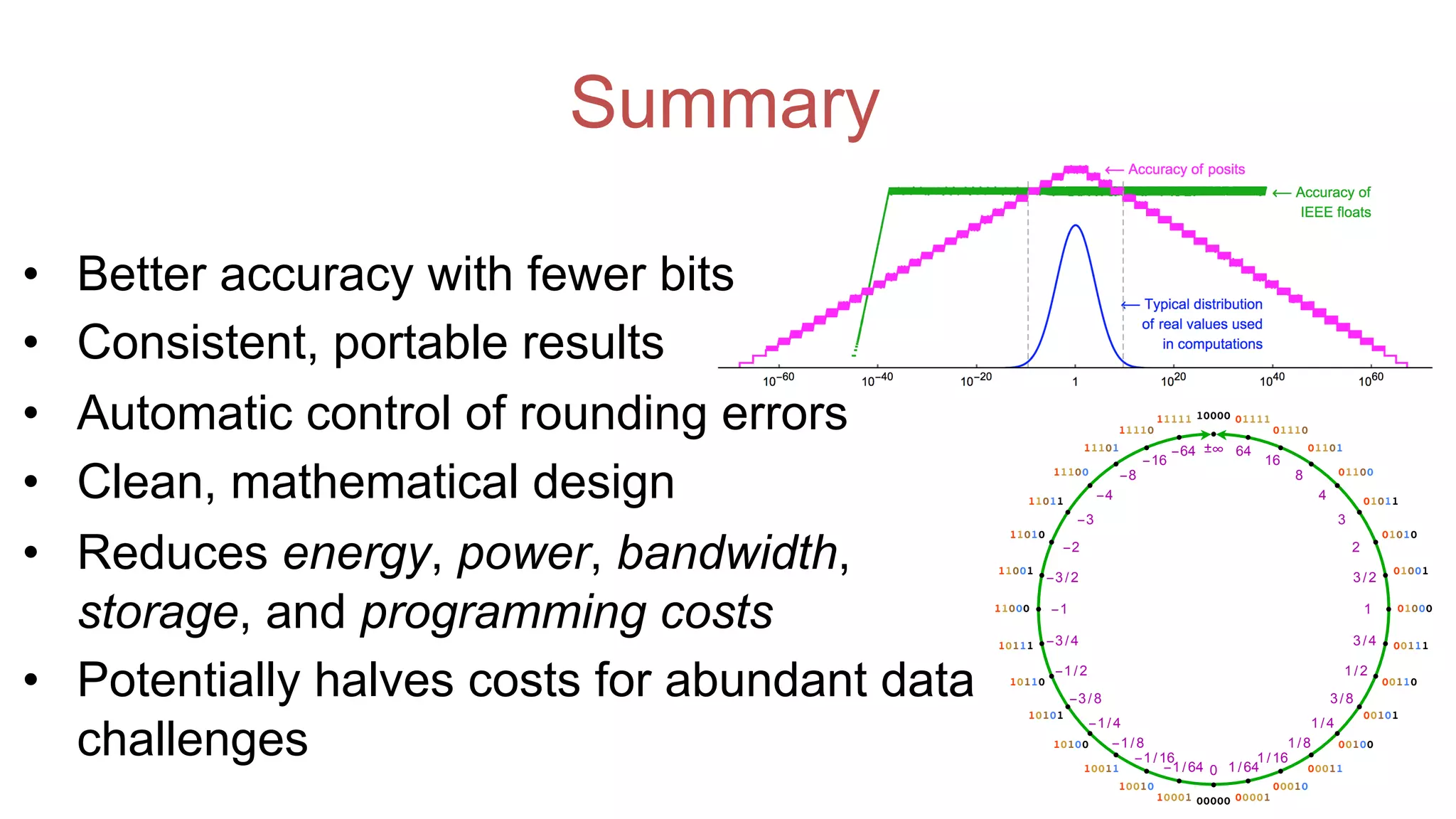
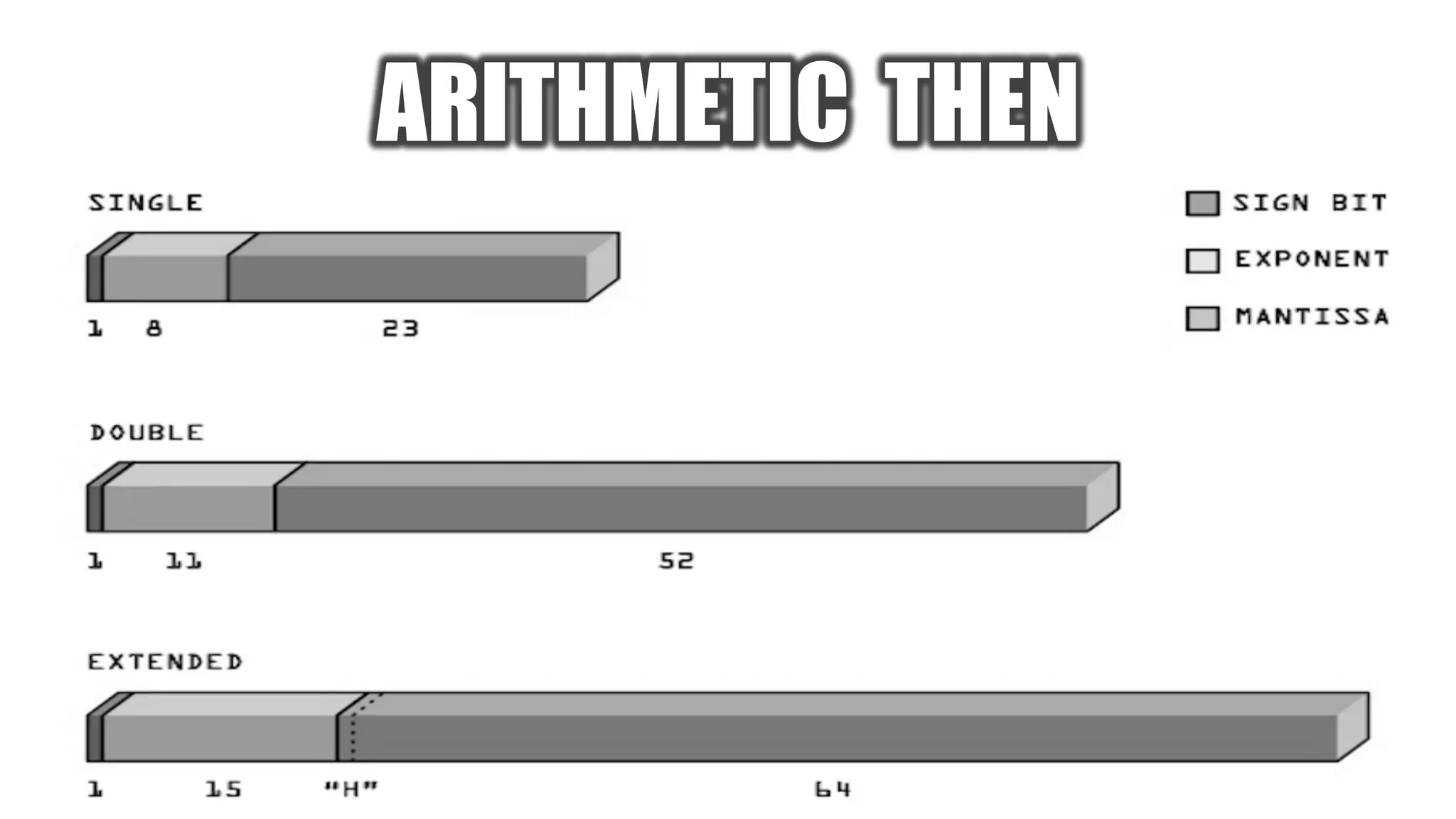
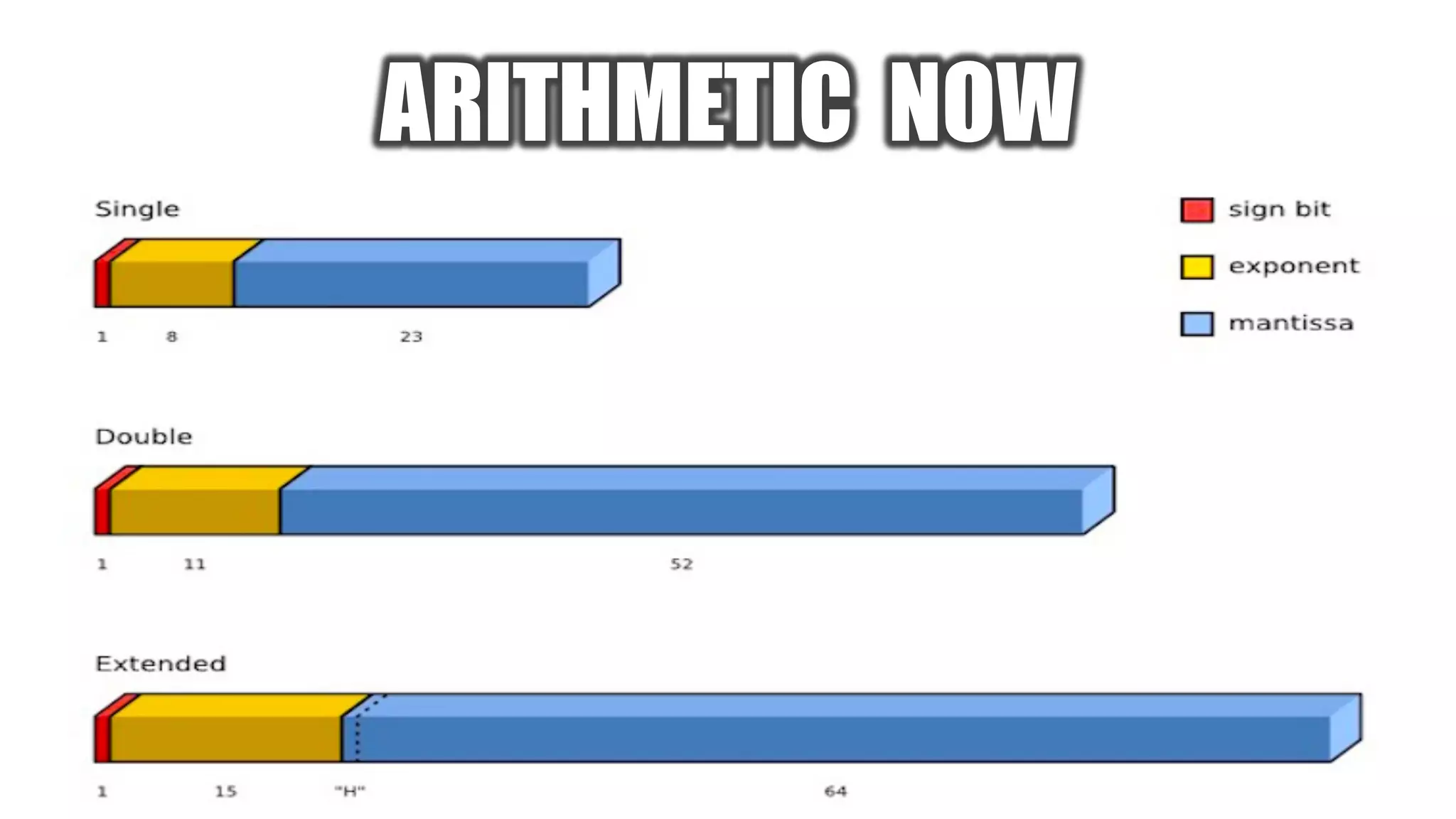
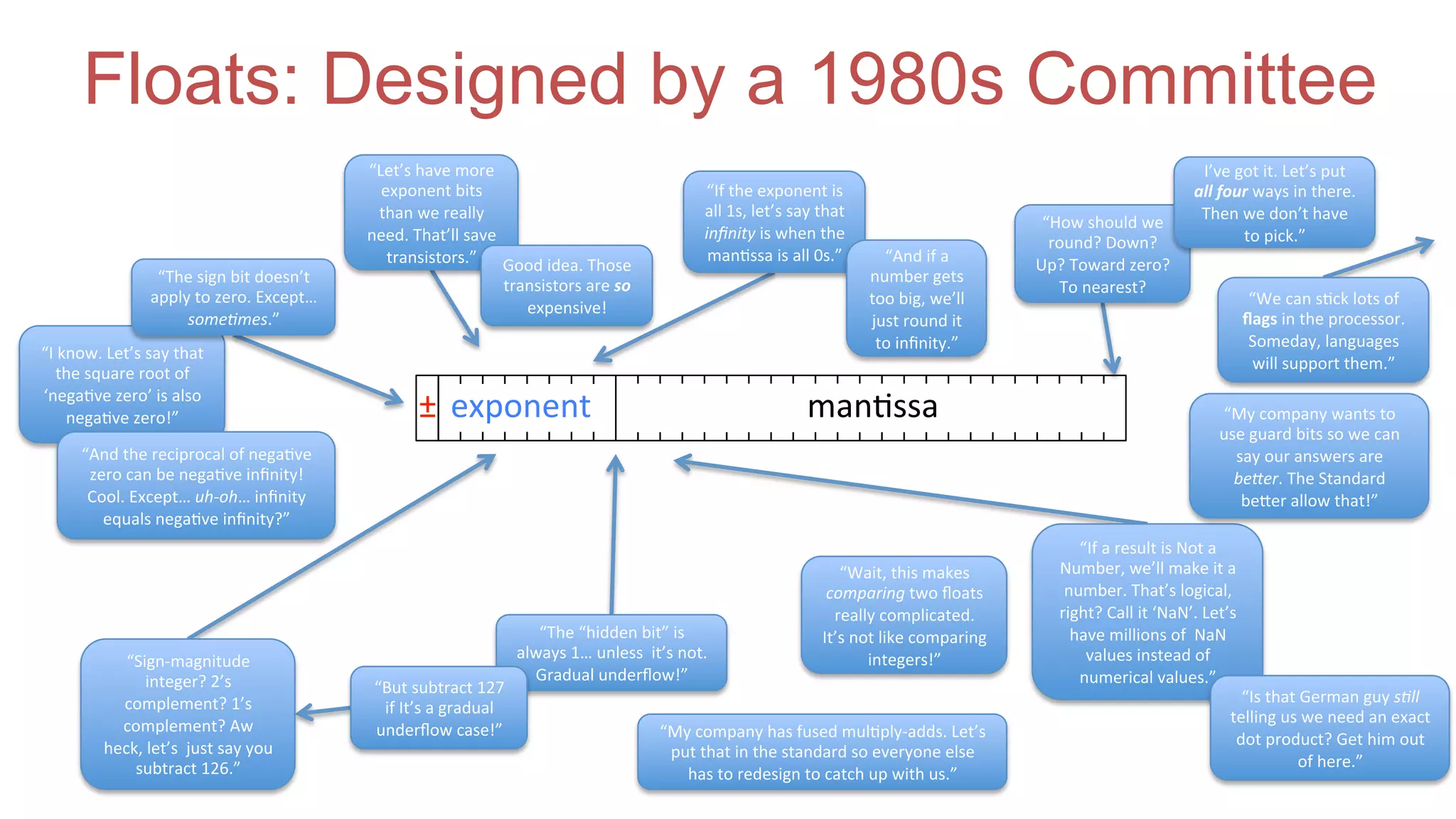
The document discusses posit arithmetic as a superior alternative to traditional floating-point systems, highlighting its benefits such as enhanced accuracy, reduced error rates, and efficient use of memory. It critiques IEEE floating-point standards for their lack of reproducibility, precision issues, and inefficiencies in calculations. The author emphasizes that posits can achieve better accuracy with fewer bits, making them more suitable for modern computational needs, particularly in big data and neural network applications.












![Contrasting Calculation “Esthetics” IEEE Standard (1985) Floats, f = n × 2m m, n are integers Intervals [f1, f2], all x such that f1 ≤ x ≤ f2 Rounded: cheap, uncertain, “good enough” Rigorous: more work, certain, mathematical If you mix the two esthetics, you end up satisfying neither. “I need the hardware to protect me from NaN and overflow in my code.” “Really? And do you keep debugger mode turned on in your produc+on sodware?”](https://image.slidesharecdn.com/beatingfloats-170804153150/75/Beating-Floating-Point-at-its-Own-Game-Posit-Arithmetic-16-2048.jpg)