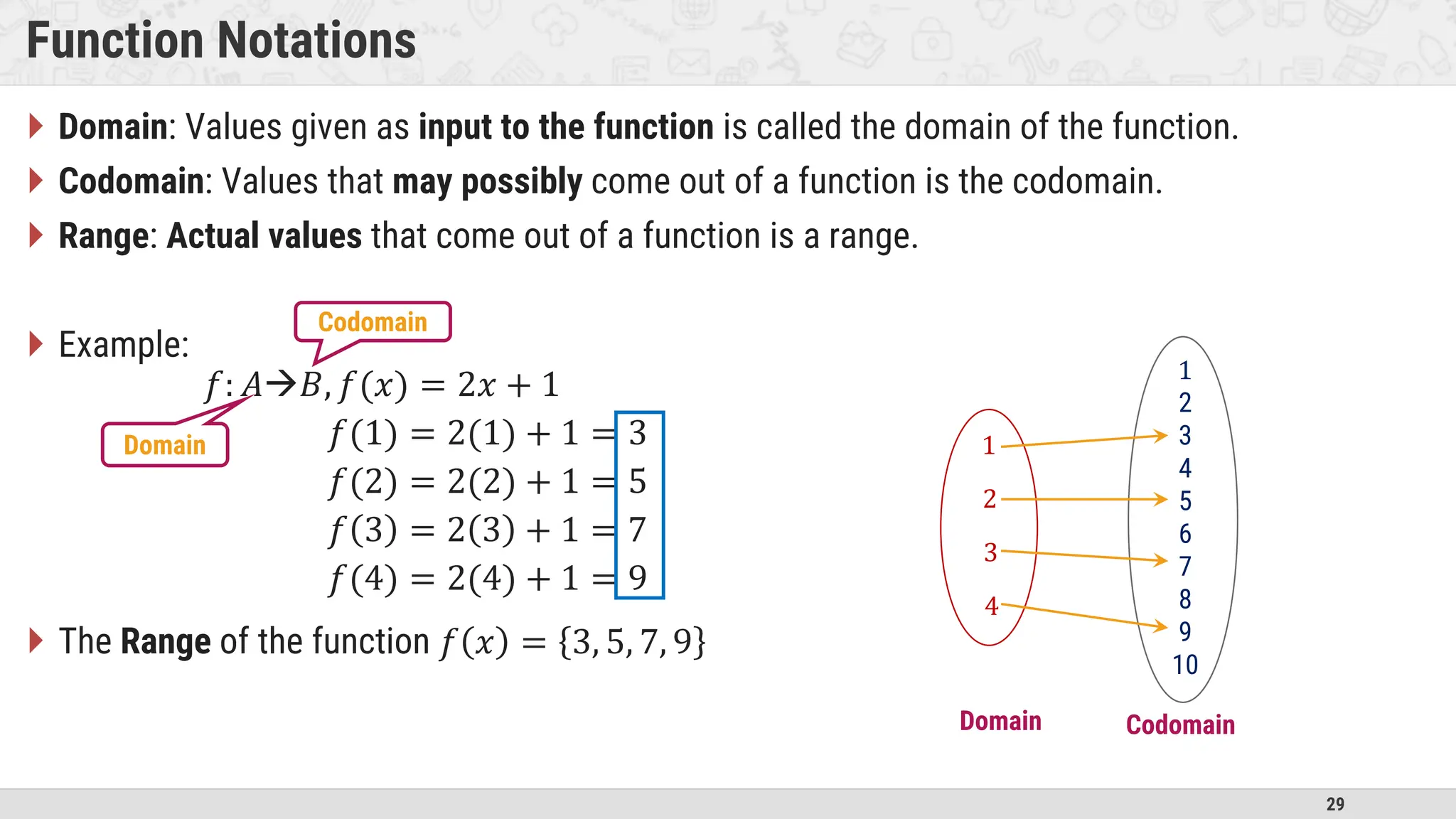
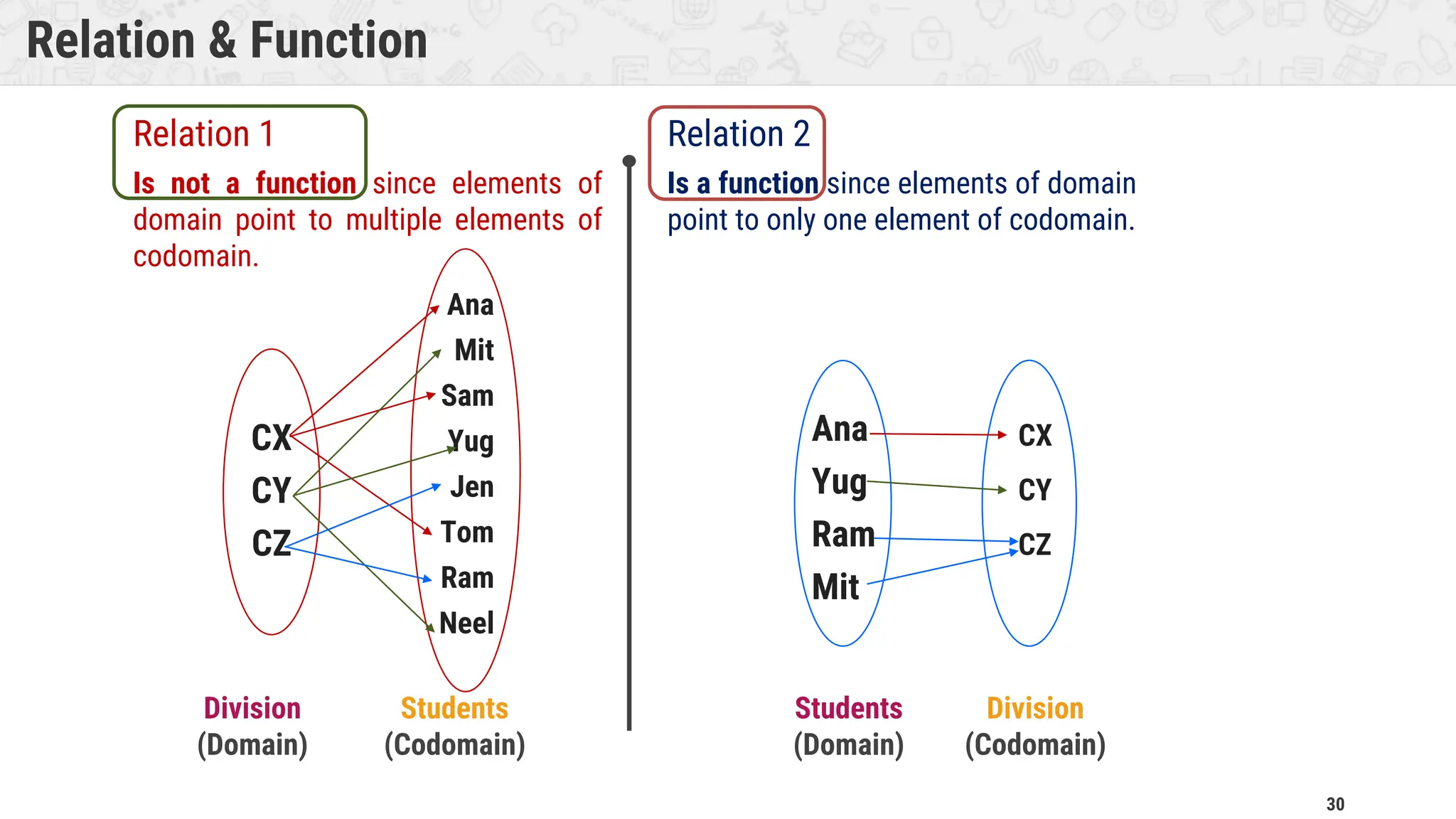
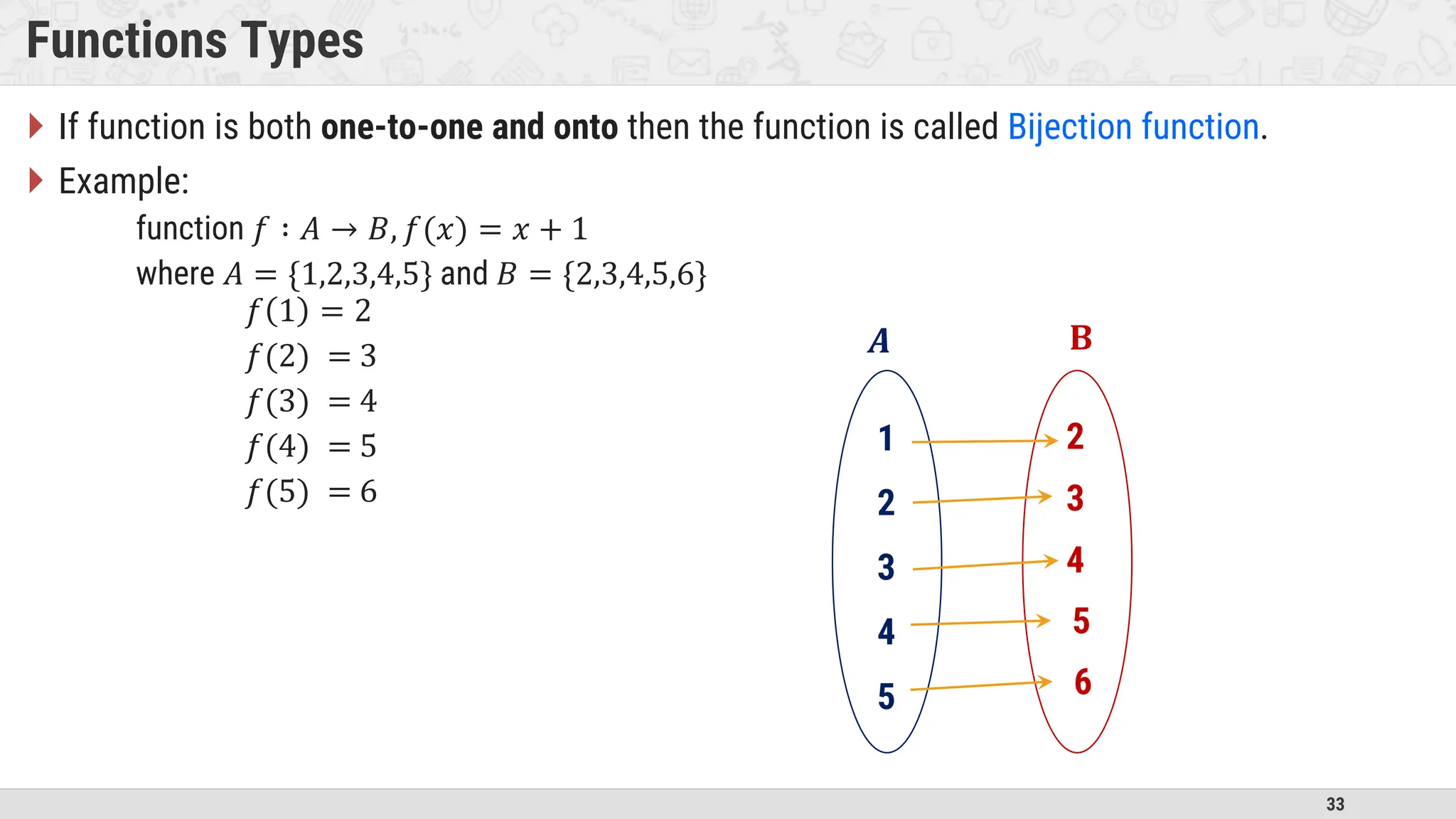
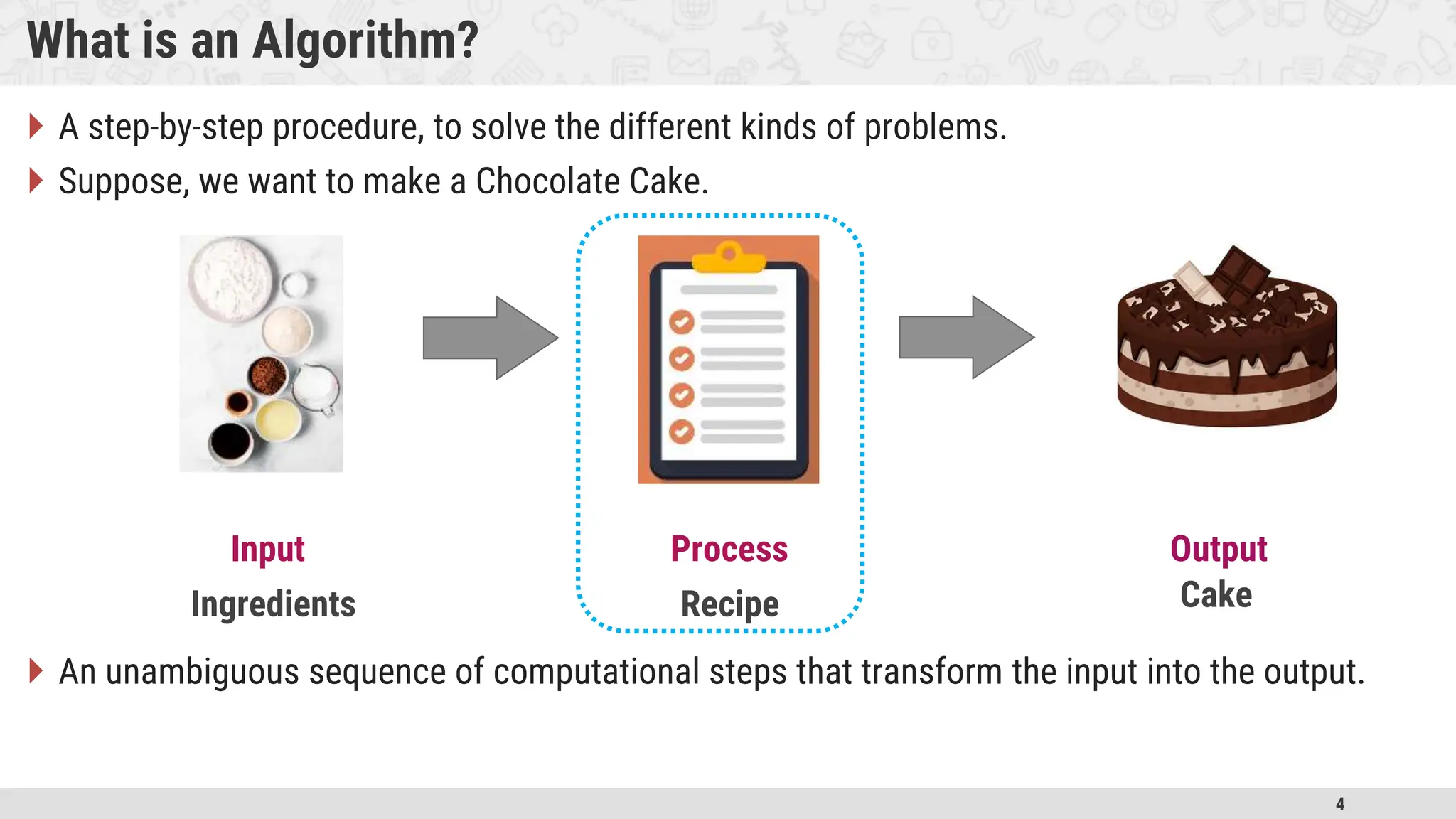
An algorithm is a step-by-step procedure to solve problems. It must be unambiguous, finite, and precisely defined. The document discusses types of algorithms and methods for multiplication. It also covers basics of set theory including sets, subsets, operations, relations, and equivalence relations. Key concepts like functions, vectors, and matrices are introduced for understanding algorithms and mathematics.






















![24 Properties of the Relation Reflexive: Let 𝐴 be a set, and let 𝑅 be a binary relation on 𝐴. Relation 𝑅 is reflexive if, Example 1 A = {1, 2} and R1 = {(a, b) | a ≤ b} so, R1 = 1,1 , 1,2 , 2,2 B = 1,2,3 , and R2 = {(1,1), (1,2), (2,1), (2,2), (3,1)} Example 2 Reflexive Not Reflexive since (𝟑, 𝟑) ∉ 𝐑𝟐 ∀𝒙: [(𝒙 ∈ 𝑨) → ((𝒙, 𝒙) ∈ 𝑹)]](https://image.slidesharecdn.com/3161605unit-11662-240401064636-a4e3c368/75/BASIC-OF-ALGORITHM-AND-MATHEMATICS-STUDENTS-24-2048.jpg)
![25 Properties of the Relation Symmetric: A relation 𝑅 on a set 𝐴 is called symmetric if (𝑦, 𝑥) ∈ 𝑅 whenever (𝑥, 𝑦) ∈ 𝑅, for some 𝑥, 𝑦 ∈ 𝐴. Example 1 A = {1,2,3} and R1 = {(a, b)|a ≠ b} R1 = {(1,2), (1,3), (2,1), (2,3), (3,1), (3,2)} B = { 1, 2, 3} and R2 = {(a, b) | a ≤ b} So, R2 = {(1,1), (1,2), (1,3), (2,2), (2,3), (3,3)} Example 2 Symmetric Asymmetric ∀𝒙: ∀𝒚: [((𝒙, 𝒚) ∈ 𝑹) → ((𝒚, 𝒙) ∈ 𝑹)]](https://image.slidesharecdn.com/3161605unit-11662-240401064636-a4e3c368/75/BASIC-OF-ALGORITHM-AND-MATHEMATICS-STUDENTS-25-2048.jpg)
![26 Properties of the Relation Transitive: A relation 𝑅 on a set 𝐴, is called transitive if whenever (𝑥, 𝑦) ∈ 𝑅 and (𝑦, 𝑧) ∈ 𝑅, then (𝑥, 𝑧) ∈ 𝑅, for 𝑥, 𝑦, 𝑧 ∈ 𝐴. Example 1 A = { 1, 2, 3} and R1 = {(a, b) | a ≤ b} So, R1 = {(1,1), (1,2), (1,3), (2,2), (2,3), (3,3)} B = 1, 2, 3,4 and R2 = a, b | 𝑤ℎ𝑒𝑟𝑒 𝑏 𝑖𝑠 𝑎 𝑠𝑢𝑐𝑐𝑒𝑠𝑠𝑜𝑟 𝑜𝑓 𝑎 So, R2 = { 1,2 , 2,3 , (3,4)} Example 2 Transitive ∀𝒙: ∀𝒚: ∀𝒛[([(𝒙, 𝒚) ∈ 𝑹] ∧ [(𝒚, 𝒛) ∈ 𝑹] → ((𝒙, 𝒛) ∈ 𝑹)] Not Transitive](https://image.slidesharecdn.com/3161605unit-11662-240401064636-a4e3c368/75/BASIC-OF-ALGORITHM-AND-MATHEMATICS-STUDENTS-26-2048.jpg)