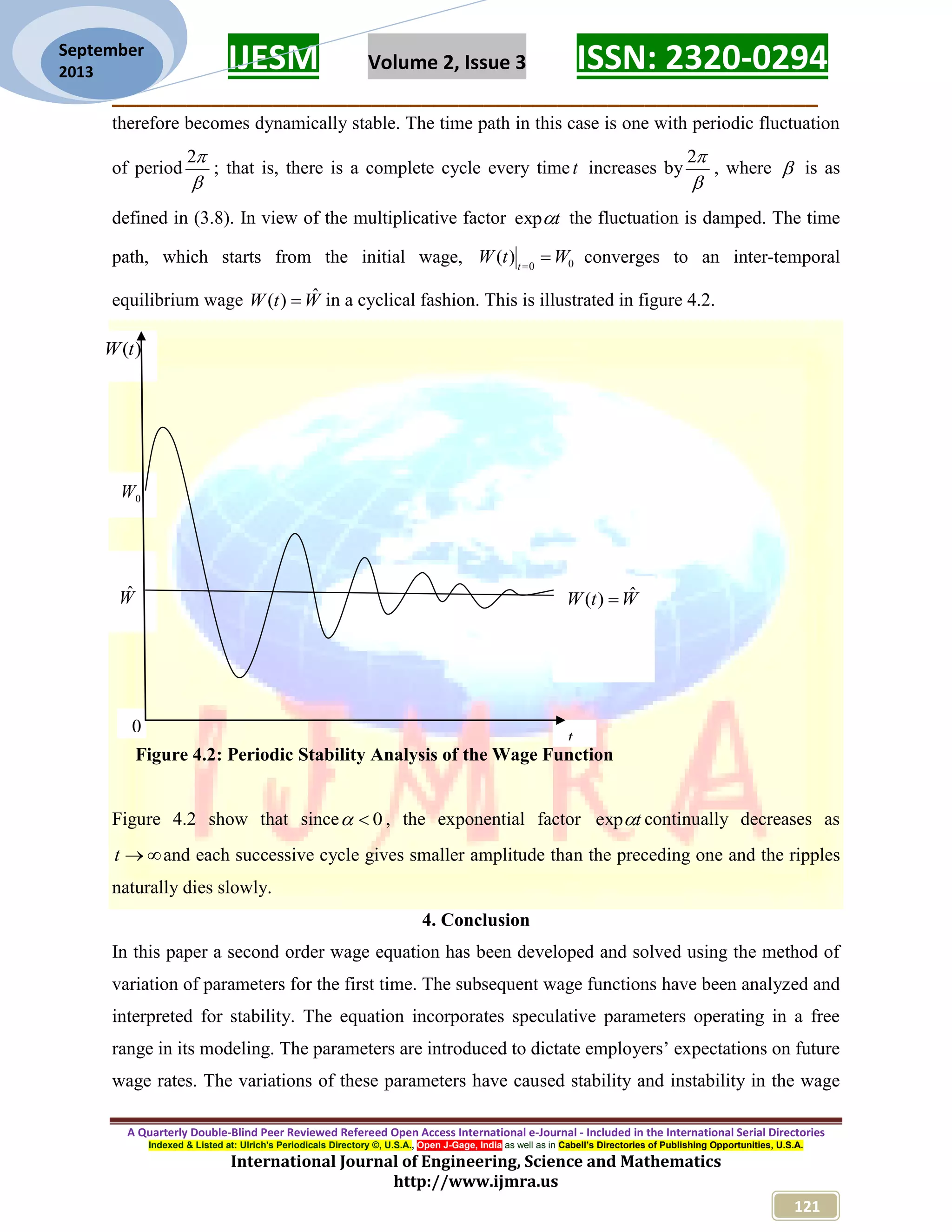
The document presents a mathematical model utilizing the method of variation of parameters to develop and analyze the stability of a second-order wage equation. It explores how various parameters affect the wage function's stability and asserts the necessity of government intervention in wage regulation to mitigate volatility. Overall, the study underscores the relationship between wage dynamics and market forces, alongside proposing an equilibrium-based approach to wage management.

![IJESM Volume 2, Issue 3 ISSN: 2320-0294 _________________________________________________________ A Quarterly Double-Blind Peer Reviewed Refereed Open Access International e-Journal - Included in the International Serial Directories Indexed & Listed at: Ulrich's Periodicals Directory ©, U.S.A., Open J-Gage, India as well as in Cabell’s Directories of Publishing Opportunities, U.S.A. International Journal of Engineering, Science and Mathematics http://www.ijmra.us 108 September 2013 1. Introduction Wages mean the reward for labor services. In [6] wage is defined as a fixed regular payment earned for work or services, typically paid on a daily or weekly basis. In [9] wage is viewed as payment for labour services to a worker, especially remuneration on an hourly, daily, weekly or by piece. It also views wage as a portion of national product that represents aggregate paid for all contributing labour and services as distinguished from the portion retained by management or reinvested in capital goods. In [10] wage is defined according to wages act of 1986. It is the sum payable to an employee by an employer in connection with that employment. It includes fees, bonuses, commissions, holiday pay or other emolument relevant to the employment whether specified in the contract of employment or not. In this paper, we consider modeling a second order differential wage equation. For example, considering deterministic price adjustment model in [7] fixed supply and demand functions at instantaneous price for security is discussed. It is argued that at equilibrium asset price, quantity demanded equals quantity supplied. This is discussed using fixed demand and supply curves while price is kept constant. It also asserts that away from the equilibrium, excess demand for security raises its price, and excess supply lowers its price. In this situation, it is argued that the sign for rate of change of price with respect to time depends on the sign of excess demand. If the demand and supply functions are made linear at constant equilibrium price, deterministic model of price adjustment is realized with respective sensitivities. In the analysis of the solution of the deterministic model, it was observed that in the long run asset price settles at a constant steady state where no further change can occur. In [4] a natural decay equation is developed. The equation describes a phenomenon where a quantity gradually decreases to zero. In the work, it is emphasized that convergence depends the sign of the proportionality parameter. If the proportionality parameter is negative then it turns into a growth equation but if it is positive, it stabilizes in the long run. In the study of slope fields for autonomous equations qualitative properties of decay equation is demonstrated. It was found that the solution could be positive, negative or zero. In all the three cases, the solution approaches zero in limit as time approaches infinity.](https://image.slidesharecdn.com/11ijmra-3923-170816113426/75/APPLICATION-OF-THE-METHOD-OF-VARIATION-OF-PARAMETERS-MATHEMATICAL-MODEL-FOR-DEVELOPING-AND-ANALYZING-STABILITY-OF-THE-WAGE-FUNCTION-2-2048.jpg)
![IJESM Volume 2, Issue 3 ISSN: 2320-0294 _________________________________________________________ A Quarterly Double-Blind Peer Reviewed Refereed Open Access International e-Journal - Included in the International Serial Directories Indexed & Listed at: Ulrich's Periodicals Directory ©, U.S.A., Open J-Gage, India as well as in Cabell’s Directories of Publishing Opportunities, U.S.A. International Journal of Engineering, Science and Mathematics http://www.ijmra.us 109 September 2013 In [1], dynamics of market prices are studied. It was found out that if the initial price function lies off the equilibrium point, in the long run stability will be realized at the equilibrium position. It also brings out clear case by case analysis of the solution of second order price equation by introducing unrestricted parameters that brings speculations in behavior of buyers and sellers. The author argued that depending on the signs of these parameters, buyers will cut or increase their purchases. Similarly, sellers will cut or increase their supplies. It was also noted that depending on signs of parameters, price function stabilizes in the long run. In [2], equilibrium solutions about a special class of static solutions are discussed. The study found that if a system starts exactly at equilibrium position, then it remains there forever. The study further found that in real systems, small disturbances often a rise which moves a system away from equilibrium state. Such disturbances, regardless of their origin give rise to initial conditions which do not coincide with equilibrium condition. If the system is not at equilibrium point, then some of its derivatives will be non zero and the system therefore exhibits a dynamic behavior, which can be monitored by watching orbits in its phase space. The resistance-inductance electric current circuit for constant electromotive force is modeled into a differential equation in [3].The stability of the solution is studied in the long run and is found to be a constant, which is the ratio of constant electromotive force to resistance. It was also found that if electromotive force is periodic, in the long run, current executes harmonic oscillations. In this case, steady state solution is the periodic part of the solution. The resistance-capacitor electric current circuit equation is also discussed for constant electromotive force. The solution was an exponential function, which converges to zero in the long run. Also, in resistance- inductance-capacitance series circuit, a second order equation was developed. Its solution consists of an exponential homogeneous part and a periodic integral part. The study found out that the homogeneous part converges to zero as time approaches infinity, while the periodic part exhibits practically harmonic oscillations. The literature is silent and it is worthwhile developing a second order wage equation, solve it and discuss its stability. The solutions of linear second order ordinary differential equations are presented in [5; 8] using the method of variation of parameters.](https://image.slidesharecdn.com/11ijmra-3923-170816113426/75/APPLICATION-OF-THE-METHOD-OF-VARIATION-OF-PARAMETERS-MATHEMATICAL-MODEL-FOR-DEVELOPING-AND-ANALYZING-STABILITY-OF-THE-WAGE-FUNCTION-3-2048.jpg)