An efficient image compression algorithm using dct biorthogonal wavelet transform with arithmetic coding

An efficient image compression algorithm using dct biorthogonal wavelet transform with arithmetic coding

• 1.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 _______________________________________________________________________________________ Volume: 04 Issue: 02 | Feb-2015, Available @ http://www.ijret.org 94 AN EFFICIENT IMAGE COMPRESSION ALGORITHM USING DCT- BIORTHOGONAL WAVELET TRANSFORM WITH ARITHMETIC CODING Priyatosh Halder1 1 Radar Section, Air Force Jodhpur, Rajasthan, India Abstract Recently the digital imaging applications is increasing significantly and it leads the requirement of effective image compression techniques. Image compression removes the redundant information from an image. By using it we can able to store only the necessary information which helps to reduce the transmission bandwidth, transmission time and storage size of image. This paper proposed a new image compression technique using DCT-Biorthogonal Wavelet Transform with arithmetic coding for improvement the visual quality of an image. It is a simple technique for getting better compression results. In this new algorithm firstly Biorthogonal wavelet transform is applied and then 2D DCT-Biorthogonal wavelet transform is applied on each block of the low frequency sub band. Finally, split all values from each transformed block and arithmetic coding is applied for image compression. Keywords: Arithmetic coding, Biorthogonal wavelet Transform, DCT, Image Compression. --------------------------------------------------------------------***---------------------------------------------------------------------- 1. INTRODUCTION Now a day, it is a great challenge to handle huge amount of data due to explosive growth of multimedia and internet technology. The data are in the various forms like graphics, image, audio etc. This brings the problem at transmission bandwidth, storage which leads the efficient compression. Since last few years increasing the efforts on the embedded wavelet coding algorithms [1-3]. Beside very good compression performance it can also reconstruct a reasonable good quality image. The image compression can be divided into two types: lossy and lossless image compression [4]. It is possible to recover the original image by lossless compression whereas losses of some amount of information occur in case of lossy compression. In many applications lossy compression is preferred since it provides large compression ratio [5]. Image compression can be obtained from the various types of transformation techniques like DCT [6], DFT, DWT etc. In traditional DCT based JPEG [7] compression system represents image as a superposition of cosine function of different discrete frequencies. The discrete cosine transform (DCT) is a popular compression scheme because it can able to give optimal performance and easily implemented with a reasonable cost. So it is used in several compression algorithms like JPEG for still images and MPEG [8] for moving images. Many attempts have been taken for improving the compression scheme [9, 10] by utilizing and identifying the features within the images. In any image compression algorithm there are three major steps: transform and quantization, modeling and ordering and finally entropy coding. In the transform step inter-pixel redundancy reduces and energy compaction occurs. To achieve better compression quantization, modeling and ordering are used. In the final stage the quantized outputs are sent to the entropy encoder. This step helps to generate bit stream which represent efficient quantized output. In my proposed method a new algorithm is investigated using modeling and ordering in wavelet domain [11]. It is seen that many attempts has been taken to design an efficient image coding techniques with which the geometry of edge singularities of image is exploited. Over the past few years, a number of image compression algorithms like EZW [12], EBCOT [9], JPEG 2000 [13], GW [14] and SPHIT [7] have introduced. This paper can be represented in the following ways that: in section II explains the review of literature. Section III describes the proposed method of DCT-Biorthogonal wavelet transform based image compression with arithmetic coding. The results and analysis are represented in section IV. Finally the section V contains the conclusion and future work. 2. LITERATURE REVIEW Ronald A. De Vore et al. in [15] explained a new image compression method based on wavelet decompositions. This theory relates a) the error between the original and compressed image the rate of decay occurs as the size of the compressed image representation increases b) in certain smoothness classes the smoothness of the image called Besov spaces. Within this theory, the error occurred by the quantization of wavelet transform coefficients is described. It is shown that wavelet-based methods are near optimal within a larger class of stable transform based, nonlinear methods of image compression possible if pictures can be
• 2.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 _______________________________________________________________________________________ Volume: 04 Issue: 02 | Feb-2015, Available @ http://www.ijret.org 95 characterized by their membership in the smoothness classes considered here. Based on previous experimental research on the spatial-frequency intensity response of the human visual system, it is argued that in most instances the error incurred in image compression should be measured in the integral sense instead of the mean-square sense. G.K. Kharate et al. in [16] described that the presently wavelet packet and discrete wavelet transform has emerged as popular techniques for image compression. The comparison of compression performance of Biorthogonal, Daubechies, Coiflets and other wavelets along with results for different frequency images is presented here. Based on the result, it can be concluded that proper selection of mother wavelet on the basis of nature of images and improves compression ratio and quality remarkably. Sanjeev Pragada et at. in [17] described that current denoising techniques which are used in the classical orthonormal wavelets for decomposition of an image corrupted with additive white Gaussian noise. For which various thresholding strategies are built. Because of their poor performance the use of available biorthogonal wavelets in image denoising is less common. Here it is presented a method to design image-matched biorthogonal wavelet based on their potential for denoising. It is conducted experiments on various image datasets namely Satellite, Natural and Medical images with the designed wavelets using two existing thresholding strategies. Here in the every dataset the biorthogonal wavelets show an average improvement of 35% in MSE for low SNR values (0 to 18db). This improvement was also seen in the visual comparison and PSNR. This point has an importance of matching when using wavelet-based denoising. Han Sae Song et al. in [18] presented a new DCT-based embedded image compression algorithm. From the ones in the neighbouring blocks the magnitudes of DCT coefficients are estimated and in the encoding the coefficients with larger estimates are given higher priority. As contexts for arithmetic coding this priority information is also used. This method finds more significant coefficients as compare to the conventional methods. Hence it provides higher coding gain. Sunil Malviya et al. in [19] proposed a new scheme for image compression using Discrete Wavelet Transform taking into account sub-band features in frequency domains. This method involves two steps firstly a two levels discrete wavelet transforms on the selected input image. The original images is decomposed at different 8x8 blocks and apply Walsh-Wavelet Transform on each block of the low frequency sub-band. Apply Arithmetic Coding on each sub- band independently after dividing each sub-band by a factor. Transform each block from LL2 and then divide each block 8x8 separated into DC value and finally compressed by Arithmetic coding. After thoroughly studying the different image compression algorithms have been presented here, some missing techniques come in my mind. This can be filled up by DCT- Biorthogonal wavelet transform using arithmetic coding. 3. PROPOSED METHOD The following steps represent the summarizing form of our proposed method for image compression: 1. First select an input image from database. 2. Divide the image into 8x8 blocks. 3. Apply the Biorthogonal wavelet transform for compression. 4. From the standard parameter set the quantization factor parameters QF1 and QF2. 5. From the range 1-10 set the compression ratio factor. 6. Apply the DCT-Biorthogonal wavelet transform and then use the arithmetic coding for compression. Step 6 consists of the following steps: i. Two level discrete Biorthogonal wavelet transform. ii. On each block of the low frequency sub-band apply 2D DCT-Biorthogonal wavelet transform. iii. From each transform block 8x8 split all the vlues. iv. By using arithmetic coding compress each sub-band. The first part of DCT-Biorthogonal wavelet transform compression steps for high frequency, domains and then second part of it for low frequency. 7. From each transform block 8x8 split all DC values. 8. Use Arithmetic coding for compression of each sub- band. 9. Finally by the compression output image is obtained. Fig -1: Flow chart of proposed method
• 3.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 _______________________________________________________________________________________ Volume: 04 Issue: 02 | Feb-2015, Available @ http://www.ijret.org 96 The above figure shows the flow chart of proposed method. Here firstly, an input image is taken and divide it into 8x8 blocks. Hence biorthogonal wavelet transform is applied on it. The quantization factor and compression ratio is chosen and DCT-biorthogonal wavelet transform is applied on 8x8 block low frequency sub-band. Then compress each sub- band with the help of arithmetic coding and split DC values of 8x8 blocks. Use arithmetic coding to compress each sub- band and output image will get finally. 4. RESULTS AND ANALYSIS Here as a dataset some classic image like Mandrill image, Lena image and Barbara image is used. The size of the each image is 256x256. The following figure 2 shows the selected three classic images as a test image. Here for compression biorthogonal 6.8 wavelet, value of each quantization factor (QF1 and QF2) 0.02 and compression ratio factor 2 is selected. For comparing the results of proposed method with the existing methods the PSNR (in dB) value is chosen. Fig -2: Test Images The following table 1 shows the comparison result of the proposed algorithm and different existing method such as EZW, EBCOT, JPEG 2000, GW and SPHIT for the above mentioned three test images. Table -1: Comparison of PSNR results Methods PSNR (in dB) Mandrill Lena Barbara EZW 32.23 30.38 28.54 EBCOT 31.96 28.58 29.36 JPEG 2000 31.90 29.58 30.96 GW 30.20 31.39 32.84 SPHIT 30.90 29.30 30.32 PROPOSED METHOD 32.75 33.63 34.39 From the above table it is seen that using the proposed method gives the PSNR results 32.75dB, 33.63 dB and 34.39 dB for the Mandrill image, Lena image and Barbara image respectively. And for all cases the performance of the proposed algorithm based on DCT-Biorthogonal wavelet transform using arithmetic coding is better. The chart 1 shows the representation of the above results in the form of bar graph. Chart -1: Comparison of compression results (PSNR) of various methods
• 4.
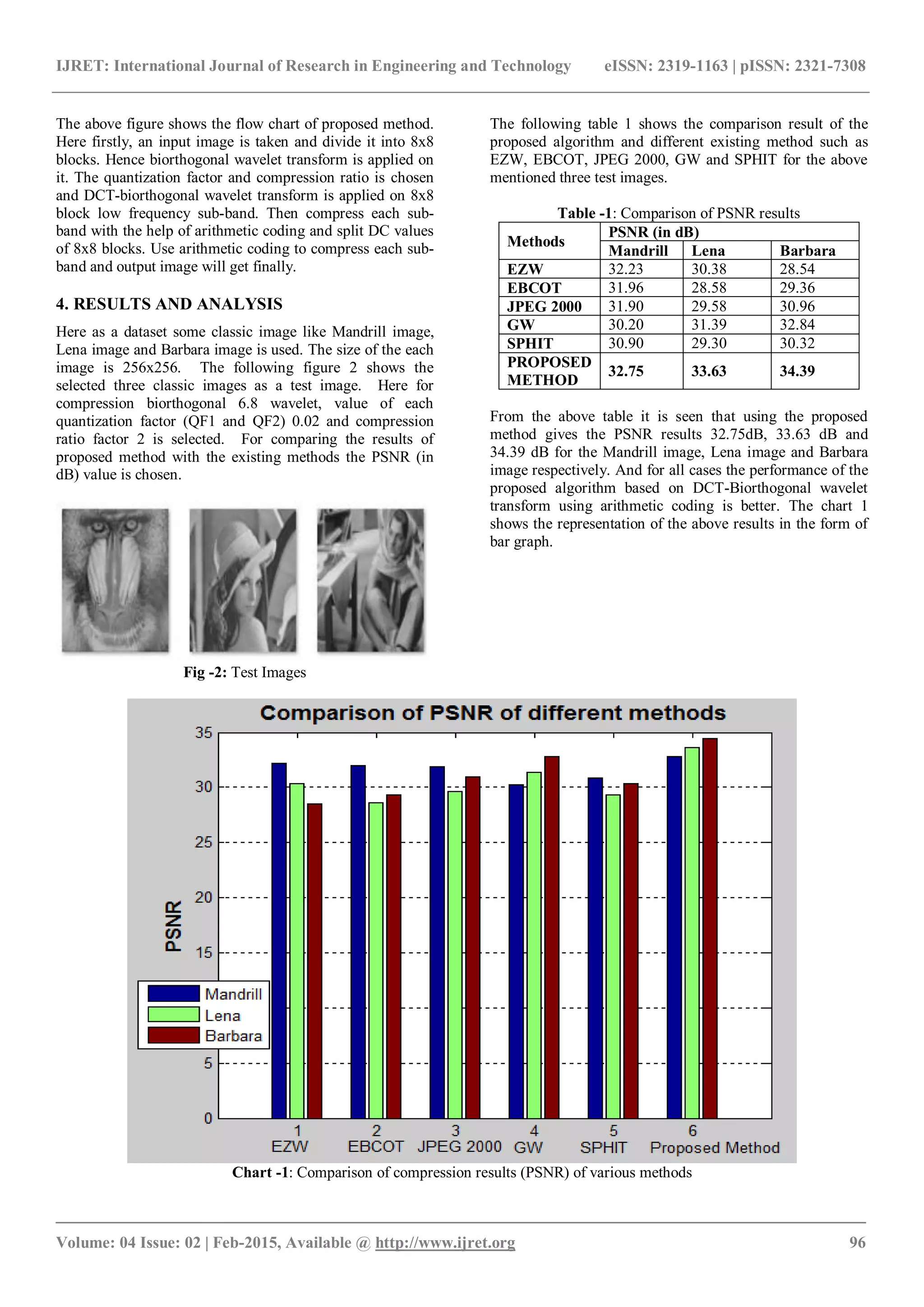
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 _______________________________________________________________________________________ Volume: 04 Issue: 02 | Feb-2015, Available @ http://www.ijret.org 97 From the chart 1 it is clear that the performance of the proposed method is better than the existing EZW, EBCOT, JPEG 2000, GW and SPHIT method. 5. CONCLUSION AND FUTURE WORK This paper represents an image compression algorithm that adopts DCT-Biorthogonal wavelets transform with the arithmetic coding. This algorithm is applied on several types of images. It is seen that this method removes the redundancy from images and also it significantly reduces the blocking artifacts and false contouring effects. This method gives better results as compare to different existing compression methods. However, the performance of this method can be extended by using different wavelet and different transform with various entropy encoding techniques. In future some more efforts are required to give on it as the image compression is still a challenging problem. ACKNOWLEDGEMENTS I would like to thank to my friend Nalini Mittal who has motivated me to complete this work. Special thanks to my father who always supports my innovative ideas. REFERENCES [1]. Jerome M. Shapiro, “Embedded Image coding using Zerotrees of Wavelet coefficients”, IEEE Transactions on Signal processing December 1993. [2]. A. Said and Pearlman, “A new fast and efficient image codec based on set partitioning in hierarchical trees”, IEEE Trans. Circuits Syst. Video Techno., vol 6, pp 243-250, June 1996. [3]. Marcus J. Nadenau, Julian Richel and Murat Kunt, “Visually improved Image compression by combing Conventional Wavelet codec with texture Modeling”, IEEE Transactions on Image processing vol 11, Nov 2007pp 1284-1294. [4]. M. A. Losada, G. Tohumoglu, D. Fraile, and A. Artes, “Multi-iteration wavelet zerotree coding for image compression”, Sci. Signal Process, vol. 80, pp. 1281-1287, 2000. [5]. G.K. Wallace, “The JPEG still picture compression standard”, Communication ACM vol 34, pp 30-44 Apr 1991. [6]. Bryan E. Usevitch, “A tutorial on modern lossy image compression: foundations of JPEG 2000, IEEE signal processing magazine Sept 2001. [7]. A. Said and W. A. Pearlman, “A new, fast and efficient image codec based on set portioning in hierarchical trees”, IEEE Trans. Circuits Syst. Video Technol., vol. 6, no. 3, pp 243-250, Jun, 1996. [8]. S. Servetto, K. Ramchandran, and M. Orchard, “Image coding based on a morphological representation of wavelet data”, IEEE Trans. Image Processing, vol. 8, pp. 1161-1173, Sept. 1999. [9]. D. Taubman, “High performance scalable image compression with EBCOT”, IEEE Trans. Image Processing, vol. 9, pp. 1158-1170, July 2000. [10]. K. peng and J.C. Kieffer, “Embedded Image Compression Based on Wavelet Pixel Classification and Sorting”, IEEE Transactions on Image Processing, vol. 13, no. 8, pp. 1011-1017, Aug 2004. [11]. M. A. Lasoda, G. Tohumoglu, D. Fraile, and A. Artes, “Multi-iteration wavelet zerotree coding for image compression”, Sci. Signal Process., vol. 80, pp. 1281-1287, 2000. [12]. J. M. Shapiro, “Embedded image coding using zerotrees of wavelet coifficients”, IEEE Trans. Signal Process., vol. 41, no. 12, pp. 3445-3462, Dec. 1993. [13]. A. Criminisi, P. Perez, and K. Toyama, “Region filling and object removal by exemplar-based image inpainting”, IEEE Trans. Image Process., vol. 13, no. 9, pp. 1200-1212, Sep. 2004. [14]. D. Alani, A. Averbuch and S. Dekel, “Image coding with geometric wavelets”, IEEE Trans. Image Process., vol. 16, no. 1, pp. 69-77, Jan. 2007. [15]. Ronald A. DeVore, Bjorn Jawerth, and Bradley J. Lucier, “Image Compression through Wavelet Transform Coding”, IEEE Transactions on Information Theory, vol. 38. no. 2, pp. 719-746 March 1992. [16]. G.K. Kharate, A.A. Ghatol and P.P. Rege, “Selection of Mother Wavelet for Image Compression on Basis of Image”, IEEE - ICSCN 2007, MIT Campus, Anna University, Chennai, India. Feb. 22-24, 2007. pp. 281-285. [17]. Sanjeev Pragada and Jayanthi Sivaswamy, “Image denoising using matched biorthogonal wavelets”, Sixth Indian Conference on Computer Vision, Graphics & Image Processing, IEEE. 2008. pp. 25-32. [18]. Han Sae Song and Nam Ik Cho, “DCT-Based Embedded Image Compression With a New Coefficient Sorting Method”, IEEE Signal Processing Letters, vol. 16, No. 5, pp. 410-413, May 2009. [19]. Sunil Malviya, Neelesh Gupta and Vibhanshu Shirvastava, “2D-Discrete Walsh Wavelet Transform for Image Compression with Arithmetic Coding”, 4th ICCCNT - 2013 July 4 - 6, 2013, Tiruchengode, India BIOGRAPHY Priyatosh Halder received the M. Tech degree in Electronics and Communication Engineering from Sri Sukhmani Institute of Engineering and Technology, Dera Bassi (Punjab), India. Presently he is working in Indian Air Force. He is a member of IEEE and IEI. His research interest is digital image processing.