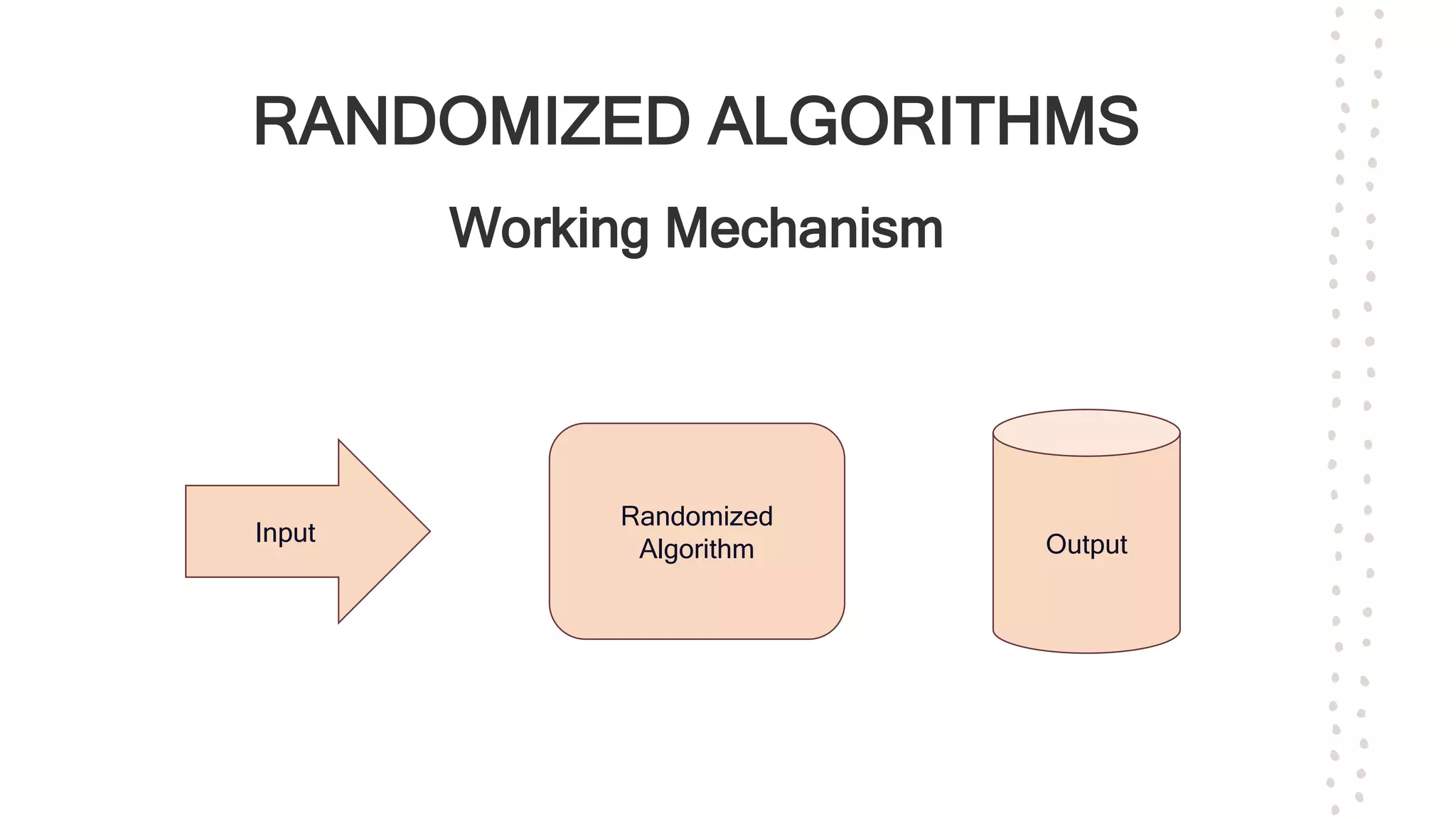
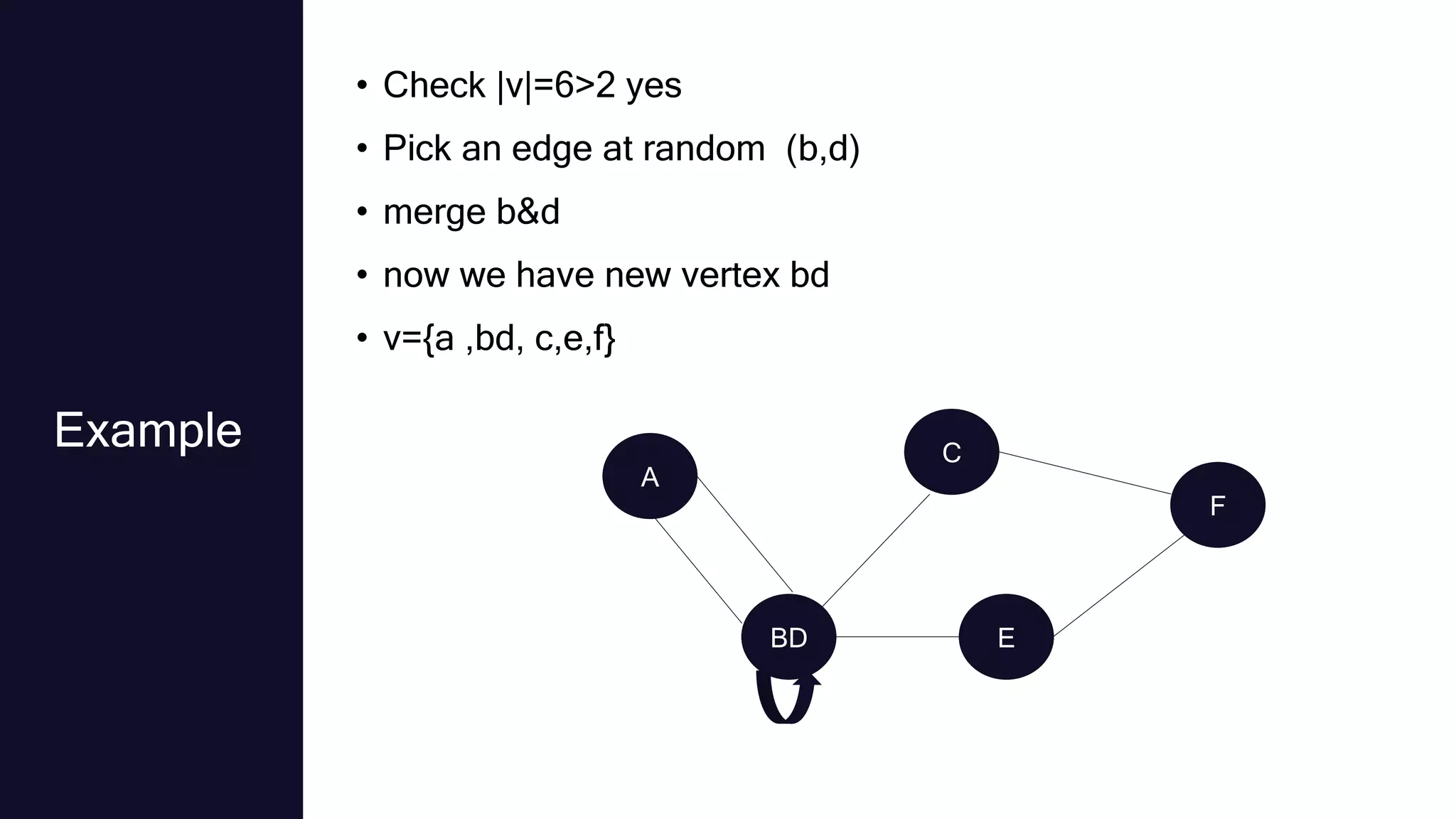
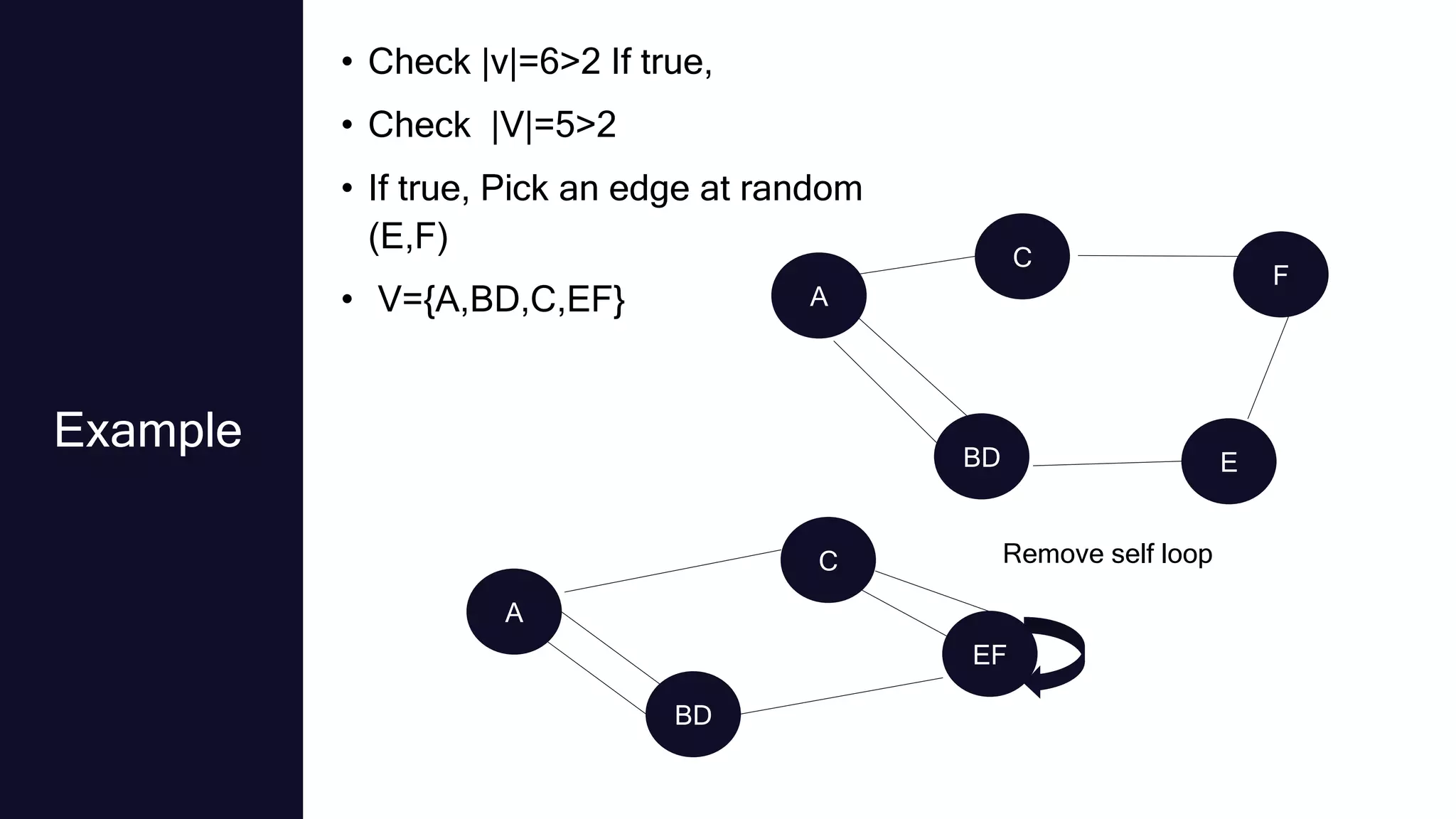
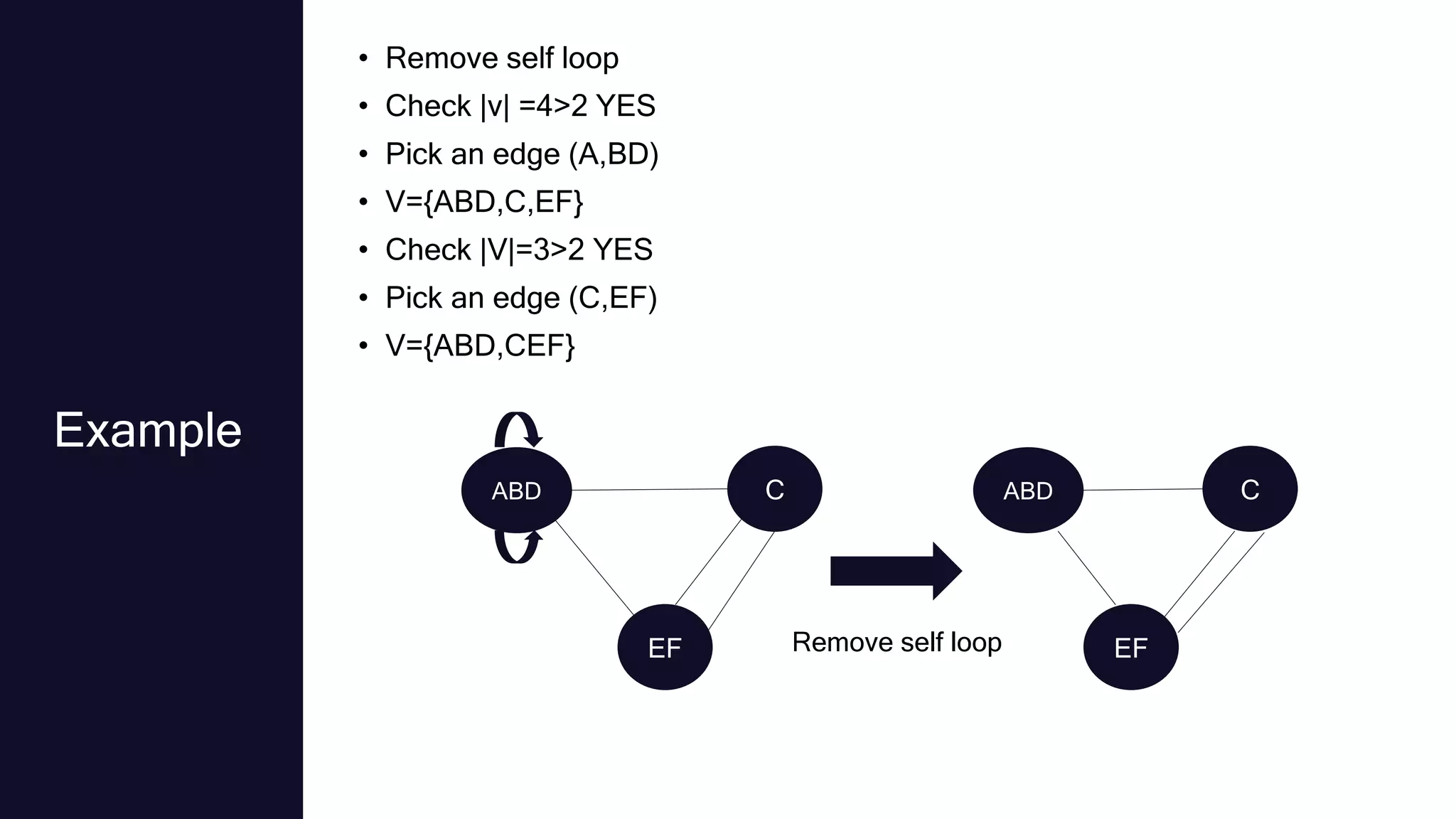
Randomized algorithms were first used in number theory in 1917 and their study was later spurred by discoveries of randomized primality tests in the 1970s. Randomized algorithms can solve problems faster than deterministic algorithms when the problem size becomes extremely large. Randomized algorithms introduce randomness into the logic of an algorithm to reduce complexity and space requirements. There are two main types: Las Vegas algorithms always produce the correct output but have random running times, while Monte Carlo algorithms have deterministic running times but may produce incorrect outputs. Randomized algorithms are commonly used for problems involving numbers, data structures, graphs, and mathematical programming where average-case solutions are acceptable.