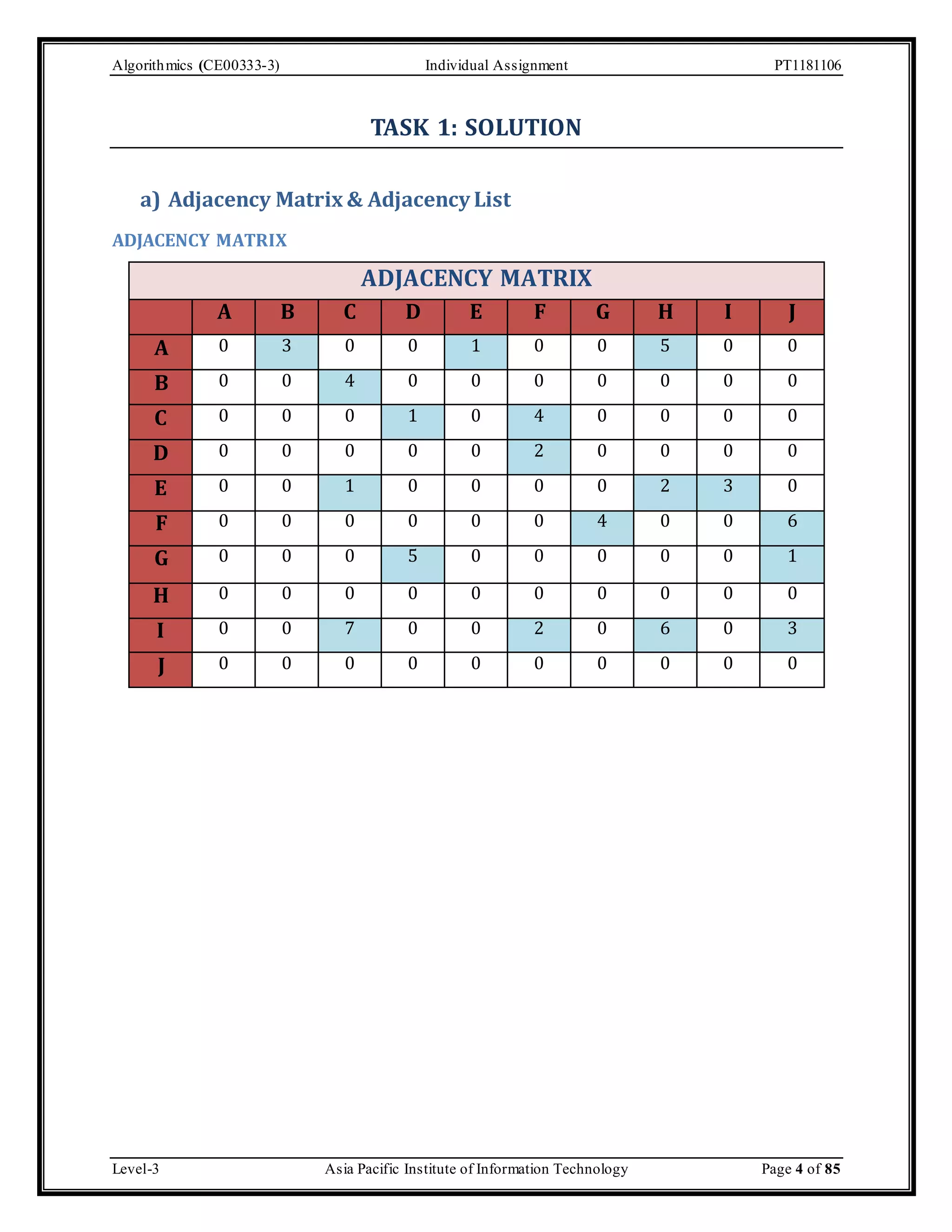
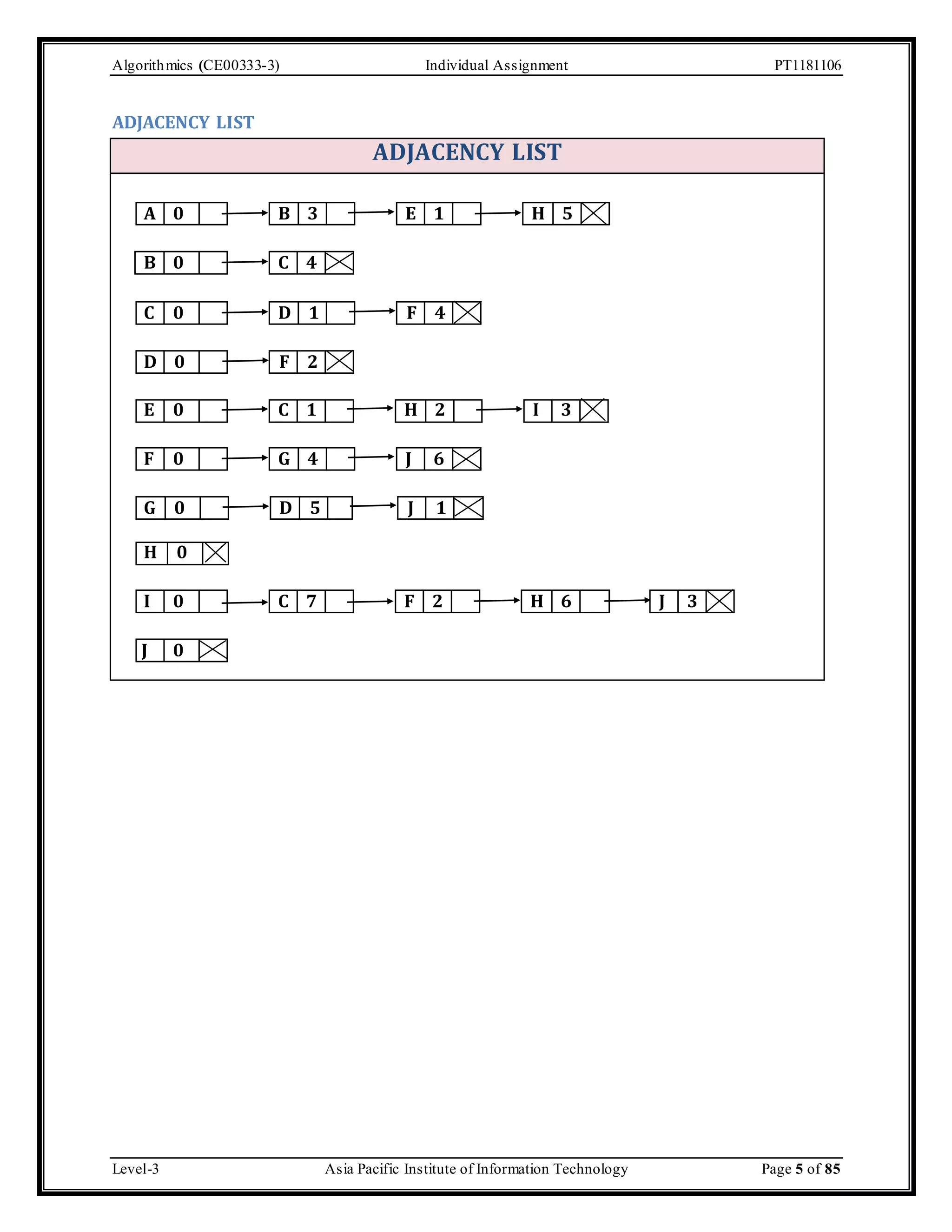
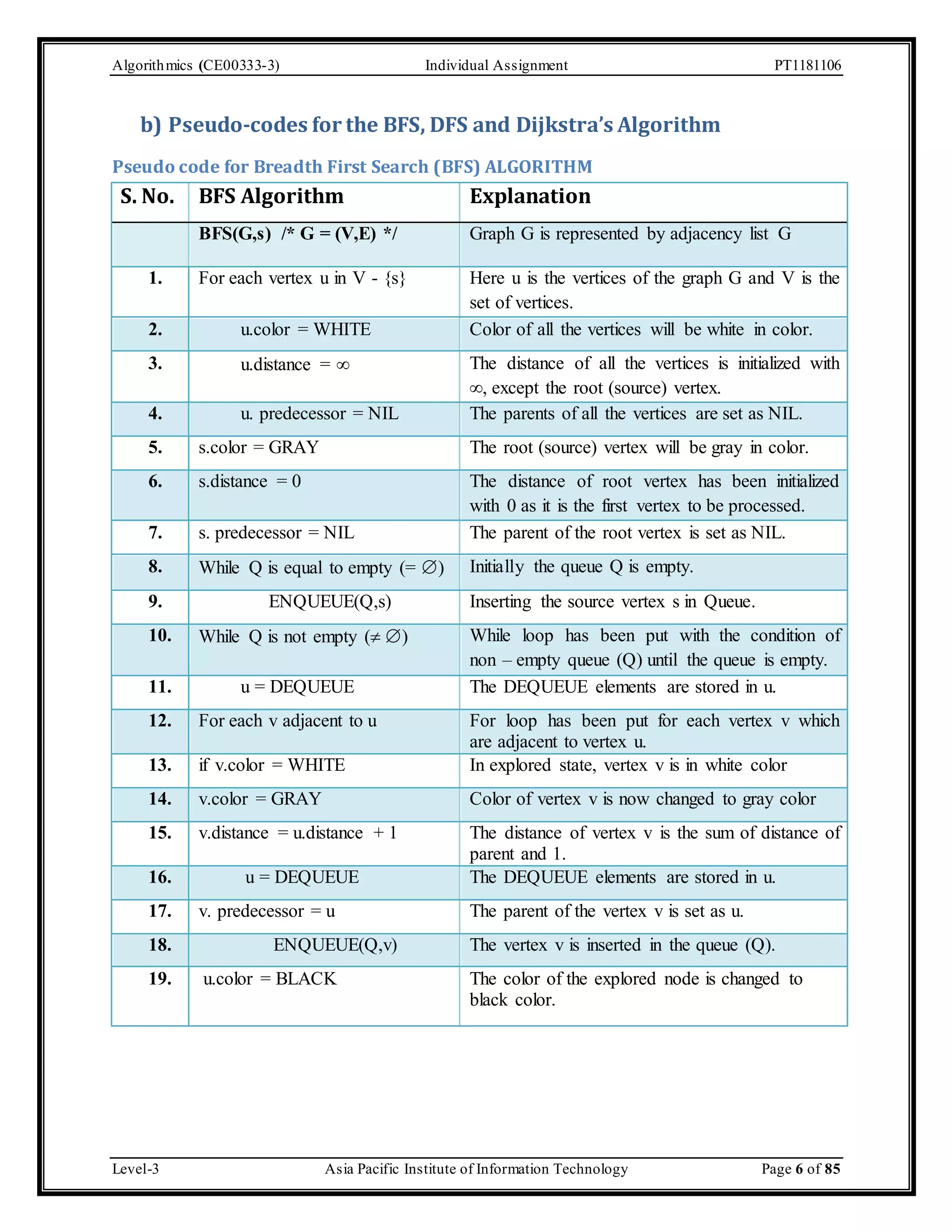
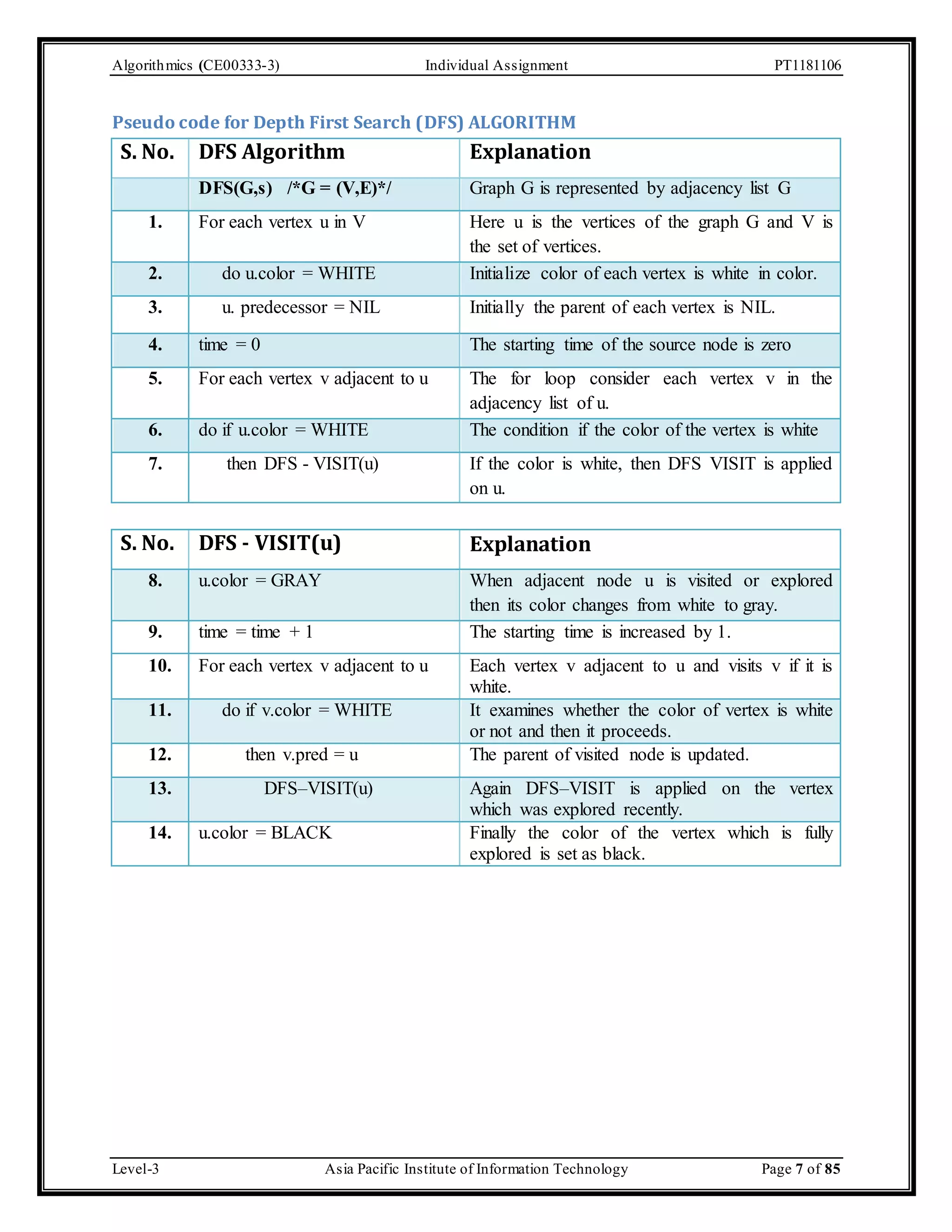
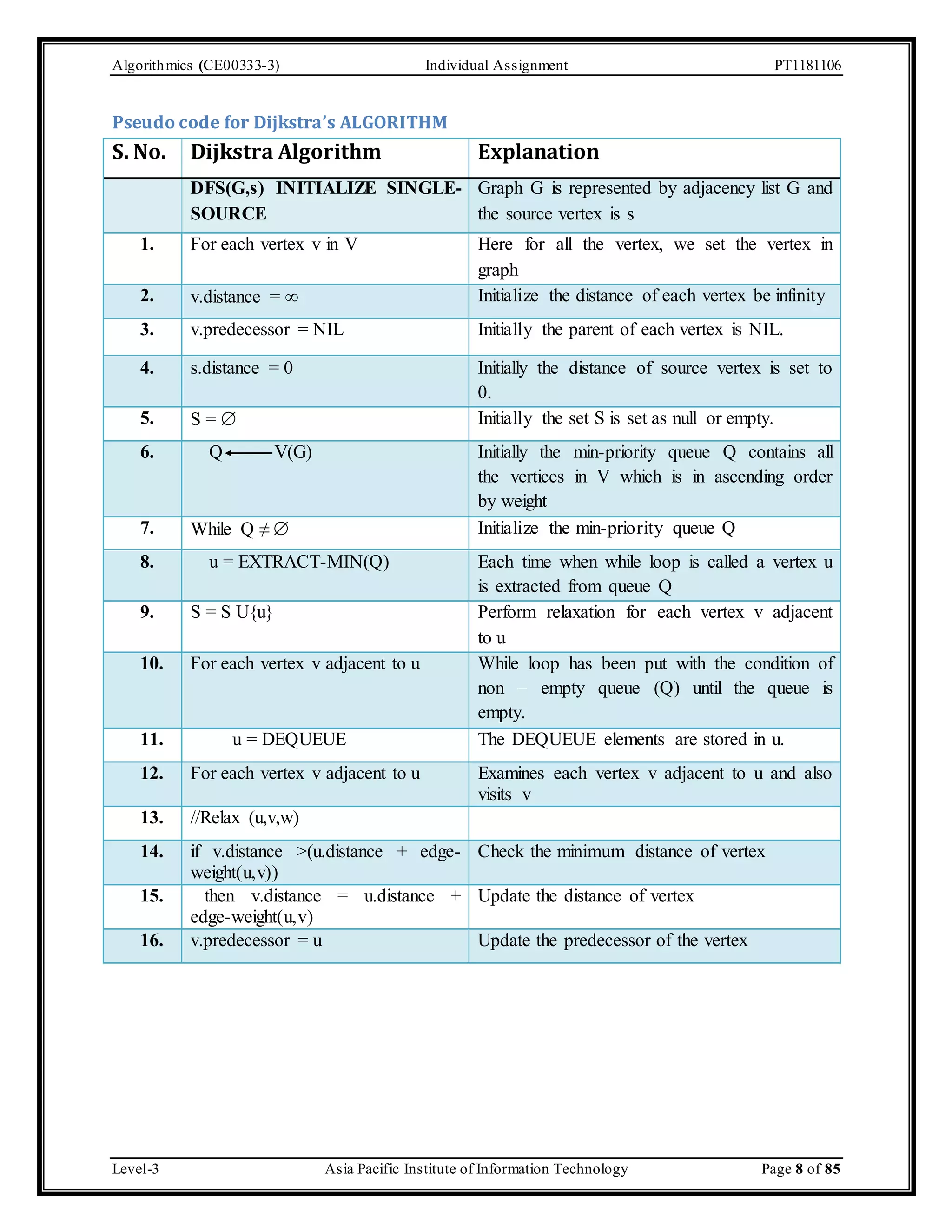
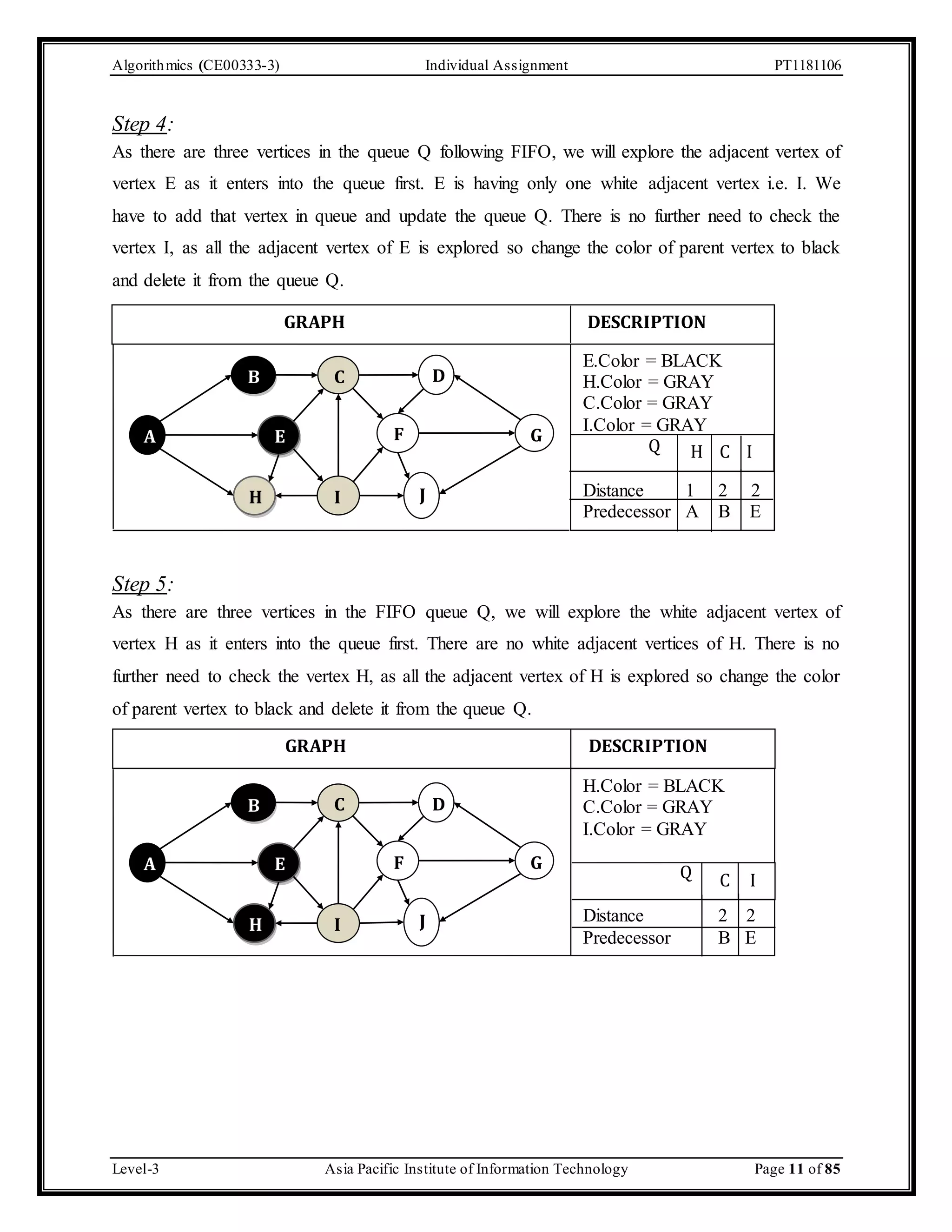
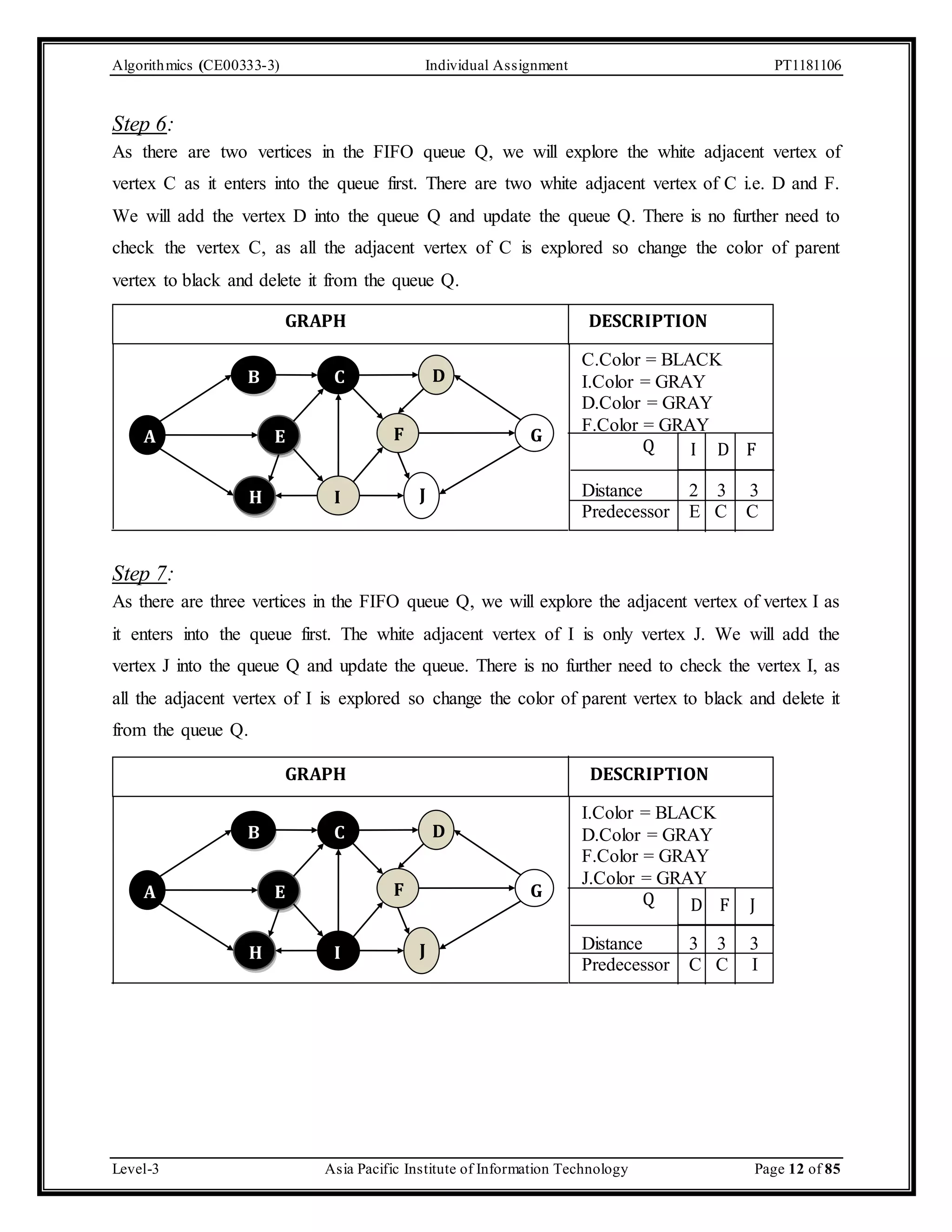
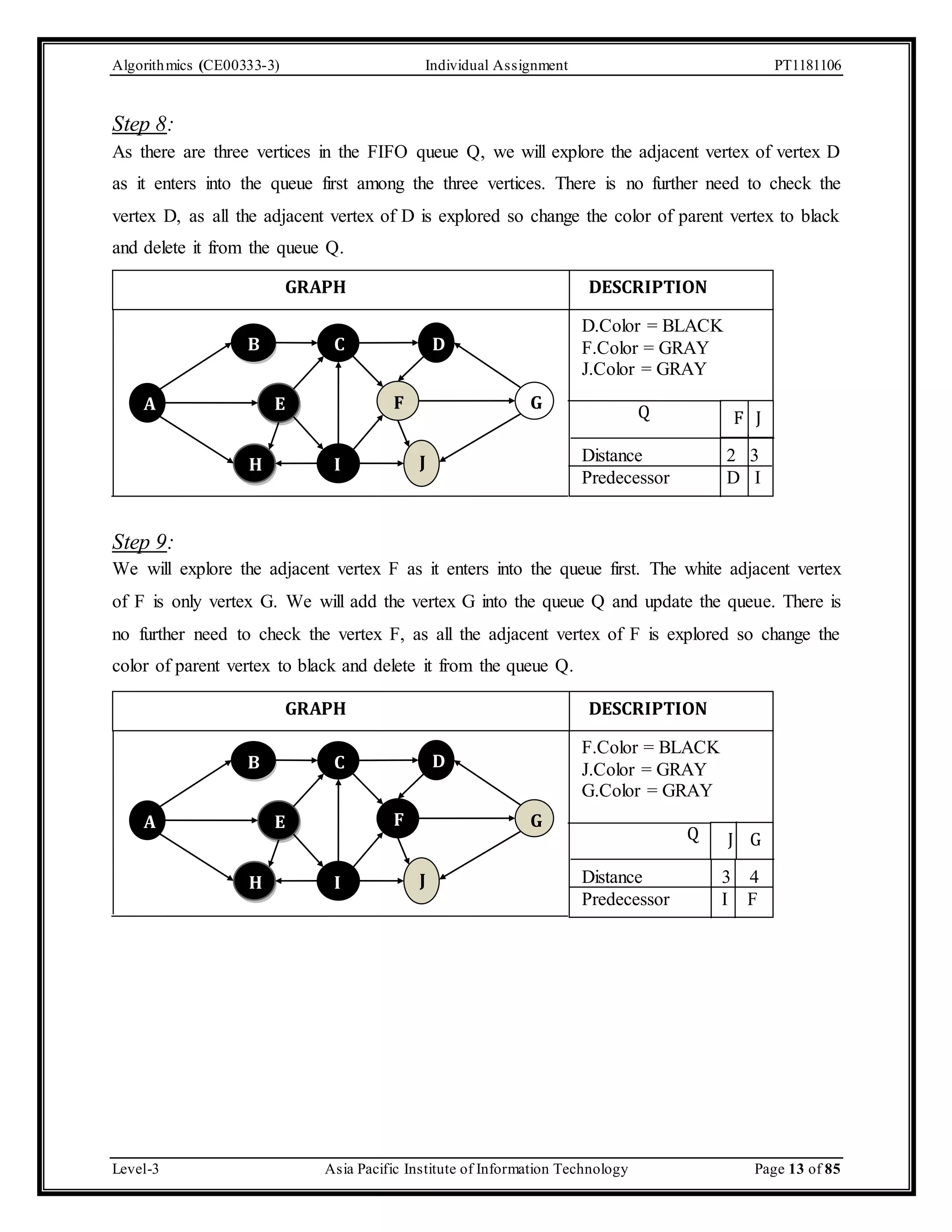
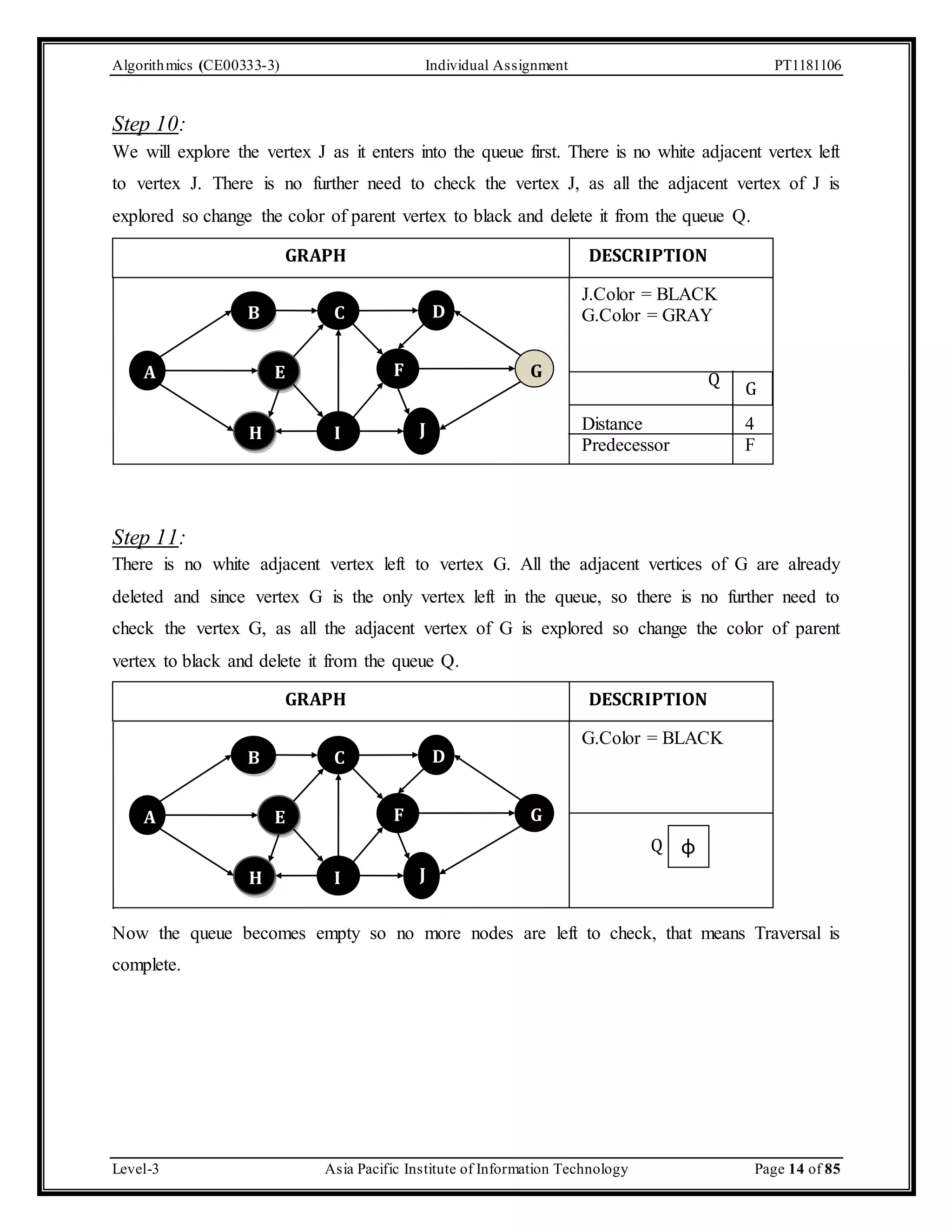
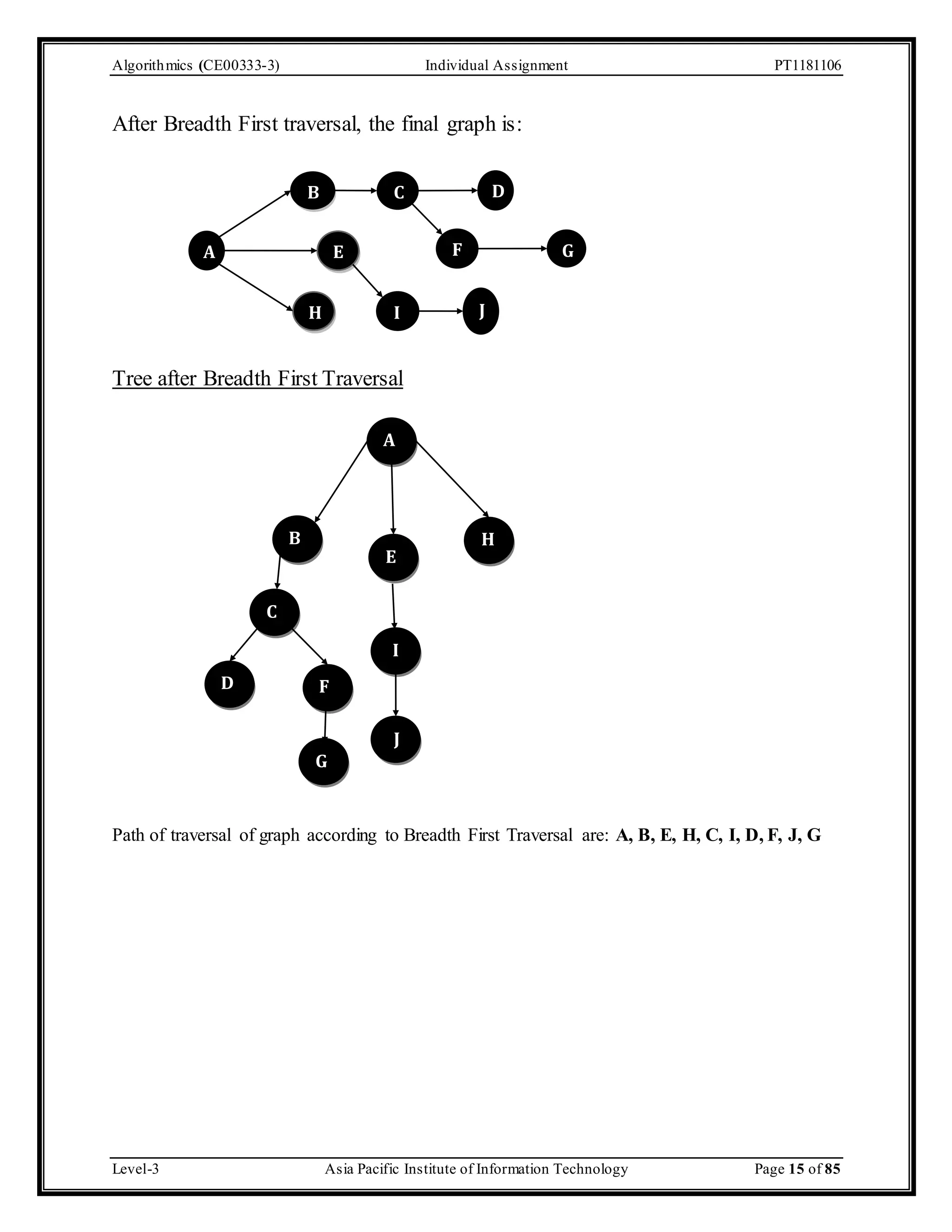
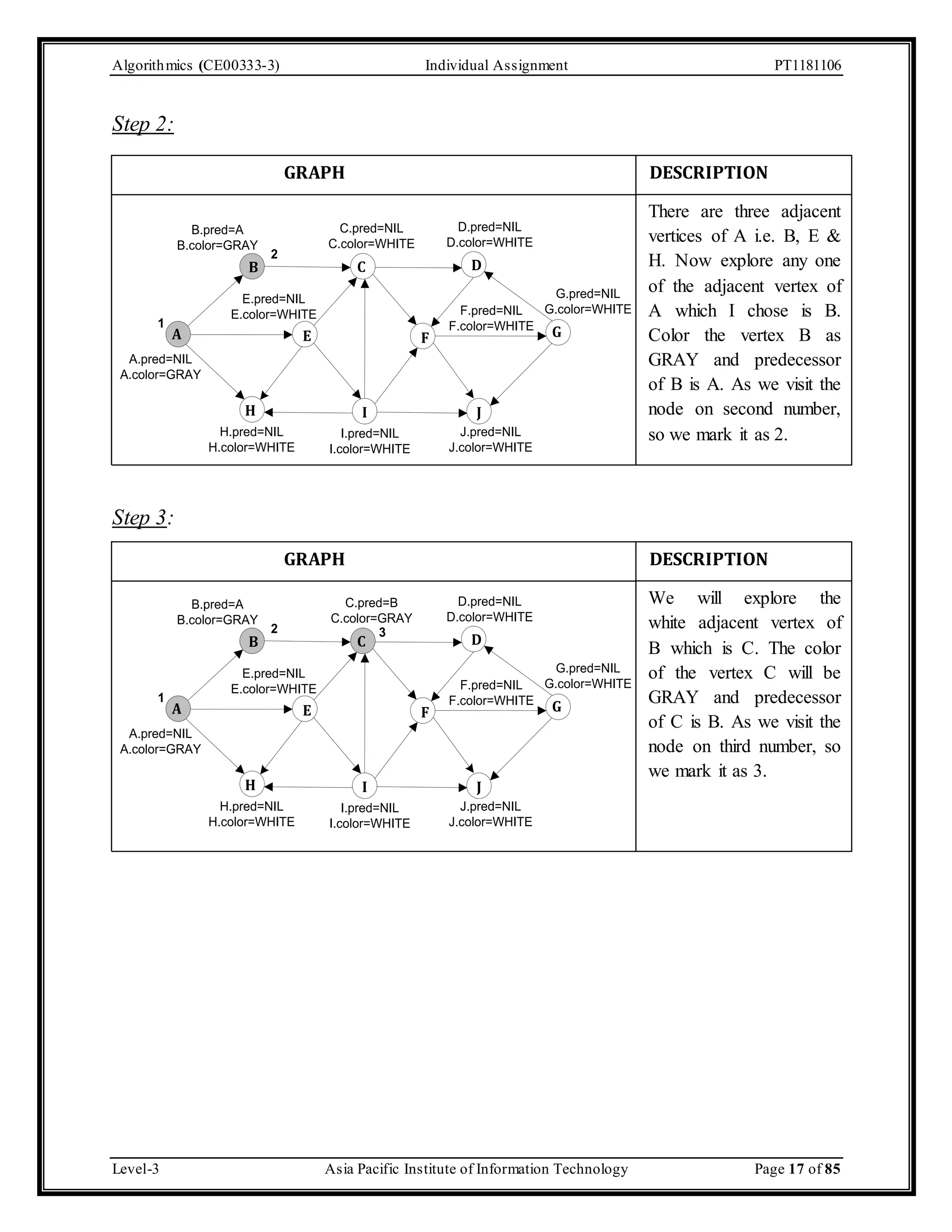
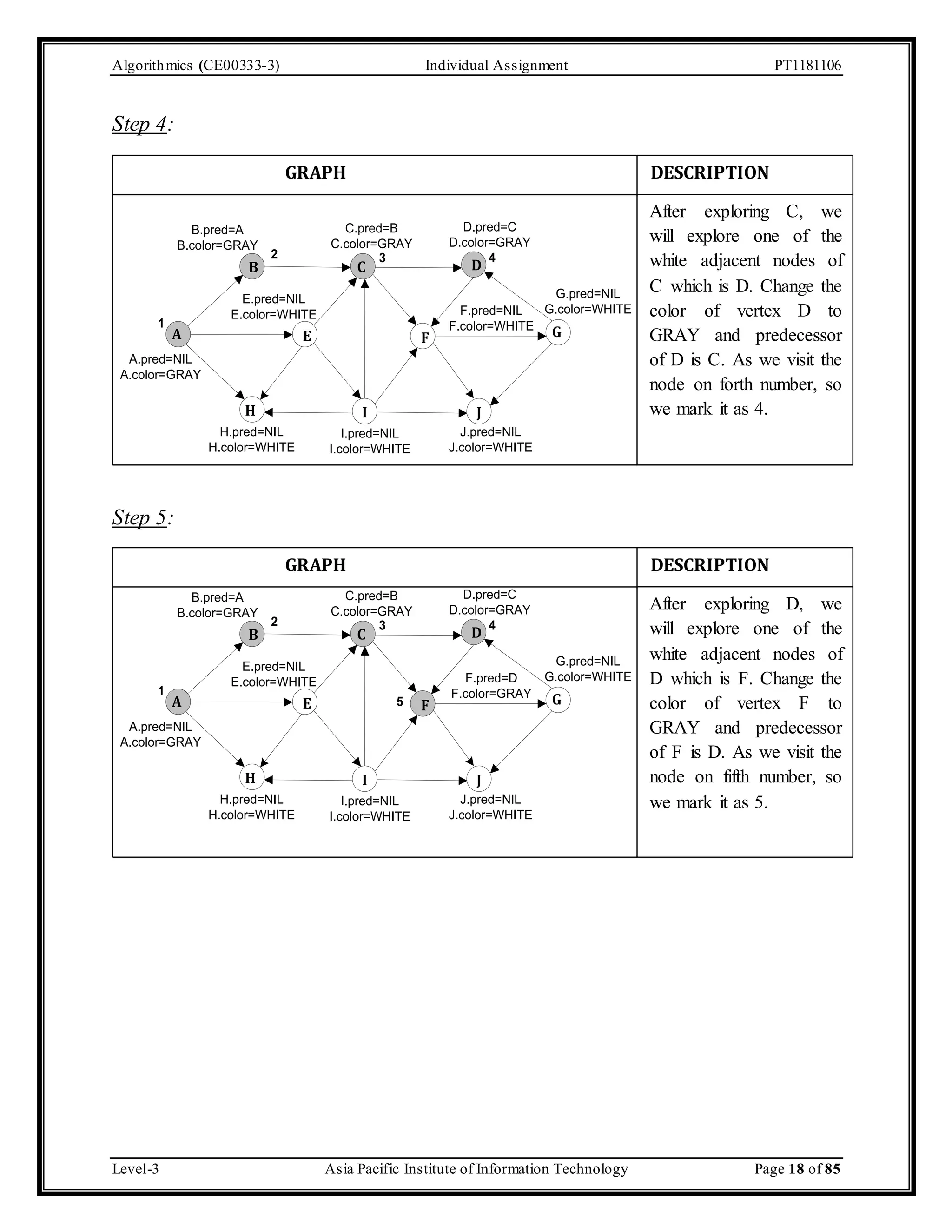
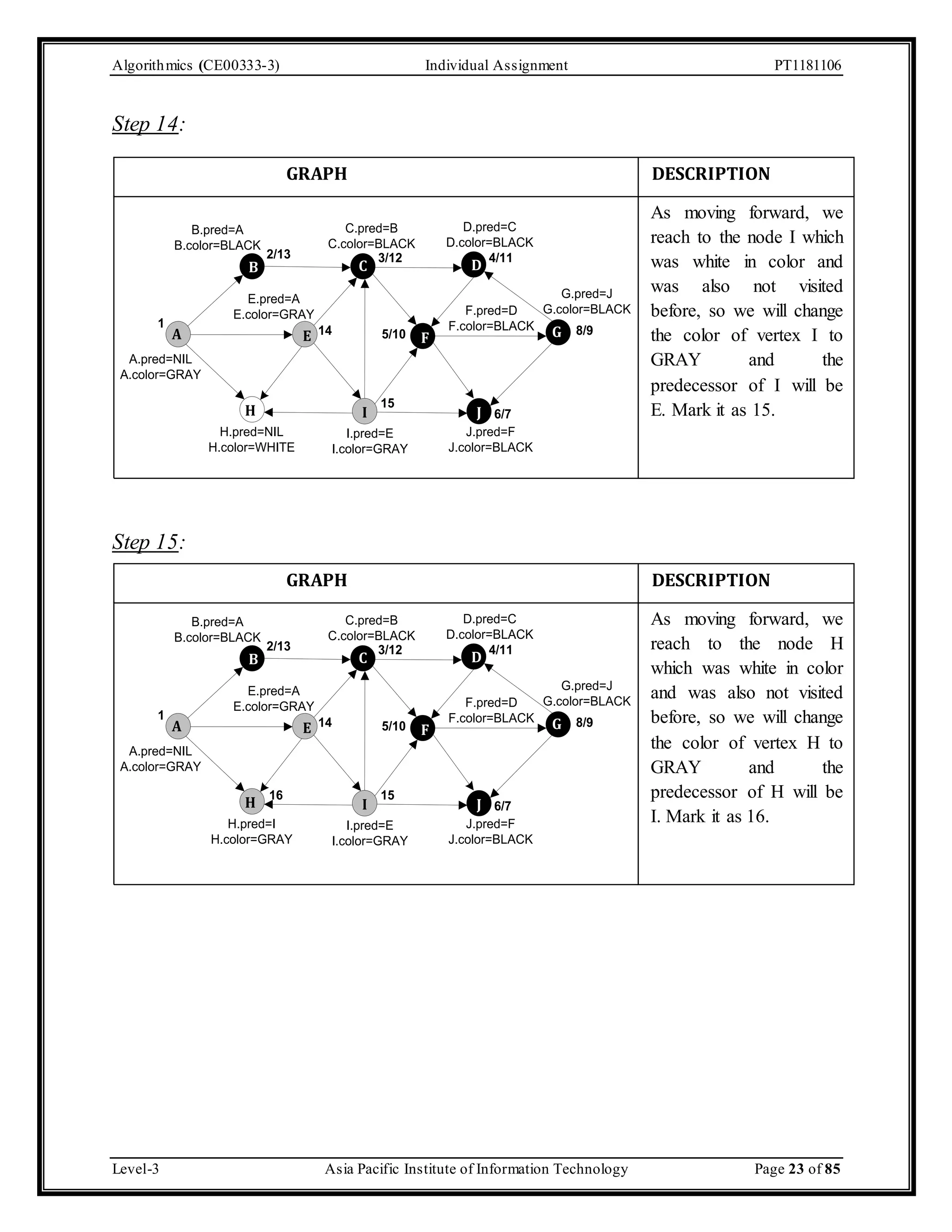
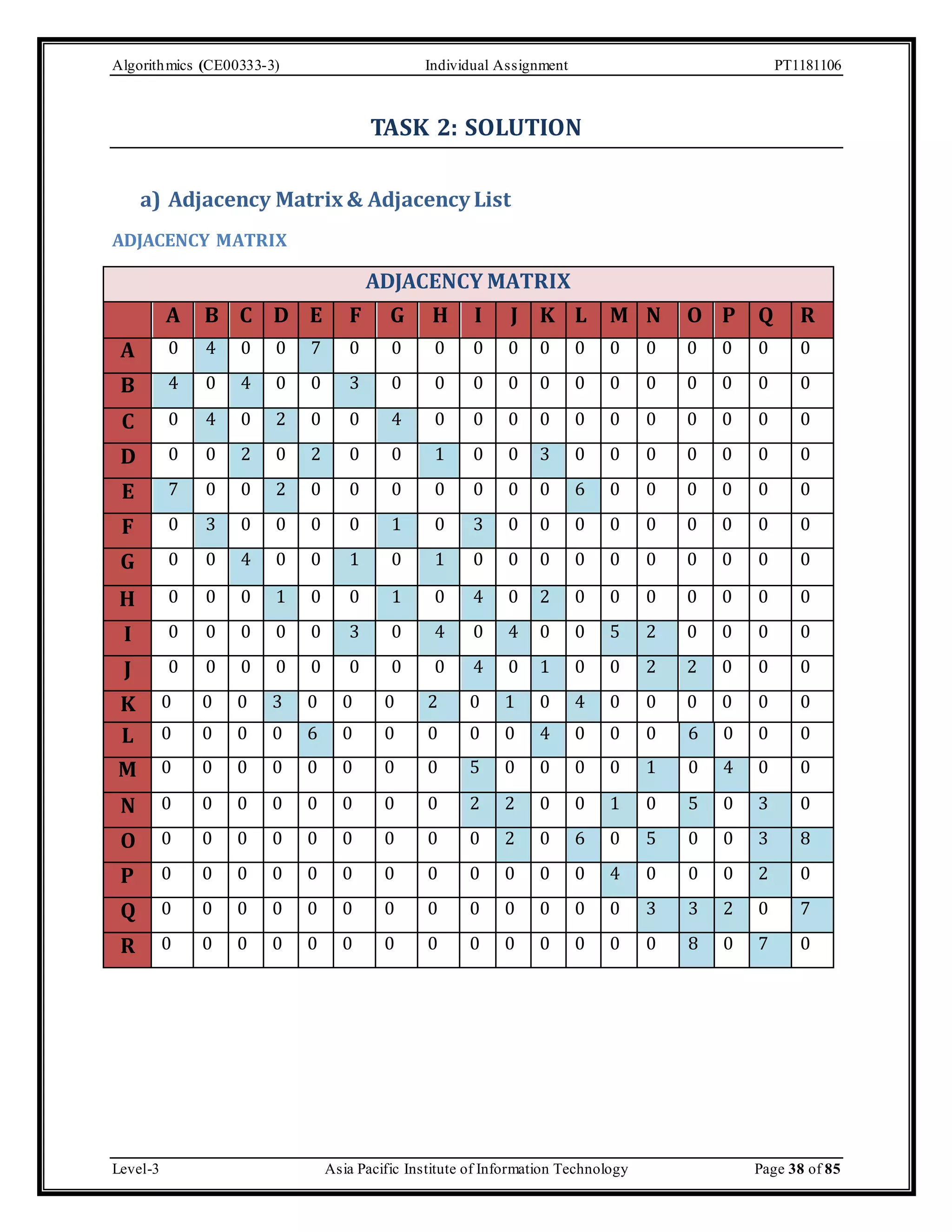
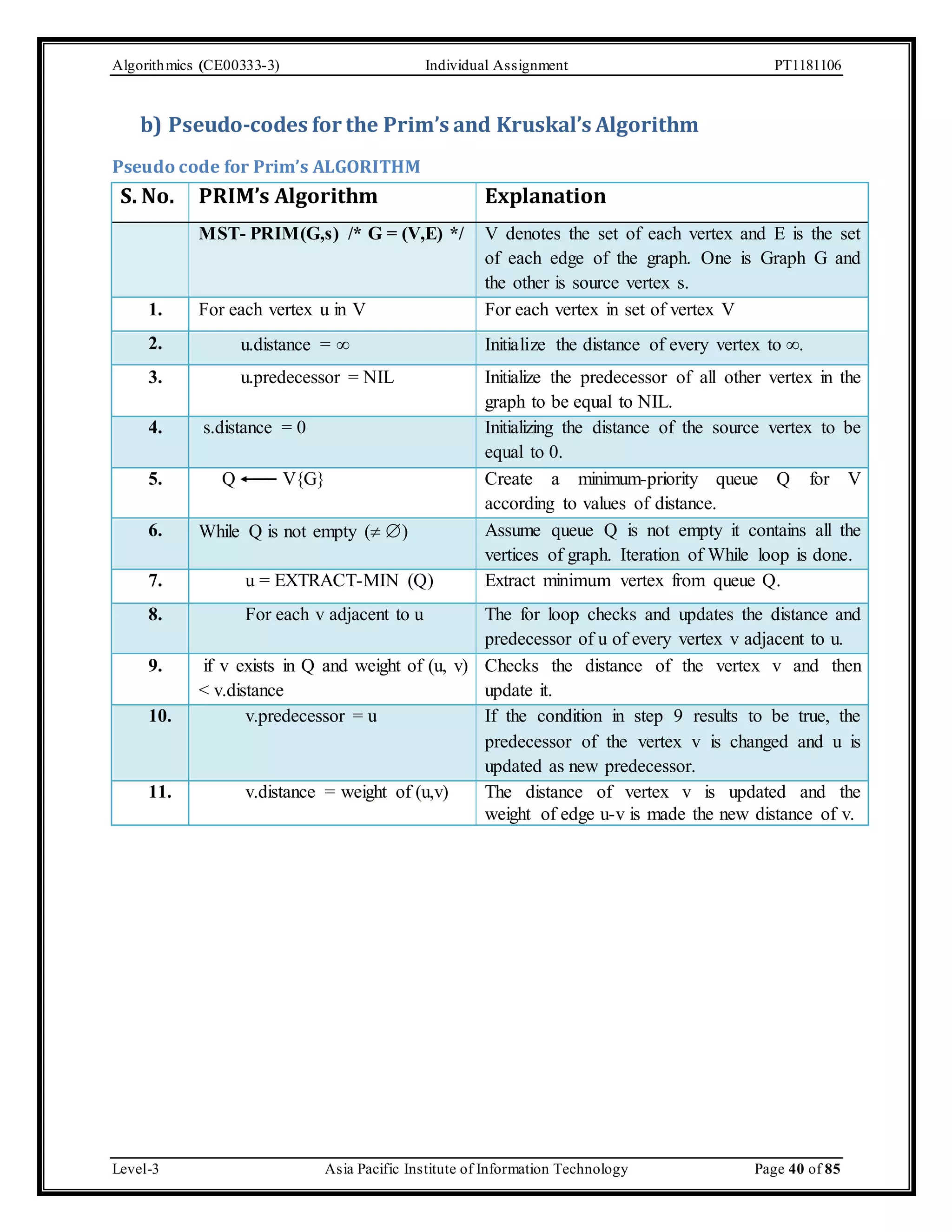
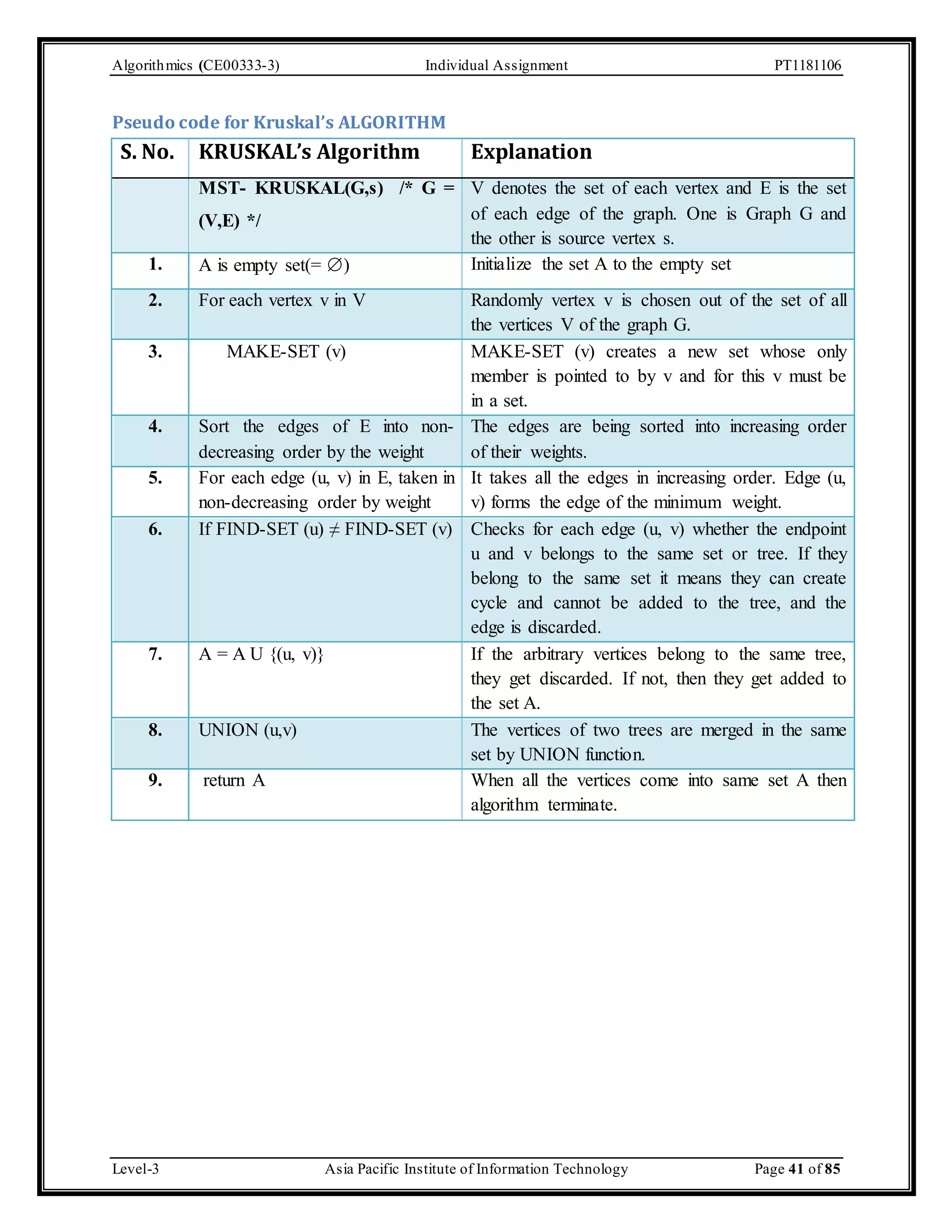
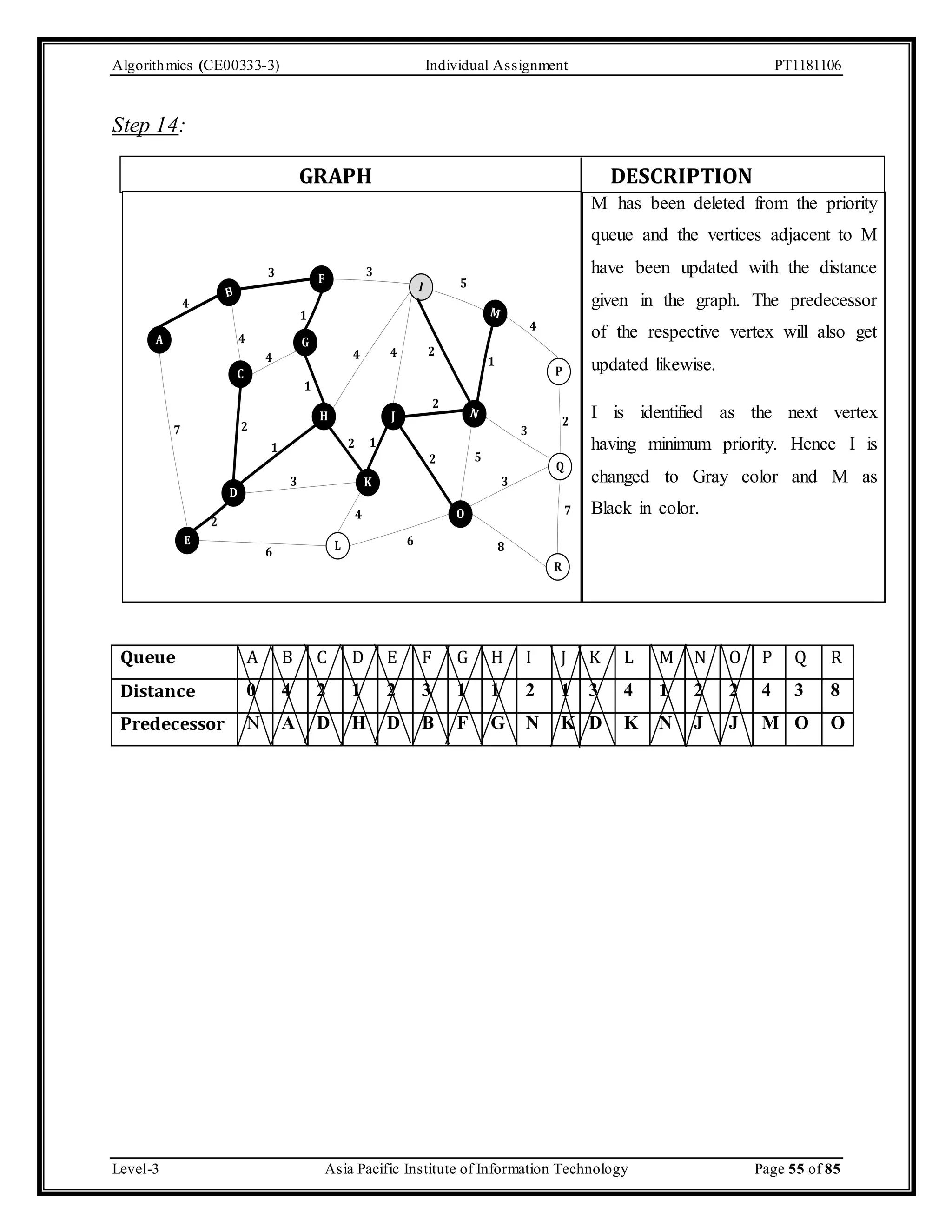
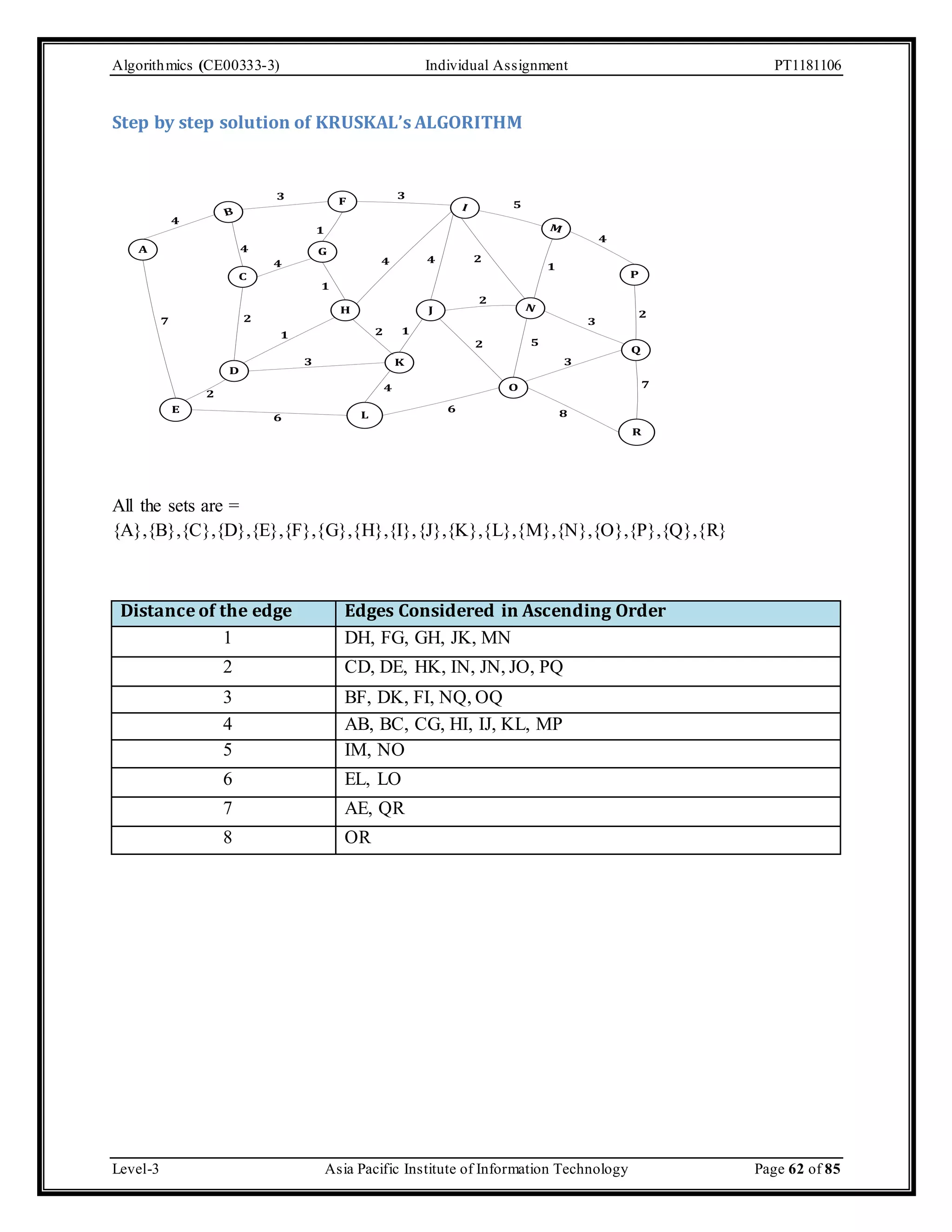
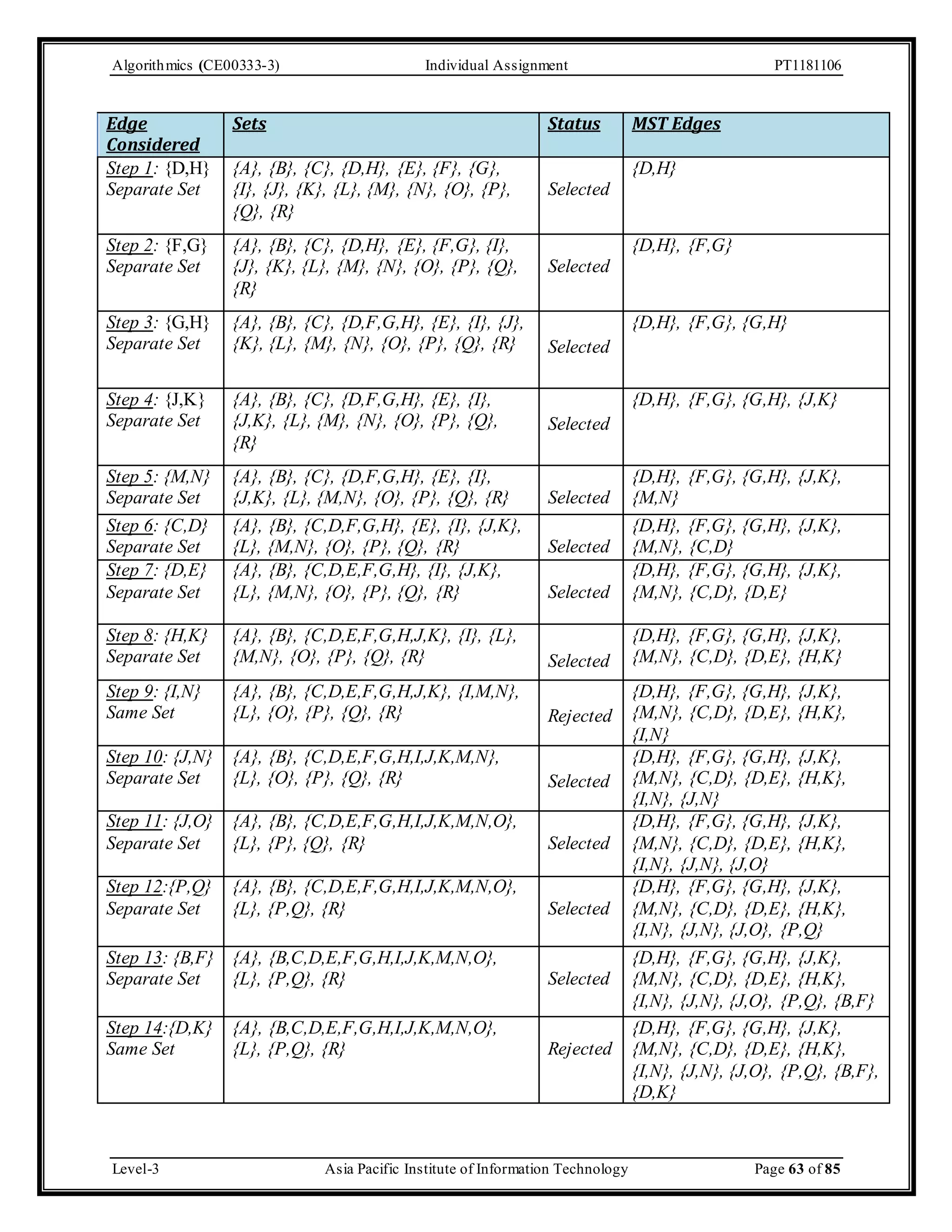
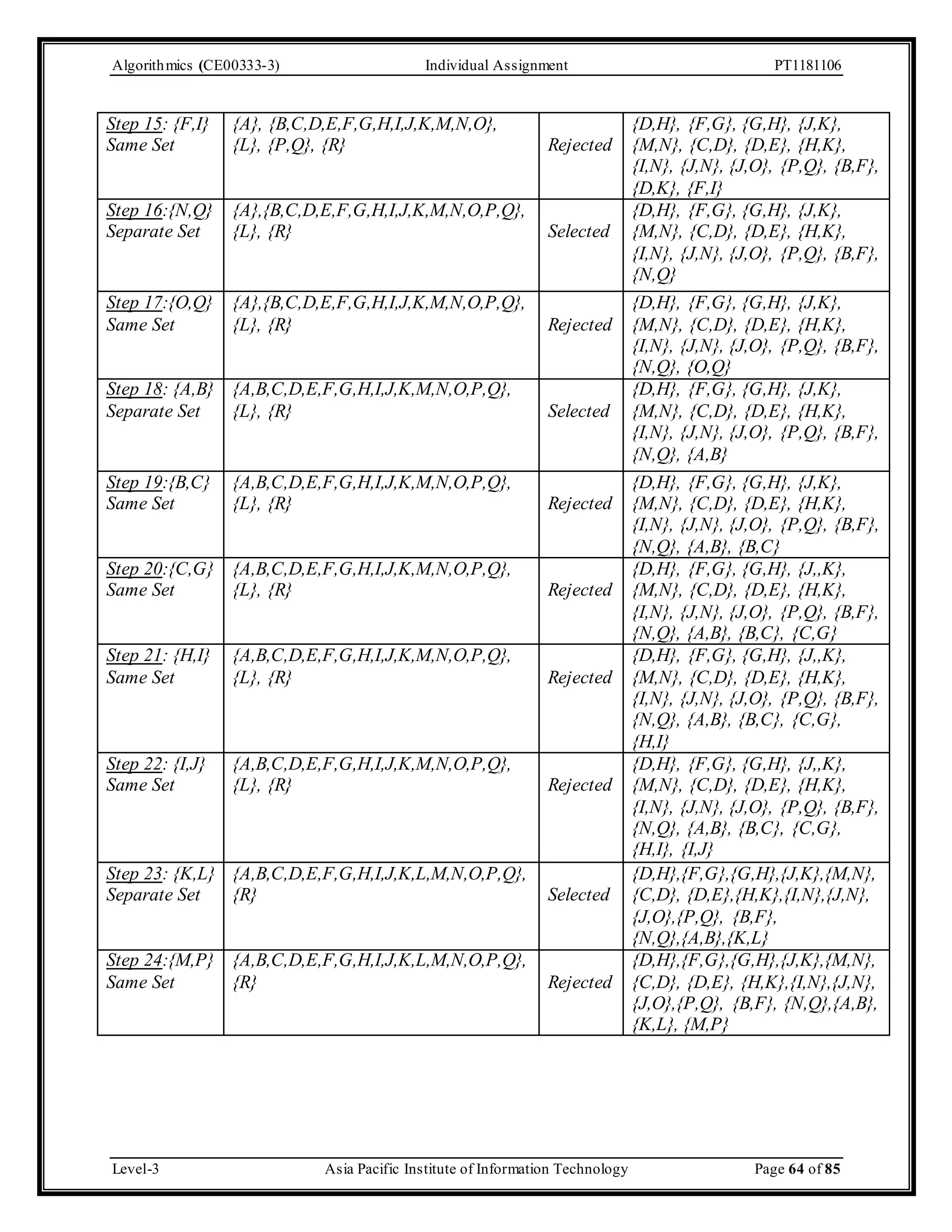
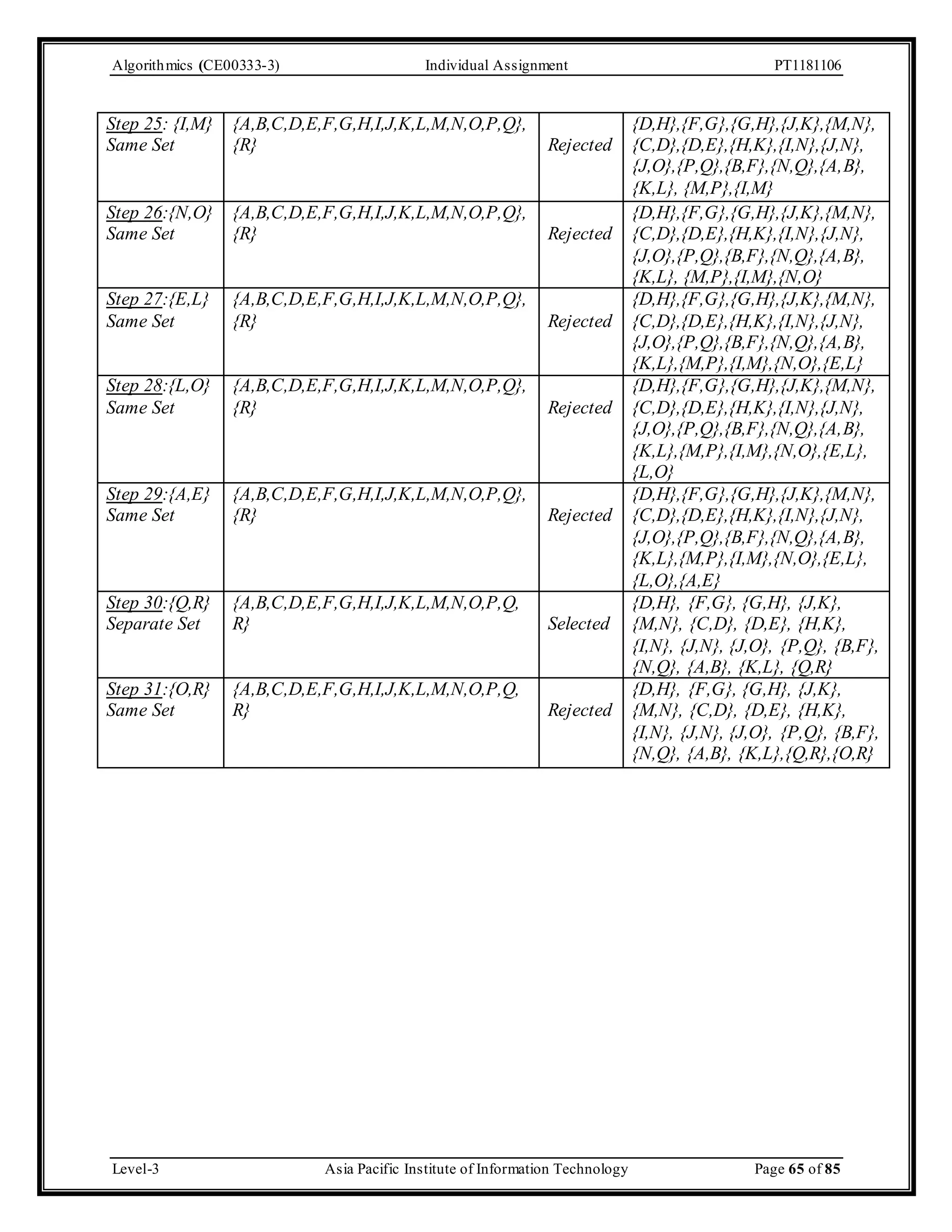
The document outlines an individual assignment for algorithmics focusing on graph theory applications, including scenarios, solutions, and algorithms like BFS, DFS, Dijkstra’s, Prim's, and Kruskal's. It provides detailed pseudo-codes, step-by-step solutions, adjacency matrices, and lists for various graph problems. Additionally, it discusses the efficiencies of these algorithms in terms of time complexity.



![Algorithmics (CE00333-3) Individual Assignment PT1181106 c) Step by step solution for the BFS, DFS and Dijkstra’s of the given graph. Step by step solution of BFS ALGORITHM (unweighted) Here it has been mentioned in the scenario that we have to assume that the graph is unweighted. Initially the color of the entire vertex is white and its distance is initialized to ∞. The parent or predecessor of all the vertices is initially NIL. The BFS uses First in First Out queue (FIFO) to store vertices which become gray after traversal. A Step 1: GRAPH DESCRIPTION B C H G D J I E F All the vertices will be in WHITE in color. Distance of all the vertices will be ∞ Parent of all the vertices will be = NIL Let’s assume the source vertex is node A. So first discover the source vertex A and add into queue Q. Also change the color of vertex A to gray and it distance and predecessor to 0. All other vertices will be white in color. GRAPH DESCRIPTION B C H G D J I E F A Source node = A [Let] A.Color = GRAY Q A Distance = 0 Predecessor = NIL Level-3 Asia Pacific Institute of Information Technology Page 9 of 85](https://image.slidesharecdn.com/algofinal-141210182027-conversion-gate01/75/Algorithms-9-2048.jpg)




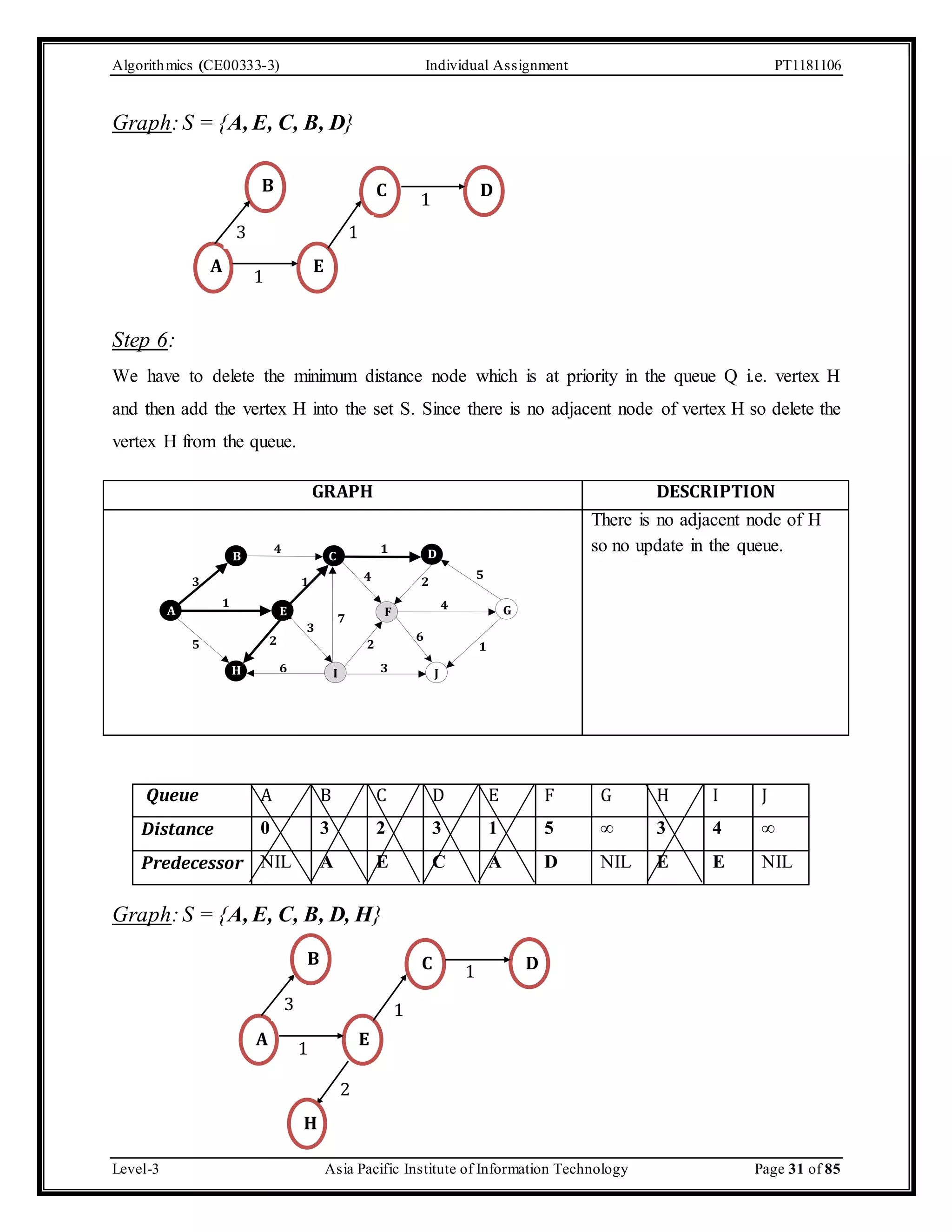
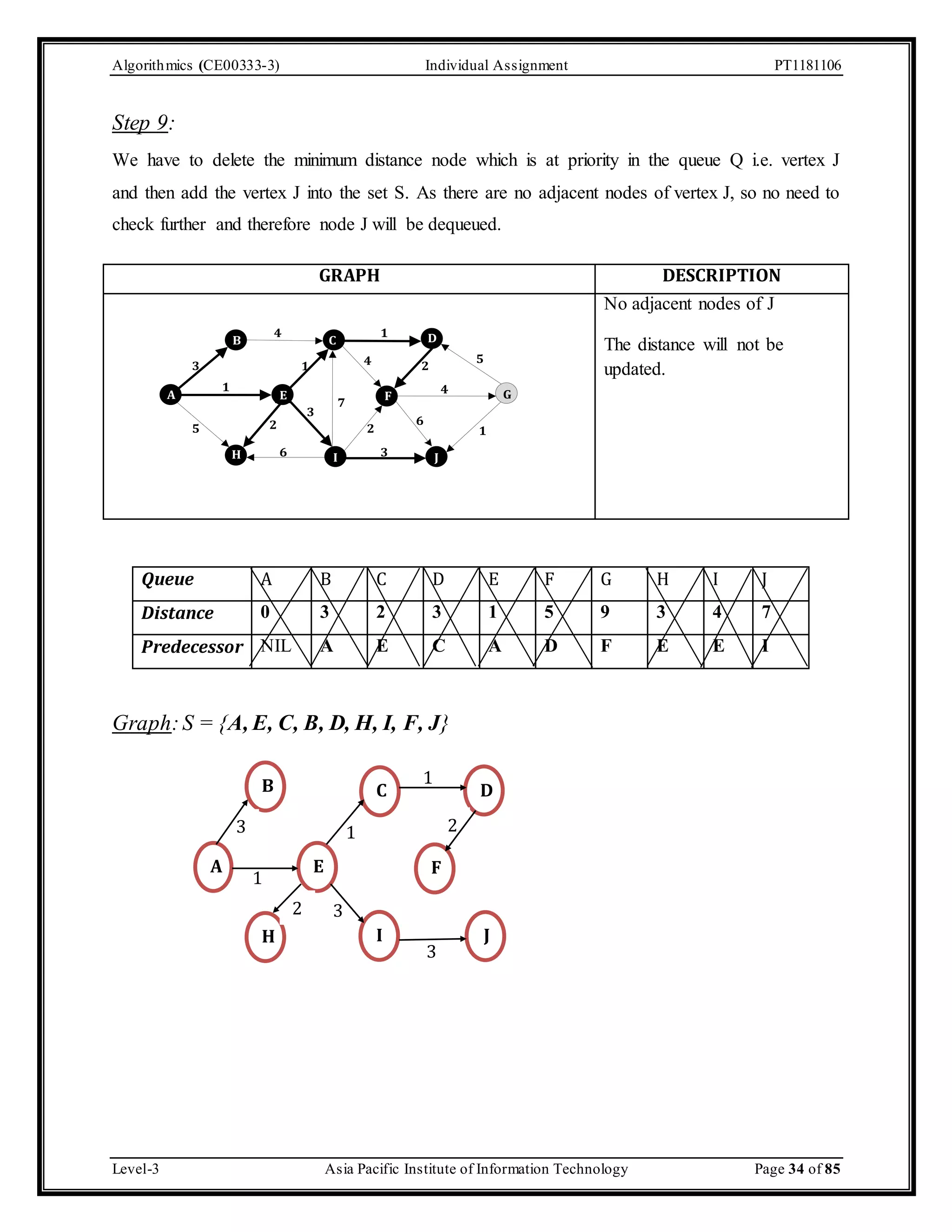
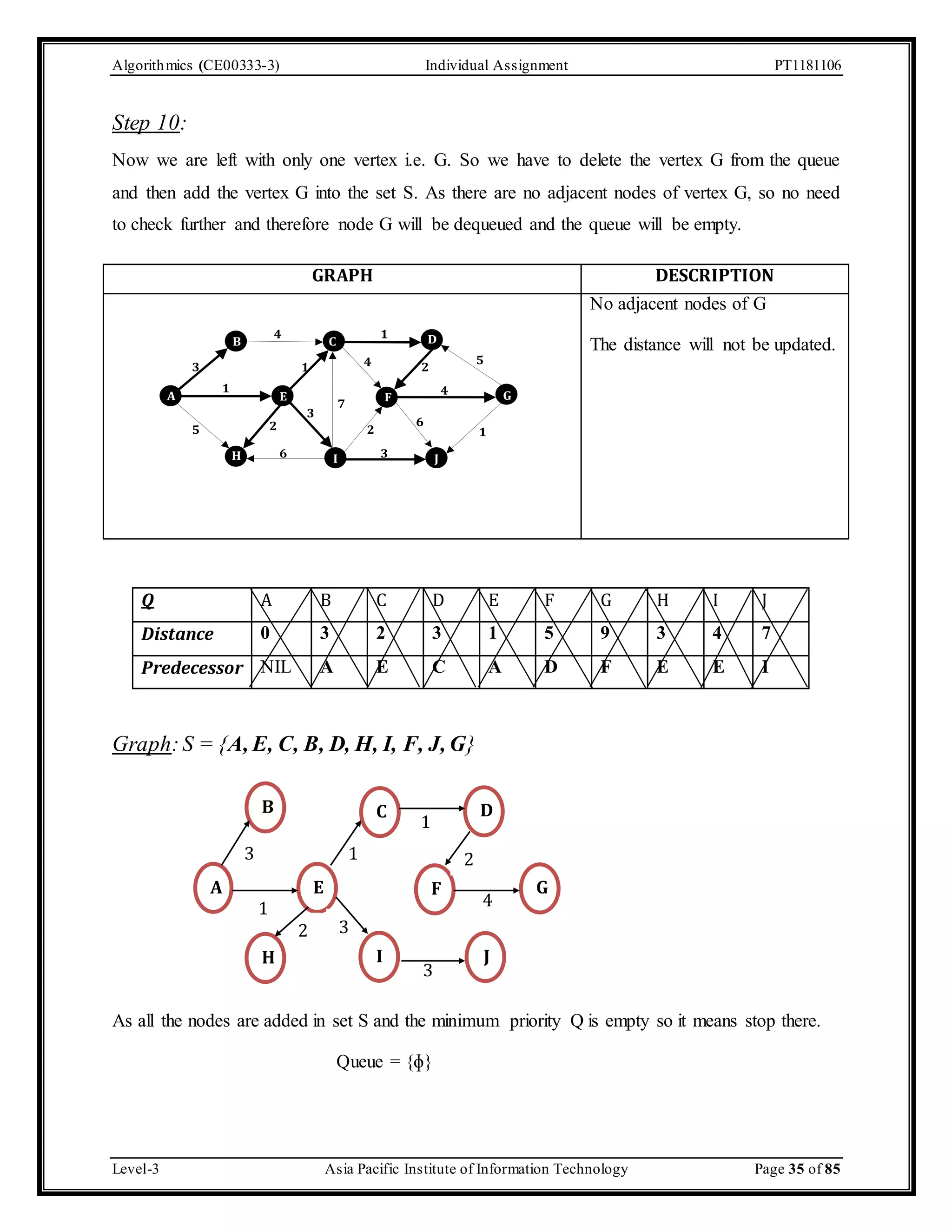
![Algorithmics (CE00333-3) Individual Assignment PT1181106 Step by step solution of Dijkstra’s Algorithm Here it has been mentioned in the scenario that we have to assume that the graph is weighted. Initially the color of the entire vertex is white and its distance is initialized to ∞ except the source vertex A whose distance will be 0. The parent or predecessor of all the vertices is initially NIL. GRAPH DESCRIPTION A 4 1 B C D 3 1 5 4 2 1 4 E F G 3 2 7 5 2 6 3 6 H I J 1 Source vertex = A [Let] The distance of all the vertices will be ∞ except the source vertex A whose distance will be 0. Predecessor of all the vertices will be NIL. Queue A B C D E F G H I J Distance 0 ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ Predecessor NIL NIL NIL NIL NIL NIL NIL NIL NIL NIL Step 1: As we have assumed the source node as vertex A, A is having the minimum distance as 0. Add it to S and relax all the nodes adjacent to source node A. The adjacent nodes of A are B, E & H. Update all the predecessor of all the adjacent nodes and we will dequeue the source node A. GRAPH DESCRIPTION A 4 1 B C D 3 1 5 4 2 1 4 E F G 3 2 7 5 2 6 3 6 H I J 1 Adjacent nodes of A = B, E, H Predecessor of B, E and H = A and rest all the vertices will be NIL. Distance of all the adjacent nodes will be updated. Level-3 Asia Pacific Institute of Information Technology Page 26 of 85](https://image.slidesharecdn.com/algofinal-141210182027-conversion-gate01/75/Algorithms-26-2048.jpg)






![Algorithmics (CE00333-3) Individual Assignment PT1181106 d) Efficiencies for the BFS, DFS and Dijkstra’s Algorithm Time Complexity of BFS Algorithm The space complexity of BFS is expressed as O|V|. Every vertex is added only once in the queue thus occupies O(1) space and vertex V occupies O(V). As every vertex is initialized, added in the queue and dequeued from the queue at most once. The operation of enqueuing takes O(1) time so the total time taken by V vertex is O(V). Because adjacency vertex of each vertex is scanned only when vertex is de-queued, so each adjacent vertex is discovered at least once when directed and two times when undirected. The for-loop inside the while loop is executed at most |E| times if G is a directed graph or 2|E| times if G is undirected. Time Complexity of DFS Algorithm In the case of DFS, each vertex is initialized once and initialization of source node takes O(V) times and DFS-VISIT takes place only once for each vertex in which check white vertex and make it GRAY in color by traversing all its adjacent node which take at most O(E) time and thus complexity is O(V+E). The complexity of DFS is O(V+E). Time Complexity of DIJKSTRA Algorithm EXTRACT-MIN is invoked once per vertex i.e., V times and each EXTRACT-MIN operation takes O(V) time since we have to search through the entire array. Each edge in the adjacency list Adj[v] is examined exactly once during the course of the algorithm. Since the total number of edges in all the adjacency lists is |E|, there a total of |E| iterations of this for loop. These operations are known as DECREASE-KEY operations. Other operations inside the for loop take O(1) time. Time = |V| O (V) + |E| O (1) = O (V2 + E) = O (V2) The above running time resulted from assuming that Q is implemented as an array. The time depends on different Q implementations. The efficiency of Dijkstra’s algorithm can be increased when using binary heap or Fibonacci heap. Complexity: depends on the complexity of the min-heap implementation. Level-3 Asia Pacific Institute of Information Technology Page 36 of 85](https://image.slidesharecdn.com/algofinal-141210182027-conversion-gate01/75/Algorithms-36-2048.jpg)





















![Algorithmics (CE00333-3) Individual Assignment PT1181106 c) Complexity of Heap Sort in terms of Big-oh Notation MAX-HEAPIFY(A, i, n) 1. l ← LEFT(i) 2. r ← RIGHT(i) 3. if l ≤ n and A[l] > A[i] 4. then largest ←l 5. else largest ←i 6. if r ≤ n and A[r] > A[largest] 7. then largest ←r 8. if largest i 9. then exchange A[i] ↔ A[largest] 10. MAX-HEAPIFY(A, largest, n) TASK DESCRIPTION ih n n T i h i 0 ( ) Cost of HEAPIFY at level i number of nodes at that level h i h i i 0 2 Replace the values of ni and hi computed before h h i h i h i 2 2 0 Multiply by 2h both at the nominator and denominator and 1 write 2i as 2 i h h k k k 0 2 2 Change variables: k = h - i k 2 k 0 k n The sum above is smaller than the sum of all elements to and h = lgn The sum above is smaller than 2 Running time of BUILD-MAX-HEAP: T(n) = O(n) O(n) Level-3 Asia Pacific Institute of Information Technology Page 84 of 85](https://image.slidesharecdn.com/algofinal-141210182027-conversion-gate01/75/Algorithms-84-2048.jpg)
![Algorithmics (CE00333-3) Individual Assignment PT1181106 REFERENCES Websites: 1. Breadth First Search PersonalKent, (2010). Breadth First Search – PersonalKent. [online] Available at: http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/breadthSearc h.htm [Accessed 21 Oct. 2014] 2. Depth First Search Brpreiss, (2012). Depth First Traversal – Brpreiss, [online] Available at: http://www.brpreiss.com/books/opus4/html/page551.html Depth First Tranversal by Bruno R. Preiss, P.Eng. [Accessed 23 Oct. 2014] 3. Dijkstra Algorithm Ryan Mark (2004) Dijkstra’s Algorithm [Online]. Available from : http://www.cs.bham.ac.uk/~mdr/teaching/modules04/java2/DijkstraAlgo.html [Accessed From: 28 Oct. 2014] 4. Time Complexity of Algorithm GeeksforGeeks, (2012). Greedy Algorithms | Set 2 (Kruskal’s Minimum Spanning Tree Algorithm) - GeeksforGeeks. [online] Available at: http://www.geeksforgeeks.org/greedy-algorithms- set-2-kruskals-minimum-spanning-tree-mst/ [Accessed 30 Oct. 2014]. 5. Prim’s Algorithm Papaioannou Panagiotis (1992) Prims Algorithm [Online] Available From: http://students.ceid.upatras.gr/~papagel/project/prim.htm [Accessed 1 Nov. 2014] 6. Krusk al’s Algorithm Kruskal J.B.(1989) Kruskal’s Algorithm [Online] Available from: http://lcm.csa.iisc.ernet.in/dsa/node184.html [Accessed 3 Nov. 2014] Books: 7. Data Structure and algorithm analysis Weiss, M. (1995). Data structures and algorithm analysis. Redwood City, Calif.: Benjamin/Cummings Pub. Co. 8. Fundamentals of computer algorithm Satraj sahni (2008). Fundamental of computer algorithm. 2nd ed. New delhi: Universities Press India pvt. Level-3 Asia Pacific Institute of Information Technology Page 85 of 85](https://image.slidesharecdn.com/algofinal-141210182027-conversion-gate01/75/Algorithms-85-2048.jpg)