A novel energy efficient data gathering algorithm for wireless sensor networks using artificial intelligence

A novel energy efficient data gathering algorithm for wireless sensor networks using artificial intelligence

• 1.
  IAES International Journalof Artificial Intelligence (IJ-AI) Vol. 13, No. 4, December 2024, pp. 3827~3836 ISSN: 2252-8938, DOI: 10.11591/ijai.v13.i4.pp3827-3836  3827 Journal homepage: http://ijai.iaescore.com A novel energy efficient data gathering algorithm for wireless sensor networks using artificial intelligence Swapna Chavva1 , Vijayashree R. Budyal2 1 Department of Electronics and Communication Engineering, Sri Venkateshwara College of Engineering, Visvesvaraya Technological University, Bengaluru, India 2 Department of Information Science and Engineering, Sai Vidya Institute of Technology, Bengaluru, India Article Info ABSTRACT Article history: Received Dec 3, 2023 Revised Apr 8, 2024 Accepted Apr 17, 2024 Energy efficiency is challenging task in wireless sensor network (WSN), it is the main barrier in extending network lifespan. In WSN, maximum energy is wasted during data gathering, hence energy efficient algorithms using artificial intelligence can be designed, that preserves energy while data gathering. Thus, our proposed methodology, A novel energy efficient data gathering algorithm using artificial intelligence for wireless sensor networks (NDGAI), uses novel artificial intelligence algorithms and addresses issue of energy consumption while gathering data. In our proposed work, mobile element is utilized to gather information from sensor nodes in the clusters, formed using amended-expectation-maximization. Each cluster should have a cluster leader and a virtual-point. These cluster leaders are formed utilizing fuzzy logic technique. Virtual-points are formed in the range of cluster leader, only when cluster leader has data. The mobile element reaches virtual point by taking the optimal path, that determined by the hybrid artificial intelligence algorithms, such as artificial-bee-colony (ABC) technique and particle swarm optimization (PSO) algorithms. Thus, by properly performing clustering, cluster leader selection, virtual-point selection and optimal path determination, lead to improved network lifetime and energy saving while gathering the data. Results are simulated and compared with scalable grid- based data gathering algorithm for environmental monitoring wireless sensor networks (SGBDN) and proposed algorithm performs better. Keywords: Cluster leader Clustering Fuzzy logic Mobile element Virtual points Wireless sensor network This is an open access article under the CC BY-SA license. Corresponding Author: Swapna Chavva Department of Electronics and Communication Engineering, Sri Venkateshwara College of Engineering Bengaluru, India Email: swapnaeng@gmail.com 1. INTRODUCTION Large number of sensors are deployed in the field, termed as wireless sensor network (WSN) [1]. These sensors helps in sensing the environment and communicates the same with base station and from base station to the user and helps the user to monitor and control the environment remotely. Thus, WSN has wide range of applications in military surveillance, agriculture, medical domain [2]–[5], and helps to monitor information such as temperature, pressure, and humidity. While gathering the information from the sensor node lot of power is consumed to transmit the information from each sensor to the base station [6]. The low energy adaptive clustering hierarchy (LEACH) [7] is one of the hierarchical clustering method where the network is partitioned or clustered and based on the probability one of the node is selected as cluster head (CH). In order to make the network last longer, mobile elements are used. These mobile elements [8], [9] go to the CH and receive data from the network. Several artificial intelligence methods, which are a subset of machine learning [10]–[12], can be used to boost efficiency and lower energy use.
• 2.
   ISSN: 2252-8938 IntJ Artif Intell, Vol. 13, No. 4, December 2024: 3827-3836 3828 In our proposed work, a novel energy efficient data gathering algorithm for wireless sensor networks using artificial intelligence (NDGAI) the base station is considered to be at the center. The network consists of hundred of nodes (also known as motes) and the entire network is sub divided into optimal number of clusters by using gap statistics algorithm along with amended expected maximization (AEM). The cluster leader is selected based on the fuzzy logic near the centroid of the each cluster. The mobile element has to reach all the clusters and gather the information. The stop points are the virtual points that are considered with in the communication range of the cluster leader and the mobile elements reaches these virtual points and gather the data. The path of the mobile elements is determined by particle swarm optimization (PSO) algorithm with artificial bee colony (ABC) named as PSO-ABC algorithm is used, which solves the travelling salesman problem. The residue of paper is categorized as literature review in section 2, section 3 presents the system model and assumptions, section 4 consists of proposed work, section 5 consists of simulation results, and finally section 6 deals with the conclusions. 2. LITERTAURE REVIEW Heinzelman et al. [13] proposed an hierarchical routing algorithm known as LEACH. Here the network is divided into clusters and CH’s are selected based on the probability function, that selects the node with high energy as CH. However, the performance of the network degrades as the CH sends the data directly to the base station. Salem and Shudifat [14] has proposed an enhanced version of LEACH protocol. The CH is selected based on the distance function in such a way that the distance is low from base station and this helps to reduce the energy consumption by increasing the network life time. According to Younis and Fahmy [15], an algorithm is designed in which CH’s are selected by considering the node residual energy and degree of the node to its neighbours and achieves unvarying CH distribution in the entire network. However more energy is utilized when data is transmitted directly to the base station. Lindsey and Raghavendra [16] has proposed an algorithm, power-efficient gathering in sensor information systems (PEGASIS), in which chain among the sensor nodes are formed and the node transit its information to a nearest neighbour nodes and then finally to the base station. But the nodes close to the base station die faster, which shortens the life of the network. CH selection is also looked at in [17]. This method gets the lowest lag by stopping the process for O (loglog N) when N nodes are given and giving a path loss exponent of 2. The hierarchical grouping method is used in [18]. Each cluster has a CH that gathers data from the other cluster members, adds it all together, and sends it to the base station by the closest CH. Each CH in a cluster takes a turn based on the time. As time goes on, though, the leftover energy may be less than the cutoff energy, which breaks the transmission link. As the utilization of wireless sensor networks is increasing drastically there is lot of research happening and the authors have designed algorithms based on mobile node [19]. In other words, a mobile node was used. This node sends data to the base station from the CH or the cluster. One idea from Cho et al. [20] is to use mobile sinks to collect data as part of a programme. In the P-LEACH algorithm that was created, the groups are shaped like circles and are split into four separate areas. Each of these areas can effectively track mobile sinks and save energy. On the other hand, the suggested method has more data that is duplicated. Gao et al. [21] have used integer-linear-programming problem and proposed maximum amount shortest path and reduced energy consumption, by finding optimal mapping between its members and sub-sink. Si et al. [22] has employed a data gathering method based on fuzzy rule-based CH selection by considering residual energy of nodes, degree of centrality, sink distance and number of neighbour nodes. This ensures uniform CH distribution. Along with CH election, intra cluster data aggregation using correlation function in fuzzy theory is adopted [23]. 3. SYSTEM MODEL AND ASSUMPTIONS The main motivation for our proposed work NDGAI is to find optimal number of cluster, cluster leader selection, virtual points selection and path selection for mobile element using artificial intelligence to the existing algorithms. In our proposed work, S number of sensor nodes are deployed in the m2 network area. The location of the sensor nodes in known by using the localization technique. The network is based on the hierarchical network [24], i.e., it consists of clusters with k cluster centroids denoted as k1,k2,k3.......kn. Each cluster consists of cluster leader, virtual points points between cluster leader and base station [25], mobile element to gather the information from cluster leader and a center base station. 3.1. Assumptions The following are some of the assumptions that are considered in WSN. Those assumptions are listed as follows: All the nodes are deployed according to Gaussian distribution function. The communication range of all the sensor nodes including mobile element have the communication range of R and is able to communicate properly.
• 3.
  Int J ArtifIntell ISSN: 2252-8938  A novel energy efficient data gathering algorithm for wireless sensor networks using … (Swapna Chavva) 3829 4. PROPOSED WORK The proposed work NDGAI deals with the data gathering from the sensor nodes in the WSN. Whilst sending and receiving the data packets, lot of energy is consumed respectively as given by (1) and (2). 𝑒𝑡𝑟 = { 𝑙𝐸𝑒𝑙𝑒 + 𝜀𝑓𝑠𝑑2 d<d𝑜 𝑙𝐸𝑒𝑙𝑒 + 𝑙𝜀𝑎𝑚𝑝𝑙𝑖𝑑4 d ≥ 𝑑𝑜 (1) 𝑒𝑟𝑡 = 𝑙𝐸𝑒𝑙𝑒 (2) Where energy required for transmission is given by etr; energy required for receiving is denoted as ert transmitted bits is denoted by l; each bit transit energy is Eele; energy cost for transmission and reception of signal is given by ϵfsd2 and ϵfsd4; transmission distance is denoted as d, d0 is the error free receiving distance. Thus from (1) it is clear that the energy required for transmitting the data is directly proportion to the square of the communication distance. 4.1. Clustering phase Clustering the sensor network means dividing the entire network into sub networks. The benefits of clustering include tactical resource usage, scalability of network, elevated performance and to avoid longer distance multi hop communication. Because of these advantages clustering is considered to be one of the major step in data gathering in WSN. a. Gap statistics method to determine optimal number of clusters: In gap statistics method the maximum number of cluster kmax has to be defined initially. Let the number of nodes to be 1, 2, 3, .........., N and the number of clusters be k1, k2, ......, kmax. The optimal number of clusters can be evaluated by using the following steps. Step.1: calculate squared Euclidean distance 𝐷𝑝𝑞 2 between pth node with the qth node using (3). 𝐷𝑝𝑞 2 = ∑ (𝑝𝑖 − 𝑞𝑖)2 𝑀 𝑖=1 (3) Let kr denote the indices of observations in cluster r and 𝑁𝑟 = |𝐾𝑟| Step.2: calculate the summation between the pairs of distances of all the nodes that belong to the cluster r, using (4). 𝐷𝑟 = ∑ 𝐷𝑝𝑞 𝑝,𝑞∈𝐾𝑟 (4) Step.3: measure dispersion within intra-cluster, denoted by 𝑊𝑘, which gives the pooled summation of squares within cluster means and is given by (5). 𝑊𝑘 = ∑ 1 2𝑁𝑟 𝑘 𝑟=1 D𝑟 (5) Step.4: generate D reference points using uniform random distribution. Cluster each of these data points by considering k1, k2…….kmax. By considering all these data points calculate the different sizes of clusters, enumerate dispersion within intra-cluster given by 𝑊𝑘𝑑. Step.5: compute the deviation between 𝑊𝑘 and 𝑊𝑘𝑑 using (6) and standard deviation can be calculated using (7). 𝐺𝑎𝑝𝑛(𝑘) = 1 𝐷 ∑ (𝑙𝑜𝑔( 𝑊𝑘𝑑) − 𝐷 𝑑=1 𝑙𝑜𝑔( 𝑊𝑘)) (6) 𝑆𝑘 = [ 1 𝐷 ∑ (𝑙𝑜𝑔( 𝑊𝑘𝑑) − 𝐷 𝑑=1 𝑙𝑜𝑔( 𝑊𝑘))] [√1 + 1 𝐷 ] (7) Step.6: finally, the optimal number of cluster value is calculated in such a way that the smallest value of k provided the condition stated in (8) is satisfied. 𝐺𝑎𝑝𝑛(𝑘) ≥ 𝐺𝑎𝑝𝑛(𝑘 + 1) − 𝑆𝑘+1 (8) Thus, using gap statistics, the optimal number of clusters are determined. When the optimal number of clusters are identified, clusters are formed by using amended expectation maximization algorithm which is a statistical method to determine maximum likelihood function.
• 4.
   ISSN: 2252-8938 IntJ Artif Intell, Vol. 13, No. 4, December 2024: 3827-3836 3830 b. AEM algorithm: expectation maximization algorithm is a statistical approach and belongs to unsupervised learning method and is used in the formation of clusters in the WSN. expectation maximization algorithm is one of the soft clustering algorithms, which means that the clusters may overlap, i.e., the node may belong to more than one cluster and the amount of relationship of the node with each cluster is identified by calculating the degree of responsibility of the node to the cluster. Hence to calculate the Euclidean distance the generalized formula adopted is given in (9). 𝐷𝑝𝑛 = √(𝑥𝑝 − 𝑥𝑛)2 − (𝑦𝑝 − 𝑦𝑛)2 (9) The node in a WSN belongs to a particular cluster if its distance to the centroid points is less when compared with the distance from other centroids. After initial clusters are formed the mean value for each cluster denoted by µk is calculated by considering the average of all the nodes that belong to a particular cluster. Covariance, ξk is calculated using (10). 𝜉𝑘 = 1 𝑁 ∑ ( 𝑁 𝑛=1 𝑥𝑛 − 𝜇𝑥)(𝑦𝑛 − 𝜇𝑦) (10) Thus the initial cluster parameters µk and ξk are obtained and these are the position vectors of cluster centroids. During initialization step, nodes in WSN are deployed according to the Gaussian distribution function with probability function, given by (11). 𝑃(𝑥𝑛) = ∑ 𝜋𝑘𝑁 ( 𝑥𝑛 𝜇𝑘 , 𝜉𝑘) 𝑘 (11) Where xn is the nth node position vector, k are the number of clusters, µk is the mixing coefficient and the value of πk depends on the number of clusters and the condition on πk calculated based on µk and it is a 22 diagonal matrix. 𝑁 ( 𝑥𝑛 𝜇𝑘 , 𝜉𝑘) is the Gaussian distribution function given by (12). 𝑁 ( 𝑥𝑛 𝜇𝑘 , 𝜉𝑘) = 1 (2𝜋)|𝜉𝑘| 𝑒𝑥𝑝 [− 1 2 (𝑥𝑛 − 𝜇𝑥)𝑇 𝜉−1 (𝑥𝑛 − 𝜇𝑘)] (12) During expectation step, the degree of responsibility, of each node to the cluster has to be calculated. Degree of responsibility, denoted as Γkn can be obtained using (13). Γ𝑘𝑛 = 𝜋𝑘𝑁( 𝑥𝑛 𝜇𝑘 ,𝜉𝑘) ∑ 𝜋𝑗𝑁 𝐾 𝑗=1 ( 𝑥𝑛 𝜇𝑗 ,𝜉𝑗) (13) As a next step, maximization step has to be executed. In this step using the degree of responsibility function, which is obtained in the expectation step has to be used to find the new parameters of the cluster centroids. This can be updated with the new values as shown from (14)-(17). The new mean value is calculated as in (14). 𝜇𝑘 𝑛𝑒𝑤 = 1 𝑁𝑘 ∑ 𝛤 𝑘𝑛𝑥𝑛 𝑁 𝑛=1 (14) The total number of nodes that belong to cluster K is given by (15). 𝑁𝑘 = ∑ 𝛤 𝑘𝑛𝑥𝑛 𝑁 𝑛=1 (15) The mixing coefficient πk can be updated using (16). 𝜋𝑘 𝑛𝑒𝑤 = 𝑁𝑘 𝑁 (16) Covariance can be updated by using (17). 𝜉𝑘 𝑛𝑒𝑤 = 1 𝑁𝑘 ∑ 𝛤 𝑘𝑛 𝑁 𝑛=1 (𝑥𝑛 − 𝜇𝑘 𝑛𝑒𝑤 )(𝑥𝑛 − 𝜇𝑘 𝑛𝑒𝑤 )𝑇 (17)
• 5.
  Int J ArtifIntell ISSN: 2252-8938  A novel energy efficient data gathering algorithm for wireless sensor networks using … (Swapna Chavva) 3831 After updating the parameters of the centroid of the cluster, as a last step, the expectation maximization algorithm is evaluated by evaluating convergence of log likelihood function as given in (18). 𝑃 = 𝑙𝑛 𝑝 ( 𝑥𝑛 𝜇𝑘 , 𝜉𝑘, 𝜋𝑘) = ∑ 𝑙𝑛 (∑ 𝜋𝑘𝑁 ( 𝑥𝑛 𝜇𝑘 , 𝜉𝑘) 𝐾 𝑘=1 ) 𝑁 𝑛=1 (18) 4.2. Cluster leader and virtual point selection Cluster leader election phase: following the clusters formation, the cluster leader has to be determined near the centroid, so that all the nodes within the cluster can send their gathered information to the cluster leader. It mainly consists of four parts. They are i) Fuzzifier, ii) Fuzzy rule base system, iii) intelligent fuzzy inference system (IIS), and iv) Defuzzifier, as shown in Figure 1. Figure 1. Fuzzy logic controller system a) Fuzzifier: fuzzifier converts crisp numbers from the inputs to the fuzzy set of values. The inputs to this Fuzzifier are: − Closeness of node to the cluster centroid (CCC): node centrality conveys the information that how much near the node is to the centroid in each cluster. Thus CC can be calculated by using (19). 𝐶𝐶𝐶 = √𝐷𝑛𝑘, 𝐶𝑘 (19) − Neighbour nodes: it tells us how many nodes are surrounded by the elected cluster leader and the equation to calculate neighbour nodes is given in (20). 𝑁𝑁 = 𝐿 𝑀 (20) where L is the number of neighbours and M is the total number of nodes in the cluster. The more the value of neighbour nodes the more the chances to be the cluster leader. − Direction of node towards base station (DBS): it tells us that how much the node is near to the base station. It can be calculated using (21). 𝐷𝐵𝑆 = √𝐷𝑛𝑘,𝑏 (21) where nk is the nth node in kth cluster and b is the location of base station. The less the DBS value, the more the chances to become cluster leader. Pos = [VeryHigh, High, MediumHigh, MediumLow, Low, VeryLow] b) Defuzzifier: defuzzifier helps in defuzzification. Deffuzifier takes the fuzzy output set from the IIS and provides crisp output, that helps in determining the cluster leader accurately. Thus to obtain the crisp output from defuzzifier, the centroid method, which is also known as the center of area is used. In this method the center point is determined, where the area under the curve on both sides of this point is equal and the same is obtained by using (22). ∫ 𝜇𝐴(𝑥)𝑑𝑥 = ∫ 𝜇𝐴(𝑥)𝑑𝑥 𝑏 𝑥∗ 𝑥∗ 𝑎 (22)
• 6.
   ISSN: 2252-8938 IntJ Artif Intell, Vol. 13, No. 4, December 2024: 3827-3836 3832 Virtual points election phase: the selection of virtual point is very important to reduce the path length of the mobile element. Selecting the optimal number of virtual points has to be achieved, so that the data is collected effectively. The distance from the cluster leader and the base station can be calculated by using Euclidean distance and then by subtracting the range of communication as shown in (23). 𝐷𝐶,𝐵 = √(𝑐𝑖 − 𝑏1)2 − (𝑐𝑗 − 𝑏2)2 (23) where i is the ith cluster leader, (ci, cj) are the cluster leader ordinates and (b1, b2) are the base station coordinates. Thus by using (23) the exact point of virtual points can be obtained. 4.3. Path determination phase The search is made in such a way that the objective function value is minimized. The objective function is fixed by considering the parameters such as in (24). 𝑥𝑚 = (𝐷𝑖𝑗), (𝑒𝐶𝐿), (𝑡𝑚) (24) where 𝐷𝑖𝑗 is the distance between the nodes, eCL is the energy in cluster leader, tm is the time taken by the mobile element to reach the virtual points. Thus the objective function is given as in (25). 𝑓𝑖 = 𝑚𝑖𝑛( 𝛼1𝐷𝑖𝑗 + 𝛼2𝑒𝐶𝐿 + 𝛼3𝑡𝑚 (25) Once the objective function is fixed the artificial bees that are present in the search space randomly selects an initial vector and later the best route is found from the initial population by using greedy solution. This is achieved by iterative method and employing the strategy by moving towards the better solution and by abandoning the poor solution. To determine whether the solution is best or poor, the objective function is given in (26). 𝑓𝑖𝑡𝑚 = { 1 + 𝑎𝑏𝑠(𝑓𝑖) if 𝑓𝑖 < 0 1 1 1+𝑓𝑖 if 𝑓𝑖 ≥ 0 (26) 5. SIMULATION RESULTS This section helps to analyse the simulation results of the proposed method. The performance of WSN is evaluated by implementing the proposed methodology using MATLAB. To evaluate the performance, 10001000 m sensing area is considered. The initial energy of each node is assumed to be 50 J and the energy required to transmit or receive each data packet is considered to be 50 nJ. The Table 1 gives the list of parameters considered. Table 1. Simulation parameters Simulation Parameters Values Area for sensing, 10001000 m Total nodes, S 100-200 Nodes initial energy, E 50 J Transmission energy required,etr 50 nJ Data receiving energy required, ert 50 nJ Packet length of data,P 512 bits Threshold energy of model,D0 50 J Each bits transmission energy,Ee 50 nJ/bit Amplifier coefficient,єs 5 PJ/bit/m2 Value of convergence,є 0.01 Transmission Euclidean distance, D 80 m Threshold, TH 25 J The Figure 2 represents number of clusters that can be considered by using gap statistics algorithm. The number of clusters here are determined by considering the gap between Log(Wk) and Elog(Wk). Figure 3 shows how the average energy is consumed with in the cluster and our proposed algorithm requires less energy when compared with scalable grid-based data gathering algorithm for environmental monitoring wireless sensor networks (SGBDN).
• 7.
  Int J ArtifIntell ISSN: 2252-8938  A novel energy efficient data gathering algorithm for wireless sensor networks using … (Swapna Chavva) 3833 Figure 2. Determination of optimal number of clusters Figure 3. Average energy consumed with in a cluster The network lifetime of the proposed network as the nodes varied from 10 to 200 is as shown in Figure 4. It is observed that the number of live nodes is more in the proposed algorithm when compared to the traditional algorithm. Figure 5 shows that the number of nodes that are alive after each round is given in the figure and it shows that our proposed algorithm is efficient as the nodes that that dyeing while collecting the data is less as the intra cluster distance has been reduced and the communication distance is efficiently considered. Figure 6 also shows the number nodes that are alive is reducing with the increase in time. The proposed algorithm better performs as the path determined is the shortest path. The Figure 7 shows the total energy consumed with respect to the time. As the virtual points as selected based on the information present in the cluster leader, the energy consumed will be less in the proposed algorithm. Also, the optimal path is determined by using the PSO-ABC algorithm which is used to solve the TSP problem. Hence the energy consumed has been reduced drastically.
• 8.
   ISSN: 2252-8938 IntJ Artif Intell, Vol. 13, No. 4, December 2024: 3827-3836 3834 Figure 4. Network life time using SGBDN and NDGAI Figure 5. Number of nodes alive Figure 6. Number of nodes alive as a function of time
• 9.
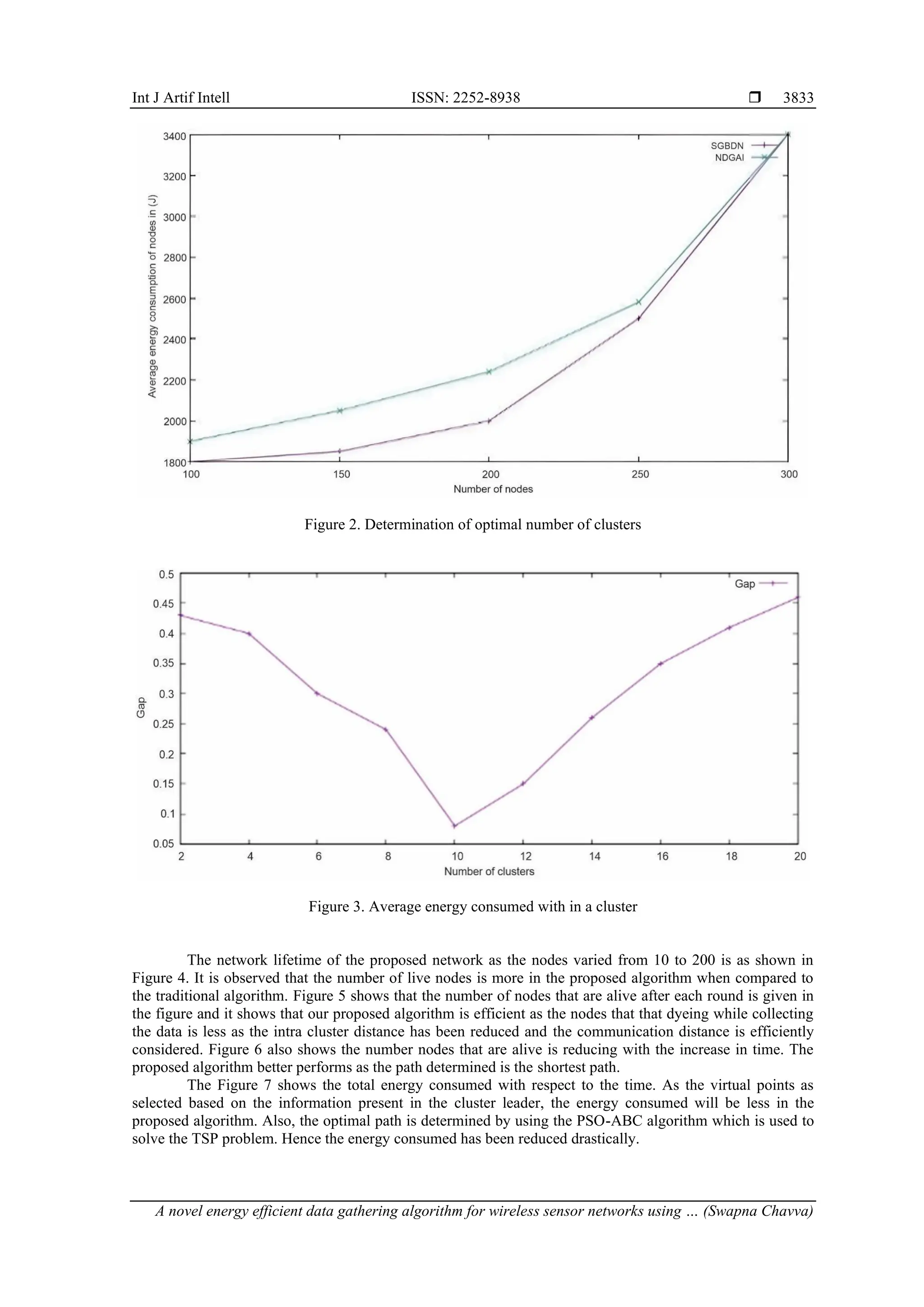
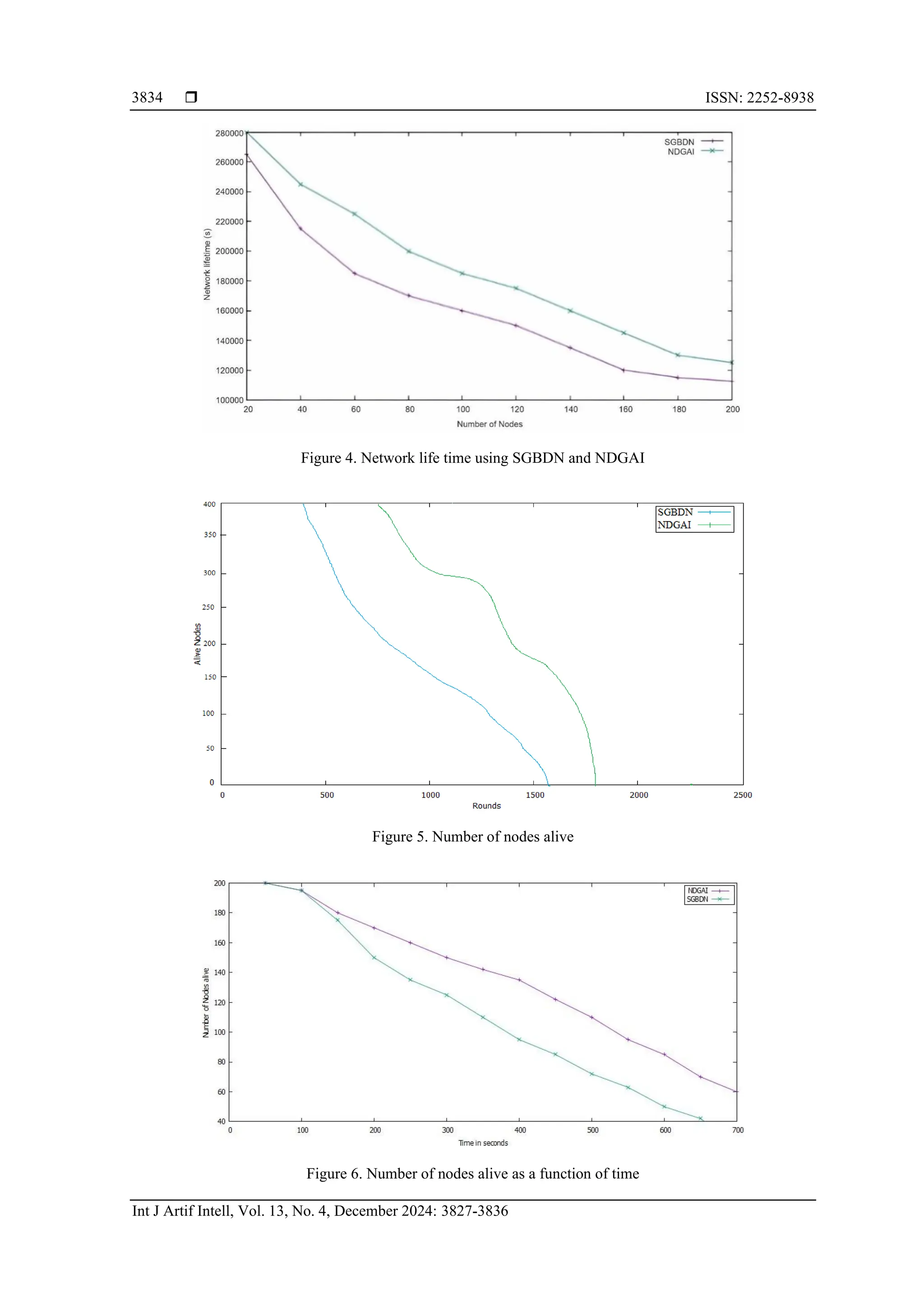
  Int J ArtifIntell ISSN: 2252-8938  A novel energy efficient data gathering algorithm for wireless sensor networks using … (Swapna Chavva) 3835 Figure 7. Total energy consumed 6. CONCLUSION The proposed methodology balances the power consumption and the energy is efficiently used while data is gathered in the WSN. NDGAI uses gap statistics algorithm along with distance function for the selecting the optimal number of clusters. The clusters which are formed are fine-tuned by using the AEM algorithm which forms the final clusters, where the cluster centroids are selected in such a way that the node density is more. Once the virtual points are formed the mobile element travels to this virtual point and collects the data from the cluster leader. The optimal path for mobile element is determined by using PSO- ABC algorithm which solves the TSP problem. Thus, the entire methodology of considering ME along with the intelligent algorithms, helps in data gathering the information in the most energy efficient way and conserves lot of energy. The simulation results also shows that the proposed methodology is very efficient and improves network lifetime. REFERENCES [1] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam, and E. Cayirci, “A survey on sensor networks,” IEEE Communications Magazine, vol. 40, no. 8, pp. 102–114, 2002, doi: 10.1109/MCOM.2002.1024422. [2] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam, and E. Cayirci, “Wireless sensor networks: A survey,” Computer Networks, vol. 38, no. 4, pp. 393–422, 2002, doi: https://doi.org/10.1016/S1389-1286(01)00302-4. [3] S. M. Diamond and M. G. Ceruti, “Application of wireless sensor network to military information integration,” in 2007 5th IEEE International Conference on Industrial Informatics, Jul. 2007, vol. 1, pp. 317–322, doi: 10.1109/INDIN.2007.4384776. [4] I. Bekmezci and F. Alagöz, “Energy efficient, delay sensitive, fault tolerant wireless sensor network for military monitoring,” International Journal of Distributed Sensor Networks, vol. 5, no. 6, pp. 729–747, Nov. 2009, doi: 10.1080/15501320902768625. [5] L. Yu, N. Wang, and X. Meng, “Real-time forest fire detection with wireless sensor networks,” in Proceedings. 2005 International Conference on Wireless Communications, Networking and Mobile Computing, 2005, vol. 2, pp. 1214–1217, doi: 10.1109/WCNM.2005.1544272. [6] K. Akkaya and M. Younis, “A survey on routing protocols for wireless sensor networks,” Ad Hoc Networks, vol. 3, no. 3, pp. 325–349, May 2005, doi: 10.1016/j.adhoc.2003.09.010. [7] W. R. Heinzelman, A. Chandrakasan, and H. Balakrishnan, “Energy-efficient communication protocol for wireless microsensor networks,” in Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, 2000, vol. 1, doi: 10.1109/HICSS.2000.926982. [8] S. Ch and V. R. Budyal, “Expectation maximization and fuzzy logic based energy efficient data collection in wireless sensor networks with mobile elements,” in 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), 2020, pp. 21–26, doi: 10.1109/SPIN48934.2020.9071055. [9] R. Zhang, J. Pan, D. Xie, and F. Wang, “NDCMC: A hybrid data collection approach for large-scale WSNs using mobile element and hierarchical clustering,” IEEE Internet of Things Journal, vol. 3, 2015, doi: 10.1109/JIOT.2015.2490162. [10] S. B. Kotsiantis, I. Zaharakis, P. Pintelas, and Others, “Supervised machine learning: A review of classification techniques,” Emerging artificial intelligence applications in computer engineering, vol. 160, no. 1, pp. 3–24, 2007. [11] C. Zhang, P. Patras, and H. Haddadi, “Deep learning in mobile and wireless networking: A survey,” IEEE Communications Surveys & Tutorials, vol. 21, no. 3, pp. 2224–2287, 2019, doi: 10.1109/COMST.2019.2904897. [12] X. Wang, X. Li, and V. C. M. Leung, “Artificial intelligence-based techniques for emerging heterogeneous network: state of the arts, opportunities, and challenges,” IEEE Access, vol. 3, pp. 1379–1391, 2015, doi: 10.1109/ACCESS.2015.2467174. [13] W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol architecture for wireless microsensor networks,” IEEE Transactions on Wireless Communications, vol. 1, no. 4, pp. 660–670, 2002, doi: 10.1109/TWC.2002.804190. [14] A. O. A. Salem and N. Shudifat, “Enhanced LEACH protocol for increasing a lifetime of WSNs,” Personal and Ubiquitous Computing, vol. 23, no. 5, pp. 901–907, 2019, doi: 10.1007/s00779-019-01205-4.
• 10.
   ISSN: 2252-8938 IntJ Artif Intell, Vol. 13, No. 4, December 2024: 3827-3836 3836 [15] O. Younis and S. Fahmy, “HEED: a hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks,” IEEE Transactions on Mobile Computing, vol. 3, no. 4, pp. 366–379, Oct. 2004, doi: 10.1109/TMC.2004.41. [16] S. Lindsey and C. S. Raghavendra, “PEGASIS: Power-efficient gathering in sensor information systems,” in Proceedings, IEEE Aerospace Conference, 2002, vol. 3, pp. 3-1125-3–1130, doi: 10.1109/AERO.2002.1035242. [17] Y. Jin, L. Wang, Y. Kim, and X. Yang, “EEMC: An energy-efficient multi-level clustering algorithm for large-scale wireless sensor networks,” Computer Networks, vol. 52, no. 3, pp. 542–562, Feb. 2008, doi: 10.1016/j.comnet.2007.10.005. [18] A. Manjeshwar and D. P. Agrawal, “TEEN: A routing protocol for enhanced efficiency in wireless sensor networks,” in Proceedings - 15th International Parallel and Distributed Processing Symposium, IPDPS 2001, 2001, vol. 1, no. 2001, pp. 2009– 2015, doi: 10.1109/IPDPS.2001.925197. [19] Y. Yang, M. I. Fonoage, and M. Cardei, “Improving network lifetime with mobile wireless sensor networks,” Computer Communications, vol. 33, no. 4, pp. 409–419, Mar. 2010, doi: 10.1016/j.comcom.2009.11.010. [20] S. Cho, L. Han, B. Joo, and S. Han, “P-LEACH: An efficient cluster-based technique to track mobile sinks in wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 10, no. 9, 2014, doi: 10.1155/2014/803656. [21] S. Gao, H. Zhang, and S. K. Das, “Efficient data collection in wireless sensor networks with path-constrained mobile sinks,” IEEE Transactions on Mobile Computing, vol. 10, no. 4, pp. 592–608, Apr. 2011, doi: 10.1109/TMC.2010.193. [22] W. Si, H. Shi, and P. Liu, “A collaborative data gathering mechanism based on fuzzy decision for wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 11, no. 8, Aug. 2015, doi: 10.1155/2015/952428. [23] R. Anwit and P. K. Jana, “An approximation algorithm to find optimal rendezvous points in wireless sensor networks,” International Conference on Advanced Computing Networking and Informatics, pp.193-204, 2018, doi: 10.1007/978-981-13- 2673-8_22. [24] C. Konstantopoulos, G. Pantziou, D. Gavalas, A. Mpitziopoulos, and B. Mamalis, “A rendezvous-based approach enabling energy-efficient sensory data collection with mobile sinks,” in IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 5, pp. 809-817, May 2012, doi: 10.1109/TPDS.2011.237. [25] J. Zhang, J. Tang, T. Wang, and F. Chen, “Energy-efficient data-gathering rendezvous algorithms with mobile sinks for wireless sensor networks” International Journal of Sensor Networks, vol. 23, no.4, pp. 248-257, 2017, doi: 10.1504/IJSNET.2017.083533. BIOGRAPHIES OF AUTHORS Swapna Chavva is currently pursuing her Ph.D. in Visvesvaraya Technological University, Belagavi, Karnataka, India and received M.Tech. Degree in Systems and Signal Processing from Jawaharlal Nehru Technological University, Hyderabad, Andhra Pradesh. She is currently working as an Assistant Professor at Sri Venkateshwara College of Engineering, Bengaluru, Karnataka, India. She has experience of around 15 years in teaching and 4 years in research. She can be contacted at email: swapnaeng@gmail.com. Dr. Vijayashree R. Budyal received Ph.D. degree in Electrical and Electronics from Visvesvaraya Technological University Belagavi, Karnataka, India. She is currently working as Professor at Sai Vidya Institute of Technology, Bengaluru, Karnataka, India. She has vast experience of more than 27 years in teaching. She received best research publication award from VGST, Karnataka in 2014. She can be contacted at email: vijayashreerb@gmail.com.