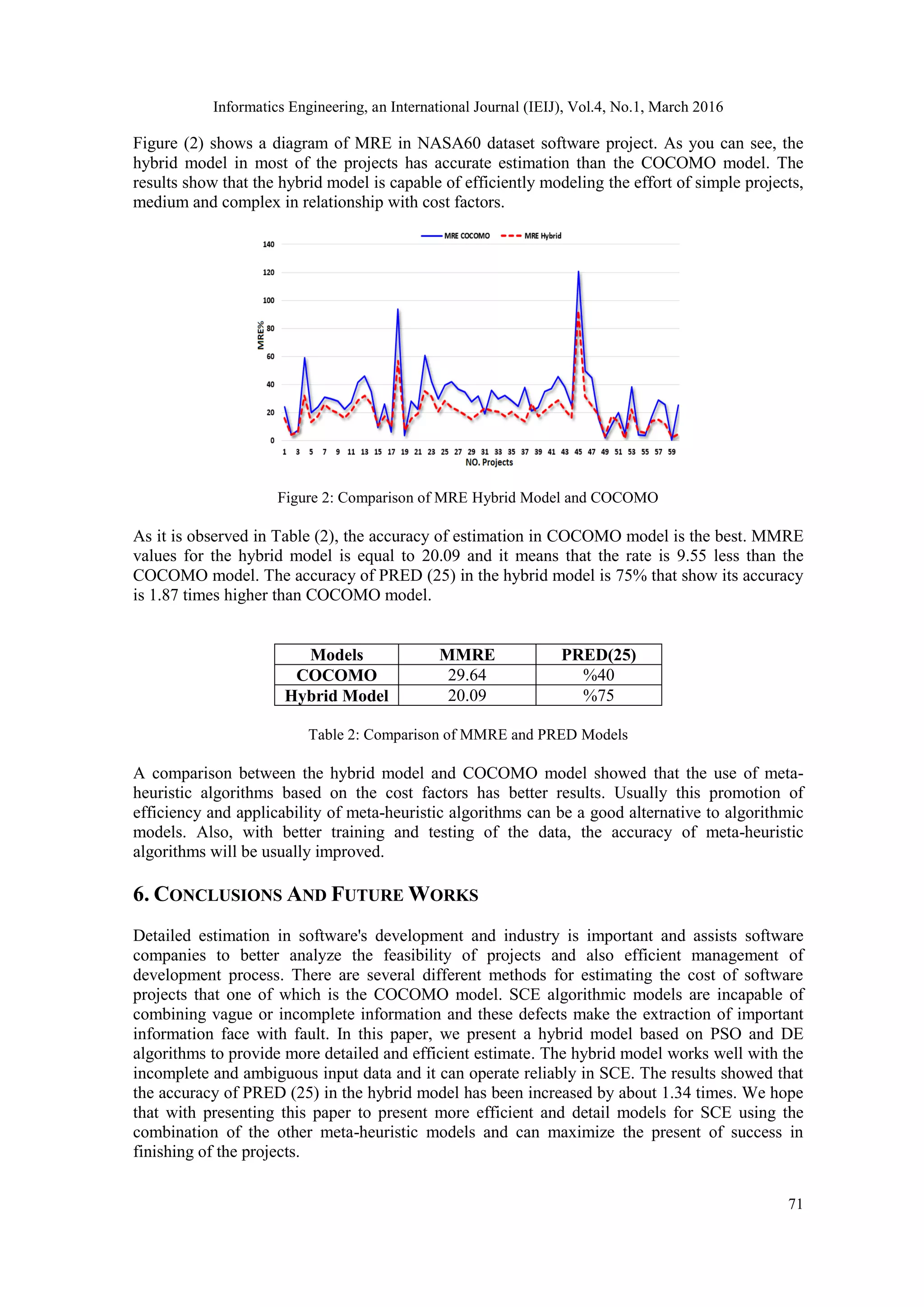
The document discusses a new hybrid model for software cost estimation (SCE) that combines particle swarm optimization (PSO) and differential evolution (DE) algorithms. This approach addresses the limitations of traditional models like COCOMO, demonstrating a reduction in mean magnitude of relative error (MMRE) by about 9.55% when tested on the NASA60 software dataset. The paper also explores the effectiveness of meta-heuristic algorithms in improving SCE accuracy compared to existing methods.
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 DOI : 10.5121/ieij.2016.4106 63 A NEW HYBRID FOR SOFTWARE COST ESTIMATION USING PARTICLE SWARM OPTIMIZATION AND DIFFERENTIAL EVOLUTION ALGORITHMS Majid Ahadi1 , Ahmad Jafarian2 Department of Computer Engineering, Urmia Branch, Islamic Azad University, Urmia, Iran ABSTRACT Software Cost Estimation (SCE) is considered one of the most important sections in software engineering that results in capabilities and well-deserved influence on the processes of cost and effort. Two factors of cost and effort in software projects determine the success and failure of projects. The project that will be completed in a certain time and manpower is a successful one and will have good profit to project managers. In most of the SCE techniques, algorithmic models such as COCOMO algorithm models have been used. COCOMO model is not capable of estimating the close approximations to the actual cost, because it runs in the form of linear. So, the models should be adapted that simultaneously with the number of Lines of Code (LOC) has the ability to estimate in a fair and accurate fashion for effort factors. Meta- heuristic algorithms can be a good model for SCE due to the ability of local and global search. In this paper, we have used the hybrid of Particle Swarm Optimization (PSO) and Differential Evolution (DE) for the SCE. Test results on NASA60 software dataset show that the rate of Mean Magnitude of Relative Error (MMRE) error on hybrid model, in comparison with COCOMO model is reduced to about 9.55%. KEYWORDS Software Cost Estimation, COCOMO, Particle Swarm Optimization, Differential Evolution 1. INTRODUCTION The SCE is always a concern for software development professionals and managers of software systems. The SCE which is due to various factors may be the result of the economic consequences of failure and disproportionate distribution of time between software teams due to the incorrect efforts and costs [1]. Managers of software development companies required to communicate with each other for determining of manpower and cost and to distinguish clear criteria with respect to previous projects [2, 3, and 4]. In the current projects we should consider new software tools and architecture for development teams. In new architectures to reduce the coding and software development, object-oriented patterns have been used [5]. In object-oriented programming model, software development teams can be linked together to avoid duplication of code [6]. This causes that less effort and cost has been done on projects. In general, estimation methods are divided into two main groups of quantitative methods and qualitative methods [7, 8]. To estimate the cost with qualitative method, generally the views and opinions of experts of software projects have been used. Usually, when the software projects' data in the past is not available, qualitative estimation methods are used. Qualitative estimation methods can be done on the basis of intuitive by applying subjective judgment, direct perception and relevant information. The quantitative estimation methods used the time that the last data will be available. Quantitative estimation methods estimate the relations between project factors and a desired future value factors.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-1-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 64 All estimation methods help managers to estimate estimations closer to reality. In some projects, no mathematical approach can be used to estimate, and the estimator performs the estimation based on criteria such as size, complexity, familiarity and team's experience. Another technique is the use of basic activities. In this method, a time has been regarded for determining the activity and the size of estimation and other criteria can be done based on it. Another method is the use of models of FP [9] and algorithmic COCOMO models [10, 11]. There are also some things that are indirectly related to the software projects, they include [12] Marketing and advertising costs Cost of meetings Costs of running of research and development Estimating LOC in software projects are from the earlier measurement technique for effort and cost. Estimation with planning and simple controlling cannot be effective and reliable. The estimated accuracy of the estimate depends on the experience of estimator. Initial estimation is an effort trying to inform staffing from the time and effort and also entering the structure and discipline on the process of the project in the case that can developed the project with the gained results [13]. In general, two methods that can be regarded for SCE include [14] Down-Up: In this approach, each component of the software system separately estimated and the results can be used to obtain estimates of the overall system. In this way the system is decomposed into different components evenly. Top-Down: This approach estimates the total cost for a system can be achieved with respect to environmental factor and by using algorithmic and non-algorithmic techniques. Poorly managed projects, probably cannot gain good success. To reduce the budget and the overall schedule and the advancement of contract parameters of projects' development should be utilized intelligent models for SCE. So, in this article we attempt to use the hybrid algorithms of PSO [15] and DE [16] for more detail and closer to the actual value of estimate. In the hybrid model has been tried to have less MMRE error value than the COCOMO model. The overall structure of the present paper is organized as follows: in Section 2, we discuss the related works have been done in the field of SCE; In Section 3, we will discuss the meta-heuristic algorithms of PSO and DE; in Section 4, we will present a proposed model however, in Section 5, we will evaluate and results and finally in Section 6 we will consider conclusions and future work. 2. RELATED WORKS SCE is one of the greatest challenges in software engineering. SCE is said to the logical prediction of required effort's process to develop or maintain software based on incomplete and ambiguous inputs. Several models have been proposed by researchers to calculate the effort. But it cannot be said with complete certainty that none of these models are careful. PSO-Chaos hybrid models is proposed for SCE effort and cost [17]. PSO algorithm combined with chaos model and compared with COCOMO model is able to reduce the amount of error MARE. Evaluation was performed on NASA60 dataset. Results indicated that the PSO model in comparison with COCOMO model whose value is equals 0.2952 is reduced MARE error to 0.1506. Also the hybrid model of PSO-Chaos shows that the MARE is reduced to 0.1153. It can be concluded that the hybrid model is more accurate than the COCOMO model.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-2-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 65 Software Effort Estimation (SEE) is regarded one of the main activities in software development. Therefore, the effective use of models to estimate the effort has a significant impact on the development of software projects. A new model to SEE was proposed using PSO algorithm [18]. The effective parameters to estimate effort have been reviewed using the PSO algorithm. Evaluation has been conducted on KEMERER dataset with 15 projects. Test results have shown that the value of MMRE error in the model is the 56.57 and in the COCOMO model is 245.39. Using PSO hybrid, the hybrid models of PSO-FCM and PSO-LA proposed for SCE [19]. Evaluation was performed on NASA60 dataset. In the hybrid model of PSO-FCM, the minimum of distance between the cluster and the sum of distance within clusters and the number of clusters as fitness parameters and improve the PSO algorithm is used. Using of Fuzzy C-Means (FCM) makes it easy that the particles have been collected in the best clusters and the fitness function has many local optimum points. In order to improve the performance of the PSO algorithm, Learning Automata (LA) can be used to regulate the behavior of particles. All particles in the PSO-LA hybrid model locally search within search space, simultaneously. In the hybrid PSO-LA model, the strategy of LA model provides the situation that particles achieve a local optimum according to reward criteria in PSO algorithm. Their experimental results show that the hybrid PSO-FCM model has less MRE error rate than the PSO-LA hybrid models. MMRE error in the PSO-FCM model is 25.36, 24.56, 24.22 and 23.86 and in the PSO-LA model is 26.32. The accuracy of PRED (25) on COCOMO Model is 40 and in the PSO-FCM Model is 61.6, 58.3, 65 and 68.3. Also in the PSO-LA model is equal to 63.3 . The hybrid of GA and Ant Colony Optimization (ACO) is proposed for the SCE [20]. In the hybrid model, effective factors in estimation are tested using the GA and trained with the ACO tests and have been achieved better results in comparison with COCOMO model. Evaluation and assessment has been done on 60 projects of NASA software projects' dataset. Their experimental results show that the combination of GA and ACO has better performance in comparison with the COCOMO models for software cost estimation and less MRE than the COCOMO model. The combination of FLANN network and PSO algorithm was used for SCE [21]. Hybrid PSO- FLANN model is a three-layer Feed Forward neural network. PSO algorithm is used to train the weight vector of FLANN. Evaluation has been made on three dataset of COCOMO 81, NASA63 and Maxwell. Test results show that PSO-FLANN model for testing and training data has good performance in MMRE and PRED criteria (25). Hybrid Model of Function Link Artificial Neural Network (FLANN) and GA were used for SCE [22]. Hybrid GA-FLANN model is a three-layer Feed Forward Network. GA algorithm is used for the hybrid model of OFWFLANN and OCFWFLANN. OFWFLANN model is used for optimizing of factors affecting the cost and OCFWFLANN model is used for training the FLANN's weight vectors. Evaluation is conducted on NASA93 dataset. Test results show that the hybrid model has good performance in testing and training of data. The use of Data-mining techniques in the field of SCE is very common nowadays [23]. Software cost estimation is simulated using techniques of Liner Regression (LR), Artificial Neural Network (ANN), Support Vector Regression (SVR) and K-Nearest-Neighbors (KNN). LR model can be used to determine the dependence of the effective traits in SCE. LR model finds the relationship between the independent factors and independent factors among the data. ANN is trying to do accurate SCE with training and testing of data. SVR models are used for optimization of the factors in SCE. KNN is a data mining technique that is used for data classification in sum of the data previously specified and their properties have been determined. The effective weight of attributes in SCE has been determined using KNN. Their experimental results show that the SVR model has less MRE than the other models.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-3-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 66 ANN-MLP model is the common methods in SCE [24]. In order to show the performance of ANN, 11 projects from 60 projects existed in NASA software dataset have been tested and trained using ANNs and have been compared with COCOMO model. It has been shown that the error of COCOMO is more than ANN error. The results show that at more than 90% of the time, ANN has much better estimation than COCOMO model. Thus, we can conclude that AI based techniques as a complementary are good alternative to the algorithmic methods. 3. META-HEURISTIC ALGORITHMS In recent years, due to the limitations of existing mathematical methods, many studies in the field of optimization issues is done using meta-heuristic algorithms [25, 26, and 27]. Meta-heuristic algorithms are the algorithms that have been inspired of animals' group behavior in nature that moved together as a group. Decision in these algorithms influenced based on the decisions of each member of the group the best status of the group. 3.1 Particle Swarm Optimization PSO algorithm was introduced in 1995 that inspired by social behavior of birds that live in large and small groups [15]. PSO algorithm is a population algorithm in which the numbers of particles that are solutions of a function with one problem form a swarm (population). Population of particles moving in space and based on their individual experience and the collective experience is trying to find the optimal solution in the search space. PSO algorithm as an optimization algorithm provides a population-based search, where each particle changes its position with time occurs. In the PSO algorithm, the particles move in a multi-dimensional search space of possible problem-solution. In this space, an assessment criterion defined and estimating the quality of solutions of the problem has been done by it. Change of the state of each particle in a group impresses by its experience and its neighbors' knowledge and search behavior of a particle is influenced by other particles. This simple behavior causes to find optimized area of the search spaces. Therefore, in the PSO algorithm, each particle upon finding an optimal positioning appropriately informed other particles, and each particle makes decision for a cost function with one determined probability based on the obtained values in order to obey from other particles and search is done n problem space using prior knowledge of the particles. This makes all the particles are not too close to each other and to effectively cope with the continuous optimization problems. In PSO algorithms, at first, individuals in group created randomly in the problem space and search can be started to find optimal solutions. In the overall structure, each person adheres of the other one that has the best fitness function, while not forgetting his own experience and obeys from the state that connected with the best fitness function. Thus, in each iteration of the algorithm, each person changes his next position according to the two values, one is the best situation that a person ever has the best (pbest) and the other is the best position that has been created by the total population. In fact it is the best pbest in the total population (gbest). Conceptually, pbest for each person is placed in a biological memory. Gbest is the basic knowledge of the population. When people change their position based on their gbest, in fact they are trying to move their knowledge's level to the population's level of knowledge. Conceptually, the best bit of all of the particles is connected all of the particles to each other. Determining the next position for each particle is done by Eq. (1) and (2).](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-4-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 67 ),.(.).(.. 22111 ibestibestii xgrcxPrcvwv ii (1) 11 iii vxx (2) In Eq. (1) c1 and c2 are learning factors. Rand () is a function to generate random numbers in the range [0, 1]. Xi is the current position and vi is the speed of moving the subjects. W is a controlling parameter that controls the speed of the current (vi) with the impact of the next speed and it creates a balance between the ability of the algorithm in global search and local search and thus we reach on average response in less time. Thus, for the optimal performance of the algorithm in the search space, the parameter of W defined according to the Eq. (3). Max MinMax Max i iww ww ))(( (3) In Eq. (3) iMax represents the maximum number of iterations in the algorithm and parameter i is a counter of iteration of finding of an optimal solution. In equation (3) parameters of WMax and WMin are initial value and final value of inertia weight respectively during the execution of the algorithm. Inertia weight linearly altered from 0.9 to 0.4 during performance of the program. Large values of W lead to global search and small amounts can lead to local search. To create a balance between local and global search, the inertia weight is evenly reduced over the implementation of the algorithm. Thus, by reducing the amount of W, search has been done more locally and around the optimal solution. 3.2 Differential Evolution DE algorithm which is an algorithm based on population were introduced in 1995 [16]. DE algorithm is a probabilistic search algorithm that solves the problems based on population. The algorithm using the distance and direction information carries out search operations from the current population. The advantages of this algorithm are speed, adjustment of parameters, its efficiency in finding the optimal solution, being parallel, high accuracy and lack of need to sorting or matrix multiplication. Algorithm of DE has the ability of searching the optimization variables and the change in direction of the coordinate in the right direction in order to find the best solutions. Algorithm of DE starts the evolutionary search process from a random initial population. Three parameters of mutation, selection and integration and three parameter of control including the number of population, scale factor and the possible integration in the DE algorithm are the most important. The steps of the process of DE algorithm are as follows: Initial Population: In the DE algorithm, the initial population or solution vectors randomly pick from the selection problem. The position vector of solutions is defined according to the Eq. (4). ),...,,( ,2,1, Diiii xxxX (4) ],1[],,1[ )).(1,0( minmaxmin DkNpiwith xxrandxx kkkik (5) Selection of the random numbers ikx from the domain of problem is done using equation (5). In Eq. (5), D is equal to the size of the solutions. Np is the number of initial population. Rand (0, 1) is the function which creates random number function (with uniform distribution) in the interval](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-5-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 68 of (0, 1). Obviously in the case of using the Eq. (5) obtained values for ikx will be put in the range of ],[ minmax ii xx and the position vector of each of the solutions is a potential response for the optimization problem. Mutation Operator: In the Mutation phase, three vectors randomly choose pairwise and differently. For any vector X in the population, a new solution is generated in each iteration according to Eq. (6). ).( ,3,2,11, GrGrGrGi xxFxv (6) In Eq. (6), 321 ,, rrr are three inequality random numbers in the range of ],1[ Np . G is the number of generated generation and the factor of F is a constant true positive rate that often is considered 0.5. Crossover Operator: Crossover operator increases diversity in the population. This operator is the same as merging operator in GA [28]. In the crossover operator, new vectors created with the combination of x and v according to Eq. (7). otherwisex jjorCRrifv u Gji randjGji Gji 1, 1, 1, )( (7) In Eq. (7), the parameter of CR is in the range [0, 1). Parameter of r randomly generated in the range of [0, 1]. Also the value of ;,...,2,1 Dj . Selection Operator: To select the best fitness vectors, vectors that have been generated by the operators of mutation and merge are compared together and whichever is fit to be transferred to the next generation. The selection operator has been done according to the Eq. (8). ),( ,1,1, GiGiGi xuValueFitnessx (8) Stopping criteria: the search process continues until a stopping criterion is met. Stopping criterion usually can be the best answer or the iteration of the algorithms based on the constancy of the fitness changes. 4. PROPOSED MODEL Accuracy of estimation and effort for software projects is very important to achieve success or error. Some of the factors of Effort Multipliers (EMs) like the complexity of the project, the experience of the team, project's time delivery, network equipment, etc., are very influential in the timely completion and budget cuts of the project [29] .SCE refers to estimate of staffing effort (Persona/ Month) and the time required for development of software production. With a suitable model for SCE, project managers can make informed decisions about resource management, control, planning, on time delivery and precise timing [29]. Hence, modeling and data analysis are important in estimating costs. Software projects always encountered a problem called time limit. This restriction is quite tangible at all stages of production and development of projects. Therefore, managers' efforts have focused on that gain maximum results with minimum resources and acquired factors. Also persistence of software companies provides added value. For achieving this goal only having adequate resources is not enough, rather, the composition and use of resources has important role that this importance affect the cost and effort. In this paper, a hybrid model based on PSO and DE on NASA60 dataset software projects has been developed to estimate the cost and effort [29] that help manufacturing commercial software companies to](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-6-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 69 assess and analyze software criteria in terms of size, complexity, time, effort and cost. In Figure (1) the flowchart of the hybrid model is shown Figure 1: Flowchart of the Hybrid Model Given that heuristic methods are powerless for solving scientific problems such as the number of non-linearity of the target function, and because the software companies affected by factors such as operating costs, production costs, production time and delivery time, estimating of the cost and effort is very difficult. Hence, to solve the aforementioned problems and enhance the strengths of speed and flexibility, hybrid algorithms of PSO and DE are used for SCE. In the hybrid model used in this paper, the mechanism of PSO algorithm can be used in order to find an initial solution and from its resulting solution is used as the initial solution for DE algorithm so that through this we quickly reach to the desired response. Convergence in the structure of used hybrid model is done globally. Because PSO Algorithm searches the limits of solution spaces for finding response that result in searching of points of solution space that has been attended less. That increases the chances of finding the right answers. Then in continue, PSO algorithm gives obtained responses to the DE algorithm so with taking advantage of producing neighbors responses and checking the around area can further move towards the optimal solutions. In the hybrid model, MMRE has been considered as the fitness function [30]. The objective of fitness function in the hybrid model is minimizing the amount of MMRE in comparison with COCOMO model. The hybrid model is repeated until the value of MMRE reduced to the desired amount. Fitness function for the hybrid model is defined in Eq. (10).](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-7-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 70 100 i ii i act estact MRE (9) niMRE n MMRE n i i ,...,2,1, 1 1 (10) Using Eq. (10) we can compare the obtained error from the estimated models. PRED is also considered an important criterion in the precision of the estimates. MMRE and PRED are the most common methods to evaluate the accuracy of prediction. PRED (x) defined according to Eq. (11) [30]. n i otherwise xifMRE n xPRED 1 ,0 ,11 )( (11) Criterion PRED (x) that is defined by MRE mostly applied in accuracy of the estimation and provides good illustrations of how the models work. In the evaluation of estimate criteria, the model that has less MRE is better than the model that has high MRE and the model that has less MMRE s better than the model that has high MMRE. Also, the model that has a higher PRED is better than the model that has high PRED. 5. EVALUATION AND RESULTS In this section, the hybrid model has been tested on NASA60 dataset software projects and the results were compared with COCOMO models. Evaluation was conducted in programming context of VC # .NET 2013. Affective parameters in the hybrid model based on testing and iteration has been represented in Table (1). Values for each of these parameters can affect the convergence and optimization of the hybrid model. So to the extent that the value of this parameter is accurate and compatible, to that extent the problem will be optimized. Parameters Value P 50 C1 1.5 C2 1.5 W 0.4 F 0.3 Pm 10 Pc 0.3 Fitness Function MMRE Table 1: Values of parameters In Table (1), P parameter determines the number of population (particle). The parameter W is the inertia weight in order to adjust the particle velocity and values of the parameters of C1 and C2 help particle learning to find the optimal points. The parameter F is a real positive constant that used to converge mutation rate. The parameter of Pm is the mutation rate, Pc parameter is the rate of integration.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-8-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 72 REFERENCES [1] F.S. Gharehchopogh, I. Maleki, A. Talebi, Using Hybrid Model of Artificial Bee Colony and Genetic Algorithms in Software Cost Estimation, 9th International Conference on Application of Information and Communication Technologies (AICT), IEEE, Rostov on Don, pp. 102-106, 2015. [2] M. Uzzafer, A Simulation Model for Strategic Management Process of Software Projects, Journal of Systems and Software, 86(1), 21-37, 2013. [3] F.S.Gharehchopogh, A. Talebi, I. Maleki, Analysis of Use Case Points Models for Software Cost Estimation, International Journal of Academic Research, Part A, 6(3), 118-124, 2014. [4] Yeong-Seok Seo, Doo-Hwan Bae, R. Jeffery, AREION: Software Effort Estimation Based on Multiple Regressions with Adaptive Recursive Data Partitioning, Information and Software Technology, 55(10), 1710-1725, 2013. [5] I. Maleki, L. Ebrahimi, S. Jodati, I. Ramesh, Analysis of Software Cost Estimation Using Fuzzy Logic, International Journal in Foundations of Computer Science & Technology (IJFCST), 4(3), 27- 41, 2014. [6] F.S. Gharehchopogh, I. Maleki, S.J. Gourabi, Object Oriented Software Engineering Models in Software Industry, International Journal of Computer Applications, 95(3), 13-16, 2014. [7] Juan J. Cuadrado-Gallego, Miguel-Ángel Sicilia, M. Garre, D. Rodríguez, An Empirical Study of Process-Related Attributes in Segmented Software Cost-Estimation Relationships, Journal of Systems and Software, 79(3), 353-361, 2006. [8] J.M. Verner, W.M. Evanco, N. Cerpa, State of the Practice: An Exploratory Analysis of Schedule Estimation and Software Project Success Prediction, Information and Software Technology, 49(2), 181-193, 2007. [9] A.J. Albrecht, J. Gaffney, Software Function, Source Lines of Code, and Development Effort Prediction: a software science validation, IEEE Transactions on Software Engineering SE, 9(6), 639- 648, 1983. [10] B.W. Boehm, Software Engineering Economics, Prentice-Hall, Englewood Cliffs, New Jersy, 1981. [11] B.W. Boehm, Software Cost Estimation with COCOMO II, Prentice Hall PTR, Englewood Cliffs, New Jersy, 2000. [12] A. Sharma, D.S. Kushwaha, Estimation of Software Development Effort from Requirements Based Complexity, Procedia Technology, Vol. 4, 716-722, 2012. [13] Y.F. Li, M. Xie, T.N. Goh, A Study of Project Selection and Feature Weighting for Analogy based Software Cost Estimation”, Journal of Systems and Software, 82(2), 241-252, 2009. [14] S.D. Conte, H.E. Dunsmore, V.Y. Shen, Software Engineering Metrics and Models, The Benjamin/Cummings Publishing Company, Inc, Menlo Park, CA, p. 214, 1986. [15] J. Kennedy, R. C. Eberhart, Particle Swarm Optimization, In Proceedings of the IEEE International Conference on Neural Networks, pp. 1942-1948, 1995. [16] R. Storn, K. Price, Minimizing the Real Functions of the ICEC’96 Contest by Differential Evolution, International Conference on Evolutionary Computation, Nagoya, Japan, 1995. [17] Z.A. Dizaji, K. Khalilpour, Particle Swarm Optimization and Chaos Theory Based Approach for Software Cost Estimation, International Journal of Academic Research, Part A, 6(3), 130-135, 2014. [18] F.S. Gharehchopogh, I. Maleki, S.R. Khaze, A Novel Particle Swarm Optimization Approach for Software Effort Estimation, International Journal of Academic Research, Part A, 6(2), 69-76, 2014. [19] F.S. Gharehchopogh, L. Ebrahimi, I. Maleki, S.J. Gourabi, A Novel PSO based Approach with Hybrid of Fuzzy C-Means and Learning Automata in Software Cost Estimation, Indian Journal of Science and Technology, 7(6), 795-803, 2014 [20] I. Maleki , A. Ghaffari, M. Masdari, A New Approach for Software Cost Estimation with Hybrid Genetic Algorithm and Ant Colony Optimization, International Journal of Innovation and Applied Studies, 5(1), 72-81, 2014. [21] T.R. Benala, K. Chinnababu, R. Mall, S. Dehuri, A Particle Swarm Optimized Functional Link Artificial Neural Network (PSO-FLANN) in Software Cost Estimation, Advances in Intelligent Systems and Computing Proceedings of the International Conference on Frontiers of Intelligent Computing, pp. 59-66, Springer-Verlag, 2013. [22] T.R. Benala, S. Dehuri, Genetic Algorithm for Optimizing Functional Link Artificial Neural Network Based Software Cost Estimation, Proceedings of the InConINDIA, pp. 75-82, Springer-Verlag, 2012.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-10-2048.jpg)
![Informatics Engineering, an International Journal (IEIJ), Vol.4, No.1, March 2016 73 [23] Z.A. Khalifelu, F.S. Gharehchopogh, Comparison and Evaluation Data Mining Techniques with Algorithmic Models in Software Cost Estimation, Elsevier, Procedia-Technology Journal, ISSN: 2212-0173, Vol. 1, pp. 65-71, 2012. [24] F.S. Gharehchopogh, Neural Networks Application in Software Cost Estimation: A Case Study, 2011 International Symposium on Innovations in Intelligent Systems and Applications (INISTA 2011), pp. 69-73, IEEE, Istanbul, Turkey, 15-18 June 2011. [25] F.S. Gharehchopogh, I. Maleki, M. Farahmandian, New Approach for Solving Dynamic Traveling Salesman Problem with Hybrid Genetic Algorithms and Ant Colony Optimization, International Journal of Computer Applications (IJCA), 53(1), 39-44, 2012. [26] F.S. Gharehchopogh, I. Maleki, B. Zebardast, A New Solutions for Continuous Optimization Functions by using Bacterial Foraging Optimization and Particle Swarm Optimization Algorithms, Elixir International Journal Computer Science and Engineering (Elixir Comp. Sci. & Engg.), Vol. 61, pp. 16655-16661, 2013. [27] I. Maleki, S.R. Khaze, M.M. Tabrizi, A. Bagherinia, A New Approach for Area Coverage Problem in Wireless Sensor Network with Hybrid Particle Swarm Optimization and Differential Evolution Algorithms, International Journal of Mobile Network Communications & Telematics (IJMNCT), 3(6), 61-75, 2013. [28] J. Holland, Adaptation in Natural and Artificial Systems, University of Michigan, Michigan, USA, 1975. [29] T. Menzies, D. Port, Zh. Chen, J. Hihn, Validation Methods for Calibrating Software Effort Models, ICSE ACM, USA, 2005. [30] S.G. MacDonell, A.R. Gray, A Comparison of Modeling Techniques for Software Development Effort Prediction, in Proceedings of International Conference on Neural Information Processing and Intelligent Information Systems, pp. 869-872, 1997.](https://image.slidesharecdn.com/4116ieij06-180823084544/75/A-NEW-HYBRID-FOR-SOFTWARE-COST-ESTIMATION-USING-PARTICLE-SWARM-OPTIMIZATION-AND-DIFFERENTIAL-EVOLUTION-ALGORITHMS-11-2048.jpg)